Robust vertex centdian facility location problem on tree networks

Abstract

This paper studies the robust vertex centdian location problem on tree networks with interval edge lengths. To obtain a robust solution, we use the minmax regret criterion. First, we obtain atmost n worst case scenario for each pair of vertices on tree networks. Then we reduce this number to $\log n$. Finally, the total time for obtaining a robust solution is equal to $O(n^{4})$. This time is reduced to $O(n^{3}\log n)$ by using the property of binary search tree and weighted centroid.

1 Introduction

The centdian location problem is the combination of $p-$center and $p-$median location problems which has been defined by Hakimi (1965), Kariv and Hakimi (1979). In a given system with specified set of clients and candidate locations, the aim of the median problem is to find the location of points on system which minimize the total weighted distances from each client to its closest established facility. Also, on this system, the center problem wants to find locations among candidate locations which minimize the maximum weighted distances of each client to its closest established facility.

If $f_{c}(x)=\max _{1\le i\le n}w_{i}d(X,v_{i})$ presents the objective function of the p-center problem and $f_{m}(x)=\sum _{1\le i\le n}w_{i}d(X,v_{i})$ denotes the objective function of the p-median problem, then the centdian problem is considered as a bi-objective model as $\min _{x}\lbrace f_{c}(x), f_{m}(x)\rbrace$. One of the methods to solve a multi-objective problem in the literature is to convert the multi-objective model into a one-objective model. This is done in several ways. The two most important methods are the $\epsilon$-constrained method and the weighted sum method (Ehrgott, 2005). The weighted sum method is also known as the combination method.

In $\epsilon$-constrained method, one of the p-center and p-median objective functions must be minimized, provided that the other objective function is not greater than $\epsilon$. The weighted sum method considers the convex combination of p-median and p-center objective functions as objective function. Revelle and Swain (1970) and Halpern (1978) introduced the first $\epsilon$-constrained method and combination method which are also called the central facilities location problem and centdian location problem, respectively. Berman et. al. described a $\epsilon$-constrained median-center problem called the modified p-median problem (Toregas et al., 1971). In this model, p-medians are to be found such that the center objective is less than $\epsilon$. For more information about this method, see (Halpern, 1979; Tamir et al., 1998). In these articles, instead of the distance function in the median objective function, they considered a non-decreasing convex function.

In the weighted sum method, the convex combination of the median and center objective functions are considered as objective function of centdian problem. In combination method, instead of convex combination, the simple sum of the median and center functions are considered. Also, in some methods, the weight of all clients are the same in both center and median problems and in some cases are different. The last case is called the double weighted centdian problem.

Halpern studied the 1-centdian location problem on general graphs and trees, in which the weight of all clients in center problem are equal to one (Halpern, 1980). Tamir et al. considered the p-centdian problem on tree networks with different weights for any client in both center and median problems, and presented an algorithm with $O(pn^{6})$ time complexity for $p\ge 4$ and $O(n^{p})$ time complexity for $p<4$ (Tamir et al., 1998).

Assume now that the input data of a problem have not an certain value. For example, consider a network with uncertain vertex weights or uncertain edge lengths or both. Then the presented algorithms in above can not solve the centdian problems on such networks. If the value of input data is specified by a distribution function, then we can use the probably optimization methods. If the value of these data is characterized by a membership function, then we can use the fuzzy optimization approaches. Assume now that the input data of a problem have not an certain value. For example, consider a network with uncertain vertex weights or uncertain edge lengths or both. Then the above mentioned algorithms can not solve the centdian problems on such networks. If the value of input data is specified by a distribution function, then we can use the probably optimization methods. If the value of these data are characterized by a membership function, then we can use the fuzzy optimization approaches. Suppose that the value of input data of a problem do not be specified by a distribution or membership function. Such problems are belong to the robust optimization models and they can be solved by existing approaches in the robust optimization. The first approach in robust optimization presented by Soyster. He considered a linear programming model in 1973 and tried to counteract to the uncertainty of data, by a conservative approach (Soyster, 1973). The final solution of his approach was far away from optimal solution, because he considered the worst cases. Mulvey et al. investigated Soyster’s approach in discrete optimization (Mulvey et al., 1995). Ben Tal et al. presented new algorithm for robust optimization, which is not efficient (Ben-Tal & Nemirovski, 2000). Bertsimas et al. introduced an algorithm, counteract the uncertainty of data by controlling the level of conservative. By using this method, they obtained the new linear optimization model, and called the robust counterpart of first model (Bertsimas & Sim, 2004). One of the important approaches in robust optimization is minmax regret criterion, which is proposed by Kouvelis and Ye (1993). In this method, the maximum difference between the cost (profit) of decision of decision maker and the cost (profit) of optimal decision is minimized.

In the robust facilly location problems, the minmax regret criterion use for obtaining the robust solution by using the combinatorial approaches. Averbakh (2003) showed that the minmax regret 1-center and 1-median problems on general graphs with uncertain edge lengths are NP-hard. These problems on special graphs, such path, tree, cycle, cactus and etc can be solved in polynomial time. Also, these problems on general graphs with uncertain vertex weights are solvable in polynomial time. Averbakh et al. considered the minmax regret 1-center problem on weighted trees with interval edge lengths and vertex weights and on un-weighted trees with interval edge lengths and presented solution methods with $O(n^{6})$ and $O(n^{2}\log n)$ time complexity, respectively (Averbakh & Berman, 2000a). Burkard et al. considered the above problems and improved theirs time complexity to $O(n^{3}\log n)$ and $O(n\log n)$, respectively (Burkard & Dollani, 2002). Also, Aloulou et al. obtained an combinatorial algorithm for minmax regret 1-center problem on general graphs and trees with time complexity $O(mn(\log n +\vert S\vert )\vert S\vert )$ and $O(n\vert S\vert (n+\log n))$, respectively (Aloulou et al., 2005). In these cases, the vertex weights of general graph and tree are described by a discrete set of scenarios such S. Kouvelis considered the minmax regret 1-median problem on trees and proposed an algorithm with $O(n^{4})$ time complexity (Kouvelis et al., 1993). Chen et al. improved this time to $O(n\vert S\vert )$ (Chen & Lin, 1998). Also, Averbakh et al. obtained two algorithms for the robust $1-$median problem on general graphs and on tree networks with time complexity $O(mn^{2}\log n)$ and $O(n\log ^{2}n)$, respectively (Averbakh & Berman, 2000b, 2003).

Conde considered the robust double weighted centdian problem on tree networks and presented an algorithm with $O(n^{3}\log n)$ time (Conde, 2008). Li et al. studied the robust centdian problem with interval vertex weights on dynamic graphs and proposed an algorithm with $O(n^{3}\log n)$ time complexity (Li et al., 2018). In this case, the weight of each node at center and median problems are the same. Up to now, the robust centdian problem with uncertainty edge lengths not investigated.

In this paper, we consider the robust vertex centdian problem on trees with interval edge lengths. We organize the paper in several sections. Section 2 defines the classic and robust vertex centdian problem on networks. We obtain a finite subset of worst case scenarios for the robust vertex centdian problem in Sect. 3 and solve the robust vertex centdian problem under these scenarios. Finally, conclusion is given in Sect. 4.

2 Problem statement

Let $T=(V, E)$ be a tree network with vertex set $V=\left\{ v_{1}, \ldots , v_{n} \right\}$ and edge set E such that each vertex $v_{i} \in V$ is associated with a non-negative weight $w_{i}$ and each edge $e \in E$ is associated with a non-negative length l(e) . For each pair of vertices $x, y \in V$, let d(x, y) be the length of shortest path between x and y. In the classical vertex centdian problem the aim is to find a vertex $v^{*}\in V$ such that it minimizes the following objective function:

$$\begin{aligned} f_{c}(x)+f_{m}(x),~~~~~~~~~~~~~~~~\forall x\in V \end{aligned}$$

(1)

where

$$\begin{aligned} f_{c}(x)=\max _{i=1,\ldots , n} w_{i}d(x, v_{i}) \end{aligned}$$

and

$$\begin{aligned} f_{m}(x)=\sum _{i=1}^{n}w_{i}d(x,v_{i}). \end{aligned}$$

Now assume that the length of edges of T do not have an exact and specified value. Let every edge $e\in E$ is indicated by an interval $\left[ l^{-}(e), l^{+}(e)\right]$ such that $l^{+}(e)\ge l^{-}(e)\ge 0$ and $l(e)\in [l^{-}(e), l^{+}(e)]$. Consider the set S as the cartesian product of these intervals. The set S is called the set of all happens of uncertain parameters. Any $s \in S$ is a scenario and $l_{e}^{s}$ is the length of edge e under this scenario. In this paper, we use the minmax regret criterion for obtaining the robust solution of uncertain centdian problem. Therefore, the robust vertex centdian problem is formulated using this criterion as follows:

$$\begin{aligned} \min _{x\in V}\max _{s\in S}[f_{c}(x,s)+f_{m}(x,s)-f_{c}(x^{*},s)-f_{m}(x^{*},s)] \end{aligned}$$

(2)

where $x^{*}$ is a vertex centdian on T under scenario $s \in S$ and

$$\begin{aligned} f_{c}(x,s)=\max _{i=1,\ldots , n} w_{i}d^{s}(x, v_{i}),~~~~ f_{m}(x,s)=\sum _{i=1}^{n}w_{i}d^{s}(x,v_{i}). \end{aligned}$$

Note that $d^{s}(x,v_{i})$ represents the length of the shortest path between x and $v_{i}$ under scenario $s\in S$. Obviously, $\vert S\vert =\infty$. Thus it is not easy to find the optimal solution of (2). Therefore, for obtaining the optimal solution of these problems, we must search the finite subset of S and solve these problems on the obtained subset. This subset of scenarios are selected so that the value of $R^{s}(x,y)= f_{c}(x,s)+f_{m}(x,s)-f_{c}(y,s)-f_{m}(y,s)$ is maximized for all pair of vertices x, y on T. Scenarios that maximize the value of $R^{s}(x,y)$ are called the worst case scenarios.

To find these scenarios, first select an arbitrary vertex on T and root the tree on this vertex. Call this vertex r. Convert this tree into a binary tree by adding at most O(n) vertices. Set the corresonding vertex weights and edge lengths equal to zero (Tamir, 1996). Let $u_{L}$ and $u_{R}$ be the left and right children of vertex r. Call the rooted subtrees in these two vertices $u_{l}$ and $u_{R}$, $T_{L}$ and $T_{R}$, respectively.

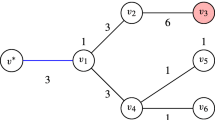
Reorder the indices of the nodes of binary tree T such that the indices of all vertices on subtree $T_{L}$ are smaller than the index of $u_{L}$. In other words, if $v_{i}$ and $v_{j}$ are the left and right descendants of vertex $v_{t}$, respectively, then $i<t$, $j<t$ and $i<j$. Also, the indices of all vertices on subtree $T_{R}$ are greater than the index of $u_{R}$. That is, if $v_{i}$ and $v_{j}$ are the left and right descendants of vertex $v_{t}$, respectively, then $i>t$, $j>t$ and $i<j$ (see Fig. 1). This reordering is performed in linear time (Korte & Vygen, 2012).

Fig. 1

An example

Let $r=v_{k}$ and $v_{1},\ldots , v_{k-1}$ be the nodes of subtree $T_{L}$ and $v_{k+1},\ldots , v_{n}$ be the nodes of subtree $T_{R}$. Also, assume that the weight of vertices of tree T are satisfied in the following inequality:

$$\begin{aligned} 0\le w_{1}\le w_{2}\le \cdots \le w_{n}. \end{aligned}$$

(3)

Now set all the leaves of subtree $T_{R}$ in the set Leav(R) . Then for each $x \in V$ and $s\in S$, we have

$$\begin{aligned} f_{c}(x,s)&=\max \left\{ \max _{1\le i\le k}w_{i}d^{s}(x,v_{i}), \max _{k+1\le i\le n}w_{i}d^{s}(x,v_{i})\right\} \nonumber \\&=\max \left\{ \max _{1\le i\le k}w_{i}d^{s}(x,v_{i}), \max _{v_{i}\in Leav(R)}w_{i}d^{s}(x,v_{i})\right\} . \end{aligned}$$

(4)

We know that for each vertex $v_{i}\in Leav(R)$, there exists at least an arbitrary vertex $v_{j}$ on unique path between x and $v_{i}$ such that

$$\begin{aligned} w_{i}d^{s}(x,v_{i})=w_{i}d^{s}(x,v_{j})+w_{i}d^{s}(v_{j},v_{i}). \end{aligned}$$

On the other hand, we know that $w_{i}d^{s}(v_{j}, v_{i})\ge 0$. Then we can conclude the following statement:

$$\begin{aligned} w_{i}d^{s}(x,v_{i})&\ge w_{i}d^{s}(x,v_{j})\\ {}&\ge w_{j}d^{s}(x,v_{j}). \end{aligned}$$

The last inequality follows from this assumption that for all $i>j$, we have $w_{i}\ge w_{j}$. As mentioned earlier, solving the problem (2) requires finding a finite number of worst-case scenarios. So the first step is to find these scenarios. For finding the worst-case scenarios, we should have information about worst case scenarios corresponding to median and center problems.

3 Worst case scenarios of the robust centdian problem

For obtaining the worst case scenarios of the robust centdian problem, first we must know about the worst case scenarios of the center and median problems. Then by using these scenarios, we can obtain the worst case scenarios of the robust centdian problem.

3.1 Worst case scenario of the robust center problem

Let x be an arbitrary vertex on tree T, $s_{x}$ be a worst case scenario according to x and $v_{x}$ be the farthest vertex from x under scenario $s_{x}$. i.e, the weighted distance of this vertex from x is maximum ($v_x$ is called the critical vertex of x). Let x, y, z be the vertices of a tree network with weights 2, 5, 1 and $d(x,y)=2, d(x,z)=4$. Then the vertex y is the critical vertex of x. Because

$$\begin{aligned} w(y)*d(x,y)>w(z)*d(x,z). \end{aligned}$$

Averbakh and Berman (2000a) showed that $s_{x}$ is satisfied in the following condition:

• 1. The edge lengths belonging to the path between x and $v_{x}$, are equal to upper bounds of the associated intervals.

• 2. The other edge lengths are equal to lower bounds of according intervals.

Define $S(x) =\bigcup _{i=1}^{n}s_{i}(x)$. It is obvious that $s_x \in S(x)$. We use (4) and conclude that $s_{x}$ belongs to $\bar{S}(x)=(\bigcup _{i=1}^{k}s_{i}(x))\bigcup (\bigcup _{v_{i}\in Leav(R)}s_{i}(x))$.

3.2 Worst case scenario of the robust median problem

Let x be a desired vertex on the tree T, $s_{x}$ be a worst case scenario for x and y be a $1-$median on the tree T under scenario $s_{x}$. Suppose $T_{u}^{v}$ and $T_{v}^{u}$ are the rooted subtrees of tree T in u and v respectively and obtained by removing edge $e=(u,v)$. Also, $T_{u}^{v}$ contains the vertex u but does not contain the vertex v and $T_{v}^{u}$ contains the vertex v but does not contain the vertex u. Assume that the total weight of the subtrees $T_{u}^{v}$ and $T_{v}^{u}$ are denoted by $W(T_{u}^{v})$ and $W(T_{v}^{u})$, respectively. Averbakh and Berman (2000b) proved that $s_{x}$ have the following properties:

• 1. The length of edge $e=(u, v)$ that belongs to path between x and y and $y \in T_{v}^{u}$, is computed as follows:

  $$\begin{aligned} l^{s_{x}}(e)= {\left\{ \begin{array}{ll} l^{+}(e) &{} if ~~~ W(T_{u}^{v})<W(T_{v}^{u}), \\ l^{-}(e) &{} if ~~~ W(T_{u}^{v})>W(T_{v}^{u}). \end{array}\right. } \end{aligned}$$

  (5)

  If $W(T_{u}^{v})=W(T_{v}^{u})$, then the length of edge e can be considered any value in the associated interval.

• 2. The length of edges not belong to path between x and y, can be any arbitrary value on the associated intervals.

Therefore, for every pair of vertices x and y on tree T a scenario can be calculated that holds in the above conditions.

3.3 Worst case scenarios of the robust centdian problems

Now consider the minmax regret vertex centdian problem presented in (2). This problem can be rewrite as follows:

$$\begin{aligned} \min _{x\in V}\max _{y\in V}\max _{s\in S}R^{s}(x, y). \end{aligned}$$

(6)

In this case, for finding a finite subset of S, we must obtain a scenario s(x, y) for all pair of nodes x and y such that it maximizes $R^{s}(x,y)$. In other words, we must compute s(x, y) satisfies in the following relation:

$$\begin{aligned} R^{s(x,y)}(x,y)=\max _{s\in S}R^{s}(x,y). \end{aligned}$$

Lemma 3.1

Assume that x and y are two arbitrary vertices on T and $s \in S$. Therefore, we can conclude the following statements:

• 1. Let $T_{x}^{y}$ be a subtree on $T_{R}$. If the critical vertex of x belongs to $T_{x}^{y}\cap Leav(R)$, then the critical vertex of y is one of the vertices in Leav(R) , in which the its index is equal or greater than the index of critical vertex of x.

• 2. Let $T_{x}^{y}$ be a subtree of $T_{L}$. If the critical vertex of x belongs to $T_{x}^{y}$, then the critical vertex of y is either one of the vertices in Leav(R) or one of the vertices with index greater than index of the critical vertex of x.

Proof

• 1. Let $v^{*}$ be the critical vertex of x under scenario s and $v^{*}$ be in the subtree $T_{R}$. Therefore, we have

  $$\begin{aligned} w(v^{*})d^{s}(x, v^{*})\ge w_{i}d^{s}(x, v_{i}), ~~~~~ \forall v_{i}\in V(T). \end{aligned}$$

  In the other hand, $\forall v_{i}\in V(T)\setminus V(T_{x}^{y})$, $w_{i}\le w(v^{*})$. Then

  $$\begin{aligned} w(v^{*})d^{s}(y, v^{*})&= w(v^{*})d^{s}(y, x)+w(v^{*})d^{s}(x,v^{*})\\ {}&\ge w(v^{*})d^{s}(y, x)+w_{i}d^{s}(x,v_{i})\\ {}&\ge w_{i}d^{s}(y, x)+w_{i}d^{s}(x,v_{i}) \end{aligned}$$

• 2. The proof of this part is the similar to the previous part.

$\square$

Lemma 3.2

Let $e=(u, v)$ be an edge on path between x and y, which is closest to x and $W(T_{u}^{v})> W(T_{v}^{u})$. Therefore, for all edge (a, b) on described path, $W(T_{a}^{b})> W(T_{b}^{a})$.

Proof

Assume that (a, b) is an arbitrary edge except e on path between x and y such that $y\in T_{b}^{a}$. Then

$$\begin{aligned} W(T_{a}^{b})=W(T_{u}^{v})+\sum _{v_{i}\in P[v, a]}w_{i},~~~~ W(T_{b}^{a})=W(T_{v}^{u})-\sum _{v_{i}\in P[v, a]}w_{i}. \end{aligned}$$

Consequently, we have

$$\begin{aligned} W(T_{b}^{a})\le W(T_{v}^{u})< W(T_{u}^{v})\le W(T_{a}^{b}). \end{aligned}$$

The first and last inequalities are inferred from the non-negativity of the weights. $\square$

Corollary 3.3

Suppose that $e=(u,v)$ is the adjacent edge of y on the path between x and y. Also, $W(T_{u}^{v})<W(T_{v}^{u})$. Then for all edge (a, b) on this path, we have

$W(T_{a}^{b})<W(T_{b}^{a})$.

In the following, we want to find the worst case scenario for all vertices x and y on the tree T. For this purpose, we must compute the values $W(T_{u}^{v})$ and $W(T_{v}^{u})$ for all edge $e=(u,v)$ on T. Let $v_{i}$ be an arbitrary vertex in $T_{L}\cup Leav(R)$. Therefore, scenario $s_{i}(x,y)$ is computed as follows:

Case 1. Let $\bar{T}_{x}$ be a rooted subtree in vertex $x\in T$, $y\notin \bar{T}_{x}$ and $v_{i}$ be a vertex on subtree $\bar{T}_{x}$. In other words, there is no edge on intersection of the paths $P[x,v_{i}]$ and P[x, y] . In this case, the length of all edges on T, under scenario $s_{i}(x,y)$ is characterized in the following way:

• 1. The length of all edges on path $P[x,v_{i}]$ equals to upper bounds of corresponding intervals.

• 2. The length of all edges on subgraph $T\setminus (P[x,y]\cup P[x,v_{i}])$ equals to lower bounds of corresponding intervals.

• 3. The length of edge $e=(u,v)$ on the path P[x, y] is calculated according to the following procedure: If $u=x$ and $W(T_{u}^{v})\ge W(T_{v}^{u})$, then the lengths of all edges on the path P[x, y] are equal to lower bounds of corresponding intervals. Because the length of these edges are equal to lower bound of intervals in both center and median problems. If $W(T_{u}^{v}) < W(T_{v}^{u})$, then we must find the closest edge (a, b) to x on the path P[x, y] , which satisfies in the condition $W(T_{a}^{b})\ge W(T_{b}^{a})$. Set the edge lengths on the path between a and the vertex y equal to lower bounds of corresponding intervals. Assume $A_{i}$ contains all edges $e=(u,v)$ on the path P[x, y] such that they satisfy in the condition $W(T_{u}^{v}) < W(T_{v}^{u})$. In other words

  $$\begin{aligned} A_{i}=\left\{ e=(u,v)\in P[x,y]:~~~ W(T_{u}^{v}) < W(T_{v}^{u})\right\} . \end{aligned}$$

  The length of edge $e \in A_{i}$ in the center problem is equal to lower bound and in the median problem is equal to upper bound of associated interval. Then the length of these edges must be computed in centdian problem, separately. Compute the weighted distance of all vertices of $\bar{T}_{x}$ from x. Suppose $v^{*}$ is a vertex on $\bar{T}_{x}$ with maximum weighted distance from x. Set the edge lengths on $A_{i}$ equals to upper bound of intervals and consider this scenario as $s_{i}^{+}(x,y)$. Compute the weighted distance of all vertices of $T\setminus \bar{T}_{x}$ from x. Assume that $v^{'}$ has the maximum weighted distance from x in $T\setminus \bar{T}_{x}$.

Subcase1: Let $w(v^{*})d^{s_{i}^{+}(x,y)}(x,v^{*})\ge w(v^{'})d^{s_{i}^{+}(x,y)}(x,v^{'})$. Therefore, $v^{*}$ is a critical vertex for x under scenario $s_{i}^{+}(x,y)$ and consequently, on scenario $s_{i}(x,y)$. According to Lemma 3.1, the critical vertex of y is on $T^{*}=\bar{T}_{x}\cup Leav(R)$. Therefore, the critical vertex of y is either $v^{*}$ or the index of this vertex is greater than the index of vertex $v^{*}$. Let $v^{''}$ be the critical vertex of y under scenario $s_{i}^{+}(x,y)$.

Remark 3.4

Let $e=(u,v)$ be an edge of $A_{i}$. Then for some $v_{j}$ with index greater than the index of vertex $v^{*}$, we have

$$\begin{aligned} -w(v^{*})+(-W(T_{u}^{v})+W(T_{v}^{u}))\ge -w_{j}+(-W(T_{u}^{v})+W(T_{v}^{u})). \end{aligned}$$

If we use Remark 3.4 and define $\triangle ^{*}_{e}= -w(v^{*})+(-W(T_{u}^{v})+W(T_{v}^{u}))$, then we conclude the following Lemma:

Lemma 3.5

If $v^{''}=v^{*}$ and $\triangle ^{*}_{e}\ge 0$, then the length of edge e on $A_{i}$ under scenario $s_{i}(x,y)$ is equal to its length under scenario $s_{i}^{+}(x,y)$.

Proof

Suppose that $\bar{s}_{i}$ is a obtained scenario from $s_{i}^{+}(x,y)$ by decreasing the length of at least one edge of $A_{i}$. Also, let $\bar{v}$ be the critical vertex of y under scenario $\bar{s}_{i}$. Then $\bar{v}=v^{*}$ or the index of $\bar{v}$ is exceed from index of $v^{*}$. If $\bar{v}=v^{*}$, then for all edge $e=(u,v) \in A_{i}$ we have

$$\begin{aligned} f(x,\bar{s}_{i})-f(y,\bar{s}_{i})&=(-w(v^{*})-W(T_{u}^{v})+W(T_{v}^{u}))d^{\bar{s}_{i}}(x,y)\\&=\triangle ^{*}_{e}d^{\bar{s}_{i}}(x,y)\\ {}&\le \triangle ^{*}_{e}d^{s_{i}^{+}(x,y)}(x,y)\\&=f(x,s_{i}^{+}(x,y))-f(y,s_{i}^{+}(x,y)). \end{aligned}$$

If $v^{''}\ne v^{*}$, then

$$\begin{aligned} f(x,\bar{s}_{i})-f(y,\bar{s}_{i})&\le w(v^{*})d^{s_{i}^{+}(x,y)}(x,v^{*})-w(v^{*})(d^{s_{i}^{+}(x,y)}(y,v^{*})-\alpha )\\&\quad +(-W(T_{u}^{v})+W(T_{v}^{u}))(d^{s_{i}^{+}(x,y)}(y,v^{*})-\alpha )\\&=w(v^{*})d^{s_{i}^{+}(x,y)}(x,v^{*})-w(v^{*})d^{s_{i}^{+}(x,y)}(y,v^{*})\\ {}&\quad +(-W(T_{u}^{v})+W(T_{v}^{u}))d^{s_{i}^{+}(x,y)}(x,y)\\ {}&\quad +(w(v^{*})+W(T_{u}^{v})-W(T_{v}^{u}))\alpha \\ {}&\le w(v^{*})d^{s_{i}^{+}(x,y)}(x,v^{*})-w(v^{''})d^{s_{i}^{+}(x,y)}(y,v^{''})\\ {}&~~+(-W(T_{u}^{v})+W(T_{v}^{u}))d^{s_{i}^{+}(x,y)}(x,y)\\&=f(x,s_{i}^{+}(x,y))-f(y,s_{i}^{+}(x,y)). \end{aligned}$$

The first inequality follows from definition of critical vertex and the second inequality concludes from $\triangle ^{*}_{e}\ge 0$. $\square$

Assume now that $v^{''}=v^{*}$ and $\triangle ^{*}_{e}<0$. According to Remark 3.4, for all $v_{j}$ with index greater than $v^{*}$, we have $\triangle ^{j}_{e}<0.$

Suppose $s_{i}^{-}(x,y)$ is a scenario contains all edges in $A_{i}$ with lower bound of corresponding intervals. Let $v^{-}$ be the critical vertex of y under this scenario.

Lemma 3.6

Let $v^{*}=v^{''}$ and $\triangle ^{j}_{e}<0$. Then the following statements are true.

• a. If $v^{*}=v^{-}$, then the length of edge $e\in A_{i}$ under scenario $s_{i}(x,y)$ is equal to length of this edge under scenario $s_{i}^{-}(x,y)$.

• b. If $v^{*}\ne v^{-}$, then the length of edge $e\in A_{i}$ under scenario $s_{i}(x,y)$ is equal to length of this edge under scenario $s_{i}^{+}(x,y)$.

Proof

• a. Let $s_{i}^{-}$ be the obtained scenario from $s_{i}^{+}(x,y)$ by decreasing the length of at least one edge on $A_{i}$. Also, assume $v^{+}$ is the critical vertex of y under scenario $s_{i}^{-}$. Therefore,

  $$\begin{aligned} f(x,s_{i}^{-})-f(y,s_{i}^{-})&=w(v^{*})d^{s_{i}^{-}}(x,v^{*})-w(v^{+})d^{s_{i}^{-}}(y,v^{+})\\&\quad +(-W(T_{u}^{v})+W(T_{v}^{u}))d^{s_{i}^{-}}(x,y)\\ {}&\le w(v^{*})d^{s_{i}^{-}}(x,v^{*})-w(v^{*})d^{s_{i}^{-}}(y,v^{*})\\&\quad +(-W(T_{u}^{v})+W(T_{v}^{u}))d^{s_{i}^{-}}(x,y)\\&=(-w(v^{*})-W(T_{u}^{v})+W(T_{v}^{u}))d^{s_{i}^{-}}(x,y)\\&=\triangle _{e}^{*}d^{s_{i}^{-}}(x,y)\\ {}&\le \triangle _{e}^{*}d^{s_{i}^{-}(x,y)}(x,y)\\ {}&= f(x,s_{i}^{-}(x,y))-f(y,s_{i}^{-}(x,y)). \end{aligned}$$

  Also, we have

  $$\begin{aligned} f(x,s_{i}^{-}(x,y))-f(y,s_{i}^{-}(x,y))&=w(v^{*})d^{s_{i}^{-}(x,y)}(x,v^{*})-w(v^{-})d^{s_{i}^{-}(x,y)}(x,v^{-})\\ {}&\quad +(-W(T_{u}^{v})+W(T_{v}^{u}))d^{s_{i}^{-}(x,y)}(x,y)\\ {}&=(-w(v^{*})-W(T_{u}^{v})\\ {}&\quad +(W(T_{v}^{u}))d^{s_{i}^{+}(x,y)}(x,y)\\ {}&\quad + (w(v^{*})+W(T_{u}^{v})-W(T_{v}^{u}))\sum _{e\in A_{i}}\alpha _{e}\\ {}&> f(x,s_{i}^{+}(x,y))-f(y,s_{i}^{+}(x,y)) \end{aligned}$$

  where $\alpha =l_{e}^{+}-l_{e}^{-}$.

• b. In this case, we have

  $$\begin{aligned}&-w(v^{*})d^{s_{i}^{+}(x,y)}(y,v^{*})+(-W(T_{u}^{v})+W(T_{v}^{u}))d^{s_{i}^{+}(x,y)}(x,y)\\ {}&\quad =-w(v^{*})d^{s_{i}^{-}(x,y)}(y,v^{*})+(-W(T_{u}^{v})+W(T_{v}^{u}))d^{s_{i}^{-}(x,y)}(x,y)\\ {}&\qquad +(w(v^{*})+W(T_{u}^{v})-W(T_{v}^{u}))\sum _{e\in A_{i}}\alpha _{e}\\ {}&\quad \ge -w(v^{-})d^{s_{i}^{-}(x,y)}(y,v^{-})+(-W(T_{u}^{v})+W(T_{v}^{u}))d^{s_{i}^{-}(x,y)}(x,y)-\triangle _{e}^{*}\sum _{e\in A_{i}}\alpha _{e}\\ {}&\quad \ge -w(v^{-})d^{s_{i}^{-}(x,y)}(y,v^{-})+(-W(T_{u}^{v})+W(T_{v}^{u}))d^{s_{i}^{-}(x,y)}(x,y). \end{aligned}$$

  If we add $w(v^{*})d ^{s_{i}^{-}(x,y)}(x,v^{*})$ to the left and right hand sides of above inequality, then we have

  $$\begin{aligned} f(x,s_{i}^{+}(x,y))-f(y,s_{i}^{+}(x,y))\ge f(x,s_{i}^{-}(x,y))-f(y,s_{i}^{-}(x,y)). \end{aligned}$$

  Because we have $w(v^{*})d ^{s_{i}^{-}(x,y)}(x,v^{*})=w(v^{*)}d ^{s_{i}^{+}(x,y)}(x,v^{*})$. By the similar way, we conclude that

  $$\begin{aligned} f(x,s_{i}^{+}(x,y))-f(y,s_{i}^{+}(x,y))\ge f(x,s_{i}^{-})-f(y,s_{i}^{-}). \end{aligned}$$

$\square$

Now suppose $v^{*}\ne v^{''}$. In this case, the objective function of centdian problem in the vertices x and y under scenario $s_{i}^{+}(x,y)$ is

$$\begin{aligned} f(x, s_{i}^{+}(x,y))-f(y, s_{i}^{+}(x,y))&=w(v^{*})d^{ s_{i}^{+}(x,y)}(x,v^{*})-w(v^{''})d^{ s_{i}^{+}(x,y)}(y,v^{''})\\ {}&+(-W(T_{u}^{v})+W(T_{v}^{u}))d^{s_{i}^{+}(x,y)}(x,y). \end{aligned}$$

Corollary 3.7

Let $v^{*}\ne v^{''}$. Therefore, the length of edge $e\in A_{i}$ under scenario $s_{i}(x,y)$ obtains as follows:

• a. If $\triangle _{e}^{*}\le 0$, then the length of this edge on scenario $s_{i}(x,y)$ is equal to its length under scenario $s_{i}^{+}(x,y)$.

• b. If for every vertex $v_{j}$ with index greater than $v^{*}$, $\triangle _{e}^{j}\ge 0$, then the length of this edge on scenario $s_{i}(x,y)$ is equal to its length under scenario $s_{i}^{+}(x,y)$.

Subcase2: Assume now that

$$\begin{aligned} w(v^{*})d^{s_{i}(x,y)}(x,v^{*})= w(v^{*})d^{s_{i}^{+}(x,y)}(x,v^{*})<w(v^{'})d^{s_{i}(x,y)}(x,v^{'}). \end{aligned}$$

Let $v^{''}\in T_{y}^{x}$. In this case, the critical vertex of y on scenario $s_{i}(x,y)$ is $v^{''}$. Because the length of all edges on the path between y and $v^{''}$, which are not in $A_{i}$, on scenarios $s_{i}(x,y)$ and $s_{i}^{+}(x,y)$ are the same.

Case2: Suppose the conditions of case1 are not met, i.e. $y\in \bar{T}_{x}$ and $v_{i}$ is not a vertex on subtree $\bar{T}_{x}$. In this case, one of the following conditions occurs. $y\in \bar{T}_{x}$ and $v_{i}$ is a vertex on subtree $T{\setminus } \bar{T}_{x}$, both vertices $y, v_{i}$ are in the subtree $T_{j}$ or $y, v_{i}$ are not in the subtree $T_{j}$. If there is no edge on intersection of paths $P[x,v_{i}]$ and P[x, y] , then the length of edges are calculated exactly like the case1. Assume now that $p[x,v_i]\cap p[x,y]\ne \emptyset$. In this case, the length of all edges on T, under scenario $s_{i}(x,y)$ is characterized in the following form:

• 1. The edge lengths on path $P[x,v_{i}]\setminus p[x,y]$ are equal to upper bounds of corresponding intervals.

• 2. The edge lengths on subgraph $T\setminus (P[x,y]\cup P[x,v_{i}])$ are equal to lower bounds of corresponding intervals.

• 3. Let $e=(u,v)\in P[x,y]\cap P[x,v_{i}]$. The length of this edge in the center problem is equal to upper bound of its corresponding interval. But this value in the median problem depends on the amount of weights $W(T_{u}^{v})$ and $W(T_{v}^{u})$. If $W(T_{u}^{v})\le W(T_{v}^{u})$, then the length of this edge in the centdian problem equals to upper bound of the corresponding interval. Let $W(T_{u}^{v}) > W(T_{v}^{u})$. Define

  $$\begin{aligned} B_{i}=\{ e=(u,v)\in P[x,y]\cap P[x,v_{i}]: ~~~W(T_{u}^{v}) > W(T_{v}^{u}) \}. \end{aligned}$$

  Set the edge lengths of this set equal to the upper bounds of their intervals. Let $w(\bar{v})d^{s}(y,\bar{v})=\max _{1\le i\le n}w_{i}d^{s}(y,v_{i})$. If $p[x,y]\cap p[x,v_{i}]\cap p[y, \bar{v}]=\emptyset$, then under the scenario $s_{i}(x,y)$ the edge lengths in the set $B_{i}$ do not decrease. Suppose this condition does not occur. Denote $\bar{V}$ as the set of all vertices of the tree T where the intersection of the path $P[x,y]\cap P[x,v_{i}]$ and the path between vertex $v\in \bar{V}$ and y is empty. Let

  $$\begin{aligned} w(v_{y})d^{s_{i}(x,y)}(y, v_{1})=\max {1\le i\le n}w_{i}d^{s_{i}(x,y)}(y,v_{i}). \end{aligned}$$

  Note that the edge lengths on the path between vertex $v \in \bar{V}$ and y are specified on the scenario $s_{i}(x,y)$. If the condition of subcase1 is met, then we set the length of these edges equal to minimum value in the desired interval. If the condition of subcase2 is met, then we set the length of these edges similar to the subcase2.

Lemma 3.8

The robust vertex centdian problem can be solved in $O(n^{4})$ time.

Proof

For each pair of vertices in $T_L \cup Leav(R)$ we compute at most O(n) worst case scenarios. The required time complexity to calculate these scenarios is linear. Because if vertices $v_i$ are selected using BFS algorithm, then it is enough to calculate only the length of one edge in each iteration. $\square$

As mentioned, at most O(n) scenarios was calculated for each pair of vertices on tree T. But some of these scenarios may be repetitive. So we are looking for ways to find these repetitive scenarios and ignore them. For this purpose, we use the concept of weight-centroid. The vertex $v^{*}$ with adjacent vertices $v_1$, $v_2$ and $v_3$ on the tree T is called the weight-centroid if the following condition is met for subtrees $T_{v_{j}}$, $j=1, 2, 3$.

$$\begin{aligned} W(T_{v_{j}})\le W(T)/2, ~~~j\in \{1, 2, 3\}. \end{aligned}$$

These subtrees are obtained by removing the vertex $v^{*}$ on the tree T. Using this concept, we obtain the following results, which show that it is not necessary that the worst case scenarios are calculated for all pair of vertices on tree T. Let $n_j$ be the number of vertices on subtree $T_j$, $j=1, 2, 3$.

Lemma 3.9

Suppose $v_i$ and x are two vertices on subtree $T_j$ and $y_1, y_2 \in V(T){\setminus } V(T_j)$. Therefore, $s_{i}(x,y_1)=s_{i}(x,y_2)$. In this case, for each $x \in V(T_j)$, there are at most one vertex y with different scenario $s_{i}(x, y)$.

Proof

Given that x and $v_i$ are in a different subtree from $y_1$ and $y_2$ (see Fig. 1), the scenarios $s_{i}(x, y_1)$ and $s_{i}(x, y_2)$ differ only in the length of edges on paths $p[y_1, v^{*}]$ and $p[y_2, v^{*}]$. Therefore, we must examine the length of edges of these two paths. According to the Corollary 3.3, on every edge (u, v) on paths $p[y_1, v^{*}]$ and $p[y_2, v^{*}]$, $W(T_{u}^{v})\ge W(T_{v}^{u})$. Then the length of the edge (u, v) is equal to lower bound of corresponding interval. The last sentence is concluded from the part 3 of case 1. Here it suffices to consider $y \in V(T) \setminus V(T_j)$ as v. $\square$

Fig. 2

Related graph of Lemma 3.9

Lemma 3.10

Suppose $v_i$ and x are two vertices on subtree $T_j$ and $y_1, y_2 \in V(T_j)$ (see Fig. 3). If $\bar{v}$ is the parent of $y_1$ and $y_2$ on path between x and r, $p[x, y_1] \cap p[v_i, x]= {\o }$ and $p[x, y_2]\cap p[v_i,x]={\o }$, then $s_{i}(x, y_1)=s_{i}(x,y_2)$. In this case, for each $x \in V(T_j)$, there are at most $\log n$ vertex y with different scenario $s_{i}(x, y)$.

Proof

This Lemma can be proved similar to Lemma 3.10. For given x and $v_i$, the number of parents for any pair of vertices $y_1$ and $y_2$ equals to the high of binary tree. The high of binary tree is at most $O(\log n)$. $\square$

Fig. 3

Related graph of Lemma 3.10

The following three Lemmas can be concluded from case2.

Lemma 3.11

Suppose $v_i$ is a vertex on subtree $T_j$ such that $p[x, v_i]\cap p[y_1, v_i]\ne {\o }, p[x,v_i]\cap p[y_2,v_i]\ne {\o }$ and $y_1, y_2$ have a common vertex on path between x and r (see Fig. 4). Then $s_{i}(x, y_1)=s_{i}(x,y_2)$. In this case, for each $x \in V(T_j)$, there is at most two y with different scenario $s_{i}(x, y)$.

Fig. 4

Related graph of Lemma 3.11

Lemma 3.12

Assume that $v_i$ is not a vertex in subtree $T_j$ and $y_1, y_2 \in V(T_j)$. If x is on path between $y_1, y_2$ (see Fig. 5), then $s_{i}(x, y_1)=s_{i}(x,y_2)$. In this case, for each $x \in V(T_j)$, there is at most one y with different scenario $s_{i}(x, y)$.

Fig. 5

Related graph of Lemma 3.12

Lemma 3.13

If $y_1, y_2$ are on path between x and $v_i$ (see Fig. 6), then $s_{i}(x, y_1)=s_{i}(x,y_2)$.

Fig. 6

Related graph of Lemma 3.13

Therefore, for each x on subtree $t_j$, it is sufficient to compute $s_{i}(x, y)$ for at most $O(\log n)$ number of vertex y. On the other hand, the number of $s_{i}(x,y)$ is n. Then for each vertex x on tree T, we can compute at most $O(n\log n)$ worst case scenarios. Each of these scenarios is calculated in linear time. Therefore, we conclude that

Lemma 3.14

The required time complexity to solve the robust centdian problem on tree networks with interval edge length is reduced to $O(n^{3}\log n)$.

Proof

For each pair of vertices, the number of worst case scenarios are atmost $O(\log n)$ and one of these scenarios is obtained in linear time. Therefore, the total time is reduced to $O(n^{3}\log n)$. $\square$

4 Conclusions

In this paper, we considered the robust centdian location problem on tree network with interval edge lengths. Here, we used the minmax regret criterion. For simplicity, we decomposed the minmax regret centdian problem to two cases. First we solved the problem in $O(n^{4})$ time complexity. Then we decreased this time to $O(n^{3}\log n)$ with using the concept of weight-centroid vertex on tree networks.