A numerical comparison of different qualitative algorithms for solving 2D inverse elastic scattering problems

Abstract

In this paper, we numerically compare several well-established and recent qualitative algorithms for the shape reconstruction of obstacles in elastic scattering based on the measured noisy full far-field data. The compared algorithms include linear sampling method, factorization method and its variant (i.e., $F_\sharp$ method), direct sampling method, and direct factorization method. To regularize the ill-conditioned far-field integral operator used in linear sampling method and factorization method, the Tikhonov regularization is used, where we compared two different regularization parameter choice technique: the generalized discrepancy principle (GDP) and the improved maximum product criterion (IMPC). The GDP requires a priori knowledge of the noise level in the far-field data, while the IMPC does not have such an impractical requirement. Extensive numerical examples are provided to illustrate the difference, similarity, advantage, and disadvantage of the tested qualitative methods under various settings. The direct sampling method and direct factorization method outperform the others in computational efficiency while achieving comparable reconstruction accuracy. We find the $F_\sharp$ method is numerically less sensitive to noise.

1 Introduction

The inverse elastic scattering problem of shape reconstruction of scattering objects from the knowledge of far-field patterns has been extensively studied (Yaman et al. 2013; Bao and Yin 2017; Bao et al. 2018). Many different quantitative and qualitative numerical algorithms were proposed in the last few decades. However, their numerical comparison are inadequately discussed, except related theoretical reviews (Colton et al. 2000b; Potthast 2005, 2006) for acoustic and electromagnetic scattering problems.

Existing numerical reconstruction algorithms for inverse scattering problems can be roughly categorized into two classes: (i) nonlinear optimization methods and (ii) qualitative methods. The nonlinear optimization approaches (Roger 1981; Murch et al. 1988; Giorgi et al. 2013) often involve an expensive iterative procedure, where a direct (forward) scattering problem needs to be (approximately) solved at each iteration. Although such optimization approaches require less number of incident fields, they do need a priori knowledge of the boundary conditions of the unknown scatterer (e.g., sound-soft or not), and its number of connected components, which may not be available in many practical applications. Moreover, the optimization iterations may converge to an incorrect approximation of the true scatterer when the provided a priori information (initial guess) is far away from the truth. The qualitative methods have the advantage of not requiring any a priori information about the unknown scatterer and were shown to be computationally faster than the nonlinear optimization methods, since they determine only an approximation of the scatterer shape and very limited information about its physical/material properties.

In this paper, we will focus on the numerical comparison of several different qualitative methods, including the linear sampling method (Colton and Kirsch 1996), factorization method (Kirsch 1998; Kirsch and Grinberg 2008) and its variant, direct sampling method (Ji et al. 2018), and direct factorization method (Leem et al. 2018a). In particular, we will provide reconstructions of 2D rigid bodies irradiated by incident elastic plane waves. In such sampling type qualitative methods, the support of the scattering obstacle is obtained by (approximately) solving a vector integral equation of the first kind and noting that a specific norm (called indicator functional) becomes unbounded or large as a sampling point lying on a rectangular grid containing the scatterer approaches its boundary.

Both linear sampling method and factorization method yield an ill-posed far-field equation, which is customarily solved via Tikhonov regularization. The regularization parameter is often computed via Morozov’s generalized discrepancy principle (GDP) (Colton et al. 1997). However, Morozov’s generalized discrepancy principle requires the computation of the zeros of the discrepancy function at each point of the grid, a process that is time-consuming (Leem et al. 2018b). The locally convergent Newton-type method is often used to compute zeros. To achieve the global convergence and significantly reduce the computational cost of finding zeros, an efficient fixed-point (FP) iteration was proposed in Bazán (2014) for approximately determining the regularization parameter. Moreover, the noise level in the data should be known a priori, something that in real-life applications is not the case in general. To avoid these difficulties, we also tested a variant of the maximum product criterion (MPC) , the so-called Improved Maximum Product Criterion (IMPC) (Bazán et al. 2012), which computes regularized solution norms and corresponding residual norms, and chooses as regularization parameter the critical point associated with the largest local maximum of the product of these norms as a function of the regularization parameter. In addition, as with MPC, IMPC does not depend on user specified input parameters (like subspace dimension or truncating parameter) and requires no a priori knowledge of the unknown noise level. IMPC extends in a very elegant way the MPC, and it has been applied with great success in reconstructing three-dimensional obstacles in acoustics (Bazán et al. 2015) and in electromagnetic scattering applications (Bazán et al. 2016).

We organize our paper as follows. In Sect. 2, the direct scattering problem for a rigid body irradiated by an incident elastic plane wave is introduced. The corresponding inverse elastic scattering problem is also presented. In Sect. 3, the compared qualitative methods and rules for choosing regularization parameter are briefly described. Extensive numerical examples with different settings are reported in Sect. 4 to illustrate some interesting similarity/difference and advantage/disadvantage of the compared methods. Finally, some concluding remarks are provided in Sect. 5.

2 Formulation of the direct and inverse scattering problem

We formulate our problem by considering the scattering process of a given time-harmonic elastic plane wave ${{ \mathbf {u}}^{{\mathrm{inc}}}}$ by an impenetrable obstacle $D\subset {\mathbb {R}}^2$ which is open, bounded, and simply connected domain with a smooth boundary $\partial D$ that is of class $C^{2}$. We assume that ${\mathbb {R}}^2$ is filled up with a homogeneous and isotropic elastic medium with Lamé constant coefficients $\mu , \lambda$, and mass density $\rho$. We further assume the strong elliptic conditions: $\mu >0$ and $2\mu +\lambda >0$. Denote by ${{\hat{\mathbf{n}}_{r}}}$ the outward unit normal vector on the boundary $\partial D$ at point ${\mathbf{r}}$, and the complement of our scatterer D, denoted by ${\mathbb {R}}^2{\setminus }{\overline{D}}$, will be referred as the exterior domain.

Let $\mathbb {S}:=\{{\mathbf{z}}\in \mathbb {R}^{2}:|{\mathbf{z}}|=1\}$ denotes the unit circle in $\mathbb {R}^2$ and $\mathbf{z}^\perp$ be the vector obtained by rotating $\mathbf{z}$ counter-clockwise by $\pi /2$. Let ${\mathbf{{u}}^{{\mathrm{inc}}}}$ be the elastic plane wave with incident direction ${{\hat{\mathbf{d}}}=(\cos \theta , \sin \theta )} \in \mathbb {S}$, which is of the linear combination form

$$\begin{aligned} \mathbf{u}^{{\mathrm{inc}}}(\mathbf{r})=a_p {\hat{\mathbf{d}}} {\mathrm{e}}^{ik_{p}\mathbf{r}\cdot \hat{\mathbf{d}}}+a_s {\hat{\mathbf{d}}^{^{\perp }}} {\mathrm{e}}^{ik_{s}\mathbf{r}\cdot \hat{\mathbf{d}}}, \end{aligned}$$

(1)

where ${k_{p}}$ is the longitudinal wave number and ${k_{s}}$ is the transverse one. Here, the vectors with hat on the top are unit vectors. At this point, we mention that our scatterer could also be irradiated only by an incident plane P-wave (longitudinal wave) with $(a_p, a_s) = (1, 0)$ or only by a plane S-wave (transverse wave) with $(a_p, a_s) = (0, 1)$.

Let $\nabla ,\nabla \cdot ,\Delta$ be the standard gradient, divergence, and Laplace operator, respectively. Define the differential operator $\Delta ^{*}$ as

$$\begin{aligned} \Delta ^{*}=\mu \Delta +(\lambda +\mu ) \nabla (\nabla \cdot ). \end{aligned}$$

(2)

The total displacement elastic field ${\mathbf{{u}}}$ is viewed as the sum of the incident field ${\mathbf{{u}}^{{\mathrm{inc}}}}$ and the scattered field ${\mathbf{{u}}^{{\mathrm{sct}}}}$, that is

$$\begin{aligned} {\mathbf{{u}}(\mathbf{r})=\mathbf{{u}}^{{\mathrm{inc}}}(\mathbf{r})+\mathbf{{u}}^{{\mathrm{sct}}}(\mathbf{r}), \quad \mathbf{r}}\in {\mathbb {R}}^{2}{\setminus }{\overline{D}}. \end{aligned}$$

(3)

The direct elastic scattering problem can be described by the boundary-value problem (Elschner and Yamamoto 2010; Hahner and Hsiao 1993): For a given incident elastic plane wave ${\mathbf{{u}}^{{\mathrm{inc}}}}$ and obstacle $D\subset \mathbb {R}^2$, find the total elastic field ${\mathbf{{u}}}\in \left[ C^{2}({\mathbb {R}}^{2}{\setminus } {\overline{D}})\right] ^{2}\cap \left[ C^{1}({\mathbb {R}}^{2}{\setminus } D)\right] ^{2}$, such that

$$\begin{aligned}&{ \Delta ^{*} \mathbf{{u}}(\mathbf{r}) +\rho \omega ^{2} \mathbf{{u}}(\mathbf{r})=\mathbf{{0}},\quad \mathbf{r}}\in {\mathbb {R}}^{2}{\setminus }{\overline{D}} \end{aligned}$$

(4)

$$\begin{aligned}&{\mathbf{{u}}(\mathbf{r})=\mathbf{{0}},\quad \mathbf{r}}\in \partial {D} \end{aligned}$$

(5)

$$\begin{aligned}&{\lim _{r\rightarrow \infty }\sqrt{r} \left( \frac{\partial {\mathbf{{u}}}^{{\mathrm{sct}}}_{\star }(\mathbf{r})}{\partial r}-ik_{\star } {\mathbf{{u}}}^{{\mathrm{sct}}}_{\star }(\mathbf{r})\right) =\mathbf{{0}}},\quad \star =p,s, \end{aligned}$$

(6)

where $r:=|\mathbf{r}|$, $\omega >0$ is the circular frequency, and $k_{p}=\omega \sqrt{\frac{\rho }{2\mu +\lambda }}$ and $k_{s}=\omega \sqrt{\frac{\rho }{\mu }}$ are wave numbers. The Dirichlet boundary condition (5) corresponds to a rigid body (scatterer) whose surface cannot be deformed by the stresses generated by the incident displacement field. The Sommerfeld–Kupradze type radiation conditions (6) hold uniformly in all directions ${{\hat{\mathbf{r}}}=\mathbf{r}/|\mathbf{r}|}$ for both P and S-components of the scattered field ${\mathbf{{u}}_{p}^{{\mathrm{sct}}}, \mathbf{{u}}_{s}^{{\mathrm{sct}}}}$, respectively. Since both $\mathbf{u}$ and $\mathbf{u}^{{\mathrm{sct}}}$ satisfy the Navier equation (4), the well-known Helmholtz decomposition leads to Kupradze (2012)

$$\begin{aligned} {\mathbf{{u}}^{{\mathrm{sct}}}(\mathbf{r})=\mathbf{{u}}^{{\mathrm{sct}}}_{p}(\mathbf{r})+\mathbf{{u}}^{{\mathrm{sct}}}_{s}(\mathbf{r})}\quad \text {with}\ {(\Delta +k_{p}^{2}) \mathbf{{u}}_{p}^{{\mathrm{sct}}}(\mathbf{r})=\mathbf{{0}}, (\Delta +k_{s}^{2}) \mathbf{{u}}_{s}^{{\mathrm{sct}}}(\mathbf{r})=\mathbf{{0}}}, \end{aligned}$$

where ${\mathbf{{u}}_{p}^{{\mathrm{sct}}}(\mathbf{r})}$ is the longitudinal part (P-wave being rotational-free), ${\mathbf{{u}}_{s}^{{\mathrm{sct}}}(\mathbf{r})}$ the transverse part (S-wave divergence-free) and ${k_{p}}$, ${k_{s}}$ are the corresponding wave numbers. The same decomposition also holds for the total field $\mathbf{{u}} (\mathbf{r})=\mathbf{{u}}_{p}(\mathbf{r})+\mathbf{{u}}_{s}(\mathbf{r})$.

The free-space Green’s dyadic (or tensor) ${{\Gamma }(\mathbf{r}, \mathbf{r'})}$ of the Navier equation (4) satisfies the following equation:

$$\begin{aligned} {\Delta ^{*}{\Gamma }(\mathbf{r}, \mathbf{r'})+\rho \omega ^{2} {\Gamma }(\mathbf{r}, \mathbf{r'})=-{I} \delta (\mathbf{r}-\mathbf{r'}),\quad \mathbf{r}, \mathbf{r'}}\in {\mathbb {R}}^{2} \end{aligned}$$

(7)

with ${\delta (\mathbf{r}-\mathbf{r'})}$ being the Dirac measure at the point ${\mathbf{r}}$, and it is given by Pelekanos and Sevroglou (2005)

$$\begin{aligned} {\Gamma }(\mathbf{r}, \mathbf{r'})= & {} {\frac{i}{4\mu } {I} H_{0}^{(1)}(k_{s}|\mathbf{r}-\mathbf{r'}|)} \nonumber \\&- \frac{i}{4\rho \omega ^2} \nabla _{\mathbf{r}}\otimes \nabla _\mathbf{r} \left[ H_{0}^{(1)}(k_{p}|\mathbf{r}-\mathbf{r'}|)-H_{0}^{(1)}(k_{s}|\mathbf{r}-\mathbf{r'}|)\right] , \end{aligned}$$

(8)

where I is an identity matrix, ${H_{0}^{(1)}({\varvec{\cdot }})}$ is the cylindrical Hankel function of the first kind and zero order, and $\otimes$ denotes the juxtaposition between two vectors (i.e., a dyadic).

From the numerical point of view, we want to avoid the dyadic nature of the fundamental solution. For the dyadic approach for elastic scattering problems, we refer to Sevroglou and Pelekanos (2001) and the references therein. In particular, let ${{\mathbf{p}}\in \mathbb {S}}$ denotes the polarization vector of an elastic point source at any ${{\mathbf{z}}}\in {\mathbb {R}}^{2}$. For any $\mathbf{r}\in {\mathbb {R}}^{2}{\setminus }\{{{\mathbf{z}}}\}$, we will adopt the notation ${{\varvec{\Gamma }}}(\mathbf{r}, {\mathbf{z}}; {\mathbf{p}}):= {\Gamma }(\mathbf{r}, {\mathbf{z}})\cdot {\mathbf{p}}$ to highlight the dependence on $\mathbf{p}$.

Using asymptotic analysis for ${\mathbf{{\Gamma }}(\mathbf{r}, {\mathbf{z}} ; {\mathbf{p}})}$, we can arrive at

$$\begin{aligned} {{{\varvec{\Gamma }}}(\mathbf{r}, {\mathbf{z}}; {\mathbf{p}})} ={{\Gamma }^{\infty }_p({\hat{\mathbf{r}}}, {\mathbf{z}}; {\mathbf{p}}) {\hat{\mathbf{r}}} \frac{{\mathrm{e}}^{ik_{p}r}}{\sqrt{r}}} +{{\Gamma }^{\infty }_s({\hat{\mathbf{r}}}, {\mathbf{z}}; {\mathbf{p}}) {\hat{\mathbf{r}}^{^{\perp }}} \frac{{\mathrm{e}}^{ik_{s}r}}{\sqrt{r}}+ O(r^{-3/2}),\quad r\rightarrow \infty }, \end{aligned}$$

(9)

where the far-field patterns ${{\varvec{\Gamma }}^{\infty }({\varvec{\cdot }}, {\mathbf{z}}; {\mathbf{p}}) =({\Gamma }^{\infty }_p({\varvec{\cdot }}, {\mathbf{z}}; {\mathbf{p}}), {\Gamma }^{\infty }_s({\varvec{\cdot }}, {\mathbf{z}}; {\mathbf{p}}))}$ of this elastic point source of the P, and S-part of ${{\Gamma }(\mathbf{r}, {\mathbf{z}}; {\mathbf{p}})}$ are given by Pelekanos and Sevroglou (2005)

$$\begin{aligned}&{{\Gamma }^{\infty }_p({\hat{\mathbf{r}}}, {\mathbf{z}}; {\mathbf{p}})=\frac{1}{\lambda +2\mu } \frac{i+1}{4\sqrt{\pi k_{p}}} {\mathrm{e}}^{-ik_{p}{\hat{\mathbf{r}}}\cdot {\mathbf{z}}} {\hat{\mathbf{r}}}\cdot {\mathbf{p}}}, \end{aligned}$$

(10)

$$\begin{aligned}&{{\Gamma }^{\infty }_s({\hat{\mathbf{r}}}, {\mathbf{z}}; {\mathbf{p}})=\frac{1}{\mu } \frac{i+1}{4\sqrt{\pi k_{s}}} {\mathrm{e}}^{-ik_{s}{\hat{\mathbf{r}}}\cdot {\mathbf{z}}} {\hat{\mathbf{r}}^{^{\perp }}}\cdot {\mathbf{p}}}, \end{aligned}$$

(11)

respectively. Exploiting Betti’s formulae, through asymptotic analysis and taking into account (9) and (10)–(11), we can arrive at the asymptotic form of the radiating solution ${\mathbf{{u}}^{{\mathrm{sct}}}}$ of the Navier equation (4)

$$\begin{aligned} {\mathbf{{u}}^{{\mathrm{sct}}}(\mathbf{r})=\mathbf{{u}}^{\infty }_p({\hat{\mathbf{r}}}) \frac{{\mathrm{e}}^{ik_{p}r}}{\sqrt{r}}+\mathbf{{u}}^{\infty }_s({\hat{\mathbf{r}}}) \frac{{\mathrm{e}}^{ik_{s}r}}{\sqrt{r}}+O(r^{-3/2})}, \end{aligned}$$

(12)

uniformly with respect to ${{\hat{\mathbf{r}}}=\mathbf{r}/|\mathbf{r}|}$ as ${r=|\mathbf{r}|\rightarrow \infty }$. The functions ${\mathbf{{u}}^{\infty }_p}$ and ${\mathbf{{u}}^{\infty }_s}$ are the corresponding far-field patterns defined on $\mathbb {S}$, and are known as the longitudinal and the transverse far-field patterns, respectively. From the point of view of the investigation of the inverse scattering problem, the far-field patterns, which consist of a measure of the scattered field at the radiation zone, are essential and useful on the numerical reconstructions of obstacles. The explicit formulae of the elastic far-field patterns ${\mathbf{{u}}^{\infty }_p}$ and ${\mathbf{{u}}^{\infty }_s}$ are omitted for brevity, which can be found in the literature, see, e.g., (Athanasiadis et al. 2006; Pelekanos and Sevroglou 2003; Sevroglou 2005).

Our interested inverse elastic scattering problem of (4)–(6) consists in the determination of the unknown boundary $\partial D$ of the rigid scatterer D, from the knowledge (with noise) of the far-field patterns ${\mathbf{{u}}^{\infty }}({\hat{\mathbf{r}}}):=({\mathbf{{u}}^{\infty }_p}({\hat{\mathbf{r}}});{{\mathbf{u}}^{\infty }_s}({\hat{\mathbf{r}}}))$ of the scattered field in all incident directions $\hat{\mathbf{d}}\in \mathbb {S}$ and observation directions $\hat{\mathbf{r}}\in \mathbb {S}$. In practical applications, we can only measure far-field pattern data from finite many directions that uniformly distributed on the unit circle. In theory, the above direct and inverse elastic scattering problem admits at most one solution (Hahner and Hsiao 1993; Li et al. 2016).

3 A brief description of compared qualitative methods

In this section, we briefly review several qualitative methods for solving the above inverse elastic scattering problem. In particular, we will consider the linear sampling method, factorization method and its variant, direct sampling method, and direct factorization method involving full far-field patterns, which are used successfully for the reconstruction of boundaries of scatterers treated in a large variety of inverse acoustic, electromagnetic, and elastic problems (Kirsch 1998; Kirsch and Grinberg 2008; Charalambopoulos et al. 2006). We will numerically compare these methods for solving inverse elastic scattering problems, and deal with reconstructions of the boundary of a rigid obstacle with homogeneous Dirichlet boundary condition.

For a given kernel ${\mathbf{g}}=(g_p,g_s)\in {\mathcal {L}}^2:=[L^2(\mathbb {S})]^2$, define the elastic Herglotz wavefunction

$$\begin{aligned} {\mathbf{v}_{\mathbf{g}}(\mathbf{r})}= {{\mathrm{e}}^{-i\pi /4}} \left[ {\int _{\mathbb {S}} \sqrt{\frac{k_{p}}{\omega }} g_{p}({\hat{\mathbf{d}}}, {\mathbf{z}}; {\mathbf{p}}) {\hat{\mathbf{d}}} {\mathrm{e}}^{ik_{p}\mathbf{r}\cdot {\hat{\mathbf{d}}}} +\sqrt{\frac{k_{s}}{\omega }} g_{s}({\hat{\mathbf{d}}}, {\mathbf{z}}; {\mathbf{p}}) {\hat{\mathbf{d}}}^{^{\perp }} {\mathrm{e}}^{ik_{s}{} \mathbf{r}\cdot {\hat{\mathbf{d}}}} ds({\hat{\mathbf{d}}})} \right] , \end{aligned}$$

(13)

which refers to a superposition of plane waves over the unit circle $\mathbb {S}$ propagating in every direction, and the components ${g_{p}({\hat{\mathbf{d}}}, {\mathbf{z}}; {\mathbf{p}}), g_{s}({\hat{\mathbf{d}}}, {\mathbf{z}}; {\mathbf{p}})}$ of $\mathbf{g}$ are, respectively, known as the longitudinal and transverse Herglotz kernels (Sevroglou and Pelekanos 2002). The far-field patterns of the scattered fields corresponding to the elastic Herglotz wave function (13) are expressed via the elastic far-field operator ${F}:{\mathcal {L}}^2\rightarrow {\mathcal {L}}^2$ given by

$$\begin{aligned} \begin{array}{lllllllll} &{}({F}{{\mathbf{g}})({\hat{\mathbf{r}}})} \\ &{}\quad ={{\mathrm{e}}^{-i\pi /4}}\left[ {\int _{\mathbb {S}}\sqrt{\frac{k_{p}}{\omega }} \mathbf{u}^{\infty }({\hat{\mathbf{r}}}, {\hat{\mathbf{d}}}, {\hat{\mathbf{d}}}) g_{p}({\hat{\mathbf{d}}}, {\mathbf{z}}; {\mathbf{p}}) +\sqrt{\frac{k_{s}}{\omega }} \mathbf{u}^{\infty }({\hat{\mathbf{r}}}, {\hat{\mathbf{d}}}, {\hat{\mathbf{d}}}^{^{\perp }}) g_{s}({\hat{\mathbf{d}}}, {\mathbf{z}}; {\mathbf{p}}) ds({\hat{\mathbf{d}}})} \right] , \end{array} \end{aligned}$$

(14)

where ${{\hat{\mathbf{r}}}, {\hat{\mathbf{d}}}}$ denote the observation and incident directions, respectively, and the far-field patterns have the form

$$\begin{aligned} {\mathbf{u}^{\infty }(\cdot , {\hat{\mathbf{d}}}, {\hat{\mathbf{d}}})}= & {} {(u^{\infty }_p(\cdot , {\hat{\mathbf{d}}}, {\hat{\mathbf{d}}}), u^{\infty }_s(\cdot , {\hat{\mathbf{d}}}, {\hat{\mathbf{d}}}))}, \end{aligned}$$

(15)

$$\begin{aligned} {\mathbf{u}^{\infty }(\cdot , {\hat{\mathbf{d}}}, {\hat{\mathbf{d}}}^{^{\perp }})}= & {} {(u^{\infty }_p(\cdot , {\hat{\mathbf{d}}}, {\hat{\mathbf{d}}}^{^\perp }), u^{\infty }_s(\cdot , {\hat{\mathbf{d}}}, {\hat{\mathbf{d}}}^{^{\perp }})).} \end{aligned}$$

(16)

Basic known properties of the above elastic far-field operator F can be found in Alves (2002), Arens (2001), Pelekanos and Sevroglou (2003), and Sevroglou (2005). In particular, the far-field operator F is known to be normal, compact, and injective, and it has a countable infinite number of nonzero eigenvalues, which lie on the circle with center $(2\pi /\omega ) i$ and radius $2\pi /\omega$ in the complex plane.

3.1 The linear sampling method and factorization method

The linear sampling method (LSM) was first introduced for inverse acoustic scattering problems and then extended to electromagnetic and elastic scattering problems (Potthast 2006). Let ${{\mathbf{p}}\in \mathbb {S}}$ be the chosen polarization vector of an elastic point source (see (9)). The basic idea of LSM is, for any ${\mathbf{z}}\in D$, to solve for a density ${{\mathbf{g}}(\cdot , {\mathbf{z}}; {\mathbf{p}})=\left( g_{p}(\cdot , {\mathbf{z}} ; {\mathbf{p}}), g_{s}(\cdot , {\mathbf{z}}; {\mathbf{p}})\right) }$ from the far-field equation

$$\begin{aligned} F{{\mathbf{g}}(\cdot , {\mathbf{z}}; {\mathbf{p}})=\phi _{{\mathbf{z}}}:={\varvec{\Gamma }}^{\infty }(\cdot , {\mathbf{z}}; {\mathbf{p}})} \end{aligned}$$

(17)

with $\phi _{\mathbf{z}}:={{\varvec{\Gamma }}^{\infty }(\cdot , {\mathbf{z}}; {\mathbf{p}})}$ is the far-field pattern of ${{{\varvec{\Gamma }}}(\mathbf{r}, {\mathbf{z}}; {\mathbf{p}})}$ given in (10) and (11). It was shown that $\Vert {\mathbf{g}}(\cdot , {\mathbf{z}}; {\mathbf{p}})\Vert _{{\mathcal {L}}^2}\rightarrow \infty$ as $\mathbf{z}$ approaches $\partial D$, which suggests to use the value of

$$\begin{aligned} {\mathbb {I}}^{{\mathrm {LSM}}}({\mathbf{z}}):=\Vert {\mathbf{g}}(\cdot , {\mathbf{z}}; {\mathbf{p}})\Vert _{{\mathcal {L}}^2} \end{aligned}$$

as an indicator function for qualitatively characterize the shape of D. In practical numerical implementations, such a simple LSM indeed demonstrates a very satisfactory reconstruction accuracy. However, it is unclear what will happen when ${\mathbf{z}}\notin D$ and Eq. (17) may not be solvable in general.

To address those theoretical drawbacks of LSM, Kirsch in Kirsch (1998) first proposed the factorization method (FM), which solves the following ‘factorized’ far-field equation:

$$\begin{aligned} (F^{*}F)^{1/4}{\mathbf{g}(\cdot , {\mathbf{z}}; {\mathbf{p}})}=\phi _{\mathbf{z}} \end{aligned}$$

(18)

with $F^{*}$ being the Hilbert adjoint operator of F. Similar to the LSM, the value of

$$\begin{aligned} {\mathbb {I}}^{\mathrm {FM}}({\mathbf{z}}):=\Vert {\mathbf{g}}(\cdot , {\mathbf{z}}; {\mathbf{p}})\Vert _{{\mathcal {L}}^2} \end{aligned}$$

with $\mathbf{g}$ given in (18) can be used as an indicator function for determining the support of the scatterer, From the knowledge of the density ${{\mathbf{g}}(\cdot , {\mathbf{z}}; {\mathbf{p}})}\in L^{2}({\mathbb {S}})$, the boundary of our obstacle can be recovered at the points where $\Vert {\mathbf{g}}(\cdot , {\mathbf{z}}; {\mathbf{p}})\Vert _{{\mathcal {L}}^2}$ becomes unbounded or has an extremely large value in numerical approximations.

The mathematical justification of FM is the key equivalence (Alves 2002; Kirsch and Grinberg 2008) (for any ${\mathbf{z}} \in {\mathbb {R}}^2$)

$$\begin{aligned} {\mathbf{z}}\in D \Longleftrightarrow {\varvec{\Gamma }}^{\infty }({\hat{\mathbf{r}}}, {\mathbf{z}}; {\mathbf{p}})\in {\mathrm {Range}}\left( (F^*F)^{1/4}\right) , \end{aligned}$$

(19)

where D is assumed to be simply connected and ${\omega ^2}$ is not an interior Dirichlet eigenvalue of $-\Delta ^*$ in D. This explicit equivalence provides a complete characterization of the support of the elastic scatterer D, leading to the above factorization method. The FM was further analyzed in Hu et al. (2012), where shape reconstructions can be achieved using only one part (P or S-part) of the far-field patterns. Very recently, this equivalence relation was further exploited for determining the interior eigenvalues (i.e., resonant frequencies) and the corresponding eigenfunctions associated with an unknown obstacle, which leads to an improved wave imaging scheme with enhanced imaging resolution (Liu et al. 2019) for certain practical scenarios.

For simplicity, we will denote $\Vert \cdot \Vert _{{\mathcal {L}}^2}$ by $\Vert \cdot \Vert$ in the following. Due to the compactness of F, the inversion of F in (17) and $(F^*F)^{1/4}$ in (18) are ill-posed, which are often treated by Tikhonov regularization for their stable approximation in the presence of noise. More specifically, let $F_\delta$ be the noisy far-field operator obtained by replacing the exact far-field pattern $\mathbf{u}^\infty$ in F by the measured noisy far-field pattern $\mathbf{u}_\delta ^\infty$, such that $\Vert F_\delta -F\Vert <\delta$. The Tikhonov regularization (Tikhonov et al. 2013; Kirsch 1998) approximates $\mathbf{g}$ by ${\mathbf{g}}_\gamma$, which is defined as the minimizer of the following Tikhonov regularized objective functional (for any fixed $\mathbf{z}$):

$$\begin{aligned} { {\mathbf{g}}_\gamma :=\mathop {\arg \min }_{\mathbf{g}\in {\mathcal {L}}^2}\ \left( \Vert A_\delta {\mathbf{g}}-\phi _{\mathbf{z}}\Vert ^2+\gamma ^2 \Vert \mathbf{g}\Vert ^2\right) ,} \end{aligned}$$

(20)

where $A_\delta =F_\delta$ or $A_\delta =(F_\delta ^*F_\delta )^{1/4}$ and $\gamma >0$ is a regularization parameter to be chosen. The above Tikhonov minimization problem (20) is mathematically equivalent to solving the regularized normal equation

$$\begin{aligned} (A_\delta ^*A_\delta +{\gamma ^2} I) {\mathbf{g}}_{\gamma }=A_\delta ^* \phi _{\mathbf{z}}. \end{aligned}$$

(21)

Let $(\{\sigma _j\},\{u_j\},\{v_j\})$ be the singular system of $F_\delta$ with $\{\sigma _j\}$ being the singular values (in decreasing order), $\{u_j\}$ and $\{v_j\}$ being the left and right singular functions, respectively, that is $F_\delta u_j=\sigma _j v_j$ and $F_\delta ^* v_j=\sigma _j u_j.$ Then, the regularized solution of (21) can be expressed in terms of the singular system $(\{\sigma _j\},\{u_j\},\{v_j\})$ according to Colton et al. (2000a) and Colton and Kress (2012)

$$\begin{aligned} {\mathbf{g}}_{\gamma }^{{\mathrm {LSM}}}=\sum _{j} \frac{\sigma _j}{{\gamma ^2}+\sigma _j^2} {(\phi _{\mathbf{z}},v_j)} u_j,\quad \text{ when } \ A_\delta =F_\delta \end{aligned}$$

(22)

or

$$\begin{aligned} {\mathbf{g}}_{\gamma }^{\mathrm {FM}}=\sum _{j} \frac{\sqrt{\sigma _j}}{{\gamma ^2}+\sigma _j} {(\phi _{\mathbf{z}},u_j)} u_j, \quad \text{ when } \ A_\delta =(F_\delta ^*F_\delta )^{1/4}. \end{aligned}$$

(23)

From the above expressions, we can see that the major operation cost of computing the regularized ${\mathbb {I}}^{{\mathrm {LSM}}}({\mathbf{z}})$ and ${\mathbb {I}}^{\mathrm {FM}}({\mathbf{z}})$ lies in the inner products between singular functions and $\phi _{\mathbf{z}}$. In finite dimension, such inner products become usually vector dot products. However, this operation could become very expensive if it is repeated for a large number of different sampling points that are necessary for a large probing domain in 3D problems.

For treating more general cases where the far-field operator F fails to be normal, we can define similar indicator functionals with F being replaced by the derived self-adjoint positive definite far-field operator $F_\sharp$ (named “F-sharp”) given by (see Grinberg and Kirsch 2004; Kirsch and Grinberg 2008)

$$\begin{aligned} F_\sharp =|{\text {Re}} (F)|+|{\text {Im}} (F)|, \end{aligned}$$

where ${\text {Re}} (A)=(A+A^*)/2$, ${\text {Im}} (A)=(A-A^*)/(2i)$, and $|B|=(B^*B)^{1/2}$. More specifically, the LSM and FM far-field linear equations now take the following form, respectively:

$$\begin{aligned} F_\sharp g_{\mathbf{z}}=\phi _{\mathbf{z}}\quad \text{ and }\quad F_\sharp ^{1/2} g_{\mathbf{z}}=\phi _{\mathbf{z}}, \end{aligned}$$

where we have used the fact that $F_\sharp ^*=F_\sharp$ and $(F_\sharp ^*F_\sharp )^{1/4}=F_\sharp ^{1/2}$. Theoretically, the condition numbers of $F_{\sharp }$ and F are of the same order, as elaborated in Sect. 4.4. However, we observed that $F_\sharp$-based methods are numerically more well conditioned than F-based methods due to the regularization effect of round-off errors, as illustrated in Fig. 12.

3.2 On the choice of regularization parameter $\gamma$

There are various a priori or a posteriori methods of choosing a good regularization parameter $\gamma$. We will focus on comparing two such methods: Morozov’s generalized discrepancy principle (GDP) (Goncharskii et al. 1973; Engl 1987; Colton and Kress 2012) and the improve maximum product criterion (IMPC) (Bazán 2014; Bazán et al. 2015), which are now briefly described as follows. Recall that GDP chooses as regularization parameter $\gamma$ the unique root of the nonlinear equation

$$\begin{aligned} G(\lambda ):= \Vert A_\delta {\mathbf{g}}_\lambda -\phi _{\mathbf{z}}\Vert ^2- \delta ^2\Vert {\mathbf{g}}_\lambda \Vert ^2=0, \end{aligned}$$

(24)

where $\delta >0$ is an estimate for $\Vert E\Vert =\Vert A_{\delta }-A\Vert$, such that $\Vert E\Vert \le \delta$. It is well known that G is convex for small $\lambda$ and concave for large $\lambda$. As a result, global and monotone convergence of the standard Newton’s method (with only local convergence) cannot be guaranteed (Lu et al. 2010) in general. This difficulty is circumvented by a fixed-point iteration (called GDP-FP) introduced by Bazán (2014), as we will see shortly.

Following (Bazán et al. 2017) closely, we now describe the GDP-FP method. To this end, we consider

$$\begin{aligned} {\mathsf{r}(\lambda )=} \Vert A_\delta {\mathbf{g}}_\lambda -\phi _{\mathbf{z}}\Vert \quad \text{ and }\quad {\mathsf{s}(\lambda )=\Vert {\mathbf{g}}_\lambda \Vert }, \end{aligned}$$

(25)

and for any initial guess $\lambda _{0}>0$, we define the fixed point iteration ($k = 0,1,2,\dots$)

$$\begin{aligned} {\lambda _{k+1}:=\xi (\lambda _k), \quad \text{ with }\ \xi (\lambda ):=\lambda } \sqrt{\frac{\delta {\mathsf{s}(\lambda )}}{\mathsf{r}(\lambda )}}. \end{aligned}$$

(26)

Bazán (2014) showed that the above-generated sequence $\{\lambda _k\}$ converges globally to the unique root of $G(\lambda )$ irrespective of the chosen initial guess. Thus, provided that the solution norm and the corresponding residual norm are available, computing the regularization parameter chosen by GDP via the above fixed-point iteration is efficient. Yet, another difficulty with GDP is that it requires knowledge of the noise level $\delta$ and poor-quality solutions may be produced when the noise level is not accurately estimated.

An alternative parameter selection criterion that avoids using knowledge of the noise level and that has been shown to produce stable reconstructions is the maximum product criterion (MPC) (Bazán et al. 2012). MPC selects as regularization parameter a maximizer of the nonlinear function,

$$\begin{aligned} {\Psi (\lambda )=\left[ \mathsf{r}(\lambda )\right] ^{2} \left[ \mathsf{s}(\lambda )\right] ^{2}} \end{aligned}$$

(27)

which is relatively simple to compute in most cases. However, MPC is not free of difficulties and it can fail when $\Psi$ has several local maxima. The improved MPC (IMPC) (Bazán et al. 2015) circumvents this problem by selecting the regularization parameter as the largest maximum point of $\Psi$ and by introducing a fixed point iteration for its computation. More specifically, the regularization parameter chosen by IMPC is computed via another fixed point iteration $(k = 0,1,2,\ldots )$

$$\begin{aligned} {\lambda _{k+1}=\chi (\lambda _k), \quad \text{ with }\ \chi (\lambda ):=\frac{\lambda ^{2} \mathsf{s}(\lambda )}{\mathsf{r}(\lambda )}} \end{aligned}$$

(28)

with a sufficiently large initial guess ${\lambda _0\in \left[ \frac{\sqrt{3}}{3}\sqrt{\sigma _1}, \sqrt{\sigma _1}\right] }$ (see Bazán et al. 2015, Thm 3.2).

We emphasize that both fixed-point approaches (26) and (28) require computing the regularized solution norm $\mathsf{s}(\lambda )$ and the corresponding residual norm $\mathsf{r}(\lambda )$ and that both of them can be efficiently implemented using the SVD of the far-field matrix ${F}^{\delta }$. In practice, the iteration of computing $\lambda _k$ as the approximation of the desired regularization parameter $\gamma$ should stop when they begin to stagnate to keep low the computational cost of the entire process. In our implementation, we choose to stop the iterations when the relative change of consecutive values is small, i.e., when

$$\begin{aligned} |\lambda _{k+1}-\lambda _{k}|\le \nu |\lambda _{k}|, \end{aligned}$$

(29)

where $\nu$ is a small tolerance parameter (e.g., $\nu =10^{-2}$). A smaller tolerance $\nu$ will lead to more accurate regularization parameter with more iterations in the above fixed-point algorithms. It is reasonable to choose a tolerance that is comparable to the level of noise, so that the regularization parameter is not overestimated with excessively high computational cost.

3.3 The direct sampling method and direct factorization method

As shown above, both LSM and FM need to invert the ill-posed far-field operator. They require a costly Tikhonov regularization procedure at each sampling point $\mathbf{z}$ to achieve a robust approximation accuracy in the presence of noise in data. Such numerical difficulty of instability is avoided in the more recently developed direct sampling methods and direct factorization method, where only matrix–vector multiplications are involved in the computation of indicator functions. Such direct methods are much faster and more robust against measurement noise, although they usually provide somewhat less sharp reconstructions than the LSM and FM. In particular, the unknown noise level and regularization parameter are not needed anymore in such direct methods, since the inversion of ill-conditioned far-field operator is circumvented.

We are particularly interested in a direct sampling method (DSM) introduced in Ji et al. (2018), where the proposed indicator functional reads

$$\begin{aligned} {\mathbb {I}}^{\mathrm {DSM}}({\mathbf{z}}):=\left|\int _{\mathbb {S}} \phi _{\mathbf{z}}^*(\mathbf{y}) F \phi _{\mathbf{z}}(\mathbf{y}) ds(\mathbf{y})\right|. \end{aligned}$$

(30)

This simple indicator functional ${\mathbb {I}}^{\mathrm {DSM}}( \mathbf{z})$ has a positive lower bound for the sampling point ${\mathbf{z}}\in D$ and it decays like the Bessel functions as the sampling point $\mathbf{z}$ goes away from the scatterer boundary $\partial D$. It is also continuously dependent on the far-field patterns and hence extremely stable with respect to data noise. We expect that the indicator ${\mathbb {I}}^{\mathrm {DSM}}( \mathbf{z})$ attains its maximum near the boundary $\partial D$ and decays monotonically like the Bessel functions as the sampling points move away from $\partial D$, which was largely verified in numerical simulations.

In view of the difference between LSM and FM and mimicking the DSM, we can define a direct factorization method (DFM) with the following indicator functional:

$$\begin{aligned} \widehat{{\mathbb {I}}}^{\mathrm {DFM}}({\mathbf{z}}):=\left|\int _{\mathbb {S}} \phi _{\mathbf{z}}^*(\mathbf{y}) (F^*F)^{1/4} \phi _{\mathbf{z}}(\mathbf{y}) ds(\mathbf{y})\right|, \end{aligned}$$

(31)

which was shown to be mathematically equivalent to the above DSM indicator ${\mathbb {I}}^{\mathrm {DSM}}( \mathbf{z})$. Apparently, both indicator functionals ${\mathbb {I}}^{\mathrm {DSM}}( \mathbf{z})$ and $\widehat{{\mathbb {I}}}^{\mathrm {FM}}({\mathbf{z}})$ are not directly derived from the above far-field equations governing the LSM and FM. To disclose their hidden connections, we can make use of a truncated Neumann series expansion of $(F^*F)^{-1/4}$ (upon appropriately rescaling) in FM to arrive at another possible more intuitive DFM indicator functional (Leem et al. 2018a)

$$\begin{aligned} {{\mathbb {I}}}^{\mathrm {DFM}}({\mathbf{z}}):=\Vert (2I- \beta (F^*F)^{1/4}) \phi _{\mathbf{z}}\Vert \approx \Vert (F^*F)^{-1/4} \phi _{\mathbf{z}}\Vert ={\mathbb {I}}^{\mathrm {FM}}({\mathbf{z}}), \end{aligned}$$

(32)

where $\beta =\frac{2}{\sqrt{\sigma _{\max } }+\sqrt{\sigma _{\min } }}$ with $\sigma _{\max }$ and $\sigma _{\min }$ being the maximum and minimal singular value of F (upon appropriate discretization). We can show that both DFM indicator functionals $\widehat{{\mathbb {I}}}^{\mathrm {DFM}}({\mathbf{z}})$ and ${{\mathbb {I}}}^{\mathrm {DFM}}({\mathbf{z}})$ are also mathematically equivalent, which hence explains the validity of the above DFM as a crude but satisfactory approximation of FM. In our simulations, we will only use ${{\mathbb {I}}}^{\mathrm {DFM}}({\mathbf{z}})$, since it usually provides sharper boundaries than $\widehat{{\mathbb {I}}}^{\mathrm {DFM}}({\mathbf{z}})$, although there is no essential difference in characterization of the scatterer. Based on our following extensive numerical tests, the profiles obtained by ${{\mathbb {I}}}^{\mathrm {DFM}}({\mathbf{z}})$ indeed seem to be much less oscillatory than those given by ${\mathbb {I}}^{\mathrm {DSM}}( \mathbf{z})$, which are clearly contaminated by undesirable artifacts outside of the scatterer, such as heavy tails or some large oscillatory peaks (see, e.g., Liu 2017).

4 Numerical examples

In this section, we will numerically compare the above-discussed different indicator functionals to reconstruct the shapes of various 2D elastic (rigid) bodies with the full far-field patterns, and P or S-part of the far-field patterns under various settings. All simulations are implemented using MATLAB 9.9 (R2020b) on a Dell Precision 7520 Laptop with Intel(R) Core(TM) i7-7700HQ CPU@2.80 GHz and 32 GB RAM. The CPU time (in seconds) is estimated using the MATLAB’s timing functions tic/toc.

For N longitudinal (pressure) waves or N transverse (shear) waves, incident from N directions ${{\hat{\mathbf{d}}}_j=(\cos \theta _j, \sin \theta _j)}$ with $\theta _j=2\pi j/N$, we assume that the far-field equation (17) and (18) is discretized as described in Hu et al. (2012), giving rise to a system of $2N\times 2N$ linear equations (with ${F}\in C^{2N\times 2N }$)

$$\begin{aligned} F{\mathbf{g}_{z}}=b_{\mathbf{z}},\quad \text{ and }\quad ({F}^{*}{F})^{1/4}{\mathbf{g}_{z}}=b_{\mathbf{z}}, \end{aligned}$$

(33)

where $b_{\mathbf{z}}$ is a discrete version of $\phi _{\mathbf{z}}$ and F (we use the same notation of brevity) is a discretized version of the far-field operator F. We shall consider the reconstruction problem in three typical cases

• (i) FF case based on the operator F (full far-field pattern),

• (ii) PP case based on the operator ${F}_p$ (part of the far-field pattern corresponding to N incident plane longitudinal waves), and

• (iii) SS case based on the operator ${F}_s$ (part of the far-field pattern corresponding to N incident plane transverse waves).

In PP (or SS) cases, a discretized version of ${F}_p$ (resp. ${F}_s$) denoted by ${F}_{p}$ (resp. ${F}_{s}$) can be extracted (as orthogonal projection) from F by taking rows 1 (resp. $N+1$) through N (resp. 2N) and columns 1 (resp. $N+1$) through N (resp. 2N). Similarly, $b_{\mathbf{z}}^{p}$ (resp. $b_{\mathbf{z}}^s$) denotes the vector of N first (resp. last) components of $b_{\mathbf{z}}$. With MATLAB matrix indexing notations, we essentially have

$$\begin{aligned} F_p= & {} F(1:N,1:N),\quad F_s=F(N+1:2N,N+1:2N),\\ b_{\mathbf{z}}^{p}= & {} b_{\mathbf{z}}(1:N),\quad b_{\mathbf{z}}^s= b_{\mathbf{z}}(N+1:2N). \end{aligned}$$

To avoid inverse crime, we construct the noisy far-field data according to

$$\begin{aligned} {F}^{\delta }={F}+\delta \Vert {F}\Vert {\mathcal {N}}, \end{aligned}$$

(34)

where ${F}^{\delta }$ is the noisy counterpart of the exact matrix F, ${\mathcal {N}}$ is a $2N\times 2N$ random Gaussian noise matrix normalized, such that $\Vert {\mathcal {N}}\Vert =1$ and $\delta$ is an error parameter which controls the amount of noise in the far-field data. The synthetic “noise-free” far-field data used in the experiments are generated as in Hu et al. (2012) using parametric forms of the integrals that represent the P-part and S-part of the scattered field.

For the implementation of LSM and FM, two different choices of Tikhonov regularization parameter are compared against the naive inversion without any regularization. In the GDP-FP and IMPC iterations, we use the SVD of ${F}^{\delta }$ (computed only once) and choose $\nu =10^{-2}$ as the stopping tolerance parameter. We mention that in all numerical examples, the number of used iterations is usually less than 10. This illustrates the excellent efficiency of GDP-FP and IMPC iterations in computing the regularization parameter. As a comparison, we also computed the Tikhonov regularization parameter based on GDP with MATLAB’s builtin nonlinear solver fzero (with default setting) that uses a combination of bisection, secant, and inverse quadratic interpolation methods. We remark that the performance of LSM-GDP and FM-GDP highly depends on the fzero solver, which seems to be much slower than the fixed-point iteration (26). This is expected, since the fzero solver obtains more accurate zeros of $G(\lambda )=0$, but it does not provide improved reconstructions. Hence, GDP-FP based on (26) is better than fzero, since it achieves a similar reconstruction quality with much less CPU time.

For the numerical reconstructions, we consider a uniform sampling grid in the square region $\left[ -5, 5 \right] \times \left[ -5, 5 \right]$ containing the unknown scatterer, with ${m=200}$ points in each direction. We select $\lambda =1$, $\mu =1$ and $\omega =2\sqrt{2}$ unless otherwise stated. We choose the polarization vector ${\mathbf{p}}=(\cos \alpha ,\sin \alpha )$ with a given $\alpha \in [0,\pi )$. In all plots, the true scatterer’s shape (in black dashed line) for generating the far-field patterns is provided on top of the reconstructed profiles for easier comparison. Figure 1 illustrates the true binary profile (with interior in red and exterior in blue) of tested scatterers.

Fig. 1

The true binary profiles of tested 2D scatterers (with a $200\times 200$ mesh size)

Fig. 2

Reconstructed kite profiles ($N=64, \alpha =7\pi /4$) with different noise levels: $\delta =0.01$ (top-left), $\delta =0.1$ (top-right), $\delta =0.3$ (bottom-left), and $\delta =0.5$ (bottom-right)

4.1 Influence of different noise levels and scatterers

We first compare the computational efficiency and reconstruction quality of the discussed methods in FF case. Figure 2 shows the reconstructed profiles of a rotated kite, where four different levels of noise $\delta =0.01,0.1,0.3,0.5$ are compared with different methods. In all figure titles, ‘LSM-NoReg’ and ‘FM-NoReg’ denote the LSM and FM without regularization, ‘LSM-GDP’ and ‘FM-GDP’ denote the LSM and FM with the regularization parameter computed by fzero, and ‘FM-GDP-FP’ and ‘FM-IMPC’ denote the FM with the regularization parameter computed by the corresponding fixed point iterations. The CPU times are also shown in the title of each subplot to illustrate the computational efficiency of each method (utilized MATLAB’s vectorized implementation whenever possible). Such CPU times should be interpreted qualitatively.

Comparing different methods across various increasing noise levels, we have the following interesting observations:

• 1. Without regularization, the reconstructed profiles by LSM quickly become unidentifiable as the noise level gets larger, and the profiles by FM seem to be less sensitive to the noise level. However, the profiles’ shapes by FM also become less visible due to large noises. The situation will get worse if a large N is used. Hence, suitable regularization is necessary for controlling the errors induced by random noise. We highlight that noise only occurs in the measured far-field data F.

• 2. With the regularization parameters chosen by GDP based on fzero solver, the reconstructed profiles by LSM and FM indeed better approximate the scatterer’s shape for all noise levels, but the CPU times become higher. The high CPU times can be dramatically reduced by the GDP-FP iteration, whose reconstructed profiles look very similar (compare subplots of ‘FM-GDP’ and ‘FM-GDP-FP’). This indicates that GDP-FP method has better efficiency than GDP with similar approximation accuracy.

• 3. With the noise level $\delta$ is unknown, the regularization parameters can be computed by the IMPC iterations, where the reconstructed profiles look even slightly better than the profiles by GDP or GDP-FP. This improved accuracy of IMPC is desirable, since it does not require the advance knowledge of the noise level, which is usually unknown or needs to be estimated when it comes to real-world applications. In GDP-based methods, the estimation of $\delta$ vastly affects the values of computed regularization parameters and hence the reconstruction quality.

• 4. The reconstructed profiles computed by DSM and DFM are very robust with respect to the noise levels, where the DFM seems to provide more accurate (less oscillatory) identification of the scatterer’s shape. Both DSM and DFM are also much faster than the other regularization-based methods. Interestingly, the DFM provides very similar profiles as the FM-IMPC, but it costs much less CPU time by avoiding computing a Tikhonov regularization parameter.

• 5. Alternatively, one can just fix a same regularization parameter in LSM and FM for all sampling points to speed up such regularization-based algorithms, which however may lead to degraded reconstruction quality. As an illustration, Fig. 3 reports the reconstructed kite profiles by LSM (denoted by ‘LSM-FixReg’) and FM (denoted by ‘FM-FixReg’) with several fixed regularization parameters $\gamma =10^{-1},10^{-2},10^{-3},10^{-4}$, where the reduced CPU times are close to the non-regularized cases. Although the reconstruction quality seems to be satisfactory for a small noise level, it deteriorates rapidly as the noise level gets larger. The LSM method seems to be more sensitive to the choice of regularization parameters.

Fig. 3

Reconstructed kite profiles $(N=64, \alpha =7\pi /4)$ by LSM and FM with fixed regularization parameters $(\gamma =10^{-1},10^{-2},10^{-3},10^{-4})$ and different noise levels: $\delta =0.01$ (top-left), $\delta =0.1$ (top-right), $\delta =0.3$ (bottom-left), and $\delta =0.5$ (bottom-right)

To objectively assess the reconstruction quality of each method, the Jaccard index (Jaccard 1908) of each profile is computed (using the MATLAB’s builtin function jaccard) against the corresponding true binary profile (see Fig. 1). The Jaccard index (also known as Jaccard similarity coefficient) is useful to access the insignificant difference in approximation accuracy of different profiles, which are not distinguishable or measurable by the human eye. In particular, the reconstructed profile is first rescaled to the range [0, 1] and then converted into a binary profile for a given cut-off threshold between 0 and 1. To measure how the reconstructed profile matches with the true binary profile at different thresholds, we plot the Jaccard index as a function of 50 thresholds uniformly distributed between 0 and 1. The total area under such a Jaccard index curve or its average value is a reasonable criterion to measure the similarity of two profiles. A larger value of average Jaccard (Avg. JAC) index in general indicates better overall reconstruction quality, in the sense of higher similarity with the true binary profile.

The Jaccard index curves corresponding to the profiles in Fig. 2 are shown in Fig. 4, where we notice the average Jaccard indices of FM-based methods (including FM-GDP, FM-GDP-FP, FM-IMPC, and DFM) are indeed slightly higher than those LSM-based algorithms (including LSM-GDP and DSM), but such difference diminishes as the noise level gets larger. Apparently, the LSM and FM without regularization give the lowest average Jaccard indices, which is compatible with our visual inspection. From the viewpoint of qualitative methods and random noises, we do not suggest to draw a definite conclusion that one method always has a better reconstruction quality than the others purely based on marginally different quantitative average Jaccard indices.

Fig. 4

The comparison of Jaccard index for the reconstructed kite profiles in Fig. 2 with different noise levels by different methods $(N=64, \alpha =7\pi /4).$ A higher average Jaccard (Avg. JAC) index indicates better overall reconstruction quality

Fig. 5

Reconstructed profiles of four different scatterers $(N=64, \alpha =7\pi /4, \delta =0.3)$

Similar observations can be obtained for the other scatterers (Ellipse, Peanut, Triangle, and Rectangle) with $\delta =0.3$, as shown in Fig. 5. In summary, appropriate regularization can greatly enhance the reconstruction quality of LSM and FM, and the regularization-free direct methods (including DSM and DFM) are very promising in terms of slightly worse reconstruction quality and superior computational efficiency (faster CPU times). For brevity, we will only report the average Jaccard index (Avg. JAC) as a simple yet objective criterion to compare the reconstruction quality.

4.2 Influence of different polarization vectors

In the far-field equations, the polarization vector $\mathbf{p}$ can be freely chosen. In Fig. 6, we show the reconstructed kite profiles with different polarization vectors and noise level $\delta =0.3$, where most cases have slightly different shapes that closely trace the true kite. Such marginal difference suggests us to use the sum of the indicator functionals with multiple polarization vectors as an improved indicator functional, whose reconstructed profiles are given in Fig. 7. In comparison with the cases with a single polarization vector, using two or more perpendicular polarization vectors indeed delivers slightly improved quality in reconstructed profiles, especially for LSM-NoReg and FM-NoReg. In particular, it seems that only two perpendicular polarization vectors with $\alpha \in \{0,\pi /2\}$ are sufficient to obtain a satisfactory (more symmetric) reconstruction.

Fig. 6

Reconstructed kite profiles with different single polarization vectors ($N=64$, top-left: $\alpha =0$, top-right: $\alpha =\pi /4$, bottom-left: $\alpha =\pi /2$, bottom-right: $\alpha =3\pi /4$)

Fig. 7

Reconstructed kite profiles by multiple polarization vectors ($N=64$, left: sum of two different $\alpha \in \{0,\pi /2\}$, right: sum of 2 different $\alpha \in \{\pi /4,3\pi /4\}$)

4.3 Influence of only P-wave or S-wave and frequencies

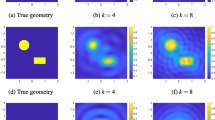
In practice, we may only have far-field data measurements with respect to P-wave or S-wave, which leads to the PP or SS cases. Figure 8 shows the constructed profiles (with $\delta =0.3$) for the interested FF, PP, and SS cases, respectively, where both $N=64$ and $N=256$ incident and observation directions are compared. The case $N=256$ leads to a much more ill-conditioned F, but the corresponding $F_\delta$ does not become significantly more ill-conditioned due to the added noise. In other words, $F_\delta$ is in general more stable to invert than F whenever the noise level $\delta$ is not too small.

As we can observe, the reconstructions corresponding to the FF case are of superior quality when compared with those of the PP and SS cases. This was expected however, since the FF case carries more data and hence more information about the scatterer. It is well known that the linear sampling method requires a large number of data to yield reliable reconstructions. Another reason is that, in general, the far-field matrix associated with the FF case is less sensitive (ill-conditioned) to noise than the matrices associated with other cases. Some details of the scatterer’s shape are somewhat incomplete and blurred in both PP and SS cases due to a reduced amount of data.

Fig. 8

Reconstructed kite profiles (top row: FF case; middle row: PP case; bottom row: SS case) of different wave cases ($N=64$ (left) and $N=256$ (right), $\alpha \in \{0,\pi /2\}$)

The obvious difference between the PP and SS case is highly dependent on the value of Lamé’s first parameter $\lambda$, which gives different values of wave numbers $k_p$ and $k_s$. Figure 9 shows the constructed profiles with two different $\lambda =-1.5$ and $\lambda =0$, where we notice the PP case seems often better when $\lambda =-1.5$ (with $k_p>k_s$), while the SS case often looks better with $\lambda =0$ (with $k_p<k_s$). The Avg. JAC values cannot differentiate some of the visual difference.

Fig. 9

Reconstructed kite profiles (top row: FF case; middle row: PP case; bottom row: SS case) with different $\lambda$ (left: $\lambda =-1.5$, right: $\lambda =0$, $N=256, \alpha \in \{0,\pi /2\}$)

Finally, we also illustrate the influence of higher frequency $\omega$ (i.e., wave numbers $k_p$ and $k_s$) in Fig. 10, where all regularized and direct methods seem to produce more similar profiles if ignoring the oscillatory effects. In the cases with higher frequency, the reconstructions by LSM without regularization seem to be highly deteriorated in the sense of visualizing the scatterer’s shape. To assemble the different characteristics with both lower and higher frequency, it is usually recommended to superimpose a range of multi-frequency data (Dennison and Devaney 2004; Bao et al. 2015) for better reconstruction quality.

Fig. 10

Reconstructed kite profiles (top row: FF case; middle row: PP case; bottom row: SS case) with higher frequency (left: $\omega =4\pi$, right: $\omega =8\pi$, $N=256, \alpha \in \{0,\pi /2\}$)

4.4 Influence of $F_\sharp$ operator

We now consider the corresponding $F_\sharp$ based methods, whose implementations are straightforward by replacing F by $F_\sharp$. Figure 11 shows the reconstructed profiles of the kite and peanut, where we observe much less difference across different methods for each case. In FF case, the obtained profiles without regularization seem to be almost as good as (or even slightly better than) the profiles generated by the regularized methods. The costly Tikhonov regularization seems to be unnecessary, since it only marginally improves the approximation quality. Such promising numerical outcomes of the $F_\sharp$-based methods without regularization can be explained by the interesting fact that the condition number of computed $F_\sharp$ is much smaller than that of F, which implies that the numerical transformation from F to $F_\sharp$ has regularization effect. In the following, we will further discuss this interesting numerical phenomena by analyzing their condition numbers. In short, due to the positive effect of round-off errors, the computed $F_\sharp$ indeed has a much smaller condition number whenever F is ill-conditioned (with many small singular values close to round-off errors). Hence, $F_\sharp$-based methods are more stable.

Fig. 11

Reconstructed kite and peanut profiles by $F_\sharp$-based methods ($N=256, \alpha =\{0,\pi /2\}$)

Let ${{\mathrm {Cond}}}(A)=\sigma _{\max }(A)/\sigma _{\min }(A)$ denotes the 2-norm condition number of a matrix A. Since F is normal and hence it is diagonalizable by a unitary matrix W, i.e., $F=W\Lambda W^*$, where the diagonal matrix $\Lambda ={{\mathrm {diag}}}(\eta _1,\eta _2,\ldots ,\eta _{2N})$ contains all the complex eigenvalues $\eta _j, j=1,2,\ldots , 2N$. By the definitions (Kirsch and Grinberg 2008), we have

$$\begin{aligned} {{\text {Re}}} (F)=W {\text {Re}}(\Lambda ) W^* =W {\mathrm {diag}}\left( {\text {Re}}(\eta _1) ,{\text {Re}}(\eta _2),\ldots ,{\text {Re}}(\eta _{2N})\right) W^* \end{aligned}$$

and

$$\begin{aligned} {\text {Im}} (F)=W {\text {Im}}(\Lambda ) W^*= W {\mathrm {diag}}\left( {\text {Im}}(\eta _1),{\text {Im}}(\eta _2), \ldots ,{\text {Im}}(\eta _{2N})\right) W^*, \end{aligned}$$

which further implies that

$$\begin{aligned} F_\sharp =W {\mathrm {diag}}\left( |{\text {Re}}(\eta _1)|+|{\text {Im}}(\eta _1)|, ,\ldots ,|{\text {Re}}(\eta _{2N})|+|{\text {Im}}(\eta _{2N})|)\right) W^*. \end{aligned}$$

Therefore, by treating $\eta _j$ as a $\mathbb {R}^2$ vector $\vec {\eta }_j:= \left[ \begin{array}{ccccccccccccccccccccccccccccccccccccc} {\text {Re}}(\eta _j)\\ {\text {Im}}(\eta _j)\end{array}\right]$, we in fact have

$$\begin{aligned} {\mathrm {Cond}}(F)=\frac{\max _{j} |\eta _j|}{\min _j |\eta _j|} =\frac{\max _{j} \sqrt{|{\text {Re}}(\eta _j)|^2+|{\text {Im}}(\eta _j)|^2}}{\min _j \sqrt{|{\text {Re}}(\eta _j)|^2+|{\text {Im}}(\eta _j)|^2}} =\frac{\max _{j} \Vert \vec {\eta }_j\Vert _2}{ \min _j \Vert \vec {\eta }_j\Vert _2} \end{aligned}$$

and

$$\begin{aligned} {\mathrm {Cond}}(F_\sharp )=\frac{\max _{j} \left( |{\text {Re}}(\eta _j)|+|{\text {Im}}(\eta _j)|\right) }{\min _j \left( |{\text {Re}}(\eta _j)|+|{\text {Im}}(\eta _j)|\right) } =\frac{\max _{j} \Vert \vec {\eta }_j\Vert _1}{\min _j \Vert \vec {\eta }_j\Vert _1}. \end{aligned}$$

From the equivalence of vector norms in $\mathbb {R}^2$ $\Vert \vec {\eta }_j\Vert _2\le \Vert \vec {\eta }_j\Vert _1\le \sqrt{2}\Vert \vec {\eta }_j\Vert _2$, we arrive at

$$\begin{aligned} \frac{1}{\sqrt{2}}\frac{\max _{j} \Vert \vec {\eta }_j\Vert _1}{ \min _j \Vert \vec {\eta }_j\Vert _1}\le \frac{\max _{j} \Vert \vec {\eta }_j\Vert _2}{ \min _j \Vert \vec {\eta }_j\Vert _2} \le \sqrt{2}\frac{\max _{j} \Vert \vec {\eta }_j\Vert _1}{ \min _j \Vert \vec {\eta }_j\Vert _1}, \end{aligned}$$

that is the following condition number estimates:

$$\begin{aligned} \frac{1}{\sqrt{2}} {\mathrm {Cond}}(F_\sharp ) \le {\mathrm {Cond}}(F) \le \sqrt{2}\ {\mathrm {Cond}}(F_\sharp ). \end{aligned}$$

(35)

Therefore, the condition number of $F_\sharp$ is theoretically of the same order as that of F.

Numerically, however, we observed that $F_\sharp$-based methods are much less sensitive to noise and the computed $F_\sharp$ using MATLAB’s matrix square root function sqrtm (Deadman et al. 2012) indeed has a significantly smaller condition number than the ill-conditioned F. In particular, we notice for an ill-conditioned F there holds ${\mathrm {Cond}}(F_\sharp )\approx \sqrt{{\mathrm {Cond}}(F)}$. This regularization effect can be roughly explained by the fact that the square rooting operation in sqrtm takes those small singular values of round-off error level (i.e., ${\mathcal {O}}(10^{-16})$) to its square root (i.e., ${\mathcal {O}}(10^{-8})$). For example, the ill-conditioned Hilbert matrix $H=\texttt {hilb}(20)$ has a large condition number of $2.1\times 10^{18}$, while its derived square root $|H|=\texttt {sqrtm}(H^*H)$ has a much smaller condition number of $1.5\times 10^9$. Such regularization effect due to round-off errors is beneficial to stable computation.

As a simple illustration, the singular values of F and $F_\sharp$ for the scatterer Kite are compared in Fig. 12, where the smallest singular value of $F_\sharp$ is much larger than that of F and the presence of random noise actually dramatically reduces the condition numbers of both F and $F_\sharp$. This essentially mitigates the necessity of sought-after regularization procedure when inverting $F_\sharp ^\delta$ for a relatively large $\delta$. However, we point out that the construction of $F_\sharp$ requires some one-time extra computation (e.g., sqrtm). The positive influence of random perturbation on the condition number has been sporadically discussed in literature, see, e.g., (Edelman 1988; Sankar et al. 2006), where the perturbed matrix was shown to be well conditioned with a high probability.

Fig. 12

Comparison of the singular values distribution of $F^\delta$ and $F_\sharp ^\delta$, respectively, for the scatterer Kite with $N=256$ (left: $\delta =0$, right: $\delta =0.1$). Notice that the condition number of $F_\sharp$ is much smaller than that of F

5 Conclusions

In this paper, several qualitative methods, including linear sampling method (LSM), factorization method (FM) and its variant (i.e., $F_\sharp$ based method), direct sampling method (DSM), and direct factorization method (DFM), are numerically compared for the shape reconstruction of 2D obstacles in elastic scattering based on the simulated noisy full far-field data. For Tikhonov regularization in linear sampling method and factorization method, we used two different regularization parameter choice techniques: the generalized discrepancy principle (GDP) and the improved maximum product criterion (IMPC). Extensive numerical examples with the use of average Jaccard index are provided to illustrate the pros and cons of each method through varying different settings, such as noise level, scatterer shape, P- or S-wave, frequency, and other contributing factors.

Based on our comprehensive numerical tests, both DFM and DSM are among the best choices in terms of both approximation accuracy and computational efficiency, although the more costly regularized LSM and FM sometimes indeed provide marginally better profiles with less artifacts. In some cases (e.g., $F_\sharp$ based methods), the costly regularization seems to be unnecessary due to smaller condition numbers. Finally, we highlight that in more realistic applications with limited aperture (Ikehata et al. 2012; Leem et al. 2019) and/or phaseless far-field data (Dong et al. 2019; Ji et al. 2019; Ji and Liu 2019), each method may display different numerical performance.