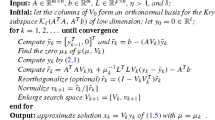Simple and Efficient Determination of the Tikhonov Regularization Parameter Chosen by the Generalized Discrepancy Principle for Discrete Ill-Posed Problems

Abstract

Discrete ill-posed problems where both the coefficient matrix and the right hand side are contaminated by noise appear in a variety of engineering applications. In this paper we consider Tikhonov regularized solutions where the regularization parameter is chosen by the generalized discrepancy principle (GDP). In contrast to Newton-based methods often used to compute such parameter, we propose a new algorithm referred to as GDP-FP, where derivatives are not required and where the regularization parameter is calculated efficiently by a fixed-point iteration procedure. The algorithm is globally and monotonically convergent. Additionally, a specialized version of GDP-FP based on a projection method, that is well-suited for large-scale Tikhonov problems, is also proposed and analyzed in detail. Numerical examples are presented to illustrate the effectiveness of the proposed algorithms on test problems from the literature.

1 Introduction

We consider linear problems of the form

$$\begin{aligned} A f = g, \qquad A\in \mathbb {R}^{n\times n} \end{aligned}$$

(1)

where the coefficient matrix $A$ arises from the discretization of ill-posed problems such as first kind Fredholm integral equations with smooth kernel. Such matrices are severely ill-conditioned and may be singular. Linear problems possessing such a matrix are frequently referred to as linear discrete ill-posed problems. In these cases the solution of (1) is very sensitive to perturbations in the data such as measurement or approximation errors, and thus regularization methods are essential for computing meaningful approximate solutions. In this paper we consider the problem of computing stable approximations to the solution of (1) for the case where the data obey the following assumptions:

A1: :

Problem (1) is consistent, ie., $g$ belongs to the column space of $A$, ${\mathcal {R}}(A)$,

A2: :

Instead of $g$ and $A$ we are given a noisy vector $\widetilde{g}$ and a noisy matrix $\widetilde{A}$ with available noise levels $\delta _g$ and $\delta _A$, respectively, such that

$$\begin{aligned} \Vert \widetilde{g}-g\Vert _2 \le \delta _g, \qquad \mathrm{and}\qquad \Vert \widetilde{A} - A\Vert _2\le \delta _A. \end{aligned}$$

(2)

Discrete ill-posed problems with data satisfying (2) appear in a number of applications such as potential theory, image processing and inverse scattering [1, 8, 9, 17, 22], among others. There are at least two well-distinguished approaches for these problems: (i) the classical Tikhonov regularization method, for which abundant literature exists, see, e.g., [11, 23, 30], and (ii) regularized total least squares methods [12, 18, 20, 22, 27–29]. Both approaches work well when the noise level in $A$ and $g$ are known accurately. However, since Tikhonov regularization is less expensive and simpler, we will concentrate only on this method.

The regularized solution determined by the method of Tikhonov is defined by

$$\begin{aligned} f_\lambda = {\mathop {\mathrm{argmin}}\limits _{f\in \mathbb {R}^n}} \left\{ \Vert \widetilde{A}f-\widetilde{g}\Vert _2^2 + \lambda ^2\Vert Lf\Vert _2^2\right\} , \end{aligned}$$

(3)

where $\lambda > 0$ is the regularization parameter and $L\in \mathbb {R}^{p\times n}$ is referred to as the regularization matrix. Notice that taking $\lambda =0$ in (3) we obtain the ordinary least squares problem

$$\begin{aligned} f_{_{\mathrm{LS}}} = {\mathop {\mathrm{argmin}}\limits _{f\in \mathbb {R}^n}}\Vert \widetilde{A}f- \widetilde{g}\Vert _2^2. \end{aligned}$$

(4)

A regularization Tikhonov problem is said to be in standard form if the matrix $L$ is the identity matrix $I_n$, otherwise the Tikhonov regularization problem is said to be in general form. The regularization matrix $L$ depends on the problem and is very often chosen as some discrete approximation to a derivative operator. The regularization parameter determines how close the regularized solution $f_\lambda$ is to the solution of (1), and should be chosen carefully.

The goal of the present paper is to construct Tikhonov regularized solutions for problem (1) with data satisfying A1–A2, using the generalized discrepancy principle (GDP) [23] as parameter choice rule. GDP is very popular due to its rigorous theoretical foundation; for a detailed analysis of GDP in a Hilbert space setting, which gives rise to error bounds including convergence rates and algorithms, the reader is referred to [21]. GDP chooses the regularization parameter as the solution of the nonlinear equation, called the discrepancy equation,

$$\begin{aligned} G(\lambda )= \Vert \widetilde{A}f_\lambda - \widetilde{g}\Vert _2^2 - ( \delta _g+\delta _A\Vert Lf_\lambda \Vert _2)^2= 0. \end{aligned}$$

(5)

The function $G$ is increasing and has a unique root under appropriate conditions. Additionally, it is convex for small $\lambda$ and concave for large $\lambda$. As a result, global and monotone convergence of Newton’s method cannot be guaranteed [29]. To overcome this difficulty, Lu et al. [21] transform the Eq. (5) into an equivalent one that depends on two free parameters $(\eta ,\nu )$ and perform an analysis to determine the set of parameters that ensure global convergence of Newton’s method. Numerical examples reported in [21] suggest that among the pairs $(\eta ,\nu )$ that guarantee convergence, there must be a pair for which the iteration converges faster, but the determination of such a pair is still lacking.

In this work, we propose a fixed-point type derivative-free algorithm for computing the regularization parameter chosen by GDP which we refer to as GDP-FP. The algorithm is shown to be globally and monotonically convergent and has convergence properties that do not depend on additional parameters as required by the algorithms proposed in [21]. GDP-FP can be readily implemented using the generalized singular value decomposition (GSVD) of the matrix pair $(\widetilde{A},L)$ when $\widetilde{A}$ and $L$ are small or of moderate size. For large scale-problems, a specialized version of GDP-FP based on a projection method is also proposed and discussed in detail. The main idea of the method introduced here is to approximate the regularized solution $f_\lambda$ by using a sequence of regularized solutions $f_\lambda ^{(k)}$ in appropriate Krylov subspaces of increasing dimension, in such a way that the regularization parameter for the projected problem is chosen as the solution of “the projected discrepancy equation”:

$$\begin{aligned} G^{(k)}(\lambda )= \Vert \widetilde{A}f_\lambda ^{(k)} - \widetilde{g}\Vert _2^2 - ( \delta _b+\delta _A\Vert Lf_\lambda ^{(k)}\Vert _2)^2= 0. \end{aligned}$$

(6)

Analogous to $G(\lambda )$, $G^{(k)}(\lambda )$ increases as $\lambda$ increases and has a unique solution under appropriate conditions.

The rest of the paper is organized as follows. Section 2 summarizes properties regarding Tikhonov regularization and some technical results to be used later on. The theoretical and computational aspects of GDP-FP are developed and discussed in Sect. 3. Section 4 starts with a review of the Golub-Kahan bidiagonalization (GKB) algorithm [4, 6], and proceeds with our specialized version of GDP-FP for large-scale problems. The proposed approach combines GKB with Tikhonov regularization in the generated Krylov subspace, where the regularization parameter for the projected problem is chosen by GDP-FP, following the ideas of the algorithm GKB-FP proposed in [4]. Again, the convergence properties of the proposed approach do not depend on user specified parameters. In Sect. 5 we provide numerical results that illustrate the effectiveness of our algorithm on test problems from the literature, including an inverse scattering problem. The paper ends with some concluding remarks.

2 Preliminaries

This section describes some technical results and the notation used throughout the paper. We start by noting that the regularized solution $f_\lambda$ can be equivalently defined as the solution of the linear least squares problem

$$\begin{aligned} \min _{f\in \mathbb {R}^n} \left\| \left( \begin{array}{c} \widetilde{A} \\ \lambda \, L \\ \end{array} \right) f - \left( \begin{array}{c} \widetilde{g} \\ 0 \\ \end{array}\right) \right\| _2. \end{aligned}$$

(7)

Hence it follows that the regularized solution $f_\lambda$ is unique when the coefficient matrix in (7) has full column rank, which means the null spaces ${\mathcal {N}}(\widetilde{A})$ and ${\mathcal {N}}(L)$ intersect trivially, i.e.,

$$\begin{aligned} {\mathcal {N}}(\widetilde{A})\cap {\mathcal {N}}(L) = \{ 0 \}, \end{aligned}$$

(8)

and the regularized solution $f_\lambda$ solves the normal equations for (7)

$$\begin{aligned} ({\widetilde{A}}^T\widetilde{A}+ \lambda ^2 L^T L) f = {\widetilde{A}}^T \widetilde{g}. \end{aligned}$$

(9)

To analyze properties of $f_\lambda$ and related quantities, we need to introduce the generalized singular value decomposition (GSVD) of the matrix pair $(\widetilde{A},L)$ [15]. For this, as usual, we assume that $L$ is $p\times n$, $\mathrm{rank}(L) = p\le n$, and that the pair $(\widetilde{A},L)$ have a GSVD

$$\begin{aligned} \widetilde{A} = U \left[ \begin{array} {cc} \Sigma &{}\quad 0 \\ 0 &{} \quad I_{n-p}\\ \end{array} \right] X^{-1}, \quad L = V\,[M;0]X^{-1}. \end{aligned}$$

(10)

Here both $U=[u_1,\ldots ,u_n]\in \mathbb {R}^{m\times n}$ and $V=[v_1,\ldots ,v_p]\in \mathbb {R}^{p\times p}$ have orthonormal columns, and $X\in \mathbb {R}^{n\times n}$ is nonsingular. Moreover, $\Sigma$ and $M$ are diagonal matrices defined by $\Sigma = \mathrm{diag}(\sigma _1,\ldots , \sigma _p)\;$, $M = \mathrm{diag}( \mu _1,\ldots ,\mu _p)$, whose entries are nonnegative and normalized such that

$$\begin{aligned} \sigma _i^2+\mu _i^2 = 1, \; \; i=1,\ldots , p. \end{aligned}$$

Then the generalized singular values of the matrix pair $(\widetilde{A}, L)$ are defined by

$$\begin{aligned} \gamma _i = \sigma _i/\mu _i, \; \; i =1,\ldots , p \end{aligned}$$

(11)

and we shall assume them to appear in nondecreasing order. With the GSVD at hand, the regularized solution can be expressed as

$$\begin{aligned} f_\lambda =\sum _{i=1}^p\frac{\gamma _i^2}{\gamma _i^2+\lambda ^2}\frac{u_i^T\widetilde{g}}{\sigma _i}\,x_i + \sum _{i=p+1}^n u_i^T\widetilde{g}\; x_i. \end{aligned}$$

(12)

Here $x_i$ denotes the $i$-th column of matrix $X$. Define also $\alpha _i = |u_i^T\widetilde{g}|^2$ (the squared Fourier coefficient of $\widetilde{g}$) and $\delta _0 = \Vert (I-UU^T)\widetilde{g}\Vert _2$ (the size of the incompatible component of $\widetilde{g}$ that lies outside the column space of $\widetilde{A}$). Further, let

$$\begin{aligned} \mathbf{y}(\lambda )&= \eta ^2(\lambda )\doteq \Vert L\,f_\lambda \Vert _2^2, \end{aligned}$$

(13)

$$\begin{aligned} \mathbf{x}(\lambda )&= \rho ^2(\lambda ) \doteq \Vert b-\widetilde{A}f_\lambda \Vert _2^2. \end{aligned}$$

(14)

In terms of the GSVD these functions reduce to

$$\begin{aligned} \mathbf{x}(\lambda ) = \displaystyle \sum _{i=1}^p \displaystyle \frac{\lambda ^4 \alpha _i}{(\gamma _i^2+\lambda ^2)^2}+\delta _0^2,\quad \mathbf{y}(\lambda ) = \displaystyle \sum _{i=1}^p \displaystyle \frac{\gamma _i^2 \alpha _i}{(\gamma _i^2+\lambda ^2)^2}. \end{aligned}$$

(15)

Hence, for $\lambda >0$, the derivatives with respect to $\lambda$ of ${ \mathbf x}(\lambda )$ and $\mathbf{y}(\lambda )$, respectively, become

$$\begin{aligned} \mathbf{x}'(\lambda ) = 4\lambda ^3\displaystyle \sum _{i=1}^p \displaystyle \frac{\gamma _i^2\alpha _i}{(\gamma _i^2+\lambda ^2)^3} > 0, \quad \mathbf{y}'(\lambda ) = -4\lambda \displaystyle \sum _{i=1}^p \displaystyle \frac{\gamma _i^2\alpha _i}{(\gamma _i^2+\lambda ^2)^3} < 0. \end{aligned}$$

(16)

Thus, the squared residual norm increases with $\lambda$ and the squared seminorm decreases. Additionally, we can exploit (16) to obtain

$$\begin{aligned} d\mathbf{y}/d\mathbf{x} = -1/\lambda ^2 \end{aligned}$$

(17)

which implies $\frac{d^2\mathbf{y}}{d\mathbf{x}^2}> 0$. So $\mathbf{y} = \mathbf{y}(\mathbf{x})$ (i.e., $\Vert Lf_\lambda \Vert _2^2$ as a function of $\Vert \widetilde{A}f_\lambda -\widetilde{g}\Vert _2^2$) is a monotonically decreasing convex function of $\mathbf{x}$. The following theorem shows that a similar result holds for the norms themselves.

Theorem 2.1

Let $f_\lambda$ denote the Tikhonov regularized solution of problem (3). Then $\Vert Lf_\lambda \Vert _2$ is a monotonically decreasing convex function of $\Vert \widetilde{A}f_\lambda -\widetilde{g} \Vert _2$. Moreover, the extreme residual norms (resp. extreme solution seminorms) corresponding to zero and infinite regularization satisfy the following properties

$$\begin{aligned} \delta _0 \le \Vert \widetilde{A}f_\lambda -\widetilde{g}\Vert \le \Vert \widetilde{g}\Vert _2, \qquad 0\le \Vert Lf_\lambda \Vert \le \Vert Lf_{_{\mathrm{LS}}}\Vert _2, \end{aligned}$$

(18)

with

$$\begin{aligned}&\lim _{\lambda \rightarrow 0}\Vert \widetilde{A}f_\lambda -\widetilde{g}\Vert = \delta _0,\quad \lim _{\lambda \rightarrow \infty }\Vert \widetilde{A}f_\lambda -\widetilde{g}\Vert = \Vert \widetilde{g}\Vert _2 \end{aligned}$$

(19)

$$\begin{aligned}&\lim _{\lambda \rightarrow 0}\Vert Lf_\lambda \Vert = \Vert Lf_{_{{LS}}}\Vert ,\quad \lim _{\lambda \rightarrow \infty }\Vert Lf_\lambda \Vert = 0 \end{aligned}$$

(20)

where $f_{_{\mathrm{LS}}}$ is the unregularized solution of (3).

Proof

See [15, Theorem 4.6.1].

Lemma 2.2

Let ${\Phi }(\lambda ) = \frac{\Vert \widetilde{A}f_\lambda -\widetilde{g}\Vert _2}{\Vert Lf_\lambda \Vert _2}.$ Then $\Phi$ is a monotonically nondecreasing function, and $\forall \lambda > 0$ we have

$$\begin{aligned} \Phi '(\lambda ) < 2\frac{\Phi (\lambda )}{\lambda }. \end{aligned}$$

(21)

Proof

To prove that ${\Phi }$ increases as $\lambda$ increases it suffices to use (16), (17) and the derivative of $\Phi$. For the second part, using the notation introduced in (13), (14) note that

$$\begin{aligned} \mathbf{x}'(\lambda ) = 2\rho (\lambda ) \rho '(\lambda ),\quad \mathrm{and},\quad \mathbf{y}'(\lambda ) = 2\eta (\lambda ) \eta '(\lambda ). \end{aligned}$$

This implies

$$\begin{aligned} \frac{d\mathbf{y}}{d\mathbf x} = \frac{1}{\Phi } \frac{d\eta }{d\rho } \Leftrightarrow \frac{d\eta }{d\rho } = -\frac{\Phi (\lambda )}{\lambda ^2}, \end{aligned}$$

where the last equality is because of (17). Taking derivative with respect to $\lambda$ on the right equality leads to

$$\begin{aligned} \frac{d^2\eta }{d\rho ^2}\rho '(\lambda ) = \frac{2\lambda \Phi (\lambda )-\lambda ^2 \Phi '(\lambda )}{\lambda ^4}. \end{aligned}$$

Now since $\rho '(\lambda )=\mathbf{x}'(\lambda )/\rho (\lambda )>0$ by (16), and since by Theorem 2.1, $\eta$ is a monotonically decreasing convex function of $\rho$, it follows that $\frac{d^2\eta }{d\rho ^2}\rho '(\lambda ) > 0$, and the the desired inequality follows. $\square$

3 Fixed-Point Approach for Computing the Tikhonov Regularization Parameter Chosen by GDP

As already commented, in the GDP errors $\delta _A$ and $\delta _g$ are taken into account and the regularization parameter is chosen as the unique solution of the nonlinear equation $G(\lambda ) = 0$. Existence and uniqueness of such solution can be explained by noting that $G$ is a monotonically increasing continuous function of $\lambda$, which is immediate to see since $G'(\lambda )> 0$ due to (16). From this observation it is clear that $G$ will have a unique root as long as

$$\begin{aligned} \lim _{\lambda \rightarrow 0^+} G(\lambda ) = \delta _0^2 - (\delta _g+\delta _A\Vert Lf_{_{{LS}}}\Vert _2)^2 <0,\quad \mathrm{and} \quad \lim _{\lambda \rightarrow \infty } G(\lambda )= \Vert \widetilde{g}\Vert _2^2-\delta _g^2>0, \end{aligned}$$

where the limit values are because of (19), (20) in Theorem 2.1. Consequently, the discrepancy equation $G(\lambda ) = 0$ will have a unique solution as long as the noise $\delta _g$ and $\delta _A$ satisfy

$$\begin{aligned} \delta _0 -\delta _A\Vert L f_{_{{LS}}}\Vert _2 <\delta _g <\Vert \widetilde{g}\Vert _2. \end{aligned}$$

(22)

If the noisy matrix $\widetilde{A}$ is nonsingular, as seen frequently when the noise is random, then $\delta _0=0$ and hence the left inequality is satisfied automatically. When $\widetilde{A}$ is singular, a reasonable condition that ensures the left inequality is $\delta _0<\delta _g$. As for the right inequality, it holds true when the amount of noise in $g$ satisfies $\delta _g\ll \Vert g\Vert _2$.

Having explained the issue of existence and uniqueness of the regularization parameter chosen by GDP, we shall now concentrate on the algorithmic aspects of methods for its computation. The special case $\delta _A = 0$ has been extensively studied by several authors and often treated with Newton’s method. An implementation of the Discrepancy principle for this very especial case is available as the Matlab function discrep in Regularization Tools by Hansen [14]. For the general case the situation is quite different. The only algorithms we are aware of are the Newton-based algorithms by Lu et al. [21] developed in a Hilbert space setting. The convergence and performance of these algorithms depend on user specified parameters.

In the following, we will develop a globally convergent algorithm for solving the discrepancy equation, with convergence properties that do not depend on any extra parameter. We will show, by means of numerical experiments, that this algorithm is capable of capturing the solution of the discrepancy equation very quickly.

We start with the following technical result.

Lemma 3.1

For $\lambda >0$ let $\vartheta (\lambda ) = \frac{\Vert \widetilde{A}f_\lambda -\widetilde{g}\Vert _2}{\delta _g+\delta _A\Vert Lf_\lambda \Vert _2}$ and $\xi (\lambda ) = \frac{\lambda ^2}{\vartheta (\lambda )}$. Then both $\vartheta (\lambda )$ and $\xi (\lambda )$ are monotonically increasing functions of $\lambda$. Moreover, the following properties hold

$$\begin{aligned} \lim _{\lambda \rightarrow 0^+}\xi (\lambda ) = \left\{ \begin{array}{ll} 0&{}\quad \mathrm{if} \;\; \delta _0 \ne 0,\\ C>0&{}\quad \mathrm{if}\;\; \delta _0 = 0\\ \end{array}\right. \end{aligned}$$

(23)

for some constant $C$.

Proof

The proof that $\vartheta$ increases as $\lambda$ increases is analogous to the proof what $\Phi$ is increasing, see Lemma 2.2. Therefore we will prove the assertion for function $\xi$ only. In fact, differentiation of $\xi (\lambda )\vartheta (\lambda ) = \lambda ^2$ with respect to $\lambda$ yields

$$\begin{aligned} \xi (\lambda )\vartheta '(\lambda )+\xi '(\lambda )\vartheta (\lambda ) = 2\lambda . \end{aligned}$$

Hence

$$\begin{aligned} \xi '(\lambda ) \vartheta (\lambda ) = \frac{2\lambda \vartheta (\lambda )- \lambda ^2\vartheta '(\lambda )}{\vartheta (\lambda )}. \end{aligned}$$

(24)

Further, since $\vartheta (\lambda )= c(\lambda )\Phi (\lambda )$ with $c(\lambda )=\frac{\eta (\lambda )}{\delta _b+\delta _A\,\eta (\lambda )}$, and $-\frac{\vartheta (\lambda )}{\lambda ^2}= c(\lambda ) \left( -\frac{\Phi (\lambda )}{\lambda ^2}\right) ,$ taking derivative with respect to $\lambda$ in this last equality we have

$$\begin{aligned} \frac{2\lambda {\vartheta }(\lambda )-\lambda ^2{\vartheta }'(\lambda )}{\lambda ^4}= c(\lambda )\left( \frac{2\lambda \Phi (\lambda )-\lambda ^2 \Phi '(\lambda )}{\lambda ^4}\right) -\left( \frac{\Phi (\lambda )}{\lambda ^2}\right) c'(\lambda ). \end{aligned}$$

(25)

Since $c'(\lambda )< 0$, which follows from the definition of $c$, and since $2\lambda \Phi (\lambda )-\lambda ^2\Phi '(\lambda )>0$ by Lemma 2.2, using these inequalities in (25) we obtain $\xi '(\lambda )>0$, which proves that $\xi$ is increasing.

The limit values in (23) are immediate consequences of (15) together with (19), (20). This concludes the proof. $\square$

We are in a position to describe the main results of this section.

Theorem 3.2

Let $\vartheta$ and $\xi$ be the functions defined in Lemma 3.1 and let $\zeta (\lambda ) = \sqrt{\xi (\lambda )}$. Assume that (22) holds true. Then the following properties hold

• (a) The parameter chosen by GDP, $\lambda _{_{\mathrm{GDP}}},$ is the unique solution of the nonlinear equation $\vartheta (\lambda ) = 1$.

• (b) $\zeta$ is a monotonically increasing function having a unique nonzero fixed-point at $\lambda = \lambda _{_{\mathrm{GDP}}}$ such that $\zeta (\lambda )\ge \lambda$ if $0<\lambda \le \lambda _{_{\mathrm{GDP}}}$, and $\zeta (\lambda )\le \lambda$ if $\lambda \ge \lambda _{_{\mathrm{GDP}}}$. Additionally,

  $$\begin{aligned} \lambda _{_{\mathrm{GDP}}}\le \gamma _1\sqrt{\frac{ \delta _b}{\rho (\gamma _1)} +\frac{\delta _A}{\gamma _1}} \end{aligned}$$

  (26)

  as long as $\delta _g\gamma _1+\delta _A\rho (\gamma _1)\le \rho (\gamma _1)\gamma _1$.

• (c) For given $\lambda _0>0$ consider the sequence $\{\lambda _j\}$ defined by

  $$\begin{aligned} \lambda _{j+1} = \zeta (\lambda _j), \; j\ge 0. \end{aligned}$$

  (27)

  Then $\displaystyle \lim _{j\rightarrow \infty } \lambda _j = \lambda _{_{\mathrm{GDP}}}$ irrespective of the initial guess chosen.

Proof

The equation $\vartheta (\lambda ) = 1$ comes as another way of writing (5) and item (a) holds true because $\vartheta (\lambda )$ is a monotonically increasing function by Lemma 3.1.

We start the proof of item (b) with the observation that $\zeta$ increases monotonically because of its definition and Lemma 3.1. Now since $\lambda _{_{\mathrm{GDP}}}$ is a solution of $\vartheta (\lambda ) = 1$, then

$$\begin{aligned} \zeta (\lambda _{_{\mathrm{GDP}}}) = \frac{\lambda _{_{\mathrm{GDP}}}}{ \sqrt{\vartheta ( \lambda _{_{\mathrm{GDP}}})}} = \lambda _{_{\mathrm{GDP}}}, \end{aligned}$$

and thus $\lambda _{_{\mathrm{GDP}}}$ is a fixed-point of $\zeta$. Conversely, if $\lambda ^*$ is a fixed-point of $\zeta$, which means $\zeta (\lambda ^*)=\lambda ^*$, then it follows that $\vartheta (\lambda ^*) = 1$ and, due to item (a), we obtain $\lambda ^*= \lambda _{_{\mathrm{GDP}}}$. This implies that $\zeta$ has a unique nonzero fixed-point at $\lambda =\lambda _{_{\mathrm{GDP}}}.$

We now proceed with the observation that $\zeta '(\lambda _{_{\mathrm{GDP}}})<1.$ We shall prove this by contradiction. In fact, assume $\zeta '(\lambda _{_{\mathrm{GDP}}})\ge 1.$ Then since $\vartheta ( \lambda _{_{\mathrm{GDP}}}) = 1$ by item ($a$) and since

$$\begin{aligned} \zeta '(\lambda ) = (\vartheta (\lambda ))^{-1/2}-\frac{\lambda }{2} \vartheta '(\lambda )(\vartheta (\lambda ))^{-3/2}, \end{aligned}$$

(28)

taking $\lambda = \lambda _{_{\mathrm{GDP}}}$ we obtain

$$\begin{aligned} 1\le \zeta '(\lambda _{_{\mathrm{GDP}}}) = 1 - \frac{\lambda _{_{\mathrm{GDP}}}}{2}\vartheta '( \lambda _{_{\mathrm{GDP}}}), \end{aligned}$$

or equivalently $\vartheta '(\lambda _{_{\mathrm{GDP}}})\le 0$, which is a contradiction as $\vartheta$ is increasing. Therefore we must have $\zeta '(\lambda _{_{\mathrm{GDP}}})<1$. Using this property, the monotonicity of $\zeta$ and the fact $\zeta$ has a unique nonzero fixed-point, we conclude that $\zeta (\lambda )\ge \lambda$ if $0<\lambda \le \lambda _{_{\mathrm{GDP}}}$ and $\zeta (\lambda )\le \lambda$ if $\lambda \ge \lambda _{_{\mathrm{GDP}}}$.

To prove the last part of item (b) we use the monotonicity of $\vartheta$ and Theorem 2.1 and deduce that for all $\lambda > 0$

$$\begin{aligned} \zeta (\lambda ) \ge \lambda \sqrt{\frac{\delta _b}{\Vert \widetilde{g}\Vert _2} }. \end{aligned}$$

(29)

We now recall from [2, Lemma1] that for $\lambda \ge \gamma _1$ we have $\rho (\lambda )/\eta (\lambda )\ge \lambda$. Thus, for $\lambda \ge \gamma _1$ we have

$$\begin{aligned} \frac{1}{\vartheta (\lambda )} = \frac{\delta _b +\delta _A\eta (\lambda )}{\rho (\lambda )} \le \frac{\delta _b}{\rho (\lambda )}+\frac{\delta _A}{\lambda } \le \frac{\delta _b}{\rho (\gamma _1)}+\frac{\delta _A}{\gamma _1},\end{aligned}$$

(30)

where the last inequality is because $\rho$ is increasing, see (17). Combination of (29) and (30) shows that for $\lambda \ge \gamma _1$ we have

$$\begin{aligned} \sqrt{\frac{\delta _b}{\Vert \widetilde{g}\Vert _2} } \,\lambda \le \zeta (\lambda ) \le \sqrt{ \frac{\delta _b}{\rho (\gamma _1)}+\frac{\delta _A}{\gamma _1}} \,\lambda . \end{aligned}$$

(31)

We now use the assumption $\delta _g\gamma _1+\delta _A\rho (\gamma _1)\le \rho (\gamma _1)\gamma _1$ and deduce that the slope of the upper bound in (31) is not larger than 1. This proves inequality (26) and ends the proof of item b).

Finally, since $\zeta$ is also an increasing function it follows that $\{\lambda _k\}$ will be either an increasing sequence if $\lambda _0< \lambda _{_{\mathrm{GDP}}}$ or a decreasing sequence if $\lambda _0> \lambda _{_{\mathrm{GDP}}}$. This concludes the proof. $\square$

From Theorem 3.2 we conclude that the regularization parameter chosen by GDP can be determined by a monotonically and globally convergent fixed-point iteration procedure as defined in (27). We will refer to this algorithm as GDP-FP. Moreover, from the nearly linear behavior of $\zeta$ for $\lambda \ge \gamma _1$ and the small slope of the bounds as described in (31), we deduce that the sequence (27) can converge rapidly when the iterative procedure is initialized either with $\lambda _0\approx \gamma _1$ or with $\lambda _0$ chosen as the a priori upper bound (26), the latter option being valid for relatively low noise levels. Finally, we note that if $\delta _g= 0$

$$\begin{aligned} \lambda _{_{\mathrm{GDP}}}\le \sqrt{\gamma _1}\sqrt{\delta _A}, \end{aligned}$$

(32)

while if $\delta _A= 0$, the upper bound (26) reduces to

$$\begin{aligned} \lambda _{_{\mathrm{GDP}}}\le \gamma _1\sqrt{\frac{\delta _g}{\rho (\gamma _1)}}, \end{aligned}$$

(33)

which is closely related to one given by Vinokurov [31].

The statements of Theorem 3.2 as well as the comments above are illustrated in Fig. 1.

Fig. 1

Functions $\vartheta$ and $\zeta$ (left) and behavior of sequence $\{\lambda _k\}$ for $\lambda _0 > \lambda _{_{\mathrm{GDP}}}$ (right) with the choice $\lambda _0 = \gamma _1$. This example corresponds to deriv2 test problem from [14] with $n =512$. To simulate noise we take $\widetilde{g}= g +e$ and $\widetilde{A} = A+ E$, were $e$ is Gaussian random vector such that $\Vert e\Vert _2/\Vert g\Vert _2 = 0.01$, and $E$ is a Gaussian random matrix such that $\Vert E\Vert _2/\Vert A\Vert _2 = 0.01$

We close the section with a description of our fixed-point algorithm for determining the regularization parameter $\lambda _{_{\mathrm{GDP}}}$ and the corresponding regularized solution $f_{\lambda _{_{\mathrm{GDP}}}}$

The computation of the GSVD of the matrix pair $(A,L)$ is quite expensive and for this reason, the GSVD is of interest only for small to medium-sized problems. For large-scale problems, we will see in the next section that projection methods are reliable options.

4 Projection Approach for Large-Scale Problems

In this section we show how to construct regularized solutions $f_\lambda$ for the case where the dimensions of $\widetilde{A}$ and $L$ are such that the computation of the GSVD of the matrix pair $(\widetilde{A},L)$ is infeasible or unattractive. The idea here is to construct approximate solutions to $f_{\lambda _{_{\mathrm{GDP}}}}$ by “projecting” the large-scale problem onto a subspace of small dimension. More precisely, let $\{{\mathcal {V}}_k\}$, $k\ge 1$, be an appropriate nested family of $k$-dimensional subspaces in $\mathbb {R}^n$. Then the idea is to determine approximations $f_\lambda ^{(k)}\in {\mathcal {V}}_k$ to $f_\lambda$ by solving the constrained Tikhonov problem

$$\begin{aligned} f_\lambda ^{(k)} = {\mathop {\mathrm{argmin}}\limits _{f\in {\mathcal {V}}_k}}\Vert \widetilde{A} f-\widetilde{g}\Vert _2^2 + \lambda ^2\Vert Lf\Vert _2^2 \end{aligned}$$

(34)

where the regularization parameter is chosen in a proper way. Problem (34) is often referred to as the projected problem and methods which use $f_\lambda ^{(k)}$ as approximations to $f_\lambda$ are referred to as projection methods. For the moment, we assume that the Tikhonov problem is in standard form and we will concentrate on a projection method based on the Golub-Kahan bidiagonalization (GKB) algorithm [6] where the regularization parameter for the projected problem is chosen by GDP. A projection approach for Tikhonov regularization in general form will be addressed at the end of the section.

4.1 Review of GKB and LSQR

Application of $k<n$ GKB steps to $\widetilde{A}$ with initial vector $\widetilde{g}/\Vert \widetilde{g}\Vert _2$ yields three matrices: a lower bidiagonal matrix $B_k\in \mathbb {R}^{(k+1)\times k}$ and two matrices $U_{k+1}\in \mathbb {R}^{m\times (k+1)}$ and $V_k \in \mathbb {R}^{n\times k}$ with orthonormal columns, such that

$$\begin{aligned} \beta _1U_{k+1}e_1 = \widetilde{g}&= \beta _1u_1, \end{aligned}$$

(35)

$$\begin{aligned} \widetilde{A}V_k&= U_{k+1}B_k, \end{aligned}$$

(36)

$$\begin{aligned} {\widetilde{A}}^TU_{k+1}&= V_kB_k^T + \alpha _{k+1}v_{k+1}e_{k+1}^T, \end{aligned}$$

(37)

where $e_k$ denotes the $k$-th unit vector in $\mathbb {R}^{k+1}$. The columns of $V_k$ provide an orthonormal basis for the generated Krylov subspace ${\mathcal {K}}_k({\widetilde{A}}^T \widetilde{A},\widetilde{A}^T\widetilde{g}\}$, an excellent choice for use when solving ill-posed problems [6, 7, 14]. GKB iterations constitute the basis for the LSQR method [24, 25]. LSQR is designed to construct approximate solutions to the least squares problem (4) defined by $f^{(k)}= V_ky^{(k)}$, where $y^{(k)}$ solves the projected least squares problem

$$\begin{aligned} \min _{y\in \mathbb {R}^{k}} \Vert B_ky-\beta _1e_1\Vert _2. \end{aligned}$$

(38)

In practical computations $f^{(k)}$ is computed via a QR factorization of $B_k$ which allows for an efficient updating of the LSQR iterates; the reader is referred to [24] for details. LSQR is also well suited for solving the “damped least squares problem” [24]

$$\begin{aligned} f_\lambda = \arg \min _{f\in \mathbb {R}^n}\left\| \left( \begin{array}{c} \widetilde{g} \\ 0 \\ \end{array} \right) - \left( \begin{array}{c} \widetilde{A} \\ \lambda I_n \\ \end{array} \right) f \right\| _2, \end{aligned}$$

(39)

where $\lambda$ is a fixed regularization parameter. In this case, the $k$th approximate solution is taken to be

$$\begin{aligned} f^{(k)}_\lambda = V_ky^{(k)}_\lambda , \end{aligned}$$

(40)

where $y^{(k)}_\lambda$ solves the regularized projected problem

$$\begin{aligned} y^{(k)}_\lambda = \arg \min _{y\in \mathbb {R}^k}\left\| \left( \begin{array}{c} \beta _1e_1 \\ 0 \\ \end{array} \right) - \left( \begin{array}{c} B_k \\ \lambda I_k \\ \end{array} \right) y \right\| _2 \end{aligned}$$

(41)

which can be handled efficiently using the QR factorization of $\left( \begin{array}{c} B_k\\ \lambda I_k\\ \end{array} \right) .$ As for $f_\lambda ^{(k)}$, it can be computed using (40). Alternatively, as shown by Paige and Saunders [24], for fixed $\lambda$ the regularized solution $f_\lambda ^{(k)}$ can be computed through an updating formula which does not require any storage of $V_k$. Note that due to (35) and (36), the residual vector $r_\lambda ^{(k)}=\widetilde{g}-\widetilde{A}f_\lambda ^{(k)}$ and the regularized solution $f_\lambda ^{(k)}$ satisfy

$$\begin{aligned} \Vert r_\lambda ^{(k)}\Vert&= \Vert U_{k+1}^T(\beta _1e_1-B_ky_\lambda ^{(k)})\Vert = \Vert \beta _1e_1-B_ky_\lambda ^{(k)}\Vert ,\end{aligned}$$

(42)

$$\begin{aligned} \Vert f_\lambda ^{(k)}\Vert&= \Vert y_\lambda ^{(k)}\Vert . \end{aligned}$$

(43)

In addition, if we let the singular value decomposition of $B_k$ be

$$\begin{aligned} B_k = P_k\left( \begin{array}{c} \Sigma _k\\ 0 \\ \end{array} \right) Q_k^T = \sum _{i=1}^k\sigma _i^{(k)}p_iq_i^T, \end{aligned}$$

(44)

where $P_k\in \mathbb {R}^{(k+1)\times (k+1)}$ and $Q_k\in \mathbb {R}^{k\times k}$ are orthogonal, and $\Sigma _k = \mathrm{diag}(\sigma _1^{(k)},\ldots ,\sigma _k^{(k)})$ with $\sigma _1^{(k)}\ge \sigma _2^{(k)}\ge \cdots \ge \sigma _k^{(k)}>0.$ Then it is immediate to check that

$$\begin{aligned} \Vert y_\lambda ^{(k)}\Vert _2^2 = \beta _1^2\sum _{i=1}^k\frac{[\sigma _i^{(k)}]^2 \xi _{1i}^2}{([\sigma _i^{(k)}]^2+\lambda ^2)^2},\qquad \Vert r_\lambda ^{(k)}\Vert _2^2 = \beta _1^2\sum _{i=1}^k\frac{\lambda ^4\xi _{1i}^2}{([\sigma _i^{(k)}]^2+\lambda ^2)^2} + {\delta _0^{(k)}}^2 \end{aligned}$$

(45)

where $\xi _{1i}$ denotes the $i$-th component of the first row of matrix $P_k$, and $\delta _0^{(k)}$ is the 2-norm of the incompatible part of $\beta _1 e_1$ that lies outside ${\mathcal {R}}(B_k)$. Moreover, analogous to the squared residual norm $\mathbf{x}(\lambda )$ and the squared solution norm $\mathbf{y}(\lambda )$, $\Vert r_\lambda ^{(k)}\Vert _2^2$ is a monotonically increasing function and $\Vert y_\lambda ^{(k)}\Vert _2^2$ is a monotonically decreasing function.

The following technical result will be used in the sequel.

Theorem 4.1

For fixed $\lambda >0$ the norm of the solution $f_\lambda ^{(k)}$ and corresponding norm of the residual vector $r_\lambda ^{(k)}$ satisfy

$$\begin{aligned} \Vert f_\lambda ^{(k+1)}\Vert \ge \Vert f_\lambda ^{(k)}\Vert , \qquad \Vert r_\lambda ^{(k+1)}\Vert \le \Vert r_\lambda ^{(k)}\Vert , \quad k=0,\ldots , n-1. \end{aligned}$$

(46)

Proof

See [4, Theorem 2.1].

4.2 Proposed Method

In order to introduce our projection method we shall assume that the GKB procedure is used to compute the approximate solutions $f_\lambda ^{(k)}$ and the corresponding residuals $r_\lambda ^{(k)}$. Based on these functions let us consider the finite sequence of functions $\vartheta ^{(k)}:\mathbb {R}^{+}\rightarrow \mathbb {R}$, $k=1,\ldots ,n$, defined by

$$\begin{aligned} \vartheta ^{(k)}(\lambda ) = \frac{\rho ^{(k)}(\lambda )}{ \delta _g+\delta _A\eta ^{(k)}(\lambda )}, \end{aligned}$$

(47)

where $\rho ^{(k)}(\lambda ) = \Vert r^{(k)}_\lambda \Vert _2,$ and $\eta ^{(k)}(\lambda ) = \Vert y_\lambda ^{(k)} \Vert _2$, and the finite sequence of functions $\zeta ^{(k)}:\mathbb {R}^{+}\rightarrow \mathbb {R}$, $k=1,\ldots ,n$, defined by

$$\begin{aligned} \zeta ^{(k)}(\lambda ) = \frac{\lambda }{\sqrt{\vartheta ^{(k)}(\lambda )}}. \end{aligned}$$

(48)

Since $\rho ^{(k)}$ and $\eta ^{(k)}$ are monotonic, some calculations show that ${\vartheta ^{(k)}}'(\lambda )>0$ and ${\zeta ^{(k)}}'(\lambda )>0$. Therefore, both ${\vartheta ^{(k)}}$ and ${\zeta ^{(k)}}$ are monotonically increasing functions. Our projected method relies on the fact that we can construct a sequence of fixed-points ${\lambda ^{(k)}}^*$ of $\zeta ^{(k)}$ which approximates $\lambda _{_{\mathrm{GDP}}}$ as $k$ increases. For this, due to the monotonicity of $\vartheta ^{(k)}$ and $\zeta ^{(k)}$ it is clear that ${\lambda ^{(k)}}^*$ is a fixed-point of $\zeta ^{(k)}$ if and only if ${\lambda ^{(k)}}^*$ is the unique solution of the “projected discrepancy equation” ${\vartheta ^{(k)}}(\lambda )=1$.

The following theorem describes how the sequence $\zeta ^{(k)}$ relates to the function $\zeta$ of the original and large-scale problem and shows that $\zeta ^{(k)}$ always has a unique nonzero fixed-point.

Theorem 4.2

Assume that exact arithmetic is used and that the GKB procedure runs $n$ steps without interruption. Then for all $\lambda >0$ it holds

$$\begin{aligned} \zeta ^{(k+1)}(\lambda )\ge \zeta ^{(k)}(\lambda ),\; \; k=1, \ldots , n-1. \end{aligned}$$

(49)

Consequently, $\zeta (\lambda )\ge \zeta ^{(k)}(\lambda )$ for $k =1, \ldots ,n.$ Additionally, if the condition (22) is satisfied, then $\zeta ^{(k)}$ always has a unique nonzero fixed-point that is the unique solution of the nonlinear equation (6).

Proof

The first inequality is straightforward from Theorem 3.2. The second inequality follows upon taking $k = n-1$ in (49). To prove the last assertion we shall analyze the sign of the function $h^{(k)}(\lambda ) = \zeta ^{(k)}(\lambda )- \lambda$ for $\lambda >0$. In fact, if (22) is satisfied, then $\lambda _{_{\mathrm{GDP}}}$ is a nonzero fixed-point of $\zeta$ due to Theorem (3.2), and thus we must have $\zeta ^{(k)}(\lambda )< \lambda$ when $\lambda > \lambda _{_{\mathrm{GDP}}}$ as we have seen that $\zeta (\lambda )\ge \zeta ^{(k)}(\lambda )$ for $\lambda >0$. Therefore, for $\lambda > \lambda _{_{\mathrm{GDP}}}$ we have

$$\begin{aligned} h^{(k)}(\lambda ) <0. \end{aligned}$$

(50)

Now notice that the behavior of $h$ near the origin depends on the constant $\delta _0^{(k)}\ne 0$, see (45) and (48). Notice also that by Lemma 3.1 we have $\lim _{\lambda \rightarrow 0^+} h^{(k)}(\lambda ) = 0$ if $\delta _0^{(k)}\ne 0$ and $\lim _{\lambda \rightarrow 0^+} h^{(k)}(\lambda ) > 0$ if $\delta _0^{(k)}= 0$. This tells us that only the case $\delta _0^{(k)}\ne 0$ must be considered when analyzing the function $h^{(k)}$ for $\lambda$ near zero and that this analysis requires information about the derivative of $h$. We then use (28) and obtain

$$\begin{aligned} {h^{(k)}}^\prime (0) = {\zeta ^{(k)}}'(0) -1= \sqrt{\frac{\delta _g+\delta _A\Vert f_\lambda ^{(k)}\Vert _2}{\delta _0^{(k)}}} -1> 0, \end{aligned}$$

(51)

the inequality being valid as $\delta _0^{(k)}\le \delta _g$. But this implies that ${\zeta ^{(k)}}'(0) > 1$. This inequality implies that there must be an open interval, say $I= (0,\overline{\lambda })\subset (0,\lambda _{_{\mathrm{GDP}}})$, such that $\zeta ^{(k)}(\lambda )>\lambda$ for all $\lambda \in I$, and thus we must have

$$\begin{aligned} h^{(k)}(\lambda ) >0 \quad \forall \lambda \in I. \end{aligned}$$

(52)

We now use (50)–(52) and conclude that $h^{(k)}$ has a root ${\lambda ^{(k)}}^*$, or equivalently that ${\lambda ^{(k)}}^*$ is a nonzero fixed-point of $\zeta ^{(k)}$. Uniqueness of ${\lambda ^{(k)}}^*$ follows from the monotonicity properties of $\zeta ^{(k)}$ and $\vartheta ^{(k)}$, and this concludes the proof. $\square$

To better explain the relevance of Theorem 4.2, it is instructive to note that as the GKB algorithm proceeds, more and more information associated with the largest singular values of $\widetilde{A}$ is captured [6, 15]. As a consequence, the sequence $\zeta ^{(k)}(\lambda )$ will quickly capture the information of $\zeta (\lambda )$ for a range of values of $\lambda$ inside the part of the singular values of $A$ that is captured by the GKB procedure in $k$ steps. This is illustrated in Fig. 2 where are depicted some functions $\zeta ^{(k)}$ as well as its limit value $\zeta (\lambda )$ for the deriv2 test problem. Notice that in a wide range of $\lambda$ values which include the parameter $\lambda _{_{\mathrm{GDP}}}$, the functions $\zeta ^{(k)}$ remain remarkably close to $\zeta$ even for small $k$.

Fig. 2

Functions $\zeta$ and $\zeta ^{(k)}$ for some values of $k$. This example corresponds to deriv2 test problem from [14] with the same data as in Fig. 1

Now for given $k\ge 1$ and arbitrarily chosen initial guess $\lambda _0^{(k)}>0$, consider the sequence $\{\lambda _j^{(k)}\}$ defined by

$$\begin{aligned} \lambda _{j+1}^{(k)} = \zeta ^{(k)}(\lambda ^{(k)}_{j}), \end{aligned}$$

(53)

and assume it converges to a fixed-point ${\lambda ^{(k)}}^*$ of $\zeta ^{(k)}$; when this is true we prove that the sequence ${\lambda ^{(k)}}^{*}$ converges to $\lambda _{_{\mathrm{GDP}}}$ from below in at most $n$ GKB steps. This is the subject of the following theorem.

Theorem 4.3

Under the hypotheses of Theorem 4.2, for $k\ge 1$ let ${\lambda ^{(k)}}^*$ be the unique nonzero fixed-point of $\zeta ^{(k)}$. Then the sequence of fixed-points $\{{\lambda ^{(k)}}^*\}_k$ is nondecreasing and ${\lambda ^{(k)}}^*$ converges to $\lambda _{_{\mathrm{GDP}}}$ in at most $n$ GKB steps.

Proof

Let ${\lambda ^{(k)}}^*$ be a fixed-point of $\zeta ^{(k)}(\lambda )$. Due to Theorem 4.2 we have

$$\begin{aligned} \zeta ^{(k+1)}({\lambda ^{(k)}}^*) \ge \zeta ^{(k)}({\lambda ^{(k)}}^*) = {\lambda ^{(k)}}^*. \end{aligned}$$

(54)

If ${\lambda ^{(k)}}^*$ is also a fixed-point of $\zeta ^{(k+1)}$ there is nothing to prove. Assume then that $\zeta ^{(k+1)}({\lambda ^{(k)}}^*)>{\lambda ^{(k)}}^*$ and consider the sequence $\lambda _{j+1} = \zeta ^{(k+1)}(\lambda _j)$, $\; j\ge 0$, with starting value $\lambda _0 = {\lambda ^{(k)}}^*.$ Based on the fact that $\zeta ^{(k+1)}$ increases as $\lambda$ increases, it follows that $\lambda _j$ forms a nondecreasing sequence, and therefore $\{\lambda _j\}$ converges to a fixed-point of $\zeta ^{(k+1)}$, i.e.,

$$\begin{aligned} \lim _{j\rightarrow \infty } \lambda _j = {\lambda ^{(k+1)}}^*= \zeta ( {\lambda ^{(k+1)}}^*) \end{aligned}$$

with ${\lambda ^{(k+1)}}^*\ge {\lambda ^{(k)}}^*$. Now since after $n$ GKB steps the Krylov space equals $\mathbb {R}^n$, it follows that $\zeta ^{(n)}$ equals $\zeta$ and so $\{{\lambda ^{(k)}}^*\}$ must converge to $\lambda _{_{\mathrm{GDP}}}$ in at most $n$ GKB steps, and the proof concludes. $\square$

The main consequence of Theorem 4.3 is that we can construct approximations to $\lambda _{_{\mathrm{GDP}}}$ using a nondecreasing finite sequence of fixed-points $\lambda ^{(k)*}$ of $\zeta ^{(k)}$, which as illustrated above can converge very quickly due to the approximation properties of the Krylov subspace generated by the GKB procedure. From the practical point of view, this gives rise to an algorithm for computing $\lambda _{_{\mathrm{GDP}}}$ and the corresponding regularized solution which we will refer to as PGDP-FP. The main steps of PGDP-FP can be summarized as follows:

We will refer to each GKB iteration as an outer iteration and to iterations during fixed computations for each $k$ as inner iterations. For practical purposes, we note that computing fixed-points for each $k$ requires solving the projected problem (41) for several values of $\lambda$ and for increasing values of $k$. This can be done following the ideas of the LSQR algorithm at a cost of approximately ${\mathcal {O}}(k)$ arithmetic operations [10, 25]. Moreover, since very often a fairly small number of steps is required for convergence, the overall cost of PGDP-FP is dominated by $k$ matrix-vector products with $\widetilde{A}$ and $\widetilde{A}^T$ for some moderate number $k$. In addition, to introduce savings for the algorithm to be efficient and competitive, the fixed-point $\lambda ^{(k)*}$ at stage $k$ can be used as initial guess for computing the fixed-point at stage $(k$+1) since, as demonstrated before, the sequence of fixed-points ${\lambda ^{(k)}}^*$ is nondecreasing. Taking into account the monotonicity of ${\lambda ^{(k)}}^*$, we choose to stop the outer iterations when the relative change of consecutive fixed-points,

$$\begin{aligned} \left| {\lambda ^{(k+1)}}^*-{\lambda ^{(k)}}^*\right| < \epsilon {\lambda ^{(k)}}^*, \end{aligned}$$

(55)

is sufficiently small, where $\epsilon$ is a tolerance parameter.

4.3 Extension to General Form Tikhonov Regularization

For some problems, standard-form Tikhonov regularization does not produce suitable regularized solutions and it is convenient to consider instead general-form Tikhonov regularized solutions. The purpose of this subsection is to briefly describe two approaches to extend GDP-FP to general-form Tikhonov regularization: one approach which implicitly transforms the general-form Tikhonov problem (3) into a related problem in standard form, and another approach where such transformation is not necessary.

For the first approach, note that the Tikhonov problem (3) can always be transformed into a Tikhonov problem in standard form [10]

$$\begin{aligned} \overline{f}_\lambda = {\mathop {\mathrm{argmin}}\limits _{\overline{f}\in \mathbb {R}^n}}\Vert \overline{A}\, \overline{f}- \overline{g}\Vert _2^2 + \lambda ^2\Vert \overline{f}\Vert _2^2. \end{aligned}$$

(56)

For the case where $L$ is invertible the standard-form transformation becomes $\overline{A} = \widetilde{A} L^{-1},$ $\overline{g} = {\widetilde{g}}$, and the back-transformation is $f_\lambda = L^{-1}\overline{f}_\lambda .$

When $L$ is not invertible the transformation takes the form

$$\begin{aligned} f_{\lambda } = L_{\widetilde{A}}^\dag \overline{f}_\lambda + f_N,\quad \overline{A} = \widetilde{A}L_{\widetilde{A}}^\dagger , \quad \overline{g} = \widetilde{g}-\widetilde{A}f_N, \end{aligned}$$

(57)

where $f_N$ lies in the null space of $L$ and

$$\begin{aligned} L_{\widetilde{A}}^\dagger = \left( I_n - \left( \widetilde{A}\left( I_n - L^\dagger L\right) \right) ^\dagger \widetilde{A} \right) L^\dagger , \end{aligned}$$

is the $\widetilde{A}$-weighted generalized inverse of $L$. If we know a full rank matrix $W$ whose columns span the null space ${\mathcal {N}}(L)$, then $f_N = W\left( \widetilde{A}W\right) ^\dagger \widetilde{g},$ and the $\widetilde{A}$-weighted generalized inverse of $L$ reduces to $L_{\widetilde{A}}^\dagger = \left( I_n-W\left( \widetilde{A}\,W\right) ^\dagger \widetilde{A}\right) L^\dagger$.

Therefore our first extension of GDP-FP to large-scale general-form Tikhonov regularization is to apply PGDP-FP to the transformed problem (56) assuming that the transformed matrix $\overline{A}$ is never explicitly formed. Once $\overline{f}_\lambda$ is determined, the regularized solution $f_\lambda$ is computed by using the back-transformation (57). This approach is well suited when the matrix-vector products with $\overline{A}$ and ${\overline{A}}^T$ are performed efficiently. That is, this approach works well when the computation of matrix-vector products with $L_{\widetilde{A}}^\dag$ is feasible and performed efficiently, as often occurs in applications involving sparse regularization matrices e.g., banded regularization matrices with small bandwidth and regularization matrices defined via Kronecker products, among others. For examples and situations where the transformation to standard form is feasible, the reader is referred to [5, 26].

Our second approach considers the case where $L$ is a regularization matrix such that the computation of matrix-vector products with $L_{\widetilde{A}}^\dag$ is infeasible or unattractive. We follow an approach suggested by Hochstenbach and Reichel [16] recently exploited in connection with an extension of GKB-FP, an algorithm for large-scale general-form Tiknonov problems discussed in [5]. The main idea here is to determine regularized solutions as defined in (34) where the subspace ${\mathcal {V}}_k$ is chosen as the Krylov subspace ${\mathcal {K}}_k({\widetilde{A}}^T{\widetilde{A}}, {\widetilde{A}}^T\widetilde{g})$ generated by GKB and the regularization parameter is chosen by GDP. In other words, we apply the GKB procedure to $\widetilde{A}$, which produces the partial decomposition (35)–(37), and compute regularized solutions as

$$\begin{aligned} f_\lambda ^{(k)} = V_k y_\lambda ^{(k)},\quad y_\lambda ^{(k)} = {\mathop {\mathrm{argmin}}\limits _{y\in \mathbb {R}^k}} \{\Vert \widetilde{A}V_k y - \widetilde{g}\Vert _2^2+ \lambda ^2\Vert LV_ky\Vert _2^2\}, \end{aligned}$$

(58)

where the regularization $\lambda$ is determined as the unique solution of the nonlinear equation (6). Note that if we use the QR factorization of the product $LV_k$, $LV_k = Q_kR_k$, based on (35), (36) the above least squares problem reduces to one of the form

$$\begin{aligned} y_\lambda ^{(k)}= \displaystyle {\mathop {\mathrm{argmin}}\limits _{y\in \mathbb {R}^k}} \{\Vert B_ky-\beta _1e_1\Vert _2^2+ \lambda ^2\Vert R_ky\Vert _2^2\} \end{aligned}$$

(59)

which can be computed efficiently in several ways, e.g., by a direct method or by first transforming the stacked matrix $[B_k^T\; \lambda R_k^T]^T$ to upper triangular form, as done when implementing GKB-FP [4]. We can now compute the functions $\vartheta ^{(k)}$ and $\zeta ^{(k)}$ as defined in (47), (48) and then follow the same ideas as PGKB-FP. That is, for chosen $p>1$ and $k\ge p$, we determine the solution ${\lambda ^{(k)}}^*$ of the nonlinear function $\vartheta ^{(k)}(\lambda )=1$, repeating the process until the stopping criterion (55) is satisfied.

In practice the QR factorization $LV_k = Q_kR_k$ is calculated only once at step $k= p$ and updated in subsequent steps. Algorithms for updating the QR factorization can be found in [13, Chapter 12].

5 Numerical Examples

We illustrate the effectiveness of GDP-FP and PGDP-FP considering two test problems involving first kind integral equations

$$\begin{aligned} \int _0^1K(s,t)\mathbf{f}(t)dt = \mathbf{g}(s), \;\; 0\le s\le 1, \end{aligned}$$

(60)

which have been discussed in [21], and a third test problem from inverse scattering. Our computations were carried out in Matlab with about 16 significant decimal digits. Since the special case $\delta _A=0$ has been discussed and illustrated in several papers, we will only concentrate here on the case $\delta _A\ne 0$.

Example 1:

In this test problem the kernel $K(s,t)$ and the functions $\mathbf{f}$ and $\mathbf{g}$ are defined by

$$\begin{aligned} K(s,t) = \left\{ \begin{array}{l} s(1-t) \quad \mathrm{for}\quad s\le t,\\ t(1-s) \quad \mathrm{for}\quad s\ge t. \end{array}\right. , \quad \mathbf{f}(t) = 4t(t-1), \quad \mathbf{g}(s) = \frac{s}{3}(s^3-2s^2+1). \end{aligned}$$

Discretization of (60) leads to a discrete ill-posed problem where $A$, $f$, and $g$ depend on how the approximation is made. In this example the matrix $A\in \mathbb {R}^{n\times n}$ is generated by using the Matlab function deriv2 from [14], the vector $f$ has coordinates $f_j = \sqrt{\Delta t}(t_j-{\Delta t}/2)$, where $t_j = j\Delta t$, $\Delta t = 1/n,$ and $g = A f$. To simulate noisy data we take $\widetilde{A} = A+ E$ and $\widetilde{g} = g+e$, where $e$ and $E$ are a scaled Gaussian random vector and a scaled Gaussian random matrix, respectively, such that for chosen $\epsilon _A$ and $\epsilon _g$ we have $\Vert E\Vert _2/\Vert A\Vert _2 = \epsilon _A$ and $\Vert e\Vert _2/\Vert g\Vert _2 = \epsilon _g$. In this example we take $\epsilon _A= \epsilon _g= 0.03$. GDP-FP is implemented by using the SVD of $A$, which means we choose $L= I$, and PGDP-FP is implemented with complete reorthogonalization, taking $\epsilon = 10^{-5}$ and $p = 3$. To simulate a medium sized problem we choose $n = 1{,}200$.

Figure 3 displays the results obtained with GDP-FP and PGDP-FP, as well as the results obtained with the L-curve method (LC) [15] which are included here for comparison purposes. From the results we see that LC may not be a good option in cases where both the matrix $A$ and the vector $b$ are noise-corrupted, and that the solutions produced by PGDP-FP and by GDP-FP, respectively, are indistinguishable (albeit slightly oscillating), as seen in Fig. 3 (second row). We also report important numbers such as the computed regularization parameters, relative errors associated with each regularized solution, etc., see Table 1. This table shows that GDP-FP converged in $j=6$ iterations and that PGDP-FP spent $k = 4$ outer iterations, i.e., the regularized solution determined with PGDP-FP lives in a Krylov subspace of dimension $k = 4$.

Fig. 3

First row (left): solution produced by L-curve. First row (right): Exact solution $f$ (solid line), solution $f_{\lambda }$ determined by GDP-FP (dash-dotted line) and solution $f_\lambda ^{(4)}$ determined by PGDP-FP (dotted line). Second row: relative error in $f_\lambda$ (left) and relative error in $f_\lambda ^{(4)}$ (right)

Table 1 Index $j$ refers to the number of iterates spent by GDP-FP, and index $k$ refers to the dimension of the Krylov subspace used to approximate $\lambda _{_{{GDP}}}$

We now show that the small oscillations in the regularized solution can be suppressed provided that a suitable regularization matrix is chosen. To this end we follow [21] and choose an invertible regularization matrix defined by $L = \frac{(n+1)}{\pi }\, T^{1/2}$ with

$$\begin{aligned} T = \left( \begin{array}{cccc} 2&{}\quad -1&{}&{} \\ -1&{}\quad \ddots &{}\quad \ddots &{}\\ &{}\quad \ddots &{}\quad \ddots &{}\quad -1\\ &{} &{}\quad -1 &{}\quad 2\end{array} \right) . \end{aligned}$$

(61)

With this choice of $L$ we transform the general-form Tikhonov problem (3) into a problem in standard form, as described in Sect. 4.3, and then determine the solution of the transformed problem via PGDP-FP. The solution $f_\lambda ^{(k)}$ obtained with PGDP-FP is then recovered using the corresponding back-transformation. Figure 4 displays results for the case $n =1{,}200$ and $\epsilon _A= \epsilon _g= 0.003$. In this case PGDP-FP performed $k = 5$ outer iterations. Note that the choice of $L$ yields a smooth regularized solution.

Fig. 4

$f$ (solid line) and $f_\lambda ^{(5)}$ (dotted line) with the choice $L = \frac{n+1}{\pi }T^{1/2}$. In this case we obtain $\lambda = 0.0096$, and $\Vert f-f_\lambda ^{(5)}\Vert /\Vert f\Vert _2 = 0.0339$

Example 2:

We now consider the first kind integral equation (60) with the same kernel $K(s,t)$ as in Example 1 but with the following two choices for $\mathbf{f}$ and $\mathbf{g}$

(a) :

$\mathbf{f}(t) = t, \quad \mathbf{g}(s) = \frac{s}{6}(s^2-1).$

(b) :

$\mathbf{f}(t) = e^{t}, \quad \mathbf{g}(s)= e^{s} + (1-e)s - 1$

Although in many problems the matrix $L$ is chosen as a scaled discrete differential operator, the purpose of the above test problems is to illustrate that such a choice may not be appropriate if the operator is not properly scaled. To this end we choose again $n= 1{,}200$ and use the same noise level as in the previous example.

For the test problem with f and g defined in (a) we consider one case where $L=I$ and two additional cases where $L\ne I$. Figure 5 (first row) displays the regularized solutions obtained with GDP-FP and PGDP-FP for the first case, as well as the relative errors associated with each solution. In this case both GDP-FP and PGDP-FP are implemented as in Example 1. The solution produced by PGDP-FP lives in a Krylov subspace of dimension $k=5$ and remains very close to that produced by GDP-FP, as it is clearly visible in Fig. 5, first row (left). However, the large relative errors in both solutions indicate that the choice $L=I$ is unsatisfactory and motivates the use of other regularization matrices.

Fig. 5

First row (left): Exact solution $f$ (solid line), $f_{\lambda }$ obtained with GDP-FP (dash-dotted line) and $f_{\lambda }^{(5)}$ obtained with PGDP-FP (dotted line). First row (right): relative error in $f_{\lambda }$ and relative error in $f_{\lambda }^{(5)}$. Second row (left): $f$ (solid line), $f_{\lambda }$ for $L= \frac{n+1}{\pi }T^{1/2}$ (dash-dotted line) and $f_{\lambda }$ for $L = L_2$ (dotted line). Second row (right): relative errors associated with the solutions obtained with $L= \frac{n+1}{\pi }T^{1/2}$ (dash-dotted line) and $L = L_2$ (dotted line), respectively

The second part of the example considers two choices for the regularization matrix: $L= \frac{n+1}{\pi }T^{1/2}$ as defined in the previous example, and $L=L_2$ where

$$\begin{aligned} L_2 = \left( \begin{array}{ccccc} -1&{}\quad 2&{}\quad -1&{}&{} \\ &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\\ &{} &{}\quad -1 &{}\quad 2&{}\quad -1\end{array} \right) \end{aligned}$$

(62)

is a rectangular matrix of size $(n-2)\times n$.

For the case where $L$ is invertible we use the extension of GDP-FP to general-form Tikhonov regularization considered in Example 1, while for the case where $L$ is rectangular, we use the extension of GDP-FP which performs computations with the $\widetilde{A}$-weighted pseudoinverse of $L$, as described in Sect. 4.3, taking advantage of the fact that $L$ has a known null subspace.

The computed regularized solutions $f_\lambda$ (obtained with the GSVD of the matrix pair $(\widetilde{A},L)$) and corresponding relative errors are displayed in Fig. 5, second row. The solutions obtained with the projection approach are very similar to those obtained with the GSVD and therefore are not shown here. Note that the results obtained with $L$ invertible are very similar to those obtained with $L=I$ (same figure, first row) and therefore of poor quality. This does not occur with the regularized solution obtained with $L = L_2$ whose quality is apparent.

We now describe results for the test problem with f and g defined in (b). For this problem, in addition to the choices for $L$ used in the test problem with data in (a), we consider the choice $L= \mathsf{D}$, where D is a rank-deficient square matrix defined by

$$\begin{aligned} \mathsf{D} = \beta (L_2^TL_2)^{1/4}, \quad \beta >0, \end{aligned}$$

(63)

with scaling factor $\beta = (n+1)/\pi$. This choice is motivated by a theoretical result by Lu et al. [21] that, for invertible ${\mathcal {L}}$, suggests choosing a scaling factor $\beta$ such that $L = \beta {\mathcal {L}}$ satisfies $\Vert L^{-1} \Vert _2\le 1$, see Theorem 2.1 in [21], and justifies the choice of the square regularization matrix $L$ in Example 1 defined via the matrix $T^{1/2}$. In order to mimic this result inverse is replaced by Moore-Penrose pseudo inverse and the scaling factor $\beta$ is chosen so that $\Vert \mathsf{D}^\dag \Vert _2\le 1.$ The computed regularized solutions $f_\lambda$ obtained with the GSVD of the matrix pair $(\widetilde{A},L)$ are displayed in Fig. 6. Notice that, contrary to the excellent results obtained with the regularization matrix $L = L_2$ in Example 1, the results in this case are of poor quality; a similar observation applies to the results obtained with the square and invertible regularization matrix. On the other hand, notice that the quality of the regularized solution obtained with $L = \mathsf{D}$ is excellent.

Fig. 6

Exact solution (solid line) and regularized solution $f_{\lambda }$ obtained with GDP-FP (dash-dotted line). First row (left): results for $L= \frac{n+1}{\pi }T^{1/2}$. First row (right): results for $L = L_2$. Second row: results for $L = \mathsf{D}$. For this this example, the computed regularization parameters are $\lambda = 0.00093,\, 0.00097$ and $0.00019$, while the corresponding relative errors are $\Vert f-f_\lambda \Vert _2/\Vert f\Vert _2= 0.3111, 0.6030$ and $0.0091$, respectively

Example 3: Inverse scattering

The propagation of time-harmonic acoustic fields in a homogeneous medium, in the presence of a sound soft obstacle $D$, is modeled by the exterior boundary value problem (direct obstacle scattering problem) [8]

$$\begin{aligned} \left\{ \begin{array}{l} \triangle u(x)+k^2 u(x)=0,\quad x\in \mathbb {R}{^2}\setminus \overline{D}\\ u(x)\doteq u^{s}+u^{i}(x)=0,\quad x\in \partial {D}\\ (\frac{\partial u^s}{\partial r}-iku^s)={\large O}(\frac{1}{r}), \quad r = |x|\rightarrow \infty \end{array}\right. \end{aligned}$$

where $k$ is a real positive wavenumber, $u^i$ is an incident wave, and $u^s$ is the scattered wave outside $D$. In addition, $u^s$ has the following asymptotic behavior

$$\begin{aligned} u^s(x)=u_{\infty }(\hat{x})\frac{e^{ikr}}{\sqrt{r}}+{\large O}(r^{-3/2}), \end{aligned}$$

(64)

where $u_{\infty }$ is defined on the unit circle $\Omega$ and called the far field-pattern of the scattered wave. Our interest here is to identify the shape of $D$ from measurements of $u_\infty$ by using a variant of the linear sampling method (LSM) [9]. The basis of LSM is the far-field equation

$$\begin{aligned} (F\,w_{z})(\hat{{x}})=\frac{e^{i\pi /4}}{\sqrt{8\pi k}} e^{-ik\hat{{ x}}{ \cdot z}}, \quad \hat{x} = x/|x|, \;\; z\in \mathbb {R}^2, \end{aligned}$$

(65)

where $F:L^2(\Omega )\rightarrow L^2(\Omega )$ is a linear compact operator, the Far-field operator, given by

$$\begin{aligned} (F\,w)(\hat{{x}})= \int _{\Omega } u_\infty (\hat{{x}}; \hat{{ d}})\,w(\hat{{d}})\,\, ds(\hat{{d}}),\,\,\,\,\,\hat{d}\in \Omega . \end{aligned}$$

(66)

LSM is based on the the observation that the solution $g_z$ of (65) has a large norm for $z$ outside and close to $\partial D$. Hence, characterizations of $D$ are obtained by plotting the norm $\Vert w_z\Vert$. However, a difficulty with LSM is that (65) is not always solvable. Kirsch [17] was able to overcome this difficulty with the introduction of a variant of LSM based on the following linear equation

$$\begin{aligned} (F^\star F)^{1/4}w_z = \frac{e^{i\pi /4}}{\sqrt{8\pi k}} e^{-ik\hat{{ x}}{ \cdot z}}. \end{aligned}$$

(67)

In this variant, the shape of $D$ is characterized analogously as in LSM, i.e., by inspecting for which $z$ the norm $\Vert g_z\Vert$ is large. In practice, Kirsch’s method deals with a finite dimensional counterpart of (67) obtained by replacing $F$ for a perturbed finite-dimensional far-field operator of the form $\widetilde{F}_d = F_d +E\in \mathbb {C}^{n\times n}$, where $n$ denotes the number of observed incident waves and the number of outgoing directions, and $F_d$ has singular values decaying quickly to zero, which means $F_d$ is severely ill-conditioned. Hence, regularization is needed in order to compute stable approximations to the solution $w_z$ of (67). Following [17], we approximate $w_z$ by using a regularized solution $w_{\lambda ,z}$ constructed by the method of Tikhonov:

$$\begin{aligned} w_{\lambda ,z} = {\mathop {\mathrm{argmin}}\limits _{w \in \mathbb {C}^{n}}}\{\Vert r_z-\widetilde{A}_d\, w\Vert _2^2+\lambda ^2\Vert w\Vert _2^2\} \end{aligned}$$

(68)

where the regularization parameter is chosen by the GDP. Here, $r_z$ denotes the discrete right hand side of (67) and $\widetilde{A}_d = (\widetilde{F}_d^*\widetilde{F}_d^*)^{1/4}$. Regarding GDP, note that the discrepancy function in this case becomes

$$\begin{aligned} G_z(\lambda )=\Vert \widetilde{A}_d\,w_{\lambda ,z}-r_z\Vert _2^2-\delta _A^2 \Vert w_{\lambda ,z}\Vert _2^2, \end{aligned}$$

which, in terms of the SVD of $\widetilde{F}_d$ reads

$$\begin{aligned} G_z(\lambda ) = \displaystyle \sum _{i=1}^n \displaystyle \frac{\lambda ^4-\delta _A^2\sigma _i}{(\sigma _i+\lambda ^2)^2}\alpha _i \end{aligned}$$

(69)

where $\sigma _i$ denote the singular values de $\widetilde{F}_d$ and $\alpha _i= |v_i^*r_z|^2$, the squared Fourier coefficients of $r_z$ with respect to the singular vectors of $\widetilde{F}_d$.

Summarizing, the characterization of the object can be done as follows:

• For each $z$ in a grid containing the object $D$, solve the Tikhonov problem (68) with the regularization parameter being chosen by GDP.

• Characterize the object by using a plot of the map $z\rightarrow W(z)= 1/\Vert w_{\lambda ,z}\Vert _2^2$.

To illustrate the efficiency of GDP-FP in this class of problems, we choose a test problem which has been considered in [3, 19]. In this case the object to be characterized is a kite located in a grid of $50\times 50$ points, the far field matrix $\widetilde{F}_d$ is $32\times 32$ (i.e., we use 32 incident observed directions), and the relative noise level in $\widetilde{F}_d$ is 5 % (which implied a relative noise level in $\widetilde{A}_d$ of approximately 15 %). To simulate perturbed data, we generate Gaussian random matrices $E_1$, $E_2$ and use a far-field matrix defined by

$$\begin{aligned} \widetilde{F}_d = F_d+ \delta (E_1+i\, E_2)\Vert F_d\Vert _2, \;\; \delta >0, \end{aligned}$$

for given $\delta$, where $F_d$ is constructed by using the Nyström method [8].

To assess the efficiency of GDP-FP when compared to other method used to solve the scattering inverse problem, we also compute the regularization parameter by using regula falsi method as done in [17]. The tolerance parameter for stopping both GDP-FP and regula falsi is set to $\epsilon =10^{-5}$. For this example, the reconstruction obtained with GDP-FP is about 12 times faster than the one obtained with regula falsi. The profile of the kite and its reconstructed version are displayed in Fig. 7.

Fig. 7

Kite and its reconstruction via Kirsch’s method with GDP as parameter choice rule

6 Conclusions

We derived a fixed-point algorithm for determining the Tikhonov regularization parameter chosen by the GDP for discrete ill-posed problems. The algorithm is monotonically and globally convergent and easy to implement using the GSVD of the coefficient matrix. A special version of the algorithm based on the Golub-Kahan bidiagonalization procedure, that is well suited for large-scale problem, is also developed and discussed in detail. The algorithms are numerically illustrated using three test problems from the Regularization Tools [14] and an additional test problem from inverse scattering [9]. In addition, the issue of selecting a proper scaling in connection with discrete differential operators was also illustrated. The numerical results indicate that the algorithms are quite fast and therefore promising for discrete ill-posed problems with noisy operator and noisy data.