Numerical solution of a class of third-kind Volterra integral equations using Jacobi wavelets

Abstract

We propose a spectral collocation method, based on the generalized Jacobi wavelets along with the Gauss–Jacobi quadrature formula, for solving a class of third-kind Volterra integral equations. To do this, the interval of integration is first transformed into the interval [− 1, 1], by considering a suitable change of variable. Then, by introducing special Jacobi parameters, the integral part is approximated using the Gauss–Jacobi quadrature rule. An approximation of the unknown function is considered in terms of Jacobi wavelets functions with unknown coefficients, which must be determined. By substituting this approximation into the equation, and collocating the resulting equation at a set of collocation points, a system of linear algebraic equations is obtained. Then, we suggest a method to determine the number of basis functions necessary to attain a certain precision. Finally, some examples are included to illustrate the applicability, efficiency, and accuracy of the new scheme.

1 Introduction

In this paper, we consider the following Volterra integral equation (VIE)

$$ t^{\beta} u(t)=f(t)+{{\int}_{0}^{t}}(t-x)^{-\alpha}\kappa(t,x)u(x)dx, \quad t\in [0,T], $$

(1)

where β > 0, α ∈ [0,1), α + β ≥ 1, f(t) = t^βg(t) with a continuous function g, and κ is continuous on the domain Δ := {(t, x) : 0 ≤ x ≤ t ≤ T} and is of the form

$$ \kappa(t,x)=x^{\alpha+\beta-1}\kappa_{1}(t,x), $$

where κ₁ is continuous on Δ. The existence of the term t^β in the left-hand side of (1) gives it special properties, which are distinct from those of VIEs of the second kind (where the left-hand side is always different from zero), and also distinct from those of the first kind (where the left-hand side is constant and equal to zero). This is why in the literature they are often mentioned as VIEs of the third kind. This class of equations has attracted the attention of researchers in the last years. The existence, uniqueness, and regularity of solutions to (1) were discussed in [1]. In that paper, the authors have derived necessary conditions to convert the equation into a cordial VIE, a class of VIEs which was studied in detail in [2, 3]. This made possible to apply to (1) some results known for cordial equations. In particular, the case α + β > 1 is of special interest, because in this case, if κ₁(t, x) > 0, the integral operator associated to (1) is not compact and it is not possible to assure the solvability of the equation by classical numerical methods. In [1], the authors have introduced a modified graded mesh and proved that with such mesh the collocation method is applicable and has the same convergence order as for regular equations.

In [4], two of the authors of the present paper have applied a different approach, which consisted in expanding the solution as a series of adjusted hat functions and approximating the integral operator by an operational matrix. The advantage of that approach is that it reduces the problem to a system of linear equations with a simple structure, which splits into subsystems of three equations, making the method efficient and easy to implement [4]. A limitation of this technique is that the optimal convergence order (O(h⁴)) can be attained only under the condition that the solution satisfies u ∈ C⁴([0, T]), which is not the case in many applications.

It is worth remarking here that there is a close connection between equations of class (1) and fractional differential equations [5]. Actually, the kernel of (1) has the same form as the one of a fractional differential equation, and if we consider the case κ(t, x) ≡ 1, then the integral operator is the Riemann–Liouville operator of order 1 − α. Therefore, it makes sense to apply to this class of equations numerical approaches that have recently been applied with success to fractional differential equations and related problems [5].

One of these techniques were wavelets, a set of functions built by dilation and translation of a single function φ(t), which is called the mother wavelet. These functions are known as a very powerful computational tool. The term wavelet was introduced by Jean Morlet about 1975 and the theory of the wavelet transform was developed by him and Alex Grossmann in the 80s [6, 7]. Some developments exist concerning the multiresolution analysis algorithm based on wavelets [8] and the construction of compactly supported orthonormal wavelet basis [9]. Wavelets form an unconditional (Riesz) basis for L²(R), in the sense that any function in L²(R) can be decomposed and reconstructed in terms of wavelets [10]. Many authors have constructed and used different types of wavelets, such as B-spline [11], Haar [12], Chebyshev [13], Legendre [14], and Bernoulli [15] wavelets. The advantage of employing wavelets, in comparison with other basis functions, is that when using them one can improve the accuracy of the approximation in two different ways: (i) by increasing the degree of the mother function (assuming that it is a polynomial); (ii) by increasing the level of resolution, that is, reducing the support of each basis function.

We underline that the application of wavelets has special advantages in the case of equations with non-smooth solutions, as it is the case of (1). In such cases, increasing the degree of the polynomial approximation is not a way to improve the accuracy of the approximation; however, such improvement can be obtained by increasing the level of resolution.

In a recent work [16], Legendre wavelets were applied to the numerical solution of fractional delay-type integro-differential equations. In the present paper we will apply a close technique to approximate the solution of (1).

The paper is organized as follows. Section 2 is devoted to the required preliminaries for presenting the numerical technique. In Section 3, we give some error bounds for the best approximation of a given function by a generalized Jacobi wavelet. Section 4 is concerned with the presentation of a new numerical method for solving equations of type Eq. (1). In Section 5, we suggest a criterion to determine the number of basis functions. Numerical examples are considered in Section 6 to confirm the high accuracy and efficiency of this new numerical technique. Finally, concluding remarks are given in Section 7.

2 Preliminaries

In this section, we present some definitions and basic concepts that will be used in the sequel.

2.1 Jacobi wavelets

The Jacobi polynomials $\left \{P_{i}^{(\nu ,\gamma )}(t)\right \}_{i=0}^{\infty }$, ν, γ > − 1, t ∈ [− 1, 1], are a set of orthogonal functions with respect to the weight function

$$ w^{(\nu,\gamma)}(t)=(1-t)^{\nu}(1+t)^{\gamma}, $$

with the following orthogonality property:

$$ {\int}_{-1}^{1}w^{(\nu,\gamma)}(t) P_{i}^{(\nu,\gamma)}(t)P_{j}^{(\nu,\gamma)}(t)dt=h_{i}^{(\nu,\gamma)}\delta_{ij}, $$

where δ_ij is the Kronecker delta and

$$ h_{i}^{(\nu,\gamma)}=\frac{2^{\nu+\gamma+1}{\Gamma}(\nu+i+1) {\Gamma}(\gamma+i+1)}{i!(\nu+\gamma+2i+1){\Gamma}(\nu+\gamma+i+1)}. $$

The Jacobi polynomials include a variety of orthogonal polynomials by considering different admissible values for the Jacobi parameters ν and γ. The most popular cases are the Legendre polynomials, which correspond to ν = γ = 0, Chebyshev polynomials of the first-kind, which correspond to ν = γ = − 0.5, and Chebyshev polynomials of the second-kind, which correspond to ν = γ = 0.5.

We define the generalized Jacobi wavelets functions on the interval [0, T) as follows:

$$ \psi_{n,m}^{(\nu,\gamma)}(t) =\left\{ \begin{array}{ll} 2^{\frac{k}{2}}\sqrt{\frac{1}{h_{m}^{(\nu,\gamma)}T}} P_{m}^{(\nu,\gamma)}\left( \frac{2^{k}}{T}t-2n+1\right), & \frac{n-1}{2^{k-1}}T\leq t<\frac{n}{2^{k-1}}T,\\ 0,&\text{otherwise}, \end{array} \right. $$

where k = 1, 2, 3, … is the level of resolution, n = 1, 2, 3, … , 2^k− 1, m = 0, 1, 2, … , is the degree of the Jacobi polynomial, and t is the normalized time. The interested reader can refer to [17, 18] for more details on wavelets. Jacobi wavelet functions are orthonormal with respect to the weight function

$$ w_{k}^{(\nu,\gamma)}(t) =\left\{ \begin{array}{ll} w_{1,k}^{(\nu,\gamma)}(t),& 0\leq t < \frac{1}{2^{k-1}}T,\\ w_{2,k}^{(\nu,\gamma)}(t),& \frac{1}{2^{k-1}}T\leq t < \frac{2}{2^{k-1}}T,\\ \quad {\vdots} &\\ w_{2^{k-1},k}^{(\nu,\gamma)}(t),& \frac{2^{k-1}-1}{2^{k-1}}T\leq t < T, \end{array} \right. $$

where

$$ w_{n,k}^{(\nu,\gamma)}(t)=w^{(\nu,\gamma)}\left( \frac{2^{k}}{T}t-2n+1\right), \quad n=1,2,\ldots, 2^{k-1}. $$

An arbitrary function u ∈ L²[0, T) may be approximated using Jacobi wavelet functions as

$$ u(t)\simeq {\Psi}_{k,M}^{(\nu,\gamma)}(t) =\sum\limits_{n=1}^{2^{k-1}}\sum\limits_{m=0}^{M}u_{n,m}\psi_{n,m}^{(\nu,\gamma)}(t), $$

where

$$ \begin{array}{lll} u_{n,m}&=\langle u(t),\psi_{n,m}^{(\nu,\gamma)}(t)\rangle_{w_{k}^{(\nu,\gamma)}}\\ &={{\int}_{0}^{T}} w_{k}^{(\nu,\gamma)}(t)u(t)\psi_{n,m}^{(\nu,\gamma)}(t)dt\\ &={\int}_{\frac{n-1}{2^{k-1}}T}^{\frac{n}{2^{k-1}}T} w_{n,k}^{(\nu,\gamma)}(t)u(t)\psi_{n,m}^{(\nu,\gamma)}(t)dt. \end{array} $$

2.2 Gauss–Jacobi quadrature rule

For a given function u, the Gauss–Jacobi quadrature formula is given by

$$ {\int}_{-1}^{1}(1-t)^{\nu}(1+t)^{\gamma}u(t)dt =\sum\limits_{l=1}^{N}\omega_{l}u(t_{l})+R_{N}(u), $$

where t_l, l = 1,…, N, are the roots of $P_{N}^{(\nu ,\lambda )}$, ω_l, l = 1,…, N, are the corresponding weights given by (see [19]):

$$ \omega_{l}=\frac{2^{\nu+\gamma+1}{\Gamma}(\nu+N+1){\Gamma}(\gamma+N+1)}{N! {\Gamma}(\nu+\gamma+N+1)(\frac{d}{dt}P_{N}^{(\nu,\gamma)}(t_{l}))^{2}(1-{t_{l}^{2}})}, $$

(2)

and R_N(u) is the remainder term which is as follows:

$$ \begin{array}{ll} R_{N}(u)=& \frac{2^{\nu+\gamma+2N+1}N!{\Gamma}(\nu+N+1){\Gamma}(\gamma+N+1) {\Gamma}(\nu+\gamma+N+1)}{(\nu+\gamma+2N+1)({\Gamma}(\nu+\gamma+2N+1))^{2}}\\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\times\frac{u^{(2N)}(\eta)}{(2N)!},\quad \eta\in(-1,1). \end{array} $$

(3)

According to the remainder term (3), the Gauss–Jacobi quadrature rule is exact for all polynomials of degree less than or equal to 2N − 1. This rule is valid if u possesses no singularity in (− 1, 1). It should be noted that the roots and weights of the Gauss–Jacobi quadrature rule can be obtained using numerical algorithms (see, e.g., [20]).

3 Best approximation errors

The aim of this section is to give some estimates for the error of the Jacobi wavelets approximation of a function u in terms of Sobolev norms and seminorms. With this purpose, we extend to the case of Jacobi wavelets some results which were obtained in [21] for the best approximation error by Jacobi polynomials in Sobolev spaces. The main result of this section is Theorem 1, which establishes a relationship between the regularity of a given function and the convergence rate of its approximation by Jacobi wavelets.

We first introduce some notations that will be used in this paper. Suppose that $L^{2}_{w^{*}}(a,b)$ is the space of measurable functions whose square is Lebesgue integrable in (a, b) relative to the weight function w^∗. The inner product and norm of $L^{2}_{w^{*}}(a,b)$ are, respectively, defined by

$$ \langle u,v\rangle_{w^{*}} ={{\int}_{a}^{b}} w^{*}(t)u(t)v(t)dt, \quad \forall~u,v\in L^{2}_{w^{*}}(a,b), $$

and

$$ \left\| u\right\|_{L_{w^{*}}^{2}(a,b)} =\sqrt{\langle u,u\rangle_{w^{*}}}. $$

The Sobolev norm of integer order r ≥ 0 in the interval (a, b), is given by

$$ \parallel u \parallel_{H_{w^{*}}^{r}(a,b)} =\left( {\sum\limits^{r}_{j=0}\parallel u^{(j)} \parallel^{2}_{L_{w^{*}}^{2}(a,b)}} \right)^{\frac{1}{2}}, $$

(4)

where u^(j) denotes the j th derivative of u and $H_{w^{*}}^{r}(a,b)$ is a weighted Sobolev space relative to the weight function w^∗.

For ease of use, for some fixed values of − 1 < ν, γ < 1, we set

$$ \psi_{i,j}(t):=\psi_{i,j}^{(\nu,\gamma)}(t), ~ w(t):=w^{(\nu,\gamma)}(t), ~ w_{k}(t):=w_{k}^{(\nu,\gamma)}(t), ~ w_{n,k}(t):=w_{n,k}^{(\nu,\gamma)}(t). $$

For starting the error discussion, first, we recall the following lemma from [21].

Lemma 1 (See 21)

Assume that $u\in H_{w}^{\mu }(-1,1)$ with μ ≥ 0 and $L_{M}(u) \in \mathbb {P}_{M}$ denotes the truncated Jacobi series of u, where $\mathbb {P}_{M}$ is the space of all polynomials of degree less than or equal to M. Then,

$$ \parallel{ u-L_{M}(u)} \parallel_{{L_{w}^{2}}(-1,1)} \leq CM^{-\mu}|u|_{H_{w}^{\mu;M}(-1,1)}, $$

(5)

where

$$ \mid u \mid_{H_{w}^{\mu;M}(-1,1)} =\left( {\sum\limits^{\mu}_{j=\min\{\mu,M+1\}}\parallel u^{(j)}\parallel^{2}_{{L_{w}^{2}}(-1,1)}} \right)^{\frac{1}{2}} $$

(6)

and C is a positive constant independent of the function u and integer M. Also, for 1 ≤ r ≤ μ, one has

$$ \parallel{ u-L_{M}(u)} \parallel_{{H_{w}^{r}}(-1,1)} \leq CM^{2r-\frac{1}{2}-\mu}|u|_{H_{w}^{\mu;M}(-1,1)}. $$

(7)

Suppose that π_M(I_{k, n}) denotes the set of all functions whose restriction on each subinterval $I_{k,n}=\left (\frac {n-1}{2^{k-1}}T, \frac {n}{2^{k-1}}T\right )$, n = 1, 2, … , 2^k− 1, are polynomials of degree at most M. Then, the following lemma holds.

Lemma 2

Let $u_{n} : I_{k,n} \rightarrow \mathbb {R}$, n = 1, 2, … , 2^k− 1, be functions in $H_{w_{n,k}}^{\mu }(I_{k,n})$ with μ ≥ 0. Consider the function ${u}_{n}: (-1,1) \rightarrow \mathbb {R}$ defined by $(\bar {u}_{n})(t)=u_{n}\left (\frac {T}{2^{k}}(t+2n-1)\right )$ for all t ∈ (− 1, 1). Then, for 0 ≤ j ≤ μ, we have

$$ \parallel (\bar{u}_{n})^{(j)} \parallel_{{L_{w}^{2}}(-1,1)} =\left( {\frac{2^{k}}{T}}\right)^{\frac{1}{2}-j}\parallel u^{(j)}_{n}\parallel_{L_{w_{n,k}}^{2}(I_{k,n})}. $$

Proof

Using the definition of the L²-norm and the change of variable $t^{\prime }=\frac {T}{2^{k}}(t+2n-1)$, we have

$$ \begin{array}{llll} \parallel{{{{\bar {u}_{n}}}^{(j)}}} \parallel_{{{L_{w}^{2}}}(- 1,1)}^{2} &= {\int}_{- 1}^{1} w(t) |{\bar{u}_{n}}^{(j)} (t)|^{2}dt \\ &={\int}_{- 1}^{1} w(t)\left|{u_{n}}^{(j)} \left( \frac{T}{2^{k}}(t+2n-1)\right)\right|^{2}dt \\ &= {\int}_{\frac{{n - 1}}{2^{k-1}}T}^{\frac{n}{2^{k-1}}T} w_{n,k}(t^{\prime})\left( \frac{2^{k}}{T}\right)^{-2j}\left|u_{n}^{(j)}(t^{\prime})\right|^{2}\left( \frac{2^{k}}{T}\right)dt^{\prime}\\ &= \left( \frac{2^{k}}{T}\right)^{1 - 2j}\parallel {u_{n}^{(j)}}\parallel_{{L_{w_{n,k}}^{2}}(I_{k,n})}^{2}, \end{array} $$

which proves the lemma. □

In order to continue the discussion, for convenience, we introduce the following seminorm for $u \in H_{w_{k}}^{\mu }(0,T)$, 0 ≤ r ≤ μ, M ≥ 0 and k ≥ 1, which replaces the seminorm (6) in the case of a wavelet approximation:

$$ \mid u \mid_{H_{w_{k}}^{r;\mu;M;k}(0,T)} =\left( {\sum\limits^{\mu}_{j=\min\{\mu,M+1\}} \left( 2^{k}\right)^{2r-2j} \parallel u^{(j)} \parallel^{2}_{L_{w_{k}}^{2}(0,T)}} \right)^{\frac{1}{2}}. $$

(8)

If we choose M such that M ≥ μ − 1, it can be easily seen that

$$ \mid u \mid_{H_{w_{k}}^{r;\mu;M;k}(0,T)} =\left( 2^{k}\right)^{r-\mu} \parallel u^{(\mu)} \parallel_{L_{w_{k}}^{2}(0,T)}. $$

(9)

The next theorem provides an estimate of the best approximation error, when Jacobi wavelets are used, in terms of the seminorm defined by (8).

Theorem 1

Suppose that $u \in H_{w_{k}}^{\mu }(0,T)$ with μ ≥ 0 and

$${\Psi}_{k,M}(u)=\sum\limits_{n = 1}^{{2^{k - 1}}}{\sum\limits_{m = 0}^{M} {{u_{n,m}}{\psi_{n,m}}(t)} },$$

is the best approximation of u based on the Jacobi wavelets. Then,

$$ \parallel{u - {\Psi}_{k,M}(u)} \parallel_{{L_{w_k}^2}(0,T)} \leq CM^{-\mu}|u|_{H_{w_k}^{0;\mu;M;k}(0,T)}, $$

(10)

and, for 1 ≤ r ≤ μ,

$$ \parallel{u - {\Psi}_{k,M}(u)} \parallel_{{H_{w_{k}}^{r}}(0,T)} \leq CM^{2r-\frac{1}{2}-\mu}|u|_{H_{w_{k}}^{r;\mu;M;k}(0,T)}, $$

(11)

where in (10) and (11) the constant C denotes a positive constant that is independent of M and k but depends on the length T.

Proof

Consider the function $u_{n}:I_{k,n}\rightarrow \mathbb {R}$ such that u_n(t) = u(t) for all t ∈ I_{k, n}. Then, from (4) and Lemma 2 for 0 ≤ r ≤ μ, we have

$$ \begin{array}{llll} \left\| {{u} - {{\Psi}_{k,M}}({u})} \right\|_{H_{w_{k}}^{r}(0,T )}^{2} &= \sum\limits_{n = 1}^{{2^{k - 1}}} {\left\| {{u_{n}} - \sum\limits_{m=0}^{M } {{u_{n,m}}{\psi_{n,m}}(t)} } \right\|}_{H_{w_{n,k}}^{r}({I_{k,n}})}^{2}\\ &= \sum\limits_{n = 1}^{2^{k - 1}}{\sum}_{j=0}^{r}\left\|{u^{(j)}_{n}} - \left( \sum\limits_{m=0}^{M } {{u_{n,m}}{\psi_{n,m}}(t)}\right)^{(j)} \right\|_{L_{w_{n,k}}^{2}(I_{k,n} )}\\ &=\sum\limits_{n = 1}^{2^{k - 1}} \sum\limits_{j = 0}^{r} {\left( \frac{2^{k}}{T}\right)}^{2j - 1}{\left\| {\bar u}_{n}^{(j)} -{\left( L_{M}({\bar u}_{n})\right)}^{(j)} \right\|}_{{L_{w}^{2}}(- 1,1)}^{2}\\ &\leq C_{1}\sum\limits_{n = 1}^{2^{k - 1}} \sum\limits_{j = 0}^{r} {\left( 2^{k}\right)}^{2j - 1}{\left\| {\bar u}_{n}^{(j)} -{\left( L_{M}({\bar u}_{n})\right)}^{(j)} \right\|}_{{L_{w}^{2}}(- 1,1)}^{2}. \end{array} $$

(12)

By setting r = 0 in (12), we obtain

$$ \begin{array}{llll} \left\|u - {\Psi}_{k,M }(u) \right\|_{L_{w_{k}}^{2}(0,T )}^{2} &\leq C_{1}\sum\limits_{n = 1}^{2^{k - 1}} {\left( 2^{k}\right)}^{-1}{\left\| {\bar u}_{n} -{\left( L_{M}({\bar u}_{n})\right)}\right\|}_{{L_{w}^{2}}(-1,1)}^{2}\\ &\leq C_{2}M^{-2\mu}{\left( 2^{k}\right)}^{- 1}\sum\limits_{n = 1}^{2^{k - 1}} {\sum}^{\mu}_{j=\min\{\mu,M+1\}}{\left\| {\bar u}_{n}^{(j)}\right\|}_{{L_{w}^{2}}(- 1,1)}^{2}\\ &\leq CM^{-2\mu}{\sum}^{\mu}_{j=\min\{\mu,M+1\}}{\left( 2^{k}\right)}^{- 2j} \sum\limits_{n = 1}^{2^{k - 1}}{\left\| { u}_{n}^{(j)}\right\|}_{L_{w_{n,k}}^{2}(I_{n,k})}^{2}\\ &= CM^{-2\mu}{\sum}^{\mu}_{j=\min\{\mu,M+1\}}{\left( 2^{k}\right)}^{- 2j}{\left\| {u}^{(j)}\right\|}_{L_{w_{k}}^{2}(0,T)}^{2}, \end{array} $$

where we have used (5) and Lemma 2. This completes the proof of (10). Furthermore, using (12) for 1 ≤ r ≤ μ and k ≥ 1, we get:

$$ \begin{array}{@{}rcl@{}} \left\| {{u} - {{\Psi}_{k,M}}({u})} \right\|_{H_{w_{k}}^{r}(0,T )}^{2} &\leq& C_{1}{\left( 2^{k}\right)}^{2r - 1} \sum\limits_{n = 1}^{2^{k - 1}} \sum\limits_{j = 0}^{r} {\left\| {\bar u}_{n}^{(j)} -{\left( L_{M}({\bar u}_{n})\right)}^{(j)} \right\|}_{{L_{w}^{2}}(- 1,1)}^{2}\\ &=&C_{1}{\left( 2^{k}\right)}^{2r - 1} \sum\limits_{n = 1}^{2^{k - 1}}{ \left\| {\bar u}_{n} -{L_{M}({\bar u}_{n})} \right\|}_{{H^{r}_{w}}(- 1,1)}^{2}\\ &\leq& C_{2}M^{4r-1-2\mu}{\left( 2^{k}\right)}^{2r - 1}\sum\limits_{n = 1}^{2^{k - 1}} {\sum}^{\mu}_{j=\min\{\mu,M+1\}}{\left\| {\bar u}_{n}^{(j)}\right\|}_{{L_{w}^{2}}(- 1,1)}^{2}\\ &=&C_{2}M^{4r-1-2\mu}{\left( 2^{k}\right)}^{2r - 1}{\sum}^{\mu}_{j=\min\{\mu,M+1\}} \sum\limits_{n = 1}^{2^{k - 1}}{\left\| {\bar u}_{n}^{(j)}\right\|}_{{L_{w}^{2}}(- 1,1)}^{2}\\ &\leq& CM^{4r-1-2\mu}{\sum}^{\mu}_{j=\min\{\mu,M+1\}}\left( 2^{k}\right)^{2r-2j} \sum\limits_{n = 1}^{2^{k - 1}}\left\| u_{n}^{(j)}\right\|^{2}_{L^{2}_{w_{n,k}(I_{k,n})}}\\ &=& CM^{4r-1-2\mu}{\sum}^{\mu}_{j=\min\{\mu,M+1\}}\left( 2^{k}\right)^{2r-2j}\left\| u^{(j)}\right\|^{2}_{L^{2}_{w_{k}(0,T)}},\\ \end{array} $$

where we have used (4), (7), and Lemma 2. Therefore, we have proved (11). □

Remark 1

We can also obtain estimates for the Jacobi wavelets approximation in terms of the L²-norm. With M ≥ μ − 1, if we combine (9) with (10), we get

$$ \parallel{u - {\Psi}_{k,M}(u)} \parallel_{{L_{w_{k}}^{2}}(0,T)} \leq CM^{-\mu}2^{-\mu k} \parallel u^{(\mu)} \parallel_{L_{w_{k}}^{2}(0,T)}; $$

from (9) and(10), we obtain

$$ \parallel{u - {\Psi}_{k,M}(u)} \parallel_{{H_{w_{k}}^{r}}(0,T)} \leq CM^{2r-\frac{1}{2}-\mu}\left( 2^{k}\right)^{r-\mu} \parallel u^{(\mu)} \parallel_{L_{w_{k}}^{2}(0,T)},\quad r\geq 1. $$

4 Method of solution

In this section, we propose a method for solving the VIE (1). To this end, by using a suitable change of variable, we transform the interval of the integral to [− 1,1]. Suppose that

$$ s=2\left( \frac{x}{t}\right)-1,\quad ds=\frac{2}{t}dx. $$

Therefore, (1) is transformed into the following integral equation:

$$ t^{\beta} u(t)=f(t)+{\left( \frac{t}{2}\right)}^{1-\alpha} {\int}_{-1}^{1}(1-s)^{-\alpha}\kappa(t,\frac{t}{2}(s+1)) u(\frac{t}{2}(s+1))ds. $$

(13)

In order to compute the integral part of (13), we set ν = −α and γ = 0 as the Jacobi parameters and use the Gauss–Jacobi quadrature rule. Then, we have

$$ t^{\beta} u(t)=f(t)+{\left( \frac{t}{2}\right)}^{1-\alpha}{\sum}_{l=1}^{N} \omega_{l}\kappa(t,\frac{t}{2}(s_{l}+1))u(\frac{t}{2}(s_{l}+1)), $$

(14)

where s_l are the zeros of $P_{N}^{(-\alpha ,0)}$ and w_l are given using (2) as

$$ \omega_{l}=\frac{2^{1-\alpha}}{\left( \frac{d}{dx} P_{N}^{(-\alpha,0)}(s_{l})\right)^{2}\left( 1-{s_{l}^{2}}\right)}, \quad l=1,2,\ldots,N. $$

We consider an approximation of the solution of (1) in terms of the Jacobi wavelets functions as follows:

$$ u(t)\simeq{\sum}_{i=1}^{2^{k-1}}{\sum}_{j=0}^{M} u_{i,j}\psi_{i,j}^{(\nu,\gamma)}(t), $$

(15)

where the Jacobi wavelets coefficients u_{i, j} are unknown. In order to determine these unknown coefficients, we substitute (15) into (14) and get

$$ \begin{array}{ll} {\sum}_{i=1}^{2^{k-1}}{\sum}_{j=0}^{M}&\left[t^{\beta} \psi_{i,j}^{(\nu,\gamma)}(t) -{\left( \frac{t}{2}\right)}^{1-\alpha}{\sum}_{l=1}^{N}\omega_{l} \kappa\left( t,\frac{t}{2}(s_{l}+1)\right)\right.\\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\left.\times\psi_{i,j}^{(\nu,\gamma)}\left( \frac{t}{2}(s_{l}+1)\right)\right]u_{i,j}=f(t). \end{array} $$

(16)

In this step, we define the following collocation points

$$ t_{n,m}=\frac{T}{2^{k}}\left( \tau_{m}+2n-1\right), \quad n=1,2,\ldots,2^{k-1},~m=0,1,\ldots,M, $$

where τ_m, m = 0,1,…, M, are the zeros of $P_{M+1}^{(\nu ,\gamma )}$. Therefore, t_{n, m} are the shifted Gauss–Jacobi points in the interval $\left (\frac {n-1}{2^{k-1}}T,\frac {n}{2^{k-1}}T\right )$, corresponding to the Jacobi parameters ν and γ. By collocating (16) at the points t_{n, m}, we obtain

$$ \begin{array}{ll} {\sum}_{i=1}^{2^{k-1}}{\sum}_{j=0}^{M}\left[t_{n,m}^{\beta} \psi_{i,j}^{(\nu,\gamma)}(t_{n,m})-\right.&{\left( \frac{t_{n,m}}{2}\right)}^{1-\alpha} {\sum}_{l=1}^{N}\omega_{l}\kappa\left( t,\frac{t_{n,m}}{2}(s_{l}+1)\right)\\ &\quad\quad\quad\left.\times \psi_{i,j}^{(\nu,\gamma)}\left( \frac{t_{n,m}}{2}(s_{l}+1)\right)\right]u_{i,j}=f(t_{n,m}). \end{array} $$

(17)

By considering n = 1,2,…,2^k− 1 and m = 0,1,…, M, in the above equation, we have a system of linear algebraic equations that can be rewritten as the following matrix form:

$$ AU=F, $$

(18)

where

$$ U=\left[\begin{array}{cc} u_{1,0}\\ u_{1,1}\\ \vdots\\ u_{1,M}\\ \vdots\\ u_{2^{k-1},0}\\ u_{2^{k-1},1}\\ \vdots\\ u_{2^{k-1},M} \end{array} \right],\quad \quad F=\left[\begin{array}{c} f(t_{1,0})\\ f(t_{1,1})\\ \vdots\\ f(t_{1,M})\\ \vdots\\ f(t_{2^{k-1},0})\\ f(t_{2^{k-1},1})\\ \vdots\\ f(t_{2^{k-1},M}) \end{array} \right], $$

and the entries of the rows of the matrix A are the expressions in the bracket in (17), which vary corresponding to the values of i and j, i.e., the coefficients of u_{i, j}, i = 1,2,…,2^k− 1, j = 0,1,…, M, for t_{n, m}, that are all nonzero and positive. Since the functions $\psi _{i,j}^{(\nu ,\gamma )}$ are orthonormal and the nodes t_{n, m} are pairwise distinct, the matrix A is nonsingular. Therefore, (18) is uniquely solvable. By solving this system using a direct method, the unknown coefficients u_{i, j} are obtained. Finally, an approximation of the solution of (1) is given by (15).

5 A criterion for choosing the number of wavelets

Now we discuss the choice of adequate values of k and M (number of basis functions). To do this, we suppose that u(⋅) ∈ C^2N([0, T]) and κ(⋅,⋅) ∈ C^2N([0, T] × [0, T]). Using the error of the Gauss–Jacobi quadrature rule given by (3), and substituting ν = −α and γ = 0 in it, the exact solution of (1) satisfies the equation

$$ t^{\beta} u(t)=f(t)+{\left( \frac{t}{2}\right)}^{1-\alpha}\left[{\sum}_{l=1}^{N} \omega_{l}\kappa\left( t,\frac{t}{2}(s_{l}+1)\right)u\left( \frac{t}{2}(s_{l}+1)\right) +R_{N}(\kappa u)\right], $$

where

$$ \begin{array}{l} R_{N}(\kappa u)=\frac{2^{-\alpha+2N+1}(N!)^{2}\left( {\Gamma}(-\alpha+N+1)\right)^{2}}{ (2N)!(-\alpha+2N+1)\left( {\Gamma}(-\alpha+2N+1)\right)^{2}}\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\times {\left( \frac{t}{2}\right)}^{2N}\frac{\partial^{2N} \left( \kappa(t,x)u(x)\right)}{\partial x^{2N}}|_{x=\eta}, \end{array} $$

for η ∈ (0, T). Therefore, we have

$$ \begin{array}{ll} t^{\beta} u(t)=f(t)+{\left( \frac{t}{2}\right)}^{1-\alpha} &\left( {\sum}_{l=1}^{N}\omega_{l}\kappa\left( t,\frac{t}{2}(s_{l}+1)\right) u\left( \frac{t}{2}(s_{l}+1)\right)\right)\\ &\quad\quad\quad+t^{1-\alpha+2N}\xi_{\alpha,N}\frac{\partial^{2N}\left( \kappa(t,x)u(x)\right)}{\partial x^{2N}}|_{x=\eta}, \end{array} $$

where

$$ \xi_{\alpha,N}=\frac{(N!)^{2}\left( {\Gamma}(-\alpha+N+1)\right)^{2}}{(2N)! (-\alpha+2N+1)\left( {\Gamma}(-\alpha+2N+1)\right)^{2}}. $$

Suppose that t≠ 0. Then we obtain that

$$ \begin{array}{ll} u(t)=g(t)+2^{\alpha-1}{t}^{1-\alpha-\beta} &\left( {\sum}_{l=1}^{N}\omega_{l}\kappa\left( t,\frac{t}{2}(s_{l}+1)\right) u\left( \frac{t}{2}(s_{l}+1)\right)\right)\\ &\quad\quad\quad+t^{1-\alpha-\beta+2N}\xi_{\alpha,N} \frac{\partial^{2N}\left( \kappa(t,x)u(x)\right)}{\partial x^{2N}}|_{x=\eta}. \end{array} $$

(19)

Let $U_{k,M}(t)=\sum \limits _{i=1}^{2^{k-1}}\sum \limits _{j=0}^{M}u_{i,j} \psi _{i,j}^{(\nu ,\gamma )}(t)$ be the numerical solution of (1) obtained by the proposed method in Section 4. From the definition of the Jacobi wavelets, for the collocation points t_{n, m}, n = 1,…,2^k− 1, m = 0,1,…, M, we have

$$ U_{k,M}(t_{n,m})=\sum\limits_{j=0}^{M}u_{n,j}\psi_{n,j}^{(\nu,\gamma)}(t_{n,m}), \quad n=1,\ldots,2^{k-1}. $$

By definition, the restriction of the functions $\psi _{n,j}^{(\nu ,\gamma )}(t)$, n = 1,…,2^k− 1, on the subinterval I_{k, n}, which we denote here by $\rho _{n,j}^{(\nu ,\gamma )}(t)$, is smooth. Therefore, we can define

$$ \zeta_{n,j}=\max_{x,t\in I_{k,n}}\left|\frac{\partial^{2N}\left( \kappa(t,x)\rho_{n,j}^{(\nu,\gamma)}(x)\right)}{\partial x^{2N}}\right|. $$

For a given ε > 0, since all the collocation points, t_{n, m}, n = 1,…,2^k− 1, m = 0,1,…, M, are positive, using (19), we can choose k and M such that for all t_{n, m}, the following criterion holds:

$$ \begin{array}{@{}rcl@{}} \left|U_{k,M}(t_{n,m})-g(t_{n,m})-2^{\alpha-1}t_{n,m}^{1-\alpha-\beta}\left( {\sum}_{l=1}^{N}\omega_{l}\kappa\left( t_{n,m},\frac{t_{n,m}}{2}(s_{l}+1)\right)\right.\right.\\ \left.\left.U_{k,M}\left( \frac{t_{n,m}}{2}(s_{l}+1)\right)\right)\right|+t_{n,m}^{1-\alpha-\beta+2N}\xi_{\alpha,N}\left| {\sum}_{j=0}^{M}u_{n,j}\zeta_{n,j}\right|<\varepsilon. \end{array} $$

6 Numerical examples

In this section, we consider three examples of VIEs of the third-kind and apply the proposed method to them. The weighted L²-norm is used to show the accuracy of the method. In all the examples, we have used N = 10 in the Gauss–Jacobi quadrature formula and the following notation is used to show the convergence of the method

$$ \text{Ratio}=\frac{e(k-1)}{e(k)}, $$

where e(k) is the L²-error obtained with resolution k.

Example 1

As the first example, we consider the following third-kind VIE, which is an equation of Abel type [1, 4]:

$$ t^{2/3}u(t)=f(t)+{{\int}_{0}^{t}} \frac{\sqrt{3}}{3\pi} x^{1/3}(t-x)^{-2/3}u(x)dx, \quad t\in[0,1], $$

where

$$ f(t)=t^{\frac{47}{12}}\left( 1-\frac{\Gamma(\frac{1}{3}) {\Gamma}(\frac{55}{12})}{\pi\sqrt{3}{\Gamma}(\frac{59}{12})}\right). $$

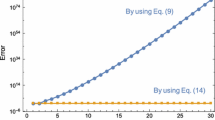
The exact solution of this equation is $u(t)=t^{\frac {13}{4}}$, which belongs to the space H³([0,1]). We have employed the method for this example with different values of M, k, ν and γ, and reported the results in Tables 1, 2 and Fig. 1. Table 1 displays the weighted L²-norm of the error for three different classes of the Jacobi parameters, which include ν = γ = 0.5 (second-kind Chebyshev wavelets), ν = γ = 0 (Legendre wavelets), and ν = γ = − 0.5 (first-kind Chebyshev wavelets) with different values of M and k. Moreover, the ratio of the error versus k is given in this table. It can be seen from Table 1 that the method converges faster in the case of the second-kind Chebyshev wavelets. In Table 2, we compare the maximum absolute error at the collocation points obtained by our method with the error of the collocation method introduced in [1], and the operational matrix method based on the adjusted hat functions [4]. From this table, it can be seen that our method gives more accurate results with less collocation points (we have used 192) than the method of [1] (N = 256) and also, has higher accuracy with a smaller number of basis functions (we have used 192) than the method of [4] (193). In Fig. 1, we show the error function obtained by the method based on the second-kind Chebyshev wavelets with M = 6, k = 4 (left) and M = 6, k = 6 (right).

Fig. 1

(Example 1.) Plot of the error function with ν = γ = 0.5 and M = 6, k = 4 (left), and M = 6, k = 6 (right)

Table 1 Example 1.) Numerical results with different values of M and k

Table 2 (Example 1.) Comparison of the maximum absolute error

Example 2

Consider the following third-kind VIE, which is used in the modelling of some heat conduction problems with mixed-type boundary conditions [1, 4]:

$$ tu(t)=\frac{6}{7}t^{3}\sqrt{t}+{{\int}_{0}^{t}} \frac{1}{2}u(x)dx, \quad t\in[0,1]. $$

This equation has the exact solution $u(t)=t^{\frac {5}{2}}$ (u ∈ H²([0,1])). The numerical results are given in Tables 3, 4 and Fig. 2. The L²-norms and the ratio of the error given in Table 3 confirm the superiority of the second-kind Chebyshev wavelets compared to the Legendre wavelets and first-kind Chebyshev wavelets. The method converges slower in this example than in the previous one, which could be expected, due to the lower regularity of the solution. A comparison between the maximum absolute error at collocation points of the present method and the methods given in [1] and [4] is presented in Table 4. Moreover, the error functions in the case of the second-kind Chebyshev wavelets with M = 6, k = 4 and M = 6, k = 6, can be seen in Fig. 2.

Fig. 2

(Example 2) Plot of the error function with ν = γ = 0.5 and M = 6, k = 4 (left), and M = 6, k = 6 (right)

Table 3 (Example 2.) Numerical results with different values of M and k

Table 4 (Example 2.) Comparison of the maximum absolute error

Example 3

Consider the following VIE of the third kind:

$$ t^{3/2}u(t)=f(t)+{{\int}_{0}^{t}} \frac{\sqrt{2}}{2 \pi } x (t-x)^{-1/2 }u(x)dx, \quad x\in[0,1], $$

where

$$ f(t)=t^{33/10} \left( 1-\frac{\Gamma \left( \frac{19}{5}\right)}{\sqrt{2 \pi} {\Gamma} \left( \frac{43}{10}\right)}\right). $$

This equation has the exact solution $u(t)=t^{\frac {9}{5}}$ (u ∈ H¹([0,1])). The numerical results for this example are displayed in Table 5 and Fig. 3, which confirm the higher accuracy of the second-kind Chebyshev wavelets method compared with the Legendre wavelets and first-kind Chebyshev wavelets methods. Since the exact solution in this case is not so smooth as in the previous examples, the method converges slower.

Fig. 3

(Example 3.) Plot of the error function with ν = γ = 0.5 and M = 6, k = 4 (left), and M = 6, k = 6 (right)

Table 5 (Example 3.) Numerical results with different values of M and k

7 Concluding remarks

In this work, a numerical method based on Jacobi wavelets has been introduced for solving a class of Volterra integral equations of the third-kind. First, the Jacobi wavelet functions have been introduced. Some error bounds are presented for the best approximation of a given function using the Jacobi wavelets. A numerical method based on the Jacobi wavelets, together with the use of the Gauss–Jacobi quadrature formula, has been proposed in order to solve Volterra integral equations of the third-kind. A criterion has been introduced for choosing the number of basis functions necessary to reach a specified accuracy. Numerical results have been included to show the applicability and high accuracy of this new technique. Our results confirm that the new method has higher accuracy than the other existing methods to solve the considered class of equations.