1 Introduction

The hyperbolic conservation laws arise in many scientific as well as technological fields, such as the Euler equations in gas dynamics, shallow water equations, and so on. In this article, we are concerned with numerically solving hyperbolic conservation laws in one space dimension with the below form

$$\begin{aligned} U_t + F(U)_x = 0, \end{aligned}$$
(1)

where U is the state vector; F(U) is the physical flux. In recent years, researchers have paid more and more attention to the arbitrary high-order methods for hyperbolic conservation laws (Toro et al. 2001; Titarev and Toro 2002, 2005; Pedro et al. 2014).

The discontinuous Galerkin (DG) methods are popular to solve the hyperbolic conservation laws. The traditional DG methods by Cockburn and Shu (1989, 1998) and Cockburn et al. (1989, 1990) are semi-discrete methods, apply the multi-stage Runge–Kutta approach (Gottlieb et al. 2009) to obtain high-order temporal accuracy, and are known as the RKDG methods. A brief historic review as well as the latest developments can be found in Cockburn et al. (2000) and Shu (2016) and the references cited therein. The RKDG methods enjoy the advantage of simplicity, but need to construct the inter-cell numerical flux and to calculate volume integrations at each stage; therefore, the RKDG methods are very time consuming relatively.

Alternatively, Qiu et al. (2005) developed a DG method using the Lax–Wendroff (LWDG) approach for the temporal discretization; the resulting LWDG method is one stage and explicit. In addition, Dumbser and Munz (2005a, 2005b) and Dumbser (2005) originally developed a new DG method with the one-stage ADER approach (Toro et al. 2001; Titarev and Toro 2002, 2005) for the temporal discretization. Subsequently, Dumbser and collaborators conducted a series of researches for this subject (Zanotti et al. 2015; Fambri et al. 2017, 2018; Rannabauer et al. 2018). The key ingredient of the DG methods (Zanotti et al. 2015; Fambri et al. 2017, 2018; Rannabauer et al. 2018) is to construct high-order inter-cell numerical flux. The inter-cell state is expressed in a form of temporal Taylor series expansion, where the temporal derivatives are described by the spatial derivatives using the governing PDE repeatedly. This procedure is known as the Cauchy–Kowalewski procedure [also termed as the Lax–Wendroff procedure in the literature Harten (1987)]. In addition, one also need to solve generalized Riemann problems at inter-cells to obtain the state itself and its spatial derivatives. However, the Cauchy–Kowalewski procedure is very cumbersome especially for high-dimensional problems. Therefore, the replacement or simplification of the Cauchy–Kowalewski procedure is very welcome. It is noteworthy that Dumbser and Munz (2006) have proposed an efficient algorithm for the Cauchy–Kowalewski procedure. More recently, Dumbser et al. (2014) and Duan and Tang (2020) have adopted the local continuous space-time Galerkin predictor approach (Dumbser et al. 2008) to replace the Cauchy–Kovalewski procedure under the framework of DG methods.

The key objective of this article is to develop a new DG method with the ADER approach for the temporal discretization, which is called as the ADER-DG method accordingly. The method here applies the differential transformation procedure Ayaz (2003, 2004) and Kurnaza et al. (2005) instead of the Cauchy–Kowalewski procedure as in Zanotti et al. (2015), Fambri et al. (2017, 2018) and Rannabauer et al. (2018) to express the spatiotemporal expansion coefficients of the solution through the low-order spatial expansion coefficients and enables us to avoid solving the generalized Riemann problem at inter-cells.

In comparison with the traditional RKDG methods (Cockburn and Shu 1989, 1998; Cockburn et al. 1989, 1990), the proposed method is one stage and fully discrete, which is welcome in many practical applications due to its simplicity and the low computer storage. Moreover, the one-stage reformulation greatly reduces the frequency of inter-process communications, and is desirable for the parallel computing. The current method is free of solving generalized Riemann problems at inter-cells, compared with the existing methods (Zanotti et al. 2015; Fambri et al. 2017, 2018; Rannabauer et al. 2018), which apply the Cauchy–Kowalewski procedure. The differential transformation procedure is more concise and more efficient than the Cauchy–Kowalewski procedure (Norman and Finkel 2012). The space–time polynomial representation of the solution on each space-time control volume leads to precise calculations for the volume integral and the numerical flux and avoids the use of costly numerical quadrature rule.

This article is organized as follows. In Sect. 2, we present a new ADER-DG method with differential transformation procedure. Section 3 contains extensive examples to illustrate the performances of the current method. Some conclusions are given in Sect. 4.

2 Construction of ADER-DG method

2.1 Mesh and solution space

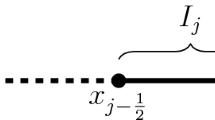
We first divide the spatial domain of interest with cells \(I_j = \left[ x_{j-\frac{1}{2}}, \; x_{j+\frac{1}{2}} \right] \), for \(j=1,2,\ldots ,N\), and we set \( x_j=\frac{1}{2}\left( x_{j-\frac{1}{2}}+x_{j+\frac{1}{2}}\right) \) and \( \tau _j=x_{j+\frac{1}{2}}-x_{j-\frac{1}{2}} \) as the mesh center and the mesh size, respectively. The notation \(\tau =\max \nolimits _{1\le j\le N} \tau _j\) stands for the Maximum mesh size and the notation \(\Omega _j=I_j\times \left[ t^n, t^{n+1}\right] \) represents the space-time control volume with \(\left[ t^n, t^{n+1}\right] \) being the time interval.

Herein, we take the approximation solution space as follows

$$\begin{aligned} V_{\tau }^k = \left\{ \varphi (x,t): \varphi (x,t)\big |_{\Omega _j} \in P^k( \Omega _j)\right\} , \end{aligned}$$

where \(P^k(\Omega _j)\) denotes the set of space-time polynomials of degree up to k on \(\Omega _j\).

2.2 General formulation of ADER-DG method

Multiplication of (1) with an arbitrary spatial test function \(\phi (x)\) and using the integration by parts on \(\Omega _j\) yield the following weak form

$$\begin{aligned}&\int \limits _{I_j} U\left( x, t^{n+1} \right) \, \phi (x) \; \mathrm{d}x - \int \limits _{I_j} U(x, t^{n}) \, \phi (x) \; \mathrm{d}x \\&\qquad + \int \limits _{t^n}^{t^{n+1}} F\left( x_{j+\frac{1}{2}}, t\right) \; \mathrm{d}t \cdot \phi \left( x^-_{j+\frac{1}{2}}\right) - \int \limits _{t^n}^{t^{n+1}}F\left( x_{j-\frac{1}{2}}, t\right) \; \mathrm{d}t \cdot \phi \left( x^+_{j-\frac{1}{2}}\right) - \iint \limits _{ \Omega _j } F (x,t) \, \phi _x \; \mathrm{d}x \mathrm{d}t \\&\quad = 0, \quad \mathrm {for} \; j=1,2, \ldots , N. \end{aligned}$$

Here, we take the physical flux as a binary function with \(F(x,t) = F(U(x,t))\) for the sake of easy presentation.

The fully discrete ADER-DG method for solving (1) is defined as follows: for all test functions \( \phi (x) = (x-x_j)^{k_x}\) with \(k_x = 0, 1, \ldots , k\) from \(V_{\tau }^k\), the solution \(U_{\tau }(x,t) \in V_{\tau }^k\) satisfies the following equality

$$\begin{aligned} \begin{aligned}&\int \limits _{ I_j} U_{\tau }\left( x, t^{n+1}\right) \, \phi (x) \; \mathrm{d}x \\&\quad = \int \limits _{ I_j} U_{\tau }(x, t^{n}) \, \phi (x) \; \mathrm{d}x - \widehat{F}_{j+\frac{1}{2}} \cdot \phi \left( x^-_{j+\frac{1}{2}}\right) + \widehat{F}_{j-\frac{1}{2}} \cdot \phi \left( x^+_{j-\frac{1}{2}}\right) \\&+ \iint \limits _{ \Omega _j } F_{\tau }(x,t) \, \phi _x \; \mathrm{d}x \mathrm{d}t, \quad \mathrm {for} \; j=1,2, \ldots , N. \end{aligned} \end{aligned}$$
(2)

Here, the numerical flux \(\widehat{F}_{j+\frac{1}{2}}\) is used to approximate the time integration of the physical flux at inter-cell, i.e., \( \int \nolimits _{t^n}^{t^{n+1}} F\left( x_{j+\frac{1}{2}}, t \right) \; \mathrm{d}t\).

Herein, on each space–time control volume \(\Omega _j\), we take \(U_{\tau }(x,t)\) (the subscript j is ignored for the sake of simplicity) in a piecewise space–time polynomial form to approximate the unknown solution U(x, t). At time \(t^n\), we have \(U_{\tau }(x,t^n)\) at hands as a linear combination of spatial polynomials

$$\begin{aligned} U_{\tau }(x,t^n) = \sum \limits _{k_x = 0}^k \widetilde{U}(k_x, 0)(x-x_j)^{k_x}, \end{aligned}$$

with \( \widetilde{U}(k_x, 0)\) being the expansion coefficient in space. Our basic goal is to construct the following space-time polynomial

$$\begin{aligned} U_{\tau }(x,t) = \sum \limits _{k_t = 0}^k \sum \limits _{k_x= 0}^{k-k_t} \widetilde{U}(k_x, k_t)(x-x_j)^{k_x}(t-t^n)^{k_t} \in V_{\tau }^k, \end{aligned}$$

on \(\Omega _j\) in the whole time interval \([t^n,t^{n+1}]\). Here, \( \widetilde{U}(k_x, k_t)\) denote the space–time-dependent degrees of freedom (DOF) on \(\Omega _j\). In the following, we will obtain \(\widetilde{U}(k_x, k_t)\) from \(\widetilde{U}(k_x, 0)\) at the old time level \(t^n\) repeatedly using the differential transformation procedure presented in Sect.  2.2.1.

The evolution from \(U_{\tau }(x,t^n)\) to \(U_{\tau }(x,t^{n+1})\) needs the evaluation of the right hand side of (2): a space integral, a space–time integral as well as the construction of numerical fluxes at intercells.

2.2.1 A brief review of differential transformation procedure

The key component of DG methods (Zanotti et al. 2015; Fambri et al. 2017, 2018; Rannabauer et al. 2018) is to repeatedly differentiate the PDE and to express the temporal derivatives through the spatial ones using the Cauchy–Kowalewski procedure. However, the Cauchy–Kowalewski procedure becomes more cumbersome especially for higher order derivatives due to chain rules. To reduce the cost of the Cauchy–Kowalewski procedure, Dumbser and Munz (2006) have proposed an efficient algorithm based on the Leibnize rule for two-dimensional Euler equations under the DG frame. More recently, Dumbser et al. (2014) and Duan and Tang (2020) have employed the local continuous space–time Galerkin predictor approach to replace the Cauchy–Kovalewski procedure (Dumbser et al. 2008) in the framework of DG methods.

Herein, we apply the differential transformation procedure to replace the Cauchy–Kowalewski procedure. The differential transformation procedure was originally proposed for nonlinear initial value problems in the electric circuit analysis (Pukhov 1982; Zhou 1986). Ayaz generalized this procedure to two-dimensional case (Ayaz 2003) and system case (Ayaz 2004; Kurnaza et al. 2005) conducted the extension to n-dimensional case. Recently, by means of this procedure, Norman and Finkel (2012) have developed a multi-moment finite volume scheme for one-dimensional balance laws.

The detailed definition of the differential transformation procedure is as follows. Suppose that a function u(x, t) in cell \(I_j\) at time \(t^n\) is known, the differential transformation is defined as in Ayaz (2003, 2004) and Kurnaza et al. (2005)

$$\begin{aligned} \tilde{u}(k_x,k_t) = \dfrac{1}{k_x! k_t!} \dfrac{\partial ^{k_x+k_t}u(x, t)}{\partial x^{k_x} \partial t^{k_t}}\bigg |_{x=x_j, t=t^n}, \;\; \mathrm {with} \;\; u(x,t) = \sum \limits _{k_t = 0}^{k} \sum \limits _{k_x = 0}^{ k-k_t} \tilde{u}(k_x,k_t) (x-x_j)^{k_x} (t-t^n)^{k_t},\nonumber \\ \end{aligned}$$
(3)

where u(x, t) is the original function and \(\tilde{u}(k_x,k_t) \) denotes the transformed function. In fact, the transformed function \(\tilde{u}(k_x, k_t)\) denotes the expansion coefficient of the truncated Taylor series expansion. The transformed functions used in this article are shown in Table 1.

Table 1 Transformed functions of some functions encountered in this article
Full size table

Subsequently, we exemplify the differential transformation procedure with the non-linear Burgers’ equation

$$\begin{aligned} u_t + f(u)_x =0, \end{aligned}$$
(4)

where \( \displaystyle f(u)=\frac{1}{2} u^2\) denotes the physical flux. Combining the rules in Table 1, we implement the differential transformation procedure at both ends of (4) and obtain the below equality for the transformed functions

$$\begin{aligned} (k_t+1) \tilde{u}(k_x, k_t+1) + (k_x+1) \tilde{f}(k_x+1, k_t)=0, \end{aligned}$$

which leads to the following recurrence formula

$$\begin{aligned} \tilde{u}(k_x, k_t+1) = -\dfrac{k_x+1}{k_t+1} \tilde{f}(k_x+1, k_t), \end{aligned}$$
(5)

with

$$\begin{aligned} \tilde{f}(k_x,k_t) = \frac{1}{2}\sum \limits _{r=0}^{k_x}\sum \limits _{s=0}^{k_t} \tilde{u}(r,s)\tilde{u}(k_x-r,k_t-s). \end{aligned}$$

We here take the physical flux f(u) as a binary function with \(f(x,t) = f(u(x,t))\). On basis of \(\tilde{u}(k_x, 0), \, k_x=0,1,\ldots ,k\) coming from \( u_{\tau }(x,t^n) = \sum \nolimits _{k_x=0}^{k} \tilde{u}(k_x, 0)(x-x_j)^{k_x} \) at time \(t^n\) and applying the above recurrence relation (5) repeatedly, we obtain

$$\begin{aligned} \tilde{u}(k_x, k_t) \quad \mathrm {and} \quad \tilde{f}(k_x, k_t) , \; \mathrm {for} \; k_t=0,1,\ldots , k; \; k_x=0,1,\ldots ,k-k_t. \end{aligned}$$

Next, we achieve

$$\begin{aligned} u_{\tau }(x,t)&= \sum \limits _{k_t=0}^{k} \sum \limits _{k_x=0}^{k-k_t} \tilde{u}(k_x,k_t)(x-x_j)^{k_x}(t-t^n)^{k_t} \in V_{\tau }^k, \\ f_{\tau }(x,t)&= \sum \limits _{k_t=0}^{k} \sum \limits _{k_x=0}^{k-k_t} \tilde{f}(k_x,k_t)(x-x_j)^{k_x}(t-t^n)^{k_t} \in V_{\tau }^k, \end{aligned}$$

on the space–time control volume \(\Omega _j\). We present the detailed steps of the procedure for Burgers’ equation in Appendix A.

Remark 1

Actually, to implement the differential transformation procedure for a given function is to obtain its transformed functions namely the expansion coefficients of the Taylor series form. Moreover, the differential transformation procedure converts a PDE into a series of recurrence relations for expansion coefficients of the solution in a Taylor series form.

2.2.2 The differential transformation procedure for Euler equations

Let us deal with the Euler equations in the gas dynamics

$$\begin{aligned} \left\{ \begin{array}{l} \rho _t + (\rho u)_x = 0, \\ (\rho u)_t + (\rho u^2 + p)_x = 0, \\ E_t + (u(E+p))_x= 0. \end{array} \right. \end{aligned}$$
(6)

Here, \(\rho \) is the density, u is the velocity, E is the total energy, p is the pressure, which is related to the total energy by

$$\begin{aligned} E=\frac{p}{\gamma -1}+\frac{1}{2}\rho u^2 \end{aligned}$$
(7)

with \(\gamma =1.4\) as the specific heats ratio. We can rewrite the system (6) in the conservative form (1) with the following conservative variable and physical flux

$$\begin{aligned} U = \left( \begin{array}{c} \rho \\ \rho u\\ E \end{array} \right) , \quad F(U) = \left( \begin{array}{c} \rho u\\ \rho u^2+p\\ u(E+p) \end{array} \right) . \end{aligned}$$

Suppose in cell \(I_j\) and at time \(t=t^n\), the solution \(U_{\tau }(x,t^n)\) are known in the form

$$\begin{aligned} U_\tau (x,t^n) = \left( \rho _{\tau }(x,t^n) , (\rho u)_{\tau }(x,t^n) , E_{\tau }(x,t^n) \right) ^{\top } =\sum \limits _{k_x=0}^k \widetilde{U}(k_x,0)(x-x_j)^{k_x}. \end{aligned}$$
(8)

Then, using the Table   1, we implement the differential transformation procedure on both ends of system (1) in a componentwise manner; we obtain the following equality of the transformed functions in a vector form

$$\begin{aligned} (k_t+1) \widetilde{U}(k_x, k_t+1) + (k_x+1) \widetilde{F}(k_x+1, k_t) = 0, \end{aligned}$$
(9)

with the below auxiliary variables

$$\begin{aligned} \begin{aligned} \widetilde{F}(k_x,k_t)&= \left( \begin{array} {c} (\widetilde{\rho u})(k_x,k_t) \\ (\gamma -1) \widetilde{E}(k_x,k_t) + \frac{1}{2} (3-\gamma ) \widetilde{G_3} (k_x,k_t) \\ \gamma \widetilde{G_5}(k_x,k_t) - \frac{1}{2} (\gamma - 1) \widetilde{G_6}(k_x,k_t) \end{array} \right) , \\ \widetilde{G_{1}}(k_x,k_t)&=-\frac{1}{\tilde{\rho }(0,0)}\sum \limits _{r=0}^{k_x}\sum \limits _{s=0}^{k_t}\tilde{\rho }(r,s)\widetilde{G_{1}}(k_x-r,k_t-s),\\ \widetilde{G_{2}}(k_x,k_t)&=\sum \limits _{r=0}^{k_x}\sum \limits _{s=0}^{k_t}(\widetilde{\rho u})(r,s)(\widetilde{\rho u})(k_x-r,k_t-s),\\ \widetilde{G_3}(k_x,k_t)&=\sum \limits _{r=0}^{k_x}\sum \limits _{s=0}^{k_t}\widetilde{G_{2}}(r,s)\widetilde{G_{1}}(k_x-r,k_t-s),\\ \widetilde{G_4}(k_x,k_t)&= \sum \limits _{r=0}^{k_x}\sum \limits _{s=0}^{k_t}\widetilde{\rho u}(r,s)\widetilde{G_1}(k_x-r,k_t-s),\\ \widetilde{G_5}(k_x,k_t)&= \sum \limits _{r=0}^{k_x}\sum \limits _{s=0}^{k_t}\widetilde{ G_4}(r,s)\widetilde{E}(k_x-r,k_t-s),\\ \widetilde{G_{6}}(k_x,k_t)&= \sum \limits _{r=0}^{k_x}\sum \limits _{s=0}^{k_t} \widetilde{G_4}(r,s)\widetilde{G_3}(k_x-r,k_t-s), \end{aligned} \end{aligned}$$

where we ignore the subscript j for the clarity of presentation. Moreover, Eq. (9) leads to the following recurrence formula

$$\begin{aligned} \widetilde{U}(k_x, k_t+1) = -\dfrac{k_x+1}{k_t+1}\widetilde{F}(k_x+1, k_t). \end{aligned}$$
(10)

Then, starting from

$$\begin{aligned} \widetilde{U}(k_x,0) = \left( \tilde{\rho }(k_x, 0), (\widetilde{\rho u})(k_x, 0), \widetilde{E}(k_x, 0) \right) ^{\top }, \; \mathrm {for} \; k_x=0,1,\ldots ,k, \end{aligned}$$

we can circularly get

$$\begin{aligned} \widetilde{U}(k_x,k_t) \quad \mathrm {and} \quad \widetilde{F}(k_x,k_t) , \; \mathrm {for} \;k_t=0,1,\ldots , k; \; k_x=0,1,\ldots ,k-k_t, \end{aligned}$$

by repeatedly using the recurrence formula (10). Subsequently, we obtain \( U_{\tau }(x,t)\) and \(F_{\tau }(x,t) \) as follows

$$\begin{aligned} U_{\tau }(x,t)&= \sum \limits _{k_t = 0}^k \sum \limits _{k_x= 0}^{k-k_t} \widetilde{U}(k_x, k_t)(x-x_j)^{k_x}(t-t^n)^{k_t} \in V_{\tau }^k, \\ F_{\tau }(x,t)&= \sum \limits _{k_t = 0}^k \sum \limits _{k_x= 0}^{k-k_t}\widetilde{F}(k_x, k_t)(x-x_j)^{k_x}(t-t^n)^{k_t} \in V_{\tau }^k, \end{aligned}$$

on each space–time control volume \(\Omega _j, \; \mathrm {for} \; j=1,2,\ldots ,N\) to approximate the unknown conservative state U(x, t) and the physical flux \(F(x,t)= F(U(x,t))\). We present the specific steps in Appendix B.

In the above formulae (10), we apply the following relations

$$\begin{aligned} \rho u^2 + p&= \rho u^2 + (\gamma - 1) \left( E - \frac{1}{2} \rho u^2 \right) = (\gamma - 1) E + \frac{1}{2} (3-\gamma ) \rho u^2 , \\ u(E+p)&= u \left( E+ (\gamma - 1) \left( E - \frac{1}{2} \rho u^2 \right) \right) = \gamma u E - \frac{1}{2} (\gamma - 1)u(\rho u^2), \end{aligned}$$

due to the equation of state (7).

Remark 2

The key function of the differential transformation procedure is to supply the temporal evolution, locally for each cell, of the existing solution \(U_{\tau }(x,t^n)\) at time \(t^n\).

Remark 3

The Cauchy–Kowalewski procedure uses the symbolic expansions of the PDE itself directly, which needs costly recomputations of many terms and leads to exponential increase in complexity. While, the differential transformation procedure is considerably cheaper than the Cauchy–Kowalewski procedure and achieves the same aim with a predictable polynomial complexity.

2.2.3 Construction of high order numerical fluxes

To construct high-order numerical flux in ADER schemes (Toro et al. 2001; Titarev and Toro 2002, 2005; Dumbser and Munz 2005a, b, 2006; Dumbser 2005), one first expand the inter-cell state in a time Taylor series form, where the temporal derivatives are expressed by the spatial derivatives using the Cauchy–Kowalewski procedure. To get the spatial derivatives, one also need to solve generalized Riemann problems at inter-cells.

After applying the differential transformation procedure in cell \(I_j\) at time \(t^n\), we have \(U_{\tau }(x,t) \) as well as \(F_{\tau }(x,t) \) on \(\Omega _j\) at hands, and then we adopt the simple and efficient Lax–Friedrichs flux

$$\begin{aligned} \widehat{F}_{j+\frac{1}{2}} = \frac{1}{2} \int \limits _{t^n}^{t^{n+1}} \left( F_{\tau }\left( x^-_{j+\frac{1}{2}}, t\right) + F_{\tau } \left( x^+_{j+\frac{1}{2}}, t \right) - \alpha \left( U_{\tau }\left( x^+_{j+\frac{1}{2}}, t\right) - U_{\tau }\left( x^-_{j+\frac{1}{2}}, t\right) \right) \right) \,\mathrm{d}t,\nonumber \\ \end{aligned}$$
(11)

where \(\alpha \) is an estimate of largest wave speed on the whole spatial domain.

Because \(U_{\tau }(x,t)\) and \(F_{\tau }(x,t)\) are all space–time polynomials on \(\Omega _j\), we can adopt precise calculations for the numerical flux in (11) in stead of resorting to the costly numerical quadrature rule.

In addition, for the space integral and the space–time integral in (2), we also apply the precise calculations and substitute them into (2), then obtain the fully discrete ADER-DG method (2).

Remark 4

The present construction means of the numerical fluxes is free of solving generalized Riemann problem at inter-cells.

2.3 Implementation details of ADER-DG method

Here, we summarize the proposed method within one time step \(t^n\longrightarrow t^{n+1}\) as follows:

  1. (i)

    Initially, we obtain \(\widetilde{U}(k_x,0), \; k_x=0,1,\ldots , k,\) from U(x, 0) in each cell \(I_j\), for \(j=1,2,\ldots , N\).

  2. (ii)

    At time \(t^n\), by the recursive steps (10), we acquire \(\widetilde{U}(k_x, k_t)\) and \(\widetilde{F}(k_x, k_t)\) on basis of \(\widetilde{U}(k_x,0)\), then obtain \(U_{\tau }(x,t)\) and \(F_{\tau }(x,t)\).

  3. (iii)

    Construct numerical fluxes \(\widehat{F}_{j+ \frac{1}{2}}\) using the formula (11).

  4. (iv)

    Obtain \(U_{\tau } (x,t^{n+1})\) according to the one-step formula (2).

  5. (v)

    Apply a slope limiter on \(U_{\tau }\left( x,t^{n+1}\right) \) when needed.

Remark 5

The one-dimensional method proposed here can be directly generalized to high-dimensional problems. To handle the multi-dimensional problems, we need to pay special attention on the differential transformation procedure. In practice, in comparison to the one-dimensional case, we need to add an extra layer on the program for the differential transformation procedures, see Appendices A and B. In addition, we also need to be careful when initializing.

3 Numerical results

In this section, we conduct classical examples to validate the performance of the current method. In the following computations, we take the polynomial of degree two and four (i.e., \(k=2\) and \(k=4\)) , and set the CFL constant as 0.18 and 0.1, respectively.

3.1 The scalar case

3.1.1 Linear advection equation

We first consider the linear advection equation as in (Jiang and Shu 1996a)

$$\begin{aligned} \left\{ \begin{array}{ll} u_t + u_x =0, &{} -1\le x \le 1, \\ u(x,0) = u_0(x), &{} \mathrm { periodic}, \end{array} \right. \end{aligned}$$

where

$$\begin{aligned}&u_0(x) = \left\{ \begin{array}{ll} \frac{1}{6} \left( \mathcal {G}(x,\beta ,z-\delta ) + \mathcal {G}(x,\beta ,z+\delta ) + 4 \mathcal {G}(x,\beta ,z) \right) , &{} -0.8\le x \le -0.6, \\ 1, &{} -0.4\le x \le -0.2, \\ 1 - | 10(x-0.1) |, &{} 0 \le x \le 0.2, \\ \frac{1}{6} \left( \mathcal {F}(x,\alpha ,a-\delta ) + \mathcal {F}(x,\alpha ,a+\delta ) + 4 \mathcal {F}(x,\alpha ,a) \right) , &{} 0.4\le x \le 0.6, \\ 0, &{} \mathrm {otherwise}, \end{array} \right. \\&\mathcal {G}(x,\beta ,z) = \displaystyle e^{-\beta (x-z)^2}, \\&\mathcal {F}(x,\alpha ,a) = \sqrt{\max \left( 1-\alpha ^2(x-a)^2, 0 \right) }. \end{aligned}$$

The above constants are set as \(a=0.5\), \(z=-0.7\), \(\delta =0.005\), \(\alpha = 10\), and \(\beta = \log 2/36 \delta ^2\). The solution includes a smooth but narrow combination of Gaussians, a square, a triangle, as well as an half ellipse.

We compute this example until \(t=8\) on a mesh with 200 cells and show the numerical results by the third order as well as the fifth-order methods in Fig.   1. Both the ADER-DG methods perform well for the four types of waves in the initial data. The numerical solution by the fifth-order method is clearly sharper than that by the third-order method.

Fig. 1
figure 1

Linear advection equation by third-order (left) and fifth-order (right) ADER-DG methods. Solutions at \(t=8\)

Full size image

3.1.2 Burgers’ equation

Then, we conduct the ADER-DG method for non-linear Burgers’ equation (4) coupled with two different initial conditions:

$$\begin{aligned} u(x,0) = 0.5 + \sin (\pi x), \; x\in [0,2] \quad \mathrm {and} \quad u(x,0) = \left\{ \begin{array}{ll} -0.5 &{} x \le 0.5,\\ 1 &{} x \le 1, \\ 0 &{} \mathrm {else}, \end{array} \right. \; x\in [0, 1.5]. \end{aligned}$$

The first case develops a shock; the second one produces a shock as well as a rarefaction at the same time. The numerical solutions of the two examples in comparison with the exact solutions are shown in Fig.   2. The numerical solutions obviously agree well with the exact solutions, and the discontinuities are all well resolved.

Fig. 2
figure 2

Burgers’ equation by third-order (left) and fifth-order (right) ADER-DG methods. Top: solutions of the first example at \(t=1.5/\pi \); Bottom: solutions of the second example at \(t = 0.5\) (right)

Full size image

3.2 The system case

3.2.1 Testing the order of accuracy

On the basis of the Euler equations (6), we testify the order of accuracy using an example with exact solutions from (Qiu and Shu 2003)

$$\begin{aligned} \rho (x,t) = 1 + 0.2\sin (\pi (x-t)) , \quad u(x,t)=1, \quad p(x,t)=1, \quad x \in [0,2], \end{aligned}$$

and we exert periodic boundary conditions at both ends of the spatial domain. For this example, we only apply the polynomial of degree four. The errors at time \(t=2\) and orders of accuracy are shown in Table   2. The solutions clearly converge at the optimal rate.

3.2.2 Sod problem

The initial conditions are as in (Sod 1978)

$$\begin{aligned} (\rho ,u,p)(x,0) = \left\{ \begin{array}{ll} (1, 0, 1) &{} \text{ if } \; \ x \le 0, \\ (0.125, 0, 0.1) &{} \mathrm {if} \; \ x>0, \end{array} \right. \end{aligned}$$

on \([-5,5]\). This example develops a rarefaction fan, a contact discontinuity as well as a shock at the same time. The computed density at time \(t=2\) is shown in Fig.   3. The numerical results keep sharp discontinuity transition and the contact discontinuities are also considerably well resolved.

Table 2 The errors and orders of accuracy for density
Full size table

3.2.3 Lax problem

The initial conditions are defined by

$$\begin{aligned} (\rho ,u,p)(x,0) = \left\{ \begin{array}{ll}(0.445,0.698,3.528) &{} \mathrm {if} \; x\le 0,\\ (0.5,0,0.571) &{} \mathrm {if} \; x>0, \end{array} \right. \end{aligned}$$

on \([-5,5]\). This example develops a shock as well as a contact discontinuity, which is difficult to resolve accurately. The computed density at time \(t=1.3\) compared with the exact one are shown in Fig.   4. The strong shock is equally well resolved by means of both methods.

Fig. 3
figure 3

Sod problem by third-order (left) and fifth-order (right) ADER-DG methods. Density at \(t = 2\)

Full size image
Fig. 4
figure 4

Lax problem by third-order (left) and fifth-order (right) ADER-DG methods. Density at \(t = 1.3\)

Full size image

3.2.4 Shu–Osher problem

The initial data are given by (Shu and Osher 1988)

$$\begin{aligned} (\rho ,u,p)(x,0) = \left\{ \begin{array}{ll} (3.857143,2.629369,10.333333) &{} \mathrm {if} \; x < -4, \\ (1+0.2\sin (5x),0,1) &{} \mathrm {if} \; x \ge -4, \end{array} \right. \end{aligned}$$

on \([-5,5]\). This example produces a shock interacting with complex smooth regions. We present the computed density at time \(t=1.8\) in Fig.   5, which fits well with the reference solution.

Fig. 5
figure 5

Shu-Osher problem by third-order (left) and fifth-order (right) ADER-DG methods. Density at \(t = 1.8\)

Full size image

3.2.5 Blast wave problem

The following example involves interaction of blast waves and its initial conditions are given by (Woodward and Colella 1984)

$$\begin{aligned} (\rho ,u,p)(x,0) =\left\{ \begin{array}{ll} (1,0,1000) &{}\quad \mathrm {if} \; 0\le x<0.1,\\ (1,0,0.01) &{}\quad \mathrm {if} \; 0.1\le x<0.9,\\ (1,0,100) &{}\quad \mathrm {if} \; 0.9\le x\le 1,\end{array} \right. \end{aligned}$$

on an unity domain [0, 1]. We impose a reflective boundary condition at both ends of the spatial domain, see Woodward and Colella (1984) for more details. We carry out the simulation on a mesh with 400 cells up to time \(t=0.038\) and present the computed density as well as the reference one in Fig.   6. The numerical results obviously keep a steep discontinuity transition.

Fig. 6
figure 6

Blast wave problem by third-order (left) and fifth-order (right) ADER-DG methods. Density at \(t = 0.038\)

Full size image

3.2.6 123 problem

The initial conditions are given by (Toro 1999)

$$\begin{aligned} (\rho ,u,p)(x,0) = \left\{ \begin{array}{ll} (1, -2, 0.4) &{} \mathrm {if} \; x<0.5, \\ (1, 2, 0.4) &{} \mathrm {if} \; x>0.5, \end{array} \right. \end{aligned}$$

on [0, 1]. We present the computed density at time \(t=0.15\) on a mesh with 200 cells in comparison with the exact one in Fig.   7. The central expansion regions are all well resolved by the current methods.

Fig. 7
figure 7

123 problem by third-order (left) and fifth-order (right) ADER-DG methods. Density at \(t =0.15\)

Full size image
Fig. 8
figure 8

Modified shock/turbulence interaction problem by third-order (left) and fifth-order (right) ADER-DG methods. Upper: density at \(t =5\); Bottom: pressure at \(t =5\)

Full size image

3.2.7 Modified shock/turbulence interaction

Then, we conduct an example (Toro and Titarev 2005) that is actually a modification of the shock/turbulence problem developed in Jiang and Shu (1996b) and Balsara and Shu (2000). The modification mainly includes three parts: (i) a weaker shock wave, (ii) a density fluctuation with frequency four times higher and (iii) a ending time ten times larger. This example produces a right facing shock wave running into a high-frequency density perturbation. As time develops, a shock moves into this density perturbation, which spreads upstream. In practice, this example can also be regarded as an extension of the Shu–Osher problem in Sect. 3.2.4 and is applied to validate a severely oscillatory wave interacting with a shock. Especially, the example here is more appropriate for testing the performance of the current high-order method. We use the following initial conditions

$$\begin{aligned} (\rho ,u,p)(x,0) = \left\{ \begin{array}{ll} (1.515695, 0.523346, 1.805) &{} \mathrm {if} \; x \le -4.5,\\ \left( 1+0.1\sin \left( {20} \pi x\right) , 0, 1\right) &{} \mathrm {if} \; x> -4.5, \end{array} \right. \end{aligned}$$

on \([-5,5]\). We implement the computation on a very refined mesh with 1000 cells up to time \(t=5\) and show the computed density in Fig.   8. Both methods produce excellent resolution for these high-frequency oscillations.

In addition, we also compare the CPU time for examples from Sects. 3.2.2–3.2.7 by the third-order ADER-DG method and the third-order RKDG method, see Table   3. As shown in the Table   3, the third-order ADER-DG method can save at least 38% of CPU time, and even save 70% of CPU time compared with the RKDG method with the same order of accuracy.

Table 3 For the CPU time, the gain of ADER-DG in terms of percentage with regard to the RKDG method
Full size table

3.2.8 Vortex evolution problem

In the end, we apply a one-dimensional example similar to the two-dimensional example from Shu (1997). This example here is used to validate the proposed method with regard to the conservation of a vortex for long time evolution. The setup of this example is as follows. The mean flow is \(\rho =1, p=1,u=1\) on the spatial domain [0, 10]. We add, to the mean flow, an isentropic vortex (perturbation in velocity u and the temperature \(T=p/\rho \) and no perturbation in the entropy \(S=p/\rho ^{\gamma }\)) as follows

$$\begin{aligned} \delta u = \dfrac{\varepsilon }{2\pi }e^{ \left( 0.5(1-(x-5)^2) \right) }(x-5), \quad \delta T = -\dfrac{(\gamma - 1)\varepsilon ^2}{8 \gamma \pi } e^{ 1-(x-5)^2}, \end{aligned}$$

with \(\varepsilon = 5\).

We impose periodic boundary conditions and carry our this example on different meshes with 100 and 200 cells. The numerical results by the third-order ADER-DG method at \(t=100\) (after 10 time periods) are shown in Table   9. As we can see from Table   9, the ADER-DG method can keep a good conservation of the vortex even for a larger time modelling. In addition, with the refinement of the mesh, the conservation of the vortex is improved.

Fig. 9
figure 9

Vortex evolution problem by third-order ADER-DG method. Density at \(t =100\)

Full size image

4 Summary and conclusions

In this article, we develop a new DG method with the one-stage ADER approach for the temporal discretization. The key component of this method is to express the spatiotemporal expansion coefficients of the solution through the low-order spatial expansion coefficients using the differential transformation procedure recursively. So, we can obtain the solution in a space–time polynomial form on each space–time control volume starting from the solution at time \(t^n\) using the differential transformation procedure repeatedly. Since the numerical solutions are in space–time polynomial forms, we can adopt precise calculations for the numerical fluxes as well as the volume integrations, and avoid using the numerical quadrature rules correspondingly.

The differential transformation procedure is more efficient and the coding is more concise than the Cauchy–Kowalewski procedure. Compared with the RKDG methods, the current method needs less computer memory due to no intermediate stages. Thanks to the explicit one-step nature and the compact stencil, the current ADER-DG method is an ideal candidate for parallel computing on supercomputers. In addition, the proposed method avoids solving the generalized Riemann problems at inter-cells. Moreover, we can easily proceed to arbitrary high-order accuracy in space and time without much coding effort. In summary, the resulting method is one step, one stage, and fully discrete.

Several classical examples demonstrate the high-order accuracy, good resolution for discontinuous solutions and high computational efficiency. Extension to two-dimensional cases constitutes our ongoing research.