A New Lax–Wendroff Discontinuous Galerkin Method with Superconvergence

Abstract

Superconvergence of discontinuous Galerkin (DG) methods for hyperbolic conservation laws has been intensively studied in different settings in the past. For example, the numerical solution by a semi-discrete DG scheme is superconvergent with order $2k+1$ in the negative-order norms, when the solution is globally smooth. Hence the accuracy of the numerical solution can be enhanced to $(2k+1)$th order accuracy by simply applying a carefully designed post-processor (Cockburn et al. in Math Comput 72:577–606, 2003). In this paper, we investigate superconvergence for the DG schemes coupled with Lax–Wendroff (LW) time discretization (LWDG). Through numerical experiments, we find that the original LWDG scheme developed in Qiu et al. (Comput Methods Appl Mech Eng 194:4528–4543, 2005) does not exhibit superconvergence properties mentioned above. In order to restore superconvergence, we propose to use the techniques from the local DG scheme to reconstruct high order spatial derivatives, while, in the original LWDG formulation, the high order derivatives are obtained by direct differentiation of the numerical solution. A collection of 1-D and 2-D numerical experiments are presented to verify superconvergence properties of the newly proposed LWDG scheme. We also perform Fourier analysis via symbolic computations to investigate the superconvergence of the proposed scheme.

1 Introduction

The discontinuous Galerkin (DG) methods are a class of finite element methods, designed for solving hyperbolic problems and many others [13]. A distinct feature of the DG methods is to use piecewise polynomial spaces of degree $k$ with discontinuities at cell boundaries as trial and test function spaces. Due to many attractive properties of DG methods, such as the ease of handling complicated geometries and boundary conditions, the compactness and the flexility for unstructured meshes and so on, these methods are becoming increasingly popular in many applications [10, 11, 27].

In this paper, we consider another distinguished property of the DG scheme, namely, superconvergence. In particular, we are interested in two types of superconvergence behaviors. One is the accuracy enhancement by post-processing the numerical solution, the other one is the long time behavior of numerical errors. It is showed in [9] that a semi-discrete DG solution converges with $(2k+1)$th order accuracy in the negative-order norm, when the problem is linear and the solution is globally smooth. Based on the error estimate, the DG solution on translation invariant grids can be post-processed via a kernel convolution with B-spline functions. The post-processed solution is proved to converge with order $2k+1$ in the $L^{2}$ norm [4, 9]. A similar superconvergence result for the local DG (LDG) methods solving convection–diffusion problems is provided in [18]. On the other hand, it is shown in [6–8, 30] that the semi-discrete DG or LDG solution is closer to the Radau projection of the exact solution [$(k+2)$th order] than the exact solution itself [$(k+1)$th order]. More recently, Cao et al. constructed another special projection of the exact solution, which is even closer to the DG solution than the Radau projection [$(2k+1)$th order], see [5]. Consequently, the error of a DG solution will not significantly grow over a long time period. Some related work of adopting Fourier analysis to investigate superconvergence properties for DG schemes includes [2, 3, 16, 17, 25, 26, 31].

The semi-discrete DG scheme can be further combined with certain time integrators. For example, one can choose the strong stability persevering (SSP) Runge–Kutta (RK) method [14] to achieve high order accuracy in both space and time. As an alternative, the one-step one-stage high order Lax–Wendroff (LW) type time discretization [21] attracts lots of attentions due to its compactness and low-storage requirement [22, 23]. The LW procedure is known as the Cauchy–Kowalewski type time discretization in the literature, which relies on converting each time derivative in a truncated temporal Taylor expansion (with expected accuracy) of the solution into spatial derivatives by repeatedly using the underlying differential equation and its differentiated forms. The original LWDG scheme is proposed by Qiu et. al in [22] for the hyperbolic conservation laws and extended to Hamilton–Jacobi equations in [15]. In this paper, we would like to investigate superconvergence properties of the LWDG scheme. To the best of our knowledge, there is no superconvergence results reported in the literature for the LWDG schemes. The numerical results documented in [6, 9] indicates that the RKDG scheme exhibits superconvergence properties if the spatial error dominates, whereas the results reported in Sect. 2 below show that such superconvergence can not be observed numerically for the original LWDG schemes in [22].

In order to restore superconvergence in the LWDG framework, we modify the original scheme by borrowing techniques from the LDG scheme. In particular, the high order spatial derivatives in the LW procedure are reconstructed through a LDG formulation, while they are obtained by direct differentiation of the numerical solution for the original LWDG scheme. In addition, for the newly proposed LWDG scheme, flux terms appeared in the LDG framework provide extra freedom to design appropriate numerical fluxes for numerical stability. Numerical experiments demonstrate that the modified LWDG scheme is stable and high order accurate. Moreover, it is observed that the proposed scheme displays similar superconvergence properties as a RKDG scheme. In order to theoretically reveal superconvergence of the new LWDG scheme, we follow the analysis in [16] to study the eigen-structures of the amplification matrix in the Fourier analysis framework. In [29], the dispersion and dissipation error analysis for the original LWDG scheme is provided.

The paper is organized as follows. In Sect. 2, a review of DG and LDG methods is given. In Sect. 3, we review superconvergence properties of DG schemes and perform a numerical study to show that the original LWDG scheme does not exhibit superconvergence in terms of accuracy enhancement by applying a post-processor (Sect. 3.1) and long time behavior of errors (Sect. 3.2). In Sect. 4, we formulate a new LWDG scheme for the linear and non-linear hyperbolic conservation laws and the Euler system. Some implementation details are also discussed. In Sect. 5, we symbolically analyze the eigen-structures of the amplification matrices of the proposed LWDG scheme as well as the original LWDG scheme when $k=1,\,2$. In Sect. 6, numerical examples for scalar and system of equations in one and two spatial dimensions are provided to verify superconvergence properties of the proposed scheme. Some interesting observations are discussed based on our understanding. Conclusions are given in Sect. 7.

2 Review: DG, LDG Methods and LW Time Discretization

In this section, we briefly review the DG and LDG methods for solving hyperbolic conservation laws and diffusion equations, respectively. We only consider 1-D cases for simplicity. The original LW time discretization coupled with DG methods will also be discussed.

2.1 DG Scheme

We first review the DG scheme for the following 1-D hyperbolic conservation laws problem

$$\begin{aligned} u_{t}+ f( u)_{x}=0, \quad x\in [a,b], \quad t>0, \end{aligned}$$

(2.1)

with suitable initial and boundary conditions.

Consider a partition of the computational domain $[a,b]$ into $N$ cells as follows:

$$\begin{aligned} a=x_{\frac{1}{2}}<x_{\frac{3}{2}}<\cdots <x_{N+\frac{1}{2}}=b. \end{aligned}$$

Denote the cell by $I_j=[x_{j-\frac{1}{2}},x_{j+\frac{1}{2}}]$ and the cell center by $x_j=\frac{1}{2}\left( x_{j+\frac{1}{2}}+x_{j-\frac{1}{2}}\right)$, for $j=1,\ldots ,N$. The length of the cell is denoted by $\Delta x_j = x_{j+\frac{1}{2}}-x_{j-\frac{1}{2}}$ and the mesh size $\Delta x=\max _{1\le j\le N}\Delta x_j$. Define the approximation space as

$$\begin{aligned} V_{h}^k=\left\{ v:v|_{I_j}\in P^k(I_j); \quad 1\le j\le N\right\} , \end{aligned}$$

(2.2)

where $P^k(I_j)$ denotes the set of polynomials of degree up to $k$ on cell $I_j$. The semi-discrete DG method for solving (2.1) is defined as follows: find $u_{h}\in V_{h}^k$ such that $\forall v\in V_{h}^k$, we have

$$\begin{aligned} \int _{I_j}(u_{h})_tv\,d x- \int _{I_j} f(u_{h})v_{x}\;d x+ \hat{f}_{j+\frac{1}{2}}v^{-}_{j+\frac{1}{2}} - \hat{f}_{j-\frac{1}{2}}v^{+}_{j-\frac{1}{2}}=0,\quad j=1,\ldots ,N. \end{aligned}$$

(2.3)

Here and below $u_{h}^{+}=u_{h}(x^{+}),\,u_{h}^{-}=u_{h}(x^{-})$ denote the right and left limits of the function $u_{h}$ at a spatial location $x$, respectively. The monotone numerical flux $\hat{f}:=\hat{f}(u_{h}^{-},u_{h}^{+})$ as the exact or approximate Riemann solver is defined at the cell interface. In the simulation, one can choose a standard monotone flux such as the Lax–Friedrichs flux. It was shown in [20] that the numerical solution $u_{h}$ by the semi-discrete DG scheme is $L^{2}$ stable, i.e.,

$$\begin{aligned} \frac{d}{dt}\int _a^b u_{h}^{2}\quad dx\le 0, \end{aligned}$$

(2.4)

when the periodic boundary conditions are imposed.

2.2 LDG Scheme

In this subsection, we review the LDG scheme [12] for the following 1-D diffusion equation:

$$\begin{aligned} u_t = ( c(u)u_{x})_{x},\quad x\in [a,b],\quad t>0, \end{aligned}$$

(2.5)

with suitable initial and boundary conditions. Here we assume $c(u)\ge 0$. The domain discretization is same as the DG scheme (2.3). In order to define the LDG scheme, we rewrite Eq. (2.5) into the following system by introducing an auxiliary variable $p=\sqrt{c(u)}u_{x}$:

$$\begin{aligned} u_{t}&= (q'p)_{x}, \end{aligned}$$

(2.6)

$$\begin{aligned} p&= q_{x}, \end{aligned}$$

(2.7)

where $q(u) = \int ^u\sqrt{c(s)}~ds$. The semi-discrete LDG method for solving (2.6)–(2.7) is defined as follows: find $u_{h},~p_{h}\in V_{h}^k$ such that $\forall v,~w\in V_{h}^k$, we have

$$\begin{aligned}&\int _{I_j}(u_{h})_tv\;dx + \int _{I_j}q'p_{h}v_{x}\;d x -\widehat{q'p_{h}}_{j+\frac{1}{2}}v^{-}_{j+\frac{1}{2}} + \widehat{q'p_{h}}_{j-\frac{1}{2}}v^{+}_{j-\frac{1}{2}}=0,\end{aligned}$$

(2.8)

$$\begin{aligned}&\int _{I_j}p_{h} w\;dx + \int _{I_j}q w_{x}\;dx -\hat{q}_{j+\frac{1}{2}}w^{-}_{j+\frac{1}{2}} +\hat{q}_{j-\frac{1}{2}}w^{+}_{j-\frac{1}{2}}=0, \end{aligned}$$

(2.9)

for $j=1,\ldots ,N$. $\widehat{q'p_{h}}$ and $\hat{q}$ are numerical fluxes that are carefully designed for semi-discrete $L^{2}$ stability. For example, in [12], the following numerical fluxes were proposed,

$$\begin{aligned}&\widehat{q'p_{h}} =\frac{[\![ q(u_{h})]\!]}{[\![u_{h} ]\!]}p_{h}^{-},\end{aligned}$$

(2.10)

$$\begin{aligned}&\hat{q}=q(u_{h}^{+}), \end{aligned}$$

(2.11)

where

$$\begin{aligned}{}[\![ u_{h} ]\!]=u_{h}^{+}-u_{h}^{-} \end{aligned}$$

denotes the jump of function $u_{h}$ at a spatial location.

The following semi-discrete $L^{2}$ stability property is proved in [12],

$$\begin{aligned} \frac{d}{dt}\int _a^b u_{h}^{2}\;dx + 2\int _a^b p_{h}^{2}\;dx = 0, \end{aligned}$$

(2.12)

when the periodic boundary conditions are imposed.

2.3 Time Discretization: LW Method

The LW time discretization, as an alternative to the method-of-line RK time discretization, was proposed for the DG scheme in [22]. We consider the 1-D conservation law (2.1). The formulation of LW type time discretization starts with a Taylor expansion in time for the solution $u$. For example, for third order temporal discretization, we have

$$\begin{aligned} u(x,t+\Delta t) \approx u(x,t) + \Delta t u_t(x,t) + \frac{\Delta t^{2}}{2} u_{tt}(x,t) + \frac{\Delta t^3}{6} u_{ttt}(x,t). \end{aligned}$$

(2.13)

The temporal derivatives in (2.13) are then converted into spatial derivatives via the original differential equation (2.1) and its differentiated versions:

$$\begin{aligned} u_t&= - f(u)_{x}, \end{aligned}$$

(2.14)

$$\begin{aligned} u_{tt}&= \left( f'(u)f(u)_{x}\right) _{x}, \end{aligned}$$

(2.15)

$$\begin{aligned} u_{ttt}&= -\left( f''(u)\left( f(u)_{x}\right) ^{2} + f'(u)\left( f'(u)f(u)_{x}\right) _{x}\right) _{x}. \end{aligned}$$

(2.16)

Substituting (2.14)–(2.16) into (2.13) gives

$$\begin{aligned}&u(x,t+\Delta t) \approx u(x,t)\nonumber \\&\qquad {}-\Delta t\left( f(u) -\frac{\Delta t}{2}f'(u)f(u)_{x} + \frac{\Delta t^{2}}{6}\left( f''(u)\left( f(u)_{x}\right) ^{2} + f'(u)\left( f'(u)f(u)_{x}\right) _{x}\right) \right) _{x} \nonumber \\&\quad = u(x,t) - \Delta t F(u,\Delta t)_{x}, \end{aligned}$$

(2.17)

where

$$\begin{aligned} F=f(u) -\frac{\Delta t}{2}f'(u)f(u)_{x} + \frac{\Delta t^{2}}{6}\left( f''(u)\left( f(u)_{x}\right) ^{2} + f'(u)\left( f'(u)f(u)_{x}\right) _{x}\right) \end{aligned}$$

(2.18)

is a new flux function. The LWDG formulation is defined based on (2.17) as follows: given $u^{n}_{h} \in V^k_{h}$, find $u_{h}^{n+1}\in V_{h}^k$ such that $\forall v\in V_{h}^k$, we have

$$\begin{aligned} \int _{I_j}u^{n+1}_{h}v\,d x = \int _{I_j}u^{n}_{h}v\,d x + \Delta t_n\left( \int _{I_j} F\left( u^{n}_{h},\Delta t_n\right) v_{x}\;d x - \hat{F}_{j+\frac{1}{2}}v^{-}_{j+\frac{1}{2}} + \hat{F}_{j-\frac{1}{2}}v^{+}_{j-\frac{1}{2}}\right) , \end{aligned}$$

(2.19)

for $j=1,\ldots ,N$ and $n=0,\,1,\ldots$. Here $u^{n}_{h}$ approximates the solution of (2.1) at time $t^{n}$, and $\Delta t_n=t^{n+1}-t^{n}$. The numerical flux $\hat{F}_{j+\frac{1}{2}}$ is defined as

$$\begin{aligned} \hat{F}_{j+\frac{1}{2}} = \frac{1}{2}\left( \left( F\left( \left( u^{n}_{h}\right) ^{+}_{j+\frac{1}{2}},\Delta t_n\right) +F\left( \left( u^{n}_{h}\right) ^{-}_{j+\frac{1}{2}},\Delta t_n\right) \right) -\alpha \left( \left( u^{n}_{h}\right) ^{+}_{j+\frac{1}{2}}-\left( u^{n}_{h}\right) ^{-}_{j+\frac{1}{2}}\right) \right) , \end{aligned}$$

(2.20)

where $\alpha = \max _u{|f'(u)|}$ with the maximum taken in the computational domain $[a,b]$. Here $f(u^{n}_{h})_{x}$ and $\left( f'(u^{n}_{h})f(u^{n}_{h})_{x}\right) _{x}$ in $F$ (2.18) are obtained by direct differentiation of the numerical solution, i.e.,

$$\begin{aligned}&f\left( u^{n}_{h}\right) _{x} = f'\left( u^{n}_{h}\right) \left( u^{n}_{h}\right) _{x},\\&\quad \left( f'\left( u^{n}_{h}\right) f\left( u^{n}_{h}\right) _{x}\right) _{x} = f'\left( u^{n}_{h}\right) \left( 2f''\left( u^{n}_{h}\right) \left( u^{n}_{h}\right) _{x}^{2} + f'\left( u^{n}_{h}\right) \left( u^{n}_{h}\right) _{xx}\right) . \end{aligned}$$

Note that the numerical flux $\hat{F}_{j+\frac{1}{2}}$ is very similar to the Lax–Friedrichs flux.

3 Superconvergence Properties and Numerical Evidences

In this section, we review superconvergence properties of DG schemes and assess the numerical performance of the corresponding properties for the LWDG schemes proposed in [22].

3.1 Enhanced Accuracy by Post-processing

It has been proved in [9] that a semi-discrete DG solution for a linear hyperbolic equation is superconvergent in the negative-order norms with order of $2k+1$ assuming that the solution is globally smooth. Because of this, the order convergence can be enhanced from $(k+1)$th order to $(2k+1)$th order by applying a post-processor [4], when the mesh is translation invariant. Specifically, such better approximated solution $u^\star _{h}$ is obtained by convolving the numerical solution with a convolution kernel $K_{h}$ that is a linear combination of B-splines [4, 9],

$$\begin{aligned} u^\star _{h} = K_{h} \star u_{h}. \end{aligned}$$

(3.1)

We refer to [4, 9] for the details of construction and analysis of the kernel. Along this line, a similar estimation of the LDG scheme for solving linear convection–diffusion equations was given in [18], and of the DG scheme for solving nonlinear scalar hyperbolic conservation laws was provided in [19]. The numerical results reported in [9] show that the $(2k+1)$th order of convergence is achieved, when a high order SSP RK scheme is used for time discretization. Note that the time step $\Delta t$ is chosen small enough such that the spatial error dominates.

Now, we study the convergence property of the post-processed solutions for the LWDG scheme (2.19) with numerical flux specified in Eq. (2.20) for the following linear advection problem:

$$\begin{aligned}&u_t + u_{x} = 0, \quad x\in [0,2\pi ],\nonumber \\&u(x,t=0) = \sin {x}, \end{aligned}$$

(3.2)

with the periodic boundary conditions. In particular, we use the LWDG scheme (2.19) to solve the model problem and post-process the numerical solution at final time step. The numerical mesh is set to be uniform. The numerical solution is computed up to time T = 1 and we let $\Delta t=\text {CFL}\Delta x$ with CFL = 0.01, thereby making the spatial error dominant.

In Table 1, we report the $L^{2}$ and $L^\infty$ errors and orders of accuracy, before and after applying the post-processing procedure. It is observed that the magnitude of numerical errors is reduced by applying the post-processor, however the order of accuracy remains $k+1$.

Table 1 Linear advection. LWDG scheme in [22]

3.2 Long Time Behavior of Errors

It is discovered that the DG errors do not significantly grow over a very long time period [6]. Such behavior of error could be explained by the superconvergence of the DG solution in approximating the Radau projection of the exact solution [6, 8, 30]. In particular, numerical analysis for solving the linear advection equation (3.2) in [30] shows that the Radau projection of the exact solution $\mathbf {P}u$ satisfies

$$\begin{aligned} \Vert \mathbf {P}u - u_{h}\Vert \le C_1(1+\text {T}^{2})\Delta x^{k+2}. \end{aligned}$$

It leads to the following error estimation:

$$\begin{aligned} \Vert e\Vert \le C_{0}\Delta x^{k+1} + C_1(1+\text {T}^{2})\Delta x^{k+2}, \end{aligned}$$

(3.3)

where $C_{0}$ and $C_{1}$ are positive constant. Note that the first term, which is independent of time, will dominate the error until $\text {T}={\mathcal {O}}(1/\sqrt{\Delta x})$. In [16], an optimal error estimation was obtained via Fourier analysis. If the mesh is assumed to be uniform and the boundary condition is periodic, the numerical error by a DG scheme (when $k=1,~ 2,~ 3$) for the linear advection equation (3.2) can be decomposed into three parts:

$$\begin{aligned} \Vert e\Vert \le C_{0} \Delta x^{k+1} + \text {T} C_1 \Delta x^{2k+1} + C_2\exp \left( -\frac{C\text {T}}{\Delta x}\right) \Delta x^{k+1}, \end{aligned}$$

(3.4)

where $C_{0}$, $C_1$, $C_2$ and $C$ are positive constant. The claim indicates that the error does not significantly grow until $\hbox {T}={\mathcal {O}}(1/\Delta x^k)$.

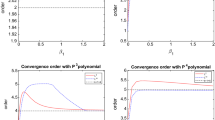
We use the model problem (3.2) to compare the LWDG schemes with the RKDG schemes in the context of the long time behavior of numerical errors. We use $P^{2}$ as the approximation space and let $N=50$, CFL = 0.01. Note that both schemes are third order accurate in space and time. We compute the numerical solutions using the two types of DG schemes up to time T = 500, and plot the time evolution history of the $L^{2}$ errors in Fig. 1. It is observed that the numerical error by the RKDG scheme does not significantly grow for a long time simulation. In fact, the magnitude of error at T = 500 is comparable to that at the very beginning of the simulation. Contrarily, the error by the LWDG scheme begins to noticeably grow around T = 20, and the growth rate is observed to be linear after some time.

Fig. 1

Long time behavior of errors. 1-D linear advection. The RKDG $P^{2}$ scheme versus the original LWDG $P^{2}$ scheme. $\hbox {CFL}=0.01$

In [16], the following error is defined and studied for the DG scheme:

$$\begin{aligned} \bar{e} = u_{h}(t=2\pi )-u_{h}(t=4\pi ). \end{aligned}$$

(3.5)

It is proved in [16] that the error $\bar{e}$ by a RKDG scheme (when $k=1,\,2,\,3$) is in the order of $2k+1$ for spatial accuracy. Here, we check the error $\bar{e}$ for the LWDG scheme when solving the model equation (3.2). In Table 2, we report the $L^{2}$ norms of error $\bar{e}$ and orders of accuracy. Only $(k+1)$th order of accuracy is observed for the LWDG scheme.

Table 2 Linear advection

In summary, several superconvergence properties of a semi-discrete DG scheme, including accuracy enhancement by post-processing the numerical solution and long time behaviors of errors, are maintained by the a discrete RKDG scheme, whereas they are not numerically observed when the original LW temporal discretization [22] is used. In the next section, we propose a new LWDG scheme, which aims to restore superconvergence properties mentioned above.

4 A New LWDG with LDG for High Order Spatial Derivatives

In the section, we formulate a new LWDG scheme for solving linear and non-linear hyperbolic conservation laws. Some stability issues will be discussed.

4.1 Linear Advection Equations

In this subsection, we still consider the linear advection equation (3.2). As the original LWDG scheme, we start with the Taylor expansion of the solution in time as in Eq. (2.13) for achieving third order temporal accuracy. By repeatedly using the underlying differential equation and its differentiation versions, we obtain

$$\begin{aligned} u(t+\Delta t) \approx u(t) - \Delta t u_{x} + \frac{\Delta t^{2}}{2} u_{xx} - \frac{\Delta t^3}{6} u_{xxx}. \end{aligned}$$

(4.1)

Note that the original LWDG formulation uses direct differentiation of the solution to obtain high order spatial derivatives. However, in the new formulation, we propose to use the LDG techniques to reconstruct high order derivatives instead. To illustrate the idea of using an LW time discretization procedure in the LDG framework, we consider solving the following partial differential equation (PDE) by an LDG scheme:

$$\begin{aligned} u_t = \epsilon _1 u_{x} + \epsilon _2 u_{xx}+\epsilon _3 u_{xxx}, \end{aligned}$$

(4.2)

where $\epsilon _1<0$, $\epsilon _2>0$, and $\epsilon _3<0$ are constant. Two auxiliary variables are introduced,

$$\begin{aligned} p = u_{x},\quad q = p_{x}. \end{aligned}$$

The corresponding semi-discrete LDG scheme is to find $u_{h},~p_{h},~q_{h}\in V_{h}^k$ such that $\forall v,~w,~s\in V_{h}^k$, we have

$$\begin{aligned} \int _{I_j}(u_{h})_tv\;dx&= -\int _{I_j}(\epsilon _1 u_{h}+\epsilon _2p_{h}+\epsilon _3q_{h})v_{x}\;dx +(\epsilon _1(\hat{u}_{h})_{j+1/2}\nonumber \\&\quad +\,\epsilon _2(\hat{p}_{h})_{j+1/2}+\epsilon _3 (\hat{q}_{h})^{n}_{j+1/2})v_{j+1/2}^{-} \nonumber \\&\quad -\,(\epsilon _1 (\hat{u}_{h})_{j-1/2}+\epsilon _2(\hat{p}_{h})_{j-1/2} +\epsilon _3(\hat{q}_{h})_{j-1/2})v_{j-1/2}^{+} ,\nonumber \\ \int _{I_j}p_{h}w\;dx&= -\int _{I_j}u_{h}w_{x}\;dx+(\tilde{u}_{h})_{j+1/2} w^{-}_{j+1/2}-(\tilde{u}_{h})_{j-1/2}w^{+}_{j-1/2}, \nonumber \\ \int _{I_j}q_{h}s\;dx&= -\int _{I_j}p_{h}s_{x}\;dx+(\tilde{p}_{h})_{j+1/2} s^{-}_{j+1/2}-(\tilde{p}_{h})_{j-1/2}s^{+}_{j-1/2}, \end{aligned}$$

(4.3)

for $j=1,\ldots ,N$. Here $u_{h}$, $p_{h}$ and $q_{h}$ approximate the solution, and its first and second order spatial derivatives of (4.2), respectively. $\hat{u}_{h}$, $\tilde{u}_{h}$, $\hat{p}_{h}$, $\tilde{p}_{h}$, and $\hat{q}_{h}$ are numerical fluxes chosen according to stability consideration as in [12, 28]:

$$\begin{aligned} \hat{u}_{h}=u_{h}^{-},\quad \hat{p}_{h}=p_{h}^{+},\quad \tilde{u}_{h}=u_{h}^{-},\quad \hat{q}_{h} =q_{h}^{+},\quad \tilde{p}_{h}=p_{h}^{+}. \end{aligned}$$

(4.4)

Similar to the semi-discrete LDG scheme for solving the convection–diffusion equations [12] and KdV-type equations [28], we have the following proposition:

Proposition 4.1

The semi-discrete LDG scheme (4.3) equipped with the alternating numerical fluxes (4.4) is $L^{2}$ stable.

Proof

The proof is similar to that in [28], thus omitted for brevity.

Based on the semi-discrete LDG scheme (4.3) for Eq. (4.2), we define the new LWDG formulation as follows: given $u_{h}^{n} \in V_{h}^k$, find $p^{n}_{h},~q^{n}_{h},~u^{n+1}_{h}\in V_{h}^k$ such that $\forall v,~w,~s\in V_{h}^k$, we have

$$\begin{aligned} \int _{I_j}u_{h}^{n+1}vdx&= \int _{I_j}u_{h}^{n}vdx+\Delta t\left( \int _{I_j}(u_{h}^{n}-\frac{\Delta t}{2}p_{h}^{n}+\frac{\Delta t^{2}}{6}q_{h}^{n})v_{xdx}\right. \nonumber \\&\quad {} -\left( \left( \hat{u}^{n}_{h}\right) _{j+1/2}-\frac{\Delta t}{2}\left( \hat{p}^{n}_{h}\right) _{j+1/2}+\frac{\Delta t^{2}}{6}\left( \hat{q}^{n}_{h}\right) _{j+1/2}\right) v_{j+1/2}^{-} \nonumber \\&\quad \left. +\left( \left( \hat{u}^{n}_{h}\right) _{j-1/2}-\frac{\Delta t}{2}\left( \hat{p}^{n}_{h}\right) _{j-1/2}+\frac{\Delta t^{2}}{6}\left( \hat{q}^{n}_{h}\right) _{j-1/2}\right) v_{j-1/2}^{+}\right) ,\end{aligned}$$

(4.5)

$$\begin{aligned} \int _{I_j}p^{n}_{h}wdx&= -\int _{I_j}u_{h}^{n}w_{xdx}+\left( \tilde{u}^{n}_{h}\right) _{j+1/2}w^{-}_{j+1/2}-\left( \tilde{u}^{n}_{h}\right) _{j-1/2}w^{+}_{j-1/2},\end{aligned}$$

(4.6)

$$\begin{aligned} \int _{I_j}q^{n}_{h}sdx&= -\int _{I_j}p_{h}^{n}s_{xdx}+\left( \tilde{p}^{n}_{h}\right) _{j+1/2}s^{-}_{j+1/2}-\left( \tilde{p}^{n}_{h}\right) _{j-1/2}s^{+}_{j-1/2}, \end{aligned}$$

(4.7)

for $j=1,\ldots ,N$ and $n=0,\,1,\ldots$. Here $u^{n}_{h}$, $p^{n}_{h}$ and $q^{n}_{h}$ approximate the solution, and its first and second order spatial derivatives of (2.1) at time $t^{n}$, respectively. $\hat{u}^{n}_{h}$, $\tilde{u}^{n}_{h}$, $\hat{p}^{n}_{h}$, $\tilde{p}^{n}_{h}$, and $\hat{q}^{n}_{h}$ are the numerical fluxes chosen as in (4.4).

Note that the proposed LWDG scheme (4.5 4.6 4.7) is formulated by applying the forward Euler time discretization to the semi-discrete LDG scheme (4.3) with $\epsilon _1=-1$, $\epsilon _2=\frac{\Delta t}{2}$, and $\epsilon _3=-\frac{\Delta t^{2}}{6}$.

4.2 Nonlinear Scalar Conservation Laws

Now, we consider a 1-D nonlinear scalar hyperbolic conservation law (2.1). Similar to the linear case, we start with the second order Taylor expansion of the solution. Again, in order to formulate a new LWDG scheme, we first consider the following PDE:

$$\begin{aligned} u_t = \epsilon _1 f(u)_{x} + \epsilon _2\left( f'(u)f(u)_{x}\right) _{x}, \end{aligned}$$

(4.8)

where $\epsilon _1<0$ and $\epsilon _2>0$ are constant. By introducing the auxiliary variable

$$\begin{aligned} p = f(u)_{x}, \end{aligned}$$

we define the corresponding semi-discrete LDG scheme for Eq. (4.8): find $u_{h},~p_{h}\in V_{h}^k$ such that $\forall v,~w\in V_{h}^k$, we have

$$\begin{aligned} \int _{I_j}(u_{h})_tvdx&= -\int _{I_j}\left( \epsilon _1 f(u_{h})+\epsilon _2f'(u_{h})p_{h}\right) v_{xdx} +\left( \epsilon _1\hat{f}_{j+1/2}+\epsilon _2\widehat{f'p}_{j+1/2}\right) v_{j+1/2}^{-} \nonumber \\&\quad -\,\left( \epsilon _1\hat{f}_{j-1/2}+\epsilon _2\widehat{f'p}_{j-1/2}\right) v_{j-1/2}^{+} ,\nonumber \\ \int _{I_j}p_{h}wdx&= -\int _{I_j}f(u_{h})w_{xdx}+\tilde{f}_{j+1/2}w^{-}_{j+1/2} -\tilde{f}_{j-1/2}w^{+}_{j-1/2}, \end{aligned}$$

(4.9)

for $j=1,\ldots ,N$. Here $\hat{f}_{j+1/2}$, $\widehat{f'p}_{j+1/2}$ and $\tilde{f}_{j+1/2}$ are the numerical fluxes, which are carefully chosen for the stability consideration as follows:

$$\begin{aligned}&\hat{f}_{j+1/2}:\ \text {standard monotone numerical flux},\nonumber \\&\widehat{f'p}_{j+1/2}=\frac{[\![ f(u_{h})]\!]_{j+1/2}}{[\![ u_{h}]\!]_{j+1/2}}(p_{h})_{j+1/2}^{+},\nonumber \\&\tilde{f}_{j+1/2}=f((u_{h})_{j+1/2}^{-}). \end{aligned}$$

(4.10)

The resulting semi-discrete scheme features a similar stability property as the linear case. In particular, we have the following proposition.

Proposition 4.2

The semi-discrete LDG scheme (4.9) with the numerical fluxes (4.10) is $L^{2}$ stable.

Proof

Over cell $I_j$, let $v=u_{h}$ and $w=p_{h}$ in scheme (4.9), we can derive the following cell entropy inequality,

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\int _{I_j} u_{h}^{2}dx + \epsilon _2\int _{I_j} p_{h}^{2}dx=\hat{H}_{j+1/2}-\hat{H}_{j-1/2} + \Theta _{j-1/2}, \end{aligned}$$

(4.11)

where $\hat{H}_{j+1/2}$ is the numerical entropy flux defined by

$$\begin{aligned} \hat{H}_{j+1/2}&= -\epsilon _1\left( F\left( (u_{h})_{j+1/2}^{-}\right) - (u_{h})_{j+1/2}^{-}\hat{f}_{j+1/2}\right) \\&\quad {}+\epsilon _2\frac{[\![ f(u_{h})]\!]_{j+1/2}}{[\![ u_{h}]\!]_{j+1/2}}(p_{h})_{j+1/2}^{+}(u_{h})_{j+1/2}^{-} \end{aligned}$$

with $F(u)=\int ^u f(s)ds$, and

$$\begin{aligned} \Theta _{j-1/2}=\epsilon _1\left( [\![ F(u_{h})]\!] _{j-1/2} - \hat{f}_{j-1/2}[\![ u_{h}]\!]_{j-1/2}\right) \le 0 \end{aligned}$$

because of the monotonicity of the numerical flux $\hat{f}$ and $\epsilon _1<0$. The $L^{2}$ stability follows by summing up (4.11) over $j$. $\square$

Similar to the linear case, one can formulate a LWDG scheme for solving (2.1) based on the semi-discrete scheme (4.9) with second order accuracy in time: find $p^{n}_{h},~u^{n+1}_{h}\in V^k_{h}$ such that, $\forall v,~w\in V^k_{h}$, we have

$$\begin{aligned} \int _{I_j}u^{n+1}_{h}v\;dx&= \int _{I_j}u^{n}_{h}v\;dx+\Delta t\left( \int _{I_j}\left( f\left( u^{n}_{h}\right) -\frac{\Delta t}{2}f'\left( u^{n}_{h}\right) p^{n}_{h}\right) v_{x}\;dx\right. \nonumber \\&\quad {} -\left. \left( \hat{f}_{j+1/2}-\frac{\Delta t}{2}\widehat{f'p^{n}_{h}}_{j+1/2}\right) v_{j+1/2}^{-} +\left( \hat{f}_{j-1/2}-\frac{\Delta t}{2}\widehat{f'p^{n}_{h}}_{j-1/2}\right) v_{j-1/2}^{+}\right) ,\nonumber \\ \int _{I_j}p^{n}_{h}w\;dx&= -\int _{I_j}f\left( u^{n}_{h}\right) w_{x}\;dx +\tilde{f}_{j+1/2}w^{-}_{j+1/2}-\tilde{f}_{j-1/2}w^{+}_{j-1/2}, \end{aligned}$$

(4.12)

for $j=1,\ldots ,N$ and $n=0,\,1,\ldots$. The numerical fluxes $\hat{f}_{j+1/2}$, $\widehat{f'p}_{j+1/2}$, and $\tilde{f}_{j+1/2}$ are chosen as (4.10). Again, note that the new LWDG scheme (4.12) is defined by the semi-discrete LDG scheme (4.9) coupled with the forward Euler time discretization with $\epsilon _1=-1$ and $\epsilon _2=-\frac{\Delta t}{2}$.

The higher temporal order accuracy can be attained by incorporating more time derivatives in the Taylor expansion. For example, the third order temporal derivative can be added to achieve third order accuracy. However, we find it difficult to formulate a semi-discrete LDG scheme, for which the $L^{2}$ stability can be proved, when solving the following PDE,

$$\begin{aligned} u_t = \epsilon _1 f(u)_{x} + \epsilon _2\left( f'(u)f(u)_{x}\right) _{x} + \epsilon _3\left( f''(u)\left( f(u)_{x}\right) ^{2} + f'(u)\left( f'(u)f(u)_{x}\right) _{x}\right) _{x}.\nonumber \\ \end{aligned}$$

(4.13)

Here, $\epsilon _1<0$, $\epsilon _2>0$, and $\epsilon _3<0$ are constant. On the other hand, we can mimic the procedure of the linear case by introducing another auxiliary variable

$$\begin{aligned} q= \left( f'(u)p\right) _{x}, \end{aligned}$$

and obtain

$$\begin{aligned} f''(u)\left( f(u)_{x}\right) ^{2} + f'(u)\left( f'(u)f(u)_{x}\right) _{x}=f''(u)p^{2}+f'(u)q. \end{aligned}$$

Similar to the scheme (4.12), we can develop a LWDG scheme with third order accuracy in time. The simple alternating fluxes are chosen for the third order terms in simulations [27, 28]. From our extensive numerical tests, the proposed third order scheme appears to be stable.

Remark 4.3

The proposed scheme can be directly extended to high dimensional problems as the original LWDG scheme. However, much more auxiliary variables are needed. From this point of view, the proposed scheme is much more involved in implementation than the original LWDG scheme when solving high dimensional problems.

4.3 Hyperbolic System: Euler System

The proposed scheme can be extended for solving hyperbolic systems. To illustrate the idea, we consider the 1-D Euler system

$$\begin{aligned} \left( \begin{array}{c} \displaystyle \rho \\ \displaystyle M\\ \displaystyle E \end{array}\right) _t + \left( \begin{array}{c} \displaystyle M \\ \displaystyle vM + P \\ \displaystyle v(E+P) \end{array}\right) _{x}=0, \end{aligned}$$

(4.14)

where $\rho$ is density, $v$ is velocity, $M=\rho v$ is momentum, $E$ is total energy and $P$ is pressure given by the equation of state $P=(\gamma -1)(E-\frac{1}{2} vM)$ with $\gamma =1.4$. Below, we consider a second order accurate LW procedure by repeatedly using the Euler equation (4.14) and its differentiation versions, we have

$$\begin{aligned} \rho (t+\Delta t)&\approx \rho (t) + \Delta t \rho _t + \frac{\Delta t^{2}}{2} \rho _{tt} \nonumber \\&= \rho (t) - \Delta t M_{x} + \frac{\Delta t^{2}}{2}(vM + P)_{xx}, \nonumber \\ M(t+\Delta t)&\approx M(t) + \Delta t M_t + \frac{\Delta t^{2}}{2} M_{tt} \nonumber \\&= M(t) - \Delta t (vM+P)_{x} + \frac{\Delta t^{2}}{2}\bigg ((\gamma -1)(v(E+P))_{x} \nonumber \\&\quad +\,(3-\gamma )v(vM+P)_{x} + \frac{\gamma -3}{2}v^{2}M_{x}\bigg )_{x},\nonumber \\ E(t+\Delta t)&\approx E(t) + \Delta t E_t + \frac{\Delta t^{2}}{2} E_{tt} \nonumber \\&= E(t) - \Delta t (v(E+P))_{x} + \frac{\Delta t^{2}}{2}\left( \left( \frac{3}{2}(\gamma -1)+\gamma \frac{E}{P}\right) \left( vM+P\right) _{x}\right. \nonumber \\&\quad +\left. \left( (\gamma -1)v^3-\frac{\gamma Ev}{\rho }\right) M_{x}+ \gamma v(v(E+P))_{x} \right) _{x}. \end{aligned}$$

(4.15)

Similar to the scalar case, define the following three auxiliary variables

$$\begin{aligned} p= M_{x}, \quad q = (vM + P)_{x}, \quad r = (v(E+P))_{x}. \end{aligned}$$

(4.16)

Plugging (4.16) into (4.15), we obtain

$$\begin{aligned} \rho (t+\Delta t)&\approx \rho (t) - \Delta t M_{x} + \frac{\Delta t^{2}}{2}q_{x} \nonumber \\ M(t+\Delta t)&\approx M(t) - \Delta t (vM+P)_{x} + \frac{\Delta t^{2}}{2}\bigg (\frac{\gamma -3}{2}v^{2}p +(3-\gamma )vq+(\gamma -1)r\bigg )_{x}\nonumber \\ E(t+\Delta t)&\approx E(t) - \Delta t (v(E+P))_{x} + \frac{\Delta t^{2}}{2}\left( \left( (\gamma -1)v^3-\frac{\gamma vE}{\rho }\right) p\right. \nonumber \\&\quad \left. +\left( \frac{3}{2}(\gamma -1)+\gamma \frac{E}{P}\right) q+ \gamma vr \right) _{x}. \end{aligned}$$

(4.17)

Then, a second order LWDG method can be formulated based on (4.16) and (4.17). Again, higher order accuracy can be obtained by incorporating more derivatives in the truncated Taylor expansion (4.15) and introducing the corresponding auxiliary variables. In the simulation, we adopt the Godunov flux for the first order spatial derivative and the alternating fluxes for the high order derivatives in the LDG framework. The details of the formulation are omitted for brevity.

5 Fourier Analysis

In this section, we apply the classical Fourier analysis to the newly proposed LWDG scheme to study its superconvergence properties. In particular, we follow the approach in [16] to analyze the eigen-structure of the amplification matrix for the LWDG schemes via symbolic computations.

Under the assumption of uniform meshes and periodic boundary conditions, Fourier analysis for the 1-D linear advection equation (3.2) is performed by assuming the initial condition to be a plane wave

$$\begin{aligned} u(x,0) = exp(i\omega x), \end{aligned}$$

(5.1)

where $\omega$ is the wave number. The numerical solution for a DG scheme can be represented as

$$\begin{aligned} u^{n}(x) = \sum _{l=0}^k u^{n}_{l,j}\phi _{l,j}(x),\quad x\in I_j, \end{aligned}$$

(5.2)

where $u^{n}_{l,j}$ are the degrees of freedom and $\phi _{l,j}(x)$ are the basis functions of $V^k_{h}$ over cell $I_j$. We adopt the scaled Legendre orthogonal polynomial basis in the following discussion, i.e.,

$$\begin{aligned} \phi _{0,j}(x) = 1,\quad \phi _{1,j}(x) = \frac{x-x_j}{\Delta x},\quad \phi _{2,j}(x) =\left( \frac{x-x_j}{\Delta x}\right) ^{2}-\frac{1}{12},\ldots \end{aligned}$$

We first note that a fully discrete DG scheme can be written in a matrix form

(5.3)

where ${\varvec{u}}^{n}_j= (u^{n}_{0,j},\ldots ,u^{n}_{k,j})^T$, and $(j-m_{0},\ldots ,j+m_1)$ is the stencil. For example, denote by $\beta =\frac{\Delta t}{\Delta x}$, we have

for the proposed LWDG scheme of $P^1$ DG spatial discretization combined with a second order LW procedure.

Assume

(5.4)

substituting which into the DG scheme (5.3) provides the following iterative equation for the coefficient vector $\hat{\mathbf{u}}^{n}$,

(5.5)

where $G$ is the amplification matrix, given by

$$\begin{aligned} G=\sum _{m=-m_{0}}^{m_1}A_{m} exp(im\xi ), \quad \xi =\omega \Delta x. \end{aligned}$$

(5.6)

It is observed from the symbolic computations that $G$ is diagonalizable. Denote the $k+1$ eigenvalues as $\lambda _{0},\ldots , \lambda _{k}$. The linear stability requires $|\lambda _l|\le 1,\,l=0,\ldots ,k$. Note that there is only one physically relevant eigenvalue, denoted by $\lambda _{0}$, which approximates the analytical eigenvalue $exp(-i\omega \Delta t)$. Under certain CFL time step restriction, the other $k$ non-physical eigenvalues will be damped exponentially fast as one evolves the numerical solution in time.

Below, we will analyze the dispersion and dissipation errors for the physically relevant eigenvalue $\lambda _{0}$ via symbolic computations. Note that such analysis of RKDG schemes and original LWDG schemes are given in [16] and [29], respectively. The comparison between the two LWDG schemes will be drown based on the dispersion and dissipation errors analysis, which can partially explain why the new LWDG scheme exhibits superconvergence but the original one does not.

We perform symbolic computations on Mathematica. Below is a summary for the two LWDG schemes when $k=1,\,2$. Note that, when $k=3$, the symbolic computation becomes prohibitively complicated for the LWDG schemes. Moreover, it is even more difficult to deal with the case of $k>=4$ in the current Fourier analysis framework, where an algebraic equation with degree greater than 4 needs to be solved symbolically. We assume $0<\beta \le 1$ and $\omega \Delta x\ll 1$ in the asymptotic expansions.

• New LWDG scheme

  • $P^1$ case

    $$\begin{aligned} \lambda _{0} = 1 - i\omega \Delta t - \frac{\omega ^{2}}{2}\Delta t^{2} - \frac{i\omega ^4}{72}\Delta t\Delta x^3 +{\mathcal {O}}(\Delta t\Delta x^4) \end{aligned}$$

  • $P^{2}$ case

    $$\begin{aligned} \lambda _{0}&= 1 - i\omega \Delta t - \frac{\omega ^{2}}{2}\Delta t^{2} + \frac{i\omega ^{3}}{6}\Delta t^3 - \frac{i\omega ^6}{7200}\Delta t\Delta x^5 +{\mathcal {O}}(\Delta t\Delta x^6) \end{aligned}$$

• Original LWDG scheme [29]

  • $P^1$ case

    $$\begin{aligned} \lambda _{0} = 1 - i\omega \Delta t - \frac{\omega ^{2}}{2}\Delta t^{2} - \frac{i\omega ^3}{12}\Delta t^{2}\Delta x +{\mathcal {O}}(\Delta t\Delta x^3) \end{aligned}$$

  • $P^{2}$ case

    $$\begin{aligned} \lambda _{0}&= 1 - i\omega \Delta t - \frac{\omega ^{2}}{2}\Delta t^{2} + \frac{i\omega ^3}{6}\Delta t^3 \\&\quad - \frac{\omega ^4}{120}\left( \frac{(20\beta + 5)\Delta t^4- 2\Delta t^3 \Delta x -\Delta t^{2} \Delta x^{2}}{1+\beta }\right) +{\mathcal {O}}(\Delta t\Delta x^4)\\ \end{aligned}$$

The normalized dispersion and dissipation error of the physically relevant eigenvalue $\lambda _{0}$ is defined as

$$\begin{aligned} e_{0} = \frac{1}{\Delta t} (\lambda _{0} - exp(-i\omega \Delta t)). \end{aligned}$$

(5.7)

In [16], the error $e_{0}$ is analyzed for the RKDG schemes. It is found that $e_{0}$ is $(2k+1)$th order accurate in space and $p$th order accurate in time with the approximation space $V_{h}^k$ and a $p$th order SSP RK method. Such extra high order accuracy of $e_{0}$ in space contributes to the superconvergence for RKDG. Below, we analyze the error $e_{0}$ for the two LWDG schemes. We only consider $P^1$ and $P^{2}$ cases, and adopt a LW time discretization procedure such that the resulting LWDG scheme has the same order of accuracy in space and time. Denote $e_{0}^N$ and $e_{0}^{O}$ as the normalized dispersion and dissipation errors (5.7) for the new (N) and original (O) LWDG scheme, respectively.

By a simple Taylor expansion of Eq. (5.7) with $\lambda _{0}$ computed above, we have the following.

• $P^1$ case

  $$\begin{aligned} e_{0}^N&= -\frac{\omega ^4}{72}\Delta x^3 - \frac{i\omega ^3}{6}\Delta t^{2} + {\mathcal {O}}(\Delta x^4+\Delta t^3),\end{aligned}$$

  (5.8)
  $$\begin{aligned} e_{0}^{O}&= -\frac{i\omega ^3}{12}\Delta t\Delta x - \frac{i\omega ^3}{6}\Delta t^{2} + {\mathcal {O}}(\Delta x^3++\Delta t^3). \end{aligned}$$

  (5.9)

• $P^{2}$ case

  $$\begin{aligned} e_{0}^N&= -\frac{i\omega ^6}{7200}\Delta x^5 - \frac{\omega ^4}{24}\Delta t^3 + {\mathcal {O}}(\Delta x^6+\Delta t^4),\end{aligned}$$

  (5.10)
  $$\begin{aligned} e_{0}^{O}&= -\frac{\omega ^4}{\beta +1}\left( \frac{(5 \beta +2) }{24 }\Delta t^3 -\frac{ 1}{60 }\Delta t^{2} \Delta x-\frac{ 1}{120 }\Delta t\Delta x^{2}\right) + {\mathcal {O}}(\Delta x^3+\Delta t^4). \end{aligned}$$

  (5.11)

Discussion First we note that the order of the leading term in $e_{0}^N$ as shown in (5.8 5.9) is the same as that from the RKDG scheme, which is $(2k+1)$th order in space and $(k+1)$th order in time for both $P^1$ and $P^{2}$ cases. With the similar argument in [16], it is implied that the numerical error by the new LWDG scheme does not significantly grow if the spatial error dominates. In fact, we only need to choose sufficiently small CFL number to reduce the temporal error. In the simulation, we let CFL = 0.01 and the superconvergent $(2k+1)$th order accuracy can be numerically observed when the mesh is relatively coarse, e.g. see Table 3. Also note that the $(2k+1)$th order superconvergence only occurs in space, while the temporal accuracy for $e_{0}^N$ is still $k+1$. On the other hand, under the assumption $\beta <1$, error $e_{0}^{O}$ by the original LWDG scheme is dominated by

$$\begin{aligned} e_{0}^{O}={\mathcal {O}}(\Delta t\Delta x^k), \end{aligned}$$

rather than an extra high order term ${\mathcal {O}}(\Delta x^{2k+1})$ as in the new LWDG scheme.

Table 3 1-D linear advection

Finally, we briefly address the efficiency of the proposed method in terms of the CFL time step restrictions obtained from linear stability. In the Fourier analysis framework, the upper bound of CFL numbers can be derived. Such a technique is adopted in [22] to obtain the CFL upper bounds for the original LWDG schemes, which are approximately $0.22$ for the $P^1$ case and $0.12$ for the $P^{2}$ case. We perform the same analysis for the proposed LWDG schemes to derive the upper bound of CFL numbers. They are approximately $0.20$ and $0.11$ for the $P^1$ and $P^{2}$ cases, which are slightly smaller than those for the original LWDG schemes.

6 Numerical Examples

In this section, we provide a collection of 1-D and 2-D numerical examples to investigate the superconvergence properties of the newly proposed LWDG schemes in different settings. In the simulations, we choose relatively small CFL numbers, e.g., CFL = 0.01, such that the spatial error dominates. We remark that if a large CFL number is taken, the relatively low order temporal accuracy may pollute the superconvergent $(2k+1)$th order of accuracy in space. Thus only the low order temporal accuracy can be numerically observed. This is also true for the RKDG schemes, see [9].

6.1 1-D Linear Advection Equation

Consider the linear advection problem:

$$\begin{aligned} u_t+u_{x}=0, \quad x\in [0,2\pi ], \end{aligned}$$

(6.1)

with the initial condition

$$\begin{aligned} u(x,0)= \sin (x), \end{aligned}$$

(6.2)

and the periodic boundary conditions. In the simulation, we choose $\Delta t=\hbox {CFL}\Delta x$ with $\hbox {CFL}=0.01$. In Table 3, we report the $L^{2}$ and the $L^\infty$ errors and the orders of accuracy before and after the post-processing procedure for the proposed LWDG scheme. Unlike the original LWDG scheme, it is clearly observed that the magnitude of numerical errors by the new LWDG schemes is greatly reduced through the post-processing procedure and the orders of accuracy are also enhanced from $k+1$ to $2k+1$. The observation indicates that numerical error of the new LWDG scheme is order of $2k+1$ in space in terms of negative-order norms. A rigorous proof of the claim is subject to future investigation.

Then we test the long time behavior of the $L^{2}$ errors by the proposed LWDG scheme in comparison to that by the original LWDG scheme. In Fig. 2, we report the time evolution of numerical errors by the two types of LWDG $P^{2}$ schemes with $N=50$ up to time T = 500. It is observed that the error by the new LWDG scheme does not significantly grow over a long period of time, which is very similar to the result by the RKDG $P^{2}$ scheme shown in Fig. 1. Also note that the error by the original LWDG scheme grows linearly with respect to time.

Fig. 2

Long time behavior of errors. 1-D linear advection. Original LWDG $P^{2}$ versus new LWDG $P^{2}$ scheme. $\hbox {CFL}=0.01$

In [16], the following error is defined and studied for RKDG schemes:

$$\begin{aligned} \bar{e} = u_{h}(t=2\pi )-u_{h}(t=4\pi ). \end{aligned}$$

(6.3)

For a RKDG scheme, the error $\bar{e}$ is in the order of $2k+1$ in space, which indicates that the numerical error will not significantly grow for a long time period. Here, we also check the error $\bar{e}$ for the proposed LWDG scheme. In Table 4, we report the $L^{2}$ norms of error $\bar{e}$ and orders of accuracy. Similar to the RKDG scheme, $(2k+1)$th order of accuracy is observed, which implies that the numerical error by the new LWDG scheme does not significantly grow for a long time period. The observation is consistent with the results given in Fig. 2. Also note that the original LWDG scheme does not enjoy such superconvergence property.

Table 4 1-D linear advection

In Fig. 3, we plot the errors of the numerical solutions before and after post-processing, and errors $\bar{e}$ in absolute value and in logarithmic scale for the new LWDG $P^{2}$ scheme and the original LWDG $P^{2}$ scheme. It is observed that, for both schemes, the post-processed errors and errors $\bar{e}$ are much less oscillatory and also much smaller in magnitude than the pre-processed errors. Moreover, note that the magnitude of post-processed errors and errors $\bar{e}$ by the new LWDG scheme is smaller than that by the original LWDG scheme, as the former ones are fifth order accurate in space, but the latter ones are only third order.

Fig. 3

Linear advection. The new LWDG $P^{2}$ scheme (left column). The original LWDG $P^{2}$ scheme (right column). Before post-processing (top). After post-processing (middle). Error $\bar{e}$ (bottom). $\hbox {CFL}=0.01$. $\hbox {T}=4\pi$

At last, we would like to report the convergence behavior for the proposed LWDG schemes at the right-shifted Radau points as well as for the cell averages. Denote the $l^\infty$ error at the right-shifted Radau points by

$$\begin{aligned} e_{R}(\text {t}) = \displaystyle \max _{\begin{array}{c} 0\le j\le N\\ 0\le l\le k \end{array}} |u_{h}(x_{l,j},t)-u(x_{l,j},t)|, \end{aligned}$$

where $x_{l,j}$, $l=0,\ldots ,k$ are the $k+1$ right-shifted Radau points on cell $I_j$, and denote the $l^{2}$ error for the cell average by

$$\begin{aligned} e_{A}(\text {t}) = \left( \frac{1}{N}\sum _{j=1}^N\left( \frac{1}{\Delta x_j}\int _{I_j}u_{h}(x,t)-u(x,t)dx\right) ^{2}\right) ^{\frac{1}{2}}. \end{aligned}$$

For a semi-discrete DG scheme, it has been shown in [5, 30] that the error $e_{R}(\text {t})$ and the error $e_{A}(\text {t})$ converge with order of $k+2$ and $2k+1$, respectively. The numerical results reported in [30, 31] also indicate that the fully-discrete RKDG scheme exhibits the same superconvergence when the spatial error dominates. In Tables 5 and 6, we report the errors $e_{R}$ and $e_{A}$, respectively, and the associated orders of accuracy at time T = 1. Similar to the RKDG schemes, $(k+2)$th order accuracy for $e_{R}$ and $(2k+1)$th order accuracy for $e_{A}$ are observed. We remark that the chosen alternating fluxes in (4.4) are crucial for observing the superconvergence numerically at the shifted Radau points. In particular, for stability consideration, we can also take $\tilde{u}_{h}=u_{h}^{+}$ and $\hat{p}_{h}=p_{h}^{-}$ in (4.4), and the numerical performance of such a choice is quick similar to the original one (4.4), including the accuracy enhancement by postprocessing the numerical solution and the long time behavior of errors. However, the superconvergence results at the right-shifted Radau points are lost. Such a phenomenon can be explained as follows. When solving the 1-D linear diffusion equation (2.5) with $c(u)=1$ by the LDG method (2.8)–(2.9), it has been pointed out in [7] that the superconvergence at the Radau points depends on the choice of alternating fluxes (2.10)–(2.11). Specifically, taking $\hat{q}=u^{+}$ and $\widehat{q'p_{h}}=p_{h}^{-}$ will lead to superconvergence at the left-shifted Radau points, while taking $\hat{q}=u^{-}$ and $\widehat{q'p_{h}}=p_{h}^{+}$ will lead to superconvergence at the right-shifted Radau points, see [1, 6]. Now consider the LDG scheme (4.3) for solving (4.2). For the first order term, one can only take $\hat{u}_{h}=u^{-}$ for stability issue, which results in the superconvergence at the right-shifted Radau points. For the second order term, taking $\hat{p}_{h}=p_{h}^{+}$ and accordingly $\tilde{u}_{h}=u_{h}^{-}$ will also lead to superconvergence at the right-shifted Radau points, which is consistent with the first order term. Consequently, the superconvergence at the right-shifted Radau points are preserved. On the other hand, if $\hat{p}_{h}=p_{h}^{-}$ and $\tilde{u}_{h}=u_{h}^{+}$ are taken, then inconsistency occurs, and hence the superconvergence at the right-shfited Radau points is destroyed. We also remark that the superconvergence at the shifted Radau points and for the cell averages can not be numerically observed for the original LWDG schemes.

Table 5 1-D linear advection

Table 6 1-D linear advection

6.2 1-D Nonlinear Burgers’ Equation

Consider 1-D nonlinear Burgers’ equation:

$$\begin{aligned} u_t+\left( \frac{u^{2}}{2}\right) _{x}=0, \quad x\in [0,2\pi ], \end{aligned}$$

(6.4)

with the initial condition

$$\begin{aligned} u(x,0)= \sin (x)+2, \end{aligned}$$

(6.5)

and the periodic boundary conditions. The time step is simply chosen as $\Delta t=\hbox {CFL}\Delta x$ with $\hbox {CFL}=0.01$. In Table 7, we report the $L^{2}$ errors and the orders of accuracy before and after the post-processing procedure for both the proposed LWDG scheme and the original LWDG scheme. The superconvergent results are clearly observed for the new scheme. However, similar to the linear case, the post-processed error is only order of $k+1$ by the original LWDG scheme. We remark that using a upwind flux, e.g., the Godunov flux, for the first order derivative term is crucial to obtain superconvergent results in the proposed LWDG formulation. If a general monotone numerical flux such as the Lax–Friedrichs flux is used, the $(2k+1)$th order superconvergence result may not be observed. In Fig. 4, we plot errors of the numerical solution before and after post-processing in absolute value and in logarithmic scale for both LWDG $P^{2}$ schemes. The highly oscillatory nature of the pre-processed errors is observed for both schemes. The post-processed errors do not oscillate much and the magnitude is also much smaller. Again the magnitude of the post-processed errors by the new LWDG scheme is much smaller than that by the original LWDG scheme.

Fig. 4

Burgers’ equation (6.4). New LWDG scheme (left column). Original LWDG scheme (right column). $P^{2}$ is used. Before post-processing (top). After post-processing (bottom). $\hbox {CFL}=0.01$, $\hbox {T}=0.2$

Table 7 Burgers’ equation (6.4)

In order to study error $\bar{e}$ for the Burgers’ equation, we add a source term to Eq. (6.4) such that $\sin (x+t)+2$ is the exact solution. A similar strategy is used in [16]. We consider the following Burgers’ equation with a source term:

$$\begin{aligned} u_t+\left( \frac{u^{2}}{2}\right) _{x}=(\sin (x+t)+3)\cos (x+t), \quad x\in [0,2\pi ], \end{aligned}$$

(6.6)

with the initial condition

$$\begin{aligned} u(x,0)= \sin (x)+2, \end{aligned}$$

and the periodic boundary condition. We report the $L^{2}$ norms of error $\bar{e}$ and the orders of accuracy in Table 8 for the proposed LWDG scheme and the original LWDG scheme. $(2k+1)$th order of accuracy is clearly observed for the new LWDG scheme. Again, such superconvergence result is not observed for the original LWDG scheme. In Fig. 5, we plot numerical errors and errors $\bar{e}$ in absolute value and in logarithmic scale for both LWDG $P^{2}$ schemes. Note that, the error $\bar{e}$ is much less oscillatory and smaller in magnitude than the pre-processed error for the two schemes, however, the magnitude of the error $\bar{e}$ by the new LWDG scheme is much smaller than that by the original LWDG scheme.

Fig. 5

Burgers’ equation (6.6). New LWDG $P^{2}$ scheme (left column). Original LWDG $P^{2}$ scheme (right column). Before post-processing (top). Error $\bar{e}$ (bottom). $\hbox {CFL}=0.01$. $\hbox {T}=4\pi$

Table 8 Burgers’ equation (6.6)

6.3 1-D Euler System

Consider 1-D Euler system (4.14). Let the initial condition to be

$$\begin{aligned} \rho (x,0) = 1+0.2\sin (\pi x),\quad v(x,0)=1\quad \text {and}\quad P(x,0)=1, \end{aligned}$$

subject to 2-periodic boundary conditions. The exact solution is $\rho (x,t) = 1+0.2\sin (\pi (x-t)),\ v(x,t)=1\ \text {and}\ P(x,t)=1.$ We compute the numerical solution up to T = 2. In Table 9, we report the $L^{2}$ and $L^\infty$ errors and the orders of accuracy for density $\rho$ before and after applying the post-processing procedure for the new LWDG scheme. Similar superconvergence property is observed as the scalar cases. In the simulation, the Godunov flux is used for the first order derivatives in order to obtain the superconvergence result.

Table 9 1-D Euler system

Then we check the error $\bar{e}$ which is defined as

$$\begin{aligned} \bar{e} = \rho _{h}(t=2)-\rho _{h}(t=4), \end{aligned}$$

since the period of the solution in time is 2. The $L^{2}$ norms of error $\bar{e}$ and orders of accuracy are reported in Table 10 for $P^1$ and $P^{2}$. $(2k+1)$th order accuracy is observed.

Table 10 1-D Euler system

We also use the following benchmark Lax problem, for which discontinuous solution structures will be developed, to test the performance of the proposed LWDG scheme. Consider the Riemann initial condition:

$$\begin{aligned} (\rho ,v,P)=(0.455,0.689,3.528)\quad x\le 0;\quad (\rho ,v,P)=(0.5,0,0.571)\quad x>0. \end{aligned}$$

(6.7)

A robust WENO limiting procedure with the TVB limiter as a troubled cell indicator is used to suppress the spurious oscillations [24]. In Figs. 6 and 7, we plot the numerical solutions of density $\rho$ at T = 1.3 with different TVB constant $M$. Comparable numerical results by the proposed LWDG scheme are observed to those by the original LWDG scheme [22].

Fig. 6

1-D Euler system. Lax problem. Density $\rho$. New LWDG scheme. TVB constant $M=1$. $P^1$ (left). $P^{2}$ (right). N = 200. $\hbox {T}=1.3$

Fig. 7

1-D Euler system. Lax problem. Density $\rho$. New LWDG scheme. TVB constant $M=50$. $P^1$ (left). $P^{2}$ (right). N = 200. $\hbox {T}=1.3$

6.4 2-D Linear Advection Equation

Consider the following 2-D linear advection equation

$$\begin{aligned} u_t + u_{x} + u_y = 0,\quad x\times y \in [0,2\pi ]\times [0,2\pi ], \end{aligned}$$

(6.8)

with the initial condition

$$\begin{aligned} u(x,y,0)= \sin (x+y), \end{aligned}$$

(6.9)

and the periodic boundary conditions. The time step is chosen as

$$\begin{aligned} \Delta t=\frac{\text {CFL}}{\frac{1}{\Delta x}+\frac{1}{\Delta y}}, \end{aligned}$$

where we set CFL = 0.01 to make the spatial error dominant in the simulation. In Table 11, we report the $L^{2}$ and $L^\infty$ errors and the orders of accuracy before and after applying the post-processor for the proposed LWDG scheme. Similar to the results for the 1-D advection problem, $(k+1)$th order of accuracy is observed for the pre-processed errors in both $L^{2}$ and $L^\infty$ norms. Moreover, post-processed numerical solutions are superconvergent with the order of $2k+1$, which implies that numerical error is also order of $2k+1$ in space in negative-order norms for the 2-D case.

Table 11 2-D linear advection

Then, we would like to test the long time behavior of the numerical errors. We set the mesh size as $N_{x}\times N_y=50\times 50$ and report the numerical errors for the two LWDG $P^{2}$ scheme at time $T= 1, 20, 50, 100, 200$ in Table 12. We observe that the numerical error by the new LWDG scheme does not significantly grow for a long time period, which indicates, as the RKDG scheme shown in [6], the new LWDG scheme features similar superconvergence property for the 2-D linear advection problem. However, as the 1-D case, the error by the original LWDG scheme is observed to noticeably grow at the beginning of the simulation.

Table 12 Long time behavior of errors

Finally, we study the error $\bar{e}$ which is defined as

$$\begin{aligned} \bar{e}=u_{h}(t=\pi )-u_{h}(t=2\pi ). \end{aligned}$$

As the results reported in [16], error $\bar{e}$ by the RKDG scheme is order of $2k+1$ in space for solving the 2-D linear advection problem. In Table 13, we report the $L^{2}$ norms of error $\bar{e}$ and orders of accuracy. The $(2k+1)$th order of accuracy is observed. Such superconvergent behavior of error $\bar{e}$ implies that the numerical error by the proposed LWDG scheme solving the 2-D linear advection problem does not significantly grow for a long time simulation. At last, we want to point out that, similar to the 1-D cases, the original LWDG scheme for the 2-D advection problem does not exhibit any superconvergence discussed above. We omit the numerical results from the original LWDG schemes for brevity.

Table 13 2-D linear advection

7 Conclusion

In this paper, we discuss the superconvergence properties of the discontinuous DG methods LW time discretization. Numerical results indicate that the original LWDG scheme does not possess several important superconvergence properties including accuracy enhancement by applying a post-processor and long time behaviors of numerical errors. In order to restore the superconvergence in the LW framework, we formulated a new LWDG scheme, in which the techniques borrowed from the LDG scheme were adopted to obtain high order spatial derivatives. Fourier analysis via symbolic computations was used to theoretically investigate the superconvergence property. Future research directions include to establish stability analysis and error estimate for the proposed LWDG scheme.