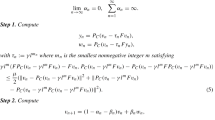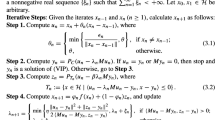1 Introduction

We focus on the following classical variational inequality (VI) ([9, 10]) which consists in finding a point \(x^*\in C\) such that

$$\begin{aligned} \langle Ax^*,x-x^*\rangle \ge 0 \ \ \forall x\in C, \end{aligned}$$
(1.1)

where C is a nonempty closed convex subset in a real Hilbert space H,  and is a single-valued mapping \(A: H\rightarrow H\). As commonly done, we denote by VI(C, A) the solution set of VI (1.1). Variational inequalities are fundamental in a broad range of mathematical and applied sciences; the theoretical and algorithmic foundations as well as the applications of variational inequalities have been extensively studied in the literature and continue to attract intensive research. For the current state of the art in a finite-dimensional setting, see for instance [8] and the extensive list of references therein.

Many authors have proposed and analyzed several iterative methods for solving the variational inequality (1.1). The simplest one is the following projection method, which can be seen as an extension of the projected gradient method introduced for solving optimization problems.

$$\begin{aligned} x_{n+1}=P_C(x_n-\lambda Ax_n), \end{aligned}$$
(1.2)

for each \(n\ge 1\), where \(P_C\) denotes the metric projection from H onto C. It is known that the assumptions which imply convergence of this method are quite restrictive and require A to be L-Lipschitz continuous and \(\alpha \)-strongly monotone (see Chapter 13 in [19]) and \( \lambda \in \left( 0, \dfrac{2\alpha }{L^2}\right) \).

One way to weaken the (1.2) convergence assumptions, Korpelevich [20] (also independently by [1]) proposed a double projection method known as the extragradient method in Euclidean space when A is monotone and L-Lipschitz continuous. The iterative step of the method is as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0\in C,\\ y_n=P_C(x_n-\lambda _n Ax_n),\\ x_{n+1}=P_C(x_n-\lambda _n Ay_n), \end{array}\right. } \end{aligned}$$

where \(\lambda _n \in \left( 0,\dfrac{1}{L}\right) \).

In recent years, the extragradient method was further extended to infinite-dimensional spaces in various ways, see, e.g. [2,3,4,5, 16, 23, 24, 30,31,32, 34] and the references therein.

Obviously, when A is not Lipschitz continuous or its Lipschitz constant L is difficult to compute/approximate, Korpelevich’s method fails since the step-size \(\lambda _n\) depends on this. So, Iusem [14] proposed the following algorithm in a way to avoid this obstacle.

Algorithm 1.1

figure a

Similar extensions have been developed by many authors, for example Khobotov [18] and Marcotte [25]. These algorithms assume that A is monotone and continuous on C. Thus, in this spirit, we wish to construct an extragradient modification which converges under a weaker condition in Hilbert spaces. To be more specific, we assume that A is a uniformly continuous pseudo-monotone operator. Our scheme also make use of a different Armijo-type line-search and then A is only assumed to be pseudo-monotone on C in the sense of Karamardian [17]. Weak and strong convergence of these proposed algorithms is established in real Hilbert spaces.

The paper is organized as follows. We first recall some basic definitions and results in Sect. 2. Our algorithms are presented and analyzed in Sect. 3. In Sect. 4, we present some numerical experiments which demonstrate the algorithms performances as well as provide a preliminary computational overview by comparing it with some related algorithms.

2 Preliminaries

Let H be a real Hilbert space and C be a nonempty, closed and convex subset of H. The weak convergence of \(\{x_n\}_{n=1}^{\infty }\) to x is denoted by \(x_{n}\rightharpoonup x\) as \(n\rightarrow \infty \), while the strong convergence of \(\{x_n\}_{n=1}^{\infty }\) to x is written as \(x_n\rightarrow x\) as \(n\rightarrow \infty .\) For each \(x,y\in H\) and \(\alpha \in {\mathbb {R}}\), we have

$$\begin{aligned}&\Vert x+y\Vert ^2\le \Vert x\Vert ^2+2\langle y,x+y\rangle .\\&\Vert \alpha x+(1-\alpha )y\Vert ^2=\alpha \Vert x\Vert ^2+(1-\alpha )\Vert y\Vert ^2-\alpha (1-\alpha )\Vert x-y\Vert ^2. \end{aligned}$$

Definition 2.1

Let \(T:H\rightarrow H\) be an operator.

  1. 1.

    The operator T is called L-Lipschitz continuous with \(L>0\) if

    $$\begin{aligned} \Vert Tx-Ty\Vert \le L \Vert x-y\Vert \ \ \ \forall x,y \in H. \end{aligned}$$
    (2.1)

    if \(L=1\) then the operator T is called nonexpansive and if \(L\in (0,1)\), T is called a contraction.

  2. 2.

    The operator T is called monotone if

    $$\begin{aligned} \langle Tx-Ty,x-y \rangle \ge 0 \ \ \ \forall x,y \in H. \end{aligned}$$
    (2.2)
  3. 3.

    The operator T is called pseudo-monotone if

    $$\begin{aligned} \langle Tx,y-x \rangle \ge 0 \Longrightarrow \langle Ty,y-x \rangle \ge 0 \ \ \ \forall x,y \in H. \end{aligned}$$
    (2.3)
  4. 4.

    The operator T is called \(\alpha \)-strongly monotone if there exists a constant \(\alpha >0\) such that

    $$\begin{aligned} \langle Tx-Ty,x-y\rangle \ge \alpha \Vert x-y\Vert ^2 \ \ \forall x,y\in H. \end{aligned}$$
  5. 5.

    The operator T is called sequentially weakly continuous if for each sequence \(\{x_n\}\) we have: \(\{x_n\}\) converges weakly to x implies \({Tx_n}\) converges weakly to Tx.

It is easy to see that every monotone operator is pseudo-monotone, but the converse is not true.

For every point \(x\in H\), there exists a unique nearest point in C, denoted by \(P_Cx\) such that \(\Vert x-P_Cx\Vert \le \Vert x-y\Vert \ \forall y\in C\). \(P_C\) is called the metric projection of H onto C. It is known that \(P_C\) is nonexpansive.

Lemma 2.2

[12] Let C be a nonempty closed convex subset of a real Hilbert space H. Given \(x\in H\) and \(z\in C\). Then \(z=P_Cx\Longleftrightarrow \langle x-z,z-y\rangle \ge 0 \ \ \forall y\in C.\)

Lemma 2.3

[12] Let C be a closed and convex subset in a real Hilbert space H,  \(x\in H\). Then

  1. (i)

    \(\Vert P_Cx-P_Cy\Vert ^2\le \langle P_C x-P_C y,x-y\rangle \ \forall y\in C\);

  2. (ii)

    \(\Vert P_C x-y\Vert ^2\le \Vert x-y\Vert ^2-\Vert x-P_Cx\Vert ^2 \ \forall y\in C;\)

  3. (iii)

    \(\langle (I-P_C)x-(I-P_C)y,x-y\rangle \ge \Vert (I-P_C)x-(I-P_C)y\Vert ^2 \ \forall y\in C.\)

For properties of the metric projection, the interested reader could be referred to [12, Section 3].

The following Lemmas are useful for the convergence of our proposed methods.

Lemma 2.4

[7] For \(x\in H\) and \(\alpha \ge \beta >0\) the following inequalities hold.

$$\begin{aligned}&\dfrac{\Vert x-P_{C}(x-\alpha Ax)\Vert }{\alpha }\le \dfrac{\Vert x-P_C(x-\beta Ax)\Vert }{\beta },\\&\Vert x-P_{C}(x-\beta Ax)\Vert \le \Vert x-P_C(x-\alpha Ax)\Vert . \end{aligned}$$

Lemma 2.5

[15] Let \(H_1\) and \(H_2\) be two real Hilbert spaces. Suppose \(A : H_1 \rightarrow H_2\) is uniformly continuous on bounded subsets of \(H_1\) and M is a bounded subset of \(H_1\). Then A(M) (the image of M under A) is bounded.

Lemma 2.6

([6], Lemma 2.1) Consider the problem VI(C, A) with C being a nonempty, closed, convex subset of a real Hilbert space H and \(A : C \rightarrow H\) being pseudo-monotone and continuous. Then, \(x^*\) is a solution of VI(C, A) if and only if

$$\begin{aligned} \langle Ax, x - x^*\rangle \ge 0 \ \ \forall x \in C. \end{aligned}$$

Lemma 2.7

[26] Let C be a nonempty set of H and \(\{x_n\}\) be a sequence in H such that the following two conditions hold:

  1. (i)

    for every \(x\in C\), \(\lim _{n\rightarrow \infty }\Vert x_n-x\Vert \) exists;

  2. (ii)

    every sequential weak cluster point of \(\{x_n\}\) is in C.

Then \(\{x_n\}\) converges weakly to a point in C.

Lemma 2.8

[22] Let \(\{a_n\}\) be a sequence of non-negative real numbers such that there exists a subsequence \(\{a_{n_i}\}\) of \(\{a_n\}\) such that \(a_{n_{i}}<a_{n_{i}+1}\) for all \(i\in {\mathbb {N}}\). Then there exists a nondecreasing sequence \(\{m_k\}\) of \({\mathbb {N}}\) such that \(\lim _{k\rightarrow \infty }m_k=\infty \) and the following properties are satisfied by all (sufficiently large) number \(k\in {\mathbb {N}}\):

$$\begin{aligned} a_{m_k}\le a_{m_{k}+1} \text { and } a_k\le a_{m_k+1}. \end{aligned}$$

In fact, \(m_k\) is the largest number n in the set \(\{1,2,\ldots ,k\}\) such that \(a_n<a_{n+1}\).

The next technical lemma is very useful and used by many authors, for example Liu [21] and Xu [35]. Furthermore, a variant of Lemma 2.9 has already been used by Reich in [29].

Lemma 2.9

Let \(\{a_n\}\) be sequence of non-negative real numbers such that:

$$\begin{aligned} a_{n+1}\le (1-\alpha _n)a_n+\alpha _n b_n, \end{aligned}$$

where \(\{\alpha _n\}\subset (0,1)\) and \(\{b_n\}\) is a sequence such that

  1. (a)

    \(\sum _{n=0}^\infty \alpha _n=\infty \);

  2. (b)

    \(\limsup _{n\rightarrow \infty }b_n\le 0.\)

Then \(\lim _{n\rightarrow \infty }a_n=0.\)

3 Main results

In this section, we introduce the two new extragradient modifications for solving the VI (1.1). We present the weak and strong convergence of the schemes under the assumptions.

Condition 3.1

The feasible set C of the VI (1.1) is a nonempty, closed, and convex subset of the real Hilbert space H.

Condition 3.2

The VI (1.1) associated operator \(A:C\rightarrow H\) is a pseudo-monotone, sequentially weakly continuous on C and uniformly continuous on bounded subsets of C.

Condition 3.3

The solution set of the VI (1.1) is nonempty, that is VI\((C,A)\ne \emptyset \).

3.1 Weak convergence

Algorithm 3.1

figure b

We start the algorithm’s convergence analysis by proving that (3.1) terminates after finite steps.

Lemma 3.2

Assume that Conditions 3.1–3.3 hold. The Armijo line-search rule (3.1) is well defined. In addition, we have \(\lambda _n\le \gamma .\)

Proof

If \(x_n\in VI(C,A)\) then \(x_n=P_{C}(x_n-\gamma Ax_n)\) and \(m_n=0\). We consider the situation \(x_n\notin VI(C,A)\) and assume the contrary that for all m we have

$$\begin{aligned}&\gamma l^m \langle Ax_n-AP_C(x_n-\gamma l^m Ax_n), x_n-P_C(x_n-\gamma l^m Ax_n)\rangle \nonumber \\&\quad > \mu \Vert x_n-P_C(x_n-\gamma l^m Ax_n)\Vert ^2 \end{aligned}$$
(3.2)

By Cauchy–Schwartz inequality, we have

$$\begin{aligned}&\gamma l^m \langle Ax_n-AP_C(x_n-\gamma l^m Ax_n), x_n-P_C(x_n-\gamma l^m Ax_n)\rangle \nonumber \\&\quad \le \gamma l^m \Vert Ax_n-AP_C(x_n-\gamma l^m Ax_n)\Vert \Vert x_n-P_C(x_n-\gamma l^m Ax_n)\Vert . \end{aligned}$$
(3.3)

Combining (3.2) and (3.3) we find

$$\begin{aligned} \gamma l^m\Vert Ax_n-AP_C(x_n-\gamma l^m Ax_n)\Vert > \mu \Vert x_n-P_C(x_n-\gamma l^m Ax_n)\Vert . \end{aligned}$$

This implies that

$$\begin{aligned} \Vert Ax_n-AP_C(x_n-\gamma l^m Ax_n)\Vert > \mu \dfrac{\Vert x_n-P_C(x_n-\gamma l^m Ax_n)\Vert }{\gamma l^m}. \end{aligned}$$
(3.4)

Since \(x_n\in C\) for all n and \(P_C\) is continuous, we have \(\lim _{m\rightarrow \infty }\Vert x_n-P_C(x_n-\gamma l^m Ax_n)\Vert =0.\) Since A is uniformly continuous on bounded subsets of C (Condition 3.2), we get that

$$\begin{aligned} \lim _{m\rightarrow \infty }\Vert Ax_n-AP_C(x_n-\gamma l^m Ax_n)\Vert =0. \end{aligned}$$
(3.5)

Combining (3.4) and (3.5) we get

$$\begin{aligned} \lim _{m\rightarrow \infty }\dfrac{\Vert x_n-P_C(x_n-\gamma l^m Ax_n)\Vert }{\gamma l^m}=0. \end{aligned}$$
(3.6)

Assume that \(z_m=P_C(x_n-\gamma l^m Ax_n)\) we have

$$\begin{aligned} \langle z_m-x_n+\gamma l^m Ax_n,x-z_m\rangle \ge 0 \ \ \forall x\in C. \end{aligned}$$

This implies that

$$\begin{aligned} \langle \dfrac{ z_m-x_n}{\gamma l^m},x-z_m\rangle +\langle Ax_n,x-z_m\rangle \ge 0 \ \ \forall x\in C. \end{aligned}$$
(3.7)

Taking the limit \(m\rightarrow \infty \) in (3.7) and using (3.6), we obtain

$$\begin{aligned} \langle Ax_n,x-x_n\rangle \ge 0 \ \ \forall x\in C, \end{aligned}$$

which implies that \(x_n\in VI(C,A)\) this is a contraction. \(\square \)

Remark 3.3

  1. 1.

    In the proof of Lemma 3.2 we do not use the pseudomonotonicity of A.

  2. 2.

    Now we show that if \(x_n=y_n\) then stop and \(x_n\) is a solution of VI(C, A). Indeed, we have \(0<\lambda _n\le \gamma \), which together with Lemma 2.4 we get

    $$\begin{aligned} 0=\dfrac{\Vert x_n-y_n\Vert }{\lambda _n}=\dfrac{\Vert x_n-P_C(x_n-\lambda _n Ax_n)\Vert }{\lambda _n}\ge \dfrac{\Vert x_n-P_C(x_n-\gamma Ax_n)\Vert }{\gamma }. \end{aligned}$$

    This implies that \(x_n\) is a solution of VI(C, A).

Lemma 3.4

Assume that Conditions 3.1–3.3 hold and let \(\{x_n\}\) be any sequence generated by Algorithm 3.1. Then we have

$$\begin{aligned} \langle Ax_n, x_n-y_n\rangle \ge \dfrac{1}{\gamma }\Vert x_n-y_n\Vert ^2. \end{aligned}$$

Proof

Recall one of the metric projection property

$$\begin{aligned} \Vert x-P_Cy\Vert ^2\le \langle x-y,x-P_Cy\rangle \text { for all } x\in C \text { and } y\in H. \end{aligned}$$

By denoting \(y=x_n-\lambda _n Ax_n\) and \(x=x_n\), we get

$$\begin{aligned} \Vert x_n-P_C(x_n-\lambda _n Ax_n)\Vert ^2\le {{\lambda _n}} \langle Ax_n, x_n-P_C(x_n-\lambda _n Ax_n)\rangle , \end{aligned}$$

thus

$$\begin{aligned} \langle Ax_n, x_n-y_n\rangle \ge \lambda _n^{-1}\Vert x_n-y_n\Vert ^2, \end{aligned}$$

which, together with \(\lambda _n\le \gamma \) we find

$$\begin{aligned} \langle Ax_n, x_n-y_n\rangle \ge \dfrac{1}{\gamma }\Vert x_n-y_n\Vert ^2. \end{aligned}$$

\(\square \)

Lemma 3.5

Assume that Conditions 3.1–3.3 hold and let \(\{x_n\}\) be any sequence generated by Algorithm 3.1. Then we have

$$\begin{aligned} \langle Ay_n,x_n-p\rangle \ge \dfrac{1-\mu }{\gamma }\Vert x_n-y_n\Vert ^2. \end{aligned}$$

Proof

Indeed, let \(p\in VI(C,A)\), since \(y_n\in C\), we have \(\langle Ap, y_n-p\rangle \ge 0\). Due to the pseudomonotonicity of A, we get

$$\begin{aligned} \langle Ay_n,y_n-p\rangle \ge 0. \end{aligned}$$
(3.8)

On the other hand, according to Lemma 3.4 we have

$$\begin{aligned} \langle Ax_n,x_n-y_n\rangle \ge \dfrac{1}{\lambda _n}\Vert x_n-y_n\Vert ^2. \end{aligned}$$
(3.9)

Now, using (3.1), (3.8) and (3.9), we get

$$\begin{aligned} \langle Ay_n,x_n-p\rangle&=\langle Ay_n,x_n-y_n\rangle +\langle Ay_n,y_n-p\rangle \\&\ge \langle Ay_n,x_n-y_n\rangle \\&= \langle Ax_n,x_n-y_n\rangle -\langle Ax_n-Ay_n,x_n-y_n\rangle \\&\ge \dfrac{1}{\lambda _n}\Vert x_n-y_n\Vert ^2-\dfrac{\mu }{\lambda _n}\Vert x_n-y_n\Vert ^2 \\&=\dfrac{1-\mu }{\lambda _n}\Vert x_n-y_n\Vert ^2. \end{aligned}$$

Since \(\lambda _n\le \gamma \) we get

$$\begin{aligned} \langle Ay_n,x_n-p\rangle \ge \dfrac{1-\mu }{\gamma }\Vert x_n-y_n\Vert ^2. \end{aligned}$$

\(\square \)

Remark 3.6

From Lemma 3.5 we see that if \(Ay_n=0\) then \(x_n=y_n\), this implies that \(x_n\) is a solution of VI(C, A).

Lemma 3.7

Assume that Conditions 3.1–3.3 hold and let \(\{x_n\}\) be any sequence generated by Algorithm 3.1. If there exists a subsequence \(\{x_{n_k}\}\) of \(\{x_n\}\) such that \(\{x_{n_k}\}\) converges weakly to \(z\in C\) and \(\lim _{k\rightarrow \infty }\Vert x_{n_k}-y_{n_k}\Vert =0\), then \(z\in VI(C,A).\)

Proof

We have \(y_{n_k}=P_C(x_{n_k}-\lambda _{n_k}Ax_{n_k})\) thus,

$$\begin{aligned} \langle x_{n_k}-\lambda _{n_k}Ax_{n_k}-y_{n_k},x-y_{n_k}\rangle \le 0 \ \ \forall x\in C, \end{aligned}$$

or equivalently

$$\begin{aligned} \dfrac{1}{\lambda _{n_k}}\langle x_{n_k}-y_{n_k},x-y_{n_k}\rangle \le \langle Ax_{n_k},x-y_{n_k}\rangle \ \ \forall x\in C. \end{aligned}$$

This implies that

$$\begin{aligned} \dfrac{1}{\lambda _{n_k}}\langle x_{n_k}-y_{n_k},x-y_{n_k}\rangle +\langle Ax_{n_k},y_{n_k}-x_{n_k}\rangle \le \langle Ax_{n_k},x-x_{n_k}\rangle \ \ \forall x\in C. \end{aligned}$$
(3.10)

Now, we show that

$$\begin{aligned} \liminf _{k\rightarrow \infty }\langle Ax_{n_k},x-x_{n_k}\rangle \ge 0. \end{aligned}$$
(3.11)

For showing this, we consider two possible cases. Suppose first that \(\liminf _{k\rightarrow \infty }\lambda _{n_k}>0\). We have \(\{x_{n_k}\}\) is a bounded sequence, A is uniformly continuous on bounded subsets of C. By Lemma 2.6, we get that \(\{Ax_{n_k}\}\) is bounded. Taking \(k\rightarrow \infty \) in (3.10) since \(\Vert x_{n_k}-y_{n_k}\Vert \rightarrow 0\), we get

$$\begin{aligned} \liminf _{k\rightarrow \infty }\langle Ax_{n_k},x-x_{n_k}\rangle \ge 0. \end{aligned}$$

Now, we assume that \(\liminf _{k\rightarrow \infty }\lambda _{n_k}=0\). Assume \(z_{n_k}=P_{C}(x_{n_k}-\lambda _{n_k}.l^{-1}Ax_{n_k})\), we have \(\lambda _{n_k}l^{-1}>\lambda _{n_k}\). Applying Lemma 3.5, we obtain

$$\begin{aligned} \Vert x_{n_k}-z_{n_k}\Vert \le \dfrac{1}{l}\Vert x_{n_k}-y_{n_k}\Vert \rightarrow 0 \text { as } k\rightarrow \infty . \end{aligned}$$

Consequently, \(z_{n_k}\rightharpoonup z\in C\), this implies that \(\{z_{n_k}\}\) is bounded, and due to Condition 3.2, we get that

$$\begin{aligned} \Vert Ax_{n_k}-Az_{n_k}\Vert \rightarrow 0 \text { as } k\rightarrow \infty . \end{aligned}$$
(3.12)

By the Armijo line-search rule (3.1), we have

$$\begin{aligned} \lambda _{n_k}.l^{-1}\Vert Ax_{n_k}-AP_C(x_{n_k}-\lambda _{n_k}l^{-1} Ax_{n_k})\Vert > \mu \Vert x_{n_k}-P_C(x_{n_k}-\lambda _{n_k}l^{-1} Ax_{n_k})\Vert . \end{aligned}$$

That is,

$$\begin{aligned} \dfrac{1}{\mu }\Vert Ax_{n_k}-Az_{n_k}\Vert >\dfrac{\Vert x_{n_k}-z_{n_k}\Vert }{\lambda _{n_k}l^{-1}}. \end{aligned}$$
(3.13)

Combining (3.12) and (3.13), we obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }\dfrac{\Vert x_{n_k}-z_{n_k}\Vert }{\lambda _{n_k}l^{-1}}=0. \end{aligned}$$

Furthermore, we have

$$\begin{aligned} \langle x_{n_k}-\lambda _{n_k} l^{-1}Ax_{n_k}-z_{n_k},x-z_{n_k}\rangle \le 0 \ \ \forall x\in C. \end{aligned}$$

This implies that

$$\begin{aligned} \dfrac{1}{\lambda _{n_k}l^{-1}}\langle x_{n_k}-z_{n_k},x-z_{n_k}\rangle +\langle Ax_{n_k},z_{n_k}-x_{n_k}\rangle \le \langle Ax_{n_k},x-x_{n_k}\rangle \ \ \forall x\in C. \end{aligned}$$
(3.14)

Taking the limit \(k\rightarrow \infty \) in (3.14), we get

$$\begin{aligned} \liminf _{k\rightarrow \infty }\langle Ax_{n_k},x-x_{n_k}\rangle \ge 0. \end{aligned}$$

Therefore, the inequality (3.11) is proved. Next, we show that \(z\in \mathrm{VI}(C,A)\).

Now we choose a sequence \(\{\epsilon _k\}\) of positive numbers decreasing and tending to 0. For each k, we denote by \(N_k\) the smallest positive integer such that

$$\begin{aligned} \langle Ax_{n_j},x-x_{n_j}\rangle +\epsilon _k \ge 0 \ \ \forall j\ge N_k, \end{aligned}$$
(3.15)

where the existence of \(N_k\) follows from (3.11). Since \(\{ \epsilon _k\}\) is decreasing, it is easy to see that the sequence \(\{N_k\}\) is increasing. Furthermore, for each k, since \(\{x_{N_k}\}\subset C\) we have \(Ax_{N_k}\ne 0\) and, setting

$$\begin{aligned} v_{N_k} = \dfrac{Ax_{N_k}}{\Vert Ax_{N_k}\Vert ^2 }, \end{aligned}$$

we have \(\langle Ax_{N_k}, x_{N_k}\rangle = 1\) for each k. Now, we can deduce from (3.15) that for each k

$$\begin{aligned} \langle Ax_{N_k}, x+\epsilon _k v_{N_k}-x_{N_k}\rangle \ge 0. \end{aligned}$$

Since the fact that A is pseudo-monotone, we get

$$\begin{aligned} \langle A(x+\epsilon _k v_{N_k}), x+\epsilon _k v_{N_k}-x_{N_k}\rangle \ge 0. \end{aligned}$$

This implies that

$$\begin{aligned} \langle Ax, x-x_{N_k}\rangle \ge \langle Ax-A(x+\epsilon _k v_{N_k}), x+\epsilon _k v_{N_k}-x_{N_k} \rangle -\epsilon _k \langle Ax, v_{N_k}\rangle . \end{aligned}$$
(3.16)

Now, we show that \(\lim _{k\rightarrow \infty }\epsilon _k v_{N_k}=0\). Indeed, we have \(x_{n_k}\rightharpoonup z \text { as } k \rightarrow \infty \). Since A is sequentially weakly continuous on C, \(\{ Ax_{n_k}\}\) converges weakly to Az. We have that \(Az \ne 0\) (otherwise, z is a solution). Since the norm mapping is sequentially weakly lower semicontinuous, we have

$$\begin{aligned} 0 < \Vert Az\Vert \le \liminf _{k\rightarrow \infty }\Vert Ax_{n_k}\Vert . \end{aligned}$$

Since \(\{x_{N_k}\}\subset \{x_{n_k}\}\) and \(\epsilon _k \rightarrow 0\) as \(k \rightarrow \infty \), we obtain

$$\begin{aligned} 0 \le \limsup _{k\rightarrow \infty } \Vert \epsilon _k v_{N_k} \Vert = \limsup _{k\rightarrow \infty } \left( \dfrac{\epsilon _k}{\Vert Ax_{n_k}\Vert }\right) \le \dfrac{\limsup _{k\rightarrow \infty }\epsilon _k }{\liminf _{k\rightarrow \infty }\Vert Ax_{n_k}\Vert }=0, \end{aligned}$$

which implies that \(\lim _{k\rightarrow \infty } \epsilon _k v_{N_k} = 0.\)

Now, letting \(k\rightarrow \infty \), then the right-hand side of (3.16) tends to zero by A is uniformly continuous, \(\{x_{N_k}\}, \{v_{N_k}\}\) are bounded and \(\lim _{k\rightarrow \infty }\epsilon _k v_{N_k}=0\). Thus, we get

$$\begin{aligned} \liminf _{k\rightarrow \infty }\langle Ax,x-x_{N_k}\rangle \ge 0. \end{aligned}$$

Hence, for all \(x\in C\) we have

$$\begin{aligned} \langle Ax, x-z\rangle =\lim _{k\rightarrow \infty } \langle Ax, x-x_{N_k}\rangle =\liminf _{k\rightarrow \infty } \langle Ax, x-x_{N_k}\rangle \ge 0. \end{aligned}$$

By Lemma 2.6, we obtain \(z\in VI(C,A)\) and the proof is complete. \(\square \)

Remark 3.8

When the mapping A is monotone, it is not necessary to impose the sequential weak continuity on A.

Theorem 3.9

Assume that Conditions 3.1–3.3 hold. Then any sequence \(\{x_n\}\) generated by Algorithm 3.1 converges weakly to an element of VI(C, A).

Proof

We divide the proof into two claims.

Claim 1

We show that

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2\le \Vert x_n-p\Vert ^2-\dfrac{(1-\mu )^2}{\gamma ^2} \dfrac{\Vert x_n-y_n\Vert ^4}{\Vert Ay_n\Vert ^2}. \end{aligned}$$

Indeed, since \(P_C\) is nonexpansive we get

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&=\Vert P_{C}(x_n-\beta _n Ay_n)-P_Cp\Vert ^2\le \Vert x_n-\beta _n Ay_n-p\Vert ^2\\&=\Vert x_n-p\Vert ^2-2\beta _n \langle Ay_n,x_n-p\rangle +\beta _n^2\Vert Ay_n\Vert ^2, \end{aligned}$$

which, together with Lemma 3.5 we obtain

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2\le&\Vert x_n-p\Vert ^2-2\beta _n \dfrac{1-\mu }{\gamma }\Vert x_n-y_n\Vert ^2 +\beta _n^2\Vert Ay_n\Vert ^2. \end{aligned}$$
(3.17)

Substituting \(\beta _n=\dfrac{1-\mu }{\gamma }\dfrac{\Vert x_n-y_n\Vert ^2}{\Vert Ay_n\Vert ^2}\) into (3.17), we get

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&\le \Vert x_n-p\Vert ^2-2\dfrac{(1-\mu )^2}{\gamma ^2} \dfrac{\Vert x_n-y_n\Vert ^4}{\Vert Ay_n\Vert ^2}+\dfrac{(1-\mu )^2}{\gamma ^2}\dfrac{\Vert x_n-y_n\Vert ^4}{\Vert Ay_n\Vert ^2}\\&=\Vert x_n-p\Vert ^2-\dfrac{(1-\mu )^2}{\gamma ^2} \dfrac{\Vert x_n-y_n\Vert ^4}{\Vert Ay_n\Vert ^2}. \end{aligned}$$

Claim 2

Now, we show that \(\{x_n\}\) converges weakly to an element of VI(C, A). Thanks to Claim 1, we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert \le \Vert x_n-p\Vert \ \ \forall p\in VI(C,A). \end{aligned}$$

This implies that for all \(p\in VI(C,A)\) then \(\lim _{n\rightarrow \infty }\Vert x_{n}-p\Vert \) exists, thus the sequence \(\{x_n\}\) is bounded. Consequently, \(\{y_n\}\) is bounded.

On the other hand, according to Claim 1, we get

$$\begin{aligned} \dfrac{(1-\mu )^2}{\gamma ^2}\dfrac{\Vert x_n-y_n\Vert ^4}{\Vert Ay_n\Vert ^2}\le \Vert x_n-p\Vert ^2-\Vert x_{n+1}-p\Vert ^2 \end{aligned}$$

which implies that

$$\begin{aligned} \lim _{n\rightarrow \infty }\dfrac{\Vert x_n-y_n\Vert ^4}{\Vert Ay_n\Vert ^2}=0. \end{aligned}$$
(3.18)

Since \(\{y_n\}\subset C\) is bounded, A is uniformly continuous on bounded subsets of C, according to Lemma 2.5 we get \(\{Ay_n\}\) is bounded, which together with (3.18) we get

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_n-y_n\Vert =0. \end{aligned}$$
(3.19)

Since \(\{x_n\}\) is a bounded sequence, there exists the subsequence \(\{x_{n_k}\}\) of \(\{x_{n}\}\) such that \(\{x_{n_k}\}\) converges weakly to \(z\in C\). It implies from Lemma 3.7 and (3.19) that \(z\in \mathrm{VI}(C,A)\).

Therefore, we showed that:

  1. (i)

    For every \(p \in \mathrm{VI}(C,A)\), then \(\lim _{n\rightarrow \infty }\Vert x_n-p\Vert \) exists;

  2. (ii)

    Every sequential weak cluster point of the sequence \(\{x_n\}\) is in VI(C, A).

By Lemma 2.7 the sequence \(\{x_n\}\) converges weakly to an element of \(\mathrm{VI}(C,A).\)

\(\square \)

Remark 3.10

Our result is more general than related results in the literature and hence might be applied for a wider class of mappings. For example, we next present the advantage of our method compared with the recent result [33, Theorem 3.1].

As in Theorem 3.9, \(A:C\rightarrow H\) is assumed to be uniformly continuous on bounded subsets instead of Lipschitz continuous in [33].

3.2 Strong convergence

In this subsection, we introduce our second extragradient modification which is based on Halpern method [13] (see also [28]) and hence has a strong convergence property. An additional assumption for the analysis of our method is the following.

Condition 3.4

Let \(\{\alpha _n\}\) be a real sequences in (0, 1) such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\alpha _n=0, \sum _{n=1}^\infty \alpha _n=\infty . \end{aligned}$$

The proposed algorithm is of the form

Algorithm 3.11

figure c

Theorem 3.12

Assume that Conditions 3.1–3.4 hold. Then any sequence \(\{x_n\}\) generated by Algorithm 3.11 converges strongly to \(p\in \mathrm{VI}(C,A)\), where \(p=P_{\mathrm{VI}(C,A)}x_0.\)

Proof

Similar to the proof of Theorem 3.9, and in order to keep it simple, we divide the proof into four claims.

Claim 1

We prove that \(\{x_n\}\) is bounded. Indeed, thanks to Claim 1 in the proof of Theorem 3.9, we have

$$\begin{aligned} \Vert z_n-p\Vert ^2\le \Vert x_n-p\Vert ^2 -\dfrac{(1-\mu )^2}{\gamma ^2}\dfrac{\Vert x_n-y_n\Vert ^4}{\Vert Ay_n\Vert ^2}. \end{aligned}$$
(3.20)

This implies that

$$\begin{aligned} \Vert z_n-p\Vert \le \Vert x_n-p\Vert . \end{aligned}$$
(3.21)

Using (3.21), we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert =&\Vert \alpha _n x_0+(1-\alpha _n)z_n-p\Vert \\&=\Vert \alpha _n (x_0-p)+(1-\alpha _n)(z_n-p)\Vert \\&\le \alpha _n \Vert x_0-p\Vert +(1-\alpha _n)\Vert z_n-p\Vert \\&\le \alpha _n\Vert x_0-p\Vert +(1-\alpha _n)\Vert x_n-p\Vert \\&\le \max \{\Vert x_0-p\Vert , \Vert x_n-p\Vert \}\\&\le \cdots \le \Vert x_0-p\Vert . \end{aligned}$$

Thus, the sequence \(\{x_n\}\subset C\) is bounded. Consequently, the sequences \(\{y_n\}, \{z_n\}, \{Ay_n\}\) are bounded.

Claim 2

We prove that

$$\begin{aligned} \dfrac{(1-\mu )^2}{\gamma ^2}\dfrac{\Vert x_n-y_n\Vert ^4}{\Vert Ay_n\Vert ^2} \le \Vert x_n-p\Vert ^2-\Vert x_{n+1}-p\Vert ^2+\alpha _n M, \end{aligned}$$

for some \(M>0.\) Indeed, we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&=\Vert \alpha _n(x_0-p)+(1-\alpha _n)(z_n-p)\Vert ^2 \nonumber \\&\le (1-\alpha _n)\Vert z_n-p\Vert ^2+2\alpha _n \langle x_0-p,x_{n+1}-p\rangle \nonumber \\&\le \Vert z_n-p\Vert ^2+2\alpha _n \langle x_0-p,x_{n+1}-p\rangle . \end{aligned}$$
(3.22)

Substituting (3.20) into (3.23), we get

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2 \le \Vert x_n-p\Vert ^2-\dfrac{(1-\mu )^2}{\gamma ^2}\dfrac{\Vert x_n-y_n\Vert ^4}{\Vert Ay_n\Vert ^2}+2\alpha _n \langle x_0-p,x_{n+1}-p\rangle . \end{aligned}$$

This implies that

$$\begin{aligned} \dfrac{(1-\mu )^2}{\gamma ^2}\dfrac{\Vert x_n-y_n\Vert ^4}{\Vert Ay_n\Vert ^2}&\le \Vert x_n-p\Vert ^2-\Vert x_{n+1}-p\Vert ^2+2\alpha _n \langle x_0-p,x_{n+1}-p\rangle \\&\le \Vert x_n-p\Vert ^2-\Vert x_{n+1}-p\Vert ^2+2\alpha _n \Vert x_0-p\Vert \Vert x_{n+1}-p\Vert \\&\le \Vert x_n-p\Vert ^2-\Vert x_{n+1}-p\Vert ^2+\alpha _n D, \end{aligned}$$

where \(D:=\sup \{2\Vert x_0-p\Vert \Vert x_{n+1}-p\Vert : n\in {\mathbb {N}}\}\).

Claim 3

We prove that

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2\le (1-\alpha _n)\Vert x_n-p\Vert ^2+2\alpha _n\langle x_0-p,x_{n+1}-p\rangle . \end{aligned}$$

Using (3.21) we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&=\Vert \alpha _n(x_0-p)+(1-\alpha _n)(z_n-p)\Vert ^2 \nonumber \\&\le (1-\alpha _n)\Vert z_n-p\Vert ^2+2\alpha _n \langle x_0-p,x_{n+1}-p\rangle \nonumber \\&\le (1-\alpha _n)\Vert x_n-p\Vert ^2+2\alpha _n \langle x_0-p,x_{n+1}-p\rangle . \end{aligned}$$
(3.23)

Claim 4

Now, we will show that the sequence \(\{\Vert x_n-p\Vert ^2\}\) converges to zero by considering two possible cases on the sequence \(\{\Vert x_n-p\Vert ^2\}\).

Case 1: There exists an \(N\in {\mathbb N}\) such that \(\Vert x_{n+1}-p\Vert ^2\le \Vert x_n-p\Vert ^2\) for all \(n\ge N.\) This implies that \(\lim _{n\rightarrow \infty }\Vert x_n-p\Vert ^2\) exists. It implies from Claim 2 that

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert x_n-y_n\Vert =0. \end{aligned}$$
(3.24)

On the other hand,

$$\begin{aligned} \Vert z_{n}-x_n\Vert&=\Vert P_C(x_n-\beta _n Ay_n)-P_{C}x_n\Vert \\&\le \Vert x_n-\beta _n Ay_n-x_n\Vert =\beta _n \Vert Ay_n\Vert =\dfrac{1-\mu }{\gamma }\dfrac{\Vert x_n-y_n\Vert ^2}{\Vert Ay_n\Vert }. \end{aligned}$$

Using (3.24), it implies that

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert z_n-x_n\Vert =0. \end{aligned}$$

Since \(\{x_n\}\subset C\) is a bounded sequence, we assume that there exists a subsequence \(\{x_{n_j}\}\) of \(\{x_n\}\) such that \(x_{n_j}\rightharpoonup z\in C\) and

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle x_0-p,x_{n}-p\rangle =\lim _{j\rightarrow \infty }\langle x_0-p,x_{n_j}-p\rangle =\langle x_0-p,z-p\rangle . \end{aligned}$$
(3.25)

Since \( \lim _{n\rightarrow \infty } \Vert x_n-y_n\Vert =0\) and \(x_{n_j}\rightharpoonup z\in C\), according Lemma 3.7, we get \(z\in VI(C,A)\). On the other hand,

$$\begin{aligned} \Vert x_{n+1}-z_{n}\Vert =\alpha _{n}\Vert x_0-z_{n}\Vert \rightarrow 0 \text { as } n\rightarrow \infty . \end{aligned}$$

Thus

$$\begin{aligned} \Vert x_{n+1}-x_{n}\Vert =\Vert x_{n+1}-z_{n}\Vert +\Vert z_{n}-x_{n}\Vert \rightarrow 0 \text { as } n\rightarrow \infty . \end{aligned}$$
(3.26)

Using (3.26), \(p=P_{VI(C,A)}x_0\) and \(x_{n_k} \rightharpoonup z\in VI(C,A)\), we get

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle x_0-p, x_{n+1}-p\rangle \le \langle x_0-p, z-p\rangle \le 0, \end{aligned}$$

which, together with Claim 3, it implies from Lemma 2.9 that

$$\begin{aligned} x_n\rightarrow p \text { as } n\rightarrow \infty . \end{aligned}$$

Case 2: There exists a subsequence \(\{\Vert x_{n_j}-p\Vert ^2\}\) of \(\{\Vert x_{n}-p\Vert ^2\}\) such that \(\Vert x_{n_j}-p\Vert ^2 < \Vert x_{n_j+1}-p\Vert ^2\) for all \(j\in {\mathbb {N}}\). In this case, it follows from Lemma 2.8 that there exists a nondecreasing sequence \(\{m_k\}\) of \({\mathbb {N}}\) such that \(\lim _{k\rightarrow \infty }m_k=\infty \) and the following inequalities hold for all \(k\in {\mathbb {N}}\):

$$\begin{aligned} \Vert x_{m_k}-p\Vert ^2\le \Vert x_{m_k+1}-p\Vert ^2 \text { and } \Vert x_{k}-p\Vert ^2\le \Vert x_{m_k+1}-p\Vert ^2. \end{aligned}$$
(3.27)

According to Claim 2, we have

$$\begin{aligned} \dfrac{(1-\mu )^2}{\gamma ^2}\dfrac{\Vert x_{m_k}-y_{m_k}\Vert ^4}{\Vert Ay_{m_k}\Vert ^2} \le \Vert x_{m_k}-p\Vert ^2-\Vert x_{{m_k}+1}-p\Vert ^2+\alpha _{m_k} M,&\le \alpha _{m_k} M. \end{aligned}$$

This implies that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{m_k}-y_{m_k}\Vert =0. \end{aligned}$$

As proved in the first case, we obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert z_{m_k}-x_{m_k}\Vert =0 \end{aligned}$$

and

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{m_k+1}-x_{m_k}\Vert =0 \end{aligned}$$

and

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle x_0-p,x_{{m_k}+1}-p\rangle \le 0. \end{aligned}$$
(3.28)

Combining (3.27) and Claim 3, we obtain

$$\begin{aligned} \Vert x_{m_k+1}-p\Vert ^2&\le (1-\alpha _{m_k})\Vert x_{m_k}-p\Vert ^2+2\alpha _{m_k}\langle x_0-p,x_{{m_k}+1}\rangle \\&\le (1-\alpha _{m_k})\Vert x_{m_k+1}-p\Vert ^2+2\alpha _{m_k}\langle x_0-p,x_{{m_k}+1}-p\rangle . \end{aligned}$$

This implies that

$$\begin{aligned} \Vert x_{m_k+1}-p\Vert ^2\le 2\langle x_0-p,x_{{m_k}+1}-p\rangle , \end{aligned}$$

which, together with (3.27) we get

$$\begin{aligned} \Vert x_{k}-p\Vert ^2\le \Vert x_{m_k+1}-p\Vert ^2\le 2\langle x_0-p,x_{{m_k}+1}-p\rangle . \end{aligned}$$
(3.29)

It implies from (3.28) and (3.29) that \(\limsup _{k\rightarrow \infty }\Vert x_{k}-p\Vert ^2=0\), that is \(x_k\rightarrow p\) as \(k\rightarrow \infty .\) \(\square \)

To end this section, we next present an academic example of variational inequality problem in an infinite dimensional space, where the cost function A is pseudo-monotone, L-Lipschitz continuous and sequentially weakly continuous on C but A fails to be a monotone mapping on H.

Example

Consider the Hilbert space

$$\begin{aligned} H=l_2:=\left\{ u=(u_1,u_2,\ldots ,u_n,\ldots ) \mid \sum _{n=1}^\infty |u_n|^2<+\infty \right\} \end{aligned}$$

equipped with the inner product and induced norm on H:

$$\begin{aligned} \langle u,v\rangle =\sum _{n=1}^\infty u_n v_n \text { and } \Vert u\Vert =\sqrt{\langle u,u\rangle } \end{aligned}$$

for any \(u=(u_1,u_2,\ldots ,u_n,\ldots ), v=(v_1,v_2,\ldots ,v_n,\ldots )\in H.\)

Consider the set and the mapping:

$$\begin{aligned} C= & {} \{u=(u_1,u_2,\ldots ,u_i,\ldots )\in H \mid |u_i|\le \dfrac{1}{i}, i=1,2,\ldots ,n,\ldots \},\\ Au= & {} \left( (\Vert u\Vert +\alpha )-\dfrac{1}{\Vert u\Vert +\alpha }\right) u, \end{aligned}$$

where \(\alpha >1\) is a positive real number.

With this C and A, it is easy to see that VI\((C,A)=\{0\}\) and moreover, A is pseudo-monotone, sequentially weakly continuous and uniformly continuous on C but A fails to be Lipschitz continuous on H.

First observe that since \(\alpha >1\), we get that

$$\begin{aligned} \left( (\Vert u\Vert +\alpha )-\dfrac{1}{\Vert u\Vert +\alpha }\right) >0 \ \ \forall u\in C. \end{aligned}$$

Now let \(u,v\in C\) be such that \(\langle Au,v-u\rangle \ge 0\). This implies that \(\langle u,v-u\rangle \ge 0\).

Consequently,

$$\begin{aligned} \langle Av,v-u\rangle&=\left( (\Vert u\Vert +\alpha )-\dfrac{1}{\Vert u\Vert +\alpha }\right) \langle v,v-u\rangle \\&\ge \left( (\Vert u\Vert +\alpha )-\dfrac{1}{\Vert u\Vert +\alpha }\right) \left( \langle v,v-u\rangle - \langle u,v-u\rangle \right) \\&=\left( (\Vert u\Vert +\alpha )-\dfrac{1}{\Vert u\Vert +\alpha }\right) \Vert v-u\Vert ^2\ge 0, \end{aligned}$$

meaning that A is pseudo-monotone.

Now, since C is compact, the mapping A is uniformly continuous and sequentially weakly continuous on C.

Finally, we show that A is not Lipschitz continuous on H. Assume to the contrary that A is Lipschitz continuous on H, i.e., there exists \(L>0\) such that

$$\begin{aligned} \Vert Au-Av\Vert \le L\Vert u-v\Vert \ \ \forall u,v\in H. \end{aligned}$$

Let \(u=(L,0,...,0,...)\) and \(v=(0,0,...,0,...)\), then

$$\begin{aligned} \Vert Au-Av\Vert =\Vert Au\Vert =\left( (\Vert u\Vert +\alpha )-\dfrac{1}{\Vert u\Vert +\alpha }\right) \Vert u\Vert =\left( (L+\alpha )-\dfrac{1}{L+\alpha }\right) L. \end{aligned}$$

Thus, \(\Vert Au-Av\Vert \le L\Vert u-v\Vert \) is equivalent to

$$\begin{aligned} \left( (L+\alpha )-\dfrac{1}{L+\alpha }\right) L\le L^2, \end{aligned}$$

equivalently

$$\begin{aligned} L+\alpha \le L+\dfrac{1}{L+\alpha }<L+1, \end{aligned}$$

which implies that \(\alpha <1\), and this leads to a contraction and thus A is not Lipschitz continuous on H.

Remark 3.13

It should be emphasized here that the example established in Section 4 in [33] is not sequentially weakly continuous.

Remark 3.14

Thank to the referee’s comment, we wish to point out that since the proximity operator of a proper, lower semicontinuous and convex function is a generalization of the metric projection and our convergence analysis mainly use the firmly nonexpansiveness of the metric projection, and it is known that the proximity operator is indeed firmly nonexpansive, our proposed method can be modified to solve a more general variational inequalities.

4 Numerical illustrations

In this section, we present an example illustrating the behavior and advantages of our proposed schemes. The numerical example which is the Kojima–Shindo Nonlinear Complementarity Problem (NCP), see e.g., [27].

Example

In this example, we test our algorithms behavior for solving The Kojima–Shindo Nonlinear Complementarity Problem (NCP) with \(n=4\), see e.g., [27]. The cpu time is measured in seconds using the intrinsic MATLAB function cpu time. The VI feasible set is \(C:=\{x\in {\mathbb {R}}_{+}^{4}\mid x_{1}+x_{2}+x_{3}+x_{4}=4\}\) and A is given as follows:

$$\begin{aligned} A(x_{1},x_{2},x_{3},x_{4}):=\left[ \begin{array} [c]{c} 3x_{1}^{2}+2x_{1}x_{2}+2x_{2}^{2}+x_{3}+3x_{4}-6\\ 2x_{1}^{2}+x_{1}+x_{2}^{2}+10x_{3}+2x_{4}-2\\ 3x_{1}^{2}+x_{1}x_{2}+2x_{2}^{2}+2x_{3}+9x_{4}-9\\ x_{1}^{2}+3x_{2}^{2}+2x_{3}+3x_{4}-3 \end{array} \right] . \end{aligned}$$
(4.1)

The solution if the problem is \((\sqrt{6}/2,0,0,0.5)\). In our experiments, we choose the stopping criteria as \(\left\| x_{n}-y_n\right\| \le 10^{-3}\). The projection onto the feasible set C is performed using CVX version 1.22. Other parameters are: \(\gamma =0.2, l=0.3, \mu =0.6\), we choose the stopping criterion \(||x_n-y_n||<10^{-5}\). In [11, Algorithm 3.1], we choose \(\varepsilon =0.2, \beta =0.5\) and \(\alpha _{-1}=0.7\).

The starting point for all experiments is \(x_0=(1,1,1,1)\). All computations were performed using MATLAB R2017a on an Intel Core i5-4200U 2.3 GHz running 64-bit Windows. In Fig. 1, the performances of Algorithms 3.1, 3.11 and [11, Algorithm 3.1] are presented.

Fig. 1
figure 1

Illustration of Algorithms 3.1, 3.11 and [11, Algorithm 3.1]

Full size image

In Table 1, the complementary data of Fig. 1 is presented.

Table 1 Algorithms 3.1, 3.11 and [11, Algorithm 3.1]
Full size table

5 Conclusions

In this paper, we proposed two extragradient extensions for solving non-Lipschitzian pseudo-monotone variational inequalities in real Hilbert spaces. Under suitable and standard conditions, we establish weak and strong convergence theorems of the proposed schemes. Our work extends and generalizes some existing results in the literature and academic and numerical experiments demonstrate the behavior and potential applicability of the methods.