1 Introduction

Consider the unconstrained nonlinear optimization problem:

$$\begin{aligned} \min f(x), \ \ \ x \in \mathbb {R}^n, \end{aligned}$$

where \(f:\mathbb {R}^n\rightarrow \mathbb {R}, \) is twice continuously differentiable.

The conjugate gradient (CG) methods are popular in solving large-scale unconstrained minimization problems, since they avoid storing matrices. One step of these iterative methods is defined as follows:

$$\begin{aligned} x_{k+1} = x_k + \alpha _k d_k, \end{aligned}$$
(1)

where \(\alpha _k>0\) is a step length and \(d_k\) is the search direction defined by:

$$\begin{aligned} d_k=\left\{ \begin{array}{ll} -g_k, &{} \hbox { for } \quad k = 0, \\ -g_k+\beta _k d_{k-1}, &{} \hbox {for } \quad k> 0, \end{array} \right. \end{aligned}$$
(2)

where \(g_{k} = \nabla f (x_{k})\) and \(\beta _k \) being a scalar called the CG parameter. Different choices for the CG parameter in (2) lead to different CG methods.

The step length \(\alpha _k\) is determined by an exact/inexact line search technique Nocedal and Wright (2006). Throughout our work here, we utilize the strong Wolfe conditions for determining the step length as follows Nocedal and Wright (2006):

$$\begin{aligned}&f(x_k + \alpha _k d_k) \le f(x_k) +\sigma _1 \alpha _k g_k^{T} d_k,\\&\Big \vert g(x_k + \alpha _k d_k)^{T} d_k \Big \vert \le \sigma _2 \Big \vert g(x_k)^{T} d_k \Big \vert , \end{aligned}$$

with \(0<\sigma _1<\sigma _2<1.\)

Well-known CG methods include those proposed by Hestenes–Stiefel (HS) (1952), Fletcher–Reeves (FR) (1964), and Polak–Ribire (PR) (Polak and Ribiére 1969; Polyak 1969).

Zoutendijk (1970) established the global convergence of the FR method with the exact line search. Al-Baali (1985) extended this result using inexact line search. Powell (1977) showed that the FR method had a poor performance in practice. In this regard, although PR and HS methods work very well in practice, their global convergence is not guaranteed. To overcome this problem, Powell (1984) suggested another modified conjugate parameter.

Recently, Dai and Liao (2001) proposed some formulae for \(\beta _k\) by exploiting a conjugacy condition based on the standard secant relation:

$$\begin{aligned} B_{k+1}s_k=y_k , \end{aligned}$$
(3)

where \( s_{k} = x_{k+1} -x_{k}\) and \(y_k=g_{k+1}-g_{k}\).

The usual secant relation employs only the gradients and the available function values are ignored. To get a higher order accuracy of approximating the Hessian matrix of the objective function, several researchers have modified the usual secant relation (3) to make full use of both the gradient and function values (see Wei et al. 2006; Yuan and Wei 2010; Yabe and Takano 2004; Zhang and Xu 2001). Wei et al. (2006), using Taylor’s series, modified (3) as follows:

$$\begin{aligned} B_{k+1}s_k=y_k + \frac{\vartheta _k}{\Vert s_k\Vert ^{2}} s_k, \end{aligned}$$
(4)

where \(\vartheta _{k}=2 (f_{k}-f_{k+1})+ (g_{k}+g_{k+1})^T s_{k}.\) Recently, Yuan and Wei (2010) extended the modified secant relation (4) as follows:

$$\begin{aligned} B_{k+1}s_k={\tilde{y}}_k, \end{aligned}$$
(5)

where \({\tilde{y}}_k =y_k + \frac{\max (\vartheta _k , 0)}{\Vert s_k\Vert ^{2}} s_k\).

Such modified secant relations make use of both the available gradient and function values only at the latest available point. Ford and Moghrabi (1997, (1993, (1994) employed interpolating polynomials, and introduced a different secant relation utilizing information from three most recent points.

Ford and Moghrabi (1993), by constructing interpolating quadratic curves for x(t), modified the secant relation (3) as follows:

$$\begin{aligned} B_{k+1}r_k=w_k, \quad r_k=s_k-\psi s_{k-1}, \quad w_k=y_k-\psi y_{k-1}, \end{aligned}$$
(6)

where

$$\begin{aligned} \psi =\frac{\delta ^{2}}{1+2\delta }, \quad \delta =\frac{t_2-t_1}{t_1-t_0}. \end{aligned}$$
(7)

Notice that \(t_0, t_1\) and \(t_2\) are chosen, such that:

$$\begin{aligned} x(t_0)=x_{k-1},\quad x(t_1)=x_{k},\quad x(t_2)=x_{k+1}. \end{aligned}$$
(8)

We observe that the modified secant method (6) utilizes information from the three most recent iterates, but does not utilize function values. Here, we use Taylor’s series to construct alternative estimates of the secant relation, using both the available gradient and function values. Moreover, we utilize the information from the three most recent points instead of merely the last two points. Then, we make use of the new secant relation and the idea of Dai and Liao (2001) and Moghrabi (2019) to obtain a new formula for \(\beta _k\) (see Eq. (48)).

The rest of our work is organized as follows. In Sect. 2, we briefly discuss the conjugacy condition proposed by Dai and Liao. In Sect. 3, we use Taylor’s series to construct alternative estimates of the secant relation and by considering this relation we introduce a new formula for CG parameter. In Sect. 4, we investigate the convergence of our proposed method. In Sect. 5, we report numerical results. We conclude in Sect. 6.

2 Dai–Liao’s nonlinear CG methods

Here, we summarize review Dai–Liao’s conjugacy condition. These methods are obtained based on the standard secant equation:

$$\begin{aligned} B_ks_{k-1}=y_{k-1}, \end{aligned}$$
(9)

where \(B_k\) is an approximation of the Hessian of f at \(x_k\).

The search direction \(d_k\) is a quasi-Newton direction obtained by solving:

$$\begin{aligned} B_kd=-g_k. \end{aligned}$$
(10)

It is well known that the search direction generated by the linear CG methods satisfies the following conjugacy conditions:

$$\begin{aligned} d_{i}^{T}Qd_{j}=0,~~~\forall i\ne j, \end{aligned}$$

where Q is a positive definite Hessian matrix of the quadratic objective function.

For a general nonlinear function f,  using the mean value theorem for f(x),  there exists \(\tau \in (0, 1)\), such that:

$$\begin{aligned} d_{k}^{T}y_{k-1}=\alpha _{k-1}d_{k}^{T} \nabla ^2 f(x_{k-1} +\tau \alpha _{k-1} d_{k-1})d_{k-1}. \end{aligned}$$
(11)

Hence, it is reasonable to replace (11) with:

$$\begin{aligned} d_{k}^{T}y_{k-1}=0. \end{aligned}$$

Using (9) and (10), we have:

$$\begin{aligned} d_{k}^{T}y_{k-1}=d_{k}^{T}( B_ks_{k-1})=-g_{k}^{T}s_{k-1}. \end{aligned}$$
(12)

Dai and Liao (2001) modified the conjugacy condition (12) as follows:

$$\begin{aligned} d_{k}^{T}y_{k-1}=-tg_{k}^{T}s_{k-1}, \end{aligned}$$
(13)

where t is a scaler. Then, using (2) and (13), they obtained the following new formula for \(\beta _{k}\):

$$\begin{aligned} \beta _{k}^{DL}=\frac{ g_{k}^{T} (y_{k-1}-ts_{k-1})}{d_{k-1}^{T} y_{k-1}}. \end{aligned}$$

Recently, several CG methods based on other secant relations have been investigated (see Babaie-Kafaki et al. 2010; Li et al. 2007; Yabe and Takano 2004). In addition, using the multi-step secant relation (6), Ford et al. (2008) derived following formulas for \(\beta _{k}\):

$$\begin{aligned} \beta _{k}^{FNY}=\frac{ g_{k}^{T} (w_{k-1}-tr_{k-1})}{d_{k-1}^{T}w_{k-1}}. \end{aligned}$$
(14)

3 Two-step conjugate gradient method

Here, we use Taylor’s series to construct alternative estimates of the secant relation to approximate the second curvature of the objective function with a high accuracy. Then, we propose a CG parameter by considering a new secant relation and adapting the idea of Dai and Liao (2001).

3.1 A modified secant relation

Here, we intend to make use of three iterates \(x_{k-1},\)\(x_{k}\), and \(x_{k+1},\) generated by some quasi-Newton algorithm. Let

$$\begin{aligned} \varphi (t)=f(x(t)), \end{aligned}$$

where x(t) is a differentiable curve in \(\mathbb {R}^n.\) Since function f is adequately smooth, it is obvious that \(\varphi (t)\) is sufficiently smooth.

Using the chain rule to function \(\varphi (t)\):

$$\begin{aligned} \varphi '(t)=\left( \frac{{\text {d}}x}{{\text {d}}t}\right) ^{T}g(x(t)) \end{aligned}$$
(15)

and

$$\begin{aligned} \varphi ''(t)=\left( \frac{{\text {d}}x}{{\text {d}}t}\right) ^{T}G(x(t))\left( \frac{{\text {d}}x}{{\text {d}}t}\right) +\left( \frac{{\text {d}}^{2}x}{{\text {d}}t^{2}}\right) ^{T}g(x(t)). \end{aligned}$$
(16)

Now, suppose that x(t) is the quadratic polynomial interpolating, so that:

$$\begin{aligned} x(t_0)=x_{k-1}, \quad x(t_1)=x_{k}, \quad x(t_2)=x_{k+1}. \end{aligned}$$

Of course, there are various choices for x(t). Using Lagrange interpolation, we have:

$$\begin{aligned} x(t)\equiv \sum _{j=0}^{2} L_j(t)x_{k+j-1}, \end{aligned}$$
(17)

where \(L_j(t), \quad j=0, 1, 2,\) are the basic Lagrange polynomials:

$$\begin{aligned} L_j(t)=\prod _{i=0,i\ne j}^{2}\frac{t-t_i}{t_j-t_i}. \end{aligned}$$

Taking the derivative of (17), we obtain:

$$\begin{aligned} \frac{{\text {d}}x(t)}{{\text {d}}t}\equiv \sum _{j=0}^{2} L'_j(t)x_{k+j-1}. \end{aligned}$$
(18)

On the other hand, we know:

$$\begin{aligned} \sum _{j=0}^{2}L'_j(t)=0. \end{aligned}$$
(19)

Using (19), we can write (18) as:

$$\begin{aligned} \frac{{\text {d}}x(t)}{{\text {d}}t}\equiv L'_2(t)\Big (s_k -\frac{L'_0(t)}{L'_2(t)}s_{k-1} \Big ). \end{aligned}$$
(20)

Moreover, by taking the derivative of (20), we have:

$$\begin{aligned} \frac{{\text {d}}^{2}x(t)}{{\text {d}}^{2}t}\equiv L''_2(t)\Big (s_k -\frac{L''_0(t)}{L''_2(t)}s_{k-1} \Big ). \end{aligned}$$
(21)

Clearly, we can represent (20) and (21) as follows:

$$\begin{aligned} \frac{{\text {d}}x(t)}{{\text {d}}t}\equiv L'_2(t)\Big (s_k -\psi s_{k-1} \Big ), \end{aligned}$$
(22)

and

$$\begin{aligned} \frac{{\text {d}}^{2}x(t)}{{\text {d}}^{2}t}\equiv L''_2(t)\Big (s_k -\delta s_{k-1} \Big ), \end{aligned}$$
(23)

where \(\psi \) and \(\delta \) are given by (7).

To determine \(\delta \) and \(\psi \) in (7), the values \(t_j, j=0, 1, 2,\) are needed. For this purpose, we consider one of the successful approaches that was introduced by Ford and Moghrabi (1993). Consider a norm of the general form:

$$\begin{aligned} \Vert z\Vert _{M}=\{z^{T}Mz\}^{\frac{1}{2}}, \end{aligned}$$

where M is some symmetric positive definite matrix. By choosing \(t_2=0\) and taking M be the identity matrix, \(t_1\) and \(t_0\) can be computed as follows:

$$\begin{aligned} t_1=-\Vert s_k\Vert , ~~t_0=-\Vert s_k\Vert -\Vert s_{k-1}\Vert . \end{aligned}$$
(24)

Using the Taylor’s expansion formula for the function \(\varphi \),

$$\begin{aligned} \varphi (t)\simeq \varphi (0)+t\varphi '(0)+\frac{t^{2}}{2}\varphi ''(0); \end{aligned}$$
(25)

that is:

$$\begin{aligned} {t^{2}}\varphi ''(0)\simeq 2\Big (\varphi (t)-\varphi (0)-t\varphi '(0)\Big ). \end{aligned}$$
(26)

Substituting \(t =t_1\) in (26), and using (15), (16) and the fact that \(\varphi (t_2)=f_{k+1}\), \(\varphi (t_1)=f_{k}, \) the relation (26) implies that:

$$\begin{aligned} \begin{array}{l} \Vert s_k\Vert ^{2} \left( \frac{{\text {d}}x}{{\text {d}}t}\vert _{ t=0}\right) ^{T}G_{k+1}\left( \frac{{\text {d}}x}{{\text {d}}t}\vert _{ t=0}\right) +\Vert s_k\Vert ^{2}\left( \frac{{\text {d}}^{2}x}{{\text {d}}t^{2}}\right) ^Tg_{k+1}\\ \simeq 2(f_{k}-f_{k+1})+2\Vert s_k\Vert \left( \frac{{\text {d}}x}{{\text {d}}t}\vert _{ t=0}\right) ^{T}g_{k+1};\end{array} \end{aligned}$$

that is:

$$\begin{aligned}&{\left( \Vert s_k\Vert \frac{{\text {d}}x}{{\text {d}}t}\vert _{ t=0}\right) ^{T}}G_{k+1} {\left( \Vert s_k\Vert \frac{{\text {d}}x}{{\text {d}}t}\vert _{ t=0}\right) }\nonumber \\&\quad \simeq 2(f_{k}-f_{k+1})+2{\left( \Vert s_k\Vert \frac{{\text {d}}x}{{\text {d}}t}\vert _{ t=0}\right) ^{T}}g_{k+1}-\Vert s_k\Vert ^{2}\left( \frac{{\text {d}}^{2}x}{{\text {d}}t^{2}}\right) ^Tg_{k+1}. \end{aligned}$$
(27)

By considering \(\{t_j\}_{j=0}^{2},\) as (24), the relations (22) and (23) can be written as:

$$\begin{aligned} \frac{{\text {d}}x}{{\text {d}}t}\vert _{t=0}=\frac{\eta _1}{\Vert s_k\Vert }(s_k-\psi s_{k-1}), \end{aligned}$$
(28)

and

$$\begin{aligned} \frac{{\text {d}}^{2}x}{{\text {d}}t^{2}}=\frac{2(s_k-\delta s_{k-1})}{t_{0}t_{1}}, \end{aligned}$$

where \(\psi \) and \(\delta \) are defined by (7), and \(\eta _1\) is given by:

$$\begin{aligned} \eta _1=\frac{t_0+t_1}{t_0}. \end{aligned}$$

This implies that:

$$\begin{aligned} -\Vert s_k\Vert ^{2}\left( \frac{{\text {d}}^{2}x}{{\text {d}}t^{2}}\right) ^{T}g_{k+1}=-2\eta _{2}{(s_k-\delta s_{k-1})^{T}g_{k+1}}, \end{aligned}$$
(29)

where

$$\begin{aligned} \eta _2= -\frac{\Vert s_k\Vert }{t_0}. \end{aligned}$$

Now, using (28) and (29) and the fact that \(y_{k}=g_{k+1}-g_{k}\) and considering \(B_{k+1}\) as a new approximation of \(G_{k+1}\), the relation (27) implies that:

$$\begin{aligned} {\overline{s}}_k^{T}B_{k+1}{\overline{s}}_k={\overline{s}}_k^{T}(y_k-\psi y_{k-1})+\vartheta _k, \end{aligned}$$
(30)

with

$$\begin{aligned} {\overline{s}}_k=\eta _1(s_k-\psi s_{k-1}), \end{aligned}$$
(31)

and

$$\begin{aligned} \vartheta _k= 2(f_{k}-f_{k+1})-2\eta _2(s_k-\delta s_{k-1})^Tg_{k+1}+{\overline{s}}_k^{T}(g_{k+1}+(1+\psi )g_k-\psi g_{k-1}). \end{aligned}$$

Equation (30) provides a new modified secant relation as follows:

$$\begin{aligned} B_{k+1} {\overline{s}}_k={\overline{y}}_k, \end{aligned}$$
(32)

where \({\overline{s}}_k\) is given by (31) and \({\overline{y}}_k\) defined by:

$$\begin{aligned} {\overline{y}}_k= y_k-\psi y_{k-1}+\frac{\vartheta _k}{\Vert {\overline{s}}_k\Vert ^{2}}{\overline{s}}_k. \end{aligned}$$
(33)

We note that this new secant relation contains information from the three most recent points where the usual secant relation makes use of the information merely at the two latest points. Moreover, both the available gradient and function values are being utilized, while the modified BFGS of Ford and Moghrabi (6) made use of only the gradient information from the three most recent points, but ignored the available function values.

A merit of the new modified secant method can be seen from the following theorem.

Theorem 1

Suppose that the function f is sufficiently smooth. If \(\Vert s_k \Vert ,\) is small enough, then we have:

$$\begin{aligned} {\overline{s}}_{k}^{T}(G_{k+1}{\overline{s}}_{k} -{\overline{y}}_{k})=\frac{1}{3} {\overline{s}}_{k}^T (T_{k+1} {\overline{s}}_{k}) {\overline{s}}_{k}+O (\parallel {\overline{s}}_{k}\parallel ^{4}), \end{aligned}$$
(34)

and

$$\begin{aligned} r_{k}^{T}(G_{k+1}r_k -w_{k})=\frac{1}{2} {\overline{s}}_{k}^T (T_{k+1} {\overline{s}}_{k}) {\overline{s}}_{k}+O (\parallel {\overline{s}}_{k} \parallel ^{4}), \end{aligned}$$
(35)

where

$$\begin{aligned} {\overline{s}}_k^T (T_{k+1} {\overline{s}}_k) {\overline{s}}_k=\sum _{i,j,l=1}^n \frac{\partial ^{3} f(x_{k+1})}{\partial x^i \partial x^j \partial x^l } \partial {\overline{s}}_{k}^i \partial {\overline{s}}_{k}^j \partial {\overline{s}}_{k}^l. \end{aligned}$$
(36)

Proof

The result follows straightforwardly from (25). \(\square \)

Theorem 1 implies that the quantity \({\overline{s}}_{k}^{T}{\overline{y}}_{k}\) generated by the modified secant method approximates the second curvature \( {\overline{s}}_{k}^{T}G_{k+1} {\overline{s}}_{k}\) with a higher accuracy than the quantity \(r_{k}^{T}w_{k}\) does.

Remark 1

It is easy to see that:

$$\begin{aligned} \eta _1 =\frac{t_0+t_1}{t_0} \le 1+\frac{t_1}{t_0} = 1+\frac{\Vert s_k\Vert }{\Vert s_k\Vert +\Vert s_{k-1}\Vert }\le 2. \end{aligned}$$
(37)

This relation implies that:

$$\begin{aligned} 1 \le \eta _1 \le 2. \end{aligned}$$
(38)

Moreover:

$$\begin{aligned} \eta _2= \frac{\Vert s_k\Vert }{\Vert s_k\Vert +\Vert s_{k-1}\Vert }\le 1. \end{aligned}$$
(39)

Here, we consider some common assumptions.

Assumption A

The level set \(D = \{x \mid f(x) \le f(x_0)\}\) is bounded.

Assumption B

The function f is continuously differentiable on D, and there is a constant \(L \ge 0\), such that, for all \( x, y \in D,\)\(\parallel g(x) - g(y) \parallel \le L \parallel x - y \parallel \).

It is clear that assumptions A and B imply that there is a positive constant \(\gamma \), such that:

$$\begin{aligned} \Vert g(x) \Vert \le \gamma , \quad \forall \quad x\in D. \end{aligned}$$

Lemma 1

Suppose that the assumption A holds and \({\overline{s}}_k\) defined by (31). Then, we have:

$$\begin{aligned} \frac{1}{2}\Vert s_k\Vert \le \Vert {\overline{s}}_k\Vert \le 3\Vert s_k\Vert . \end{aligned}$$
(40)

Proof

By the definitions of \(t_0, t_1\) and \(t_2\), we can get:

$$\begin{aligned} \delta =\frac{\Vert s_k\Vert }{\Vert s_{k-1}\Vert }. \end{aligned}$$

We see that \(\delta >0\) and \(\eta _{1} =\frac{t_0+t_1}{t_0}>0,\) then we can deduce the following inequalities:

$$\begin{aligned} \psi =\frac{\delta ^{2}}{1+2\delta }<\frac{\delta ^{2}}{2\delta }=\frac{\Vert s_k\Vert }{2\Vert s_{k-1}\Vert }. \end{aligned}$$
(41)

Now, using (31), (38), and (41), we have:

$$\begin{aligned} \Vert {\overline{s}}_k\Vert \le { \eta _1 } (\Vert s_k \Vert + \psi \Vert s_{k-1}\Vert ) \le 3\Vert s_k \Vert . \end{aligned}$$
(42)

Moreover, we can give:

$$\begin{aligned} \Vert {\overline{s}}_k\Vert \ge {\eta _1 } (\Vert s_k \Vert - \psi \Vert s_{k-1}\Vert ) \ge \frac{1}{2} \Vert s_k \Vert . \end{aligned}$$
(43)

Hence, (42) and (43) give the desired result (40). \(\square \)

3.2 A new formula for \(\beta _k\)

Here, considering the approach proposed by Dai and Liao, and using our modified secant relation given by (32), we propose a new conjugacy relation:

$$\begin{aligned} d_{k}^{T}{{\overline{y}}}_{k-1}=-tg_{k}^{T}{\overline{s}}_{k-1}. \end{aligned}$$
(44)

Using the conjugacy relation (44), we present a new formula for \(\beta _k\):

$$\begin{aligned} \beta _{k}=\frac{ g_{k}^{T} ({{\overline{y}}}_{k-1}-t{\overline{s}}_{k-1})}{d_{k-1}^{T}{{\overline{y}}}_{k-1}}. \end{aligned}$$
(45)

For a general function f,  it is possible that the denominator, \(d_{k-1}^{T} {{\overline{y}}}_{k-1},\) in (45) becomes zero. To overcome the difficulty, we make a modification on (32) as follows:

$$\begin{aligned} B_{k+1} {\overline{s}}_k=y_k^{*} , \end{aligned}$$
(46)

with

$$\begin{aligned} y_k^{*} ={\overline{y}}_k +h_k {\overline{s}}_k,\quad h_k=C\Vert g_k\Vert +\max \left( -\frac{{\overline{y}}_k^T {\overline{s}}_k}{\Vert {\overline{s}}_k\Vert ^{2}},0\right) , \end{aligned}$$
(47)

where C is a positive constant.

Now, using the secant relation (46), we obtain another CG parameter as follows:

$$\begin{aligned} \beta _{k}^{{\text {new}}}=\frac{ g_{k}^{T} (y^{*}_{k-1}-ts_{k-1})}{d_{k-1}^{T} y^{*}_{k-1}}. \end{aligned}$$
(48)

From (38) and (47), it is not difficult to see that:

$$\begin{aligned}&d_{k-1}^{T}y^{*}_{k-1} \ge C \Vert g_{k-1}\Vert d_{k-1}^{T} {\overline{s}}_{k-1}\nonumber \\&\quad \ge \frac{1}{2}C \Vert g_{k-1}\Vert d_{k-1}^{T} {s}_{k-1} \ge \frac{1}{2}C\alpha ^{-1}_{k-1} \Vert g_{k-1}\Vert \Vert s_{k-1}\Vert ^{2}>0. \end{aligned}$$
(49)

We can now give a new CG algorithm using our proposed CG parameter given by (48) as follows.

Algorithm 1: New conjugate gradient method

Step 1: Give \( \varepsilon , \) as a tolerance for stopping criterion, \( C>0, \)\( \lambda > 0 \), \(\sigma _1 \in (0,1)\) and \(\sigma _2\in (\sigma _1,1),\) a starting point \(x_0 \in \mathbb {R}^n.\) Set \(\alpha _{initial}=1\), \(d_0=-g_0,\) and \(k = 0\).

Step 2: If \(\Vert g_k \Vert <\varepsilon \) then stop.

Step 3: Compute the step length \(\alpha _k\) to satisfy the strong Wolfe conditions with the initial step length set to \(\alpha _{initial}\).

Step 4 : Set \(x_{k+1} = x_k + \alpha _k d_k.\)

Step 5 : Compute \({\overline{s}}_k\) and \(y_{k}^{*}\) by (31) and (47), respectively. Then, calculate \(\beta _{k} \) by:

$$\begin{aligned} \beta _{k}\equiv \beta ^{{\text {New}}}_{k} =\frac{ g_{k+1}^{T} (y^{*}_{k}-ts_{k})}{d_{k+1}^{T} y^{*}_{k}}. \end{aligned}$$

Step 6 : Compute \(d_{k+1}\) by \(d_{k+1}=-g_{k+1}+\beta _kd_k\).

Step7: Compute the initial step length by:

$$\begin{aligned} \alpha _{{\text {initial}}}=\lambda \frac{ \Vert s_{k} \Vert }{\Vert d_{k+1}\Vert }. \end{aligned}$$

Step 8 : Set \(k = k + 1\) and go to Step 2.

In the next section, we proceed to establish the global convergence of Algorithm 1.

4 Convergence analysis

First, we consider the following definition.

Definition 1

For the search directions \(\{d_k\}\), we say that the descent condition holds if and only if:

$$\begin{aligned} g_{k}^{T}d_{k}<0, \quad \forall \quad k\ge 0. \end{aligned}$$

To establish convergence of Algorithm 1, we first provide some lemmas.

Lemma 2

Let f satisfies assumptions A and B. For \({\overline{y}}_{k}\) defined by (33), we have:

$$\begin{aligned} \Vert {\overline{y}}_{k} \Vert \le M_1 \Vert s_{k-1}\Vert , \end{aligned}$$
(50)

where \(M_1 > 0\) is a constant.

Proof

Using assumptions A and B and Remark 1, we obtain:

$$\begin{aligned} \begin{array}{ll} \vert \vartheta _k \vert &{} = \vert 2(f_{k}-f_{k+1})-2\eta _{2}(s_k-\delta s_{k-1})g_{k+1}+{\overline{s}}_k^{T}(g_{k+1}+(1+\psi )g_k-\psi g_{k-1})\vert \\ &{} = \vert -2g(x_{k}+\theta s_k)s_k-2\eta _{2}(s_k-\delta s_{k-1})g_{k+1}+{\overline{s}}_k^{T}(g_{k+1}\\ &{} \quad +(1+\psi )g_k-\psi g_{k-1})\vert \\ &{} \le \Vert 2 (g_{k+1}-g(x_{k}+\theta s_k)) s_k\Vert +2\delta \Vert s_{k-1}\Vert g_{k+1}\Vert +\Vert {\overline{s}}_k \Vert \Vert (g_{k+1}\\ &{} \quad +(1+\psi )g_k-\psi g_{k-1})\Vert \\ &{} \le 2L(1-\theta )\Vert s_k \Vert ^{2}+2\gamma {\Vert s_k \Vert } +2m_2(1+\psi )\gamma \Vert {s}_k\Vert , \end{array} \end{aligned}$$

where \(\theta \in [0, 1]\). Thus, we can deduce that there exists constant \(a_1>0\), such that:

$$\begin{aligned} \vert \vartheta _k \vert \le a_1\Vert s_k\Vert ^{2}. \end{aligned}$$

Also, from definition of \({\overline{y}}_k\) and relation (40), we have:

$$\begin{aligned} \Vert {\overline{y}}_k\Vert= & {} \Vert y_k-\psi y_{k-1}+\frac{\vartheta _k}{\Vert {\overline{s}}_k\Vert ^{2}}{\overline{s}}_k\Vert \\\le & {} \Vert y_k\Vert + \vert \psi \vert \Vert y_{k-1}\Vert +\frac{\vert \vartheta _k \vert }{\Vert {\overline{s}}_k\Vert ^{2}}\Vert {\overline{s}}_k\Vert \\\le & {} L \Vert s_k\Vert + \vert \psi \vert L \Vert s_{k-1}\Vert +2{a_{3}}\Vert {\overline{s}}_k\Vert \\\le & {} \frac{3}{2}L \Vert s_k\Vert +6\Vert {s}_k\Vert . \end{aligned}$$

Therefore, the inequality (50) holds with \(M_1=\frac{3}{2}L+6a_1.\)\(\square \)

Corollary 1

Let f satisfies assumptions A and B, and \(y^{*}_{k}\) be defined by (47). Then, there exists a constant \(M_2>0\), such that:

$$\begin{aligned} \Vert y_{k} ^{*}\Vert \le M_2 \Vert s_{k}\Vert . \end{aligned}$$
(51)

Proof

Considering Lemma 2 and assumptions A and B, we have:

$$\begin{aligned} \Vert y_{k} ^{*}\Vert&=\Vert {\overline{y}}_{k}+r_{k} {\overline{s}}_{k}\Vert \\&=\Vert {\overline{y}}_{k}+\left( C\Vert g_{k}\Vert +\max \left( -\frac{{\overline{y}}_{k}^{T} {\overline{s}}_{k}}{\Vert {\overline{s}}_{k} \Vert ^{2}},0\right) \right) {\overline{s}}_{k}\Vert \\&\le \Vert {\overline{y}}_{k}\Vert + C\Vert g_{k}\Vert \Vert {\overline{s}}_{k} \Vert + \frac{\vert {\overline{y}}_{k}^{T} {\overline{s}}_{k}\vert }{\Vert {\overline{s}}_{k} \Vert ^{2}}\Vert {\overline{s}}_{k }\Vert \\&\le 2 \Vert {\overline{y}}_{k}\Vert + C\Vert g_{k}\Vert \Vert {\overline{s}}_{k} \Vert \le (2M_1 +Cm_2\gamma ) \Vert {s}_{k} \Vert , \end{aligned}$$

which implies (51) with \(M_2=(2M_1 +Cm_2\gamma ) \Vert {s}_{k}\Vert .\)\(\square \)

For any CG method using the strong Wolfe line search conditions, the following general result was established in Dai et al. (1999).

Lemma 3

Dai et al. (Dai et al. 1999) Let assumptions A and B hold. Consider any CG method in the form (1)–(2), where \(d_k\) is a descent direction and \(\alpha _{k}\) is computed using the strong Wolfe line search conditions. If

$$\begin{aligned} \sum _{k\ge 1}{} \frac{1}{\Vert d_k \Vert }=\infty , \end{aligned}$$
(52)

then we have:

$$\begin{aligned} \liminf _{k\longrightarrow \infty }g(x_k)=0. \end{aligned}$$

Next, we establish the global convergence of Algorithm 1.

Theorem 2

Let f satisfies the Assumptions A, B and \(\{x_k\}\) be generated by Algorithm 1. Then, we have:

$$\begin{aligned} \liminf _{k\rightarrow \infty }g(x_k)=0. \end{aligned}$$
(53)
Table 1 Problems from the CUTEr library
Full size table

Proof

In view of Lemma 3, it suffices to show that (52) holds.

From (49), we have:

$$\begin{aligned} d_{k-1}^{T}y^{*}_{k-1} \ge \frac{1}{2}C\alpha ^{-1}_{k-1} \Vert g_{k-1}\Vert \Vert s_{k-1}\Vert ^{2}. \end{aligned}$$
(54)

On the other hand, using (40), we have:

$$\begin{aligned}&\vert g_{k}^{T} y^{*}_{k-1}-tg_{k}^{T}{\overline{s}}_{k-1}\vert \le \vert g_{k}^{T} y^{*}_{k-1}\vert +t\vert g_{k}^{T}{\overline{s}}_{k-1}\vert \end{aligned}$$
(55)
$$\begin{aligned}&\quad \le \Vert g_{k}\Vert \Vert y^{*}_{k-1}\Vert +3 t\Vert g_{k} \Vert \Vert s_{k-1}\Vert \nonumber \\&\quad \le M \Vert g_k\Vert \Vert s_{k-1}\Vert +3t \Vert g_k\Vert \Vert s_{k-1}\Vert \nonumber \\&\quad \le (M+3t) \Vert g_k\Vert \Vert s_{k-1}\Vert . \end{aligned}$$
(56)

Consequently, from (2), (54) and (56), we have:

$$\begin{aligned} \Vert d_k\Vert= & {} \Vert - g_k+ \beta ^{{\text {New}}}_{k} d_{k-1}\Vert \\\le & {} \Vert g_k\Vert +\vert \beta ^{{\text {New}}}_{k} \vert \Vert d_{k-1}\Vert \\= & {} \Vert g_k\Vert + \frac{ \vert g_{k}^{T} y^{*}_{k-1}-tg_{k}^{T} s_{k-1}\vert }{\vert d_{k-1}^{T} y^{*}_{k-1}\vert } \Vert d_{k-1}\Vert \\\le & {} \gamma +2 \frac{( M+3 t )\Vert s_{k-1}\Vert }{C\alpha ^{-1}_{k-1} \Vert s_{k-1}\Vert ^{2}} \Vert d_{k-1}\Vert \\\le & {} \gamma + 2 \frac{(M+3 t ) }{ C}. \end{aligned}$$

Now, summing up over k,  we get:

$$\begin{aligned} \sum _{k\ge 1}^{} \frac{1}{\Vert d_k\Vert }\ge \frac{C}{ C\gamma +2( M+ t )} \sum _{k\ge 1}^{}1=\infty . \end{aligned}$$

Thus, by Lemma 3, the proof is complete. \(\square \)

5 Numerical results

Numerical results presented by Ford et al. (2008) show that the CG methods with \({\beta }^{FNY}_k\) as given by (14), perform better than the DL method of Dai and Liao (2001), the YT method of Yabe and Takano (2004), and HS method of Hestenes and Stiefel (1952). Thus, here, we compare the performance of our CG method, denoted by M1, with the aforementioned CG method proposed in Ford et al. (2008), denoted by M2. Therefore, our results are reported for the following two algorithms:

M1: Our proposed method (Algorithm 1).

M2: The CG method of Ford et al. (2008) (Algorithm 1 with \( \beta ^{FNY}_k\) as given by (14)).

Since CG methods are mainly designed for large-scale problems, our experiments were made on a set of 75 test problems of the CUTEr library Gould et al. (2015) with the minimum dimension being equal to 1000. A summary of these problems is given in Table 1.

Fig. 1
figure 1

The Dolan–Moré performance profiles using number of function evaluations

Full size image
Fig. 2
figure 2

The Dolan–Moré performance profiles using number of iterations

Full size image
Fig. 3
figure 3

The Dolan–More performance profiles using CPU times

Full size image

All the codes were written in Matlab 2011 and run on a PC with CPU Intel(R) Core(TM) i5-4200 3.6 GHz, 4 GB of RAM memory, and Centos 6.2 server Linux operating system. The algorithms stop when

$$\begin{aligned} \Vert g_k\Vert \le 10^{-6}, \end{aligned}$$

or the total number of iterates exceeds 3000.

We note that we terminated an algorithm and considered it as failed on a problem, when the number of iterations exceeded 3000.

For the two algorithms in all cases, the steplength \(\alpha _k\) is computed using the strong Wolfe conditions with \(\sigma _1 =0.001,\)\(\sigma _2 =0.1.\) For this, we used the line search procedure of Moré and Thuente (1994). Moreover, we set \(C=10^{-6}\) in the relation (47).

It is remarkable that numerical performance of the DL method is very dependent on the choice of the parameter t. Recently, work has been done to propose proper selections of t. Here, we utilize the parameter t,  as follows Babaie-Kafaki and Ghanbari (2014):

$$\begin{aligned} t_k=\frac{\Vert y_{k}\Vert }{\Vert s_{k}\Vert }. \end{aligned}$$
(57)

We used the performance profiles of Dolan and Moré (2002) to evaluate the performance of these two algorithms with respect to CPU time, the number of iterations, and the total number of function and gradient evaluations computed as:

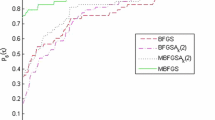
$$\begin{aligned} N_{\text {f}} + 3N_{\text {g}}, \end{aligned}$$

where \(N_{\text {f}}\) and \(N_{\text {g}}\), respectively, denote the number of function and gradient evaluations. Figures 1, 2, and 3 demonstrate the results of the comparisons. From these figures, it is clearly observed that Algorithm 1 (M1) is more efficient as compared to the method of Ford et al. (2008).

6 Conclusion

We presented a secant relation for unconstrained optimization problems and approximated the second curvature of the objective function with a high accuracy. Then, based on the proposed secant relation and adapting the approach of Dai–Liao, we presented a conjugate gradient method to solve unconstrained optimization problems. An interesting feature of the proposed method was taking both the gradient and function values into account. Another important property of the proposed method was the utilization of information from the three most recent iterates instead of the last two iterates. Under suitable assumptions, we have established the global convergence of the proposed method without a convexity assumption on the objective function. Numerical results on the collection of problems in CUTER show that the proposed method is efficient as compared to the conjugate gradient method proposed by Ford et al.