1 Introduction

Consider the unconstrained nonlinear optimization problem

$$\begin{aligned} \min f(x), \;\;\; x \in \mathbb {R}^n, \end{aligned}$$
(1)

where f is twice continuously differentiable. The quasi-Newton methods are popular iterative methods for solving (1), whose iterates are constructed as follows:

$$\begin{aligned} x_{k+1} = x_k + \alpha _k d_k , \end{aligned}$$

where \(\alpha _k\) is a step size and \(d_k\) is a descent direction obtained by solving \(B_k d_k=-g_k,\) where \(g_k =\bigtriangledown f(x_k)\) and \(B_k \) is an approximation of the Hessian matrix of f at \(x_k\) which satisfies the secant equation.

The standard secant equation can be established as follows (see Dennis and Schnabel 1983). We have

$$\begin{aligned} g_{k+1}-g_{k}=\int _{0}^{1}\bigtriangledown ^2 f(x_k +ts_k){\mathrm{d}t} {s_k}, \end{aligned}$$
(2)

where \(s_k=x_{k+1}-x_k.\) Since \(B_{k+1}\) is to approximate \(G(x_{k+1})=\nabla ^2 f(x_{k+1}),\) the secant equation is defined to be

$$\begin{aligned} B_{k+1} s_k=y_k, \end{aligned}$$
(3)

where \(y_k=g_{k+1}-g_k\). The relation (3) is sometimes called the standard secant equation.

A famous family of quasi-Newton methods is Broyden family Broyden (1965) in which the updates are defined by

$$\begin{aligned} B_{k+1}=B_{k}-\frac{B_k s_k s_{k}^\mathrm{T} B_k}{s_{k}^\mathrm{T} B_k s_k}+\frac{y_{k}y_{k}^\mathrm{T}}{s_{k}^\mathrm{T} y_{k} }+\mu w_k w^\mathrm{T}_{k},~~~~w_k=( s^\mathrm{T}_{k}B_k s_k)^{1/2}\left[ \frac{y_k}{s^\mathrm{T}_{k}y_k }-\frac{B_k s_k}{s^\mathrm{T}_{k}B_k s_k}\right] , \end{aligned}$$
(4)

where \(\mu \) is a scale parameter. The BFGS, DFP and SR1 updates are obtained by setting \(\mu =0\), \(\mu =1\) and \(\mu =1/(1-s^\mathrm{T}_{k}B_k s_k/s^\mathrm{T}_{k}y_k ),\) respectively.

Among quasi-Newton methods, the most efficient method is the BFGS method Broyden (1970).

When f is convex, the global convergence of the BFGS method have been studied by some authors (see Byrd and Nocedal 1989; Byrd et al. 1987; Griewank 1991; Powell 1976; Toint 1986). However, the BFGS method is very efficient as regards numerical performance, but Dai (2003) have constructed an example to show that this method may fail for non-convex functions with inexact Wolfe line searches. In addition, Mascarenhas (2004) showed that the nonconvergence of the standard BFGS method even with exact line search.

Global convergence of the BFGS method for the general functions under Wolfe line search is still an open problem. Recently, Yuan et al. (2017, 2018) provided a positive answer, and proved the global convergence of BFGS method under a modified weak Wolfe–Powell line search technique for general functions.

To obtain better quasi-Newton methods, many modified methods have been presented (see Li and Fukushima 2001a, b; Wei et al. 2006; Yuan and Wei 2009, 2010; Yuan et al. 2017, 2018; Zhang et al. 1999; Zhang and Xu 2001).

Li and Fukushima (2001a, b) made a modification on the standard BFGS method as follows:

$$\begin{aligned} B_{k+1}s_{k}=\overline{y}_{k}, \end{aligned}$$
(5)

with

$$\begin{aligned} \overline{y}_{k}=y_{k}+r_k s_{k},~~ r_k=C\Vert g_{k}\Vert ^{2}+\max \left( -\frac{y_{k}^\mathrm{T} s_{k}}{\Vert s_{k} \Vert ^{2}},0\right) , \end{aligned}$$
(6)

where C is a positive constant.

They showed this method is globally convergent without a convexity assumption on the objective function f.

The usual secant equation employs only the gradients and the available function values are ignored. To get a higher order accuracy of approximating the Hessian matrix of the objective function, several researchers have modified the usual secant equation (3) to make full use of both the gradient and function values (see Wei et al. 2006; Yuan and Wei 2009, 2010; Yuan et al. 2017, 2018; Zhang et al. 1999; Zhang and Xu 2001).

Wei et al. (2006), using Taylor’s series, modified (3) as follows:

$$\begin{aligned} B_{k+1}s_k=\tilde{y}_k, \end{aligned}$$
(7)

where \(\tilde{y}_k=y_k + \frac{\vartheta _k}{\Vert s_k\Vert ^{2}} s_k\) and \(\vartheta _{k}=2 (f_{k}-f_{k+1})+ (g_{k}+g_{k+1})^\mathrm{T} s_{k}.\)

Recently, Yuan and Wei (2010) considered an extension of the modified secant equation (7) as follows:

$$\begin{aligned} B_{k+1}s_k=y_k + \frac{\max (\vartheta _k , 0)}{\Vert s_k\Vert ^{2}} s_k. \end{aligned}$$
(8)

Numerical results of Yuan and Wei (2010) showed that the modified BFGS method suggested by Yuan and Wei outperformed the CG methods proposed by Wei et al. (2006) and Li and Fukushima (2001b) and the standard BFGS method Broyden (1970).

Such modified secant equations make use of both the available gradient and function values only at the last two points. Here, we employ chain rule, and introduced a different secant relation utilizing information from three most recent points and using both the available gradient and function values. Then, we make use of the new secant equation in a BFGS updating formula.

This work is organized as follows: In Sect. 2, we first employ chain rule to derive an alternative secant equation and then we outline our proposed algorithm. In Sect. 3, we investigate the global convergence of the proposed method. Finally, in Sect. 4, we report some numerical results.

2 Two-step BFGS method

In this section, we obtain a new secant equation. Next, we use this secant equation and we give the algorithm.

2.1 Proposed modified secant equation

Here, we intend to make use of three iterates \(x_{k-1},\) \(x_{k}\) and \(x_{k+1}\) generated by some quasi-Newton algorithm. Using chain rule to function \(\bigtriangledown ^2 f(X(t)),\) we know

$$\begin{aligned} g(X(1))-g(X(-1))=\int _{-1}^{1}\bigtriangledown ^2 f(X(t))\frac{{\mathrm{{d}}X(t)}}{{\mathrm{{d}}t}}\mathrm{{d}}t, \end{aligned}$$
(9)

where X(t) is a differentiable curve in \(\mathbb {R}^n.\)

Now, suppose that X(t) is the interpolating curve so that

$$\begin{aligned} X(-1)=x_{k-1},~~~~~~~X(0)=x_{k},~~~~~~~X(1)=x_{k+1}. \end{aligned}$$
(10)

Of course there are various choices for X(t). Here, motivated by Ford and Saadallah (1987), we define a nonlinear interpolating with a free parameter as follows:

$$\begin{aligned} X(t)\equiv x(t,\theta ) \equiv q(t)\frac{1}{1+t\theta }, \end{aligned}$$
(11)

where \(q(t)=a_0 + a_1 t + a_2 t^2\) (\(\{a_i\}_{i=0}^{2}\) are constant vectors) and \(\theta \) is a parameter to be chosen later.

Since \(q(t)=x(t,\theta ) (1+t\theta )\) is a second degree polynomial and hence, may be written in its Lagrangian form

$$\begin{aligned} q(t)=\sum _{j=0}^{2} L_j(t)q(t_j), \end{aligned}$$
(12)

where \(q(t_j)=x(t_j,\theta )(1+t_j \theta )\) and the \(L_j(t)\) are the basic Lagrange polynomials:

$$\begin{aligned} L_{j}(t)=\prod _{i=0,i\ne j}^{2}\frac{t-t_i}{t_j-t_i}, j=0, 1, 2. \end{aligned}$$
(13)

After some algebraic manipulations, (12) can be written as

$$\begin{aligned} q(t) \equiv \bigg [\frac{t(t+1)(1+\theta )}{2}x_{k+1}+(1-t^{2})x_k+\frac{t(t-1)(1-\theta )}{2}x_{k-1}\bigg ]. \end{aligned}$$
(14)

Therefore

$$\begin{aligned} x(t,\theta ) \equiv \bigg [\frac{t(t+1)(1+\theta )}{2}x_{k+1}+(1-t^{2})x_k+\frac{t(t-1)(1-\theta )}{2}x_{k-1}\bigg ]\frac{1}{1+t\theta }. \end{aligned}$$
(15)

Taking the derivative from both sides of (15), we obtain:

$$\begin{aligned} \frac{\mathrm{d}x(t,\theta )}{\mathrm{d}t}\simeq & {} \Bigg (\frac{(1+2t)(1+\theta )}{2}x_{k+1}-2tx_k+\frac{(2t-1)(1-\theta )}{2}x_{k-1}\Bigg ) \frac{1}{1+t\theta }\nonumber \\&+ \bigg (\frac{t(t+1)(1+\theta )}{2}x_{k+1}+(1-t^{2})x_k+\frac{t(t-1)(1-\theta )}{2}x_{k-1}\bigg )\frac{-\theta }{(1+t\theta )^{2}}.\nonumber \\ \end{aligned}$$
(16)

On the other hand, using Lagrange interpolation we have

$$\begin{aligned} \bigtriangledown ^2 f(x(t,\theta ))\simeq \sum _{j=0}^{2} L_j(t)\bigtriangledown ^2 f(x_{k+j-1}). \end{aligned}$$
(17)

Substituting relation (17) into (9), we obtain:

$$\begin{aligned} g(x_{k+1})-g(x_{k-1})= & {} \int _{-1}^{1}\bigtriangledown ^2 f(X(t)) \frac{\mathrm{d}X(t)}{\mathrm{d}t}\mathrm{d}t\nonumber \\= & {} \sum _{j=0}^{2}\int _{-1}^{1} L_j(t) \bigtriangledown ^2 f(x_{k+j-1}) \frac{\mathrm{d}X(t)}{\mathrm{d}t}\mathrm{d}t, \end{aligned}$$
(18)

where \(\frac{\mathrm{d}X(t)}{\mathrm{d}t}\equiv \frac{\mathrm{d}x(t,\theta )}{\mathrm{d}t}\) given by (16).

Now, by considering \(B_{k+1}\) as a new approximation of \(\nabla ^2 f(x_{k+1}),\) (18) leads to

$$\begin{aligned} B_{k+1}\int _{-1}^{1}L_2(t) \frac{\mathrm{d}X(t)}{\mathrm{d}t}\mathrm{d}t= & {} g(x_{k+1})-g(x_{k-1})\nonumber \\&- B_k\int _{-1}^{1} L_1(t) \frac{\mathrm{d}X(t)}{\mathrm{d}t}\mathrm{d}t- B_{k-1}\int _{-1}^{1} L_0(t) \frac{\mathrm{d}X(t)}{\mathrm{d}t}\mathrm{d}t,\qquad \end{aligned}$$
(19)

where \(B_{k-1}\) and \(B_{k}\) approximate \(\nabla ^2 f(x_{k-1}) \) and \(\nabla ^2 f(x_{k}),\) respectively.

Equation (19) provides a new modified secant relation as follows:

$$\begin{aligned} B_{k+1} s_k^{*}=y_k ^{*}, \end{aligned}$$
(20)

where \(y_k ^{*}\) and \(s_k ^{*}\) are given by

$$\begin{aligned} s_k^{*}=\int _{-1}^{1}L_2(t) \frac{\mathrm{d}X(t)}{\mathrm{d}t}\mathrm{d}t, \end{aligned}$$
(21)

and

$$\begin{aligned} y_k ^{*}=y_k+y_{k-1}- B_k\int _{-1}^{1} L_1(t) \frac{\mathrm{d}X(t)}{\mathrm{d}t}\mathrm{d}t- B_{k-1}\int _{-1}^{1} L_0(t) \frac{\mathrm{d}X(t)}{\mathrm{d}t}\mathrm{d}t, \end{aligned}$$
(22)

with \(\frac{\mathrm{d}X(t)}{\mathrm{d}t}\equiv \frac{\mathrm{d}x(t,\theta )}{\mathrm{d}t}\) given by (16).

Now, the issue is choosing a strategy to determine a numerical value for \(\theta \). Define

$$\begin{aligned} \varphi (t,\theta )=f(x(t,\theta )). \end{aligned}$$
(23)

Clearly we have

$$\begin{aligned} \int _{-1}^{1} \varphi '(t,\theta )=f_{k+1}-f_{k-1}. \end{aligned}$$
(24)

On the other hand, a reasonable estimate of the integral would be given by

$$\begin{aligned} \int _{-1}^{1} \varphi '(t,\theta )\simeq & {} 2\varphi '(0,\theta )\nonumber \\= & {} 2x'(0,\theta )g_k. \end{aligned}$$
(25)

Remark A

In constructing this estimate of the integral, we are using advantage of the fact that \(t=0\) is an interior point of the interval of integration \([-1,1].\)

On the other hand, from Eq. (16) we have

$$\begin{aligned} x'(0,\theta )\simeq \frac{1}{2}\left[ s_{k}+s_{k-1}+\theta s_k -\theta s_{k-1}\right] . \end{aligned}$$
(26)

From (24), (25) and (26), we obtain

$$\begin{aligned} \theta \equiv \frac{f_{k+1} -f_{k-1}- s^\mathrm{T}_{k}g_{k}- s^\mathrm{T}_{k-1}g_{k}}{ s^\mathrm{T}_{k}g_{k}-s^\mathrm{T}_{k-1}g_{k}}. \end{aligned}$$
(27)

Obviously (27) is a good estimation of \(\theta \) and it dose not require expensive computations.

Also, it is easy to see that if the denominator, \((1 + t\theta )\) in (11), becomes zero over the interval \([-1,1 ],\) then the interpolating curve \(x(t,\theta )\) is undesirable. To overcome this difficulty, since the denominator \((1 + t\theta )\) is positive at \(t=0\), we impose the two conditions as follows:

$$\begin{aligned} 1 + \theta>0 \quad 1 - \theta >0 \end{aligned}$$

that is,

$$\begin{aligned} -1<\theta <1. \end{aligned}$$
(28)

In implementing the new algorithm, if the condition (28) dose not hold, then we set \(\theta =0.\)

2.2 Proposed BFGS algorithm

Here, we apply the modified secant equation given in the previous subsection then we propose new modified BFGS method such that \(B_{k+1}\) update by

$$\begin{aligned} B_{k+1}= B_{k}-\frac{B_k s^{*}_k {s^{*}_{k}}^\mathrm{T} B_k}{{s^{*}_{k}}^\mathrm{T} B_k s^{*}_k}+\frac{y_{k}^{*}{y_{k}^{*}}^\mathrm{T}}{{s^{*}_{k}}^\mathrm{T} y_{k}^{*} }, \end{aligned}$$
(29)

where \(y_k ^{*}\) and \(s_k ^{*}\) are given by

$$\begin{aligned} s_k^{*}=\int _{-1}^{1}L_2(t) \frac{\mathrm{d}X(t)}{\mathrm{d}t}\mathrm{d}t, \end{aligned}$$
(30)

and

$$\begin{aligned} y_k ^{*}=y_k+y_{k-1}- B_k\int _{-1}^{1} L_1(t) \frac{\mathrm{d}X(t)}{\mathrm{d}t}\mathrm{d}t- B_{k-1}\int _{-1}^{1} L_0(t) \frac{\mathrm{d}X(t)}{\mathrm{d}t}\mathrm{d}t, \end{aligned}$$
(31)

with \(\frac{\mathrm{d}X(t)}{\mathrm{d}t}\) and \(\theta \) are given by (16) and (27) respectively.

We note that this new modified BFGS contains information from the three most recent points where the usual BFGS method and modified BFGS method introduced by Li and Fukushima (2001b), Wei et al. (2006) and Yuan and Wei (2010), make use of the information merely at the two latest points. In addition, both the available gradient and function values are being utilized.

We know, \({s^{*}_{k}}^\mathrm{T}{y^{*}_{k}}>0,\) is sufficient to ensure \(B_{k+1}\) to be positive definite (see Nocedal and Wright 2006) and consequently, the generated search directions are descent directions. However, for a general function f,  \({s^{*}_{k}}^\mathrm{T}y^{*}_{k} \) may not be positive for all \(k\ge 0,\) and consequently \(B_{k+1}\) may not be positive definite.

For preserving positive definiteness of the updates, we set

$$\begin{aligned} B_{k+1}= \left\{ \begin{array}{ll} B_{k}-\frac{B_k s^{*}_k {s^{*} _{k}}^\mathrm{T} B_k}{{s^{*}_{k}}^\mathrm{T} B_k s^{*}_k}+\frac{y_{k}^{*}{y_{k}^{*}}^\mathrm{T}}{{s^{*}_{k}}^\mathrm{T}y_{k}^{*} }, &{} \frac{ {s_{k}^{*}}^\mathrm{T} y_{k}^{*}}{\Vert s_k^{*}\Vert ^2} \ge \delta ,\\ B_k, &{} \hbox {otherwise. } \end{array} \right. \end{aligned}$$
(32)

where \(\delta \) is a positive constant.

Remark B

From (32), it is easy to see that \({s^{*}_{k}}^\mathrm{T}y^{*}_{k}>0\) therefore the matrix \(B_{k+1}\) generated by (32), is symmetric and positive definite for all k.

We can now give a new BFGS algorithm using new secant relation (20), as Algorithm 1.

Algorithm 1: The new modified BFGS method.

Step 1: Give \( \varepsilon \) as a tolerance for convergence, \(\sigma _1 \in (0,1),\) \(\sigma _2\in (\sigma _1,1),\) a starting point \(x_0 \in \mathbb {R} ^n,\) and a positive definite matrix \(B_0.\) Set \(k = 0\).

Step 2: If \(\Vert g_k \Vert <\varepsilon \) then stop.

Step 3: Compute a search direction \( d_k\): Solve \(B_k d_k =- g_k.\)

Step 4: Compute the step length \(\alpha _k\) satisfying the following Wolfe conditions:

$$\begin{aligned}&f(x_k + \alpha _k d_k) \le f(x_k) +\sigma _1 \alpha _k g_k^\mathrm{T} d_k, \end{aligned}$$
(33)
$$\begin{aligned}&g(x_k + \alpha _k d_k)^\mathrm{T} d_k \ge \sigma _2 g(x_k)^\mathrm{T} d_k. \end{aligned}$$
(34)

Step 5: Set \(x_{k+1} = x_k + \alpha _k d_k\). Compute \(s_{k}^{*}\) and \(y_{k}^{*}\) by (30) and (31) respectively, with \(\theta \) given by (27). If \({s_{k}^{*}}^\mathrm{T} y_{k}^{*}< 10^{-4} \Vert s_{k}^{*}\Vert \Vert y_{k}^{*}\Vert \) then set \( s_{k}^{*}=s_k\) and \(y_{k}^{*}=y_k.\)

Step 6: Update \(B_{k+1}\) by (32).

Step 7: Set \(k = k + 1\) and go to Step 2.

1pc

Next, we will investigate the global convergence of Algorithm 1.

3 Convergence analysis

To establish the global convergence of the Algorithm 1, we need some commonly used assumptions.

Assumption A

(i) The level set \(D = \{x \mid f(x) \le f(x_0)\}\) is bounded, where \(x_0\) is the starting point of Algorithm 1.

(ii) The function f is twice continuously differentiable and there is constant \(L> 0,\) such that

$$\begin{aligned} \Vert G(x) -G(y) \Vert \le L \Vert x - y\Vert ,~~~ \forall x, y \in D. \end{aligned}$$

It is clear that Assumption A implies

$$\begin{aligned} \Vert G(x)\Vert \le m,~~\forall x\in D, \end{aligned}$$
(35)

where m is a positive constant

Since \(B_k\) is a approximate G(x) at \(x_k,\) similar to Yuan and Wei (2009) and Zhu (2005) we give the following assumption.

Assumption B

Assume that \(B_k\) is a good approximation to G(x) at \(x_k.\), i.e.,

$$\begin{aligned} \Vert B_k-G(x_k) \Vert \le \varepsilon _k, \end{aligned}$$
(36)

where \( \varepsilon _k \in (0, 1)\) are suitable quantities.

On the other hand, we have

$$\begin{aligned} \Vert B_k\Vert -\Vert G(x_k) \Vert \le \Vert B_k- G(x_k) \Vert \le \varepsilon _k, \end{aligned}$$

Hence, we can give

$$\begin{aligned} \Vert B_k \Vert \le \gamma , ~~~ \forall k\ge 0, \end{aligned}$$
(37)

where \(\gamma = \varepsilon _k+m.\)

Using Assumption A and the Wolfe conditions, \(\lbrace f(x_k)\rbrace \) is a nonincreasing sequence, which ensures \(\lbrace x_k \rbrace \subset D\) and the existence of \(x^{*}\) such that

$$\begin{aligned} \lim _{k\rightarrow \infty }f{(x_k)}=f(x^{*}). \end{aligned}$$
(38)

To establish the global convergence of Algorithm 1, we present the following useful Lemmas.

Lemma 3.1

Let f satisfies assumptions A and B, and \(\{x_k\}\) be generated by Algorithm 1 and there exist constants \(a_1\) and \(a_2\) such that

$$\begin{aligned} \Vert B_k s_{k} \Vert \le a_1\Vert s_{k} \Vert , ~~~~~~s_{k}^{T} B_k s_{k}\ge a_2\Vert s_{k} \Vert ^2, \end{aligned}$$
(39)

for infinitely many k. Then, we have

$$\begin{aligned} \liminf _{k\rightarrow \infty }g(x_k)=0. \end{aligned}$$
(40)

Proof

Since \(s_{k}= \alpha _k d_k,\) it is clear that (39) holds true if \(s_{k}\) is replaced by \(d_k\). From (39) and the relation \(g_{k} = - B_{k}d_k,\) we have

$$\begin{aligned} d^\mathrm{T}_k B_{k}d_k \ge a_2\Vert d_k \Vert ^2, ~~~~~~~ ~~~~~~~a_2\Vert d_k \Vert \le \Vert g_k \Vert \le a_1\Vert d_k \Vert . \end{aligned}$$
(41)

Let \(\Lambda \) be the set of indices k for which (39) hold. Using (34) and Assumption asB, we have

$$\begin{aligned} L\alpha _k \Vert d_k\Vert ^2 \ge (g_{k+1}-g_k)^\mathrm{T}d_k \ge -(1-\sigma _2)g^\mathrm{T}_k d_k. \end{aligned}$$
(42)

This implies that, for any \(k \in \Lambda ,\)

$$\begin{aligned} \alpha _k \ge \frac{-(1-\sigma _2)g^\mathrm{T}_k d_k}{L\Vert d_k\Vert ^2}=\frac{(1-\sigma _2)d_{k}^\mathrm{T}B_k d_k}{L\Vert d_k\Vert ^2}\ge \frac{(1-\sigma _2)a_2}{L}. \end{aligned}$$
(43)

Moreover, by (38), we obtain

$$\begin{aligned} \sum _{k=1}^{\infty }(f_k-f_{k+1})=\lim _{N\rightarrow \infty }\sum _{k=1}^{N}(f_k-f_{k+1})=\lim _{N\rightarrow \infty }f(x_1)-f(x_{N}))=f(x_1)-f(x^{*}), \end{aligned}$$

which yields

$$\begin{aligned} \sum _{k=1}^{\infty }(f_k-f_{k+1})<\infty . \end{aligned}$$

Using (33), we get

$$\begin{aligned} \sum _{k=1}^{\infty }\alpha _k g_k^\mathrm{T} d_k<\infty , \end{aligned}$$

which ensures

$$\begin{aligned} \lim _{k\rightarrow \infty }\alpha _k g_k^\mathrm{T}d_k=0. \end{aligned}$$

This together with (43) lead to

$$\begin{aligned} \lim _{k\in \Lambda , k\rightarrow \infty } d_k^\mathrm{T}B_k d_k=\lim _{k\in \Lambda , k\rightarrow \infty }- g_k^\mathrm{T}d_k=0. \end{aligned}$$

which a long with (41), yields (40). \(\square \)

Now, we prove the global convergence of Algorithm 1.

Theorem 3.1

Let f satisfy the assumptions A and B and \(\lbrace x_k\rbrace \) be generated by Algorithm 1. Then, we have

$$\begin{aligned} \liminf _{k\rightarrow \infty }g(x_k)=0. \end{aligned}$$
(44)

Proof

Using Lemma 3.1, it is sufficient to show relation (39) holds for infinitely many k. Using (37), we have

$$\begin{aligned} \Vert B_k s_k \Vert \le \Vert B_k \Vert \Vert s_k \Vert \le \gamma \Vert \Vert s_k \Vert . \end{aligned}$$
(45)

Since \(B_{k},\) in Algorithm 1 is symmetric and positive definite then there exists \(a_2\) such that

$$\begin{aligned} {s_{k}}^\mathrm{T} B_k s_{k} \ge a_2\Vert s_{k} \Vert ^2. \end{aligned}$$

Then, Lemma 3.1 completes the proof. \(\square \)

Table 1 Test problems taken from CUTEr library
Full size table
Fig. 1
figure 1

The Dolan–More performance profiles using number of function evaluations

Full size image
Fig. 2
figure 2

The Dolan–More performance profiles using number of iterations

Full size image
Fig. 3
figure 3

The Dolan–More performance profiles using CPU times

Full size image

4 Numerical results

We compare the performance of the following four methods on some unconstrained optimization problems:

MBFGS: proposed method (Algorithm 1).

BFGS: the usual BFGS method using (3) [2].

BFGS\(A_k(2)\): the modified BFGS method of Wei et al. using (5) Wei et al. (2006).

MBFGS\(A_k(2)\): the modified BFGS of Yuan and Wei using (7) Yuan and Wei (2010).

1pc We have tested all the considered algorithms on 120 test problems from CUTEr library Gould et al. (2003). A summary of these problems are given in Table 1. All the codes were written in Matlab 7.14.0.739 (2012a) and run on PC with CPU Intel(R) Core(TM) i5-4200 3.6 GHz, 4 GB of RAM memory and Centos 6.2 server Linux operating system. In the four algorithms, the initial matrix is set to be the identity matrix and \(\varepsilon = 106\). In Algorithm 1 we set \(\sigma _1 =0.01,\) and \(\sigma _2 =0.9 \) and \(\delta =10^{-6}\).

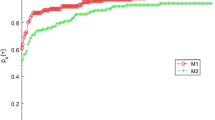
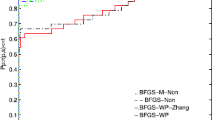
We used the performance profiles of Dolan and More (2002) to evaluate performance of these four algorithms with respect to CPU time, the number of iterations and the total number of function and gradient evaluations computed as \(N_f + nN_g\) where \(N_f\) and \(N_g\), respectively, denote the number of function and gradient evaluations (note that to account for the higher cost of \(N_g\), as compared to \(N_f\) the former is multiplied by n).

Figures 1, 2 and 3 demonstrate the results of the comparisons of the four methods. From these figures, it is clear that Algorithm 1 (MBFGS) is the most efficient in solving these 120 test problems.

5 Conclusion

We introduced a modified BFGS (MBFGS) method using a new secant equation. An interesting feature of the proposed method was taking both the gradient and function values into account. Another important property of the MBFGS method was the utilization of information from the two most recent steps instead of the last step alone. Under suitable assumptions, we established the global convergence of the proposed method. Numerical results on the collection of problems from the CUTEr library showed the proposed method to be more efficient as compared to several proposed BFGS methods in the literature.