A new family of globally convergent conjugate gradient methods

Abstract

Conjugate gradient methods are an important class of methods for unconstrained optimization, especially for large-scale problems. Recently, they have been much studied. In this paper, a new family of conjugate gradient method is proposed for unconstrained optimization. This method includes the already existing two practical nonlinear conjugate gradient methods, which produces a descent search direction at every iteration and converges globally provided that the line search satisfies the Wolfe conditions. The numerical experiments are done to test the efficiency of the new method, which implies the new method is promising. In addition the methods related to this family are uniformly discussed.

1 Introduction

Consider the unconstrained optimization problem

$$\begin{aligned} {\textit{minf}}(x),x\in R^{n} \end{aligned}$$

(1)

where f is a smooth function and its gradient is available. Conjugate gradient methods are a class of important methods for solving (1), especially for large scale problems, which have the following form:

$$\begin{aligned} x_{k+1}=x_{k}+\alpha _{k}d_{k} \end{aligned}$$

(2)

where $x_{k}$ is the current iterate, $\alpha _{k}$ is a positive scalar and called the step length which is determined by some line search, and $d_{k}$ is the search direction generated by the rule

$$\begin{aligned} d_{k}=\left\{ \begin{array}{l@{\quad }l} -g_{k} &{} {\textit{for}}\,k=1; \\ -g_{k}+\beta _{k}d_{k-1}&{} {\textit{for}}\,k\ge 2, \end{array} \right. \end{aligned}$$

(3)

where $g_{k}=\triangledown f(x_{k})$ is the gradient of f at $x_{k}$ , and $\beta _{k}$ is a scalar. The strong Wolfe conditions, namely,

$$\begin{aligned}&f\left( x_{k}+\alpha _{k}d_{k}\right) -f(x_{k})\le \delta \alpha _{k}g_{k}^{T}d_{k} \end{aligned}$$

(4)

$$\begin{aligned}&\left| g\left( x_{k}+\alpha _{k}d_{k}\right) ^{T}d_{k}\right| \le -\sigma g_{k}^{T}d_{k}, \end{aligned}$$

(5)

where $0<\delta <\sigma <1$. The scalar $\beta _{k}$ is chosen so that the method (2), (3) reduces to the linear conjugate gradient method in the case when f is convex quadratic and exact line search $\left( g(x_{k}+\alpha _{k}d_{k})^{T}d_{k}=0\right)$ is used. For general functions, however, different formula for scalar $\beta _{k}$ result in distinct nonlinear conjugate gradient methods, (see Dai and Yuan 1999; Fletcher and Reeves 1964; Polyak 1969; Fletcher 1987; Shanno 1978). Since Fletcher and Reeves (FR) introduced the linear conjugate gradient method in 1964, with

$$\begin{aligned} \beta _{k}^{FR}=\dfrac{\left\| g_{k}\right\| ^{2}}{\left\| g_{k-1}\right\| ^{2}}, \end{aligned}$$

(6)

where $\left\| .\right\|$ means the Euclidean norm. For non-quadratic objective functions, the global convergence of (FR) method was proved when the exact line search or strong Wolfe line search (Al-Baali 1985; Dai and Yuan 1996) was used. However, if the condition (5) is satisfied for $\sigma <1$, the above method of (FR) with the strong Wolfe line search can ensure a descent search direction and converge globally provided only for the case when f is quadratic (Dai et al. 2000; Dai and Yuan 1999). The conjugate descent (CD) method of Fletcher (1987), where

$$\begin{aligned} \beta _{k}^{CD}=\dfrac{\left\| g_{k}\right\| ^{2}}{-g_{k-1}^{T}d_{k-1}} , \end{aligned}$$

(7)

ensures a descent direction for general functions if the line search satisfies the strong Wolfe conditions (4), (5) with $\sigma <1$. But the global convergence of the method is proved (see Dai et al. 2000) only for the case when the line search satisfies (4) and

$$\begin{aligned} \sigma g_{k}^{T}d_{k}\le g\left( x_{k}+\alpha _{k}d_{k} \right) ^{T}d_{k}\;\le 0. \end{aligned}$$

(8)

For any positive constant $\sigma _{2}$, an example is constructed in Dai et al. (2000) showing that conjugate descent method with $\alpha _{k}$ satisfying (4) and

$$\begin{aligned} \sigma _{1}g_{k}^{T}d_{k}\le g\left( x_{k}+\alpha _{k}d_{k} \right) ^{T}d_{k}\le -\sigma _{2}g_{k}^{T}d_{k}, \end{aligned}$$

(9)

need not converge. Recently, Dai and Yuan (1999) proposed a nonlinear conjugate gradient method, which has the form (2), (3) with

$$\begin{aligned} \beta _{k}^{DY}=\dfrac{\left\| g_{k}\right\| ^{2}}{d_{k-1}^{T}y_{k-1}}, \end{aligned}$$

(10)

where $y_{k-1}=g_{k}-g_{k-1}.$ A remarkable property of the DY method is that it provides a descent search direction at every iteration and converges globally provided that the step size satisfies the Wolfe conditions, namely, (4) and

$$\begin{aligned} \sigma g_{k}^{T}d_{k}\le g\left( x_{k}+\alpha _{k}d_{k}\right) ^{T}d_{k}. \end{aligned}$$

(11)

By direct calculations, we can deduce an equivalent form for $\beta _{k}^{DY}$, namely

$$\begin{aligned} \beta _{k}^{DY}=\dfrac{g_{k}^{T}d_{k}}{g_{k-1}^{T}d_{k-1}}. \end{aligned}$$

(12)

In Dai and Yuan (2003), proposed a class of globally convergent conjugate gradient methods, in which

$$\begin{aligned} \beta _{k}=\dfrac{\left\| g_{k}\right\| ^{2}}{\lambda \left\| g_{k-1}\right\| ^{2}+\left( 1-\lambda \right) \left( d_{k-1}^{T}y_{k-1}\right) }, \end{aligned}$$

(13)

where $\lambda \in \,[0,1]$ is a parameter, and proved that the family of methods using line searches that satisfy (4) and (9) converges globally if the parameters $\sigma _{1},\sigma _{2}$, and $\lambda$ are such that

$$\begin{aligned} \sigma _{1}+\sigma _{2}\le \lambda ^{-1}. \end{aligned}$$

In addition, Sellami et al. (2015) proposed a new two-parameter family of conjugate gradient methods, in which

$$\begin{aligned} \beta _{k}=\dfrac{(1-\lambda _{k})\left\| g_{k}\right\| ^{2}+\lambda _{k}\left( -g_{k}^{T}d_{k}\right) }{\left( 1-\lambda _{k}-\mu _{k}\right) \left\| g_{k-1}\right\| ^{2}+\left( \lambda _{k}+\mu _{k}\right) \left( -g_{k-1}^{T}d_{k-1}\right) }, \end{aligned}$$

where $\lambda _{k}\in [0,1]$ and ${\mu } _{k}\in [0,1-\lambda _{k}]$ are parameters, and proved that the new two-parameter family can ensure a descent search direction at every iteration and converges globally under line search condition (4) and (9) where the scalars $\sigma _{1}$ and $\sigma _{2}$ satisfy the condition

$$\begin{aligned} \sigma _{1}+\sigma _{2}\le \dfrac{1+\mu _{k}\sigma _{1}}{1-\lambda _{k}}. \end{aligned}$$

Observing that the formula (7) and (10) share same numerators and two denominators. In this paper we can use combinations of these numerators and denominators to obtain the following new family of conjugate gradient methods

$$\begin{aligned} \beta _{k}^{*}=\dfrac{(1-\lambda )\left\| g_{k}\right\| ^{2}+\lambda \left( -g_{k}^{T}d_{k}\right) }{(1-\lambda )\left( -g_{k-1}^{T}d_{k-1}\right) +\lambda \left( -g_{k-1}^{T}d_{k-1}\right) } \end{aligned}$$

(14)

Thus by the above equality in (14), we deduce an equivalent form of $\beta _{k}^{*},$

$$\begin{aligned} \beta _{k}^{*}=\dfrac{(1-\lambda )\left\| g_{k}\right\| ^{2}+\lambda \left( -g_{k}^{T}d_{k}\right) }{-g_{k-1}^{T}d_{k-1}} \end{aligned}$$

(15)

with $\lambda \in [0,1]$ being a parameter. We see that the above formula for $\beta _{k}^{*}$ is special forms of

$$\begin{aligned} \beta _{k}^{*}=\dfrac{\phi _{k}}{\phi _{k-1}^{\prime }}, \end{aligned}$$

(16)

where $\phi _{k}$ satisfies that

$$\begin{aligned} \phi _{k}=(1-\lambda )\left\| g_{k}\right\| ^{2}+\lambda \left( -g_{k}^{T}d_{k}\right) , \end{aligned}$$

(17)

and

$$\begin{aligned} \phi _{k-1}^{\prime }=(1-\lambda )\left( -g_{k-1}^{T}d_{k-1}\right) +\lambda \left( -g_{k-1}^{T}d_{k-1}\right) =-g_{k-1}^{T}d_{k-1} \end{aligned}$$

(18)

It is clear that the formula (15) is a generalization of the two previous methods are defined by (7) and (10).

The rest of this paper is organized as follows. Some preliminaries are given in the next section. Section 3 provides two convergence theorems for the general method (2), (3) with $\beta _{k}^{*}$ defined by (16). Section 4 includes the main convergence properties of the new family of conjugate gradient methods with Wolfe line search, and we study methods related to the new nonlinear conjugate gradient method (15). The preliminary numerical results are contained in Sect. 5. Conclusions and discussions are made in the last section.

2 Preliminaries

For convenience, we assume that $g_{k}\ne 0$ for all k, for otherwise a stationary point has been found. We give the following basic assumption on the objective function.

Assumption 2.1

• (i) f is bounded below on the level set $\pounds =\left\{ x\in R^{n};f(x)\le f(x_{1})\right\}$;

• (ii) In some neighborhood N of $\pounds$, f is differentiable and its gradient g is Lipschitz continuous, namely, there exists a constant $L >0$ such that

  $$\begin{aligned} \left\| g(x)-g\left( \tilde{x}\right) \right\| \le L\left\| x-\tilde{x} \right\| ,\quad {\textit{for}}\;{\textit{all}}\, x, \tilde{x}\in N \end{aligned}$$

  (19)

  Some of the results obtained in this paper depend also on the following assumption.

Assumption 2.2

The level set $\pounds =\left\{ x\in R^{n};f(x)\le f(x_{1})\right\}$ is bounded.

If f satisfies Assumption 2.1 and 2.2, there exists a positive constant $\gamma$ such that

$$\begin{aligned} \left\| g(x)\right\| \le \gamma , \quad {\textit{for}}\;{\textit{all}}\,x\in \pounds . \end{aligned}$$

(20)

The conclusion of the following lemma, often called the Zoutendijk condition, is used to prove the global convergence of nonlinear conjugate gradient methods. It was originally given in Zoutendijk (1970).

Lemma 2.3

Suppose Assumption 2.1 holds. Let $\{x_{k}\}$ be generated by (2) and $d_{k}$ satisfy $g_{k}^{T}d_{k}<0$. If $\alpha _{k}$ is determined by the Wolfe line search (4), (11), then we have

$$\begin{aligned} \sum \limits _{k\ge 1}\dfrac{\left( g_{k}^{T}d_{k}\right) ^{2}}{\left\| d_{k}\right\| ^{2}}<\infty . \end{aligned}$$

(21)

In the latter section, we need the following lemmas, the first of which is derived from Hu and Storey (1991), Pu and Yu (1990), whereas the second is self-evident and will be used for many times.

Lemma 2.4

Suppose that $\left\{ a_{i}\right\}$ and $\left\{ b_{i}\right\}$ are positive number sequences. If

$$\begin{aligned} \sum _{k\ge 1}a_{k}=\infty , \end{aligned}$$

(22)

and there exist two constants $c_{1}$ and $c_{2}$ such that for all $k\ge 1$,

$$\begin{aligned} b_{k}\le c_{1}+c_{2}\sum _{i=1}^{k}a_{i}, \end{aligned}$$

(23)

then we have that

$$\begin{aligned} \sum _{k\ge 1}\dfrac{a_{k}}{b_{k}}=\infty . \end{aligned}$$

(24)

Lemma 2.5

Consider the following 1-dimensional function,

$$\begin{aligned} \rho (t)=\dfrac{a+bt}{c+dt},\ \ \ t\in R^{1}, \end{aligned}$$

(25)

where $a,\ b,\ c,$ and$\ d\ne 0$ are given real numbers. If

$$\begin{aligned} bc-ad>0, \end{aligned}$$

(26)

$\rho (t)$ is strictly monotonically increasing for $t<\dfrac{-c}{d }$ and $t>\dfrac{-c}{d};{ otherwise },$ if

$$\begin{aligned} bc-ad<0, \end{aligned}$$

(27)

$\rho (t)$ is strictly monotonically decreasing for $t<\dfrac{-c}{d }$ and $t>\dfrac{-c}{d}.$

3 Algorithm and convergence properties

Now we can present a new descent conjugate gradient method, namely NDCG method, as follows:

Algorithm 3.1

• Step 0: Given $x_{1}\in R$, set $d_{1}=-g_{1}$, $k=1$. If $g_{1}$= 0, then stop.

• Step 1: Find a $\alpha _{k}>0$ satisfying the Wolfe conditions (4) and (11).

• Step 2: Let $x_{k+1}=x_{k}+\alpha _{k}d_{k}$ and $g_{k+1}=g(x_{k+1})$. If $g_{k+1}=0$, then stop.

• Step 3: Compute $\beta _{k+1}^{*}$ by the formula (15) and generate $d_{k+1}$ by (3).

• Step 4: Set $k:=k+1$, go to Step 1.

In order to establish the global convergence result for the Algorithm 3.1, we will impose the following basic lemma.

For simplicity, we define

$$\begin{aligned} r_{k}=-\dfrac{g_{k}^{T}d_{k}}{\phi _{k}}, \end{aligned}$$

(28)

and

$$\begin{aligned} t_{k}=\dfrac{\left\| d_{k}\right\| ^{2}}{\phi _{k}^{2}}. \end{aligned}$$

(29)

Lemma 3.1

For the method (2), (3) with $\beta _{k}^{*}$ defined by (16),

$$\begin{aligned} t_{k}=2\sum _{i=1}^{k}\dfrac{r_{i}}{\phi _{i}}-\sum _{i=1}^{k}\dfrac{ \left\| g_{i}\right\| ^{2}}{\phi _{i}^{2}}, \end{aligned}$$

(30)

holds for all $k\ge 1.$

Proof

Since $d_{1}=-g_{1}$. (30) holds for $k=1$. For $i\ge 2$, it follows from (3) that

$$\begin{aligned} d_{i}+g_{i}=\beta _{i}^{*}d_{i-1}. \end{aligned}$$

(31)

Squaring both sides of the above equation, we get that

$$\begin{aligned} \left\| d_{i}\right\| ^{2}=-\left\| g_{i}\right\| ^{2}-2g_{i}^{T}d_{i}+\beta _{i}^{*2}\left\| d_{i-1}\right\| ^{2}. \end{aligned}$$

(32)

Dividing (32) by $\phi _{i}^{2}$ and applying (16) and (29),

$$\begin{aligned} t_{i}=\dfrac{\left\| d_{i-1}\right\| ^{2}}{\phi _{i-1}^{\prime }{}^{2}} +2\dfrac{r_{i}}{\phi _{i}}-\dfrac{\left\| g_{i}\right\| ^{2}}{\phi _{i}^{2}}. \end{aligned}$$

(33)

Using (18), (17) and since, $d_{1}=-g_{1}$ we get that

$$\begin{aligned} \dfrac{\left\| d_{1}\right\| ^{2}}{\phi _{1}^{\prime }{}^{2}}=\dfrac{ \left\| g_{1}\right\| ^{2}}{\left\| g_{1}\right\| ^{4}}=\dfrac{ \left\| g_{1}\right\| ^{2}}{\phi _{1}^{2}}. \end{aligned}$$

(34)

Summing the above expression (33) over i, we obtain

$$\begin{aligned} t_{k}=t_{1}+2\sum _{i=2}^{k}\dfrac{r_{i}}{\phi _{i}}-\sum _{i=2}^{k}\dfrac{ \left\| g_{i}\right\| ^{2}}{\phi _{i}^{2}}. \end{aligned}$$

(35)

Since $d_{1}=-g_{1}$ and $t_{1}=\dfrac{\left\| g_{1}\right\| ^{2}}{ \phi _{1}^{2}},$ the above relation is equivalent to (30). So (30) holds for $k\ge 1$. $\square$

Theorem 3.2

Suppose that $x_{1}$ is a starting point for which Assumption 2.1 holds. Consider the method (2), (3) and (16), if for all k, $d_{k}$ satisfy $g_{k}^{T}d_{k}<0$ and $\alpha _{k}$ is determined by the Wolfe line search (4), (11), and if

$$\begin{aligned} \sum _{k\ge 1}r_{k}^{2}=\infty , \end{aligned}$$

(36)

we have that

$$\begin{aligned} \lim _{k\longrightarrow \infty }\inf \left\| g_{k}\right\| =0. \end{aligned}$$

(37)

Proof

Equation (3) can be re-written as

$$\begin{aligned} g_{i}^{T}d_{i}+\left\| g_{i}\right\| ^{2}=\beta _{i}^{*}g_{i}^{T}d_{i-1}. \end{aligned}$$

(38)

Squaring both sides of the above equation, we get that

$$\begin{aligned} -2g_{i}^{T}d_{i}-\left\| g_{i}\right\| ^{2}\le \dfrac{ \left( g_{i}^{T}d_{i}\right) ^{2}}{\left\| g_{i}\right\| ^{2}}, \end{aligned}$$

(39)

dividing (39) by $\phi _{i}^{2}$ and applying (30)

$$\begin{aligned} t_{k}\le \sum _{i=1}^{k}\dfrac{r_{i}^{2}}{\left\| g_{i}\right\| ^{2}}. \end{aligned}$$

(40)

We proceed by contradiction. Assume that

$$\begin{aligned} \lim _{k\longrightarrow \infty }\inf \left\| g_{k}\right\| \ne 0. \end{aligned}$$

(41)

Then there exists a positive constant $\gamma$ such that

$$\begin{aligned} \left\| g_{k}\right\| \ge \gamma , \, \, \, for\,\, all\,\,k. \end{aligned}$$

(42)

We can see from (40) that,

$$\begin{aligned} t_{k}\le \dfrac{1}{\gamma ^{2}}\sum _{i=1}^{k}r_{i}^{2}. \end{aligned}$$

(43)

The above relation, (36) and Lemma 2.4, yield

$$\begin{aligned} \sum _{i\ge 1}\dfrac{r_{i}^{2}}{t_{i}}=\infty . \end{aligned}$$

(44)

Thus, by the definition (28) and (29), we know that (44) contradicts (21). This concludes the proof. $\square$

Theorem 3.3

Suppose that $x_{1}$ is a starting point for which Assumption 2.1 holds. Consider the method (2), (3) and (16), if for all k, $d_{k}$ satisfy $g_{k}^{T}d_{k}<0$ and $\alpha _{k}$ is determined by the Wolfe line search (4), (11), and if

$$\begin{aligned} \sum _{k\ge 1}\dfrac{\left\| g_{k}\right\| ^{2}}{\phi _{k}^{2}}=\infty , \end{aligned}$$

(45)

we have that

$$\begin{aligned} \lim _{k\longrightarrow \infty }\inf \left\| g_{k}\right\| =0. \end{aligned}$$

(46)

Proof

Noting that

$$\begin{aligned} t_{k}\ge 0\,\,\, {\textit{for}}\,\, {\textit{all}}\,\,k, \end{aligned}$$

(47)

Squaring the right side of equation (39), we get that

$$\begin{aligned} \left( -2g_{i}^{T}d_{i}-\left\| g_{i}\right\| ^{2}\right) ^{2}\ge 0. \end{aligned}$$

Hence, we have

$$\begin{aligned} 4\left( g_{i}^{T}d_{i}\right) ^{2}+\left\| g_{i}\right\| ^{4}+4\left( g_{i}^{T}d_{i}\right) \left\| g_{i}\right\| ^{2}\ge 0. \end{aligned}$$

(48)

Summing this expression over i and dividing (48) by $\left( \phi _{i}^{2}\left\| g_{i}\right\| ^{2}\right)$, we obtain

$$\begin{aligned} 4\sum \limits _{i=1}^{k}\frac{\left( g_{i}^{T}d_{i}\right) ^{2}}{\phi _{i}^{2}\left\| g_{i}\right\| ^{2}}\ge -4 \sum \limits _{i=1}^{k}\frac{\left( g_{i}^{T}d_{i}\right) }{\phi _{i}^{2}}-\sum \limits _{i=1}^{k}\frac{ \left\| g_{i}\right\| ^{2}}{\phi _{i}^{2}}. \end{aligned}$$

(49)

On the other hand, we can get from (30) and (47)

$$\begin{aligned} -2\sum \limits _{i=1}^{k}\frac{g_{i}^{T}d_{i}}{\phi _{i}^{2}}\ge \sum \limits _{i=1}^{k}\frac{ \left\| g_{i}\right\| ^{2}}{\phi _{i}^{2}}. \end{aligned}$$

Direct calculation show that,

$$\begin{aligned} -4\sum \limits _{i=1}^{k}\frac{g_{i}^{T}d_{i}}{\phi _{i}^{2}}-\sum \limits _{i=1}^{k}\frac{ \left\| g_{i}\right\| ^{2}}{\phi _{i}^{2}}\ge \sum \limits _{i=1}^{k} \frac{\left\| g_{i}\right\| ^{2}}{\phi _{i}^{2}}. \end{aligned}$$

(50)

The above relation (49) and (50) imply that

$$\begin{aligned} 4\sum \limits _{i=1}^{k}\frac{\left( g_{i}^{T}d_{i}\right) ^{2}}{\phi _{i}^{2}\left\| g_{i}\right\| ^{2}}\ge \sum \limits _{i=1}^{k}\frac{\left\| g_{i}\right\| ^{2}}{\phi _{i}^{2}}. \end{aligned}$$

Thus if (45) holds, we also have that

$$\begin{aligned} \sum _{k\ge 1}\dfrac{\left( g_{k}^{T}d_{k}\right) ^{2}}{\left\| g_{k}\right\| ^{2}\phi _{k}^{2}}=\infty . \end{aligned}$$

(51)

Because (40) still holds, it follows from (51), the definition of $r_{k}$ and Lemma 2.4, that

$$\begin{aligned} \sum _{k\ge 1}\dfrac{\left( g_{k}^{T}d_{k}\right) ^{2}}{\left\| g_{k}\right\| ^{2}\left\| d_{k}\right\| ^{2}}=\infty . \end{aligned}$$

(52)

The above relation and Lemma 2.3 clearly give (37). This completes our proof.

Thus we have proved two convergence theorems for the general method (2), (3) with $\beta _{k}^{*}$ defined by (16).

It should also be noted that the sufficient descent condition, namely

$$\begin{aligned} g_{k}^{T}d_{k}\le -c\left\| g_{k}\right\| ^{2}, \end{aligned}$$

(53)

where c is a positive constant, is not invoked in Theorems 3.2 and 3.3. The sufficient descent condition (53) was often used or implied in the previous analysis of conjugate gradient methods (see Al-Baali 1985; Gilbert and Nocedal 1992). This condition has been relaxed to the descent condition $(g_{k}^{T}d_{k}<0)$ in the convergence analysis (Dai and Yuan 1999) of the FR method and the convergence analysis (Dai et al. 2000) of any conjugate gradient method. $\square$

4 Global convergence of new conjugate gradient method

In this section, we establish some global convergence of the new family of nonlinear conjugate gradient methods under certain line searches conditions and the methods related to this family are uniformly discussed.

We consider the method (2), (3) with $\phi _{k}$ satisfying

$$\begin{aligned} \phi _{k}=(1-\lambda )\left\| g_{k}\right\| ^{2}+\lambda \left( -g_{k}^{T}d_{k}\right) , \end{aligned}$$

(54)

where $\lambda \in [0,1]$. (54) and (3) show that

$$\begin{aligned} g_{k}^{T}d_{k}= & {} -\left\| g_{k}\right\| ^{2}+\beta _{k}^{*}g_{k}^{T}d_{k-1}\nonumber \\= & {} -\left\| g_{k}\right\| ^{2}+\dfrac{(1-\lambda )\left\| g_{k}\right\| ^{2}+\lambda \left( -g_{k}^{T}d_{k}\right) }{-g_{k-1}^{T}d_{k-1}} g_{k}^{T}d_{k-1}. \end{aligned}$$

(55)

The above relation imply that

$$\begin{aligned} g_{k}^{T}d_{k}=-\dfrac{(1-\lambda )\left( -g_{k}^{T}d_{k-1}\right) -g_{k-1}^{T}d_{k-1}}{ \lambda g_{k}^{T}d_{k-1}-g_{k-1}^{T}d_{k-1}}\left\| g_{k}\right\| ^{2}. \end{aligned}$$

(56)

Thus by (55), we deduce an equivalent form of $\beta _{k}^{*},$

$$\begin{aligned} \beta _{k}^{*}=\dfrac{\left\| g_{k}\right\| ^{2}}{\lambda g_{k}^{T}d_{k-1}-g_{k-1}^{T}d_{k-1}}. \end{aligned}$$

(57)

Substituting (56) into (54), we obtain that

$$\begin{aligned} \phi _{k}=\dfrac{-g_{k-1}^{T}d_{k-1}}{\lambda g_{k}^{T}d_{k-1}-g_{k-1}^{T}d_{k-1}}\left\| g_{k}\right\| ^{2}. \end{aligned}$$

(58)

By this relation, we can show an important property of $\phi _{k}$ under Wolfe line searches and hence obtain the global convergence of the new family of nonlinear conjugate gradient methods (57) under some assumptions.

Theorem 4.1

Suppose that $x_{1}$ is a starting point for which Assumption 2.1 and 2.2 hold. Consider the method (2), (3), (16) and (54), if $g_{k}^{T}d_{k}<0$ for all k and $\alpha _{k}$ is computed by the Wolfe line search (4), (11), then

$$\begin{aligned} \dfrac{\phi _{k}}{\left\| g_{k}\right\| ^{2}}\le \left( 1-\lambda \sigma \right) ^{-1}. \end{aligned}$$

(59)

Further, the method converges in the sense that

$$\begin{aligned} \lim _{k\longrightarrow \infty }\inf \left\| g_{k}\right\| =0. \end{aligned}$$

(60)

Proof

Since (11), we have that

$$\begin{aligned} g\left( x_{k}+\alpha _{k}d_{k}\right) ^{T}d_{k}\ge \sigma g_{k}^{T}d_{k}. \end{aligned}$$

(61)

By direct calculations show that

$$\begin{aligned} \lambda g_{k}^{T}d_{k-1}-g_{k-1}^{T}d_{k-1}\ge (1-\lambda \sigma )\left( -g_{k-1}^{T}d_{k-1}\right) . \end{aligned}$$

(62)

Dividing (58) by $\left\| g_{k}\right\| ^{2}$ and applying (62) implies the truth of (59). Therefore, by (20) and (62) that

$$\begin{aligned} \sum _{k\ge 1}\dfrac{\left\| g_{k}\right\| ^{2}}{\phi _{k}^{2}}\ge \dfrac{\left( 1-\lambda \sigma \right) ^{2}}{\left\| g_{k}\right\| ^{2}}\ge \dfrac{ \left( 1-\lambda \sigma \right) ^{2}}{\gamma ^{2}}=\infty . \end{aligned}$$

(63)

Thus (37) follows from Theorem 3.3.

In the following, we can show that, for any $\lambda \in \left( 0,1\right]$ , the method (2), (3), (16) and (54) ensures the descent property of each search direction and converges globally under line search condition (4) and (9) where the scalar $\sigma _{2}$ satisfy certain condition. For this purpose, we define

$$\begin{aligned} \overline{r}_{k}=-\dfrac{g_{k}^{T}d_{k}}{\left\| g_{k}\right\| ^{2}}, \end{aligned}$$

(64)

and

$$\begin{aligned} l_{k}=\dfrac{g_{k+1}^{T}d_{k}}{g_{k}^{T}d_{k}}, \end{aligned}$$

(65)

it is obvious that $d_{k}$ is a descent direction if and only if $\overline{r }_{k}>0.$ For the above relation, (56) and (65), we can write

$$\begin{aligned} \overline{r}_{k}=\dfrac{1+(1-\lambda )l_{k-1}}{1-\lambda l_{k-1}}. \end{aligned}$$

(66)

$\square$

Theorem 4.2

Suppose that $x_{1}$ is a starting point for which Assumption 2.1 holds. Consider the method (2), (3), (16) and (54), where $\lambda \in \left[ 0,1\right)$ and $\alpha _{k}$ satisfies the line search conditions (4) and (9). If the scalar $\sigma _{2}$ in (9) is such that

$$\begin{aligned} \sigma _{2}\le (1-\lambda )^{-1}, \end{aligned}$$

(67)

then we have for all $k\ge 1$

$$\begin{aligned} 0<\bar{r}_{k}<\left( 1-\sigma _{1}\right) ^{-1}. \end{aligned}$$

(68)

Further, the method converges in the sense that (37) is true.

Proof

The right hand side of (66) is a function of $\lambda$, $l_{k-1}$ and $\overline{r}_{k-1}$, which is denoted as

$h(\lambda ,l_{k-1},\bar{r}_{k-1}).$ We prove (68) by induction. Noting that $d_{1}=-g_{1}$ and hence $\bar{r}_{1}=1$, we see that (68) is true for $k=1$ . We now suppose that (68) holds for $k-1$, namely,

$$\begin{aligned} 0<\bar{r}_{k-1}<\left( 1-\sigma _{1}\right) ^{-1}. \end{aligned}$$

(69)

It follows from (9)

$$\begin{aligned} -\sigma _{2}\le l_{k-1}\le \sigma _{1}. \end{aligned}$$

(70)

Then by Lemma 2.5, the fact that $\lambda \in \left[ 0,1\right)$, we get that

$$\begin{aligned} \bar{r}_{k}\le & {} h\left( \lambda ,\sigma _{1},\bar{r}_{k-1}\right) <h\left( \lambda ,\sigma _{1},\left( 1-\sigma _{1}\right) ^{-1}\right) \nonumber \\= & {} 1+\dfrac{\sigma _{1}}{1-\lambda \sigma _{1}} \nonumber \\\le & {} 1+\dfrac{\sigma _{1}}{1-\sigma _{1}} \nonumber \\= & {} \left( 1-\sigma _{1}\right) ^{-1}. \end{aligned}$$

(71)

On the other hand, by Lemma 2.5 and relation (67), we also have that

$$\begin{aligned} \bar{r}_{k}\ge h\left( \lambda ,-\sigma _{2},\bar{r}_{k-1}\right) >h\left( \lambda ,-\sigma _{2},\left( 1-\sigma _{1}\right) ^{-1}\right) \ge 0. \end{aligned}$$

(72)

Thus (68) is true for k, by induction, (68) holds for $k\ge 1$.

To show the truth of (37), by Theorem 3.2, it suffices to prove that

$$\begin{aligned} \max \left\{ r_{k-1},r_{k}\right\} \ge c_{1}, \end{aligned}$$

(73)

for all $k\ge 2$ and some constant $c_{1}\ge 0.$ In fact, if

$$\begin{aligned} \bar{r}_{k-1}\le 1, \end{aligned}$$

(74)

by Lemma 2.5, the fact that $\lambda \in \left[ 0,1\right) ,$ we can get that

$$\begin{aligned} \bar{r}_{k}\ge h\left( \lambda ,-\sigma _{2},1\right) \overset{\varDelta }{=}c_{2}. \end{aligned}$$

(75)

Since $c_{2}\in \left( 0,1\right) ,$ we then obtain

$$\begin{aligned} \max \left\{ \bar{r}_{k-1},\bar{r}_{k}\right\} \ge c_{2}, \end{aligned}$$

(76)

for all $k\ge 2$. By the definition (28) of $r_{k}$ and relation (54), we have that

$$\begin{aligned} r_{k}=\dfrac{\bar{r}_{k}}{1+\lambda (\bar{r}_{k}-1)}. \end{aligned}$$

(77)

Which, with (76) and lemma (23), implies that (73) holds with $c_{1}=c_{2}$. This completes our proof. $\square$

Thus we have some general convergence results are established for the new family of nonlinear conjugate gradient methods (57). It is easy to see from (57) that the new family of conjugate gradient methods includes the two nonlinear conjugate gradient methods mentioned above. For the case when $\lambda =1,$ the method is proved to generate a descent search direction at every iteration and converge globally of the DY method under the Wolfe line search conditions (4), (11) (see Dai and Yuan 1999). If $\lambda =0,$ then the method ensures a descent direction for general functions and is proved to global convergence under strong Wolfe line search (4), (5) of the method CD (see Dai et al. 2000).

In addition, the methods related to the FR method and the DY method in Hu and Storey (1991), Dai and Yuan (1999) can also be regarded as special cases of the new family methods (57). For example, to combine the nice global convergence properties of the FR method and the good numerical performances of the PRP method, namely

$$\begin{aligned} \beta _{k}^{PRP}=\dfrac{g_{k}^{T}y_{k-1}}{\left\| g_{k-1}\right\| ^{2}} . \end{aligned}$$

(78)

Hu and Storey (1991) extended the result in Al-Baali (1985) to any method (2) and (3) with $\beta _{k}$ satisfying

$$\begin{aligned} \beta _{k}\in \left[ 0,\beta _{k}^{FR}\right] . \end{aligned}$$

(79)

Gilbert and Nocedal (1992) further extended the result to the case that

$$\begin{aligned} \beta _{k}\in \left[ -\beta _{k}^{FR},\beta _{k}^{FR}\right] . \end{aligned}$$

(80)

Dai and Yuan (2001) studied the hybrid conjugate gradient algorithms and proposed the following hybrid methods

$$\begin{aligned} \beta _{k}=\max \left\{ 0,\min \left\{ \beta _{k}^{HS},\beta _{k}^{DY}\right\} \right\} . \end{aligned}$$

(81)

where $\beta _{k}^{HS}$ is the choice of Hestenes and Stiefel (1952) and $\beta _{k}^{DY}$ appears in Dai and Yuan (1999). Furthermore, Dai and Yuan (1999) proved that the method (2) and (3) with $\beta _{k}$ satisfying

$$\begin{aligned} \beta _{k}\in \left[ \dfrac{\sigma -1}{1+\sigma }\overline{\beta _{k}}, \overline{\beta _{k}}\right] , \end{aligned}$$

(82)

where $\overline{\beta _{k}}$ stands for the formula (10), and with $\alpha _{k}$ chosen by the Wolfe line search give the convergence relation (37). For methods related to the method (57). We have the following result, where $s_{k}$ is given by

$$\begin{aligned} s_{k}=\dfrac{\beta _{k}}{\beta _{k}^{*}}, \end{aligned}$$

(83)

where $\beta _{k}^{*}$ stands for the formula (15). We prove that any method (20), (21) with the strong Wolfe line search produces a descent search direction at every iteration and converges globally if the scalar $\beta _{k}$ is such that

$$\begin{aligned} -c\le s_{k}\le (1-\sigma )^{-1}, \end{aligned}$$

(84)

where $c=(1+\sigma )/ (1-\sigma )>0.$

Theorem 4.3

Suppose that $x_{1}$ is a starting point for which Assumption 2.1 holds. Consider the method (2) and (3), where

$$\begin{aligned} \beta _{k}=\dfrac{\tau _{k}\left\| g_{k}\right\| ^{2}}{\lambda g_{k}^{T}d_{k-1}-g_{k-1}^{T}d_{k-1}}, \end{aligned}$$

(85)

and where $\alpha _{k}$ is computed by the strong Wolfe line search (4) and (9) with $\sigma \le \dfrac{1}{2}$. For any $\lambda \in \left[ 0,1\right]$, if

$$\begin{aligned} \tau _{k}\in \left[ \dfrac{1+\lambda \sigma }{\sigma -1},\dfrac{1-\lambda \sigma }{1-\sigma }\right] , \end{aligned}$$

(86)

and $\beta _{k}$ is such that

$$\begin{aligned} s_{k}\in \left[ -c,(1-\sigma )^{-1}\right] , \end{aligned}$$

(87)

then if $g_{k}\ne 0$ for all $k\ge 1$, we have that

$$\begin{aligned} 0<\bar{r}_{k}<(1-\sigma )^{-1}\quad for\,\, all \,\,k\ge 1. \end{aligned}$$

(88)

Further, the method converges in the sense that (37) is true.

Proof

From relation (15), (85) and by direct calculations we can show that

$$\begin{aligned} \overline{r}_{k}=\dfrac{1-(\lambda -\tau _{k})l_{k-1}}{1-\lambda l_{k-1}}, \end{aligned}$$

(89)

and

$$\begin{aligned} s_{k}=\dfrac{\tau _{k}}{1-\lambda (1-\tau _{k})l_{k-1}}, \end{aligned}$$

(90)

where $\overline{r}_{k}$ and $l_{k}$ are defined by (64) and (65). Now the right hand side of (89) is a function of $\lambda$, $\tau _{k}$, $l_{k-1}$ and $\overline{r}_{k-1}$, which can be denoted as $h(\lambda ,\tau _{k},l_{k-1},\bar{r}_{k-1}).$ We prove (88) by induction. Noting that $d_{1}=-g_{1}$ and hence $\bar{r}_{1}=1$, we see that (4.34 ) is true for $k=1$. We now suppose that (88) holds for $k-1$, namely,

$$\begin{aligned} 0<\bar{r}_{k-1}<(1-\sigma )^{-1}. \end{aligned}$$

(91)

It follows from (5)

$$\begin{aligned} \left| l_{k-1}\right| \le \sigma . \end{aligned}$$

(92)

Then by Lemma 2.5, and the fact that $\lambda \in \left[ 0,1\right]$, we get that

$$\begin{aligned} \bar{r}_{k}\le & {} \max \left\{ h\left( \lambda ,\dfrac{1-\lambda \sigma }{1-\sigma },l_{k-1},\bar{r}_{k-1}\right) ,h\left( \lambda ,,\dfrac{1+\lambda \sigma }{\sigma -1} ,l_{k-1},\bar{r}_{k-1}\right) \right\} \nonumber \\\le & {} \max \left\{ h\left( \lambda ,,\dfrac{1-\lambda \sigma }{1-\sigma },\sigma , \bar{r}_{k-1}\right) ,h\left( \lambda ,,\dfrac{1+\lambda \sigma }{\sigma -1},-\sigma , \bar{ r}_{k-1}\right) \right\} \nonumber \\< & {} \max \left\{ h\left( \lambda ,,\dfrac{1-\lambda \sigma }{1-\sigma },\sigma ,(1-\sigma )^{-1}\right) ,h\left( \lambda ,,\dfrac{1+\lambda \sigma }{\sigma -1},-\sigma ,(1-\sigma )^{-1}\right) \right\} \nonumber \\= & {} 1+\dfrac{\sigma }{1-\sigma }=(1-\sigma )^{-1}, \end{aligned}$$

(93)

where $\sigma \le \frac{1}{2}$ is also used in the equality. For the opposite direction, we can prove that

$$\begin{aligned} \bar{r}_{k}>\min \left\{ h\left( \lambda ,,\dfrac{1-\lambda \sigma }{1-\sigma } ,-\sigma ,(1-\sigma )^{-1}\right) , \, h\left( \lambda ,,\dfrac{1+\lambda \sigma }{\sigma -1} ,\sigma ,\left( 1-\sigma \right) ^{-1}\right) \right\} \ge 0. \end{aligned}$$

(94)

Thus (88) is true for k, by induction, (88) holds for $k\ge 1$.

We now prove (37) by contradiction and assuming that

$$\begin{aligned} \left\| g(x)\right\| \ge \gamma ,\quad {{\textit{for}}\,\,\, {\textit{some}}\,\, } \gamma >0, \end{aligned}$$

(95)

for all $k\ge 1,$ since $d_{k}+g_{k}=\beta _{k}d_{k-1},$ we have that

$$\begin{aligned} \left\| d_{k}\right\| ^{2}=\beta _{k}^{2}\left\| d_{k-1}\right\| ^{2}-2g_{k}^{T}d_{k}-\left\| g_{k}\right\| ^{2}. \end{aligned}$$

(96)

Dividing both sides of (96) by $\left( g_{k}^{T}d_{k}\right) ^{2}$ and using (64) and (83), we obtain

$$\begin{aligned} \dfrac{\left\| d_{k}\right\| ^{2}}{\left( g_{k}^{T}d_{k}\right) ^{2}}= & {} \dfrac{\beta _{k}^{2}\left\| d_{k-1}\right\| ^{2}}{\left( g_{k}^{T}d_{k}\right) ^{2}}+\dfrac{2}{\bar{r}_{k}\left\| g_{k}\right\| ^{2}}-\dfrac{1}{\bar{r}_{k}^{2}\left\| g_{k}\right\| ^{2}} \nonumber \\= & {} \dfrac{\left( s_{k}\beta _{k}^{*}\right) ^{2}\left\| d_{k-1}\right\| ^{2}}{ \left( g_{k}^{T}d_{k}\right) ^{2}}+\dfrac{1}{\left\| g_{k}\right\| ^{2} } \left[ 1-\left( 1-\dfrac{1}{\bar{r}_{k}}\right) ^{2}\right] . \end{aligned}$$

(97)

In addition, by the definition (64) of $\bar{r}_{k}$, the relation (3) and (83), we get

$$\begin{aligned} \bar{r}_{k}\left\| g_{k}\right\| ^{2}=-g_{k}^{T}d_{k}=\left\| g_{k}\right\| ^{2}-s_{k}\beta _{k}^{*}g_{k}^{T}d_{k-1}, \end{aligned}$$

(98)

the above relation and the definition (65) imply that

$$\begin{aligned} s_{k}\beta _{k}^{*}=\dfrac{\left( 1-\bar{r}_{k}\right) }{l_{k-1}\left( g_{k-1}^{T}d_{k-1}\right) } \left\| g_{k}\right\| ^{2}. \end{aligned}$$

(99)

Relation (97) and (99), we obtain

$$\begin{aligned} \dfrac{\left\| d_{k}\right\| ^{2}}{\left( g_{k}^{T}d_{k}\right) ^{2}}= \dfrac{\left( 1-\bar{r}_{k}\right) ^{2}\left\| d_{k-1}\right\| ^{2}}{\bar{r} _{k}^{2}l_{k-1}^{2}\left( g_{k-1}^{T}d_{k-1}\right) ^{2}}+\dfrac{1}{\left\| g_{k}\right\| ^{2}}\left[ 1-\left( 1-\dfrac{1}{\bar{r}_{k}}\right) ^{2}\right] . \end{aligned}$$

(100)

Denote

$$\begin{aligned} m_{k}=\dfrac{1-\bar{r}_{k}}{\bar{r}_{k}l_{k-1}}, \end{aligned}$$

(101)

where $l_{k-1}\ne 0.$ Now we prove that

$$\begin{aligned} \left| m_{k}\right| \le 1, \quad for\,\, all\,\, k\ge 2. \end{aligned}$$

(102)

the right hand side of (101) is a function of $l_{k-1}$ and $\overline{r} _{k}$, which can be denoted as $h(l_{k-1},\bar{r}_{k}).$ We can get by (88), (92) and Lemma 2.5 that

$$\begin{aligned} m_{k}\le & {} \max \left\{ h\left( \sigma ,\bar{r}_{k}\right) ,h(-\sigma ,\bar{r} _{k})\right\} \nonumber \\< & {} \max \left\{ h\left( \sigma ,(1-\sigma )^{-1}\right) ,h\left( -\sigma ,(1-\sigma )^{-1}\right) \right\} =1. \end{aligned}$$

(103)

Thus we have that

$$\begin{aligned} m_{k}\ge & {} \min \left\{ h\left( -\sigma ,\bar{r}_{k}\right) ,h\left( \sigma ,\bar{r} _{k}\right) \right\} \nonumber \\> & {} \min \left\{ h\left( -\sigma ,(1-\sigma )^{-1}\right) ,h\left( \sigma ,(1-\sigma )^{-1}\right) \right\} =-1. \end{aligned}$$

(104)

Therefore (101) holds for all $k\ge 2.$

By (102) and (100), we obtain

$$\begin{aligned} \dfrac{\left\| d_{k}\right\| ^{2}}{\left( g_{k}^{T}d_{k}\right) ^{2}} \le \dfrac{\left\| d_{k-1}\right\| ^{2}}{\left( g_{k-1}^{T}d_{k-1}\right) ^{2}}+ \dfrac{1}{\left\| g_{k}\right\| ^{2}}. \end{aligned}$$

(105)

Because $\left\| d_{1}\right\| ^{2}/ \left( g_{1}^{T}d_{1}\right) ^{2}=1/ \left\| g_{1}\right\| ^{2},$ (105) shows that

$$\begin{aligned} \dfrac{\left\| d_{k}\right\| ^{2}}{\left( g_{k}^{T}d_{k}\right) ^{2}} \le \sum _{i=1}^{k}\dfrac{1}{\left\| g_{i}\right\| ^{2}}, \end{aligned}$$

(106)

for all k. Then we get from this and (95) that

$$\begin{aligned} \dfrac{\left( g_{k}^{T}d_{k}\right) ^{2}}{\left\| d_{k}\right\| ^{2}} \ge \dfrac{\gamma ^{2}}{k}, \end{aligned}$$

(107)

which implies that

$$\begin{aligned} \sum _{k\ge 1}\dfrac{\left( g_{k}^{T}d_{k}\right) ^{2}}{\left\| d_{k}\right\| ^{2}}=+\infty . \end{aligned}$$

(108)

This contradicts the Zoutendijk condition (21). Therefore (37) holds. $\square$

5 Numerical results

In this section, we will test the following four conjugate gradient algorithms:

• PRP$^{SW}$: the PRP method with the strong Wolfe conditions, where $\delta =10^{-2}$ and $\sigma =0,1$.

• PRP$_{+}^{SW}$: the PRP method with nonnegative values of $\beta _{k}=max\left\{ 0,\beta _{k}^{PRP}\right\}$ and the strong Wolfe conditions, where $\delta =10^{-2}$ and $\sigma =0,1$.

• NDCG$^{SW}$: Algorithm 3.1 with the Wolfe conditions (4) and (9), where the scalar $\sigma _{2}$ satisfy the condition (67), in addition, $\delta =10^{-2}$, $\sigma _{1}=\sigma _{2}=\sigma =0,1$, $\lambda =0,5$.

• NDCG$^{W}$: Algorithm 3.1 with the standard Wolfe conditions, where $\delta =10^{-2}$, $\sigma =0,1$, $\lambda =0,5$.

In this paper, all codes were written in Matlab and run on PC with 3.0 GHz CPU processor and 1GB RAM memory and Linux operation system. During our experiments, the strategy for the initial step length is to assume that the first-order change in the function at iterate $x_{k}$ will be the same as that obtained at the previous step (Hu and Storey 1991). In other words, we choose the initial guess $\alpha _{0}$ satisfying:

$$\begin{aligned} \alpha _{0}=\alpha _{k-1}\dfrac{\varPsi _{k-1}}{\varPsi _{k}}\,\,\,\,{\textit{for}}\,\, {\textit{all}}\,\, k>1, \end{aligned}$$

where $\varPsi _{k}=g_{k}^{T}d_{k},$ when $k=1$, we choose $\alpha _{0}=\frac{1}{\left\| g(x_{1})\right\| }$. In the case when an uphill search direction does occur, we restart the algorithm by setting $d_{k}=-g_{k}$, but this case never occurs for NDCG$^{SW}$ and NDCG$^{W}$. We stop the iteration if the inequality $\left\| g(x_{k})\right\| <10^{-6}$ 10 is satisfied. The iteration is also stopped if the number of iteration exceed 10,000, but we find that this never occurs for our tested problems. The test problems we used are described in Hillstrome et al. (1981). Each problem was tested with various values of n changing from $n=500$ to 1000.

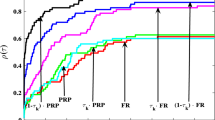
Table  1 list numerical results. The meaning of each column is as follows:

“N”	The number of the test problem
“Problem”	The name of the test problem
“n”	The dimension of the test problem
“NI”	The number of iterations
“NF”	The total number of function evaluations
“NG”	The total number of gradient evaluations
“CPUtime(s)”	The total CPU time in seconds which should be taken to compute all of these problems

Table 1 Test results on PRP$^{SW}/$ PRP$_{+}^{SW}/$ NDCG$^{SW}/$ NDCG$^{W}$ methods

We can see from the above table that, the average performances of the NDCG$^{SW}$ is better than that of the PRP method. Also see that, the NDCG$^{W}$ outperforms other three algorithms for solving these problems, especially for problems 3, 4, 7, 9, 11 and 12. Table  1, shows the performance of these methods relative to CPU time. To solve all the 26 problems, the CPU time (in seconds) required by the PRP$^{SW}$, PRP$_{+}^{SW}$, NDCG$^{SW}$ and NDCG$^{W}$ are 3.5688e+2, 3.5441e+2, 3.3435e+2 and 3.3112e+2, respectively.These preliminary results obtained are encouraging.

6 Conclusions and discussions

In this paper, we have proposed a new family of nonlinear conjugate gradient methods, and studied the global convergence of these methods. The new family not only includes the two already known simple and practical conjugate gradient methods, but has other family of conjugate gradient methods as subfamily. First, we can see that, the descent property of the search direction plays an important role in establishing some general convergence results of the method in the form (16) with weak Wolfe line search (4) and (11) even in the absence of the sufficient descent condition (3.27), namely, Theorems 3.2, 3.3, 4.1. Next, from Theorem 4.2, we proved that the new family can ensure a descent search direction at every iteration and converges globally under line search condition (4) and (9) where the scalar $\sigma _{2}$ satisfy the condition (67). From Theorem (56), we have carefully studied methods related to the method (57). Denote $s_{k}$ to be the size of $\beta _{k}$ with respect to $\beta _{k}^{*}$. If $\tau _{k}$ and $s_{k}$ belongs to some interval, namely, (86) and (87) respectively, the corresponding methods are shown to produce a descent search direction at every iteration and converge globally provided that the line search satisfies the strong Wolfe conditions (4) and (9) with $\sigma \le \frac{1}{2}.$ In summary, our computational results show that this new descent nonlinear conjugate gradient method, namely NDCG$^{W}$ method not only converges globally, but also outperforms the original PRP method in average. The results, we hope, can stimulate more study on the theory and implementations on the conjugate gradient methods with the Wolfe line search. For future research, we should investigate to find the practical performance of the method (57). Furthermore, we can investigate whether Theorems 4.2 and 4.3 can be extended to the case that $\lambda >1$ or $\lambda <0.$