A new conservative finite difference scheme for the generalized Rosenau–KdV–RLW equation

Abstract

In this paper, a new conservative fourth-order finite difference scheme is proposed for solving the generalized Rosenau–KdV–RLW equation. The solvability, convergence, and conservation of the numerical solution are discussed by the discrete energy method. The scheme is convergent of $O(\tau ^{2}+h^{4})$ and unconditionally stable. Several numerical experiment results show that the proposed scheme is efficient and reliable.

1 Introduction

Nonlinear wave phenomena play an important role in engineering and sciences. In the past, many scientists have studied about different mathematical models to explain the wave behavior, such as the KdV equation (Korteweg and Vries 1895; Ozer and Kutluay 2005; Skogestad and Kalisch 2009; Kim et al. 2012; Yan et al. 2016), the Rosenau equation (Rosenau 1986, 1988; Park 1992), the Rosenau–KdV equation (Zuo 2009; Esfahani 2011; Triki and Biswas 2013; Zheng and Zhou 2014), the Rosenau–RLW equation (Pan and Zhang 2012; Wongsaijai et al. 2014, 2019), and many others (Lu and Chen 2015; Coclite and Ruvob 2017; Mohanty and Kaur 2019; Kaur and Mohanty 2019).

In this paper, we will consider the following initial-boundary value problem of the generalized Rosenau–KdV–RLW equation (Razborova et al. 2015):

$$\begin{aligned}&u_{t}+au_{x}+b(u^{p})_{x}-cu_{xxt}+{d}u_{xxx}+u_{xxxxt}=0, \quad x\in [\alpha ,\beta ], \quad t\in [0,T], \end{aligned}$$

(1.1)

with an initial condition

$$\begin{aligned}&u(x,0)=\phi (x), \quad x\in [\alpha ,\beta ], \end{aligned}$$

(1.2)

and boundary conditions

$$\begin{aligned}&u(\alpha ,t)=u(\beta ,t)=0, \quad u_{x}(\alpha ,t)=u_{x}(\beta ,t)=0, \quad t\in [0,T], \end{aligned}$$

(1.3)

where a, b, c and d are non-negative real constants, $p\ge$ 2 is a positive integer, $\phi (x)$ is a given smooth function, u(x, t) is a real-valued function.

For Eq. (1.1), shock waves, solitary waves, and the asymptotic behavior with power law nonlinearity have been theoretically studied in Razborova et al. (2014) and Sanchez et al. (2015). Besides the theoretical analysis, Wongsaijai and Poochinapan (2014) proposed a three-level average implicit finite difference scheme, and Wang and Dai (2018) developed a linearly implicit finite difference scheme. However, both the schemes in Wongsaijai and Poochinapan (2014) and Wang and Dai (2018) are only second-order accurate. As pointed out in Ghiloufi and Omrani (2017), the conservative approximation properties of the scheme have possibly even more impacts on numerical results. Thus, the motivation of this research is to establish a fourth-order conservative finite difference scheme for Eqs. (1.1)–(1.3).

Theorem 1.1

Suppose $\phi (x)\in H_{0}^{2}[\alpha ,\beta ]$, then the problem in Eqs. (1.1)–(1.3) satisfies the following energy conservative property:

$$\begin{aligned} E(t)&=\int _{\alpha }^{\beta }\Big [u^{2}(x,t)+cu^{2}_{x}(x,t)+u^{2}_{xx}(x,t)\Big ]\mathrm{d}x=\Vert u\Vert _{L_{2}}^{2}+c\Vert u_{x}\Vert _{L_{2}}^{2}+\Vert u_{xx}\Vert _{L_{2}}^{2}\nonumber \\&\quad =\int _{\alpha }^{\beta }\Big [u^{2}(x,0)+cu^{2}_{x}(x,0)+u^{2}_{xx}(x,0)\Big ]\mathrm{d}x\nonumber \\&\quad =\int _{\alpha }^{\beta }\Big [(\phi (x))^{2}+c(\phi (x))^{2}_{x}+(\phi (x))^{2}_{xx}\Big ]\mathrm{d}x=E(0), \quad c\ge 0, \quad t\in [0,T]. \end{aligned}$$

(1.4)

Proof

From Eq. (1.1), we have

$$\begin{aligned}&u_{t}-cu_{xxt}+u_{xxxxt}=-au_{x}-b(u^{p})_{x}-{d}u_{xxx}.&\end{aligned}$$

(1.5)

Multiplying Eq. (1.5) by 2u and integrating on the interval $[\alpha ,\beta ]$, we obtain

$$\begin{aligned}&\frac{\mathrm{{d}}}{\mathrm{d}t}\int _{\alpha }^{\beta }u^{2}\mathrm{d}x-2c\int _{\alpha }^{\beta }uu_{xxt}\mathrm{d}x+2\int _{\alpha }^{\beta }uu_{xxxxt}\mathrm{d}x\nonumber \\&=-2a\int _{\alpha }^{\beta }uu_{x}\mathrm{d}x-2b\int _{\alpha }^{\beta }u(u^{p})_{x}\mathrm{d}x-2d\int _{\alpha }^{\beta }uu_{xxx}\mathrm{d}x. \end{aligned}$$

(1.6)

Using the integration by parts and considering the boundary conditions in Eq. (1.3), we have

$$\begin{aligned}&\int _{\alpha }^{\beta }uu_{x}\mathrm{d}x=\frac{1}{2}u^{2}\Big |_{\alpha }^{\beta }=0, \end{aligned}$$

(1.7)

$$\begin{aligned}&\int _{\alpha }^{\beta }uu_{xxx}\mathrm{d}x=\Big (uu_{xx}-\frac{1}{2}u_{x}^{2}\Big )\Big |_{\alpha }^{\beta }=0, \end{aligned}$$

(1.8)

$$\begin{aligned}&\int _{\alpha }^{\beta }u(u^{p})_{x}\mathrm{d}x=\Big (uu^{p}-\frac{1}{p+1}u^{p+1}\Big )\Big |_{\alpha }^{\beta }=0, \end{aligned}$$

(1.9)

$$\begin{aligned}&\int _{\alpha }^{\beta }uu_{xxt}\mathrm{d}x=\int _{\alpha }^{\beta }ud(u_{xt})=\Big (uu_{xt}\Big )\Big |_{\alpha }^{\beta }\nonumber \\&\quad -\int _{\alpha }^{\beta }u_{xt}\mathrm{d}u=-\frac{1}{2}\frac{\mathrm{{d}}}{\mathrm{d}t}\int _{\alpha }^{\beta }u_{x}^{2}\mathrm{d}x, \end{aligned}$$

(1.10)

$$\begin{aligned}&\int _{\alpha }^{\beta }uu_{xxxxt}\mathrm{d}x=\Big (uu_{xxxt}\Big )\Big |_{\alpha }^{\beta }-\int _{\alpha }^{\beta }u_{xxxt}\mathrm{d}u\nonumber \\&\quad =-\Big (u_{x}u_{xxt}\Big )\Big |_{\alpha }^{\beta }+\int _{\alpha }^{\beta }u_{xxt}u_{xx}\mathrm{d}x=\frac{1}{2}\frac{\mathrm{{d}}}{\mathrm{d}t}\int _{\alpha }^{\beta }u_{xx}^{2}\mathrm{d}x. \end{aligned}$$

(1.11)

Substituting Eqs. (1.7)–(1.11) into Eq. (1.6) gives

$$\begin{aligned}&\frac{\mathrm{{d}}}{\mathrm{d}t}\int _{\alpha }^{\beta }\Big [u^{2}(x,t)+cu^{2}_{x}(x,t)+u^{2}_{xx}(x,t)\Big ]\mathrm{d}x=0. \end{aligned}$$

Therefore, we obtain $E(t)=E(0)$, $t\in [0,T]$. $\square$

Lemma 1.2

(Wang and Dai 2018) Suppose $\phi (x)\in H_{0}^{2}[\alpha ,\beta ]$, then the solution of Eqs. (1.1)–(1.3) satisfies $\Vert u\Vert _{L_{2}}\le C$, $\Vert u_{x}\Vert _{L_{2}}\le C$, $\Vert u_{xx}\Vert _{L_{2}}\le C$, and hence $\Vert u\Vert _{L_{\infty }}\le C$, $\Vert u_{x}\Vert _{L_{\infty }}\le C$.

Theorem 1.3

Suppose $\phi (x)\in H_{0}^{2}[\alpha ,\beta ]$, then the problem in Eqs. (1.1)–(1.3) is well posed.

Proof

Assume that $u_{1}$ and $u_{2}$ are two solutions of Eqs. (1.1)–(1.3) satisfying the initial conditions $\phi ^{(1)}$ and $\phi ^{(2)}$, respectively. Let $\theta =u_{1}-u_{2}$, then $\theta$ satisfies

$$\begin{aligned}&\theta _{t}+a\theta _{x}+b[(u_{1})^{p}]_{x}-b[(u_{2})^{p}]_{x}-c\theta _{xxt}+d\theta _{xxx}+\theta _{xxxxt}=0, \end{aligned}$$

and the initial-boundary conditions:

$$\begin{aligned}&\theta (x,0)=\phi ^{(1)}-\phi ^{(2)}, \quad x\in [\alpha ,\beta ],\\&\theta (\alpha ,t)=\theta (\beta ,t)=0, ~\theta _{x}(\alpha ,t)=\theta _{x}(\beta ,t)=0,~t\in [0,T]. \end{aligned}$$

Letting

$$\begin{aligned}&E(t)=\int _{\alpha }^{\beta }(\theta ^{2}+c\theta ^{2}_{x}+\theta ^{2}_{xx})\mathrm{d}x,~c\ge 0, \end{aligned}$$

we use a similar derivation as that in the proof of Theorem 1.1 and obtain

$$\begin{aligned} \frac{\mathrm{d} E(t)}{d t}&=2\int _{\alpha }^{\beta }(\theta \theta _{t}+c\theta _{x}\theta _{xt}+\theta _{xx}\theta _{xxt})\mathrm{d}x \nonumber \\&\quad =-2\int _{\alpha }^{\beta }\theta \Big [a\theta _{x}+b[(u_{1})^{p}]_{x}-b[(u_{2})^{p}]_{x}+d\theta _{xxx}\Big ]\mathrm{d}x \nonumber \\&\quad =2b\int _{\alpha }^{\beta }\theta \Big [[(u_{2})^{p}]_{x}-[(u_{1})^{p}]_{x}\Big ]\mathrm{d}x\nonumber \\&\quad -\Big [a\theta ^{2}+2d\theta \theta _{xx}-d(\theta _{x})^{2}\Big ]\Big |_{\alpha }^{\beta } \nonumber \\&\quad =2bp\int _{\alpha }^{\beta }\theta \Big [(u_{2})^{p-1}(u_{2})_{x}-(u_{1})^{p-1}(u_{1})_{x}\Big ]\mathrm{d}x \nonumber \\&\quad =-2bp\int _{\alpha }^{\beta }\theta \theta _{x}(u_{2})^{p-1}\mathrm{d}x-2bp\int _{\alpha }^{\beta }\theta \sum _{k=0}^{p-2}(u_{2})^{p-2-k}(u_{1})^{k}(u_{1})_{x}\theta \mathrm{d}x. \end{aligned}$$

(1.12)

By Lemma 1.2, we obtain

$$\begin{aligned}&\Big |\int _{\alpha }^{\beta }\theta \theta _{x}(u_{2})^{p-1}\mathrm{d}x\Big |\le C\int _{\alpha }^{\beta }|\theta |\cdot |\theta _{x}|\mathrm{d}x\le C\Big (\int _{\alpha }^{\beta }\theta ^{2}\mathrm{d}x+\int _{\alpha }^{\beta }(\theta _{x})^{2}\mathrm{d}x\Big ),\\&\Big |\int _{\alpha }^{\beta }\theta \sum _{k=0}^{p-2}(u_{2})^{p-2-k}(u_{1})^{k}(u_{1})_{x}\theta \mathrm{d}x\Big |\le C \int _{\alpha }^{\beta }\theta ^{2}\mathrm{d}x, \end{aligned}$$

where C is a constant. Substituting the above two inequalities into Eq. (1.12), we obtain $\frac{\mathrm{d} E(t)}{d t}\le CE(t)$, $t\in [0,T]$. This leads to $E(t)\le e^{CT}E(0)$, $0\le t\le T$. Thus, if $\phi ^{(1)}=\phi ^{(2)}$, we have $\theta (x,0)=0$ and hence $E(0)=0$, implying that $E(t)=0$. By the Sobolev inequality, we obtain $\Vert \theta \Vert _{L_{\infty }}=0$ and $u_{1}=u_{2}$. Furthermore, if $\theta (x,0)<\varepsilon$, $\theta _{x}(x,0)<\varepsilon$, $\theta _{xx}(x,0)<\varepsilon$, we obtain $E(0)<\varepsilon$ and hence $E(t)\le e^{CT}E(0)\le \varepsilon e^{CT}$, $0\le t\le T$, implying that the solution is continuously dependent on the initial condition. We conclude that Eqs. (1.1)–(1.3) are well posed. $\square$

The rest of this paper is arranged as follows: Sect. 2 gives the detailed description of the fourth-order finite difference scheme and its discrete conservative property for Eqs. (1.1)–(1.3). Section 3 provides complete proofs on the solvability, convergence and stability of the proposed scheme with the convergence order $O(\tau ^{2}+h^{4})$. Section 4 presents some numerical simulations to verify the theoretical analysis. Finally, concluding remarks are given in Sect. 5.

2 Difference scheme and its discrete conservative law

The solution domain $\{(x,t)|\alpha \le x\le \beta , 0\le t\le T\}$ is covered by a uniform grid $\{(x_{j},t_{n})|x_{j}=\alpha +jh,~t_{n}=n\tau ,~j=0, \ldots ,J,~n=0, \ldots ,N\}$, with spacing $h=(\beta -\alpha )/J$, $\tau =T/N$. Denote $U^{n}_{j}\approx u(x_{j},t_{n})$, and let

$$\begin{aligned}&Z_{h}^{0}=\{U=(U_{j})|U_{-1}=U_{0}=U_{1}=U_{J-1}=U_{J}=U_{J+1}=0\}, \end{aligned}$$

(2.1)

where $j=-1,0,1, \ldots ,J-1,J,J+1$. For convenience, the following notations will be introduced:

$$\begin{aligned}&(U_{j}^{n})_{{\tilde{x}}}=\frac{1}{h}(U_{j+1}^{n}-U_{j}^{n}), \quad (U_{j}^{n})_{\bar{x}}=\frac{1}{h}(U_{j}^{n}-U_{j-1}^{n}), \quad (U_{j}^{n})_{{\hat{x}}}=\frac{1}{2h}(U_{j+1}^{n}-U_{j-1}^{n}),\\&\bar{U}^{n}_{j}=\frac{1}{2}(U^{n+1}_{j}+U^{n-1}_{j}), \quad (U_{j}^{n})_{{\hat{t}}}=\frac{1}{2\tau }(U_{j}^{n+1}-U_{j}^{n-1}), \quad (U_{j}^{n})_{{\tilde{t}}}=\frac{1}{\tau }(U_{j}^{n+1}-U_{j}^{n}),\\&\langle U^{n},V^{n}\rangle =h\sum ^{J-1}_{j=1}U_{j}^{n}V_{j}^{n}, \quad \Vert U^{n}\Vert ^{2}=\langle U^{n},U^{n}\rangle , \quad \Vert U^{n}\Vert _{\infty }=\max _{1\le j\le J-1}|U_{j}^{n}|. \end{aligned}$$

By setting

$$\begin{aligned}&w=-au_{x}-b(u^{p})_{x}+cu_{xxt}-\mathrm{d}u_{xxx}-u_{xxxxt}, \end{aligned}$$

(2.2)

Eq. (1.1) can be written as $w=u_{t}$. Using the Taylor expansion in the variable x, we obtain

$$\begin{aligned} w^{n}_{j}&=-a\Big [(U^{n}_{j})_{{\hat{x}}}-\frac{h^{2}}{6}(\partial ^{3}_{x}u)^{n}_{j}\Big ]-b\Big [[(U^{n}_{j})^{p}]_{{\hat{x}}}-\frac{h^{2}}{6}(\partial ^{3}_{x}u^{p})^{n}_{j}\Big ]+c\Big [(U^{n}_{j})_{{\tilde{x}}\bar{x}{\hat{t}}}-\frac{h^{2}}{12}(\partial ^{4}_{x}\partial _{t}u)^{n}_{j}\Big ] \nonumber \\&\qquad -d\Big [(U^{n}_{j})_{\dot{\ddot{x}}}-\frac{h^{2}}{6}(\partial ^{5}_{x}u)^{n}_{j}\Big ]-\Big [(U^{n}_{j})_{{\tilde{x}}{\tilde{x}}\bar{x}{\bar{x}}{\hat{t}}}-\frac{h^{2}}{6}(\partial ^{6}_{x}\partial _{t}u)^{n}_{j}\Big ]+O(h^{4}), \end{aligned}$$

(2.3)

where the fourth-order operator $(U_{j}^{n})_{\dot{\ddot{x}}}$ is defined as follows (Wang and Dai 2018):

$$\begin{aligned}&(U_{j}^{n})_{\dot{\ddot{x}}}=-\frac{1}{24h^{3}}(U_{j+3}^{n}-U_{j-3}^{n}) +\frac{2}{3h^{3}}(U_{j+2}^{n}-U_{j-2}^{n})-\frac{29}{24h^{3}}(U_{j+1}^{n}-U_{j-1}^{n})\nonumber \\&\qquad =u_{j}^{(3)}+\frac{h^{2}}{6}u_{j}^{(5)}+O(h^{4}). \end{aligned}$$

(2.4)

From Eq. (2.2), we have

$$\begin{aligned}&(\partial ^{6}_{x}\partial _{t}u)^{n}_{j}=-a(\partial ^{3}_{x}u)^{n}_{j}-b(\partial ^{3}_{x}u^{p})^{n}_{j}+c(\partial ^{4}_{x}\partial _{t}u)^{n}_{j}-d(\partial ^{5}_{x}u)^{n}_{j}-(\partial ^{2}_{x}w)^{n}_{j}. \end{aligned}$$

(2.5)

Substituting Eq. (2.5) into Eq. (2.3) gives

$$\begin{aligned} w^{n}_{j}&=-a(U^{n}_{j})_{{\hat{x}}}-b[(U^{n}_{j})^{p}]_{{\hat{x}}}+c(U^{n}_{j})_{{\tilde{x}}{\bar{x}}{\hat{t}}}-d(U^{n}_{j})_{\dot{\ddot{x}}}-(U^{n}_{j})_{{\tilde{x}}{\tilde{x}}\bar{x}{\bar{x}}{\hat{t}}}\\&\qquad +\frac{ch^{2}}{12}(\partial ^{4}_{x}\partial _{t}u)^{n}_{j}-\frac{h^{2}}{6}(\partial ^{2}_{x}w)^{n}_{j}+O(h^{4}). \end{aligned}$$

Using second-order accuracy for approximation, we obtain

$$\begin{aligned}&U^{n}_{j}=\bar{U}^{n}_{j}+O(\tau ^{2}), \quad w^{n}_{j}=(\partial _{t}u)^{n}_{j}=(U^{n}_{j})_{{\hat{t}}}+O(\tau ^{2}),\\&(\partial ^{2}_{x}w)^{n}_{j}=(W^{n}_{j})_{{\tilde{x}}\bar{x}}+O(h^{2}), \quad (\partial ^{4}_{x}\partial _{t}u)^{n}_{j}=(U^{n}_{j})_{{\tilde{x}}{\tilde{x}}\bar{x}{\bar{x}}{\hat{t}}}+O(h^{2}). \end{aligned}$$

Thus, the proposed difference scheme for Eqs. (1.1)–(1.3) is written as

$$\begin{aligned}&(U^{n}_{j})_{{\hat{t}}}+a(\bar{U}^{n}_{j})_{{\hat{x}}}+b[(\bar{U}^{n}_{j})^{p}]_{{\hat{x}}}+d(\bar{U}^{n}_{j})_{\dot{\ddot{x}}}+A(h)(U^{n}_{j})_{{\tilde{x}}\bar{x}{\tilde{x}}{\bar{x}}{\hat{t}}}-B(h)(U^{n}_{j})_{{\tilde{x}}{\bar{x}}{\hat{t}}}=0, \end{aligned}$$

(2.6)

$$\begin{aligned}&A(h)=1-\frac{ch^{2}}{12}, \quad B(h)=c-\frac{h^{2}}{6}, \quad j=2, \ldots ,J-2, \quad n=2, \ldots ,N, \end{aligned}$$

(2.7)

$$\begin{aligned}&U^{0}_{j}=\phi (x_{j}), \quad 0\le j\le J, \end{aligned}$$

(2.8)

$$\begin{aligned}&U^{n}_{0}=U^{n}_{J}=0,~U^{n}_{-1}=U^{n}_{1}=0,~U^{n}_{J-1}=U^{n}_{J+1}=0,~n=1, \ldots ,N. \end{aligned}$$

(2.9)

Since the scheme in Eqs. (2.6)–(2.9) is a three-level method, we need to give a two-level method to compute $U^{1}$, which is given by

$$\begin{aligned}&(U^{0}_{j})_{{\tilde{t}}}+a(U^{0.5}_{j})_{{\hat{x}}}+b[(U^{0.5}_{j})^{p}]_{{\hat{x}}}+d(U^{0.5}_{j})_{\dot{\ddot{x}}}+A(h)(U^{0}_{j})_{{\tilde{x}}\bar{x}{\tilde{x}}{\bar{x}}{\hat{t}}}-B(h)(U^{0}_{j})_{{\tilde{x}}{\bar{x}}{\hat{t}}}=0, \end{aligned}$$

(2.10)

where

$$\begin{aligned}&U_{j}^{0.5}=(U_{j}^{1}+U_{j}^{0})/2, \quad j=2, \ldots ,J-2,~n=0, \ldots ,N. \end{aligned}$$

Lemma 2.1

(Hu et al. 2008; Ye et al. 2015) For any two mesh functions $U, V\in Z_{h}^{0}$, we obtain

$$\begin{aligned}&\langle U_{{\tilde{x}}},V\rangle =-\langle U,V_{{\bar{x}}}\rangle , \langle U_{{\hat{x}}},V\rangle =-\langle U,V_{{\hat{x}}}\rangle , \end{aligned}$$

(2.11)

$$\begin{aligned}&\langle U_{{\tilde{x}}{\bar{x}}},V\rangle =-\langle U_{{\tilde{x}}},V_{{\tilde{x}}}\rangle , \quad \langle U_{{\tilde{x}}\bar{x}},U\rangle =-\Vert U_{{\tilde{x}}}\Vert ^{2}, \quad \langle U,U_{{\tilde{x}}\bar{x}{\tilde{x}}{\bar{x}}}\rangle =\Vert U_{{\tilde{x}}\bar{x}}\Vert ^{2}. \end{aligned}$$

(2.12)

Lemma 2.2

(Shao et al. 2013) For any mesh function $U\in Z_{h}^{0}$, there exist two positive constants $C_{1}$ and $C_{2}$ such that

$$\begin{aligned}&\Vert U^{n}\Vert _{\infty }\le C_{1}\Vert U^{n}\Vert +C_{2}\Vert U^{n}_{{\tilde{x}}}\Vert . \end{aligned}$$

(2.13)

Lemma 2.3

(Cai et al. 2015) For any discrete function $U\in Z_{h}^{0}$, we have

$$\begin{aligned}&\Vert U^{n}_{{\tilde{x}}}\Vert ^{2}\le \frac{4}{h^{2}}\Vert U^{n}\Vert ^{2}, \quad 0\le n\le N. \end{aligned}$$

(2.14)

Lemma 2.4

(Wongsaijai and Poochinapan 2014; Wang and Dai 2018) For any mesh function $U\in Z_{h}^{0}$, we have

$$\begin{aligned}&\langle U_{\hat{x}},U\rangle =0, \quad \langle U_{\dot{\ddot{x}}},U\rangle =0, \quad \langle U^{p}_{{\hat{x}}},U\rangle =0, \quad p\ge 2. \end{aligned}$$

(2.15)

Theorem 2.5

Suppose $\phi (x)\in H_{0}^{2}([\alpha ,\beta ])$, then the finite difference scheme in Eqs. (2.6)–(2.10) is conservative for discrete energy in sense:

$$\begin{aligned}&E^{n}\equiv \frac{\Vert U^{n+1}\Vert ^{2}+\Vert U^{n}\Vert ^{2}}{2}+B(h)\Big [\frac{\Vert U^{n+1}_{{\tilde{x}}}\Vert ^{2}+\Vert U^{n}_{{\tilde{x}}}\Vert ^{2}}{2}\Big ]\nonumber \\&\qquad +A(h)\Big [\frac{\Vert U^{n+1}_{{\tilde{x}}\bar{x}}\Vert ^{2}+\Vert U^{n}_{{\tilde{x}}\bar{x}}\Vert ^{2}}{2}\Big ]\nonumber \\&\qquad =\cdot \cdot \cdot =\Vert U^{0}\Vert ^{2}+B(h)\Vert U^{0}_{{\tilde{x}}}\Vert ^{2}+A(h)\Vert U^{0}_{{\tilde{x}}\bar{x}}\Vert ^{2}\equiv E^{0}, \quad n=0, \ldots ,N-1. \end{aligned}$$

(2.16)

Proof

Taking the inner product of Eq. (2.6) with 2${{\bar{U}}}^{n}$, we obtain

$$\begin{aligned}&\langle U^{n}_{{\hat{t}}},2{{\bar{U}}}^{n}\rangle {+}A(h)\langle U^{n}_{{\tilde{x}}{\tilde{x}}{\bar{x}}{\bar{x}}{\hat{t}}},2{\bar{U}}^{n}\rangle {-}B(h)\langle U^{n}_{{\tilde{x}}{\bar{x}}{\hat{t}}},2{\bar{U}}^{n}\rangle \nonumber \\&\quad {+}a\langle \bar{U}^{n}_{{\hat{x}}},2{\bar{U}}^{n}\rangle +b\langle (\bar{U}^{n})^{p}_{{\hat{x}}},2{\bar{U}}^{n}\rangle +d\langle \bar{U}^{n}_{\dot{\ddot{x}}},2{\bar{U}}^{n}\rangle =0. \end{aligned}$$

(2.17)

From Lemmas 2.1 and 2.4, we obtain

$$\begin{aligned}&\langle \bar{U}^{n}_{{\hat{x}}},2{\bar{U}}^{n}\rangle =0, \quad \langle (\bar{U}^{n})^{p}_{{\hat{x}}},2{\bar{U}}^{n}\rangle =0, \quad \langle \bar{U}^{n}_{\dot{\ddot{x}}},2{\bar{U}}^{n}\rangle =0,\\&\langle U^{n}_{{\hat{t}}},2{{\bar{U}}}^{n}\rangle =\Vert U^{n}\Vert _{{\hat{t}}}^{2},~\langle U^{n}_{{\tilde{x}}{\bar{x}}{\hat{t}}},2{\bar{U}}^{n}\rangle =-\Vert U_{{\tilde{x}}}^{n}\Vert _{{\hat{t}}}^{2},~\langle U^{n}_{{\tilde{x}}{\tilde{x}}{\bar{x}}{\bar{x}}{\hat{t}}},2{\bar{U}}^{n}\rangle =\Vert U_{{\tilde{x}}\bar{x}}^{n}\Vert _{{\hat{t}}}^{2}. \end{aligned}$$

Thus, Eq. (2.17) can be rewritten as

$$\begin{aligned}&\Vert U^{n}\Vert _{{\hat{t}}}^{2}+A(h)\Vert U_{{\tilde{x}}\bar{x}}^{n}\Vert _{{\hat{t}}}^{2}+B(h)\Vert U_{{\tilde{x}}}^{n}\Vert _{{\hat{t}}}^{2}=0. \end{aligned}$$

This is equivalent to

$$\begin{aligned}&\Vert U^{n+1}\Vert ^{2}+A(h)\Vert U^{n+1}_{{\tilde{x}}\bar{x}}\Vert ^{2}+B(h)\Vert U^{n+1}_{{\tilde{x}}}\Vert ^{2}=\Vert U^{n-1}\Vert ^{2}+A(h)\Vert U^{n-1}_{{\tilde{x}}\bar{x}}\Vert ^{2}+B(h)\Vert U^{n-1}_{{\tilde{x}}}\Vert ^{2}, \end{aligned}$$

where $n=1, \ldots ,N-1$. This further yields

$$\begin{aligned} E^{n}&\equiv \frac{\Vert U^{n+1}\Vert ^{2}+\Vert U^{n}\Vert ^{2}}{2}+B(h)\Big [\frac{\Vert U^{n+1}_{{\tilde{x}}}\Vert ^{2}+\Vert U^{n}_{{\tilde{x}}}\Vert ^{2}}{2}\Big ]+A(h)\Big [\frac{\Vert U^{n+1}_{{\tilde{x}}\bar{x}}\Vert ^{2}+\Vert U^{n}_{{\tilde{x}}\bar{x}}\Vert ^{2}}{2}\Big ]\nonumber \\&=\frac{\Vert U^{n}\Vert ^{2}+\Vert U^{n-1}\Vert ^{2}}{2}+B(h)\Big [\frac{\Vert U^{n}_{{\tilde{x}}}\Vert ^{2}+\Vert U^{n-1}_{{\tilde{x}}}\Vert ^{2}}{2}\Big ]+A(h)\Big [\frac{\Vert U^{n}_{{\tilde{x}}\bar{x}}\Vert ^{2}+\Vert U^{n-1}_{{\tilde{x}}\bar{x}}\Vert ^{2}}{2}\Big ]\nonumber \\&=E^{n-1}=\cdot \cdot \cdot =E^{0}, \quad n=1, \ldots ,N-1. \end{aligned}$$

(2.18)

Similarly, taking the inner product of Eq. (2.10) with 2$u^{0.5}$, we obtain

$$\begin{aligned}&\langle U^{0}_{{\tilde{t}}},2u^{0.5}\rangle +a\langle (U^{0.5}_{{\hat{x}}}),2u^{0.5}\rangle +b\langle (U^{0.5})^{p}_{{\hat{x}}},2u^{0.5}\rangle +d\langle U^{0.5}_{\dot{\ddot{x}}},2u^{0.5}\rangle \nonumber \\&\quad +A(h)\langle U^{0}_{{\tilde{x}}{\bar{x}}{\tilde{x}}{\bar{x}}{\hat{t}}},2u^{0.5}\rangle -B(h)\langle U^{0}_{{\tilde{x}}{\bar{x}}{\hat{t}}},2u^{0.5}\rangle =0. \end{aligned}$$

(2.19)

From Lemmas 2.1 and 2.4, we obtain

$$\begin{aligned}&\langle (U^{0.5}_{{\hat{x}}}),2u^{0.5}\rangle =0, \quad \langle (U^{0.5})^{p}_{{\hat{x}}},2u^{0.5}\rangle =0, \quad \langle U^{0.5}_{\dot{\ddot{x}}},2u^{0.5}\rangle =0, \end{aligned}$$

(2.20)

$$\begin{aligned}&\langle U^{0}_{{\tilde{t}}},2u^{0.5}\rangle =\Vert U^{0}\Vert _{{\tilde{t}}}^{2}, \quad \langle U^{0}_{{\tilde{x}}\bar{x}{\tilde{t}}},2U^{0.5}\rangle =-\Vert U_{{\tilde{x}}}^{0}\Vert _{{\tilde{t}}}^{2}, \quad \langle U^{0}_{{\tilde{x}}{\bar{x}}{\tilde{x}}\bar{x}{\tilde{t}}},2U^{0.5}\rangle =\Vert U_{{\tilde{x}}\bar{x}}^{0}\Vert _{{\tilde{t}}}^{2}. \end{aligned}$$

(2.21)

Substituting Eqs. (2.20)–(2.21) into Eq. (2.19), we obtain

$$\begin{aligned}&\Vert U^{0}\Vert _{{\tilde{t}}}^{2}+A(h)\Vert U_{{\tilde{x}}\bar{x}}^{0}\Vert _{{\tilde{t}}}^{2}+B(h)\Vert U_{{\tilde{x}}}^{0}\Vert _{{\tilde{t}}}^{2}=0. \end{aligned}$$

This is equivalent to

$$\begin{aligned}&\Vert U^{1}\Vert ^{2}+A(h)\Vert U^{1}_{{\tilde{x}}\bar{x}}\Vert ^{2}+B(h)\Vert U^{1}_{{\tilde{x}}}\Vert ^{2}\\&\qquad =\Vert U^{0}\Vert ^{2}+A(h)\Vert U^{0}_{{\tilde{x}}\bar{x}}\Vert ^{2}+B(h)\Vert U^{0}_{{\tilde{x}}}\Vert ^{2}. \end{aligned}$$

Thus, from the above equation and the definition of $E^{0}$, we have

$$\begin{aligned} E^{0}&=\frac{\Vert U^{1}\Vert ^{2}+\Vert U^{0}\Vert ^{2}}{2}+B(h)\Big [\frac{\Vert U^{1}_{{\tilde{x}}}\Vert ^{2}+\Vert U^{0}_{{\tilde{x}}}\Vert ^{2}}{2}\Big ]\\&\qquad +A(h)\Big [\frac{\Vert U^{1}_{{\tilde{x}}\bar{x}}\Vert ^{2}+\Vert U^{0}_{{\tilde{x}}\bar{x}}\Vert ^{2}}{2}\Big ]\\&=\Vert U^{0}\Vert ^{2}+B(h)\Vert U^{0}_{{\tilde{x}}}\Vert ^{2}+A(h)\Vert U^{0}_{{\tilde{x}}\bar{x}}\Vert ^{2}. \end{aligned}$$

$\square$

Theorem 2.6

Suppose $\phi (x)\in H_{0}^{2}([\alpha ,\beta ])$, then the solution $U^{n}$ of Eqs. (2.6)–(2.10) satisfies $\Vert U^{n}\Vert \le C$, $\Vert U^{n}_{{\tilde{x}}}\Vert \le C$, $\Vert U_{{\tilde{x}}\bar{x}}^{n}\Vert \le C$, which yield

$$\begin{aligned}&\Vert U^{n}\Vert _{\infty }\le C, \quad \Vert U_{{\tilde{x}}}^{n}\Vert _{\infty }\le C, \qquad \Vert U_{{\bar{x}}}^{n}\Vert _{\infty }\le C, \quad \Vert U_{{\hat{x}}}^{n}\Vert _{\infty }\le C, \quad 0\le n\le N. \end{aligned}$$

Proof

We prove the theorem by the mathematical induction. From Eq. (2.8), we obtain $\Vert U^{0}\Vert \le C$. We assume that

$$\begin{aligned}&\Vert U^{k}\Vert \le C, \quad \Vert U^{k}\Vert _{\infty }\le C, \quad k=0,1,2, \ldots ,n.&\end{aligned}$$

From Lemma 2.3, we obtain

$$\begin{aligned}&\Vert U^{n+1}_{{\tilde{x}}}\Vert ^{2}\le \frac{4}{h^{2}}\Vert U^{n+1}\Vert ^{2}, \quad \Vert U^{n+1}_{{\tilde{x}}\bar{x}}\Vert ^{2}\le \frac{4}{h^{2}}\Vert U_{{\tilde{x}}}^{n+1}\Vert ^{2}, \end{aligned}$$

which yield

$$\begin{aligned}&\Vert U^{n+1}\Vert ^{2}+B(h)\Vert U_{{\tilde{x}}}^{n+1}\Vert ^{2}+A(h)\Vert U_{{\tilde{x}}\bar{x}}^{n+1}\Vert ^{2}\nonumber \\&\ge \Vert U^{n+1}\Vert ^{2}+c\Vert U_{{\tilde{x}}}^{n+1}\Vert ^{2}+\Vert U_{{\tilde{x}}\bar{x}}^{n+1}\Vert ^{2}-\frac{h^{2}}{6}\frac{4}{h^{2}}\Vert U^{n+1}\Vert ^{2}\nonumber \\&\quad -\frac{ch^{2}}{12}\frac{4}{h^{2}}\Vert U_{{\tilde{x}}}^{n+1}\Vert ^{2}\nonumber \\&\ge \frac{1}{3}\Vert U^{n+1}\Vert ^{2}+\frac{2c}{3}\Vert U_{{\tilde{x}}}^{n+1}\Vert ^{2}+\Vert U_{{\tilde{x}}\bar{x}}^{n+1}\Vert ^{2}\ge 0, \quad c\ge 0, \end{aligned}$$

(2.22)

implying that $E^{n+1}\ge 0$. From Eqs. (2.16) and (2.22), we obtain $\Vert U^{n+1}\Vert \le C$, $\Vert U_{{\tilde{x}}}^{n+1}\Vert \le C$, $\Vert U_{{\tilde{x}}\bar{x}}^{n+1}\Vert \le C$. By Lemma 2.2, we further obtain

$$\begin{aligned}&\Vert U^{n+1}\Vert _{\infty }\le C, \quad \Vert U_{{\tilde{x}}}^{n+1}\Vert _{\infty }\le C, \quad \Vert U_{{\bar{x}}}^{n+1}\Vert _{\infty }\le C, \quad \Vert U_{{\hat{x}}}^{n+1}\Vert _{\infty }\le C, \end{aligned}$$

which completes the proof. $\square$

3 Solvability, convergence and stability

Theorem 3.1

The finite difference scheme in Eqs. (2.6)–(2.10) is uniquely solvable.

Proof

Using the mathematical induction, we can determine $U^{0}$ uniquely by Eq. (2.8) and choose Eq. (2.10) to compute $U^{1}$. Assume that $U^{1(\gamma _{1})}$ and $U^{1(\gamma _{2})}$ are two solutions of Eq. (2.10) and let $U^{1(\gamma )}=U^{1(\gamma _{1})}-U^{1(\gamma _{2})}$, then $U^{1(\gamma )}$ satisfies the following equation:

$$\begin{aligned}&\frac{1}{\tau }U^{1(\gamma )}_{j}+\frac{a}{2}(U^{1(\gamma )}_{j})_{{\hat{x}}}+\frac{\mathrm{{d}}}{2}(U^{1(\gamma )}_{j})_{\dot{\ddot{x}}}-\frac{1}{\tau }B(h)(U^{1(\gamma )}_{j})_{{\tilde{x}}\bar{x}}+\frac{1}{\tau }A(h)(U^{1(\gamma )}_{j})_{{\tilde{x}}{\tilde{x}}\bar{x}{\bar{x}}}=0, \end{aligned}$$

(3.1)

where $j=2, \ldots ,J-2$. By taking an inner product on both sides of Eq. (3.1) with $U^{1(\gamma )}$, we have

$$\begin{aligned}&\Vert U^{1(\gamma )}\Vert ^{2}+B(h)\Vert U^{1(\gamma )}_{{\tilde{x}}}\Vert ^{2}+A(h)\Vert U^{1(\gamma )}_{{\tilde{x}}\bar{x}}\Vert ^{2}=0. \end{aligned}$$

(3.2)

From Theorem 2.6, we get

$$\begin{aligned}&\Vert U^{1(\gamma )}\Vert ^{2}+B(h)\Vert U^{1(\gamma )}_{{\tilde{x}}}\Vert ^{2}+A(h)\Vert U^{1(\gamma )}_{{\tilde{x}}\bar{x}}\Vert ^{2}\nonumber \\&\quad \ge \frac{1}{3}\Vert U^{1(\gamma )}\Vert ^{2}+\frac{2c}{3}\Vert U^{1(\gamma )}_{{\tilde{x}}}\Vert ^{2}+\Vert U^{1(\gamma )}_{{\tilde{x}}\bar{x}}\Vert ^{2}\ge 0. \end{aligned}$$

(3.3)

Thus, from Eqs. (3.2) and (3.3), we obtain

$$\begin{aligned}&\Vert U^{1(\gamma )}\Vert ^{2}=0, \quad \Vert U^{1(\gamma )}_{{\tilde{x}}}\Vert ^{2}=0, \quad \Vert U^{1(\gamma )}_{{\tilde{x}}\bar{x}}\Vert ^{2}=0.&\end{aligned}$$

Therefore, Eq. (3.1) has the only one solution and $U^{1}$ is uniquely solvable. Now, suppose $U^{0}$, $U^{1}$,$\ldots$, $U^{n}$ to be solved uniquely. By consider the homogeneous Eq. (2.6) for $U^{n+1}$, we have

$$\begin{aligned}&\frac{1}{\tau }U^{n+1}_{j}-\frac{1}{\tau }B(h)(U^{n+1}_{j})_{{\tilde{x}}\bar{x}}+\frac{1}{\tau }A(h)(U^{n+1}_{j})_{{\tilde{x}}{\bar{x}}{\tilde{x}}{\bar{x}}}\nonumber \\&\quad +a(U^{n+1}_{j})_{{\hat{x}}}+b[U^{n+1}_{j})^{p}]_{{\hat{x}}}+d(U_{j}^{n+1})_{\dot{\ddot{x}}}=0. \end{aligned}$$

(3.4)

Computing an inner product of Eq. (3.4) with $U^{n+1}$, we obtain

$$\begin{aligned}&\Vert U^{n+1}\Vert ^{2}+A(h)\Vert U_{{\tilde{x}}\bar{x}}^{n+1}\Vert ^{2}+B(h)\Vert U_{{\tilde{x}}}^{n+1}\Vert ^{2}=0. \end{aligned}$$

(3.5)

This together with Eq. (2.22) gives

$$\begin{aligned}&\Vert U^{n+1}\Vert ^{2}=0, \quad \Vert U_{{\tilde{x}}}^{n+1}\Vert ^{2}=0, \quad \Vert U_{{\tilde{x}}\bar{x}}^{n+1}\Vert ^{2}=0. \end{aligned}$$

(3.6)

Therefore, Eq. (3.4) has the only one solution and $U^{n+1}$ is uniquely solvable. $\square$

Theorem 3.2

Suppose $\phi (x)\in H_{0}^{2}([\alpha ,\beta ])$, then the solution $U^{n}$ converges to the solution $u^{n}$ in the sense of $\Vert \cdot \Vert _{\infty }$, and the convergence rate is $O(\tau ^{2}+h^{4})$.

Proof

Let $e^{n}_{j}=u^{n}_{j}-U^{n}_{j}$, then the truncation error can be obtained as follows:

$$\begin{aligned}&R^{n}_{j}=(e^{n}_{j})_{{\hat{t}}}-B(h)(e^{n}_{j})_{{\tilde{x}}{\bar{x}}{\hat{t}}}+a(\bar{e}^{n}_{j})_{{\hat{x}}}+d(\bar{e}^{n}_{j})_{\dot{\ddot{x}}}+A(h)(e^{n}_{j})_{{\tilde{x}}\bar{x}{\tilde{x}}{\bar{x}}{\hat{t}}}+b[(\bar{u}^{n}_{j})^{p}-(\bar{U}^{n}_{j})^{p}]_{{\hat{x}}}, \end{aligned}$$

(3.7)

where $R^{n}_{j}=O(\tau ^{2}+h^{4})$. By taking an inner product on both sides of Eq. (3.7) with 2${{\bar{e}}}_{j}^{n}$,

we have

$$\begin{aligned}&(\Vert e^{n+1}\Vert ^{2}-\Vert e^{n-1}\Vert ^{2})+B(h)(\Vert e_{{\tilde{x}}}^{n+1}\Vert ^{2}-\Vert e_{{\tilde{x}}}^{n-1}\Vert ^{2})\nonumber \\&\quad +A(h)(\Vert e_{{\tilde{x}}\bar{x}}^{n+1}\Vert ^{2}-\Vert e_{{\tilde{x}}\bar{x}}^{n-1}\Vert ^{2})\nonumber \\&=2\tau \langle R^{n},2{{\bar{e}}}^{n}\rangle -2\tau \langle a(\bar{e}^{n})_{{\hat{x}}}+d(\bar{e}^{n})_{\dot{\ddot{x}}},2{\bar{e}}^{n}\rangle \nonumber \\&\quad -2\tau \langle b[(\bar{u}^{n})^{p}-(\bar{U}^{n})^{p}]_{{\hat{x}}},2{{\bar{e}}}^{n}\rangle . \end{aligned}$$

(3.8)

According to Lemmas 1.2, 2.1 and Theorem 2.6, we obtain

$$\begin{aligned} \langle [(\bar{u}^{n})^{p}-(\bar{U}^{n})^{p}]_{{\hat{x}}},2{\bar{e}}^{n}\rangle&=-h\sum _{j=1}^{J-1}\Big \{\Big [(\bar{u}_{j}^{n})^{p}-(\bar{U}_{j}^{n})^{p}\Big ]\cdot 2({\bar{e}}_{j}^{n})_{{\hat{x}}}\Big \} \nonumber \\&=-h\sum _{j=1}^{J-1}\Big \{\sum _{k=1}^{p-1}\Big [(\bar{u}_{j}^{n})^{p-k}(\bar{U}_{j}^{n})^{k}(\bar{e}_{j}^{n})\Big ]\cdot 2(\bar{e}_{j}^{n})_{{\hat{x}}}\Big \} \nonumber \\&\le C(\Vert e^{n-1}\Vert ^{2}+\Vert e^{n+1}\Vert ^{2}+\Vert e_{{\tilde{x}}}^{n-1}\Vert ^{2}+\Vert e_{{\tilde{x}}}^{n+1}\Vert ^{2}). \end{aligned}$$

(3.9)

From Lemmas 2.1, 2.3 and 2.4, we obtain

$$\begin{aligned}&\langle \bar{e}^{n}_{{\hat{x}}},2{\bar{e}}^{n}\rangle =0, \quad \langle \bar{e}^{n}_{\dot{\ddot{x}}},2{\bar{e}}^{n}\rangle =0, \end{aligned}$$

(3.10)

$$\begin{aligned}&\Vert e^{n}_{\hat{x}}\Vert ^{2}\le \Vert e^{n}_{{\tilde{x}}}\Vert ^{2}\le \frac{1}{2}\Vert e^{n}\Vert ^{2}+\frac{1}{2}\Vert e^{n}_{{\tilde{x}}\bar{x}}\Vert ^{2}, \end{aligned}$$

(3.11)

$$\begin{aligned}&\langle R^{n},2{{\bar{e}}}^{n}\rangle \le \Vert R^{n}\Vert ^{2}+\frac{1}{2}(\Vert e^{n+1}\Vert ^{2}+\Vert e^{n-1}\Vert ^{2}).&\end{aligned}$$

(3.12)

Substituting Eqs. (3.9)–(3.12) into Eq. (3.8) gives

$$\begin{aligned}&(\Vert e^{n+1}\Vert ^{2}-\Vert e^{n-1}\Vert ^{2})+B(h)(\Vert e_{{\tilde{x}}}^{n+1}\Vert ^{2}-\Vert e_{{\tilde{x}}}^{n-1}\Vert ^{2})+A(h)(\Vert e_{{\tilde{x}}\bar{x}}^{n+1}\Vert ^{2}-\Vert e_{{\tilde{x}}\bar{x}}^{n-1}\Vert ^{2})\nonumber \\&\le 2\tau \Vert R^{n}\Vert ^{2}+C\tau (\Vert e_{{\tilde{x}}\bar{x}}^{n+1}\Vert ^{2}+\Vert e_{{\tilde{x}}\bar{x}}^{n-1}\Vert ^{2}+\Vert e^{n+1}\Vert ^{2}+\Vert e^{n}\Vert ^{2}+\Vert e^{n-1}\Vert ^{2}). \end{aligned}$$

(3.13)

Setting

$$\begin{aligned}&\varLambda ^{n}\equiv \Vert e^{n}\Vert ^{2}+\Vert e^{n-1}\Vert ^{2}+B(h)(\Vert e_{{\tilde{x}}}^{n}\Vert ^{2}+\Vert e_{{\tilde{x}}}^{n-1}\Vert ^{2})+A(h)(\Vert e_{{\tilde{x}}\bar{x}}^{n}\Vert ^{2}+\Vert e_{{\tilde{x}}\bar{x}}^{n-1}\Vert ^{2}), \end{aligned}$$

then we have from Eq. (2.22) that

$$\begin{aligned}&\varLambda ^{n+1}\ge \frac{1}{3}(\Vert e^{n+1}\Vert ^{2}+\Vert e^{n}\Vert ^{2})+\frac{2c}{3}(\Vert e_{{\tilde{x}}}^{n+1}\Vert ^{2}+\Vert e_{{\tilde{x}}}^{n}\Vert ^{2})+(\Vert e_{{\tilde{x}}\bar{x}}^{n+1}\Vert ^{2}+\Vert e_{{\tilde{x}}\bar{x}}^{n}\Vert ^{2})\ge 0. \end{aligned}$$

And, Eq. (3.13) can be rewritten as

$$\begin{aligned}&\varLambda ^{n+1}-\varLambda ^{n}\le 2\tau \Vert R^{n}\Vert ^{2}+C\tau (\varLambda ^{n+1}+\varLambda ^{n}). \end{aligned}$$

Hence, we obtain

$$\begin{aligned}&(1-C\tau )(\varLambda ^{n+1}-\varLambda ^{n})\le 2\tau \Vert R^{n}\Vert ^{2}+2C\tau \varLambda ^{n}. \end{aligned}$$

If $\tau$ is sufficiently small, which satisfies $1-C\tau >0$, then we obtain

$$\begin{aligned}&\varLambda ^{n+1}-\varLambda ^{n}\le C\tau \Vert R^{n}\Vert ^{2}+C\tau \varLambda ^{n}. \end{aligned}$$

(3.14)

Summarizing Eq. (3.14) from 1 to n, we get

$$\begin{aligned}&\varLambda ^{n+1}\le \varLambda ^{1}+C\tau \sum _{k=1}^{n}\Vert R^{k}\Vert ^{2}+C\tau \sum _{k=1}^{n}\varLambda ^{k}. \end{aligned}$$

Since $e^{0}=0$ and Eq. (2.10) is used to compute $U^{1}$, we obtain

$$\begin{aligned}&e^{0}=0, \quad \varLambda ^{1}=O(\tau ^{2}+h^{4})^{2}, \end{aligned}$$

and notice that

$$\begin{aligned}&\tau \sum _{k=1}^{n}\Vert R^{k}\Vert ^{2}\le n\tau \max _{1\le k\le n}\Vert R^{k}\Vert ^{2}\le T\cdot O(\tau ^{2}+h^{4})^{2}, \end{aligned}$$

we have

$$\begin{aligned}&\varLambda ^{n+1}\le O(\tau ^{2}+h^{4})^{2}+C\tau \sum _{k=1}^{n}\varLambda ^{k}. \end{aligned}$$

From discrete Gronwall’s inequality Wang et al. (2019), we obtain $\varLambda ^{n}\le O(\tau ^{2}+h^{4})^{2}$, implying

$$\begin{aligned}&\Vert e^{n+1}\Vert ^{2}\le O(\tau ^{2}+h^{4})^{2}, \quad \Vert e_{{\tilde{x}}\bar{x}}^{n+1}\Vert ^{2}\le O(\tau ^{2}+h^{4})^{2}. \end{aligned}$$

(3.15)

Furthermore, it follows from Eqs. (3.11), (3.15) and Lemma 2.2 that

$$\begin{aligned}&\Vert e_{{\tilde{x}}}^{n+1}\Vert \le O(\tau ^{2}+h^{4}), \quad \Vert e^{n+1}\Vert _{\infty }\le O(\tau ^{2}+h^{4}). \end{aligned}$$

(3.16)

This completes the proof. $\square$

Theorem 3.3

Under the conditions of Theorem 3.2, the solution $U^{n}$ of Eqs. (2.6)–(2.10) is unconditionally stable in norm $\Vert \cdot \Vert _{\infty }$.

Table 1 Comparison of errors with $\tau =h$ at $T=20$

Fig. 1

The spatial and temporal convergence orders

Fig. 2

Numerical solutions of the Rosenau–KdV equation with $h=0.25$, $\tau =h^{2}$, $\alpha =-40$, $\beta =60$ (left) and $\alpha =-40$, $\beta$=150 (right)

Fig. 3

Absolute error distribution at $T=30$ with $\tau =h/2$, $\tau =h^{2}$, $h=0.5$ (left) and $h=0.25$ (right)

4 Numerical experiments

In this section, we choose numerical experiments to verify the correctness of our theoretical analysis results. The $L_{\infty }$ and $L_{2}$ error norms of the solution obtained from Eqs. (2.6)–(2.10) are defined as

$$\begin{aligned}&L_{2}=\Vert e^{n}\Vert _{2}=\Big [h\sum ^{J-1}_{j=1}|e_{j}^{n}|^{2}\Big ]^{\frac{1}{2}}, \quad L_{\infty }=\Vert e^{n}\Vert _{\infty }=\max _{1\le j\le J-1}|e_{j}^{n}|. \end{aligned}$$

Example 1

Consider the Rosenau–KdV equation in the case of $a=1$, $b=0.5$, $c=0$, $d=1$ and $p=2$ as follows (Wongsaijai and Poochinapan 2014):

$$\begin{aligned}&u_{t}+u_{x}+0.5(u^{2})_{x}+u_{xxx}+u_{xxxxt}=0, \quad \alpha \le x\le \beta , \quad t\in [0,T], \end{aligned}$$

(4.1)

subject to the initial condition

$$\begin{aligned}&u(x,0)=\phi (x)=35\Big (\frac{\sqrt{313}}{312}-\frac{1}{24}\Big ){{\,\mathrm{sech}\,}}^{4}\Big [\frac{1}{24}\sqrt{-26+2\sqrt{313}}x\Big ], \quad \alpha \le x\le \beta , \end{aligned}$$

and the boundary conditions

$$\begin{aligned}&u(\alpha ,t)=u(\beta ,t)=0, \quad u_{x}(\alpha ,t)=u_{x}(\beta ,t)=0. \end{aligned}$$

The analytical solution is

$$\begin{aligned}&u(x,t)=35\Big (\frac{\sqrt{313}}{312}-\frac{1}{24}\Big ){{\,\mathrm{sech}\,}}^{4}\Big \{\frac{1}{24}\sqrt{-26+2\sqrt{313}}\Big [x-\frac{1}{2}(1+\frac{\sqrt{313}}{13})t\Big ]\Big \}. \end{aligned}$$

(4.2)

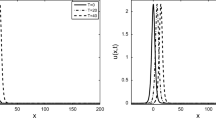
First, using different h, $x\in [-70, 100]$, $T=20$ and $\tau =h$, the comparison of error results was listed in Table 1. As seen, the results from the present scheme are more accurate than that obtained by the scheme in Hu et al. (2013). Then the spatial and temporal convergence orders for $U^{n}$ at $T=10$ with different space and time steps were drawn in Fig. 1, where $h=0.5$, 0.25, 0.125, 0.0625, $\tau =h^{2}$ in Fig. 1a, and $\tau =0.2$, 0.1, 0.05, 0.025, 0.0125, $h=\sqrt{\tau }$ in Fig. 1b. From Fig. 1, the convergence rate $O(\tau ^{2}+h^{4})$ is verified. Furthermore, the solution profiles were plotted in Fig. 2 using $h=0.25$, $\tau =h^{2}$, $\alpha =-40$, $\beta =60$, 150. The solitons at $t=30$ and 60 are in excellent agreement with the solitons at $t=0$. Finally, Fig. 3 shows absolute errors at $T=30$ with $h=1/2$, 1/4 and $\tau =h^{2}$. From Fig. 3, we can see that the maximum errors are around orders of $10^{-3}$ and $10^{-4}$, respectively. The above results indicate that our scheme in Eqs. (2.6)–(2.10) can be applied to simulate solitary propagations.

Table 2 Comparison of errors at $T=40$ with $\tau =0.1$, $h=0.25$

Table 3 Comparison of rates of convergence and CPU time at $T=40$ with $p=4$, $h=0.5$ and $\tau =h^{2}$

Table 4 Comparison of rates of convergence and CPU time at $T=40$ with $p=8$, $h=0.5$ and $\tau =h^{2}$

Fig. 4

Discrete energy by the present scheme with $h=0.25$, $\tau =h^{2}$, $p=4$ (left) and $p=8$ (right)

Fig. 5

Numerical solutions of the Rosenau–RLW equation with $p=4$, $\tau =h^{2}$, $\alpha =-60$, $\beta =120$, $h=0.25$ (left) $h=0.125$ (right)

Example 2

Consider the generalized Rosenau–RLW equation in the case of $a=1$, $b=1$, $c=1$, $d=0$ and $p\ge 2$ as follows

$$\begin{aligned}&u_{t}+u_{x}+(u^{p})_{x}-u_{xxt}+u_{xxxxt}=0, \quad -60\le x\le 120, \quad t\in [0,40], \end{aligned}$$

(4.3)

subject to the initial condition

$$\begin{aligned}&u(x,0)=\phi (x)=\exp \Big [\frac{1}{p-1}\ln \frac{(p+1)(3p+1)(p+3)}{2(p^{2}+3)(p^{2}+4p+7)}\Big ]{{\,\mathrm{sech}\,}}^{\frac{4}{p-1}}(k_{1}x), \end{aligned}$$

and the boundary conditions

$$\begin{aligned}&u(-60,t)=u(120,t)=0, \quad u_{x}(-60,t)=u_{x}(120,t)=0. \end{aligned}$$

The exact solitary wave solution is

$$\begin{aligned}&u(x,t)=\exp \Big [\frac{1}{p-1}\ln \frac{(p+1)(3p+1)(p+3)}{2(p^{2}+3)(p^{2}+4p+7)}\Big ]{{\,\mathrm{sech}\,}}^{\frac{4}{p-1}}[k_{1}(x-k_{2}t)], \end{aligned}$$

where

$$\begin{aligned}&k_{1}=\frac{p-1}{\sqrt{4p^{2}+8p+20}}, \quad k_{2}=\frac{p^{4}+4p^{3}+14p^{2}+20p+25}{p^{4}+4p^{3}+10p^{2}+12p+21}, \quad p\ge 2. \end{aligned}$$

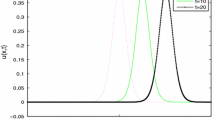
First, we made a comparison between our scheme and the scheme in Pan and Zhang (2012); Wongsaijai and Poochinapan (2014). The results in term of errors at $T=40$, and different p were listed in Tables 2, 3 and 4. One may see that the computational efficiency of the present scheme is clearly better than the ones obtained by the schemes in Pan and Zhang (2012); Wongsaijai and Poochinapan (2014). Then the conservative invariant $E^{n}$ at different times $t\in [0,60]$ was listed in Table 5, where $p=4$, 8, $h=0.25$ and $\tau =h^{2}$. We also showed the conservative law of discrete energy $E^{n}$ in Fig. 4. The obtained results in Table 5 and Fig. 4 testify that the present scheme is conservative for energy, which coincides with the theory. Finally, we simulated the wave graph of the numerical solution of Eq. (4.3). The wave graph comparison of numerical solutions obtained using $h=0.25$, 0.125, $\tau =h^{2}$ at various times are given in Figs. 5 and 6 for $p=4$ and $p=8$, respectively. From Figs. 5 and 6, we can see that the heights of the wave graph at different times are almost identical, which implies that the energy computed by the scheme is conservative.

Table 5 Discrete energy $E^{n}$ of the scheme with $p=4$, 8, $h=0.25$, $\tau =h^{2}$

Table 6 Comparison of errors at $T=30$ with $\tau =h$

Example 3

Consider the Rosenau–KdV–RLW equation in the case of $a=1$, $b=0.5$, $c=1$, $d=1$ and $p=2$ as follows:

$$\begin{aligned}&u_{t}+u_{x}+0.5(u^{2})_{x}-u_{xxt}+u_{xxx}+u_{xxxxt}=0, \quad \alpha \le x\le \beta , \quad t\in [0,T], \end{aligned}$$

(4.4)

subject to the initial condition

$$\begin{aligned}&u(x,0)=\phi (x)=-\frac{5}{456}\Big (25-13\sqrt{457}\Big ){{\,\mathrm{sech}\,}}^{4}(k_{3}x), \quad \alpha \le x\le \beta , \end{aligned}$$

and boundary conditions

$$\begin{aligned}&u(\alpha ,t)=u(\beta ,t)=0, \quad u_{x}(\alpha ,t)=u_{x}(\beta ,t)=0. \end{aligned}$$

The exact solitary wave solution is

$$\begin{aligned}&u(x,t)=-\frac{5}{456}\Big (25-13\sqrt{457}\Big ){{\,\mathrm{sech}\,}}^{4}(k_{3}x)[k_{3}(x-k_{4}t)], \end{aligned}$$

where

$$\begin{aligned}&k_{3}=\Big (\frac{-13+\sqrt{457}}{288}\Big )^{1/2},~k_{4}=\frac{241+13\sqrt{457}}{266}. \end{aligned}$$

Fig. 6

Numerical solutions of the Rosenau–RLW equation with $p=8$, $\tau =h^{2}$, $\alpha =-60$, $\beta =120$, $h=0.25$ (left) $h=0.125$ (right)

Fig. 7

Absolute error distribution at $T=30$ (left) and $T=60$ (right) with $h=0.25$, $\tau =h^{2}$, $\alpha =-40$, $\beta =160$

Fig. 8

Numerical solutions of the Rosenau–KdV–RLW equation with $h=0.25$, $\tau =h^{2}$, $\alpha =-40$, $\beta =100$ (left) and $\beta =200$ (right)

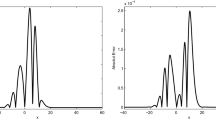
First, we compared the errors at $T=30$ and different h, using $\alpha =-40$ and $\beta =100$ as reported in Table 6. It is clear that the errors obtained by the present scheme are slightly smaller than the ones obtained by the method in Wongsaijai and Poochinapan (2014). Then we drew the absolute errors distributions with $h=0.25$, $\tau =h^{2}$, $\alpha =-40$, $\beta =160$ at $T=30$, 60 in Fig. 7. We found that the maximum error obtained by the present scheme takes place around the peak amplitude of solitary waves. At last, the curves of the numerical solutions computed by the present scheme in with $h=0.25$, $\tau =h^{2}$, $\alpha =-40$, $\beta =100$, 200 are given in Fig. 8, and we can see that the waves at $T=20\sim 60$ agree with the corresponding waves at $T=0$ quite well.

5 Conclusion

A new conservative finite difference scheme for the generalized Rosenau–KdV–RLW equation is introduced and analyzed. The scheme is unconditionally stable and convergent with order of $O(\tau ^{2}+h^{4})$. Numerical experiments confirm well the theoretical analysis and show that the present scheme is efficient and reliable.