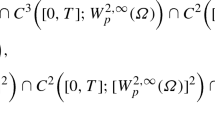Conservative and fourth-order compact difference schemes for the generalized Rosenau–Kawahara–RLW equation

Abstract

In this article, we present two conservative and fourth-order compact finite-difference schemes for solving the generalized Rosenau–Kawahara–RLW equation. The proposed schemes are energy-conserved, convergent, and unconditionally stable, and the numerical convergence orders in both $l_{2}$-norm and $l_{\infty }$-norm are of $O(\tau ^{2}+h^{4})$. Numerical experiments demonstrate that the present schemes are efficient and reliable.

1 Introduction

Nonlinear phenomena play important roles in various fields of science and engineering. In recent years, there has been a growing interest in the computation of nonlinear wave phenomena using different mathematical models. These models include the KdV equation [1,2,3], the Benjamin–Bona–Mahony equation or RLW equation [4,5,6], the Rosenau equation [7, 8], the Rosenau–RLW equation [9, 10], the Kawahara equation [11, 12], the Rosenau–Kawahara equation [13], and many others [14,15,16,17].

In this article, we consider the following initial-boundary value problem of the generalized Rosenau–Kawahara–RLW equation: [18]:

$$\begin{aligned}&u_{t}+\alpha u_{x}+\beta u^{p}u_{x}+\gamma u_{xxx}-\delta u_{xxt}+\lambda u_{xxxxt}\nonumber \\&\quad -\theta u_{xxxxx}=0,\quad x\in \Omega ,~0<t\le T, \end{aligned}$$

(1)

$$\begin{aligned}&u(x,0)=u_{0}(x),\quad x\in \Omega , \end{aligned}$$

(2)

$$\begin{aligned}&u(x_{l},t)=u_{x}(x_{l},t)=0,\nonumber \\&u(x_{r},t)=u_{x}(x_{r},t)=u_{xx}(x_{r},t)=0, \end{aligned}$$

(3)

where $\Omega = [x_{l},x_{r}]$, $0\le t\le T$, $\alpha$, $\beta$, $\gamma$, and $\theta$ are real positive constants, $\delta$ and $\lambda$ are positive constants, $p\ge 1$ is a positive integer, and $u_{0}(x)$ is a given smooth function. It should be pointed out that, here, u(x, t) represents the wave profile, which has the following asymptotic values [19]:

$$\begin{aligned} u\rightarrow 0,\quad \partial ^{n}u/\partial x^{n}\rightarrow 0,\quad {\text {as }} \ x\rightarrow {\pm \infty },\quad n\ge 1. \end{aligned}$$

(4)

Thus, the boundary conditions (3) are meaningful for the solitary solution of Eq. (1).

It is easy to verify that the problem (1)–(3) has the following conservation law [20, 21]:

$$\begin{aligned} E(t)&=\int _{x_{l}}^{x_{r}}(u^{2}+\delta u^{2}_{x}+\lambda u^{2}_{xx}){\text {d}}x=\Vert u\Vert _{L_{2}}^{2}\\&\quad +\delta \Vert u_{x}\Vert _{L_{2}}^{2}+\lambda \Vert u_{xx}\Vert _{L_{2}}^{2}\\&=\Vert u_{0}\Vert _{L_{2}}^{2}+\delta \Vert (u_{0})_{x}\Vert _{L_{2}}^{2}\\&\quad +\lambda \Vert (u_{0})_{xx}\Vert _{L_{2}}^{2}=E(0),\quad \delta>0,\quad \lambda >0,\quad t\in [0,T]. \end{aligned}$$

Lemma 1.1

(See [20]) Suppose that $u_{0}\in H_{0}^{2}(\Omega )$, and then, the solution u(x, t) of the problem (1)–(3) satisfies:

$$\begin{aligned}&\Vert u\Vert _{L^2}\le C,\quad \Vert u_x\Vert _{L^2}\le C,\quad \Vert u_{xx}\Vert _{L^2}\le C,\\&\Vert u\Vert _{L^{\infty }}\le C,\quad \Vert u_x\Vert _{L^{\infty }}\le C. \end{aligned}$$

Theorem 1.2

Suppose that $u_{0}\in H_{0}^{2}(\Omega )$, and then, the problem (1)–(3) is well posed.

Proof

Assume that $u_{1}$ and $u_{2}$ are two solutions of the problem (1)–(3) satisfying the initial conditions $u_{0}^{(1)}$ and $u_{0}^{(2)}$, respectively. Let $\eta =u_{1}-u_{2}$, and then, $\eta$ satisfies:

$$\begin{aligned}&\eta _{t}+\alpha \eta _{x}+\beta [u_{1}^{p}(u_{1})_{x}-u_{2}^{p}(u_{2})_{x}]+\gamma \eta _{xxx}-\delta \eta _{xxt}+\lambda \eta _{xxxxt}-\theta \eta _{xxxxx}=0,\nonumber \\&\eta (x,0)=u_{0}^{(1)}-u_{0}^{(2)},\quad x\in \Omega , \end{aligned}$$

(5)

$$\begin{aligned}&\eta (x_{l},t)=\eta _{x}(x_{l},t)=0,\quad \eta (x_{r},t)=\eta _{x}(x_{r},t)=\eta _{xx}(x_{r},t)=0,\quad t\in [0,T].&\end{aligned}$$

(6)

Multiplying Eq. (5) by $\eta$, and then, integrating it over $[x_{l},x_{r}]$, we obtain:

$$\begin{aligned}&\int _{x_{l}}^{x_{r}}\eta \Bigg (\eta _{t}-\delta \eta _{xxt}+\lambda \eta _{xxxxt}\Bigg ){\text {d}}x-\theta \int _{x_{l}}^{x_{r}}\eta \eta _{xxxxx}{\text {d}}x\nonumber \\&\quad =-\int _{x_{l}}^{x_{r}}\eta \Bigg (\alpha \eta _{x}+\beta [u_{1}^{p}(u_{1})_{x}-u_{2}^{p}(u_{2})_{x}]+\gamma \eta _{xxx}\Bigg ){\text {d}}x. \end{aligned}$$

(7)

Using the integration by parts and the boundary conditions (6), we have:

$$\begin{aligned}&\int _{x_{l}}^{x_{r}}\eta \eta _{x}{\text {d}}x=\frac{1}{2}(\eta ^{2})\Bigg |_{x_{l}}^{x_{r}}=0, \end{aligned}$$

(8)

$$\begin{aligned}&\int _{x_{l}}^{x_{r}}\eta \eta _{xxx}{\text {d}}x=(\eta \eta _{xx})\Bigg |_{x_{l}}^{x_{r}}-\int _{x_{l}}^{x_{r}}\eta _{xx}\eta _{x}{\text {d}}x=-\frac{1}{2}(\eta _{x})^{2}\Bigg |_{x_{l}}^{x_{r}}=0,\end{aligned}$$

(9)

$$\begin{aligned}&\int _{x_{l}}^{x_{r}}\eta \eta _{xxxxx}{\text {d}}x=(\eta \eta _{xxxx})\Bigg |_{x_{l}}^{x_{r}}-\int _{x_{l}}^{x_{r}}\eta _{xxxx}d\eta =-\int _{x_{l}}^{x_{r}}\eta _{x}d(\eta _{xxx})\nonumber \\&\quad =-(\eta _{x}\eta _{xxx})\Bigg |_{x_{l}}^{x_{r}}+\int _{x_{l}}^{x_{r}}\eta _{xxx}\eta _{xx}{\text {d}}x\nonumber \\&\quad =\frac{1}{2}(\eta _{xx})^{2}\Bigg |_{x_{l}}^{x_{r}}=-\frac{1}{2} [\eta _{xx}(x_{l},t)]^{2}. \end{aligned}$$

(10)

Letting:

$$\begin{aligned} G(t)=\int _{x_{l}}^{x_{r}}(\eta ^{2}+\delta \eta ^{2}_{x}+\lambda \eta ^{2}_{xx}){\text {d}}x,\quad \delta>0,\quad \lambda >0,\quad t\in [0,T]. \end{aligned}$$

Substituting Eqs. (8)–(10) into Eq. (7), we obtain:

$$\begin{aligned}&\frac{{\text {d}} G(t)}{{\text {d}} t}+\theta [\eta _{xx}(x_{l},t)]^{2}{\text {d}}x\nonumber \\&\quad =-2\beta \int _{x_{l}}^{x_{r}}\eta [u_{1}^{p}(u_{1})_{x}-u_{2}^{p}(u_{2})_{x}]{\text {d}}x\nonumber \\&\quad =-2\beta \int _{x_{l}}^{x_{r}}\eta [u_{1}^{p}(\eta +u_{2})_{x}-u_{2}^{p}(u_{2})_{x}]{\text {d}}x\nonumber \\&\quad =-2\beta \int _{x_{l}}^{x_{r}}\eta u_{1}^{p}\eta _{x}{\text {d}}x-2\beta \int _{x_{l}}^{x_{r}}\eta (u_{1}^{p}-u_{2}^{p})(u_{2})_{x}{\text {d}}x\nonumber \\&\quad =-2\beta \int _{x_{l}}^{x_{r}}\eta u_{1}^{p}\eta _{x}{\text {d}}x-2\beta \int _{x_{l}}^{x_{r}}\Bigg [\eta ^{2}(u_{2})_{x}\sum _{k=0}^{p-1}(u_{1})^{p-1-k}(u_{2})^{k}\Bigg ]{\text {d}}x. \end{aligned}$$

(11)

By Lemma 1.1 and the Cauchy–Schwarz inequality, we obtain:

$$\begin{aligned}&\Bigg |\int _{x_{l}}^{x_{r}}\eta u_{1}^{p}\eta _{x}{\text {d}}x\Bigg |\le C\int _{x_{l}}^{x_{r}}|\eta |\cdot |\eta _{x}|{\text {d}}x\le C\Bigg [\int _{x_{l}}^{x_{r}}\eta ^{2}{\text {d}}x+\int _{x_{l}}^{x_{r}}(\eta _{x})^{2}{\text {d}}x\Bigg ],\\&\Bigg |\int _{x_{l}}^{x_{r}}\Bigg [\eta ^{2}(u_{2})_{x}\sum _{k=0}^{p-1}(u_{1})^{p-1-k}(u_{2})^{k}\Bigg ]{\text {d}}x\Bigg |\le C \int _{x_{l}}^{x_{r}}\eta ^{2}{\text {d}}x, \end{aligned}$$

where C is a constant. Substituting the above two inequalities into Eq. (11), we obtain:

$$\begin{aligned}&\frac{{\text {d}} G(t)}{{\text {d}} t}+\theta [\eta _{xx}(x_{l},t)]^{2}{\text {d}}x\le C\Bigg [\int _{x_{l}}^{x_{r}}\eta ^{2}{\text {d}}x+\int _{x_{l}}^{x_{r}}(\eta _{x})^{2}{\text {d}}x\Bigg ],\quad \theta >0. \end{aligned}$$

Since $\theta$ is a positive constant, we have:

$$\begin{aligned} \frac{{\text {d}} G(t)}{{\text {d}} t}\le CG(t),\quad t\in [0,T]. \end{aligned}$$

This leads to:

$$\begin{aligned} G(t)\le {\text {e}}^{CT}G(0),\quad 0\le t\le T. \end{aligned}$$

Thus, if $u_{0}^{(1)}=u_{0}^{(2)}$, we have $\eta (x,0)=0$ and, hence, $G(0)=0$, implying that $G(t)=0$. By the Sobolev inequality, we obtain $\Vert \eta \Vert _{L_{\infty }}=0$ and $u_{1}=u_{2}$. Furthermore, if

$$\begin{aligned} \eta (x,0)<\varepsilon ,\quad \eta _{x}(x,0)<\varepsilon ,\quad \eta _{xx}(x,0)<\varepsilon , \end{aligned}$$

we obtain $G(0)<\varepsilon$ and hence:

$$\begin{aligned} G(t)\le {\text {e}}^{CT}G(0)\le \varepsilon {\text {e}}^{CT},\quad 0\le t\le T, \end{aligned}$$

implying that the solution is continuously dependent on the initial condition. We conclude that the problem (1)–(3) is well posed. This completes the proof. $\square$

For the generalized Rosenau–Kawahara–RLW equation (1), He and Pan [18] presented a second-order accurate implicit difference scheme, which is energy-conserved and unconditionally stable. Wang and Dai [20] proposed a fourth-order accurate conservative finite-difference scheme and their numerical analysis showed that the method can be applied to study the solitary wave traveling in a long time. Ghiloufi et al. [21] proposed two conservative finite-difference schemes for the Rosenau–Kawahara–RLW equation, and both schemes are fourth-order convergent in space variables. However, the above finite-difference schemes in Refs. [20, 21], although they have the fourth-order numerical precision, employ a nine-point discrete method. Thus, the purpose of this paper is to establish two new conservative high-order compact finite-difference schemes for solving the generalized Rosenau–Kawahara–RLW equation. The coefficient matrices of these new schemes are both seven-diagonal. And we rigorously prove that the two schemes are unconditionally stable and conserve the energy in the discrete sense.

The outline is as follows. In Sect. 2, a nonlinear conservative difference scheme for the problem (1)–(3) is described in detail, and corresponding conservation, stability, and convergence are proved. In Sect. 3, a three-time-level linearized compact finite-difference scheme is constructed. The discrete conservative law, the unique solvability, the prior error estimates, and the unconditional convergence of the difference scheme are shown. In Sect. 4, an iterative algorithm for the nonlinear compact scheme is given and its convergence is proved. In Sect. 5, we present some numerical examples to show the performance of the schemes and confirm our theoretical analysis. Finally, conclusions are drawn in the last section.

Fig. 1

Absolute error distribution of Example 5.1 computed by Scheme A (left) and Scheme B (right) with $h=0.125$ and $\tau =h^{2}$ at $T=4$

Fig. 2

Numerical solutions of Example 5.1 computed by Scheme A (left) and Scheme B (right) with $h=0.25$ and $\tau =0.1$

Fig. 3

Discrete energy for long-time simulations of Example 5.2 computed by Scheme A (left) and Scheme B (right) when $h=0.1$ and $\tau =0.01$

2 Nonlinear compact difference scheme

In this section, we propose a two-time-level nonlinear and conservative fourth-order compact finite-difference scheme for the problem (1)–(3).

2.1 Construction of nonlinear-implicit scheme

We first define the solution domain to be $[x_{l},x_{r}]\times [0,T]$, which is covered by a uniform grid $(x_{j},t^{n})$, where:

$$\begin{aligned} x_{j}=x_{l}+jh,\ t^{n}=n\tau ,\ h=(x_{r}-x_{l})/J,\ \tau =T/N, \ 0\le j\le J, \ 0\le n\le N. \end{aligned}$$

At each point $(x_{j},t^{n})$, the symbol $u(x_{j},t^{n})$ is denoted as the exact solution, while the associated numerical solution is represented by $U^{n}_{j}\approx u(x_{j},t^{n})$. The following notations are introduced for the simplicity:

$$\begin{aligned} \bar{U}^{n}_{j}&=\frac{1}{2}(U^{n+1}_{j}+U^{n-1}_{j}),\quad U^{n+\frac{1}{2}}_{j}=\frac{1}{2}(U^{n+1}_{j}+U^{n}_{j}),\\ (U_{j}^{n})_{{\hat{t}}}&=\frac{1}{2\tau }(U_{j}^{n+1}-U_{j}^{n-1}),\quad (U_{j}^{n})_{\tilde{t}}=\frac{1}{\tau }(U_{j}^{n+1}-U_{j}^{n}),\\ (U_{j}^{n})_{\tilde{x}}&=\frac{1}{h}(U_{j+1}^{n}-U_{j}^{n}),\quad (U_{j}^{n})_{\bar{x}}=\frac{1}{h}(U_{j}^{n}-U_{j-1}^{n}),\quad (U_{j}^{n})_{{\hat{x}}}=\frac{1}{2h}(U_{j+1}^{n}-U_{j-1}^{n}),\\ \langle U^{n},V^{n}\rangle&=h\sum ^{J-1}_{j=1}U^{n}_{j}V^{n}_{j},\quad \Vert U^{n}\Vert ^{2}=\langle U^{n},U^{n}\rangle ,\quad \Vert U^{n}\Vert _{\infty }=\max _{0\le j\le J}|U^{n}_{j}|. \end{aligned}$$

To get the high-order scheme, we use the following two fourth-order compact finite-difference operators [22]:

$$\begin{aligned}&{\mathcal {A}}_{x}U^{n}_{j}=U^{n}_{j}+\frac{h^{2}}{12}(U^{n}_{j})_{\tilde{x}\bar{x}}=\frac{1}{12}(U^{n}_{j-1}+10U^{n}_{j}+U^{n}_{j+1}),\\&{\mathcal {B}}_{x}U^{n}_{j}=U^{n}_{j}+\frac{h^{2}}{6}(U^{n}_{j})_{\tilde{x}\bar{x}}=\frac{1}{6}(U^{n}_{j-1}+4U^{n}_{j}+U^{n}_{j+1}),\quad 1\le j\le J,\quad 0\le n\le N. \end{aligned}$$

For the discretization of the first-order derivative $u_{x}$ and the second-order derivative $u_{xx}$ of the function u(x, t), we have the following formulas [23]:

$$\begin{aligned}&u_{x}(x_{j},t^{n})={\mathcal {B}}^{-1}_{x}(U^{n}_{j})_{\hat{x}}+O(h^{4}),\quad u_{xx}(x_{j},t^{n})={\mathcal {A}}^{-1}_{x}(U^{n}_{j})_{\tilde{x}\bar{x}}+O(h^{4}). \end{aligned}$$

Omitting the small terms $O(h^{4})$, we obtain:

$$\begin{aligned}&u_{x}(x_{j},t^{n})\approx {\mathcal {B}}^{-1}_{x}(U^{n}_{j})_{\hat{x}},\quad u_{xx}(x_{j},t^{n})\approx {\mathcal {A}}^{-1}_{x}(U^{n}_{j})_{\tilde{x}\bar{x}}.&\end{aligned}$$

We now introduce the vector and matrix notations as:

$$\begin{aligned}&U=(U_{1},U_{2},\ldots ,U_{J-1})^{\text {T}},\\&\Lambda _{h}u_{x}= [u_{x}(x_{1}),u_{x}(x_{2}),\ldots ,u_{x}(x_{J-1})]^{\text {T}},\\&\Lambda _{h}u_{xx}= [u_{xx}(x_{1}),u_{xx}(x_{2}),\ldots ,u_{xx}(x_{J-1})]^{\text {T}},\\&M_{1}=\frac{1}{12}\left( \begin{array}{ccccc} 10 &{}1 &{}0 &{}\cdots &{}0\\ 1 &{}10 &{}1 &{}\cdots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0 &{}\cdots &{}1 &{}10 &{}1\\ 0 &{}\cdots &{}0 &{}1 &{}10 \end{array} \right) _{(J-1)\times (J-1)},\\&M_{2}=\frac{1}{6}\left( \begin{array}{ccccc} 4 &{}1 &{}0 &{}\cdots &{}0\\ 1 &{}4 &{}1 &{}\cdots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0 &{}\cdots &{}1 &{}4 &{}1\\ 0 &{}\cdots &{}0 &{}1 &{}4 \end{array} \right) _{(J-1)\times (J-1)},&\end{aligned}$$

where $[,]^{\text {T}}$ is the transpose of the vector [, ]. Thus, the corresponding matrix form is:

$$\begin{aligned}&\Lambda _{h}u_{x}\approx M^{-1}_{2}U_{\hat{x}},\quad \Lambda _{h}u_{xx}\approx M^{-1}_{1}U_{\tilde{x}{\bar{x}}}.&\end{aligned}$$

Since $M_{1}$ and $M_{2}$ are two real symmetric positive definite matrices, there exist two real symmetric positive definite matrices $H_{1}$ and $H_{2}$, such that [24]:

$$\begin{aligned} H_{1}=M^{-1}_{1},\quad H_{2}=M^{-1}_{2}. \end{aligned}$$

Introducing the new functions y, z, w, d, g, and $\phi$, Eq. (1) can be written as:

$$\begin{aligned}&y_{t}=z+d,\quad d=\alpha u_{x},\quad w=u_{xx}, \end{aligned}$$

(12)

$$\begin{aligned}&g=w_{xx},\quad z=\beta \phi +\gamma w_{x}-\theta g_{x},\end{aligned}$$

(13)

$$\begin{aligned}&\phi =\frac{1}{p+1}(u^{p+1})_{x},\quad y=-u+\delta w-\lambda g. \end{aligned}$$

(14)

Therefore, the original problem (1)–(3) is changed to an equivalent system of the second-order differential equations (12)–(14). Using the above notations, we construct the nonlinear compact difference scheme for solving the system (12)–(14) as follows:

$$\begin{aligned}&(Y^{n}_{j})_{\tilde{t}}=Z^{n+\frac{1}{2}}_{j}+D^{n+\frac{1}{2}}_{j},\quad {\mathcal {B}}_{x}D^{n+\frac{1}{2}}_{j}=\alpha (U^{n+\frac{1}{2}}_{j})_{{\hat{x}}}, \end{aligned}$$

(15)

$$\begin{aligned}&{\mathcal {A}}_{x}W^{n+\frac{1}{2}}_{j}=(U^{n+\frac{1}{2}}_{j})_{\tilde{x}\bar{x}},\quad {\mathcal {A}}_{x}G^{n+\frac{1}{2}}_{j}=(W^{n+\frac{1}{2}}_{j})_{\tilde{x}\bar{x}}, \end{aligned}$$

(16)

$$\begin{aligned}&{\mathcal {B}}_{x}Z^{n+\frac{1}{2}}_{j}=\beta \phi (U^{n+\frac{1}{2}}_{j},U^{n+\frac{1}{2}}_{j})+\gamma (W^{n+\frac{1}{2}}_{j})_{\hat{x}}-\theta (G^{n+\frac{1}{2}}_{j})_{\hat{x}}, \end{aligned}$$

(17)

$$\begin{aligned}&\phi (U^{n+\frac{1}{2}}_{j},U^{n+\frac{1}{2}}_{j})=\frac{1}{p+2}\Bigg \{(U^{n+\frac{1}{2}}_{j})^{p}(U^{n+\frac{1}{2}}_{j})_{\hat{x}}+ [(U^{n+\frac{1}{2}}_{j})^{p+1}]_{\hat{x}}\Bigg \}, \end{aligned}$$

(18)

$$\begin{aligned}&Y^{n}_{j}=-U^{n}_{j}+\delta W^{n}_{j}-\lambda G^{n}_{j}. \end{aligned}$$

(19)

From Eqs. (15)–(19), we have:

$$\begin{aligned}&{\mathcal {B}}_{x}(U^{n}_{j})_{\tilde{t}}+\alpha (U_{j}^{n+\frac{1}{2}})_{{\hat{x}}}+\beta \phi (U^{n+\frac{1}{2}}_{j},U^{n+\frac{1}{2}}_{j})+\gamma {\mathcal {A}}^{-1}_{x} (U^{n+\frac{1}{2}}_{j})_{\tilde{x}{\bar{x}}{\hat{x}}}-\delta {\mathcal {A}}^{-1}_{x}{\mathcal {B}}_{x} (U^{n}_{j})_{\tilde{x}{\bar{x}}\tilde{t}}\nonumber \\&\quad +\lambda ({\mathcal {A}}^{-1}_{x})^{2}{\mathcal {B}}_{x}(U^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}\tilde{t}}-\theta ({\mathcal {A}}^{-1}_{x})^{2} (U^{n+\frac{1}{2}}_{j})_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}{\hat{x}}}=0,\quad n\ge 1,\quad j=2,\ldots ,J-2. \end{aligned}$$

(20)

Thus, the compact finite-difference scheme (20) can be rewritten in the following matrix form:

$$\begin{aligned}&U^{n}_{\tilde{t}}+\alpha H_{2}U^{n+\frac{1}{2}}_{{\hat{x}}}+\beta H_{2}\Phi (U^{n+\frac{1}{2}},U^{n+\frac{1}{2}})+\gamma H_{1}H_{2}U^{n+\frac{1}{2}}_{\tilde{x}{\bar{x}}{\hat{x}}}-\delta H_{1}U^{n}_{\tilde{x}{\bar{x}}\tilde{t}}+\lambda H_{1}^{2}U^{n}_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}\tilde{t}}\nonumber \\&\quad -\theta H_{1}^{2}H_{2}U^{n+\frac{1}{2}}_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}{\hat{x}}}=0,\quad n=0,1,2,\ldots ,N-1,&\end{aligned}$$

(21)

where

$$\begin{aligned} \Phi (U^{n+\frac{1}{2}},U^{n+\frac{1}{2}})=\Bigg [\phi (U_{1}^{n+\frac{1}{2}},U_{1}^{n+\frac{1}{2}}),\phi (U_{2}^{n+\frac{1}{2}},U_{2}^{n+\frac{1}{2}}),\ldots ,\phi (U_{J}^{n+\frac{1}{2}},U_{J}^{n+\frac{1}{2}})\Bigg ]^{\text {T}}. \end{aligned}$$

The initial condition (2) is discretized as:

$$\begin{aligned} U^{0}_{j}=u_{0}(x_{j}),\quad j=0,1,2,\ldots ,J. \end{aligned}$$

(22)

It should be pointed out that since $U^{n}_{0}=(U^{n}_{0})_{{\hat{x}}}=0$, $U^{n}_{J}=(U^{n}_{J})_{{\hat{x}}}=(U^{n}_{J})_{\tilde{x}\bar{x}}=0$ from Eq. (3) and $\partial ^{n}u/\partial x^{n}\rightarrow 0$ as $x\rightarrow {\pm \infty }$ in Eq. (4), $n\ge 1$, we may assume:

$$\begin{aligned} U^{n}_{-1}=U^{n}_{0}=U^{n}_{1}=0,\quad U^{n}_{J-1}=U^{n}_{J}=U^{n}_{J+1}=0,\quad n=0,1,\ldots ,N, \end{aligned}$$

(23)

for simplicity, where $j=-1,J+1$ are ghost points. We further denote:

$$\begin{aligned}&R_{0}^{J}=\{U=(U^{n}_{j})_{j\in Z}|U^{n}_{-1}=U^{n}_{0}=U^{n}_{1}=0,\quad U^{n}_{J-1}=U^{n}_{J}=U^{n}_{J+1}=0,\quad n=0,1,\ldots ,N\}.&\end{aligned}$$

Hence, $U^{n}\in R_{0}^{J}$, $0\le n\le N$.

2.2 Auxiliary lemmas

To analyze the discrete conservative properties for the compact finite-difference scheme (5)–(7), the following lemmas should be introduced.

Lemma 2.1

[25, 26] For any two mesh functions $U, V\in R_{0}^{J}$, we have:

$$\begin{aligned}&\langle U_{\tilde{x}},V\rangle =-\langle U,V_{\bar{x}}\rangle ,\quad \langle U_{{\hat{x}}},V\rangle =-\langle U,V_{{\hat{x}}}\rangle ,\\&\langle U_{\tilde{x}\bar{x}},U\rangle =-\Vert U_{\tilde{x}}\Vert ^{2},\quad \langle U_{\tilde{x}\tilde{x}{\bar{x}}\bar{x}},U\rangle =\Vert U_{\tilde{x}\bar{x}}\Vert ^{2},\quad \langle U_{\tilde{x}\bar{x}},V\rangle =-\langle U_{\tilde{x}},V_{\tilde{x}}\rangle =\langle U,V_{\tilde{x}{\bar{x}}}\rangle . \end{aligned}$$

Lemma 2.2

[20] For any mesh function $U^{n}\in R_{0}^{J}$, we have:

$$\begin{aligned}&\langle U^{n}_{\tilde{t}},2 U^{n+\frac{1}{2}}\rangle =\Vert U^{n}\Vert ^{2}_{\tilde{t}},\quad \langle U^{n}_{{\hat{t}}},2{{\bar{U}}}^{n}\rangle =\Vert U^{n}\Vert ^{2}_{{\hat{t}}},\\&\langle U^{n}_{\tilde{x}{\bar{x}}\tilde{t}},2 U^{n+\frac{1}{2}}\rangle =-\Vert U^{n}_{\tilde{x}}\Vert ^{2}_{\tilde{t}},\quad \langle U^{n}_{\tilde{x}{\bar{x}}{\hat{t}}},2{\bar{U}}^{n}\rangle =-\Vert U^{n}_{\tilde{x}}\Vert ^{2}_{{\hat{t}}},\\&\langle U^{n}_{\tilde{x}\tilde{x}{\bar{x}}{\bar{x}}\tilde{t}},2 U^{n+\frac{1}{2}}\rangle =\Vert U^{n}_{\tilde{x}\bar{x}}\Vert ^{2}_{\tilde{t}},\quad \langle U^{n}_{\tilde{x}\tilde{x}{\bar{x}}{\bar{x}}{\hat{t}}},2{\bar{U}}^{n}\rangle =\Vert U^{n}_{\tilde{x}\bar{x}}\Vert ^{2}_{{\hat{t}}}.&\end{aligned}$$

Lemma 2.3

[18] For any discrete function $U^{n}$ on the finite interval $[x_{l},x_{r}]$, there exist two positive constants $C_{1}$ and $C_{2}$, such that:

$$\begin{aligned}&\Vert U^{n}\Vert _{\infty }\le C_{1}\Vert U^{n}\Vert +C_{2}\Vert U^{n}_{\tilde{x}}\Vert ,\quad n=0,1,2,\ldots ,N.&\end{aligned}$$

Lemma 2.4

[27] The eigenvalues of the matrices $M_{1}$ and $M_{2}$ are, respectively, in the following forms:

$$\begin{aligned} \lambda _{M_{1},i}=\frac{1}{6}\Bigg (5+\cos \frac{i\pi }{J+1}\Bigg ), \quad \lambda _{M_{2},i}=\frac{1}{3}\Bigg (2+\cos \frac{i\pi }{J+1}\Bigg ),\quad i=1,2,\ldots ,J. \end{aligned}$$

Lemma 2.5

[24] For any real value symmetric positive definite matrices H and for $U, V\in R_{0}^{J}$, we have:

$$\begin{aligned}&\langle HU_{\hat{x}},V\rangle =-\langle HU,V_{\hat{x}}\rangle =-\langle U,HV_{\hat{x}}\rangle ,\\&\langle HU_{\tilde{x}{\bar{x}}},V\rangle =-\langle HU_{\tilde{x}},V_{\tilde{x}}\rangle =-\langle \mathfrak {R}U_{\tilde{x}},\mathfrak {R}V_{\tilde{x}}\rangle ,\\&\langle HU_{\tilde{x}{\bar{x}}},U\rangle =-\langle \mathfrak {R}U_{\tilde{x}},\mathfrak {R}U_{\tilde{x}}\rangle =-\Vert \mathfrak {R}U_{\tilde{x}}\Vert ^{2}, \end{aligned}$$

where $\mathfrak {R}$ is obtained by the Cholesky decomposition of H, denoted as $H=\mathfrak {R}^{\text {T}}\mathfrak {R}$.

Lemma 2.6

For any mesh function $U\in R_{0}^{J}$, we have:

$$\begin{aligned}&\Vert U\Vert ^{2}\le \langle H_{1}U,U\rangle =\Vert \mathfrak {R}_{1}U\Vert ^{2}\le \frac{3}{2}\Vert U\Vert ^{2},\quad \Vert U\Vert ^{2}\le \langle H_{2}U,U\rangle =\Vert \mathfrak {R}_{2}U\Vert ^{2}\le 3\Vert U\Vert ^{2},&\end{aligned}$$

where $\mathfrak {R}_{i}$ is obtained by the Cholesky decomposition of $H_{i}$, denoted as $H_{i}=\mathfrak {R}_{i}^{\text {T}}\mathfrak {R}_{i}$, $i=1,2$.

Proof

It follows from Lemma 2.4 that the eigenvalues of the matrices $M_{1}$ and $M_{2}$ satisfy:

$$\begin{aligned} \frac{2}{3}\le \lambda _{M_{1},i}\le 1,\quad ~\frac{1}{3}\le \lambda _{M_{2},i}\le 1,\quad i=1,2,\ldots ,J. \end{aligned}$$

This implies that:

$$\begin{aligned} 1\le \lambda _{H_{1},i}\le \frac{3}{2},\quad 1\le \lambda _{H_{2},i}\le 3,\quad i=1,2,\ldots ,J. \end{aligned}$$

Thus, we obtain:

$$\begin{aligned} 1\le \Vert H_{1}\Vert =\rho (H_{1})\le \frac{3}{2},\quad 1\le \Vert H_{2}\Vert =\rho (H_{2})\le 3, \end{aligned}$$

(24)

where $\rho (H_{i})$ is the spectral radius of the matrices $H_{i}$, $i=1,2$. Note that:

$$\begin{aligned}&\langle H_{i}U,U\rangle =\langle \mathfrak {R}_{i}U,\mathfrak {R}_{i}U\rangle =\Vert \mathfrak {R}_{i}U\Vert ^{2},\quad i=1,2.&\end{aligned}$$

It follows from Eq. (24) that:

$$\begin{aligned}&\Vert U\Vert ^{2}\le \langle H_{1}U,U\rangle =\Vert \mathfrak {R}_{1}U\Vert ^{2}\le \Vert H_{1}\Vert \langle U,U\rangle \le \frac{3}{2}\Vert U\Vert ^{2},\\&\Vert U\Vert ^{2}\le \langle H_{2}U,U\rangle =\Vert \mathfrak {R}_{2}U\Vert ^{2}\le \Vert H_{2}\Vert \langle U,U\rangle \le 3\Vert U\Vert ^{2}. \end{aligned}$$

This completes the proof. $\square$

Lemma 2.7

[24] For any mesh function $U\in R_{0}^{J}$, we have:

$$\begin{aligned}&\Vert U_{\hat{x}}\Vert ^{2}\le \Vert U_{\tilde{x}}\Vert ^{2},\quad \Vert U_{\tilde{x}}\Vert ^{2}=\Vert U_{\bar{x}}\Vert ^{2},\\&\Vert \mathfrak {R}_{2}U\Vert ^{2}\le C\Vert \mathfrak {R}_{1}U\Vert ^{2},\quad \Vert U\Vert ^{2}\le \Vert H_{1}U\Vert ^{2}\le C\Vert U\Vert ^{2}.&\end{aligned}$$

Lemma 2.8

[24] For any mesh function $U\in R_{0}^{J}$, we have:

$$\begin{aligned} \langle H_{2}U_{\hat{x}},U\rangle =0,\quad \langle H_{1}H_{2}U_{\tilde{x}{\bar{x}}{\hat{x}}},U\rangle =0,\quad \langle H_{2}\Phi (U,\bar{U}),\bar{U}\rangle =0. \end{aligned}$$

Lemma 2.9

For any two mesh functions $U,V\in R_{0}^{J}$, we have:

$$\begin{aligned}&\langle H_{1}^{2}U_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}},V\rangle =\langle H_{1}U_{\tilde{x}{\bar{x}}},H_{1}V_{\tilde{x}\bar{x}}\rangle ,\quad \langle H_{1}^{2}U_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}},U\rangle =\Vert H_{1}U_{\tilde{x}{\bar{x}}}\Vert ^{2}.&\end{aligned}$$

Proof

For $U,V\in R_{0}^{J}$, from Lemma 2.1, we have:

$$\begin{aligned} \langle H_{1}^{2}U_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}},V\rangle =\langle H_{1}^{2}U_{\tilde{x}{\bar{x}}},V_{\tilde{x}\bar{x}}\rangle =\langle H_{1}U_{\tilde{x}{\bar{x}}},H_{1}V_{\tilde{x}\bar{x}}\rangle . \end{aligned}$$

Furthermore, we obtain:

$$\begin{aligned}&\langle H_{1}^{2}U_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}},U\rangle =\langle H_{1}U_{\tilde{x}{\bar{x}}},H_{1}U_{\tilde{x}\bar{x}}\rangle =\Vert H_{1}U_{\tilde{x}{\bar{x}}}\Vert ^{2}.&\end{aligned}$$

This completes the proof. $\square$

Lemma 2.10

For any mesh function $U\in R_{0}^{J}$, we have:

$$\begin{aligned}&\langle H_{1}^{2}H_{2}U_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}{\hat{x}}},U\rangle =0.&\end{aligned}$$

Proof

For $U\in R_{0}^{J}$, from Lemmas 2.1 and 2.5, we have:

$$\begin{aligned}&\langle H_{1}^{2}H_{2}U_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}{\hat{x}}},U\rangle =-\langle U_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}},H_{1}^{2}H_{2}U_{{\hat{x}}}\rangle =-\langle (U_{\tilde{x}\bar{x}})_{\tilde{x}{\bar{x}}},H_{1}^{2}H_{2}U_{{\hat{x}}}\rangle \\&\quad =-\langle U_{\tilde{x}\bar{x}},H_{1}^{2}H_{2}U_{\tilde{x}{\bar{x}}{\hat{x}}}\rangle =-\langle U,H_{1}^{2}H_{2}U_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}{\hat{x}}}\rangle \\&\quad =-\langle H_{1}^{2}H_{2}U_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}{\hat{x}}},U\rangle ,&\end{aligned}$$

and then, we have $\langle H_{1}^{2}H_{2}U_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}{\hat{x}}},U\rangle =0$. This completes the proof. $\square$

2.3 Discrete conservative law

We now analyze the discrete conservation for the nonlinear compact finite-difference scheme (21)–(23).

Theorem 2.11

The nonlinear compact finite-difference scheme (21)–(23) is conservative in the sense of the discrete energy, that is:

$$\begin{aligned}&E_{1}^{n}\equiv \Vert U^{n}\Vert ^{2} +\delta \Vert \mathfrak {R}_{1}U_{\tilde{x}}^{n}\Vert ^{2}+\lambda \Vert H_{1}U_{\tilde{x}\bar{x}}^{n}\Vert ^{2}\\&\quad =E_{1}^{n-1}=\cdots =E_{1}^{0}\equiv \Vert U^{0}\Vert ^{2} +\delta \Vert \mathfrak {R}_{1}U_{\tilde{x}}^{0}\Vert ^{2}+\lambda \Vert H_{1}U_{\tilde{x}\bar{x}}^{0}\Vert ^{2}, \end{aligned}$$

where $\delta >0$, $\lambda >0$, $n=0,1,2,\ldots ,N$.

Proof

Computing the discrete inner product of Eq. (21) with 2$U^{n+\frac{1}{2}}$ and using Lemmas 2.2, 2.5, 2.8, and 2.10, we obtain:

$$\begin{aligned}&\langle U^{n}_{\tilde{t}},2U^{n+\frac{1}{2}}\rangle =\frac{1}{\tau }(\Vert U^{n+1}\Vert ^{2}-\Vert U^{n}\Vert ^{2}),\\&\langle H_{1}U^{n}_{\tilde{x}\bar{x}\tilde{t}},2U^{n+\frac{1}{2}}\rangle =-\frac{1}{\tau }(\Vert \mathfrak {R}_{1}U^{n+1}_{\tilde{x}}\Vert ^{2}-\Vert \mathfrak {R}_{1}U^{n}_{\tilde{x}}\Vert ^{2}),\\&\langle H_{1}^{2}U^{n}_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}\tilde{t}},2U^{n+\frac{1}{2}}\rangle =\frac{1}{\tau }(\Vert H_{1}U^{n+1}_{\tilde{x}\bar{x}}\Vert ^{2}-\Vert H_{1}U^{n}_{\tilde{x}\bar{x}}\Vert ^{2}),\\&\langle H_{1}H_{2}U^{n+\frac{1}{2}}_{\tilde{x}{\bar{x}}{\hat{x}}},U^{n+\frac{1}{2}}\rangle =0,\quad \langle H_{1}^{2}H_{2}U^{n+\frac{1}{2}}_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}{\hat{x}}},U^{n+\frac{1}{2}}\rangle =0,\\&\langle H_{2}U^{n+\frac{1}{2}}_{{\hat{x}}},U^{n+\frac{1}{2}}\rangle =0,\quad \langle H_{2}\Phi (U^{n+\frac{1}{2}},U^{n+\frac{1}{2}}),U^{n+\frac{1}{2}}\rangle =0. \end{aligned}$$

Therefore, we have:

$$\begin{aligned}&\frac{1}{\tau }\Vert U^{n+1}\Vert ^{2}+\frac{\delta }{\tau }\Vert \mathfrak {R}_{1}U^{n+1}_{\tilde{x}}\Vert ^{2}+\frac{\lambda }{\tau }\Vert H_{1}U^{n+1}_{\tilde{x}\bar{x}}\Vert ^{2}\\&\quad =\frac{1}{\tau }\Vert U^{n}\Vert ^{2}+\frac{\delta }{\tau }\Vert \mathfrak {R}_{1}U^{n}_{\tilde{x}}\Vert ^{2}+\frac{\lambda }{\tau }\Vert H_{1}U^{n}_{\tilde{x}\bar{x}}\Vert ^{2},\quad \delta>0, \quad \lambda >0. \end{aligned}$$

Consequently, we obtain $E_{1}^{n}=E_{1}^{n-1}=\cdots =E_{1}^{0}$. This completes the proof. $\square$

2.4 A priori estimates

Theorem 2.12

Suppose that $u_{0}\in H_{0}^{2}( [x_{l},x_{r}])$, and then, the solution $U^{n}$ of the compact finite-difference scheme (21)–(23) satisfies:

$$\begin{aligned} \Vert U^{n}\Vert \le \sqrt{E^{0}_{1}},\quad \Vert U^{n}_{\tilde{x}}\Vert \le \sqrt{\frac{E^{0}_{1}}{\delta }},\quad \Vert U^{n}_{\tilde{x}\bar{x}}\Vert \le \sqrt{\frac{E^{0}_{1}}{\lambda }},\quad \delta>0, \quad \lambda >0, \end{aligned}$$

which yield $\Vert U^{n}\Vert _{\infty }\le C$ and $\Vert U_{\tilde{x}}^{n}\Vert _{\infty }\le C$ for any $0\le n\le N$.

Proof

By the assumption that $\delta$ and $\lambda$ are positive constants, from Lemmas 2.6, 2.7 and Theorem 2.11, it yields:

$$\begin{aligned} \Vert U^{n}\Vert ^{2}+\delta \Vert U_{\tilde{x}}^{n}\Vert ^{2}+\lambda \Vert U_{\tilde{x}\bar{x}}^{n}\Vert ^{2}\le \Vert U^{n}\Vert ^{2} +\delta \Vert \mathfrak {R}_{1}U_{\tilde{x}}^{n}\Vert ^{2}+\lambda \Vert H_{1}U_{\tilde{x}\bar{x}}^{n}\Vert ^{2}=E^{0}_{1}. \end{aligned}$$

Therefore, we obtain:

$$\begin{aligned}&\Vert U^{n}\Vert \le \sqrt{E^{0}_{1}},\quad \Vert U^{n}_{\tilde{x}}\Vert \le \sqrt{\frac{E^{0}_{1}}{\delta }},\quad \Vert U^{n}_{\tilde{x}\bar{x}}\Vert \le \sqrt{\frac{E^{0}_{1}}{\lambda }},\quad \delta>0, \quad \lambda >0.&\end{aligned}$$

By Lemma 2.3, we obtain $\Vert U^{n}\Vert _{\infty }\le \tilde{C}$, $\Vert U_{\tilde{x}}^{n}\Vert _{\infty }\le \tilde{C}$, where:

$$\begin{aligned} \tilde{C}=\max \Bigg \{C_{1}\sqrt{E^{0}_{1}}+C_{2}\sqrt{\frac{E^{0}_{1}}{\delta }},~C_{1}\sqrt{\frac{E^{0}_{1}}{\delta }}+C_{2}\sqrt{\frac{E^{0}_{1}}{\lambda }}\Bigg \},\quad \delta>0, \quad \lambda >0. \end{aligned}$$

This completes the proof. $\square$

2.5 Solvability

To prove the solvability of the nonlinear compact finite-difference scheme in Eqs. (21)–(23), the following variant of Brouwer fixed point theorem will be used.

Lemma 2.13

[28,29,30] Let $({\mathcal {H}},\langle \cdot ,\cdot \rangle )$ be a finite-dimensional inner product space, $\Vert \cdot \Vert$ be the associated norm, and $g: {\mathcal {H}}\rightarrow {\mathcal {H}}$ be continuous. Assume that:

$$\begin{aligned}&\exists \xi>0,\quad \forall z\in {\mathcal {H}},\quad \Vert z\Vert =\xi ,\quad \langle g(z),z\rangle >0. \end{aligned}$$

Then, there exists a $z^{*}\in {\mathcal {H}}$, such that $g(z^{*})=0$ and $\Vert z^{*}\Vert \le \xi$.

Theorem 2.14

The compact finite-difference scheme (21)–(23) is solvable.

Proof

We know $U^{0}$ exists. To prove the theorem by using mathematical induction, we assume that $U^{1},\ldots ,U^{n}$ exist. For $n\ge 1$, we rewrite Eq. (21) in the form of:

$$\begin{aligned}&2(U^{n+\frac{1}{2}}-U^{n})+\beta H_{2}\Phi (U^{n+\frac{1}{2}},U^{n+\frac{1}{2}})+\gamma H_{1}H_{2}U^{n+\frac{1}{2}}_{\tilde{x}{\bar{x}}{\hat{x}}}-2\delta H_{1}(U^{n+\frac{1}{2}}-U^{n})_{\tilde{x}{\bar{x}}}\\&\quad +\alpha H_{2}U^{n+\frac{1}{2}}_{{\hat{x}}}+2\lambda H_{1}^{2}(U^{n+\frac{1}{2}}-U^{n})_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}}-\theta H_{1}^{2}H_{2}U^{n+\frac{1}{2}}_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}{\hat{x}}}=0. \end{aligned}$$

Let $g: R^{J}_{0}\rightarrow R^{J}_{0}$ defined by:

$$\begin{aligned}&g(V)=2(V-U^{n})+\beta H_{2}\Phi (V,V)+\gamma H_{1}H_{2}V_{\tilde{x}{\bar{x}}{\hat{x}}}-2\delta H_{1}(V-U^{n})_{\tilde{x}{\bar{x}}}\nonumber \\&\quad +\alpha H_{2}V_{{\hat{x}}}+2\lambda H_{1}^{2}(V-U^{n})_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}}-\theta H_{1}^{2}H_{2}V_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}{\hat{x}}}=0. \end{aligned}$$

(25)

Then, g is obviously continuous. Taking the inner product of Eq. (25) with V and using Lemmas 2.5, 2.8–2.10, we obtain:

$$\begin{aligned}&\langle H_{2}V_{{\hat{x}}},V\rangle =0,\quad \langle H_{1}H_{2}V_{\tilde{x}{\bar{x}}{\hat{x}}},V\rangle =0,\quad \langle H_{1}V_{\tilde{x}{\bar{x}}},V\rangle =-\Vert \mathfrak {R}_{1}V_{\tilde{x}}\Vert ^{2}, \end{aligned}$$

(26)

$$\begin{aligned}&\langle H_{2}\Phi (V,V),V\rangle =0,\quad \langle H_{1}^{2}H_{2}V_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}{\hat{x}}},V\rangle =0,\quad \langle H_{1}^{2}V_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}},V\rangle =\Vert H_{1}V_{\tilde{x}{\bar{x}}}\Vert ^{2}. \end{aligned}$$

(27)

Thus, from Eqs. (26) and (27) and Young’s inequality, we obtain:

$$\begin{aligned}&\langle g(V),V\rangle =2\Vert V\Vert ^{2}-2\langle U^{n},V\rangle +2\delta \Vert \mathfrak {R}_{1}V_{\tilde{x}}\Vert ^{2}+2\delta \langle H_{1}U^{n}_{\tilde{x}{\bar{x}}},V\rangle \\&\qquad +2\lambda \Vert H_{1}V_{\tilde{x}\bar{x}}\Vert ^{2}-2\lambda \langle H_{1}U^{n}_{\tilde{x}\bar{x}},H_{1}V_{\tilde{x}{\bar{x}}}\rangle \\&\quad \ge 2\Vert V\Vert ^{2}-(\Vert U^{n}\Vert ^{2}+\Vert V\Vert ^{2})+2\delta \Vert \mathfrak {R}_{1}V_{\tilde{x}}\Vert ^{2}-\delta (\Vert \mathfrak {R}_{1}U^{n}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{1}V_{\tilde{x}}\Vert ^{2})\\&\qquad +2\lambda \Vert H_{1}V_{\tilde{x}\bar{x}}\Vert ^{2}-2\lambda (\frac{1}{4}\Vert H_{1}U^{n}_{\tilde{x}\bar{x}}\Vert ^{2}+\Vert H_{1}V_{\tilde{x}{\bar{x}}}\Vert ^{2})\\&\quad \ge \Vert V\Vert ^{2}-(\Vert U^{n}\Vert ^{2}+\delta \Vert \mathfrak {R}_{1}U^{n}_{\tilde{x}}\Vert ^{2}+\frac{\lambda }{2}\Vert H_{1}U^{n}_{\tilde{x}\bar{x}}\Vert ^{2}),\quad \delta>0,\quad \lambda >0.&\end{aligned}$$

Hence, for:

$$\begin{aligned}&\Vert V\Vert ^{2}=\Vert U^{n}\Vert ^{2}+\delta \Vert \mathfrak {R}_{1}U^{n}_{\tilde{x}}\Vert ^{2}+\frac{\lambda }{2}\Vert H_{1}U^{n}_{\tilde{x}\bar{x}}\Vert ^{2}+1, \end{aligned}$$

then we have $\langle g(V),V\rangle >0$, and from Lemma 2.13, we deduce the existence of $V^{*}\in R_{0}^{J}$, such that $g(V^{*})=0$. Thus, the existence of $U^{n+1}=2V^{*}-U^{n}$ is obtained. This completes the proof. $\square$

2.6 Convergence and stability

Define the grid function $u^{n}_{j}=u(x_{j},t^{n})$, $\omega ^{n}_{j}=u^{n}_{j}-U^{n}_{j}$ and:

$$\begin{aligned}&V^{n}=(u^{n}_{1},u^{n}_{2},\ldots ,u^{n}_{J})^{\text {T}},\quad \Omega ^{n}=(\omega ^{n}_{1},\omega ^{n}_{2},\ldots ,\omega ^{n}_{J})^{\text {T}}, \quad R^{n}=(r^{n}_{1},r^{n}_{2},\ldots ,r^{n}_{J})^{\text {T}},&\end{aligned}$$

and then, the truncation errors of the scheme (21)–(23) satisfy:

$$\begin{aligned}&V^{n}_{\tilde{t}}+\alpha H_{2}V^{n+\frac{1}{2}}_{{\hat{x}}}+\beta H_{2}\Phi (V^{n+\frac{1}{2}},V^{n+\frac{1}{2}})+\gamma H_{1}H_{2}V^{n+\frac{1}{2}}_{\tilde{x}{\bar{x}}{\hat{x}}}-\delta H_{1}V^{n}_{\tilde{x}{\bar{x}}\tilde{t}}+\lambda H_{1}^{2}V^{n}_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}\tilde{t}}\nonumber \\&\quad -\theta H_{1}^{2}H_{2}V^{n+\frac{1}{2}}_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}{\hat{x}}}=R^{n},\quad n=0,1,2,\ldots ,N-1, \end{aligned}$$

(28)

$$\begin{aligned}&V^{0}=\Bigg (u_{0}(x_{1}),u_{0}(x_{2}),\ldots ,u_{0}(x_{J})\Bigg )^{\text {T}}, \end{aligned}$$

(29)

$$\begin{aligned}&u^{n}_{-1}=u^{n}_{0}=u^{n}_{1}=0,\quad u^{n}_{J-1}=u^{n}_{J}=u^{n}_{J+1}=0,\quad n=0,1,\ldots ,N. \end{aligned}$$

(30)

According to the Taylor expansion, we have:

$$\begin{aligned}&\mid r^{n}_{j}\mid \le C(\tau ^{2}+h^{4}),\quad j=1,2,\ldots ,J,\quad n=0,1,\ldots ,N.&\end{aligned}$$

Subtracting Eqs. (28)–(30) from Eqs. (21)–(23) and letting $\Omega ^{n}=V^{n}-U^{n}$, we obtain the following error equation:

$$\begin{aligned}&R^{n}=\Omega ^{n}_{\tilde{t}}+\alpha H_{2}\Omega ^{n+\frac{1}{2}}_{{\hat{x}}}+\beta H_{2} [\Phi (V^{n+\frac{1}{2}},V^{n+\frac{1}{2}})-\Phi (U^{n+\frac{1}{2}},U^{n+\frac{1}{2}})]+\gamma H_{1}H_{2}\Omega ^{n+\frac{1}{2}}_{\tilde{x}{\bar{x}}{\hat{x}}}\nonumber \\&\quad -\delta H_{1}\Omega ^{n}_{\tilde{x}{\bar{x}}\tilde{t}}+\lambda H_{1}^{2}\Omega ^{n}_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}\tilde{t}}-\theta H_{1}^{2}H_{2}\Omega ^{n+\frac{1}{2}}_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}{\hat{x}}},\quad n=1,2,\ldots ,N-1, \end{aligned}$$

(31)

where $\Omega ^{0}=0$.

Lemma 2.15

(See [24]) Assume that $\{S^{n}\}$ is a non-negative sequence and satisfies:

$$\begin{aligned} S^{0}\le A,\quad S^{n}\le A+B\tau \sum _{i=0}^{n-1}S^{i},\quad n=1,2,\ldots , \end{aligned}$$

where A and B are non-negative constants. Then, $S^{n}$ satisfies $S^{n}\le A{\text {e}}^{Bn\tau }$, $n=0,1,\ldots$.

Lemma 2.16

For $\Omega ^{n+\frac{1}{2}}=(\omega ^{n+\frac{1}{2}}_{1},\omega ^{n+\frac{1}{2}}_{2},\ldots ,\omega ^{n+\frac{1}{2}}_{J})^{\text {T}}$, we have:

$$\begin{aligned}&\langle H_{2} [\Phi (V^{n+\frac{1}{2}},{V}^{n+\frac{1}{2}})-\Phi (U^{n+\frac{1}{2}},{U}^{n+\frac{1}{2}})],{\Omega }^{n+\frac{1}{2}}\rangle \\&\quad \le C(\Vert \mathfrak {R}_{2}\Omega ^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n+1}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n}\Vert ^{2}).&\end{aligned}$$

Proof

According to Lemma 2.1, we obtain:

$$\begin{aligned}&\left\langle \left [ \phi \left( v^{n+\frac{1}{2}},{v}^{n+\frac{1}{2}}\right) -\phi \left( u^{n+\frac{1}{2}},{u}^{n+\frac{1}{2}}\right) \right] ,{\omega }^{n+\frac{1}{2}}\right\rangle \nonumber \\&\quad =\frac{h}{p+2}\sum ^{J-1}_{j=1}\left\{ \left( v^{n+\frac{1}{2}}_{j}\right) ^{p}\left( {v}^{n+\frac{1}{2}}_{j}\right) _{\hat{x}}-\left( u^{n+\frac{1}{2}}_{j}\right) ^{p}\left( {u}^{n+\frac{1}{2}}_{j}\right) _{\hat{x}}\right\} {\omega }_{j}^{n+\frac{1}{2}}\nonumber \\&\qquad +\frac{h}{p+2}\sum ^{J-1}_{j=1}\left\{ \left [ \left( v^{n+\frac{1}{2}}_{j}\right) ^{p}{v}^{n+\frac{1}{2}}_{j}\right] _{\hat{x}}-\left [ \left( u^{n+\frac{1}{2}}_{j}\right) ^{p}{u}^{n+\frac{1}{2}}_{j}\right] _{\hat{x}}\right\} {\omega }_{j}^{n+\frac{1}{2}}\nonumber \\&\quad =\frac{h}{p+2}\sum ^{J-1}_{j=1}\left\{ \left( v^{n+\frac{1}{2}}_{j}\right) ^{p}\left( {v}^{n+\frac{1}{2}}_{j}\right) _{\hat{x}}-\left( u^{n+\frac{1}{2}}_{j}\right) ^{p}\left( {u}^{n+\frac{1}{2}}_{j}\right) _{\hat{x}}\right\} {\omega }_{j}^{n+\frac{1}{2}}\nonumber \\&\qquad -\frac{h}{p+2}\sum ^{J-1}_{j=1}\left\{ \left( v^{n+\frac{1}{2}}_{j}\right) ^{p}{v}^{n+\frac{1}{2}}_{j}-\left( u^{n+\frac{1}{2}}_{j}\right) ^{p}{u}^{n+\frac{1}{2}}_{j}\right\} \left( {\omega }_{j}^{n+\frac{1}{2}}\right) _{\hat{x}}\nonumber \\&\quad =\frac{h}{p+2}\sum ^{J-1}_{j=1}\left\{ \left [ \left( v^{n+\frac{1}{2}}_{j}\right) ^{p}\left( {\omega }^{n+\frac{1}{2}}_{j}\right) _{\hat{x}}{\omega }_{j}^{n+\frac{1}{2}}\right] +\left( \left [ \left( v^{n+\frac{1}{2}}_{j}\right) ^{p}-\left( u^{n+\frac{1}{2}}_{j}\right) ^{p}\right] \left( {u}^{n+\frac{1}{2}}_{j}\right) _{\hat{x}}{\omega }_{j}^{n+\frac{1}{2}}\right) \right\} \nonumber \\&\qquad -\frac{h}{p+2}\sum ^{J-1}_{j=1}\left [ \left( v^{n+\frac{1}{2}}_{j}\right) ^{p}{\omega }^{n+\frac{1}{2}}_{j}\left( {\omega }_{j}^{n+\frac{1}{2}}\right) _{\hat{x}}\right] \nonumber \\&\qquad -\frac{h}{p+2}\sum ^{J-1}_{j=1}\left( \left [ \left( v^{n+\frac{1}{2}}_{j}\right) ^{p}-\left( u^{n+\frac{1}{2}}_{j}\right) ^{p}\right] {u}^{n+\frac{1}{2}}_{j}\left( {\omega }_{j}^{n+\frac{1}{2}}\right) _{\hat{x}}\right) . \end{aligned}$$

(32)

Note that:

$$\begin{aligned}&\sum ^{J-1}_{j=1}\Bigg \{\Bigg [\Bigg (v^{n+\frac{1}{2}}_{j}\Bigg )^{p}-\Bigg (u^{n+\frac{1}{2}}_{j}\Bigg )^{p}\Bigg ]\Bigg ({u}^{n+\frac{1}{2}}_{j}\Bigg )_{\hat{x}}{\omega }_{j}^{n+\frac{1}{2}}\Bigg \}\nonumber \\&\quad =\sum _{j=1}^{J}\Bigg \{\sum _{k=0}^{p-1}\Bigg [\Bigg (v_{j}^{n+\frac{1}{2}}\Bigg )^{p-1-k}\Bigg (u_{j}^{n+\frac{1}{2}}\Bigg )^{k}\Bigg ]\omega ^{n+\frac{1}{2}}_{j}\Bigg ({u}^{n+\frac{1}{2}}_{j}\Bigg )_{\hat{x}}{\omega }_{j}^{n+\frac{1}{2}}\Bigg \}, \end{aligned}$$

(33)

and

$$\begin{aligned}&\sum ^{J-1}_{j=1}\Bigg \{\Bigg [\Bigg (v^{n+\frac{1}{2}}_{j}\Bigg )^{p}-\Bigg (u^{n+\frac{1}{2}}_{j}\Bigg )^{p}]{u}^{n+\frac{1}{2}}_{j}\Bigg ({\omega }_{j}^{n+\frac{1}{2}}\Bigg )_{\hat{x}}\Bigg \}\nonumber \\&\quad =\sum _{j=1}^{J}\Bigg \{\sum _{k=0}^{p-1}\Bigg [\Bigg (v_{j}^{n+\frac{1}{2}}\Bigg )^{p-1-k}\Bigg (u_{j}^{n+\frac{1}{2}}\Bigg )^{k}\Bigg ]\omega ^{n+\frac{1}{2}}_{j}{u}^{n+\frac{1}{2}}_{j}\Bigg ({\omega }_{j}^{n+\frac{1}{2}}\Bigg )_{\hat{x}}\Bigg \}. \end{aligned}$$

(34)

It follows from the Cauchy–Schwarz inequality, Lemma 2.7, and Eqs. (32)–(34), and we obtain:

$$\begin{aligned}&\left| \left\langle \left [ \phi \left( v^{n+\frac{1}{2}},{v}^{n+\frac{1}{2}}\right) -\phi \left( u^{n+\frac{1}{2}},{u}^{n+\frac{1}{2}}\right) \right] ,{\omega }^{n+\frac{1}{2}}\right\rangle \right| \\&\quad \le C\left( \Vert {\omega }^{n+\frac{1}{2}}_{\hat{x}}\Vert ^{2}+\Vert {\omega }^{n+\frac{1}{2}}\Vert ^{2}\right) \le C\left( \Vert {\omega }^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert {\omega }^{n}_{\tilde{x}}\Vert ^{2}+\Vert {\omega }^{n+1}\Vert ^{2}+\Vert \omega ^{n}\Vert ^{2}\right) . \end{aligned}$$

Thus, applying Lemma 2.5, we have:

$$\begin{aligned}&\left\langle H_{2}\left [ \Phi \left( V^{n+\frac{1}{2}},{V}^{n+\frac{1}{2}}\right) -\Phi \left( U^{n+\frac{1}{2}},{U}^{n+\frac{1}{2}}\right) \right] ,{\Omega }^{n+\frac{1}{2}}\right\rangle \\&\quad \le C\left( \Vert \mathfrak {R}_{2}{\Omega }^{n+\frac{1}{2}}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{2}{\Omega }^{n+\frac{1}{2}}\Vert ^{2}\right) \\&\quad \le C(\Vert \mathfrak {R}_{2}\Omega ^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n+1}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n}\Vert ^{2}). \end{aligned}$$

This completes the proof. $\square$

Theorem 2.17

Assume that $u_{0}$ is sufficiently smooth and $u(x,t)\in C^{9,3}_{x,t}( [x_{l},x_{r}]\times [0,T])$, and then, the solution $U^{n}$ of the compact finite-difference scheme (21)–(23) converges to the solution of the problem (1)–(3) with the convergence rate of $O(\tau ^{2}+h^{4})$ in the sense of $\Vert \cdot \Vert$ and $\Vert \cdot \Vert _{\infty }$ norms.

Proof

Taking the inner product of Eq. (31) with 2$\Omega ^{n+\frac{1}{2}}$ and using Lemmas 2.2, 2.8–2.10, we have:

$$\begin{aligned}&\langle R^{n},2\Omega ^{n+\frac{1}{2}}\rangle = \Vert \Omega ^{n}\Vert ^{2}_{\tilde{t}}+\delta \Vert \mathfrak {R}_{1}\Omega ^{n}_{\tilde{x}}\Vert ^{2}_{\tilde{t}}+\lambda \Vert H_{1}\Omega ^{n}_{\tilde{x}\bar{x}}\Vert ^{2}_{\tilde{t}}\nonumber \\&\quad +\beta \langle H_{2} [\Phi (V^{n+\frac{1}{2}},{V}^{n+\frac{1}{2}})-\Phi (U^{n+\frac{1}{2}},{U}^{n+\frac{1}{2}})],2{\Omega }^{n+\frac{1}{2}}\rangle .&\end{aligned}$$

(35)

According to Lemmas 2.6, 2.7, and 2.16, we obtain:

$$\begin{aligned}&\langle H_{2} [\Phi (V^{n+\frac{1}{2}},{V}^{n+\frac{1}{2}})-\Phi (U^{n+\frac{1}{2}},{U}^{n+\frac{1}{2}})],2{\Omega }^{n+\frac{1}{2}}\rangle \nonumber \\&\quad \le C(\Vert \mathfrak {R}_{1}\Omega ^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Omega ^{n}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Omega ^{n+1}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Omega ^{n}\Vert ^{2})\nonumber \\&\quad \le C(\Vert \mathfrak {R}_{1}\Omega ^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Omega ^{n}_{\tilde{x}}\Vert ^{2}+\Vert \Omega ^{n+1}\Vert ^{2}+\Vert \Omega ^{n}\Vert ^{2}).&\end{aligned}$$

(36)

Furthermore, we have:

$$\begin{aligned} \langle R^{n},2\Omega ^{n+\frac{1}{2}}\rangle \le \Vert R^{n}\Vert ^{2}+\frac{1}{2}(\Vert \Omega ^{n+1}\Vert ^{2}+\Vert \Omega ^{n}\Vert ^{2}). \end{aligned}$$

(37)

Substituting Eqs. (36) and (37) into Eq. (35) gives:

$$\begin{aligned}&\Vert \Omega ^{n+1}\Vert ^{2}-\Vert \Omega ^{n}\Vert ^{2}+\delta (\Vert \mathfrak {R}_{1}\Omega ^{n+1}_{\tilde{x}}\Vert ^{2}-\Vert \mathfrak {R}_{1}\Omega ^{n}_{\tilde{x}}\Vert ^{2})+\lambda (\Vert H_{1}\Omega ^{n+1}_{\tilde{x}\bar{x}}\Vert ^{2}-\Vert H_{1}\Omega ^{n}_{\tilde{x}\bar{x}}\Vert ^{2})\nonumber \\&\quad \le C\tau (\Vert \mathfrak {R}_{1}\Omega ^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Omega ^{n}_{\tilde{x}}\Vert ^{2})+\Vert H_{1}\Omega ^{n+1}_{\tilde{x}\bar{x}}\Vert ^{2}+\Vert H_{1}\Omega ^{n}_{\tilde{x}\bar{x}}\Vert ^{2})\nonumber \\&\qquad +\tau \Vert R^{n}\Vert ^{2}+C\tau (\Vert \Omega ^{n+1}\Vert ^{2}+\Vert \Omega ^{n}\Vert ^{2}). \end{aligned}$$

(38)

Setting:

$$\begin{aligned} B_{1}^{n}\equiv \Vert \Omega ^{n}\Vert ^{2}+\delta \Vert \mathfrak {R}_{1}\Omega ^{n}_{\tilde{x}}\Vert ^{2}+\lambda \Vert H_{1}\Omega ^{n}_{\tilde{x}\bar{x}}\Vert ^{2}, \end{aligned}$$

we can obtain from Eq. (38) that:

$$\begin{aligned} B_{1}^{n}-B_{1}^{n-1}\le \tau \Vert R^{n}\Vert ^{2}+C\tau (B_{1}^{n}+B_{1}^{n-1}). \end{aligned}$$

Hence, we obtain:

$$\begin{aligned} (1-C\tau )(B_{1}^{n}-B_{1}^{n-1})\le \tau \Vert R^{n}\Vert ^{2}+2C\tau B_{1}^{n-1}. \end{aligned}$$

If $\tau$ is sufficiently small, such that $1-C\tau >0$, then we obtain:

$$\begin{aligned} B_{1}^{n}-B_{1}^{n-1}\le C\tau \Vert R^{n}\Vert ^{2}+2C\tau B_{1}^{n-1}. \end{aligned}$$

(39)

Summarizing Eq. (39) from 1 to n, we obtain:

$$\begin{aligned} B_{1}^{n}\le B_{1}^{0}+C\tau \sum _{l=1}^{n}\Vert R^{l}\Vert ^{2}+2C\tau \sum _{l=1}^{n}B_{1}^{l-1}, \end{aligned}$$

where

$$\begin{aligned} \tau \sum _{l=1}^{n}\Vert R^{l}\Vert ^{2}\le n\tau \max _{1\le l\le n}\Vert R^{l}\Vert ^{2}\le CT(\tau ^{2}+h^{4})^{2}. \end{aligned}$$

Since $\omega _{j}^{0}=0$, $j=1,2,\ldots ,J$, we have $B_{1}^{0}=0$. Therefore, from Lemma 2.15, we obtain $B_{1}^{n}\le C(\tau ^{2}+h^{4})^{2}$. This yields:

$$\begin{aligned} \Vert \Omega ^{n}\Vert \le C(\tau ^{2}+h^{4}),\quad \Vert \mathfrak {R}_{1}\Omega ^{n}_{\tilde{x}}\Vert \le C(\tau ^{2}+h^{4}),\quad \Vert H_{1}\Omega ^{n}_{\tilde{x}\bar{x}}\Vert \le C(\tau ^{2}+h^{4}). \end{aligned}$$

From Lemmas 2.6 and 2.7, we obtain:

$$\begin{aligned} \Vert \Omega ^{n}_{\tilde{x}}\Vert \le C(\tau ^{2}+h^{4}),\quad \Vert \Omega ^{n}_{\tilde{x}\bar{x}}\Vert \le C(\tau ^{2}+h^{4}). \end{aligned}$$

According to Lemma 2.3, we conclude that $\Vert \Omega ^{n}\Vert _{\infty }\le C(\tau ^{2}+h^{4})$. This completes the proof. $\square$

Theorem 2.18

Under the conditions of Theorem 2.17, the solution $U^{n}$ of compact finite-difference scheme (21)–(23) is unconditionally stable in the sense of $\Vert \cdot \Vert$ and $\Vert \cdot \Vert _{\infty }$ norms.

Proof

Suppose that there are solutions $U^{n}_{j}\in R_{0}^{J}$ and $\tilde{U}^{n}_{j}\in R_{0}^{J}$, which both satisfy the nonlinear finite-difference scheme in Eqs. (21)–(23), such that $U^{0}_{j}=u_{0}(x_{j})$ and $\tilde{U}^{0}_{j}=\tilde{u}_{0}(x_{j})$. Set $F^{n}_{j}=U^{n}_{j}-\tilde{U}^{n}_{j}$, $0\le j\le J$, $0\le n\le N$. Using a similar proof as that for Theorem 2.17, we conclude that:

$$\begin{aligned}&\Vert F^{n}\Vert \le C\Vert F^{0}\Vert ,\quad \Vert F^{n}\Vert _{\infty }\le C\Vert F^{0}\Vert _{\infty }.&\end{aligned}$$

This completes the proof. $\square$

2.7 Uniqueness

We now show the uniqueness of the numerical solution.

Theorem 2.19

The compact finite-difference scheme (21)–(23) has a unique solution.

Proof

Assume that both $U^{n}$ and $\tilde{U}^{n}$ satisfy the scheme (21)–(23), and let $\Theta ^{n}=U^{n}-\tilde{U}^{n}$, and then, we obtain:

$$\begin{aligned}&\Theta ^{n}_{\tilde{t}}+\alpha H_{2}\Theta ^{n+\frac{1}{2}}_{{\hat{x}}}+\beta H_{2} [\Phi (U^{n+\frac{1}{2}},U^{n+\frac{1}{2}})-\Phi (\tilde{U}^{n+\frac{1}{2}},\tilde{U}^{n+\frac{1}{2}})]+\gamma H_{1}H_{2}\Theta ^{n+\frac{1}{2}}_{\tilde{x}{\bar{x}}{\hat{x}}}\nonumber \\&\quad -\delta H_{1}\Theta ^{n}_{\tilde{x}{\bar{x}}\tilde{t}}+\lambda H_{1}^{2}\Theta ^{n}_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}\tilde{t}}-\theta H_{1}^{2}H_{2}\Theta ^{n+\frac{1}{2}}_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}{\hat{x}}},\quad n=0,1,2,\ldots ,N-1, \end{aligned}$$

(40)

$$\begin{aligned}&\Theta ^{0}_{j}=0,\quad 0\le j\le J, \end{aligned}$$

(41)

$$\begin{aligned}&\Theta ^{n}_{-1}=\Theta ^{n}_{0}=\Theta ^{n}_{1}=0,\quad \Theta ^{n}_{J-1}=\Theta ^{n}_{J}=\Theta ^{n}_{J+1}=0,\quad n=0,1,\ldots ,N.&\end{aligned}$$

(42)

Taking the inner product of Eq. (40) with $2\Theta ^{n+\frac{1}{2}}$ and using Lemmas 2.8–2.10, we obtain:

$$\begin{aligned}&\Vert \Theta ^{n}\Vert ^{2}_{\tilde{t}}+\delta \Vert \mathfrak {R}_{1}\Theta ^{n}_{\tilde{x}}\Vert ^{2}_{\tilde{t}}+\lambda \Vert H_{1}\Theta ^{n}_{\tilde{x}\bar{x}}\Vert ^{2}_{\tilde{t}}\\&\quad +\beta \langle H_{2} [\Phi (U^{n+\frac{1}{2}},{U}^{n+\frac{1}{2}})-\Phi (\tilde{U}^{n+\frac{1}{2}},\tilde{U}^{n+\frac{1}{2}})],2{\Theta }^{n+\frac{1}{2}}\rangle =0. \end{aligned}$$

From Lemmas 2.6, 2.7 and 2.16, we have:

$$\begin{aligned}&\Vert \Theta ^{n}\Vert ^{2}_{\tilde{t}}+\delta \Vert \mathfrak {R}_{1}\Theta ^{n}_{\tilde{x}}\Vert ^{2}_{\tilde{t}}+\lambda \Vert H_{1}\Theta ^{n}_{\tilde{x}\bar{x}}\Vert ^{2}_{\tilde{t}}\\&\quad \le C(\Vert \mathfrak {R}_{1}\Theta ^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Theta ^{n}_{\tilde{x}}\Vert ^{2}+\Vert \Theta ^{n+1}\Vert ^{2}+\Vert \Theta ^{n}\Vert ^{2})\\&\quad \le C(\Vert \Theta ^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert \Theta ^{n}_{\tilde{x}}\Vert ^{2}+\Vert \Theta ^{n+1}\Vert ^{2}+\Vert \Theta ^{n}\Vert ^{2}).&\end{aligned}$$

Applying Lemmas 2.6, 2.7, 2.15, and Eq. (42), we obtain that for $\tau$ small enough:

$$\begin{aligned} \Vert \Theta ^{n}\Vert ^{2}+\delta \Vert \Theta ^{n}_{\tilde{x}}\Vert ^{2}+\lambda \Vert \Theta ^{n}_{\tilde{x}\bar{x}}\Vert ^{2}=0,\quad \delta>0,\quad \lambda >0. \end{aligned}$$

This yields $\Theta ^{n+1}=0$; that is, Eq. (21) only admits a zero solution. Therefore, the compact finite-difference scheme in Eqs. (21)–(23) determines $U^{n+1}$ uniquely. This completes the proof. $\square$

Fig. 4

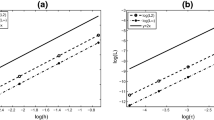
Spatial convergence order (left) and temporal convergence order (right) of Example 5.2 with different h and $\tau$ at $T=4$

Fig. 5

Absolute error distribution of Example 5.2 computed by Scheme A (left) and Scheme B (right) with $h=0.125$ and $\tau =h^{2}$ at $T=4$

Fig. 6

Numerical solutions of Example 5.2 computed by Scheme A (left) and Scheme B (right) with $h=0.25$ and $\tau =0.1$

Fig. 7

Wave surface of Examples 5.1 and 5.2 computed by Scheme A and Scheme B with $x_{l}=-40$, $x_{r}=60$ at $T=10$

3 Linearized compact difference scheme

3.1 Construction of linearized compact difference scheme

In this section, we construct a linearized compact finite-difference scheme for solving the system (12)–(14):

$$\begin{aligned}&(Y^{n}_{j})_{{\hat{t}}}=\bar{Z}^{n}_{j}+\bar{D}^{n}_{j},\quad {\mathcal {B}}_{x}\bar{D}^{n}_{j}=\alpha (\bar{U}^{n}_{j})_{{\hat{x}}}, \end{aligned}$$

(43)

$$\begin{aligned}&{\mathcal {A}}_{x}\bar{W}^{n}_{j}=(\bar{U}^{n}_{j})_{\tilde{x}\bar{x}},\quad {\mathcal {A}}_{x}\bar{G}^{n}_{j}=(\bar{W}^{n}_{j})_{\tilde{x}\bar{x}}, \end{aligned}$$

(44)

$$\begin{aligned}&{\mathcal {B}}_{x}\bar{Z}^{n}_{j}=\beta \phi (U^{n}_{j},\bar{U}^{n}_{j})+\gamma (\bar{W}^{n}_{j})_{\hat{x}}-\theta (\bar{G}^{n}_{j})_{\hat{x}}, \end{aligned}$$

(45)

$$\begin{aligned}&\phi (U^{n}_{j},\bar{U}^{n}_{j})=\frac{1}{p+2}\{(U^{n}_{j})^{p}(\bar{U}^{n}_{j})_{\hat{x}}+ [(U^{n}_{j})^{p}\bar{U}^{n}_{j}]_{\hat{x}} \}, \end{aligned}$$

(46)

$$\begin{aligned}&Y^{n}_{j}=-U^{n}_{j}+\delta W^{n}_{j}-\lambda G^{n}_{j}. \end{aligned}$$

(47)

From Eqs. (43)–(47), we have:

$$\begin{aligned}&{\mathcal {B}}_{x}(U^{n}_{j})_{{\hat{t}}}+\alpha (\bar{U}_{j}^{n})_{{\hat{x}}}+\beta \phi (U^{n}_{j},\bar{U}^{n}_{j})+\gamma {\mathcal {A}}^{-1}_{x} (\bar{U}^{n}_{j})_{\tilde{x}{\bar{x}}{\hat{x}}}-\delta {\mathcal {A}}^{-1}_{x}{\mathcal {B}}_{x} (U^{n}_{j})_{\tilde{x}{\bar{x}}{\hat{t}}}\nonumber \\&\quad +\lambda ({\mathcal {A}}^{-1}_{x})^{2}{\mathcal {B}}_{x}(U^{n}_{j})_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}{\hat{t}}}-\theta ({\mathcal {A}}^{-1}_{x})^{2} (\bar{U}^{n}_{j})_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}{\hat{x}}}=0, \end{aligned}$$

(48)

where $j=1,2,\ldots ,J$, $n=1,2,\ldots ,N-1$. Since the scheme (48) is a three-time-level method, to start the computation, we may get $U^{1}$ by the following two levels in time method (21) as:

$$\begin{aligned}&{\mathcal {B}}_{x}(U^{0}_{j})_{\tilde{t}}+\alpha (U_{j}^{\frac{1}{2}})_{{\hat{x}}}+\beta \phi (U^{\frac{1}{2}}_{j},U^{\frac{1}{2}}_{j})+\gamma {\mathcal {A}}^{-1}_{x} (U^{\frac{1}{2}}_{j})_{\tilde{x}{\bar{x}}{\hat{x}}}-\delta {\mathcal {A}}^{-1}_{x}{\mathcal {B}}_{x} (U^{0}_{j})_{\tilde{x}{\bar{x}}\tilde{t}}\nonumber \\&\quad +\lambda ({\mathcal {A}}^{-1}_{x})^{2}{\mathcal {B}}_{x}(U^{0}_{j})_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}\tilde{t}}-\theta ({\mathcal {A}}^{-1}_{x})^{2} (U^{\frac{1}{2}}_{j})_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}{\hat{x}}}=0,\quad j=1,2,\ldots ,J. \end{aligned}$$

(49)

The compact finite-difference scheme (48)–(49) can be rewritten in the following matrix form:

$$\begin{aligned}&U^{n}_{\hat{t}}+\alpha H_{2}\bar{U}^{n}_{{\hat{x}}}+\beta H_{2}\Phi (U^{n},\bar{U}^{n})+\gamma H_{1}H_{2}\bar{U}^{n}_{\tilde{x}{\bar{x}}{\hat{x}}}-\delta H_{1}U^{n}_{\tilde{x}{\bar{x}}{\hat{t}}}+\lambda H_{1}^{2}U^{n}_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}{\hat{t}}}\nonumber \\&\quad -\theta H_{1}^{2}H_{2}\bar{U}^{n}_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}{\hat{x}}}=0,\quad n=1,2,\ldots ,N-1, \end{aligned}$$

(50)

$$\begin{aligned}&U^{0}_{\tilde{t}}+\alpha H_{2}U^{\frac{1}{2}}_{{\hat{x}}}+\beta H_{2}\Phi (U^{\frac{1}{2}},U^{\frac{1}{2}})+\gamma H_{1}H_{2}U^{\frac{1}{2}}_{\tilde{x}{\bar{x}}{\hat{x}}}-\delta H_{1}U^{0}_{\tilde{x}{\bar{x}}\tilde{t}}+\lambda H_{1}^{2}U^{0}_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}\tilde{t}}\nonumber \\&\quad -\theta H_{1}^{2}H_{2}U^{\frac{1}{2}}_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}{\hat{x}}}=0, \end{aligned}$$

(51)

and the initial-boundary conditions are discretized as:

$$\begin{aligned}&U^{0}_{j}=u_{0}(x_{j}),\quad j=0,1,2,\ldots ,J, \end{aligned}$$

(52)

$$\begin{aligned}&U^{n}_{-1}=U^{n}_{0}=U^{n}_{1}=0,\quad U^{n}_{J-1}=U^{n}_{J}=U^{n}_{J+1}=0,\quad n=0,1,\ldots ,N, \end{aligned}$$

(53)

where:

$$\begin{aligned} \Phi (U^{n},\bar{U}^{n})=\Big [\phi (U_{1}^{n},\bar{U}_{1}^{n}),\phi (U_{2}^{n},\bar{U}_{2}^{n}),\ldots ,\phi (U_{n}^{n},\bar{U}_{n}^{n})\Big ]^{\text {T}}. \end{aligned}$$

3.2 Conservation

Theorem 3.1

The finite-difference scheme (50)–(53) is conservative in the sense of the discrete energy, that is:

$$\begin{aligned}&E_{2}^{n}\equiv \frac{1}{2}(\Vert U^{n+1}\Vert ^{2}+\Vert U^{n}\Vert ^{2}) +\frac{\delta }{2}(\Vert \mathfrak {R}_{1}U_{\tilde{x}}^{n+1}\Vert ^{2}+\Vert \mathfrak {R}_{1}U_{\tilde{x}}^{n}\Vert ^{2})+\frac{\lambda }{2}(\Vert H_{1}U_{\tilde{x}\bar{x}}^{n+1}\Vert ^{2}+\Vert H_{1}U_{\tilde{x}{\bar{x}}}^{n}\Vert ^{2})\\&\quad =E_{2}^{n-1}=\cdots =E_{2}^{0}\equiv \Vert U^{0}\Vert ^{2} +\delta \Vert \mathfrak {R}_{1}U_{\tilde{x}}^{0}\Vert ^{2}+\lambda \Vert H_{1}U_{\tilde{x}\bar{x}}^{0}\Vert ^{2}, \end{aligned}$$

where $\delta >0$, $\lambda >0$, $n=0,1,2,\ldots ,N-1$.

Proof

Computing the discrete inner product of Eq. (50) with 2$\bar{U}^{n}$, and from Lemmas 2.2, 2.5, 2.8–2.10, we obtain:

$$\begin{aligned}&\frac{1}{2\tau }\Vert U^{n+1}\Vert ^{2}+\frac{\delta }{2\tau }\Vert \mathfrak {R}_{1}U^{n+1}_{\tilde{x}}\Vert ^{2}+\frac{\lambda }{2\tau }\Vert H_{1}U^{n+1}_{\tilde{x}\bar{x}}\Vert ^{2} =\frac{1}{2\tau }\Vert U^{n-1}\Vert ^{2}+\frac{\delta }{2\tau }\Vert \mathfrak {R}_{1}U^{n-1}_{\tilde{x}}\Vert ^{2}+\frac{\lambda }{2\tau }\Vert H_{1}U^{n-1}_{\tilde{x}\bar{x}}\Vert ^{2}. \end{aligned}$$

Consequently, we obtain $E_{2}^{n}=E_{2}^{n-1}=\cdots =E_{2}^{0}$. Similarly, taking the inner product of Eq. (51) with $2U^{\frac{1}{2}}$ yields to:

$$\begin{aligned} \frac{1}{\tau }\Vert U^{1}\Vert ^{2}+\frac{\delta }{\tau }\Vert \mathfrak {R}_{1}U^{1}_{\tilde{x}}\Vert ^{2}+\frac{\lambda }{\tau }\Vert H_{1}U^{1}_{\tilde{x}\bar{x}}\Vert ^{2}=\frac{1}{\tau }\Vert U^{0}\Vert ^{2}+\frac{\delta }{\tau }\Vert \mathfrak {R}_{1}U^{0}_{\tilde{x}}\Vert ^{2}+\frac{\lambda }{\tau }\Vert H_{1}U^{0}_{\tilde{x}\bar{x}}\Vert ^{2}. \end{aligned}$$

Thus, we obtain:

$$\begin{aligned}&E_{2}^{0}=\Vert U^{0}\Vert ^{2} +\delta \Vert \mathfrak {R}_{1}U_{\tilde{x}}^{0}\Vert ^{2}+\lambda \Vert H_{1}U_{\tilde{x}\bar{x}}^{0}\Vert ^{2},\quad \delta>0,\quad \lambda >0.&\end{aligned}$$

This completes the proof. $\square$

3.3 Unique solvability

Theorem 3.2

The linearized compact finite-difference scheme (50)–(53) has a unique solution.

Proof

By the mathematical induction, it is obvious that $U^{0}$ and $U^{1}$ are uniquely solvable by Eqs. (52) and (51), respectively. Now, suppose that $U^{0}$, $U^{1} ,\ldots ,U^{n}$ are uniquely solved. Then, Eq. (50) is a linear system about $U^{n+1}$. By considering Eq. (50) for $U^{n+1}$, we have:

$$\begin{aligned}&\frac{1}{2\tau }U^{n+1}+\alpha H_{2}U^{n+1}_{{\hat{x}}}+\beta H_{2}\Phi (U^{n},U^{n+1})+\gamma H_{1}H_{2}U^{n+1}_{\tilde{x}\bar{x}{\hat{x}}}-\frac{\delta }{2\tau }H_{1}U^{n+1}_{\tilde{x}{\bar{x}}}\nonumber \\&\quad +\frac{\lambda }{2\tau }H_{1}^{2}U^{n+1}_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}}-\theta H_{1}^{2}H_{2}U^{n+1}_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}{\hat{x}}}=0,\quad n=1,2,\ldots ,N-1. \end{aligned}$$

(54)

Taking the inner product of Eq. (54) with $U^{n+1}$, we obtain from Lemmas 2.1, 2.8–2.10 that:

$$\begin{aligned} \frac{1}{2\tau }\Vert U^{n+1}\Vert ^{2}+\frac{\delta }{2\tau }\Vert \mathfrak {R}_{1}U^{n+1}_{\tilde{x}}\Vert ^{2}+\frac{\lambda }{2\tau }\Vert H_{1}U^{n+1}_{\tilde{x}\bar{x}}\Vert ^{2}=0,\quad \delta>0,\quad \lambda >0. \end{aligned}$$

This yields $U^{n+1}=0$; that is, Eq. (50) only admits a zero solution. Therefore, there exists a unique solution $U^{n+1}$ that satisfies Eqs. (50)–(53). This completes the proof. $\square$

3.4 A priori estimates

Theorem 3.3

Suppose that $u_{0}\in H_{0}^{2}( [x_{l},x_{r}])$, and then, the solution $U^{n}$ of the compact finite-difference scheme (50)–(53) satisfies:

$$\begin{aligned} \Vert U^{n}\Vert \le \sqrt{2E^{0}_{2}},\quad \Vert U^{n}_{\tilde{x}}\Vert \le \sqrt{\frac{2E^{0}_{2}}{\delta }}, \quad \Vert U^{n}_{\tilde{x}\bar{x}}\Vert \le \sqrt{\frac{2E^{0}_{2}}{\lambda }},\quad \delta>0,\quad \lambda >0, \end{aligned}$$

which yield $\Vert U^{n}\Vert _{\infty }\le C$ and $\Vert U_{\tilde{x}}^{n}\Vert _{\infty }\le C$ for any $0\le n\le N$.

Proof

By the assumption that $\delta$ and $\lambda$ are positive constants, from Lemmas 2.6, 2.7, and Theorem 3.1, we obtain:

$$\begin{aligned}&\Vert U^{n+1}\Vert ^{2}+\Vert U^{n}\Vert ^{2} +\delta (\Vert U_{\tilde{x}}^{n+1}\Vert ^{2}+\Vert U_{\tilde{x}}^{n}\Vert ^{2})+\lambda (\Vert U_{\tilde{x}\bar{x}}^{n+1}\Vert ^{2}+\Vert U_{\tilde{x}{\bar{x}}}^{n}\Vert ^{2})\\&\quad \le \Vert U^{n+1}\Vert ^{2}+\Vert U^{n}\Vert ^{2} +\delta (\Vert \mathfrak {R}_{1}U_{\tilde{x}}^{n+1}\Vert ^{2}+\Vert \mathfrak {R}_{1}U_{\tilde{x}}^{n}\Vert ^{2})+\lambda (\Vert H_{1}U_{\tilde{x}\bar{x}}^{n+1}\Vert ^{2}+\Vert H_{1}U_{\tilde{x}{\bar{x}}}^{n}\Vert ^{2})\\&\quad =2E^{n}_{2}=\cdots =2E^{0}_{2}. \end{aligned}$$

Therefore, we obtain:

$$\begin{aligned} \Vert U^{n}\Vert \le \sqrt{2E^{0}_{2}},\quad \Vert U^{n}_{\tilde{x}}\Vert \le \sqrt{\frac{2E^{0}_{2}}{\delta }}, \quad \Vert U^{n}_{\tilde{x}\bar{x}}\Vert \le \sqrt{\frac{2E^{0}_{2}}{\lambda }},\quad \delta>0,\quad \lambda >0. \end{aligned}$$

By Lemma 2.3, we obtain $\Vert U^{n}\Vert _{\infty }\le \bar{C}$, $\Vert U_{\tilde{x}}^{n}\Vert _{\infty }\le \bar{C}$, where:

$$\begin{aligned} \bar{C}=\max \Big \{C_{1}\sqrt{2E^{0}_{2}}+C_{2}\sqrt{\frac{2E^{0}_{2}}{\delta }}, \quad C_{1}\sqrt{\frac{2E^{0}_{2}}{\delta }}+C_{2}\sqrt{\frac{2E^{0}_{2}}{\lambda }}\Big \}. \end{aligned}$$

This completes the proof. $\square$

3.5 Convergence and stability

Lemma 3.4

For $\Omega ^{n}=(\omega ^{n}_{1},\omega ^{n}_{2},\ldots ,\omega ^{n}_{J})^{\text {T}}$, we have:

$$\begin{aligned}&\langle H_{2} [\Phi (V^{n},\bar{V}^{n})-\Phi (U^{n},\bar{U}^{n})],{{{\bar{\Omega }}}}^{n}\rangle \\&\quad \le C(\Vert \mathfrak {R}_{2}\Omega ^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n-1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n+1}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n-1}\Vert ^{2}).&\end{aligned}$$

Proof

Similar to Lemma 2.16, we obtain:

$$\begin{aligned}&\langle H_{2}(\Phi (V^{n},\bar{V}^{n})-\Phi (U^{n},\bar{U}^{n})),{{{\bar{\Omega }}}}^{n}\rangle \\&\quad \le C(\Vert \mathfrak {R}_{2}{\bar{\Omega }}^{n}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{2}{\bar{\Omega }}^{n}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n}\Vert ^{2})\\&\quad \le C(\Vert \mathfrak {R}_{2}\Omega ^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n-1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n+1}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n}\Vert ^{2}+\Vert \mathfrak {R}_{2}\Omega ^{n-1}\Vert ^{2}).&\end{aligned}$$

This completes the proof. $\square$

Theorem 3.5

Assume that $u_{0}$ is sufficiently smooth and $u(x,t)\in C^{9,3}_{x,t}( [x_{l},x_{r}]\times [0,T])$, and then, the solution $U^{n}$ of the compact finite-difference scheme (50)–(53) converges to the solution of the problem (1)–(3) with the convergence rate of $O(\tau ^{2}+h^{4})$ in the sense of $\Vert \cdot \Vert$ and $\Vert \cdot \Vert _{\infty }$ norms.

Proof

The truncation error equations of the compact finite-difference scheme in Eqs. (50)–(53) are:

$$\begin{aligned}&R^{n}=\Omega ^{n}_{{\hat{t}}}+\alpha H_{2}{\bar{\Omega }}^{n}_{{\hat{x}}}+\beta H_{2} [\Phi (V^{n},\bar{V}^{n})-\Phi (U^{n},\bar{U}^{n})]+\gamma H_{1}H_{2}{\bar{\Omega }}^{n}_{\tilde{x}{\bar{x}}{\hat{x}}}-\delta H_{1}\Omega ^{n}_{\tilde{x}{\bar{x}}{\hat{t}}}\nonumber \\&\qquad +\lambda H_{1}^{2}\Omega ^{n}_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}{\hat{t}}}-\theta H_{1}^{2}H_{2}{\bar{\Omega }}^{n}_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}{\hat{x}}},\quad n=1,2,\ldots ,N-1, \end{aligned}$$

(55)

$$\begin{aligned}&R^{0}=\Omega ^{0}_{\tilde{t}}+\alpha H_{2}\Omega ^{\frac{1}{2}}_{{\hat{x}}}+\beta H_{2} [\Phi (V^{\frac{1}{2}},V^{\frac{1}{2}})-\Phi (U^{\frac{1}{2}},U^{\frac{1}{2}})]+\gamma H_{1}H_{2}\Omega ^{\frac{1}{2}}_{\tilde{x}{\bar{x}}{\hat{x}}}-\delta H_{1}\Omega ^{0}_{\tilde{x}{\bar{x}}\tilde{t}}\nonumber \\&\qquad +\lambda H_{1}^{2}\Omega ^{0}_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}\tilde{t}}-\theta H_{1}^{2}H_{2}\Omega ^{\frac{1}{2}}_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}{\hat{x}}}. \end{aligned}$$

(56)

Taking the inner product of Eq. (55) with 2${{{\bar{\Omega }}}}^{n}$ and using Lemmas 2.2, 2.9, and 2.10, we have:

$$\begin{aligned}&2\langle R^{n},{{{\bar{\Omega }}}}^{n}\rangle = \Vert \Omega ^{n}\Vert ^{2}_{{\hat{t}}}+\delta \Vert \mathfrak {R}_{1}\Omega ^{n}_{\tilde{x}}\Vert ^{2}_{{\hat{t}}}+\lambda \Vert H_{1}\Omega ^{n}_{\tilde{x}\bar{x}}\Vert ^{2}_{{\hat{t}}}\nonumber \\&\qquad +\beta \langle H_{2} [\Phi (V^{n},\bar{V}^{n})-\Phi (U^{n},\bar{U}^{n})],2{{{\bar{\Omega }}}}^{n}\rangle . \end{aligned}$$

(57)

According to the Cauchy–Schwarz inequality and Lemmas 2.6, 2.7, and 3.4, we obtain:

$$\begin{aligned}&\langle H_{2} [\Phi (V^{n},\bar{V}^{n})-\Phi (U^{n},\bar{U}^{n})],2{{{\bar{\Omega }}}}^{n}\rangle \nonumber \\&\quad \le C(\Vert \mathfrak {R}_{1}\Omega ^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Omega ^{n-1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Omega ^{n+1}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Omega ^{n}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Omega ^{n-1}\Vert ^{2})\nonumber \\&\quad \le C(\Vert \mathfrak {R}_{1}\Omega ^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Omega ^{n-1}_{\tilde{x}}\Vert ^{2}+\Vert \Omega ^{n+1}\Vert ^{2}+\Vert \Omega ^{n}\Vert ^{2}+\Vert \Omega ^{n-1}\Vert ^{2}),&\end{aligned}$$

(58)

and

$$\begin{aligned} \langle R^{n},2{{{\bar{\Omega }}}}^{n}\rangle \le \frac{1}{2}\Vert R^{n}\Vert ^{2}+\Vert \Omega ^{n+1}\Vert ^{2}+\Vert \Omega ^{n-1}\Vert ^{2}. \end{aligned}$$

(59)

Substituting Eqs. (58) and (59) into Eq. (57) gives:

$$\begin{aligned}&\Vert \Omega ^{n+1}\Vert ^{2}-\Vert \Omega ^{n-1}\Vert ^{2}+\delta (\Vert \mathfrak {R}_{1}\Omega ^{n+1}_{\tilde{x}}\Vert ^{2}-\Vert \mathfrak {R}_{1}\Omega ^{n-1}_{\tilde{x}}\Vert ^{2})+\lambda (\Vert H_{1}\Omega ^{n+1}_{\tilde{x}\bar{x}}\Vert ^{2}-\Vert H_{1}\Omega ^{n-1}_{\tilde{x}\bar{x}}\Vert ^{2})\nonumber \\&\quad \le 2\tau \Vert R^{n}\Vert ^{2}+C\tau (\Vert \Omega ^{n+1}\Vert ^{2}+\Vert \Omega ^{n}\Vert ^{2}+\Vert \Omega ^{n-1}\Vert ^{2})+\Vert \mathfrak {R}_{1}\Omega ^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Omega ^{n}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Omega ^{n-1}_{\tilde{x}}\Vert ^{2})\nonumber \\&\qquad +C\tau (\Vert H_{1}\Omega ^{n+1}_{\tilde{x}\bar{x}}\Vert ^{2}+\Vert H_{1}\Omega ^{n}_{\tilde{x}\bar{x}}\Vert ^{2}+\Vert H_{1}\Omega ^{n-1}_{\tilde{x}\bar{x}}\Vert ^{2}).\nonumber \\ \end{aligned}$$

(60)

Setting

$$\begin{aligned} B_{2}^{n}\equiv \Vert \Omega ^{n+1}\Vert ^{2}+\Vert \Omega ^{n}\Vert ^{2}+\delta (\Vert \mathfrak {R}_{1}\Omega ^{n+1}_{\tilde{x}}\Vert ^{2}+\Vert \mathfrak {R}_{1}\Omega ^{n}_{\tilde{x}}\Vert ^{2})+\lambda (\Vert H_{1}\Omega ^{n+1}_{\tilde{x}\bar{x}}\Vert ^{2}+\Vert H_{1}\Omega ^{n}_{\tilde{x}\bar{x}}\Vert ^{2}), \end{aligned}$$

we can obtain from Eq. (60) that:

$$\begin{aligned} B_{2}^{n}-B_{2}^{n-1}\le 2\tau \Vert R^{n}\Vert ^{2}+C\tau (B_{2}^{n}+B_{2}^{n-1}). \end{aligned}$$

Hence, we obtain:

$$\begin{aligned} (1-C\tau )(B_{2}^{n}-B_{2}^{n-1})\le 2\tau \Vert R^{n}\Vert ^{2}+2C\tau B_{2}^{n-1}. \end{aligned}$$

If $\tau$ is sufficiently small, such that $1-C\tau >0$, then we obtain:

$$\begin{aligned} B_{2}^{n}-B_{2}^{n-1}\le C\tau \Vert R^{n}\Vert ^{2}+C\tau B_{2}^{n-1}. \end{aligned}$$

(61)

Summarizing Eq. (61) from 1 to n, we obtain:

$$\begin{aligned} B_{2}^{n}\le B_{2}^{0}+C\tau \sum _{l=1}^{n}\Vert R^{l}\Vert ^{2}+C\tau \sum _{l=1}^{n}B_{2}^{l-1}, \end{aligned}$$

where

$$\begin{aligned} \tau \sum _{l=1}^{n}\Vert R^{l}\Vert ^{2}\le n\tau \max _{1\le l\le n}\Vert R^{l}\Vert ^{2}\le CT(\tau ^{2}+h^{4})^{2}. \end{aligned}$$

Since $\omega _{j}^{0}=0$, $j=1,2,\ldots ,J$, we have from Lemma 2.6 that:

$$\begin{aligned} B_{2}^{0}=\Vert \Omega ^{1}\Vert ^{2}+\delta \Vert \mathfrak {R}_{1}\Omega ^{1}_{\tilde{x}}\Vert ^{2}+\lambda \Vert H_{1}\Omega ^{1}_{\tilde{x}\bar{x}}\Vert ^{2}\le C(\Vert \Omega ^{1}\Vert ^{2}+\delta \Vert \Omega ^{1}_{\tilde{x}}\Vert ^{2}+\lambda \Vert \Omega ^{1}_{\tilde{x}\bar{x}}\Vert ^{2}), \end{aligned}$$

where $\delta >0$, $\lambda >0$. Taking the inner product of Eq. (56) with 2${\Omega }^{\frac{1}{2}}$, and using a similar argument in Theorem 2.17, we obtain $B_{2}^{0}\le C(\tau ^{2}+h^{4})^{2}$. Therefore, from Lemma 2.16, we obtain $B_{2}^{n}\le C(\tau ^{2}+h^{4})^{2}$. This yield:

$$\begin{aligned} \Vert \Omega ^{n}\Vert \le C(\tau ^{2}+h^{4}),\quad \Vert \mathfrak {R}_{1}\Omega ^{n}_{\tilde{x}}\Vert \le C(\tau ^{2}+h^{4}),\quad \Vert H_{1}\Omega ^{n}_{\tilde{x}\bar{x}}\Vert \le C(\tau ^{2}+h^{4}). \end{aligned}$$

From Lemmas 2.6 and 2.7, we obtain:

$$\begin{aligned} \Vert \Omega ^{n}_{\tilde{x}}\Vert \le C(\tau ^{2}+h^{4}),\quad \Vert \Omega ^{n}_{\tilde{x}\bar{x}}\Vert \le C(\tau ^{2}+h^{4}). \end{aligned}$$

According to Lemma 2.3, we conclude that $\Vert \Omega ^{n}\Vert _{\infty }\le C(\tau ^{2}+h^{4})$. This completes the proof. $\square$

Using a similar argument, we can prove stability of the difference solution (50)–(53).

Theorem 3.6

Under the conditions of Theorem 3.5, the solution $U^{n}$ of compact finite-difference scheme (50)–(53) is unconditionally stable in the sense of $\Vert \cdot \Vert$ and $\Vert \cdot \Vert _{\infty }$ norms.

Fig. 8

Wave surface of Examples 5.1 and 5.2 computed by Scheme A and Scheme B with $x_{l}=-40$, $x_{r}=160$ at $T=20$

Fig. 9

Interaction of two solitary waves of Example 5.3 computed by Scheme A and Scheme B with $x_{l}=-200$, $x_{r}=300$ at $T=0$, 5, 10, 15, 20, and 25, respectively

4 Iterative algorithm

In this section, we give an approximate solution of nonlinear system (21)–(23) using an iterative method such as the techniques in Refs. [31, 32]. For fixed n, Eq. (20) can be written as follows:

$$\begin{aligned}&\frac{2}{\tau }{\mathcal {B}}_{x}\left( U^{n+\frac{1}{2}}_{j}-U^{n}_{j}\right) +\alpha \left( U_{j}^{n+\frac{1}{2}}\right) _{{\hat{x}}}+\beta \phi \left( U^{n+\frac{1}{2}}_{j},U^{n+\frac{1}{2}}_{j}\right) +\gamma {\mathcal {A}}^{-1}_{x} \left( U^{n+\frac{1}{2}}_{j}\right) _{\tilde{x}{\bar{x}}{\hat{x}}}\nonumber \\&\quad -\frac{2}{\tau }\delta {\mathcal {A}}^{-1}_{x}{\mathcal {B}}_{x} \left [ \left( U^{n+\frac{1}{2}}_{j}\right) _{\tilde{x}\bar{x}}-\left( U^{n}_{j}\right) _{\tilde{x}\bar{x}}\right] +\frac{2}{\tau }\lambda \left( {\mathcal {A}}^{-1}_{x}\right) ^{2}{\mathcal {B}}_{x}\left [ \left( U^{n+\frac{1}{2}}_{j}\right) _{\tilde{x}\bar{x}\tilde{x}{\bar{x}}}-(U^{n}_{j})_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}}\right] \nonumber \\&\quad -\theta \left( {\mathcal {A}}^{-1}_{x}\right) ^{2} \left( U^{n+\frac{1}{2}}_{j}\right) _{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}{\hat{x}}}=0,\quad n\ge 1,\quad j=2,\ldots ,J-2, \end{aligned}$$

(62)

which can be computed by the following iterative method:

$$\begin{aligned}&\frac{2}{\tau }{\mathcal {B}}_{x}(U^{n+\frac{1}{2}(i+1)}_{j}-U^{n}_{j})+\alpha (U_{j}^{n+\frac{1}{2}(i+1)})_{{\hat{x}}}+\beta \phi (U^{n+\frac{1}{2}(i)}_{j},U^{n+\frac{1}{2}(i)}_{j})+\gamma {\mathcal {A}}^{-1}_{x} (U^{n+\frac{1}{2}(i+1)}_{j})_{\tilde{x}{\bar{x}}{\hat{x}}}\nonumber \\&\quad -\frac{2}{\tau }\delta {\mathcal {A}}^{-1}_{x}{\mathcal {B}}_{x} [(U^{n+\frac{1}{2}(i+1)}_{j})_{\tilde{x}\bar{x}}-(U^{n}_{j})_{\tilde{x}\bar{x}}]+\frac{2}{\tau }\lambda ({\mathcal {A}}^{-1}_{x})^{2}{\mathcal {B}}_{x} [(U^{n+\frac{1}{2}(i+1)}_{j})_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}}-(U^{n}_{j})_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}}]\nonumber \\&\quad -\theta ({\mathcal {A}}^{-1}_{x})^{2} (U^{n+\frac{1}{2}(i+1)}_{j})_{\tilde{x}{\bar{x}}\tilde{x}{\bar{x}}{\hat{x}}}=0,\quad n\ge 1,\quad i=0,1,2,\ldots ,\quad j=2,\ldots ,J-2, \end{aligned}$$

(63)

where:

$$\begin{aligned}&U^{n+\frac{1}{2}(0)}_{j}=\left\{ \begin{array}{ll} U^{0}_{j},&{} n=0,\\ \frac{3}{2}U^{n}_{j}-\frac{1}{2}U^{n-1}_{j},&{} n\ge 1.\\ \end{array} \right.&\end{aligned}$$

Theorem 4.1

The iterative method (63) converges to the solution of the nonlinear compact difference scheme (20).

Proof

Let

$$\begin{aligned} \varepsilon ^{n+\frac{1}{2}(i)}_{j}=U^{n+\frac{1}{2}}_{j}-U^{n+\frac{1}{2}(i)}_{j},\quad i=0,1,2,\ldots ,\quad j=2,\ldots ,J-2, \end{aligned}$$

when $n=0$, we have:

$$\begin{aligned}&\varepsilon ^{n+\frac{1}{2}(0)}_{j}=U^{n+\frac{1}{2}}_{j}-U^{n+\frac{1}{2}(0)}_{j}=\frac{1}{2}(U^{n+1}_{j}+U^{n}_{j})-U^{n}_{j}=\frac{1}{2}(U^{n+1}_{j}-U^{n}_{j})\nonumber \\&\quad =\frac{1}{2}(U^{n+1}_{j}-v^{n+1}_{j})+\frac{1}{2}(v^{n+1}_{j}-v^{n}_{j})+\frac{1}{2}(v^{n}_{j}-U^{n}_{j})\nonumber \\&\quad =\frac{1}{2} [O(\tau ^{2}+h^{4})+O(\tau )+O(\tau ^{2}+h^{4})]=O(\tau +h^{4}).&\end{aligned}$$

(64)

If $n\ge 1$, we have:

$$\begin{aligned}&\varepsilon ^{n+\frac{1}{2}(0)}_{j}=U^{n+\frac{1}{2}}_{j}-U^{n+\frac{1}{2}(0)}_{j}\nonumber \\&\quad =\frac{1}{2}(U^{n+1}_{j}+U^{n}_{j})--(\frac{3}{2}U^{n}_{j}-\frac{1}{2}U^{n-1}_{j})=\frac{1}{2}(U^{n+1}_{j}-2U^{n}_{j}+U^{n-1}_{j})\nonumber \\&\quad =\frac{1}{2}(U^{n+1}_{j}-v^{n+1}_{j})+\frac{1}{2}(v^{n+1}_{j}-2v^{n}_{j}+v^{n-1}_{j})--(U^{n}_{j}-v^{n}_{j})+\frac{1}{2}(U^{n-1}_{j}-v^{n-1}_{j})\nonumber \\&\quad =O(\tau ^{2}+h^{4})+O(\tau ^{2})+O(\tau ^{2}+h^{4})+O(\tau ^{2}+h^{4})=O(\tau ^{2}+h^{4}). \end{aligned}$$

(65)

From Eqs. (64), (65), we have:

$$\begin{aligned}&\Vert \varepsilon ^{n+\frac{1}{2}(0)}\Vert _{\infty }=\left\{ \begin{aligned} O(\tau +h^{4}),\quad n=0,\\ O(\tau ^{2}+h^{4}),\quad n\ge 1.\\ \end{aligned} \right.&\end{aligned}$$

Therefore, for sufficiently small h and $\tau$, we have:

$$\begin{aligned}&\Vert \varepsilon ^{n+\frac{1}{2}(0)}\Vert _{\infty }\le \frac{1}{2}, \quad n=0,1,2,\ldots ,N-1.&\end{aligned}$$

Now, suppose that $\Vert \varepsilon ^{n+\frac{1}{2}(i)}\Vert _{\infty }\le \frac{1}{2}$. It follows from Theorem 2.11 that:

$$\begin{aligned} \Vert U^{n+\frac{1}{2}(i)}\Vert _{\infty }=\Vert U^{n+\frac{1}{2}}-\varepsilon ^{n+\frac{1}{2}(i)}\Vert _{\infty }\le \Vert U^{n+\frac{1}{2}}\Vert _{\infty }+\Vert \varepsilon ^{n+\frac{1}{2}(i)}\Vert _{\infty }\le C. \end{aligned}$$

Subtracting Eq. (63) from Eq. (62), we obtain:

$$\begin{aligned}&\frac{2}{\tau }{\mathcal {B}}_{x}\varepsilon ^{n+\frac{1}{2}(i+1)}_{j}+\alpha (\varepsilon _{j}^{n+\frac{1}{2}(i+1)})_{{\hat{x}}}+\beta \Big [\phi (U^{n+\frac{1}{2}}_{j},U^{n+\frac{1}{2}}_{j})-\phi (U^{n+\frac{1}{2}(i)}_{j},U^{n+\frac{1}{2}(i)}_{j})\Big ]\\&\quad +\gamma {\mathcal {A}}^{-1}_{x} (\varepsilon ^{n+\frac{1}{2}(i+1)}_{j})_{\tilde{x}{\bar{x}}{\hat{x}}}-\frac{2}{\tau }\delta {\mathcal {A}}^{-1}_{x}{\mathcal {B}}_{x} (\varepsilon ^{n+\frac{1}{2}(i+1)}_{j})_{\tilde{x}\bar{x}}+\frac{2}{\tau }\lambda ({\mathcal {A}}^{-1}_{x})^{2}{\mathcal {B}}_{x}(\varepsilon ^{n+\frac{1}{2}(i+1)}_{j})_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}}\\&\quad -\theta ({\mathcal {A}}^{-1}_{x})^{2} (\varepsilon ^{n+\frac{1}{2}(i+1)}_{j})_{\tilde{x}{\bar{x}}\tilde{x}\bar{x}{\hat{x}}}=0,\quad n\ge 1,\quad i=0,1,2,\ldots , \end{aligned}$$

which can be rewritten into the following matrix form:

$$\begin{aligned}&\frac{2}{\tau }\varepsilon ^{n+\frac{1}{2}(i+1)}+\alpha H_{2}(\varepsilon ^{n+\frac{1}{2}(i+1)})_{{\hat{x}}}+\beta H_{2}\Big [\Phi (U^{n+\frac{1}{2}},U^{n+\frac{1}{2}})-\Phi (U^{n+\frac{1}{2}(i)},U^{n+\frac{1}{2}(i)})\Big ]\nonumber \\&\quad +\gamma H_{1}H_{2} (\varepsilon ^{n+\frac{1}{2}(i+1)})_{\tilde{x}{\bar{x}}{\hat{x}}}-\frac{2}{\tau }\delta H_{1} (\varepsilon ^{n+\frac{1}{2}(i+1)})_{\tilde{x}\bar{x}}+\frac{2}{\tau }\lambda H_{1}^{2}(\varepsilon ^{n+\frac{1}{2}(i+1)})_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}}\nonumber \\&\quad -\theta H_{1}^{2}H_{2}(\varepsilon ^{n+\frac{1}{2}(i+1)})_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}{\hat{x}}}=0,\quad n\ge 1,\quad i=0,1,2,\ldots .&\end{aligned}$$

(66)

Computing the inner product of Eq. (66) with $\varepsilon ^{n+\frac{1}{2}(i+1)}$ and using Lemmas 2.1, 2.2, 2.5, 2.8–2.10, we obtain:

$$\begin{aligned}&\langle \varepsilon ^{n+\frac{1}{2}(i+1)},\varepsilon ^{n+\frac{1}{2}(i+1)}\rangle =\Vert \varepsilon ^{n+\frac{1}{2}(i+1)}\Vert ^{2}, \end{aligned}$$

(67)

$$\begin{aligned}&\langle H_{2}\varepsilon ^{n+\frac{1}{2}(i+1)}_{{\hat{x}}},\varepsilon ^{n+\frac{1}{2}(i+1)}\rangle =0, \end{aligned}$$

(68)

$$\begin{aligned}&\langle H_{1}H_{2} \varepsilon ^{n+\frac{1}{2}(i+1)}_{\tilde{x}\bar{x}{\hat{x}}},\varepsilon ^{n+\frac{1}{2}(i+1)}\rangle =0, \end{aligned}$$

(69)

$$\begin{aligned}&\langle H_{1}\varepsilon ^{n+\frac{1}{2}(i+1)}_{\tilde{x}\bar{x}},\varepsilon ^{n+\frac{1}{2}(i+1)}\rangle =-\Vert \mathfrak {R}_{1}\varepsilon ^{n+\frac{1}{2}(i+1)}_{\tilde{x}}\Vert ^{2}, \end{aligned}$$

(70)

$$\begin{aligned}&\langle H_{1}^{2}\varepsilon ^{n+\frac{1}{2}(i+1)}_{\tilde{x}\bar{x}\tilde{x}\bar{x}},\varepsilon ^{n+\frac{1}{2}(i+1)}\rangle =\Vert H_{1}\varepsilon ^{n+\frac{1}{2}(i+1)}_{\tilde{x}\bar{x}}\Vert ^{2}, \end{aligned}$$

(71)

$$\begin{aligned}&\langle H_{1}^{2}H_{2}\varepsilon ^{n+\frac{1}{2}(i+1)}_{\tilde{x}\bar{x}\tilde{x}{\bar{x}}{\hat{x}}},\varepsilon ^{n+\frac{1}{2}(i+1)}\rangle =0. \end{aligned}$$

(72)

As shown by Thomee and Murthy [33], we obtain:

$$\begin{aligned} \Vert [\Phi (U^{n+\frac{1}{2}},U^{n+\frac{1}{2}})-\Phi (U^{n+\frac{1}{2}(i)},U^{n+\frac{1}{2}(i)})]\Vert \le Ch^{-1}\Vert \varepsilon ^{n+\frac{1}{2}(i)}\Vert . \end{aligned}$$

(73)

Thus, from Eq. (73), Lemma 2.6 and the Cauchy–Schwarz inequality, we have:

$$\begin{aligned}&\langle H_{2} [\Phi (U^{n+\frac{1}{2}},U^{n+\frac{1}{2}})-\Phi (U^{n+\frac{1}{2}(i)},U^{n+\frac{1}{2}(i)})],\varepsilon ^{n+\frac{1}{2}(i+1)}\rangle \nonumber \\&\quad \le C\{\Vert [\Phi (U^{n+\frac{1}{2}},U^{n+\frac{1}{2}})-\Phi (U^{n+\frac{1}{2}(i)},U^{n+\frac{1}{2}(i)})]\Vert ^{2}+\Vert \varepsilon ^{n+\frac{1}{2}(i+1)}\Vert ^{2}\}\nonumber \\&\quad \le C(h^{-1}\Vert \varepsilon ^{n+\frac{1}{2}(i)}\Vert ^{2}+\Vert \varepsilon ^{n+\frac{1}{2}(i+1)}\Vert ^{2}). \end{aligned}$$

(74)

From Eqs. (66)–(72) and (74), we obtain:

$$\begin{aligned}&\Vert \varepsilon ^{n+\frac{1}{2}(i+1)}\Vert ^{2}+\delta \Vert \mathfrak {R}_{1}\varepsilon ^{n+\frac{1}{2}(i+1)}_{\tilde{x}}\Vert ^{2}+\lambda \Vert H_{1}\varepsilon ^{n+\frac{1}{2}(i+1)}_{\tilde{x}\bar{x}}\Vert ^{2}\nonumber \\&\quad \le C\tau \langle H_{2} [\Phi (U^{n+\frac{1}{2}(i)},U^{n+\frac{1}{2}(i)})-\Phi (U^{n+\frac{1}{2}},U^{n+\frac{1}{2}})],\varepsilon ^{n+\frac{1}{2}(i+1)}\rangle \nonumber \\&\quad \le C\tau (h^{-1}\Vert \varepsilon ^{n+\frac{1}{2}(i)}\Vert ^{2}+\Vert \varepsilon ^{n+\frac{1}{2}(i+1)}\Vert ^{2}), \end{aligned}$$

(75)

which yields:

$$\begin{aligned} (1-C\tau )\Vert \varepsilon ^{n+\frac{1}{2}(i+1)}\Vert ^{2}\le C\tau h^{-1}\Vert \varepsilon ^{n+\frac{1}{2}(i)}\Vert ^{2}; \end{aligned}$$

hence, for $1-C\tau \ge \frac{1}{2}$, we obtain:

$$\begin{aligned}&\Vert \varepsilon ^{n+\frac{1}{2}(i+1)}\Vert ^{2}\le 2C\tau h^{-1}\Vert \varepsilon ^{n+\frac{1}{2}(i)}\Vert ^{2}.&\end{aligned}$$

(76)

It follows from Lemma 2.6 and Eqs. (75)–(76) that:

$$\begin{aligned}&\Vert \varepsilon ^{n+\frac{1}{2}(i+1)}_{\tilde{x}}\Vert ^{2}\le \Vert \mathfrak {R}_{1}\varepsilon ^{n+\frac{1}{2}(i+1)}_{\tilde{x}}\Vert ^{2} \nonumber \\&\quad \le C\tau (h^{-1}\Vert \varepsilon ^{n+\frac{1}{2}(i)}\Vert ^{2}+\Vert \varepsilon ^{n+\frac{1}{2}(i+1)}\Vert ^{2})\le C\tau h^{-1}\Vert \varepsilon ^{n+\frac{1}{2}(i)}\Vert ^{2}. \end{aligned}$$

(77)

Applying Lemma 2.4 with Eqs. (76)–(77), we obtain:

$$\begin{aligned} \Vert \varepsilon ^{n+\frac{1}{2}(i+1)}\Vert ^{2}_{\infty }\le C\tau h^{-1}\Vert \varepsilon ^{n+\frac{1}{2}(i)}\Vert ^{2}\le C\tau L h^{-1}\Vert \varepsilon ^{n+\frac{1}{2}(i)}\Vert ^{2}_{\infty }. \end{aligned}$$

Therefore, if $\tau$ is sufficiently small, such that $\tau \le \frac{h}{4CL}$, we have:

$$\begin{aligned}&\Vert \varepsilon ^{n+\frac{1}{2}(i+1)}\Vert _{\infty }\le \frac{1}{2}\Vert \varepsilon ^{n+\frac{1}{2}(i)}\Vert _{\infty }\le \cdots \le \frac{1}{2^{i+1}}\Vert \varepsilon ^{n+\frac{1}{2}(0)}\Vert _{\infty }\rightarrow 0,\quad i\rightarrow +\infty .&\end{aligned}$$

Therefore, the iterative algorithm is convergent. This completes the proof. $\square$

5 Numerical experiments

In this section, we present some numerical experiments to validate our theoretical results. For convenience, we denote the nonlinear compact difference scheme (21)–(23) as Scheme A and the linearized compact difference scheme (50)–(53) as Scheme B. The generalized Rosenau–Kawahara–RLW equation (1) has the following invariant quantities [34]:

$$\begin{aligned}&I_{1}(t)=\int _{-\infty }^{+\infty }u{\text {d}}x\approx I^{n}_{1}=h\sum ^{J}_{j=0}U^{n}_{j},\\&I_{2}(t)=\int _{-\infty }^{+\infty }\frac{1}{2}u^{2}{\text {d}}x\approx I^{n}_{2}=\frac{h}{2}\sum ^{J}_{j=0}(U^{n}_{j})^{2}, \end{aligned}$$

which are computed to check the conversation of the numerical algorithm.

Example 5.1

We considered the parameters $\alpha =1$, $\beta =1$, $\gamma =2$, $\delta =1$, $\lambda =1$, $\theta =1$, and $p=2$ in Eq. (1), which gives the following Rosenau–Kawahara–RLW equation [18, 20]

$$\begin{aligned}&u_{t}+u_{x}+u^{2}u_{x}+2u_{xxx}-u_{xxt}+u_{xxxxt}-u_{xxxxx}=0, \end{aligned}$$

(78)

$$\begin{aligned}&u(x,0)=\frac{3}{4}\frac{\sqrt{370}-5\sqrt{10}}{\sqrt{5\sqrt{37}-29}}{{\,\mathrm{sech}\,}}^{2}\Big (\frac{\sqrt{\sqrt{37}-5}}{4}x\Big ), \end{aligned}$$

(79)

where the exact solution is:

$$\begin{aligned}&u(x,t)=\frac{3}{4}\frac{\sqrt{370}-5\sqrt{10}}{\sqrt{5\sqrt{37}-29}}{{\,\mathrm{sech}\,}}^{2}\Big [\frac{\sqrt{\sqrt{37}-5}}{4}\Big (x-\frac{33-5\sqrt{37}}{5\sqrt{37}-29}t\Big )\Big ]. \end{aligned}$$

(80)

In this case, we chose $x_{l}=-40$ and $x_{r}=60$. First, to investigate the accuracy of the present schemes, we computed the $\Vert \cdot \Vert _{\infty }$ norm error of the numerical solutions (78)–(80). If $\tau$ is sufficiently small, then $e(h,\tau ) =O(h^{q_{1}}+\tau ^{q_{2}})\approx O(h^{q_{1}})$. Consequently, $e(2h,\tau )/e(h,\tau )\approx 2^{q_{1}}$ and, hence, $q_{1}\approx \log _{2} [e(2h,\tau )/e(h,\tau )]$ is the convergence order with respect to h. Likewise, if h is sufficiently small, $q_{2}\approx \log _{2} [e(h,2\tau )/e(h,\tau )]$ is the convergence rate with respect to $\tau$. In our computation, we calculated the convergence orders based on the following formula as: [15, 21]:

$$\begin{aligned}&\text {Rate}_{h}=\log _{2}\Big (\frac{e(2h,\tau )}{e(h,\tau )}\Big ),\quad \text {Rate}_{\tau }=\log _{2}\Big (\frac{e(h,2\tau )}{e(h,\tau )}\Big ). \end{aligned}$$

Tables 1 and 2 give the comparison of error results and CPU times between the present schemes and the non-compact methods in [21]. From Tables 1 and 2, we can see that the convergence orders of the present schemes are equal to $O(\tau ^{2}+h^{4})$, which confirms the theoretical order of convergence obtained in Theorems 2.17 and 3.5. Furthermore, we observe that the errors from the present schemes are much smaller than that obtained based on the methods in [21]. Also, the present schemes have relatively less computational cost than the methods in [21] do. Thus, we can conclude that the present two compact schemes are more effective than the schemes in [21].

Table 1 Comparison of errors and temporal convergence order with various $\tau$ and $h=0.05$ at $T=4$ for Example 5.1

Table 2 Comparison of errors and spatial convergence order with various h and $\tau =0.0002$ at $T=4$ for Example 5.1

To show that the two compact difference schemes have the energy conservative properties, we then listed the conservative invariants $E_{1}^{n}$ and $E_{2}^{n}$ at various times in Table 3, where $h=0.1$, $\tau =0.01$. The obtained results in Table 3 verify that the present schemes preserve the discrete conservative properties very well as time increases. Moreover, we can see from Table 3 that both $E_{1}^{n}$ and $E_{2}^{n}$ are conserved in our simulations with at least five-digit correctness after decimal point. This confirms the theoretical conservation shown in Theorems 2.11 and 3.1. In Table 4, we listed the theoretical values I(t), numerical approximations $I^{n}$, and the corresponding error values $|I(t)-I^{n}|/I(t)$ for the two conserved quantities, where $[x_{l},x_{r}]= [-30,30]$, $T=1$, $h=0.125$, and $\tau =h^2$. In Fig. 1, we drew the absolute error distributions with $h=0.125$, $\tau =h^{2}$ at $T=4$. From Table 4 and Fig. 1, we can see that this numerical approximations are in good agreement with the analytical solutions. Then, we plotted the motion of solitary wave with $h=0.25$ and $\tau =0.1$ at different time levels in Fig. 2. From Fig. 2, we see that the agreement between forms of approximate solutions at $T=0$ and $T=20$, 40 is excellent. The values of the invariants $I^{n}_{1}$ and $I^{n}_{2}$ at different times are listed in Table 5. The numerical results in Fig. 2 and Table 5 indicate that the present schemes can preserve the discrete conservation properties. Thus, the present schemes are effective for studying the solitary wave traveling at long time.

Table 3 Discrete conservative energy computed by Scheme A and Scheme B with $h=0.1$ and $\tau =0.01$

Table 4 Conserved quantities and error values at $T=1$

Table 5 Invariants $I^{n}$ of the scheme at different times

Example 5.2

We considered the parameters $\alpha =1$, $\beta =1$, $\gamma =2$, $\delta =1$, $\lambda =1$, $\theta =1$, and $p=4$ in Eq. (1), which gives the following Rosenau–Kawahara–RLW equation [18, 20]:

$$\begin{aligned}&u_{t}+u_{x}+u^{4}u_{x}+2u_{xxx}-u_{xxt}+u_{xxxxt}-u_{xxxxx}=0, \end{aligned}$$

(81)

$$\begin{aligned}&u(x,0)=\Bigg [\frac{40(\sqrt{127}-10)^{2}}{3(10\sqrt{127}-109)}\Bigg ]^{\frac{1}{4}}{{\,\mathrm{sech}\,}}\Bigg (\frac{\sqrt{\sqrt{127}-10}}{3}x\Bigg ), \end{aligned}$$

(82)

where the exact solution is:

$$\begin{aligned} u(x,t)=\Bigg [\frac{40(\sqrt{127}-10)^{2}}{3(10\sqrt{127}-109)}\Bigg ]^{\frac{1}{4}}{{\,\mathrm{sech}\,}}\Bigg [\frac{\sqrt{\sqrt{127}-10}}{3}\Bigg (x-\frac{118-10\sqrt{127}}{10\sqrt{127}-109}t\Bigg )\Bigg ]. \end{aligned}$$

(83)

First, we displayed some values of discrete energy of Scheme A and Scheme B in Fig. 3, where $h=0.1$, $\tau =0.01$. The obtained results in From Fig. 3 also verify that the present two schemes are conservative perfectly for energy. Then, the spatial and temporal convergence orders for numerical solutions with different h and $\tau$ at $T=4$ are shown in Fig. 4, where the case of $h=0.8$, 0.4, 0.2, $\tau =0.0002$ is plotted in Fig. 4a, and the case of $h=0.05$, $\tau =0.4$, 0.2, 0.1 is plotted in Fig. 4b. From Fig. 4, we can also see that the convergence orders for both schemes are fourth-order accuracy in space and second-order accuracy in time. The absolute error distributions with $h=0.125$, $\tau =h^{2}$ at $T=4$ are plotted in Fig. 5. These indicate that numerical solutions are very accurate as compared with the exact solutions. The profiles of the solitary waves with $h=0.25$, $\tau =h^{2}$ at different time levels $T=0$, 30, 60 are plotted in Fig. 6. From Fig. 6, we can see that the waves at $T=30$ and 60 agree with the ones at $T=0$ quite well, which also demonstrates the accuracy and efficiency of the present schemes. The surfaces of the waves with $h=0.1$, $\tau =h^{2}$ at $T=10$ and 20 are drawn in Figs. 7 and 8, respectively. We can see that the waves travel from left to right direction without changing their shapes.

Example 5.3

We considered the interaction of two solitary waves using the following initial condition [34]:

$$\begin{aligned} u(x,0)=\sum _{i=1}^{2}A_{i}{{\,\mathrm{sech}\,}}^{\frac{4}{p}} [p\sqrt{\mu }(x-\bar{x}_{i})], \end{aligned}$$

(84)

where:

$$\begin{aligned}&A_{i}=\Big [\frac{8\mu ^{2}(\lambda c_{i}+\theta )(p+1)(p+2)(3p+4)(p+4)}{\beta }\Big ]^{\frac{1}{p}},\\&\mu =\frac{\sqrt{\upsilon }-(\theta +\alpha \lambda )(p^{2}+4p+8)}{(\lambda \gamma -\delta \theta )(p+2)^{2}},\\&\upsilon =(\alpha \lambda +\theta )^{2}(p^{2}+4p+8)^{2}+16(\lambda \gamma -\delta \theta )(\alpha \delta +\gamma )(p+2)^{2}, \end{aligned}$$

for $i=1$,2, $\bar{x}_{i}$ is arbitrary constant.

Here, we chose the parameters $\alpha =5$, $\beta =10$, $\gamma =0.2$, $\delta =0.1$, $\lambda =7$, $\theta =0.1$, and $p=2$ in Eq. (1), which gives the following Rosenau–Kawahara–RLW equation:

$$\begin{aligned} u_{t}+5u_{x}+10u^{2}u_{x}+0.2u_{xxx}-0.1u_{xxt}+7u_{xxxxt}-0.1u_{xxxxx}=0. \end{aligned}$$

(85)

In this case, the exact solution is unknown. We calculated the solution on the domain $[-250,500]\times [0,40]$, with $\bar{x}_{1}=-10$, $\bar{x}_{2}=20$, $c_{1}=1.5$, $c_{2}=0.3$, $h=0.1$, and $\tau =0.1$. Table 6 presents a comparison of the numerical errors of the invariants obtained by the present methods with those provided by B-spline collocation method [34], in which one can see that the present methods are more accurate than B-spline collocation method in Ref. [34]. Finally, the interactions of these two solitary waves at different time levels are plotted in Fig. 9. We can see that the larger wave catches up with the smaller wave during the time evolution of the solitary waves, and after the interaction, the two solitary waves regain their original shapes again.

Table 6 Comparison of error values for the invariant $I_{2}^{n}$

6 Conclusion

We have developed two conservative and fourth-order compact finite-difference schemes for the generalized Rosenau–Kawahara–RLW equation. Both schemes have been shown to be second-order convergent in time and fourth-order convergent in space. Conservation of the discrete energy, existence, uniqueness, and unconditional stability of the numerical solutions are proved. Numerical experiments show that the present schemes provide accurate numerical solutions which coincide with the theoretical results.