Magnetohydrodynamic double-diffusive natural convection for nanofluid within a trapezoidal enclosure

Abstract

Double-diffusive natural convection flow in a trapezoidal cavity with various aspect ratios in the presence of water-based nanofluid and applied magnetic field in the direction perpendicular to the bottom and top parallel walls is investigated. The bottom and top parallel walls are considered to be insulated, whereas left and right walls are assumed to be uniformly heated and cold, respectively. The numerical computation is carried out to find the streamlines, isotherms, isoconcentrations, average Nusselt number, and average Sherwood number. This study is done for various values of Rayleigh number $(10^{5}\le Ra \le 10^{7})$, Hartmann number $(0\le Ha \le 120)$, various aspect ratios $(0.5\le A \le 2)$, the solid volume fraction $(0\le \varphi \le 0.1)$, and the inclination angle of cavity $(\phi )$. It is found that the strength of vortex decreases/increases as the magnetic field parameter/aspect ratio increases. It is also found that increase in the Rayleigh number causes natural convection due to the increase in the buoyancy forces. In nanofluid, mass transfer ratio is more effective than base fluid.

1 Introduction

Fluid flow of water-based nanofluids, and heat and mass transfer due to natural convection induced by applied magnetic field in a trapezoidal enclosure have practical importance in many engineering applications and geophysical problems. Effects of magnetic field and aspect ratio of a cavity occur in a wide range of scientific field, such as geology, biology, oceanography, astrophysics, and chemical processes. These include solar collectors, nuclear reactors, solar ponds, electronic cooling, geothermal reservoirs, and chemical processing equipments.

During past few decades, studies on natural convection in a trapezoidal cavities have been under taken by many researchers. Lyiean et al. (1980) studied rate of heat transfer in natural convection within a trapezoidal cavity. Basak et al. (2009) investigated flow due to natural convection in a trapezoidal enclosure filled with porous medium. Peric (1993) examined natural convection within a trapezoidal cavity with various aspect ratios. On the other hand, some of the important studies on natural convection of nanofluid in a various enclosure can be found in Sheremet et al. (2016), Mahmoodi (2011), Ghasemi et al. (2011), Mahmoudi and Abu-Nada (2013), Das and Oha (2009), Corcione (2010), and Nasrin and Parvin (2012). Sheremet et al. (2016) investigated numerically entropy generation due to natural convection in a square cavity filled with nanofluid with hot solid object inserted by cooling the top wall and left bottom corners. Mahmoodi (2011) studied heat transfer in free convection and fluid flow in a square cavity containing nanofluid in the presence of an inside heater. Ghasemi et al. (2011) numerically examined natural convection in a square cavity filled with a water–Al$_{2}$O$_{3}$ nanofluid in the presence of horizontally applied magnetic field. Mahmoudi and Abu-Nada (2013) studied combined effect of the magnetic field and nanofluids on natural convection within a square cavity. Das and Oha (2009) examined heat transfer in natural convection within a partially heated and cooled square cavity filled with nanofluids for various thermal boundary conditions. Corcione (2010) studied buoyancy-driven heat transfer in rectangular cavity with differentially heated side walls. Nasrin and Parvin (2012) numerically investigated buoyancy-driven flow and heat transfer in a trapezoidal cavity filled with nanofluid for different temperature conditions.

Apart from these studies, there have been considerable interest to study double-diffusive natural convection of base fluid and nanoparticles in enclosure of different shapes. Chen et al. (2016) studied double-diffusive natural convection in a square enclosure filled with water-based SiO$_{2}$ nanofluid. They observed that the influences of addition of nanoparticles into base fluid are quite different between the laminar and turbulent regimes. Mahapatra et al. (2013) studied magnetohydrodynamic-mixed convection flow in an inclined enclosure with thermal radiation and heat generation. Dastmalchi et al. (2015) studied double-diffusive natural convection in a porous square cavity filled with nanofluid. It was performed for several physical conditions with various values of temperature difference between the hot and cold walls, bulk volume fraction of nanoparticles, and porosity. Tofaneli and de Lemos (2009) studied double-diffusive turbulent natural convection in a porous square cavity with opposing temperature and concentration gradients. Chen et al. (2012) studied numerically double-diffusive turbulent natural convection in a square cavity by LES-based lattice Boltzmann model with Rayleigh number up to $10^{11}$ and buoyancy ratio varying from 0.1 to 2. Parvin et al. (2013) investigated the effect of natural convection parameter Rayleigh number on double-diffusive natural convection in a partially heated square cavity filled with water-based Al$_{2}$O$_{3}$ nanofluid. Esfahani and Bordbar (2011) studied double-diffusive natural convection in a square cavity filled with different nanofluids. They observed that increasing the values of nanoparticle volume fraction, the flow strength will be reduced in the cavity. Arani et al. (2014) investigated double-diffusive natural convection of Al$_{2}$O$_{3}$–water nanofluid in a square cavity with partially heated side walls. Sivasankaran and Kandaswamy (2006) examined double-diffusive natural convection of water in a partitioned enclosure with temperature-dependent species diffusivity. Arefmanesh et al. (2015) studied the mixed convection fluid flow and heat transfer in a trapezoidal cavity filled with nanofluids by considering the effect of Brownian motion. Nayak et al. (2015) numerically studied mixed convection and entropy generation of nanofluid in a differentially heated skewed enclosure. A numerical work was carried out by Teamah and Shehata (2016) to study the effect of magnetic field on double diffusion within a trapezoidal cavity. Uddin et al. (2016) investigated unsteady double diffusion mixed convection flow due to uniform and nonuniform heating at the bottom side wall in lid-driven trapezoidal cavity in the presence of magnetic field . A few investigations on stagnation-point flow of nanofluids appear in the works of earlier researchers (Pal et al. 2014; Pal and Mandal 2015; Pal et al. 2015).

Over the years, the primitive variable and stream function–vorticity formulation are used to compute incompressible viscous flows governed by the Navier–Stokes equations. The primitive variable formulation is difficult because of the presence of the pressure term in the governing equations, whereas the stream function–vorticity formulation is difficult, because the vorticity prescribed on the boundaries. Due to these facts, the biharmonic pure stream function form of the Navier–Stokes equations, which eliminates the need to compute both pressure and vorticity, is emerging as an attractive alternative (Gupta 1975; Gupta and Kalita 2005; Kalita and Sen 2012; Pandit 2008). It is worth mentioning here that we have adopted this biharmonic strategy in our formulation.

The prime objective of this paper is to analyze numerically the flow and thermal characteristics of water-based nanofluid confined within a trapezoidal cavity by considering heating of side walls in presence of magnetic field. We also want to study the effects of aspect ratio of a trapezoidal cavity on heat and mass transfer with various angles and nanoparticles. The numerical results for streamline contours, isotherms, isoconcentrations, average Nusselt number, and average Sherwood number are presented graphically. It is found that the conduction mode of heat transfer dominates the convection mode with increase in the magnetic field. It is interesting to find that, due to the growth of number of the nanoparticles, effective viscosity is more prominent than the growth of the effective thermal conductivity at a large aspect ratio.

This paper is organized in five sections. Section 2 deals with the mathematical formulation, Sect. 3 provides numerical solution procedure, and Sect. 4 gives numerical results and discussion. In Sect. 5, we summarize the results of the present investigation.

Fig. 1

Schematic diagram of the physical domain

2 Mathematical formulation

2.1 Governing equations and boundary conditions

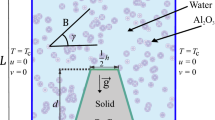
Consider the trapezoidal cavity filled with water-based nanofluid and a laminar flow is initiated due to the imposition of different kinds of temperatures and concentration conditions at the different walls under the influence of magnetic field applied in the horizontal direction. The displacement current, induced magnetic field, dissipation, and Joule heating are neglected. This is justified for the flow where magnetic Reynolds number is small. The physical domain of a trapezoidal cavity is shown in Fig. 1 with the left and the right wall inclined at angles $(\pi -\phi )$ and $\phi$, with x-axis. The governing equations for steady two-dimensional natural convection flow of a water-based nanofluid in dimensional form can be written as:

$$\begin{aligned} \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}= & {} 0, \end{aligned}$$

(1)

$$\begin{aligned} u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}= & {} - \,\frac{1}{\rho _\mathrm{nf}}\frac{\partial p}{\partial x} + \nu _\mathrm{nf} \left[ \frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} \right] -\frac{\sigma _\mathrm{nf}~ B_{0}^{2}~ u}{\rho _\mathrm{nf}}, \end{aligned}$$

(2)

$$\begin{aligned} u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}= & {} -\, \frac{1}{\rho _\mathrm{nf}}\frac{\partial p}{\partial y} + \nu _\mathrm{nf} \left[ \frac{\partial ^2 v}{\partial x^2} + \frac{\partial ^2 v}{\partial y^2} \right] \nonumber \\&+\,\frac{g(\rho \beta _\mathrm{T})_\mathrm{nf}}{\rho _\mathrm{nf}}(T-T_\mathrm{c}) -\frac{g(\rho \beta _\mathrm{S})_\mathrm{nf}}{\rho _\mathrm{nf}}(c-c_\mathrm{c}), \end{aligned}$$

(3)

$$\begin{aligned} u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}= & {} \alpha _\mathrm{nf}\left[ \frac{\partial ^2 T}{\partial x^2} + \frac{\partial ^2 T}{\partial y^2} \right] , \end{aligned}$$

(4)

$$\begin{aligned} u\frac{\partial c}{\partial x} + v\frac{\partial c}{\partial y}= & {} D \left[ \frac{\partial ^2 c}{\partial x^2} + \frac{\partial ^2 c}{\partial y^2} \right] . \end{aligned}$$

(5)

The boundary conditions of the physical problem are as follows: in all the four walls, no slip condition prevails. This condition gives $u=0,~v=0$ at the four walls. The bottom and top walls are adiabatic ($\frac{\partial T}{\partial y}=0$), whereas left wall is hot $(T=T_\mathrm{h})$ and right wall is cold $(T=T_\mathrm{c})$. The concentration gradients at the bottom and top walls are considered to be zero and concentration at left and right walls are assumed constants which are $c_\mathrm{h}$ and $c_\mathrm{c}$, respectively. Using the dimensionless quantities:

$$\begin{aligned}&X=\frac{x}{L},~ Y=\frac{y}{L},~ U=\frac{u L}{\alpha _\mathrm{f}},~ V=\frac{v L}{\alpha _\mathrm{f}},~C=\frac{c-c_\mathrm{c}}{c_\mathrm{h}-c_\mathrm{c}},\theta =\frac{T-T_\mathrm{c}}{T_\mathrm{h}-T_\mathrm{c}},~ P=\frac{pL^{2}}{\rho _\mathrm{nf} \alpha ^{2}_\mathrm{f}}, \\&Pr=\frac{\nu _\mathrm{f}}{\alpha _\mathrm{f}}, ~Ha=\sqrt{\frac{\rho _\mathrm{f}}{\mu _\mathrm{f}}}~ B_{0} L, Le=\frac{\alpha _\mathrm{f}}{D},~Ra=\frac{g~ \beta _\mathrm{f}(T_\mathrm{h}-T_\mathrm{c}) L^{3}}{\nu _{f}\alpha _\mathrm{f}},~N=\frac{\beta _\mathrm{S}(c_\mathrm{h}-c_\mathrm{c})}{\beta _\mathrm{T}(T_\mathrm{h}-T_\mathrm{c})}. \end{aligned}$$

The governing Eqs. (1)–(5) reduce to dimensionless form:

$$\begin{aligned} \frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y}= & {} 0, \end{aligned}$$

(6)

$$\begin{aligned} U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y}= & {} - \frac{\partial P}{\partial X} + \frac{\mu _\mathrm{nf}}{\rho _\mathrm{nf}\alpha _\mathrm{f}} \left[ \frac{\partial ^2 U}{\partial X^2} + \frac{\partial ^2 U}{\partial Y^2} \right] -\frac{\sigma _\mathrm{nf}\rho _\mathrm{f}}{\sigma _\mathrm{f}\rho _\mathrm{nf}} Ha^{2}~ U, \end{aligned}$$

(7)

$$\begin{aligned} U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y}= & {} - \frac{\partial P}{\partial Y} + \frac{\mu _\mathrm{nf}}{\rho _\mathrm{nf}\alpha _\mathrm{f}} \left[ \frac{\partial ^2 V}{\partial X^2} + \frac{\partial ^2 V}{\partial Y^2} \right] +\frac{(\rho \beta )_\mathrm{nf}}{\rho _\mathrm{nf}\beta _\mathrm{f}}~ Ra~ Pr ~(\theta -N~ C), \end{aligned}$$

(8)

$$\begin{aligned} U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial Y}= & {} \frac{\alpha _\mathrm{nf}}{\alpha _\mathrm{f}}\left[ \frac{\partial ^2 \theta }{\partial X^2} + \frac{\partial ^2 \theta }{\partial Y^2} \right] , \end{aligned}$$

(9)

$$\begin{aligned} U\frac{\partial C}{\partial X} + V\frac{\partial C}{\partial Y}= & {} \frac{1}{Le}\left[ \frac{\partial ^2 C}{\partial X^2} + \frac{\partial ^2 C}{\partial Y^2} \right] . \end{aligned}$$

(10)

The dimensionless initial boundary conditions are as follows:

$$\begin{aligned} U= & {} 0,~V=0 ~~ \text{ at } \text{ all } \text{ the } \text{ four } \text{ walls }, \\ \frac{\partial \theta }{\partial Y}= & {} 0=\frac{\partial C}{\partial Y}~~ \text{ at } \text{ the } \text{ bottom } \text{ and } \text{ top } \text{ walls }, \\ \theta= & {} 1=C~~ \text{ at } \text{ the } \text{ left } \text{ wall }, \\ \theta= & {} 0=C~~ \text{ at } \text{ the } \text{ right } \text{ wall }. \end{aligned}$$

We introduce stream function $(\psi )$ and vorticity $(\omega )$ in the following manner:

$$\begin{aligned} U =\frac{\partial \psi }{\partial Y}, ~~ V =-\frac{\partial \psi }{\partial X}, ~~ \omega =\frac{\partial V}{\partial X} - \frac{\partial U}{\partial Y}. \end{aligned}$$

(11)

Using Eq. (6) and eliminating P from Eqs. (7) and (8), we get

$$\begin{aligned} P_{1} \left[ \frac{\partial ^2\omega }{\partial X^2}+\frac{\partial ^2\omega }{\partial Y^2}\right] -\left[ U \frac{ \partial \omega }{\partial X}+V \frac{\partial \omega }{\partial Y}\right] +P_{2}\frac{\partial U}{\partial Y}+ P_{3}\left( \frac{\partial \theta }{\partial X}-N~\frac{\partial C}{\partial X}\right) = 0, \end{aligned}$$

(12)

where $P_{1},~ P_{2}, ~P_{3}$ are defined in Appendix. Combining three equations in Eq. (11), we get the governing equation for $\psi$ as

$$\begin{aligned} \frac{\partial ^2 \psi }{\partial X^2} + \frac{\partial ^2 \psi }{\partial Y^2} = -\omega . \end{aligned}$$

(13)

2.2 Thermophysical properties of the nanofluid

The effective density, the heat capacity, thermal expansion coefficient, and electrical conductivity of the nanofluid (see, Kefayati 2015; Xuan and Roetzel 2000) are given by the following relations:

$$\begin{aligned} \rho _\mathrm{nf}= & {} (1-\varphi )\rho _\mathrm{f}+\varphi \rho _\mathrm{p}, ~~ (\rho C_\mathrm{p})_\mathrm{nf} =(1-\varphi )(\rho C_\mathrm{p})_\mathrm{f}+\varphi (\rho C_\mathrm{p})_\mathrm{p}, \\ (\rho \beta )_\mathrm{nf}= & {} (1-\varphi )(\rho \beta )_\mathrm{f}+\varphi (\rho \beta )_\mathrm{p}, ~~ \sigma _\mathrm{nf}=\sigma _{f} \left( 1 +\frac{3(\zeta -1)\varphi }{(\zeta +2)-(\zeta -1)\varphi } \right) , \end{aligned}$$

respectively, where $\varphi$ is the volume fraction of the nanoparticle, $\zeta = \sigma _\mathrm{p}/\sigma _\mathrm{f}$, and the subscripts f and p refer to the base fluid and nanoparticle, respectively. Thermal diffusivity of the nanofluid is $\alpha _\mathrm{nf}=k_\mathrm{nf}/(\rho C_\mathrm{p})_\mathrm{nf}$, where $k_\mathrm{nf}$ is effective thermal conductivity and is given by the following expression:

$$\begin{aligned} k_\mathrm{nf}=k_\mathrm{f} \left[ \frac{k_\mathrm{p}+2k_{f}-2\varphi (k_\mathrm{f}-k_\mathrm{p})}{k_\mathrm{p}+2 k_\mathrm{f}+\varphi (k_\mathrm{f}-k_\mathrm{p})}\right] . \end{aligned}$$

Here, $k_\mathrm{f}$ and $k_\mathrm{p}$ are thermal conductivity of the base fluid and nanoparticle, respectively. The effective viscosity of the nanofluid is obtained from the Brinkman model (see, Brinkman 1952) which is expressed by

$$\begin{aligned} \mu _\mathrm{nf}=\mu _\mathrm{f}(1-\varphi )^{-2.5}, \end{aligned}$$

where $\mu _\mathrm{f}$ is the viscosity of the base fluid. The thermophysical properties of the base fluid (pure water) and the solid particle are given in Table 1.

2.3 Coordinate transformation and biharmonic formulation

Application of the boundary conditions at the various boundaries is a difficult task. The prescription of conditions at boundaries not conforming to the coordinate lines leads to severe interpolation errors. For this reason, a transformation is introduced to map irregular physical domain to square computational domain. In this study, the physical (X, Y) plane is transformed into the computational $(\xi ,\eta )$ plane using the mapping:

$$\begin{aligned} \xi =\frac{X+Y \cot \phi }{1+ 2Y \cot \phi }, ~~\eta =\frac{Y}{A}, \end{aligned}$$

where A is aspect ratio of a cavity. This mapping is employed the physical trapezoidal flow domain to computational square flow domain which is shown in Fig. 2. Equations (9), (10), (12), and (13) are transformed to

$$\begin{aligned}&P_{4} F \frac{\partial ^2 \theta }{\partial \xi ^2} + E P_{4}\frac{\partial ^2 \theta }{\partial \xi \partial \eta } + \frac{P_{4}}{A^{2}}\frac{\partial ^2 \theta }{\partial \eta ^2}=- B \frac{\partial \theta }{\partial \xi }+\frac{V}{A}\frac{\partial \theta }{\partial \eta }, \end{aligned}$$

(14)

$$\begin{aligned}&F \frac{\partial ^2 C}{\partial \xi ^2} + E \frac{\partial ^2 C}{\partial \xi \partial \eta } + \frac{1}{A^{2}}\frac{\partial ^2 C}{\partial \eta ^2}=- Le ~ P_{6} \frac{\partial C}{\partial \xi }+\frac{Le~V}{A}\frac{\partial C}{\partial \eta }, \end{aligned}$$

(15)

$$\begin{aligned}&P_{1} F \frac{\partial ^2 \omega }{\partial \xi ^2}+P_{1} E \frac{\partial ^2 \omega }{\partial \xi \partial \eta }+\frac{P_{1}}{A^{2}}\frac{\partial ^2 \omega }{\partial \eta ^2}+M\frac{\partial \omega }{\partial \xi }-\frac{V}{A}\frac{\partial \omega }{\partial \eta } \nonumber \\&\quad + P_{3} G \left( \frac{\partial \theta }{\partial \xi }-N~\frac{\partial C}{\partial \xi }\right) +P_{2}\left( \frac{E A}{2} \frac{\partial U}{\partial \xi }+\frac{1}{A} \frac{\partial U}{\partial \eta }\right) =0, \end{aligned}$$

(16)

$$\begin{aligned}&F \frac{\partial ^2 \psi }{\partial \xi ^2} + E \frac{\partial ^2 \psi }{\partial \xi \partial \eta } + \frac{1}{A^{2}}\frac{\partial ^2 \psi }{\partial \eta ^{2}}+H \frac{\partial \psi }{\partial \xi } =- \omega , \end{aligned}$$

(17)

where

$$\begin{aligned} U=\left( \frac{E A}{2} \psi _{\xi }\right) +\left( \frac{1}{A}\psi _{\eta }\right) , V=-\left( G\psi _{\xi }\right) . \end{aligned}$$

(18)

Table 1 Thermophysical properties of the base fluid (pure water) and nanoparticle

Fig. 2

Mapping of the trapezoidal domain to a square domain

Eliminating $\omega$ from Eq. (16), with the help of Eq. (17), we get

$$\begin{aligned}&P_{1} F^{2}\frac{\partial ^{4} \psi }{\partial \xi ^{4}}+2P_{1}E F\frac{\partial ^{4} \psi }{\partial \xi ^{3}\partial \eta }+ T_{5}\frac{\partial ^{4} \psi }{\partial \xi ^{2}\partial \eta ^{2}}+\frac{2 P_{1} E}{A^{2}}\frac{\partial ^{4} \psi }{\partial \xi \partial \eta ^{3}}+ \frac{P_{1}}{A^{4}}\frac{\partial ^{4} \psi }{\partial \eta ^{4}}\nonumber \\&\quad +\, T_{1}\frac{\partial ^{3} \psi }{\partial \xi ^{3}} +T_{2} \frac{\partial ^{3} \psi }{\partial \xi ^{2}\partial \eta } +T_{3}\frac{\partial ^{3} \psi }{\partial \xi \partial \eta ^{2}} \nonumber \\&\quad -\,\frac{V}{A^{3}}\frac{\partial ^{3} \psi }{\partial \eta ^{3}}+T_{4}\frac{\partial ^{2} \psi }{\partial \xi ^{2}}+ T_{6}\frac{\partial ^{2} \psi }{\partial \xi \partial \eta }+T_{7}\frac{\partial \psi }{\partial \xi }\nonumber \\&\quad - \, P_{3} G\left( \frac{\partial \theta }{\partial \xi }-N~\frac{\partial C}{\partial \xi }\right) -P_{2}\left( \frac{E A}{2}\frac{\partial U}{\partial \xi }+\frac{1}{A} \frac{\partial U}{\partial \eta }\right) =0, \end{aligned}$$

(19)

which is biharmonic equation in stream function–velocity formulation, where B,  E,  F,  $G,~ H,~M,~P_{4}, P_{6},~T_{1}, ~T_{2},~ T_{3},$ $~ T_{4},~ T_{5},~ T_{6}, \mathrm{{and}} ~T_{7}$ are defined in the Appendix.

2.4 Nusselt number

The heat transfer rate in terms of the local Nusselt number (Nu) is defined by

$$\begin{aligned} Nu=-\frac{k_\mathrm{nf}}{k_\mathrm{f}}\frac{\partial \theta }{\partial n}, \end{aligned}$$

where n is the normal direction on a plane. The local Nusselt number at right wall $(Nu_\mathrm{r})$ and left wall $(Nu_\mathrm{l})$ is defined as follows:

$$\begin{aligned} Nu_\mathrm{r}=-\sin \phi \frac{k_\mathrm{nf}}{k_\mathrm{f}} \frac{\partial \theta }{\partial X}+\cos \phi \frac{k_\mathrm{nf}}{k_\mathrm{f}} \frac{\partial \theta }{\partial Y}, Nu_\mathrm{l}=\sin \phi \frac{k_\mathrm{nf}}{k_\mathrm{f}} \frac{\partial \theta }{\partial X}+\cos \phi \frac{k_\mathrm{nf}}{k_\mathrm{f}} \frac{\partial \theta }{\partial Y}. \end{aligned}$$

The average Nusselt number at left wall $(\overline{Nu_\mathrm{l}})$ and right $(\overline{Nu_\mathrm{r}})$ walls are given by

$$\begin{aligned} \overline{Nu_\mathrm{l}}=\frac{\sin \phi }{A} \int _{0}^{\frac{A}{\sin \phi }} Nu_\mathrm{l} {\text {d}}S_{1}, \overline{Nu_\mathrm{r}}=\frac{\sin \phi }{A} \int _{0}^{\frac{A}{\sin \phi }} Nu_\mathrm{r} \mathrm{{d}}S_{2}, \end{aligned}$$

where d$S_{1}$ and d$S_{2}$ are small element lengths along the left and right walls, respectively. The average Nusselt number $(\overline{Nu})$ is defined by $\overline{Nu}=\frac{1}{2}(\overline{Nu_\mathrm{l}}+\overline{Nu_\mathrm{r}})$.

2.5 Sherwood number

The mass transfer rate in terms of the local Sherwood number (Sh) is defined by

$$\begin{aligned} {{Sh}}=-\frac{\partial C}{\partial n}, \end{aligned}$$

where n is the normal direction on a plane. The local Sherwood number at right wall $({{Sh}}_\mathrm{r})$ and left wall $({{Sh}}_\mathrm{l})$ are given by

$$\begin{aligned} {{{Sh}}_\mathrm{r}}=-\sin \phi \frac{\partial C}{\partial X}+\cos \phi \frac{\partial C}{\partial Y},~~ {{{Sh}}_\mathrm{l}}=\sin \phi \frac{\partial C}{\partial X}+\cos \phi \frac{\partial C}{\partial Y}. \end{aligned}$$

The average Sherwood number at left and right walls are defined as follows:

$$\begin{aligned} \overline{{{Sh}}_\mathrm{l}}=\frac{\sin \phi }{A} \int _{0}^{\frac{A}{\sin \phi }} {{{Sh}}_\mathrm{l}} \mathrm{{d}}S_{1}, ~~\overline{{{Sh}}_\mathrm{r}}=\frac{\sin \phi }{A} \int _{0}^{\frac{A}{\sin \phi }} Sh_\mathrm{r} \mathrm{{d}}S_{2}, \end{aligned}$$

where d$S_{1}$ and d$S_{2}$ are small element lengths along the left and right walls, respectively. The average Sherwood number $(\overline{Sh})$ is defined by $\overline{Sh}=\frac{1}{2}(\overline{{{Sh}}_\mathrm{l}}+\overline{{{Sh}}_\mathrm{r}})$.

3 Numerical solution procedure

The second-order finite-difference approximation of Eqs. (14), (15), and (19) using Appendix may be rewritten in the matrix form as follows:

$$\begin{aligned} Q {\theta }= & {} 0, \end{aligned}$$

(20)

$$\begin{aligned} R {C}= & {} 0, \end{aligned}$$

(21)

$$\begin{aligned} S {\psi }= & {} f\left( Ra,~ Pr,~ Ha,~ U, ~V, ~\theta _{\xi },~ C_{\xi },~ \psi _{\xi }, ~\psi _{\eta }\right) , \end{aligned}$$

(22)

where $\psi _{\xi }$ and $\psi _{\eta }$ can be obtained solving the following equations by Thomas algorithm:

$$\begin{aligned} (\psi _\xi )_{ i+1,j}+4(\psi _\xi )_{i,j}+(\psi _\xi )_{ i-1,j} = \frac{3}{h} (\psi _{i+1,j}-\psi _{i-1,j}), \end{aligned}$$

(23)

$$\begin{aligned} (\psi _\eta )_{i,j+1}+4(\psi _\eta )_{ i,j}+(\psi _\eta )_{ i,j-1} = \frac{3}{ h} (\psi _{i,j+1}-\psi _{i,j-1}). \end{aligned}$$

(24)

For a grid of size $m\times n$, the coefficient matrices Q, R, and S are of order mn and $\psi ,~\theta ,~$C and f are mn-component vectors. We solve this problem using outer–inner iteration procedure as described by Gupta and Kalita (2005). We solve Eqs. (20), (21), and (22) using the biconjugate gradient stabilized (BiCGStab) method which constitutes inner iterations. Once both the Eqs. (20), (21), and (22) are solved, then we solve for $\psi _{\xi }$ and $\psi _{\eta }$ using Thomas algorithm for the tridiagonal linear systems arising from Eqs. (23) and (24). This constitutes one outer iteration cycle. We use same relaxation parameter $\lambda$ inside both the inner and outer iteration cycles for $\psi$,$~\theta$, and C. After calculating $\psi _{\xi }$ and $\psi _{\eta }$, we compute U and V from Eq. (18). The computations were stopped when the maximum $\psi$ error, $\theta$ error, and C error between two successive outer iteration steps were smaller than $0.5 \times 10^{-6}$.

4 Results and discussion

In the present study, we simulate double-diffusive convection flow due to both the thermal and solutal effects in a trapezoidal cavity filled with water-based nanofluid. The effects of volume fraction of nanoparticles, type of nanoparticles, Rayleigh number, and Hartmann number on fluid flow, heat transfer characteristics, and solutal transfer characteristics in the cavity are discussed in terms of streamlines, isotherms, isoconcentrations, average Nusselt numbers, and average Sherwood numbers. Prandtl number in the present paper is considered to be 0.7.

4.1 Code validation and grid independence study

Our code is validated by comparing the results with the benchmark results of Basak et al. (2012) and Davis (1982) when pure working fluid is used in the square cavity $(\phi =90^{\circ })$ for different values of Rayleigh number and $Pr=0.71$ as shown in Table 2. In addition, validation of present results with those of Ghasemi et al. (2011) for $\psi _\mathrm{min}$ is given in Table 3 using $81 \times 81$ grids. It is observed from these tables that our results agree very well with those of the previous researchers’ results.

The grid independence test is done using different grid sizes within trapezoidal enclosure with different aspect ratios ($A= 0.5, 1$) and is presented in Table 4 for $Ra=10 ^{6}$, $Ha=40$, $N=-2$, $Le=1$, $\phi =60^{\circ }$, and $\varphi =0.05$. Considering various grids $21 \times 21$, $41 \times 41$, $81 \times 81$ and $161 \times 161$, thus we conclude that $81 \times 81$ grid is enough for all the calculations.

Table 2 Code validation for $|\psi _\mathrm{max}|$ and average Nusselt number $(\overline{Nu})$

Table 3 Code validation for $\psi _\mathrm{min}$

Table 4 Grid independence test for $|\psi _\mathrm{max}|$

4.2 Effects of Hartmann number

The effects of the Hartmann number on the streamlines, isotherms, and isoconcentrations are presented in Fig. 3a–c, respectively, for $Ra=10^{6}$, $Le=1$, $A=0.5$, $N=-2$, $\phi =60^{\circ }$. The enclosure is filled with a water-based Al$_{2}$O$_{3}$ nanofluid, which has solid volume fraction $\varphi$= 0.03. The buoyancy-driven circulating flows within the enclosure are evident for all values of the Hartmann numbers. The strength of these circulations decreases as the value of Hartmann number increases. This is evident from the fact that the maximum value of stream function in an enclosure decreases with the increase in strength of the magnetic field which is the effect of Lorentz force. It means that as strength of magnetic field increases, conduction mode of heat transfer becomes dominant to convection mode of heat transfer. The maximum values of $\psi$ are 8.48, 6.9, 4.74, and 3.21 for $Ha= 0,$ 40, 80, and 120, respectively. The results also show a conduction-dominated regime with vertical isotherms and isoconcentrations at high Hartmann number and a convection-dominated regime with horizontal isotherms and isoconcentrations at low Hartmann number. The isotherms and isoconcentrations are affected by variations in the Hartmann number. These effects are more noticeable at $Ha =0$ and 40, where an increase in the Hartmann number results in the change of path of isotherms and isoconcentrations from horizontal to vertical. This is an indication of weaker convection flows at higher Hartmann number. Figure 4a, b shows how the average Nusselt number and average Sherwood number, respectively, vary with the Hartmann number at different values of the solid volume fraction ($0 \le \varphi \le 0.1$), for $Ra= 10^{6}$, where the heat and mass transfer are only due to conduction. The average Nusselt number and average Sherwood number decrease when the Hartmann number increases. In addition, the average Nusselt number and average Sherwood number decrease when the volume friction of the nanofluid increases. In fact, the increase in volume friction $(\varphi )$ means that more nanoparticles were added in the base fluid which makes the nanofluid more viscous which in turn slowdown the fluid movement.

Fig. 3

Effects of Hartmann number (Ha) astream function $(\psi )$, b isotherms $(\theta )$, and c isoconcentrations (C) for $Le=1$, $A=0.5$, $N=-2$, $Ra=10^{6}$, and $\varphi =0.03$, $\phi =60^{\circ }$

Fig. 4

Effects of Hartmann number (Ha) versus a average Nusselt number, and b average Sherwood number for $Le=1$, $A=0.5$, $N=-2$, $Ra=10^{6}$, $0 \le \varphi \le 0.1$, and $\phi =60^{\circ }$

4.3 Effects of inclination angle

The effects of inclination angle on the streamlines, isotherms, and isoconcentrations are presented in Fig. 5a–c, respectively, for $Ra=10^{6}$, $Le=1$, $A=1$, $N=-2$, and $Ha=40$. The enclosure is filled with a water-based Al$_{2}$O$_{3}$ nanofluid, which has a solid volume fraction $\varphi$= 0.03. The buoyancy-driven circulating flows within the enclosure are evident for all values of inclination angles of a trapezoidal cavity. The strength of circulation (the maximum values of $\psi$) decreases as $\phi =30^{\circ }$ is increased $60^{\circ }$, buts when $\phi$ is increase from $60^{\circ }$ to $90^{\circ }$, the strength of this circulation increases. When inclination angle $(\phi )$ is more than $45^{\circ }$ nature of heat transfer becomes less convective but more conductive and so the curvature of streamline is reduced. As observed from Fig. 5, the inclination angle $(\phi )$ of the cavity has an important role on the eddy strength. It is interesting to note two circulation (smallest) zones exist for $\phi = 60^{\circ }$ and $90^{\circ }$. The maximum values of $\psi$ are 13.8, 13.3, 13, and 13.4 for $\phi = 30^{\circ }$, $45^{\circ }$, $60^{\circ }$ and $90^{\circ }$, respectively. Comparing Figs. 3a and 5a for $Ha=40$, the maximum values of $\psi$ increase with the increase in A. From Fig. 4b, c it is evident that the isotherms and isoconcentrations are affected by variations of inclination angle $(\phi )$, i.e., the line of isotherms and isoconcentrations in the core of the cavity tends to be horizontal as inclination angle increased. Figure 6a, b shows how the average Nusselt number and average Sherwood number, respectively, vary with inclination angle at different values of the solid volume fractions ($0 \le \varphi \le 0.1$), for fixed values of other parameters. The average Nusselt number and average Sherwood number are increased when the inclination angle is increased. The average Sherwood number decreases when the volume fraction of nanofluid increases. For small values of inclination angle, moreover, average Nusselt number decreases when volume fraction nanoparticles $(\varphi )$ increases, but, for more than a certain value of inclination angle, the opposite trend is observed.

Fig. 5

Effects of inclination angle $(\phi )$: a stream function $(\psi )$, b isotherms $(\theta )$, and c isoconcentrations (C) for $Le=1$, $A=1$, $N=-2$, $Ra=10^{6}$, and $\varphi =0.03$, $Ha=40$

Fig. 6

Effects of inclination angle $(\phi )$ versus a average Nusselt number, and b average Sherwood number for $Le=1$, $A=1$, $N=-2$, $Ra=10^{6}$, $0 \le \varphi \le 0.1$, and $Ha=40$

4.4 Effects of aspect ratio

The effects of the aspect ratio on the streamlines, isotherms, and isoconcentrations are presented in Fig. 7a–c, respectively, for $Ra=10^{6}$, $Le=1$, $Ha=40$, $N=-10$, $\phi =60^{\circ }$, and $\varphi = 0.03$, when water-based Al$_{2}$O$_{3}$ nanofluid is used. The buoyancy-driven circulating flows within the enclosure are evident for all values of the aspect ratio. The strength of these circulations increases as aspect ratio increases. Actually, once the Rayleigh number, Ra, is assigned, the increase of the cavity aspect ratio is obtained by increasing volume of the cavity. This implies that the resistance encountered by the fluid to flow across the cavity increases, and, consequently, due to the increase in the volume fraction of the nanofluid effective viscosity starts becoming excessive in comparison with the growth of the effective thermal conductivity at a larger aspect ratio. The maximum values of $\psi$ are 7.76, 20.4, 27, and 33.2 for $A= 0.5$, 1, 1.5, and 2, respectively. Comparing Figs. 3a and 7a, it is seen that, for $A=0.5, Ha=40$, the maximum strength ($\psi$) of these circulations increases with the decrease in values of N. Also one small circulation zone exists for $N=-2$, but two small circulation zone exists for $N=-10$. The results also show a conduction-dominated regime with vertical isotherms at a small value of $A (=0.5)$ and a convection-dominated regime with horizontal isotherms and isoconcentrations at high aspect ratio $(1\le A \le 2)$. The large values of A, the isotherms, and isoconcentrations remain horizontal. Figure 8a, b, respectively, shows how the average Nusselt number and average Sherwood number vary with aspect ratio (A) for various values of the solid volume fraction ($0 \le \varphi \le 0.1$). The average Nusselt number and average Sherwood number increase when aspect ratio increases. It is seen that the Sherwood number, a measure of rate of mass transfer, is optimized at the highest Ra and lowest A for both base fluid and nanofluid. In addition, mass transfer rate is more effective for nanofluid than the base fluid. This mitigation of heat transfer is mainly attributed to the effective dynamic viscosity which is predominant in the natural convection of nanofluid for low effective thermal conductivity. In addition, the average Nusselt number almost remains unchanged when the volume fraction of nanofluid increases.

Fig. 7

Effects of aspect ratio (A) a stream function $(\psi )$, b isotherms $(\theta )$, and c isoconcentrations (C) for $Le=1$, $\phi =60^{\circ }$, $N=-10$, $Ra=10^{6}$, and $\varphi =0.03$, $Ha=40$

Fig. 8

Effects of aspect ratio (A) versus a average Nusselt number and b average Sherwood number for $Le=1$, $\phi =60^{\circ }$, $N=-10$, $Ra=10^{6}$, $0 \le \varphi \le 0.1$, and $Ha=40$

Fig. 9

Effects of Rayleigh (Ra) a stream function $(\psi )$, b isotherms $(\theta )$, and c isoconcentrations (C) for $Le=1$, $\phi =60^{\circ }$, $N=-2$, $A=0.5$, $\varphi =0.03$, and $Ha=40$

Fig. 10

Effects of Rayleigh (Ra) versus a average Nusselt number, and b average Sherwood number for $Le=1$, $\phi =60^{\circ }$, $N=-2$, $A=0.5$, $0 \le \varphi \le 0.1$, and $Ha=40$

4.5 Effects of Rayleigh number

Figure 8a–c illustrate streamlines $(\psi )$, isotherms $(\theta )$, and isoconcentrations (C) for various values of Ra. The strength of these circulations increases as the Ra increases. As Ra increases, the strength of fluid flow increases and that leads to increase in thermal energy transport due to enhanced convection. This happens due to the fact that increasing buoyancy force causes natural convection in the cavity with the increase of Rayleigh number. The maximum values of $\psi$ are 1.58, 6.9, and 16.75 for $Ra =10^{5}$, $10^{6}$, and $10^{7}$, respectively. Comparison of Figs.  5a and 9a shows that, as the aspect ratio increases from 0.5 to 1, the maximum value of $\psi$ increases for $Ra= 10^{6}$. It is also noted that, when the aspect ratio $A =0.5$, single small circulation zone exists, but, for the aspect ratio $A =1$, two small circulation zones exist. Comparing Figs. 7a and 8a, it is seen that, when N increases from $-10$ to $-2$, the maximum values of $\psi$ increase for $Ra=10^{6}$, $A=0.5$, and $Ha=40$. The results also show a conduction-dominated regime with almost vertical isotherms and isoconcentrations at low $Ra (=10^{5})$ and a convection-dominated regime with almost horizontal isotherms and isoconcentrations at high $Ra (=10^{7})$. Comparison of Figs. 7c and 9c shows that, as N increases, the pattern of isoconcentrations remains almost horizontal but the pattern of isoconcentrations remains almost vertical for $Ra= 10^{6}$, $A=0.5$, $Ha=40$, $\varphi =0.03$, $Le=1$, and $\phi =60^{\circ }$. Figure 10a, b shows that the average Nusselt number and average Sherwood number, respectively, vary with Ra for different values of the solid volume fraction ($0 \le \varphi \le 0.1$). The average Nusselt number and average Sherwood number increase with increasing the value of Ra. It is interesting to note that if the solid volume fraction of water-based Al$_{2}$O$_{3}$ nanofluid increases, then average Nusselt number increases, but average Sherwood number decreases. It is found that the addition of nanoparticles has an effect on the average Nusselt number, indicating a better heat transfer. In addition, the effect of the nanoparticles is more significant at low Rayleigh number than at high Rayleigh number.

Fig. 11

Average Nusselt number (left) and average Sherwood number (right) versus volume fraction for different nanoparticles, $Le=1$, $A=0.5$, $N=-10$, $Ra=10^{6}$, and $\phi =60^{\circ }$

4.6 Effects of nanoparticles

Finally, variations of average Nusselt number and average Sherwood number with nanoparticle volume fraction for different kinds of nanoparticles consisting of Cu, Ag, Al$_{2}$O$_{3}$, and TiO$_{2}$ are compared in Fig. 11a, b. It can be seen from these figures that, for nanoparticles with larger thermal conductivity, the average Nusselt number and average Sherwood number are large. In other words, by increasing the value of volume fraction, both the average Nusselt number and average Sherwood number are decreased. For the same physical conditions, the minimum solutal transfer occurs when Al$_{2}$O$_{3}$ or TiO$_{2}$ nanoparticles with small thermal conductivity are used and the maximum heat transfer occurs when Ag or Cu nanoparticles with large thermal conductivity are used.

5 Conclusion

Fluid flow, and heat and mass transfer in a trapezoidal cavity filled with water-based nanofluid with different inclination angle $(\phi )$, aspect ratio (A), magnetic field parameter (Ha), and Rayleigh number (Ra) are studied. The main findings can be summarized as follows:

• The recirculation eddy in the cavity is reduced as the magnetic field strength increases which results in decrease of the convection heat transfer. In such case, conduction heat transfer becomes dominant.

• The maximum values of $\psi$, average Nusselt number and average Sherwood number increase when the value of A increases keeping other parameters fixed.

• The convective heat transfer is an increasing function of Rayleigh number, and hence, the mass transfer also follows this fashion.

• Increasing Hartmann number has the opposite effect than that of increasing Rayleigh number. Higher Hartmann number weakens convection for both nanofluid and base fluid. However, nanofluid provides higher value of the average Nusselt number than base fluid even when magnetic field is applied.

• The maximum value of $\psi$ increases for $(30^{\circ } \le \phi \le 60^{\circ })$ and decreases for $(60^{\circ } \le \phi \le 90^{\circ })$ for increasing values of $\psi$ when other parameters are fixed.

• In addition, we see that the average Nusselt number decreases when we use Cu, Ag, Al$_{2}$O$_{3}$, and TiO$_{2}$ as nanoparticles and the lowest value of the average Nusselt number was obtained for TiO$_{2}$ nanoparticle. This can be justified by the fact that TiO$_{2}$ nanoparticle has less thermal conductivity compared to the other type of nanoparticles.

Appendix

$$\begin{aligned} P_{1}= & {} \frac{\mu _\mathrm{nf}}{\rho _\mathrm{nf}\alpha _\mathrm{f}},~~P_{2}=\frac{\sigma _\mathrm{nf}\rho _\mathrm{f}}{\sigma _\mathrm{f}\rho _\mathrm{nf}} Ha^{2},~~P_{3} = \frac{(\rho \beta )_\mathrm{nf}}{\rho _\mathrm{nf}\beta _\mathrm{f}} Ra Pr,~~P_{4}=\frac{\alpha _\mathrm{nf}}{\alpha _\mathrm{f}}, \\ B= & {} U G+ 0.5 V E A-H~P_{4},~ P_{6}=U G + 0.5 V E A-\frac{H}{Le},\\ G= & {} \frac{1}{1+2\eta A \cot \phi },~~E=-\frac{2 G \cot \phi (2 \xi -1)}{A},~~F = G^{2}[1+ \cot ^{2}\phi (2 \xi -1)^{2}], \\ H= & {} 4 G^{2} \cot ^{2}\phi (2\xi -1),~~ M=-U G+ V G(2\xi -1)\cot \phi + P_{1} H,\\ T_{1}= & {} -8P_{1} F G^{2}(1-2\xi )\cot ^{2}\phi +P_{1} F H \\&+F M- 4 A G^{3}\cot \phi [1+(1-2\xi )^{2}\cot ^{2}\phi ],\\ T_{2}= & {} -\frac{8}{A}P_{1} F G \cot \phi - 8P_{1} E G^{2}(1-2\xi )\cot ^{2}\phi \\&+P_{1} E H-\frac{8}{A}G^{3} P_{1} \cot \phi [1+(1-2\xi )^{2}\cot ^{2}\phi ]+M E-\frac{V E}{A},\\ T_{3}= & {} -\frac{4}{A}P_{1} E G \cot \phi -\frac{8}{A^{2}}P_{1} G^{2}(1-2\xi )\cot ^{2}\phi +\frac{P_{1} H}{A^{2}}+\frac{M}{A^{2}}-\frac{V E}{A},\\ T_{4}= & {} 24 G^{2}P_{1} \cot ^{2}\phi +32P_{1} E G^{3} A(1-2\xi )\cot ^{3}\phi \\&+\,24 G^{4} P_{1} \cot ^{2} \phi [1+(1-2\xi )^{2}\cot ^{2}\phi ] \\&-\,4 M G^{2} (1-2\xi )\cot ^{2}\phi +M H+4 V G^{3} \cot \phi [1+(1-2\xi )^{2}\cot ^{2}\phi ],\\ T_{5}= & {} \frac{2 P_{1} F}{A^{2}}+P_{1} E^{2}, \\ T_{6}= & {} 16G^{2}P_{1} E \cot ^{2}\phi +\frac{32}{A}P_{1} G^{3}(1-2\xi )\cot ^{3}\phi -\frac{4}{A}M G \cot \phi \\&+\,\frac{4}{A}V G^{2}(1-2\xi )\cot ^{2}\phi -\frac{V H}{A},\\ T_{7}= & {} -32P_{1} E G^{3}A \cot ^{3}\phi -96P_{1} G^{4}(1-2\xi )\cot ^{4}\phi \\&+\,8M G^{2}\cot ^{2}\phi -16V G^{3}(1-2\xi )\cot ^{3}\phi , \\ \frac{\partial \psi }{\partial \xi }= & {} \frac{1}{2h}(\psi _{i+1,j}-\psi _{i-1,j}) + O(h^{2}),\\ \frac{\partial \psi }{\partial \eta }= & {} \frac{1}{2h}(\psi _{i,j+1}-\psi _{i,j-1})+ O(h^{2}), \\ \frac{\partial ^{2} \psi }{\partial \xi ^{2}}= & {} \frac{1}{h^{2}}(\psi _{i+1,j}-2\psi _{i,j}+\psi _{i-1,j})+ O(h^{2}), \end{aligned}$$

$$\begin{aligned} \frac{\partial ^{2} \psi }{\partial \eta ^{2}}= & {} \frac{1}{h^{2}}(\psi _{i,j+1}-2\psi _{i,j}+\psi _{i,j-1})+ O(h^{2}), \\ \frac{\partial ^{2} \psi }{\partial \xi \partial \eta }= & {} \frac{1}{4h^{2}}(\psi _{i-1,j-1}-\psi _{i+1,j-1}+\psi _{i+1,j+1}-\psi _{i-1,j+1})+ O(h^{2}),\\ \frac{\partial ^{3} \psi }{\partial \xi ^{2}\partial \eta }= & {} \frac{1}{2h^{3}}(2\psi _{i,j-1}-2\psi _{i,j+1}-\psi _{i-1,j-1}\\&-\psi _{i+1,j-1}+\psi _{i+1,j+1}+\psi _{i-1,j+1})+ O(h^{2}), \\ \frac{\partial ^{3} \psi }{\partial \xi ^{3}}= & {} \frac{1}{h^{2}}(\psi _{\xi i+1,j}-2\psi _{\xi i,j}+\psi _{\xi i-1,j})+ O(h^{2}),\\ \frac{\partial ^{3} \psi }{\partial \eta ^{3}}= & {} \frac{1}{h^{2}}(\psi _{\eta i,j+1}-2\psi _{\eta i,j}+\psi _{\eta i,j-1})+ O(h^{2}),\\ \frac{\partial ^{3} \psi }{\partial \xi \partial \eta ^{2}}= & {} \frac{1}{2h^{3}}[2\psi _{i-1,j}-2\psi _{i+1,j}-\psi _{i-1,j-1}\\&+\psi _{i+1,j-1}+\psi _{i+1,j+1}-\psi _{i-1,j+1}]+ O(h^{2}), \\ \frac{\partial ^{4} \psi }{\partial \xi ^{4}}= & {} \frac{6}{h^{4}}[h(\psi _{\xi i+1,j}-\psi _{\xi i-1,j})-2(\psi _{i+1,j}-2\psi _{i,j}+\psi _{i-1,j})]+ O(h^{2}),\\ \frac{\partial ^{4} \psi }{\partial \eta ^{4}}= & {} \frac{6}{h^{4}}[h(\psi _{\eta i,j+1}-\psi _{\eta i,j-1})-2(\psi _{i,j+1}-2\psi _{i,j}+\psi _{i,j-1})]+ O(h^{2}), \\ \frac{\partial ^{4} \psi }{\partial \xi ^{3}\partial \eta }= & {} \frac{1}{2 h^{3}}[2\psi _{\xi i,j-1}-2\psi _{\xi i,j+1}-\psi _{\xi i-1,j-1}\\&-\psi _{\xi i+1,j-1}+\psi _{\xi i+1,j+1}+\psi _{\xi i-1,j+1}]+ O(h^{2}), \\ \frac{\partial ^{4} \psi }{\partial \xi \partial \eta ^{3}}= & {} \frac{1}{2 h^{3}}[2\psi _{\eta i-1,j}-2\psi _{\eta i+1,j}-\psi _{\eta i-1,j-1}\\&+\psi _{\eta i+1,j-1}+\psi _{\eta i+1,j+1}-\psi _{\eta i-1,j+1}]+ O(h^{2}), \\ \frac{\partial ^{4} \psi }{\partial \xi ^{2}\partial \eta ^{2}}= & {} \frac{1}{h^{4}}[4\psi _{i,j}-2(\psi _{i-1,j}+\psi _{i+1,j}+\psi _{i,j-1}+\psi _{i,j+1})+\psi _{i-1,j-1}\\&+\psi _{i+1,j-1}+\psi _{i+1,j+1}-\psi _{i-1,j+1}]+ O(h^{2}). \end{aligned}$$

Here, h is the step length on a uniform rectangular mesh in the transformed domain.