Impact of finite wavy wall thickness on entropy generation and natural convection of nanofluid in cavity partially filled with non-Darcy porous layer

Abstract

This paper investigates the natural convection inside a partially layered porous cavity with a heated wavy solid wall; the geometry is encountered in compact heat exchangers. Alumina nanoparticles are included in the water to enhance the heat exchange process. The incidental entropy generation is also studied to evaluate the thermodynamic irreversibility. The nanofluid flow is taken as laminar and incompressible while the advection inertia effect in the porous layer is taken into account by adopting the Darcy–Forchheimer model. The problem is explained in the dimensionless form of the governing equations and solved by the finite element method. The Darcy number (Da), porosity of the porous layer ($\varepsilon$), number of undulations (N), and the nanoparticles volume fraction ($\phi$) are varied to assess the heat transfer and the incidental entropy generation. It is found that the waviness of the solid wall augments the average Nusselt number and minimizes the generation of entropy. The results show for some circumstances that the Nusselt number is augmented by 43.8% when N is raised from 0 (flat solid wall) to 4. It is also found that the porosity of the porous layer is a more crucial parameter than its permeability, where a 37.4% enhancement in the Nusselt number is achieved when the porosity is raised from 0.2 to 0.8.

1 Introduction

A nanofluid encompassed by an undulated-wall enclosure is an appropriate and convenient strategy to follow for enhancing the natural heat convection. If the natural convection coincides with a transport process in porous media, this will be of great interest in many technical and engineering applications. Treatment of toxicity exhausted from automobiles, heat exchangers, cooling of gas turbine blades [1], filtration processes, crystal solidification, etc. are sample examples of these applications. The topic of nanofluid has become familiar since the research of Choi and Eastman [2] who did not expect that their “hope” of enhancing heat transfer had become to be a very important field for both investigations and applications. Nanometer-sized nanoparticles dispersed in a low thermal conductivity liquid are the idea behind a nanofluid. Abundant papers can be found that established correlations of predicting the nanofluid properties [3,4,5,6,7,8,9,10] and utilized a nanofluid in heat transfer enhancement in enclosures with or without porous media [11,12,13,14,15,16,17,18,19]. In addition, critical review studies that display and re-correlate the most interested works have demonstrated the importance of this field of investigation [20,21,22,23,24,25,26,27,28]. Nanofluids are also widely implemented in promoting the heat convection in porous media. Sun and Pop [16] have recorded the precedence in investigating the natural convection in a triangular cavity saturated with a porous medium using the Darcy model. Chamkha and Ismael [17] studied the natural convection in an irregular porous cavity heated by a triangular solid. Based on the solid size and Rayleigh number, they reported that the heat exchange may be improved or dropped with increasing values of volume fraction of nanoparticles. [29] reported a numerical solution of the magnetohydrodynamics flow of a micropolar nanofluid within a porous channel.

Cavities confining different media of different permeabilities have been studied early because of their critical applications in filtration and storing of radiative waste. The early experiments of Beavers and Joseph [30] demonstrated the unconfirmed no slip boundary condition regarding the tangential velocity at the interface between the clear and porous layer, which agree theoretically with the Darcy law. Because it possesses the feasibility of equating the viscosities of interfering different permeability layers, the Darcy–Brinkman model is used to represent the flow within the porous medium. Chamkha and Ismael [31] concluded that the natural convection in a partly-porous cavity can be enhanced by adding copper nanoparticles when the porous layer has a low permeability. Ismael and Chamkha [32] have demonstrated the feasibility of using nanofluids in partially porous cavities using a combination of various models of the most effective physical properties, namely the dynamic viscosity and the thermal conductivity. Sheremet and Trifonova [33] studied unsteady free convection in a vertical cylinder including two overlapping fluid and porous layers walled by a conductive solid. They used Beavers–Joseph boundary condition and reported that the Nusselt number declines with increasing the porous layer height, while it increases with increasing values of the Darcy number. Alsabery et al. [34] adopted the Darcy model along with the Beavers and Joseph boundary conditions to simulate the free convection in a tilted partly-porous cavity saturated with various nanoparticles. They imposed periodic temperatures on the cavity vertical walls. Gibanov et al. [35] studied the mixed convection in an interesting geometry that is a ventilated square cavity containing a triangular porous layer. With their geometry, it was found that the heat transfer decreased when the Darcy number grew from $10^{-7}$ up to $10^{-3}$, then the heat transfer was enhanced. They discussed the formation of the buoyancy circulation inside the vented cavity. Ismael and Ghalib [36] controlled the natural convection and the thermosolutal convection inside a partially porous cavity using a conductive square cylinder. They found that the growth of the Darcy number significantly enhanced both the convective heat and mass transfers. They suggested that the best position of the conductive cylinder was in the vicinity of the hot wall, within the porous layer. Ismael [37] performed a double diffusive mixed convection in a novel lid-driven partially porous cavity with a moving curved wall. Diverse roles of the Rayleigh number, speed of the moving wall, buoyancy ratio and the Lewis number were reported in detail. It is worth to mention that in [36, 37], the impact of tortuous paths of the porous layer was taken into account and found to have notable effects on the transport processes. However, it should not be understood that early works regarding the partially porous cavity have not been highlighted, but for the sake of brevity, readers may find most of them reviewed in [22,23,24,25,26,27,28].

To determine the extent of energy destruction accompanying the natural convection, the analysis of entropy can be included in the analysis [38]. Yilbas et al. [39] remarked that within the free convection in a rectangular cavity, the strengthening of the circulation along the horizontal axis increases the local entropy generation. Famouri and Hooman [40] showed that when the entropy resulting from fluid friction irreversibility FFI is absent, the entropy due to heat transfer irreversibility HTI increases monotonically with the temperature difference that is set differentially on the cavity vertical walls. A heated slab partitioned their cavity. Ilis et al. [41] showed that at a high Rayleigh number, the entropy generation in different cavities with the same area was due to the fluid friction irreversibility. Basak et al. [42] investigated the entropy generation and natural convection in a cavity containing a liquid metal or aqueous solution saturated in a porous medium with different boundary conditions. For an optimal entropy generation rate, they indicated an intermediate value of the Darcy number. Lam and Prakash [43] implemented porous inserts to eliminate hot spots produced by eddies generated when an impinging jet strikes a series of protruding heat sources. The heat sources are fixed on an impingement plate. They noticed that the heat exchange and the entropy boost with increasing values of the Darcy and Reynolds numbers. Oztop et al. [44] performed a three-dimensional simulation of entropy generation and free convection in a cubical partially open cavity. It was found that the edge of the location of the opening was the dominant parameter of the rate of entropy generation. Bondareva et al. [45] worked on the free convection of a nanofluid and entropy generation in an open triangular cavity and reported an increase in the rate of entropy generation with copper nanoparticles loading. Armaghani et al. [46] investigated the free convection and the generated entropy in an inclined partially porous cavity filled with a nanofluid. It has been shown the maximal heat transfer and minimal entropy generation (preferred thermal performance) can be obtained by adjusting the Rayleigh number, inclination of the cavity and the size of the porous layer. Aly et al. [47] worked on the mixed convection and the entropy generation inside a lid-driven partially layered cavity saturated with a Cu-water nanofluid. A wavy porous layer was fixed in the middle of the cavity resulting in dividing the volume to three layers. Their results demonstrated the supremacy of HTI with decreasing values of the Darcy number. Alsabery et al. [48], the team of the current paper, have conducted an analysis about mixed convection and the related entropy generation in a wavy-walled cavity filled with a nanofluid and containing a central rotating circular cylinder. It has been noted that at higher Rayleigh numbers, a deterioration of the Nusselt number occurs. In addition, the rotation of the cylinder switches the dominance of FFI.

Hence, based on this brief survey, it can be concluded that the natural convection and entropy generation analyses have not been investigated inside a partially porous cavity heated from below by a wavy solid wall. Therefore, the current paper aims to include the nanofluid effect filled in such a cavity. The waviness of the solid wavy wall and the porosity of the porous layer are some of the important parameters that are expected to govern the heat exchange and the accompanying thermodynamic irreversibility.

2 Mathematical formulation

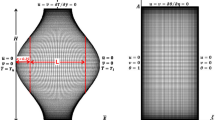
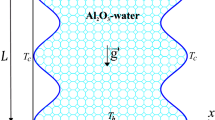
The current numerical work explains the steady two-dimensional (2D) entropy generation and natural convection problem in a porous wavy-walled cavity with length L, as illustrated in Fig. 1. The wavy-walled cavity is divided to three segments, the first layer (top segment) is filled with a nanofluid, the second layer (middle segment) is filled with a porous medium that is saturated with a nanofluid, while the third layer (bottom segment) is assumed to be a solid wall. The bottom wavy solid wall has a constant hot temperature $T_\mathrm{h}$, while the vertical (left and right) walls are preserved at a constant cold temperature $T_\mathrm{c}$. The horizontal top wall is kept adiabatic. The boundaries of the domain are impermeable and the nanofluid is made of water and $\text {Al}_2\text {O}_3$ nanoparticles fill the wavy cavity. The Forchheimer–Brinkman-extended Darcy model and the Boussinesq approximation are applicable. The local thermodynamic equilibrium condition is assumed for the convective nanofluid and the solid matrix in the porous layer. The type of the porous media is presumed to be glass balls ($k_\mathrm{m}=1.05\,\mathrm{W/m}\,^\circ \mathrm{C}$). While the type of the solid wavy wall is considered to be brickwork ($k_\mathrm{w}=0.76\mathrm{W/m}\,^\circ \mathrm{C}$). The continuity, momentum and energy equations for laminar and steady Newtonian fluid flow with the consideration of the above-mentioned assumptions are written as following:

For the nanofluid layer [48]:

$$\begin{aligned}&\frac{{\partial u_{\mathrm{nf}}}}{{\partial x}} + \frac{{\partial v_{\mathrm{{nf}}}}}{{\partial y}} = 0, \end{aligned}$$

(1)

$$\begin{aligned}&u_{\mathrm{{nf}}}\frac{{\partial u_{\mathrm{{nf}}}}}{{\partial x}} + v_{\mathrm{{nf}}}\frac{{\partial u_{\mathrm{{nf}}}}}{{\partial y}}\nonumber \\&\quad = - \frac{1}{\rho _{\mathrm{{nf}}} }\frac{{\partial p}}{{\partial x}} +\frac{\mu _{\mathrm{{nf}}}}{\rho _{\mathrm{{nf}}}} \left( {\frac{{\partial ^2 u_{\mathrm{{nf}}}}}{{\partial x^2 }} + \frac{{\partial ^2 u_{\mathrm{{nf}}}}}{{\partial y^2 }}} \right) , \end{aligned}$$

(2)

$$\begin{aligned}&u_{\mathrm{{nf}}}\frac{{\partial v_{\mathrm{{nf}}}}}{{\partial x}} + v_{\mathrm{{nf}}}\frac{{\partial v_{\mathrm{{nf}}}}}{{\partial y}}\nonumber \\&\quad = - \frac{1}{\rho _{\mathrm{{nf}}} }\frac{{\partial p}}{{\partial y}} +\frac{\mu _{\mathrm{{nf}}}}{\rho _{\mathrm{{nf}}}} \left( {\frac{{\partial ^2 v_{\mathrm{{nf}}}}}{{\partial x^2 }} + \frac{{\partial ^2 v_{\mathrm{{nf}}}}}{{\partial y^2 }}} \right) \nonumber \\&\quad \quad + \beta _{\mathrm{{nf}}} g \left( T_{\mathrm{{nf}}}-T_{c}\right) , \end{aligned}$$

(3)

$$\begin{aligned}&{u_{\mathrm{{nf}}}}\frac{{\partial {T_{\mathrm{{nf}}}}}}{{\partial x}} + {v_{\mathrm{{nf}}}}\frac{{\partial {T_{\mathrm{{nf}}}}}}{{\partial y}} = \frac{k_{\mathrm{{nf}}}}{(\rho C_{p})_{\mathrm{{nf}}}}\left( {\frac{{{\partial ^2}{T_{\mathrm{{nf}}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{T_{\mathrm{{nf}}}}}}{{\partial {y^2}}}} \right) . \end{aligned}$$

(4)

For the porous layer [49]:

$$\begin{aligned}&\frac{{\partial u_{\mathrm{{m}}}}}{{\partial x}} + \frac{{\partial v_{\mathrm{{m}}}}}{{\partial y}} = 0, \end{aligned}$$

(5)

$$\begin{aligned}&\frac{\rho _{\mathrm{{nf}}}}{\varepsilon ^2} \left( u_{\mathrm{{m}}}\frac{{\partial u_{\mathrm{{m}}}}}{{\partial x}} + v_{\mathrm{{m}}}\frac{{\partial u_{\mathrm{{m}}}}}{{\partial y}}\right) \nonumber \\&\quad = - \frac{{\partial p}}{{\partial x}} + \frac{\mu _{\mathrm{{nf}}}}{\varepsilon }\,\left( {\frac{{{\partial ^2}u_{\mathrm{{m}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}u_{\mathrm{{m}}}}}{{\partial {y^2}}}} \right) \nonumber \\&\quad \quad -\left( \frac{\mu _{\mathrm{{nf}}}}{K}u_{\mathrm{{m}}}- F \frac{\rho _{\mathrm{{nf}}} u_{\mathrm{{m}}} \left| \mathbf{u} \right| }{\sqrt{K}} \right) , \end{aligned}$$

(6)

$$\begin{aligned}&\frac{\rho _{\mathrm{{nf}}}}{\varepsilon ^2} \left( u_{\mathrm{{m}}}\frac{{\partial v_{\mathrm{{m}}}}}{{\partial x}} + v_{\mathrm{{m}}}\frac{{\partial v_{\mathrm{{m}}}}}{{\partial y}}\right) \nonumber \\&\quad = - \frac{{\partial p}}{{\partial y}} + \frac{\mu _{\mathrm{{nf}}}}{\varepsilon }\,\left( {\frac{{{\partial ^2}v_{\mathrm{{m}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}v_{\mathrm{{m}}}}}{{\partial {y^2}}}} \right) \nonumber \\&\quad\quad -\left( \frac{\mu _{\mathrm{{nf}}}}{K}v_{\mathrm{{m}}}- F \frac{\rho _{\mathrm{{nf}}} v_{\mathrm{{m}}} \left| \mathbf{u} \right| }{\sqrt{K}} \right) + (\rho \beta )_{\mathrm{{nf}}} \text {g}(T_{\mathrm{{m}}} - {T_\mathrm{c}}), \end{aligned}$$

(7)

$$\begin{aligned}&u_{\mathrm{{m}}}\frac{{\partial T_{\mathrm{{m}}}}}{{\partial x}} + v_{\mathrm{{m}}}\frac{{\partial T_{\mathrm{{m}}}}}{{\partial y}} = \frac{k_{\mathrm{eff}}}{(\rho C_{p})_{\mathrm{{nf}}}} \left( {\frac{{{\partial ^2}T_{\mathrm{{m}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}T_{\mathrm{{m}}}}}{{\partial {y^2}}}} \right) . \end{aligned}$$

(8)

The energy equation of the wavy solid wall is:

$$\begin{aligned} \frac{{{\partial ^2}{T_{\mathrm{w}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{T_{\mathrm{w}}}}}{{\partial {y^2}}} = 0, \end{aligned}$$

(9)

where the subscripts m and w stand for the porous media and solid wall, respectively. x and y present the components of the fluid velocity, $\left| \mathbf{u} \right| =\sqrt{u^2 + v^2}$ is the Darcy velocity, $\text {g}$ is the acceleration due to gravity, $F=\frac{b}{\sqrt{a}\varepsilon ^{3/2}}$ represents Forchheimer’s coefficient, with $a=150$ and $b=1.75$. $k_{\mathrm{eff}}$ shows the effective thermal conductivity of nanofluid saturated porous medium, $\varepsilon$ is the porosity of the medium and K is the permeability of the porous medium that is described as the following [50]:

$$\begin{aligned} K=\frac{\varepsilon ^{3} d^2_\mathrm{m}}{150 (1-\varepsilon )^2}. \end{aligned}$$

(10)

Fig. 1

Physical model of convection in a wavy-walled cavity together with the coordinate system

Here, $d_\mathrm{m}$ shows the average particle size of the porous bed.

The thermo-physical properties of $\mathrm{Al}_{2}\mathrm{O}_{3}$-water nanofluid including heat capacitance ($(\rho C_p)_{\mathrm{{nf}}}$), effective thermal diffusivity ($\alpha _{\mathrm{{nf}}}$), effective density ($\rho _{\mathrm{{nf}}}$) and the thermal expansion coefficient ($\beta _{\mathrm{{nf}}}$) can be explained respectfully by the following [5, 51]:

$$\begin{aligned}&(\rho C_p)_{\mathrm{{nf}}}=(1-\phi )(\rho C_p)_{f}+\phi (\rho C_p)_{p}, \end{aligned}$$

(11)

$$\begin{aligned}&\alpha _{\mathrm{{nf}}}=\frac{k_{\mathrm{{nf}}}}{(\rho C_p)_{\mathrm{{nf}}}}, \end{aligned}$$

(12)

$$\begin{aligned}&\rho _{\mathrm{{nf}}}=(1-\phi )\rho _{f}+\phi \rho _{p}, \end{aligned}$$

(13)

$$\begin{aligned}&{(\rho \beta )_{\mathrm{{nf}}}} = (1 - \phi ){(\rho \beta )_{f}} + \phi {(\rho \beta )_{p}}. \end{aligned}$$

(14)

The dynamic viscosity ratio ($\frac{\mu _{\mathrm{{nf}}}}{\mu _\mathrm{{f}}}$) of water-$\hbox {Al}_{2}\hbox {O}_{3}$ nanofluids for 33nm particle size in the ambient condition is described by [5] as follows:

$$\begin{aligned} \frac{\mu _{\mathrm{{nf}}}}{\mu _\mathrm{{f}}} = 1/\left( 1-34.87\left( d_p/d_\mathrm{{f}}\right) ^{-0.3}\phi ^{1.03}\right) . \end{aligned}$$

(15)

And the thermal conductivity ratio ($\frac{k_{\mathrm{{nf}}}}{k_{f}}$) of water-$\hbox {Al}_{2}\hbox {O}_{3}$ nanofluids is calculated by [5] as follows:

$$\begin{aligned} \frac{k_{\mathrm{{nf}}}}{k_{f}}= 1 + 4.4 \text {Re}_B^{0.4} \text {Pr}^{0.66} \left( \frac{T}{T_{fr}}\right) ^{10} \left( \frac{k_p}{k_\mathrm{{f}}}\right) ^{0.03} \phi ^{0.66}, \end{aligned}$$

(16)

where $\text {Re}_B$ is defined as

$$\begin{aligned} \text {Re}_B=\frac{\rho _\mathrm{{f}} u_B d_p}{\mu _\mathrm{{f}}}, \quad u_B = \frac{2k_b T}{\pi \mu _\mathrm{{f}} d_p^2}. \end{aligned}$$

(17)

The range of the nanoparticles volume fraction in [5] work is ($0\le \phi \le 0.04$). Here, $k_b=1.380648 \times 10^{-23} (J/K)$ is the Boltzmann constant. $l_\mathrm{{f}}=0.17$nm is the mean path of fluid particles. $d_\mathrm{{f}}$ is the molecular diameter of water given as [5]:

$$\begin{aligned} d_\mathrm{{f}} = \frac{6 M}{N \pi \rho _\mathrm{{f}}}, \end{aligned}$$

(18)

where M is the molecular weight of the base fluid, N is the Avogadro number and $\rho _\mathrm{{f}}$ is the density of the base fluid at standard temperature (310 K). By presenting the following non-dimensional variables:

$$\begin{aligned}(X,Y)&=\frac{(x,y)}{L},\,\, U_\mathrm{nf,m}=\frac{u_\mathrm{nf,m}L}{\alpha _\mathrm{{f}}},\,\, V_\mathrm{nf,m}=\frac{v_\mathrm{nf,m}L}{\alpha _\mathrm{{f}}},\nonumber \\ \theta _{\mathrm{{nf}}}&=\frac{T_{\mathrm{{nf}}} - T_\mathrm{c}}{T_\mathrm{h} - T_\mathrm{c}},\,\, \theta _\mathrm{m}=\frac{T_\mathrm{m} - T_\mathrm{c}}{T_\mathrm{h} - T_\mathrm{c}},\nonumber \\\theta _\mathrm{w}&=\frac{T_\mathrm{w} - T_\mathrm{c}}{T_\mathrm{h} - T_\mathrm{c}}, \,\, P=\frac{pL^2}{\rho _{f} \alpha _\mathrm{{f}}^2}, \,\, k_{\mathrm{eff}}=\varepsilon k_{\mathrm{{nf}}}+(1-\varepsilon )k_\mathrm{m}, \nonumber \\ C_F &= \frac{1.75}{\sqrt{150}}. \end{aligned}$$

(19)

The dimensionless governing equations are demonstrated as:

In the nanofluid layer:

$$\begin{aligned}&\frac{{\partial U_{\mathrm{{nf}}}}}{{\partial X}} + \frac{{\partial V_{\mathrm{{nf}}}}}{{\partial Y}} = 0, \end{aligned}$$

(20)

$$\begin{aligned}&U_{\mathrm{{nf}}}\frac{{\partial U_{\mathrm{{nf}}}}}{{\partial X}} + V_{\mathrm{{nf}}}\frac{{\partial U_{\mathrm{{nf}}}}}{{\partial Y}} = - \frac{{\partial P}}{{\partial X}} \nonumber \\&\qquad + \Pr \frac{\rho _{f}}{\rho _{\mathrm{{nf}}}} \frac{\mu _{\mathrm{{nf}}}}{\mu _{f}} \left( {\frac{{{\partial ^2}U_{\mathrm{{nf}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}U_{\mathrm{{nf}}}}}{{\partial {Y^2}}}} \right) , \end{aligned}$$

(21)

$$\begin{aligned}&U_{\mathrm{{nf}}}\frac{{\partial V_{\mathrm{{nf}}}}}{{\partial X}} + V_{\mathrm{{nf}}}\frac{{\partial V_{\mathrm{{nf}}}}}{{\partial Y}} = - \frac{{\partial P}}{{\partial Y}} \nonumber \\&\qquad + \Pr \frac{\rho _{f}}{\rho _{\mathrm{{nf}}}} \frac{\mu _{\mathrm{{nf}}}}{\mu _{f}} \left( {\frac{{{\partial ^2}V_{\mathrm{{nf}}}}}{{\partial {X^2}}} + \frac{{{\partial ^2}V_{\mathrm{{nf}}}}}{{\partial {Y^2}}}} \right) \nonumber \\&\qquad + \frac{(\rho \beta )_{\mathrm{{nf}}}}{\rho _{\mathrm{{nf}}} \beta _{f}} {Ra} \, {\Pr } \, \theta , \end{aligned}$$

(22)

$$\begin{aligned}&U_{\mathrm{{nf}}}\frac{{\partial \theta _{\mathrm{{nf}}}}}{{\partial X}} + V_{\mathrm{{nf}}}\frac{{\partial \theta _{\mathrm{{nf}}}}}{{\partial Y}}\nonumber \\&\quad = \frac{(\rho C_p)_{f}}{(\rho C_p)_{\mathrm{{nf}}}} \frac{k_{\mathrm{{nf}}}}{k_{f}} \left( \frac{{{\partial ^2}\theta _{\mathrm{{nf}}}}}{{\partial {X^2}}} + \frac{{{\partial ^2}\theta _{\mathrm{{nf}}}}}{{\partial {Y^2}}}\right) . \end{aligned}$$

(23)

In the porous layer:

$$\begin{aligned}&\frac{{\partial U_{\mathrm{{m}}}}}{{\partial X}} + \frac{{\partial V_{\mathrm{{m}}}}}{{\partial Y}} = 0, \end{aligned}$$

(24)

$$\begin{aligned}&\frac{1}{\varepsilon ^2}\left( U_{\mathrm{{m}}}\frac{\partial U_{\mathrm{{m}}}}{\partial X} + V_{\mathrm{{m}}}\frac{\partial U_{\mathrm{{m}}}}{\partial Y}\right) \nonumber \\&\quad = - \frac{\partial P}{\partial X}+ \frac{\rho _{f}}{\rho _{\mathrm{{nf}}}} \frac{\mu _{\mathrm{{nf}}}}{\mu _{f}} \frac{\Pr }{\varepsilon }\left( \frac{\partial ^2 U_{\mathrm{{m}}}}{\partial X^2} + \frac{\partial ^2 U_{\mathrm{{m}}}}{\partial Y^2}\right) \nonumber \\&\qquad - \frac{\rho _{f}}{\rho _{\mathrm{{nf}}}} \frac{\mu _{\mathrm{{nf}}}}{\mu _{f}} \frac{\Pr }{Da}U_{\mathrm{{m}}}- \frac{C_F\sqrt{U^2_{\mathrm{{m}}} + V^2_{\mathrm{{m}}}}}{\sqrt{Da}} \frac{U_{\mathrm{{m}}}}{\varepsilon ^{3/2}}, \end{aligned}$$

(25)

$$\begin{aligned}&\frac{1}{\varepsilon ^2}\left( U_{\mathrm{{m}}}\frac{\partial V_{\mathrm{{m}}}}{\partial X} + V_{\mathrm{{m}}}\frac{\partial V_{\mathrm{{m}}}}{\partial Y}\right) \nonumber \\&\quad = - \frac{\partial P}{\partial Y}+ \frac{\rho _{f}}{\rho _{\mathrm{{nf}}}} \frac{\mu _{\mathrm{{nf}}}}{\mu _{f}} \frac{\Pr }{\varepsilon }\left( \frac{\partial ^2 V_{\mathrm{{m}}}}{\partial X^2} + \frac{\partial ^2 V_{\mathrm{{m}}}}{\partial Y^2}\right) \nonumber \\&\qquad - \frac{\rho _{f}}{\rho _{\mathrm{{nf}}}} \frac{\mu _{\mathrm{{nf}}}}{\mu _{f}} \frac{\Pr }{Da}V_{\mathrm{{m}}}- \frac{C_F\sqrt{U^2_{\mathrm{{m}}} + V^2_{\mathrm{{m}}}}}{\sqrt{Da}} \frac{V_{\mathrm{{m}}}}{\varepsilon ^{3/2}} \nonumber \\&\qquad + \frac{(\rho \beta )_{\mathrm{{nf}}}}{\rho _{\mathrm{{nf}}} \beta _{f}} {Ra} \, {\Pr } \, \theta , \end{aligned}$$

(26)

$$\begin{aligned}&U_{\mathrm{{m}}}\frac{{\partial \theta _{\mathrm{{m}}}}}{{\partial X}} + V_{\mathrm{{m}}}\frac{{\partial \theta _{\mathrm{{m}}}}}{{\partial Y}} \nonumber \\&\quad = \frac{k_{\mathrm{eff}}}{k_{f}} \frac{(\rho C_p)_{f}}{(\rho C_p)_{\mathrm{{nf}}}} \left( \frac{{{\partial ^2}\theta _{\mathrm{{m}}}}}{{\partial {X^2}}} + \frac{{{\partial ^2}\theta _{\mathrm{{m}}}}}{{\partial {Y^2}}}\right) . \end{aligned}$$

(27)

In the wavy solid wall:

$$\begin{aligned} \frac{{{\partial ^2}\theta _\mathrm{w}}}{{\partial {X^2}}} + \frac{{{\partial ^2}\theta _\mathrm{w}}}{{\partial {Y^2}}} = 0. \end{aligned}$$

(28)

The dimensionless boundary conditions of Eqs. (20)–(28) are:

$$\begin{aligned}&\text {On the bottom hot wavy wall:} \nonumber \\&U = V = 0,\,\, \theta _{\mathrm{w}}=1,\,\, A(1-\cos (2N\pi Y)),\nonumber \\&\quad 0\le X\le 1, \end{aligned}$$

(29)

$$\begin{aligned}&\text {On the left cold vertical wall:} \nonumber \\&U = V = 0,\,\, \theta _{\mathrm{{nf}}}=\theta _{\mathrm{{m}}}=\theta _{\mathrm{w}}=0,\nonumber \\&\quad X=0,\,\, 0\le Y\le 1, \end{aligned}$$

(30)

$$\begin{aligned}&\text {On the right cold vertical wall:} \nonumber \\&U = V = 0,\,\, \theta _{\mathrm{{nf}}}=\theta _{\mathrm{{m}}}=\theta _{\mathrm{w}}=0,\nonumber \\&\quad X=1,\,\, 0\le Y\le 1, \end{aligned}$$

(31)

$$\begin{aligned}&\text {On the top adiabatic horizontal wall:} \nonumber \\&U = V = 0,\,\, \frac{\partial \theta _{\mathrm{{nf}}}}{\partial Y}=0,\,\, 0\le X \le 1,\,\, Y=1, \end{aligned}$$

(32)

$$\begin{aligned}&\text {On the interface wavy wall:} \nonumber \\&U = V = 0,\,\, \frac{\partial \theta _\mathrm{m}}{\partial n} = K_{r}\frac{\partial \theta _{\mathrm{w}}}{\partial n},\nonumber \\&\quad D+A(1-\cos (2N\pi Y)),\,\, 0\le X\le 1. \end{aligned}$$

(33)

At the wall between the nanofluid and porous layers, the dimensionless boundary conditions can be concluded from continuity of tangential and normal velocities, shear and normal stresses, temperature and the heat flux across the wall, and suppose that the dynamic viscosity in both nanofluid and porous layers is the same ($\mu _{\mathrm{{nf}}} = \mu _{\mathrm{{m}}}$). Hence, the wall dimensionless boundary conditions are described as follows:

$$\begin{aligned} \theta _{\mathrm{{nf}}}{\mid _{Y = {H^+ }}}& = \theta _{\mathrm{{m}}}{\mid _{Y = {H^- }}}, \end{aligned}$$

(34)

$$\begin{aligned} \frac{{\partial {\theta _{\mathrm{{nf}}}}}}{{\partial Y}}{\bigg |_{Y = {H^+ }}}&= \frac{k_{\mathrm{eff}}}{k_{\mathrm{{nf}}}} \frac{{\partial {\theta _\mathrm{m}}}}{{\partial Y}}{\bigg |_{Y = {H^- }}}, \end{aligned}$$

(35)

$$\begin{aligned} {U_{\mathrm{{nf}}}}{\mid _{Y = {H^+ }}}& = {U_\mathrm{m}}{\mid _{Y = {H^- }}}, \end{aligned}$$

(36)

$$\begin{aligned} {V_{\mathrm{{nf}}}}{\mid _{Y = {H^+ }}}& = {V_\mathrm{m}}{\mid _{Y = {H^- }}}, \end{aligned}$$

(37)

where D is the thickness of the wavy solid wall, H is the thickness of the nanofluid layer and the subscripts $+$ and − indicate that the respective quantities are evaluated while approaching the interface from the nanofluid and porous layers, respectively. $Ra = \frac{g \beta _\mathrm{{f}} \left( T_\mathrm{h}-T_\mathrm{c} \right) L^3}{\nu _{f} \alpha _{f}}$ is the Rayleigh number of the base fluid and $\Pr =\frac{\nu _\mathrm{{f}}}{\alpha _\mathrm{{f}}}$ is the Prandtl number of the base fluid. And $K_{r} = {k_\mathrm{w}}/{k_{\mathrm{eff}}}$ describes the thermal conductivity ratio. The local Nusselt number on the interface wavy wall between the solid and porous layer is evaluated as the following:

$$\begin{aligned} Nu_{i} = \frac{k_{\mathrm{eff}}}{k_{f}} \left( \frac{\partial \theta _{\mathrm{{m}}}}{\partial n}\right) _{n}. \end{aligned}$$

(38)

Finally, average Nusselt number on the interface wavy wall between the solid and porous layer is the following:

$$\begin{aligned} \overline{\mathrm{Nu}}_{i} = \int _{0}^{n} \mathrm{Nu}_{i} {\mathrm{d}}n. \end{aligned}$$

(39)

The entropy generation of the nanofluid layer is given by [41, 48]:

$$\begin{aligned} S_{\mathrm{{nf}}}& = \frac{k_{\mathrm{{nf}}}}{T_0^2} \left[ \left( \frac{\partial T}{\partial x}\right) ^2 + \left( \frac{\partial T}{\partial y}\right) ^2 \right] \nonumber \\&+ \frac{\mu _{\mathrm{{nf}}}}{T_0} \left[ 2\left( \frac{\partial u}{\partial x}\right) ^2 + 2\left( \frac{\partial v}{\partial y}\right) ^2 + \left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial x} \right) ^2 \right] . \end{aligned}$$

(40)

The entropy generation relation of the porous layer is given by [38]

$$\begin{aligned} S_{\mathrm{{m}}}& = \frac{k_\mathrm{eff}}{T_0^2} \left[ \left( \frac{\partial T}{\partial x}\right) ^2 + \left( \frac{\partial T}{\partial y}\right) ^2 \right] \nonumber \\&\quad + \frac{\mu _{f}}{T_0} \left[ 2\left( \frac{\partial u}{\partial x}\right) ^2 + 2\left( \frac{\partial v}{\partial y}\right) ^2 + \left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial x} \right) ^2 \right] \nonumber \\&\quad +\,\frac{\mu _{f}}{K T_0}\left( u^2+v^2\right) . \end{aligned}$$

(41)

In dimensionless form, Eq. (40) can be expressed as:

$$\begin{aligned} S_{\text {GEN},\mathrm{nf}}& = \frac{k_{\mathrm{{nf}}}}{k_\mathrm{{f}}} \left[ \left( \frac{\partial \theta }{\partial X}\right) ^2 + \left( \frac{\partial \theta }{\partial Y}\right) ^2 \right] \nonumber \\&\quad + \frac{\mu _{\mathrm{{nf}}}}{\mu _\mathrm{{f}}} N_{\mathrm{{nf}}} \left\{ 2 \left[ \left( \frac{\partial U}{\partial X}\right) ^2 + \left( \frac{\partial V}{\partial Y}\right) ^2 \right] \right. \nonumber \\&\quad \left. + \left( \frac{\partial ^2 U}{\partial Y^2} + \frac{\partial ^2 V}{\partial X^2} \right) ^2 \right\} , \end{aligned}$$

(42)

where $N_{\mathrm{{nf}}}$ is the irreversibility distribution ratio in the nanofluid layer which can be expressed as:

$$\begin{aligned} N_{\mathrm{{nf}}}=\frac{\mu _\mathrm{{f}} T_0}{k_\mathrm{{f}}} \left( \frac{\alpha _\mathrm{{f}}}{L(\varDelta T)}\right) ^2, \end{aligned}$$

(43)

and $S_{\text {GEN}, nf}$ presents the dimensionless entropy generation rate:

$$\begin{aligned} S_{\text {GEN}, nf}=S_{\text {gen}, nf}\frac{T_0^2 L^2}{k_\mathrm{{f}} (\varDelta T)^2}. \end{aligned}$$

(44)

The terms of Eq. (42) can be separated according to the following form:

$$\begin{aligned} S_{\text {GEN}, nf}= S_{nf, \theta } + S_{nf, \varPsi }, \end{aligned}$$

(45)

where $S_{nf, \theta }$ and $S_{nf, \varPsi }$ are showing the entropy generation due to HTI and FFI of the nanofluid layer, respectively.

$$\begin{aligned} S_{nf, \theta }& = \frac{k_{\mathrm{{nf}}}}{k_\mathrm{{f}}} \left[ \left( \frac{\partial \theta }{\partial X}\right) ^2 + \left( \frac{\partial \theta }{\partial Y}\right) ^2 \right] , \end{aligned}$$

(46)

$$\begin{aligned} S_{nf, \varPsi }& = \frac{\mu _{\mathrm{{nf}}}}{\mu _\mathrm{{f}}} N_{\mathrm{{nf}}} \left\{ 2 \left[ \left( \frac{\partial U}{\partial X}\right) ^2 + \left( \frac{\partial V}{\partial Y}\right) ^2 \right] \right. \nonumber \\&\quad + \left. \left( \frac{\partial ^2 U}{\partial Y^2} + \frac{\partial ^2 V}{\partial X^2} \right) ^2 \right\} . \end{aligned}$$

(47)

In dimensionless form, Eq. (41) can be expressed as:

$$\begin{aligned} S_{\text {GEN}, \mathrm{m}}& = \frac{k_\mathrm{eff}}{k_\mathrm{{f}}} \left[ \left( \frac{\partial \theta }{\partial X}\right) ^2 + \left( \frac{\partial \theta }{\partial Y}\right) ^2 \right] + \frac{\mu _{\mathrm{{nf}}}}{\mu _\mathrm{{f}}} N_{\mathrm{{m}}} \nonumber \\&\quad \times \left\{ Da \left[ 2 \left( \left( \frac{\partial U}{\partial X}\right) ^2 + \left( \frac{\partial V}{\partial Y}\right) ^2 \right) \right. \right. \nonumber \\&\quad \left. \left. + \left( \frac{\partial ^2 U}{\partial Y^2} + \frac{\partial ^2 V}{\partial X^2} \right) ^2 \right] + \left( U^2+V^2\right) \right\} , \end{aligned}$$

(48)

where $N_{\mathrm{{m}}}=\frac{\mu _\mathrm{{f}} T_0}{k_\mathrm{{f}}} \left( \frac{\alpha _\mathrm{{f}}^2}{K(\varDelta T)^2}\right)$ is the irreversibility distribution ratio in the porous layer and $S_{\text {GEN},\mathrm{m}}=S_{\text {gen},m}\frac{T_0^2 L^2}{k_\mathrm{{f}} (\varDelta T)^2}$.

The terms of Eq. (48) can be separated in the following form:

$$\begin{aligned} S_{\text {GEN}, m}= S_{m, \theta } + S_{m, \varPsi }, \end{aligned}$$

(49)

where $S_{m, \theta }$ and $S_{m, \varPsi }$ are presenting the entropy generation due to HTI and FFI of the porous layer, respectively.

$$\begin{aligned} S_{m, \theta }& = \frac{k_\mathrm{eff}}{k_\mathrm{{f}}} \left[ \left( \frac{\partial \theta }{\partial X}\right) ^2 + \left( \frac{\partial \theta }{\partial Y}\right) ^2 \right] , \end{aligned}$$

(50)

$$\begin{aligned} S_{m, \varPsi }& = \frac{\mu _{\mathrm{{nf}}}}{\mu _\mathrm{{f}}} N_{\mathrm{{m}}} \nonumber \\&\quad \times \left\{ Da \left[ 2 \left( \left( \frac{\partial U}{\partial X}\right) ^2 + \left( \frac{\partial V}{\partial Y}\right) ^2 \right) \right. \right. \nonumber \\&\quad + \left. \left. \left( \frac{\partial ^2 U}{\partial Y^2} + \frac{\partial ^2 V}{\partial X^2} \right) ^2 \right] + \left( U^2+V^2\right) \right\} . \end{aligned}$$

(51)

In the dimensionless form, the local entropy generation can be expressed as:

$$\begin{aligned} S_{\text {GEN}} = S_{\text {GEN}, nf} + S_{\text {GEN}, m}. \end{aligned}$$

(52)

The global entropy generation (GEG) is evaluated by integrating Eq. (52) over the considered domain

$$\begin{aligned} \text {GEG}& = \int S_{\text {GEN}} {\mathrm{d}}X {\mathrm{d}}Y = \int S_{\text {GEN}, nf} {\mathrm{d}}X {\mathrm{d}}Y\nonumber \\&\quad + \int S_{\text {GEN}, m} {\mathrm{d}}X {\mathrm{d}}Y. \end{aligned}$$

(53)

The modified Bejan number (Be) is defined as follows:

$$\begin{aligned} Be = \frac{\int S_{nf, \theta } {\mathrm{d}}X {\mathrm{d}}Y + \int S_{m, \theta } {\mathrm{d}}X {\mathrm{d}}Y}{\text {GEG}}. \end{aligned}$$

(54)

When $Be > 0.5$, the HTI is the dominant, while when $Be < 0.5$, the FFI is the dominant.

3 Numerical method and validation

The dimensionless governing equations Eqs. (20)–(28) subject to the selected dimensionless boundary conditions Eqs. (29)–(37) are solved with Galerkin weighted residual finite element method. The computational domain is discretized into triangular elements (see Fig. 2) for each of the flow variables within the computational domain. Newton-Raphson iteration algorithm was utilized for simplifying the nonlinear terms in the momentum equations. The convergence of the solution is assumed when the relative error for each of the variables satisfies the following convergence criteria:

$$\begin{aligned} \left| \frac{\varGamma ^{i+1}-\varGamma ^{i}}{\varGamma ^{i+1}}\right| \le \eta , \end{aligned}$$

here i shows the iteration number and $\eta$ is the convergence criterion. In the current work, the convergence criterion was set at $\eta =10^{-6}$.

Fig. 2

FEM grid-points distribution for the grid size of 9721 elements

To validate the numerical code of the current data, a comparison is made between the current work results and the numerical one described by Khanafer et al. [52] for the case of natural convection heat transfer in a wavy non-Darcian porous cavity, as shown in Fig. 3. In addition, the resulting figures and the one examined by Singh and Thorpe [53] and Sheremet and Trifonova [33] are compared for the case of natural convection in a square cavity including a fluid layer overlying a porous layer, as presented in Fig. 4. Figure 5 describes a validation for the used thermal conductivity ratio and dynamic viscosity ratio with two different experimental results and the numerical results of Corcione et al. [6] as well. Based on the above validations, the numerical outcomes of the present numerical code amount to a high degree of reliability.

Fig. 3

a Streamlines of (left) Khanafer et al. [52] and (right) present study; b isotherms of (left) Khanafer et al. [52] and (right) present study for $\mathrm{Ra}=10^{5}$, $\mathrm{Da}=10^{-2}$, $\varepsilon =0.9$, $N=3$, $D=0$ and $\mathrm{Pr}=1$

Fig. 4

Streamlines (left) and isotherms (right) for $\mathrm{Ra}=10^{6}, \mathrm{Da}=10^{-5}, \phi =0, N=0, H=0.5, D=0$ and $\Pr =0.71$. Singh and Thorpe [53] (a), Sheremet and Trifonova [33] (b) and present study (c)

Fig. 5

Comparisons of a thermal conductivity ratio with Chon et al. [7] and Corcione et al. [6] and b dynamic viscosity ratio with Ho et al. [8] and Corcione et al. [6] at $Ra=3.37\times 10^{5}$, $N=0$, $H=1$ and $D=0$

4 Results and discussion

Results explained by the contours of stream function, temperature, and the entropy are discussed in this section. The governing of four parameters are varied as follows; Darcy number ($10^{-6} \le Da \le 10^{-2}$), nanoparticle volume fraction ($0\le \phi \le 0.04$), number of undulations ($0 \le N \le 4$) and the porosity of the medium ($0.2 \le \varepsilon \le 0.8$). Rayleigh number, amplitude of the wavy wall, Prandtl number and the coefficient of interphase heat transfer are fixed at $Ra=10^{6}$, $A=0.1$, $H=10$ and $\Pr =4.623$, respectively. The local velocity distribution, local and average Nusselt numbers along with the Bejan number are also evaluated and for diverse values of Da and $\phi$. Table 1 displays the thermos-physical properties of the nanofluid at $T=310$K.

Table 1 Thermo-physical properties of water with $\hbox {Al}_{2}\hbox {O}_{3}$ nanoparticles at $T=310\,\mathrm{K}$ [54]

Although the present study is achieved at an average temperature (310 K), which brings Prandtl number to be 4.623; however, other values of Prandtl number have also been assessed. Table 2 depicts the effect of Prandtl number on the interface Nusselt number, Bejan number and the average temperature within the cavity. It can be seen that Nusselt number increases with $\Pr$. This is an expected fashion because the dominance of the momentum diffusivity over the thermal one. As such, the improvement in heat transfer rejects more heat from the nanofluid. Thus, the average temperature inside the cavity declines. The increase in momentum diffusivity leads to more generation of entropy due to fluid friction (FFI) and this, in turn, decreases Bejan number which is directly proportional with entropy generation due to heat transfer (HTI).

Table 2 Variations of interface average Nusselt number ($\overline{\mathrm{Nu}}_{i}$), Bejan number (Be) and dimensionless temperature ($\theta$) with $\Pr$ at $\mathrm{Da}=10^{-3}$, $\phi =0.02$ and $N=3$

4.1 Effect of Darcy number (Da)

By fixing the volume fraction, number of undulation, and the porosity at $\phi =0.02$, $N=3$ and $\varepsilon =0.5$, respectively, the impact of dimensionless permeability (Darcy number) on the three contour maps (streamlines, isotherms, and isentropic lines) is shown plotted in Fig. 6. The top horizontal wall blocks the flow and heat transfer, and thus, when the nanofluid reaches there, it circulates in two counter rotating vortices. Although the advection effect is included in the model of the motion within the porous layer, the nanofluid looks stagnant within the porous layer of lower Darcy number (Fig. 6a). This is because of the large drag exerted by this layer. The nanofluid within the clear layer seems colder than that within the porous layer, which exhibits almost horizontal isotherms. Along the segments of the wavy wall closer to the cold vertical walls, the temperature gradient concentrates notably and resulting in a concentrated entropy generation. Moreover, the isentropic lines depict three other sources to the entropy generation that are localized at situations where the nanofluid in contact with vertical cold walls and at the region where the two vortices are met. It can be inferred that these sources are caused by the fluid friction irreversibility (FFI). Now, the impact of Darcy number can be understood clearly via Fig. 6b–d, that is, increasing Da provides less dragged paths resulting in more free circulating nanofluids which can be seen by the inception of the streamlines circulations in the porous layer and the strengthening of that circulating in the nanofluid layer. The aspect of the isotherms switches to the plume like behavior with increasing Darcy number. The isentropic lines reveal that the FFI localized in the nanofluid regions is more dominant than that generated due to HTI in the porous layer. However, when Da is increased from $10^{-3}$ to $10^{-2}$, the intension in the global entropy generation is about one order of magnitude. These results agree well with the outcomes of Yilbas et al. [39] and Lam and Prakash [43].

Fig. 6

Variations of (left) streamlines, (middle) isotherms, and (right) isentropic lines evolution by Darcy number (Da) for $\phi =0.02$, $N=3$ and $\varepsilon =0.5$

For the same parameters of Fig. 6, the local distribution of the non-dimensional velocity component normal to the interface between the porous and clear layers is portrayed in Fig. 7a with different values of Da for $\phi =0.02$, $N=3$ and $\varepsilon =0.5$. In the figure, when $\mathrm{Da}=10^{-5}$ the velocity V is negligible due to the limitation of fluid circulation within the clear fluid. For higher Da values, the velocity exhibits maximum upward at the mid distance of the interface, and two other peaks downward within the porous layer on either side of the upward one. The maximum upward one corresponds to the strong fluid movement resulting from meeting the two counter rotating vortices. However, the three peaks are higher for higher Da values due to the increased permeability of the porous layer. Figure 7b depicts the variations of the local Nusselt number along the wavy wall. It is clearly vision that the greater the Darcy number, is the greater the local Nusselt number. Since the nanofluid circulation is restricted near them, the two troughs of the wavy wall exhibit lower Nusselt number because less heat is conveyed to the fluid. While, the three crests exhibit the peaks of the local Nusselt number. Because the temperature differences, the peaks of the lateral crests, which are nearer to the cold vertical walls, are greater than the peak of central crest. However, there are some perturbations of the local Nusselt number in the three peaks; these perturbations result from the detached circulation at the tips of the three crests that can be identified by the thickness of the thermal boundary layers appeared in Fig. 6.

Fig. 7

Variations of a local velocity distribution (V) along X at the wall between the nanofluid and porous layers and b local Nusselt numbers with the wavy wall and b interface wavy wall for different Da at $\phi =0.02$, $N=3$ and $\varepsilon =0.5$

Hence, the overall increase in the average Nusselt number versus Darcy number is plausible now as shown in Fig. 8a which agree also with Sheremet and Trifonova [33]. This increase is not linear where at $\phi =0.04$, the percentage increase in Nusselt number when Da is raised from $10^{-5}$ to $10^{-4}$ is 6.7%, whereas when Da is raised from $10^{-4}$ to $10^{-3}$ becomes 29.7%. Figure 8b shows that Bejan number (Be) is less than 0.5 only for $\mathrm{Da}=10^{-2}$, otherwise it is greater than 0.5. This indicates to the dominance of the FFI when $\mathrm{Da} \le 10^{-2}$, otherwise the HTI is dominant ($Be > 0.5$). The same result was reported also by Aly et al. [47]. However, Be is an increasing function of Da up to $\mathrm{Da}=10^{-4}$, at $\mathrm{Da}=10^{-5}$ the extremely drag of the porous layer contributes to the weakness of the energy transport thus, the FFI looks less than that at $\mathrm{Da}=10^{-4}$.

Fig. 8

Variations of a interface average Nusselt number and b Bejan number with $\phi$ for different Da at $N=3$ and $\varepsilon =0.5$

4.2 Effect of nanofluid volume fraction ($\phi$)

For the sake of inspecting the effect of nanoparticles volume fraction, Da, N, and $\varepsilon$ were fixed at $10^{-3}$, 3 and 0.5, respectively. Figure 9 displays unremarkable variations in the patterns of the streamlines, isotherms and isentropic lines with $\phi$. The two pertinent physical properties that play a significant role in the natural convection are the thermal conductivity and the dynamic viscosity. According to Corcione [5] model, both these properties augment with increasing $\phi$. Hence, along with the augmented transferred energy, the viscous force increases also. Therefore, the magnitude of the stream function decreases with $\phi$ and the cores of the two counter rotating vortices shrink slightly. Due to the suppressed intensity of the nanofluid flow, the global entropy generation decreases also. Contrarily, Bondareva et al. [45] reported an increase in entropy with increasing values of the volume fraction of the nanofluid. This is because their open cavity permits to freely flow. The distribution of the velocity component normal to the clear/porous layers interface and the local Nusselt number along the wavy interface are shown in Fig. 10a, b, respectively. The trend of the V component is similar to that shown in Fig. 7a with slight increments of peaks associated with higher volume fraction. On the other hand, Fig. 10b demonstrates that the reduction in flow intensity with $\phi$ does not affect the energy conveyed resulting from the enhanced thermal conductivity, where the local Nusselt number augments with $\phi$. The average Nusselt number depicted in Fig. 11a supports this evidence, where, for example, at $\mathrm{Da}=10^{-3}$, the average Nusselt number enhanced about 15% when $\phi$ is set at 0.04, while at $\mathrm{Da}=10^{-2}$, the percentage increase is about 16.4%. This figure demonstrates also the rapid increase in the average Nusselt number when Darcy number changes from $10^{-4}$ to $10^{-3}$. It is appropriate to mention here that Chamkha and Ismael [31] and Ismael and Chamkha [32] have captured similar action of $\phi$ on the average Nusselt number. Figure 11b shows that Bejan number increases slightly with $\phi$ over the range $\mathrm{Da}<10^{-4}$. This is because the viscous forces growing with increasing $\phi$. Nevertheless, around the value of $\mathrm{Da}=10^{-4}$, the pure fluid ($\phi =0$) manifests the largest Bejan number.

Fig. 9

Variations of (left) streamlines, (middle) isotherms, and (right) isentropic lines evolution by nanoparticles volume fraction ($\phi$) for $\mathrm{Da}=10^{-3}$, $N=3$ and $\varepsilon =0.5$

Fig. 10

Variations of a local velocity distribution (V) along X at the wall between the nanofluid and porous layers and b local Nusselt numbers with the interface wavy wall for different $\phi$ at $\mathrm{Da}=10^{-3}$, $N=3$ and $\varepsilon =0.5$

Fig. 11

Variations of a interface average Nusselt number and b Bejan number with Da for different $\phi$ at $N=3$ and $\varepsilon =0.5$

4.3 Effect of undulations (N)

To inspect the effect of the number of undulations N, Da, $\phi$ and $\varepsilon$ are fixed at $10^{-3}$, 0.02 and 0.5, respectively. Figure 12 distinguishes between the streamlines, isotherms and isentropic lines of wavy walls and the flat wall ($N=0$). For $N=0$ (Fig. 12a), the regular space of the cavity permits in producing four counter rotating vortices. The two symmetric vortices of the nanofluid layer are stronger than that in the porous layer. The isotherms show intensified temperature gradient within the solid wall with a plume protruding from the hot wall. The generation of entropy is concentrated in the nanofluid layer as can be seen from the isentropic lines. When $N=1$ (Fig. 12b), the hot bottom wall elongates and thus provides more energy to the porous layer, but this in turns produces a humped surface which squeezes the nearby recirculation resulting in a bit increase in the magnitude of the stream function. Qualitatively, the isotherms do not change while the isentropic lines demonstrate more and more concentration of the entropy generation within the nanofluid layer. For $N=2$ (Fig. 12c) and 3 (Fig. 12d), the roughed wavy surface obstructs the circulation in the porous layer which seem chaotic. The isotherms present some stratification pattern close to the troughs. The global isentropic generation decreases with increasing N up to 2, but when $N=4$, it increases. This can be associated with the increasing of N which reduces the space in which the nanofluid circulates and thus reduces the FFI, but when increased excessively, the humps produce substantial surfaces for FFI. Regarding the local distributions of V, Fig. 13a portrays that for flat wall, the upward and downward peaks are almost equal due to the absence of drag exerted by the wall undulation. For undulated walls, the upward peak is greater than downward peaks and this is clearly vision with $N=3$. Figure 13b shows that the local Nusselt numbers for $N=0,1$ are almost similar where it has two peaks in the vicinity of the vertical cold walls while at the middle of the solid wall, which corresponds to the situation of concourse of the two vortices, Nusselt number manifests lower peak. At the concourse of the counter rotating vortices, the fluid is stagnant, thus little heat exchanges there. The drops in the local Nusselt number at the solid wall edges are due to the ends effect. Hence, the same elucidation can be thought for the other curves of N. It is worth noting that the number of undulations lengthens the hot solid wall, which in turn augments the average Nusselt number as portrayed in Fig. 14a. The percentages increase in the average Nusselt number when N raises from 0 to 4 are 43.8% at $\mathrm{Da}=10^{-6}$ and 21.8% at $\mathrm{Da}=10^{-2}$. Figure 14b displays that there is a critical value of the Darcy number, namely $\mathrm{Da}*=3\times 10^{-4}$. For $\mathrm{Da} \le Da*$, the flat solid wall experiences higher Bejan number which is unchanging with Da, whereas for $\mathrm{Da} > \mathrm{Da}*$, Bejan number decreases rapidly. Within this range, the HTI increase with increasing N but still less than FFI.

Fig. 12

Variations of (left) streamlines, (middle) isotherms, and (right) isentropic lines evolution by number of undulations (N) for $\mathrm{Da}=10^{-3}$, $\phi =0.02$ and $\varepsilon =0.5$

Fig. 13

Variations of a local velocity distribution (V) along X at the wall between the nanofluid and porous layers and b local Nusselt numbers with the interface wavy wall for different N at $\mathrm{Da}=10^{-3}$, $\phi =0.02$ and $\varepsilon =0.5$

Fig. 14

Variations of a interface average Nusselt number and b Bejan number with Da for different N at $\phi =0.02$ and $\varepsilon =0.5$

4.4 Effect of porosity of the medium ($\varepsilon$)

Regarding the porous layer, the ratio of the empty spaces (voids) to the total volume of the layer is identified by the porosity ($\varepsilon$). The effect of porosity is tested in this category for $\mathrm{Da}=10^{-3}$, $\phi =0.02$ and $N=3$ and depicted in Figs. 15, 16 and 17. In Fig. 15, the streamlines demonstrate that with increasing $\varepsilon$, the recirculation in the porous layer expands and penetrates the valleys created by the wavy wall. This is due to the free paths available with increasing $\varepsilon$, which can be utilized by the advection inertia effect and demonstrated by the strengthening of the stream function. The notable variation of the isotherms with $\varepsilon$ is characterized by thinning the thermal boundary layer close to the wavy solid wall. The isentropic lines show different behavior with $\varepsilon$ that is the at very low voids (Fig. 15a), the porous layer looks idle where the entropy generation owing to the nanofluid layer. Nevertheless, it is expected that the tortuous paths lead to more friction and hence more thermodynamic irreversibility can be seen at the edges of the solid wavy wall. When $\varepsilon$ is set at 0.4 (Fig. 15b), more free space is available and this permits to free flow within the porous layer and more heat exchange, and thus, abrupt reduction in the global entropy generation rate is observed. The global generation rate at $\varepsilon =0.6$ is about 767 and at $\varepsilon =0.8$ it slightly increases to about 801. This slight improvement can be assigned to the free paths available in the porous layer permit to stronger circulations that in turn cause FFI. The patterns of V and $Nu_i$ along the interface lines are pictured in Fig. 16a and b, respectively. Owing to the availability of voids and the diminishing of drag, the three peaks of V are greater with higher porosity as shown in Fig. 16a. The local Nusselt number shown in Fig. 16b is previously discussed, but the effect of $\varepsilon$ is difficult to understand in this case, thus it relies on the variations of the average Nusselt number exhibited in Fig. 17a. The figure reveals that the higher porosity medium manifests higher heat transfer rate, where the percentage gain in the average Nusselt number when $\varepsilon$ is raised from 0.2 to 0.8 is 37.4% at $\mathrm{Da}=10^{-6}$ and 17.7 at $\mathrm{Da}=10^{-2}$. Figure 17b portrays that Bejan number increases with $\varepsilon$ along the whole studied Da values. Also it is affected by $\varepsilon$ notably for higher Da values. To enable scholars who are interested in this subject to use, numeric data results explained in Fig. 17 have been calculated in Table 3.

Fig. 15

Variations of (left) streamlines, (middle) isotherms, and (right) isentropic lines evolution by porosity of the medium ($\varepsilon$) for $\mathrm{Da}=10^{-3}$, $\phi =0.02$ and $N=3$

Fig. 16

Variations of a local velocity distribution (V) along X at the wall between the nanofluid and porous layers and b local Nusselt numbers with the interface wavy wall for different $\varepsilon$ at $\mathrm{Da}=10^{-3}$, $\phi =0.02$ and $N=3$

Fig. 17

Variations of a interface average Nusselt number and b Bejan number with Da for different $\varepsilon$ at $\phi =0.02$ and $N=3$

Table 3 Variations of interface average Nusselt number $\overline{\mathrm{Nu}}_{i}$ and Bejan number Be with Da for different $\varepsilon$ at $\phi =0.02$ and $N=3$

5 Conclusions

Free convection in a composite cavity with a solid wavy wall is investigated numerically in this paper. $\mathrm {Al}_2\mathrm {O}_3$-water nanofluid is filled in and saturates the cavity. The advection inertia effect is included in modeling the momentum exchange in the porous layer. The Galerkin weighted residual finite element scheme is employed in the numerical computation of the results. The following observations are drawn from the present study.

• 1. Although it confuses the circulations within the porous layer, the waviness of the solid wall augments the average Nusselt number and minimizes the global rate of entropy generation. For example, at specified conditions, the percentage increase in the average Nusselt number when the number of undulations rises from 0 to 4 is 43.8%. There is a critical Darcy number ($\mathrm{Da}^*= 3\times 10^{-4}$) that identifies the variations of the Bejan number with the waviness.

• 2. The higher the porosity of the medium is, the higher the average Nusselt number where about 37.4% enhancement in the average Nusselt number is obtained when the porosity is raised from 0.2 to 0.8 at $\mathrm{Da}=10^{-6}$. An abrupt reduction in the global rate of entropy generation is obtained when the porosity is set greater than 0.2.

• 3. When the Darcy number is increased, the average Nusselt number augments moderately, whereas the global rate of energy generation increases rapidly. The FFI localized in the nanofluid regions is more dominant than that generated due to HTI in the porous layer. However, when Da is increased from $10^{-3}$ to $10^{-2}$, the intension in the global entropy generation is about one order of magnitude.

• 4. The nanofluid volume fraction enhances the average Nusselt number and decreases the global rate of the entropy generation.