1 Introduction

Many physical and engineering applications naturally require multiscale solutions. This is especially true for problems related to metamaterials, composite materials, and porous media flows; see Chen and Lipton (2013), Berlyand and Novikov (2002), Cao et al. (2003), Li (2011), Ozgun and Kuzuoglu (2013), Epov et al. (2015), Zhou et al. (2012). The mathematical and numerical analysis for these problems are challenging since they are governed by elliptic equations with high-contrast coefficients (Hou and Wu 1997; Chen and Hou 2013; Ming and Yue 2006; Galvis and Efendiev 2010; Calo et al. 2014). For instance, in the modeling of composite materials, their conducting or elastic properties are modeled by discontinuous coefficients. The value of the coefficient can vary several orders of magnitude across discontinuities. Problems with these jumps are referred to as high-contrast problems. Similarly, the coefficient is denoted as a high-contrast coefficient. See for instance Calo et al. (2014), Galvis and Ki Kang (2014), Efendiev et al. (2013), Efendiev and Galvis (2012), Bourgat (1977).

We seek to understand how the high-contrast variations in the material properties affect the structure of the solution. In terms of the model, these variations appear in the coefficients of the differential equations. We expand our previous work (Calo et al. 2014), where we construct an asymptotic expansion to represent solutions. The asymptotic expansion is obtained in terms of the high-contrast in the material properties. In this paper, we use this asymptotic expansion to design numerical solutions for high-contrast problems. The asymptotic expansion helps us derive elegant numerical strategies and to understand the local behavior of the solution. In addition, the asymptotic expansion can be used to study functionals of solutions and describe their behavior with respect to the contrast or other important parameters. The asymptotic expansion in Calo et al. (2014) uses globally supported harmonic extensions of subdomains indicator functions referred to as harmonic characteristic functions. We modify the construction presented in Calo et al. (2014) to approximate the harmonic characteristic function in the local neighborhood of each inclusion. Thus, to make practical use of the expansion we avoid computing each characteristic function in the whole domain. This modification renders the method computationally tractable while the reduction in accuracy is not significant. For the case of dense distributions of inclusions, we observe numerically that the optimal size for the support of the basis functions is of the order of the representative distance between inclusions. We perform numerical tests that show the good performance of the proposed multiscale finite element method (MsFEM). The construction and analysis of localized exponentially decaying basis for numerical homogenization has been seen in Berlyand and Kolpakov (2001), Henning et al. (2014), Owhadi et al. (2014). We use a finite element method (FEM) and assume that there is a fine-mesh that completely resolves the geometrical configuration of the inclusions in the domain. That is, the fine-scale finite element formulation fully captures the solution behavior. To compute the solution of the linear system at this fine resolution is not practical, and therefore a multiscale finite element strategy is needed to compute a coarse-scale representation that captures relevant information of the targeted fine-scale solution. The coarse dimension in our simulations corresponds to the total number of inclusions. Nevertheless, a coarser scale may be needed for some applications. In this case, it is possible to use the framework of the generalized finite element method to design and analyze a coarser scale for computations. For a detailed discussion, see Efendiev et al. (2013) and references therein. In some more demanding applications, an efficient iterative domain decomposition method could also be designed and analyzed for these problems. This is under investigation and will be presented elsewhere.

The problem of computing solutions of elliptic problems related to modern artificial materials such as dispersed and/or densely packed composite materials has been considered by some researchers recently. For instance, in Wen and Ding (2004) the computation of effective properties of dispersed composite materials is considered. They use a classical multiscale finite element method. We recall that the application of the classical finite element method may lead to the presence of resonance errors due to the chosen local boundary conditions, see Hetmaniuk (2011). In Peterseim and Carstensen (2013) the authors develop a finite element method based on a network approximation of the conductivity for particle composites.

The rest of the paper is organized as follows. In Sect. 2, we setup the problem. In Sect. 3, we summarize the asymptotic expansion procedure described in Calo et al. (2014). We also introduce the definition of harmonic characteristic functions, which help us determine the individual terms of the expansion. In Sect. 4, we illustrate some aspects of the asymptotic expansion using some finite element computations. Section 5 constructs multiscale finite elements using the asymptotic expansion described in the previous sections. In particular, we approximate the leading term of the expansion with localized harmonic characteristic functions. We then apply this approximation to the case of dense high-contrast inclusions. In Sect. 6, we present some numerical experiments using the methods proposed. Finally, in Sect. 7 we draw some conclusions.

2 Problem setup

We use the notation introduced in Calo et al. (2014). We consider a second-order elliptic problems of the form,

$$\begin{aligned} -\text{ div } (\kappa (x) \nabla u(x))=f(x),\ \text{ in } D, \end{aligned}$$
(1)

with Dirichlet data defined by \(u=g\) on \(\partial D\). We assume that \(\kappa (x)>0\). Here \(D\subset \mathbb {R}^d\) is the disjoint union of a background domain \(D_0\) and subdomains that represent the inclusions, i.e., \(D=D_0\cup (\bigcup _{m=1}^M \overline{D}_m)\). We assume that \(D_1,\dots ,D_M\) are connected polygonal domains (or domains with smooth boundaries). Additionally, we require that each inclusion \(D_m\), \(m=1,\dots ,M\) is compactly included in the open set \(D\setminus \bigcup _{\ell =1, \ell \not =m}^M\overline{D}_\ell \), i.e., \(\overline{D}_m\subset D\setminus \bigcup _{\ell =1, \ell \not =m}^M \overline{D}_\ell \). Given \(w\in H^1(D)\) we also use the notation \(w^{(m)}\), for the restriction of w to the domain \(D_m\), that is,

$$\begin{aligned} w^{(m)}=w\big |_{D_m}, \quad m=0,1,\dots ,M. \end{aligned}$$

Let \(\kappa \) be defined by

$$\begin{aligned} \kappa (x)=\left\{ \begin{array}{c@{\quad }c} \eta ,&{} x\in D_m, ~~m=1,\dots ,M, \\ 1,&{} x\in D_0=D\setminus \bigcup _{m=1}^M\overline{D}_m. \end{array}\right. \end{aligned}$$
(2)

Following Calo et al. (2014), we represent the solution by an asymptotic expansion in terms of the contrast \(\eta \). We assume that \(\eta \) is a large parameter. The expansion reads,

$$\begin{aligned} u_\eta =u_0+\frac{1}{\eta }u_1+\frac{1}{\eta ^2}u_2+\dots = \sum _{j=0}^\infty \eta ^{-j} u_{j}, \end{aligned}$$
(3)

with coefficients \(\{u_j\}_{j=0}^\infty \subset H^1(D)\) and such that they satisfy the following Dirichlet boundary conditions,

$$\begin{aligned} u_0=g \text{ on } \partial D \quad \text{ and } \quad u_{j}=0 \text{ on } \partial D \text{ for } j\ge 1. \end{aligned}$$
(4)

We consider the weak formulation of (1). Find \(u\in H^1(D)\) such that

$$\begin{aligned} \int _D \kappa (x)\nabla u(x) \cdot \nabla v(x)\mathrm{d}x=\int _D f(x)v(x)\mathrm{d}x,\quad \text{ for } \text{ all } v\in H^1_0(D). \end{aligned}$$
(5)

We put \(\Omega = \bigcup _{m=1}^{M}D_m\) and substitute (3) into (5) to obtain the following expression for all \(v\in H_0^1(D)\),

$$\begin{aligned} \sum _{j=0}^\infty \eta ^{-j}\int _{D_0}\nabla u_j \cdot \nabla v + \sum _{j=0}^\infty \eta ^{-j+1}\int _{\Omega }\nabla u_j \cdot \nabla v =\int _D fv. \end{aligned}$$

We change the index in the last sum of the right-hand side, then

$$\begin{aligned} \eta \int _{\Omega }\nabla u_0 \cdot \nabla v + \sum _{j=0}^\infty \eta ^{-j}\left( \int _{D_0}\nabla u_{j} \cdot \nabla v + \int _{\Omega }\nabla u_{j+1} \cdot \nabla v\right) =\int _D fv, \end{aligned}$$

for all \(v\in H_0^1(D)\). In brief, we obtain the following equations after matching powers of \(\eta \)

$$\begin{aligned} \int _{\Omega }\nabla u_0 \cdot \nabla v =0, \end{aligned}$$
(6)
$$\begin{aligned} \int _{D_0}\nabla u_0 \cdot \nabla v +\sum _{m=1}^{M}\int _{D_m}\nabla u_1 \cdot \nabla v=\int _D fv, \end{aligned}$$
(7)

and for \(j\ge 1\),

$$\begin{aligned} \int _{D_0}\nabla u_j \cdot \nabla v +\sum _{m=1}^{M}\int _{D_m}\nabla u_{j+1} \cdot \nabla v=0, \end{aligned}$$
(8)

which are valid for all \(v\in H_0^1(D)\).

3 Asymptotic expansion

Now we compute the terms in the asymptotic expansion (3). For more details on the construction and related expansions we refer to Calo et al. (2014), Poveda et al. (2016).

First, we recall the set of constants functions inside de inclusions

$$\begin{aligned} V_{\text{ const }}=\left\{ v\in H_0^1(D), \text{ such } \text{ that } v\big |_{D_m} \text{ is } \text{ constant } \text{ for } \text{ all } m=1,\dots ,M\right\} . \end{aligned}$$

By the Eq. (6) we have that \(u_0\) is constant in each high-conductivity inclusion and solves the background problem

$$\begin{aligned} \int _{D_0}\nabla u_0 \cdot \nabla z&= \int _D fz\quad \text{ for } \text{ all } z\in V_{\text{ const }}\end{aligned}$$
(9)
$$\begin{aligned} u_0&= g\quad \text{ on } \partial D. \end{aligned}$$
(10)

Let \(\delta _{m\ell }\) represent the Kronecker delta, which is equal to 1 when \(m=\ell \) and 0 otherwise. For each \(m=1,\dots , M\) we introduce the harmonic characteristic function of \(D_m\), \(\chi _{D_{m}}\in H_{0}^{1}(D)\), with the condition

$$\begin{aligned} \chi _{D_{m}}\equiv \delta _{m\ell },\quad \text{ in } D_{\ell }, \text{ for } \ell =1,\dots ,M, \end{aligned}$$
(11)

which is equal to the harmonic extension of its boundary data to the interior of \(D_{0}\). We then have,

$$\begin{aligned} \Delta \chi _{D_m}&=0, \quad \text{ in } D_0,\nonumber \\ \chi _{D_m}&=0, \quad \text{ on } \partial D \text{ and } \partial D_\ell , \, m\ne \ell , \, \ell =1,2,\dots ,M \\ \chi _{D_m}&=1, \quad \text{ on } \partial D_m.\nonumber \end{aligned}$$
(12)

The asymptotic limit \(u_0\) in (3) can be explicitly written in term of the harmonic characteristic functions and a boundary corrector; see Calo et al. (2014). In fact, we get,

$$\begin{aligned} u_0=u_{0,0}+\sum _{m=1}^{M}c_m(u_0)\chi _{D_m}, \end{aligned}$$
(13)

where \(u_{0,0}\in H^1(D)\), for \(m=1,\dots ,M\), and \(u_{0,0}\) solves the following problem posed in the background \(D_0\),

$$\begin{aligned} -\Delta u_{0,0}&=f, \quad \text{ in } D_0,\\\nonumber u_{0,0}&=g, \quad \text{ on } \partial D\\ u_{0,0}&=0, \quad \text{ on } \partial D_m, m=1,\dots ,M.\nonumber \end{aligned}$$
(14)

\(u_{0,0}\) is globally supported but it is forced to vanish in all interior inclusions boundaries. The constants in (13) solve an M dimensional linear system. Let \(\mathbf {c}=(c_1(u_0),\dots ,c_M(u_0))\in \mathbb {R}^M\), then we have that

$$\begin{aligned} \mathbf {A}_\mathrm{geom}\mathbf {c}=\mathbf {b}, \end{aligned}$$
(15)

where \(\mathbf {A}_\mathrm{geom}=[a_{m\ell }]\) and \(\mathbf {b}=(b_1,\dots ,b_M)\in \mathbb {R}^M\) are defined by

$$\begin{aligned} a_{m\ell }= & {} \int _{D}\nabla \chi _{D_m}\cdot \nabla \chi _{D_{\ell }}, \end{aligned}$$
(16)

and

$$\begin{aligned} b_{\ell }= & {} \int _{D}f\chi _{D_{\ell }}-\int _{D_0}\nabla u_{0,0}\cdot \nabla \chi _{D_{\ell }}, \end{aligned}$$
(17)

respectively. The expression \(\sum _{m=1}^{M}c_m(u_0)\chi _{D_m}\) is the Galerkin projection of \(u_0-u_{0,0}\) into the space \(\text{ Span }\left\{ \chi _{D_m}\right\} _{m=1}^{M}\).

Now for the sake of completeness, we briefly describe the next individual terms of the asymptotic expansion. We have for \(j=1,2,\dots ,\)

$$\begin{aligned} u_{j}=\widetilde{u}_{j}+\sum _{m=1}^{M}c_{j,m}\chi _{D_{m}}, \end{aligned}$$
(18)

where the function \(\widetilde{u}_{j}\) is defined in three steps:

  1. 1.

    Solve a Neumann problem in each inclusion with data from \(u_{j-1}\) with \(j=1,2,\dots \). We have the restriction of \(u_j\) to the subdomain \(D_m\) with \(m=1,\dots ,M\) ( i.e., \(u_j\big |_{D_m}=u_j^{(m)}\)), that is

    $$\begin{aligned} u_j=\widetilde{u}_j+c_{j,m},\quad \text{ with } \int _{D_m}\widetilde{u}_j=0,\quad \text{ for } \text{ all } m=1,\dots ,M, \end{aligned}$$

    and \(\widetilde{u}_j\) satisfies the Neumann problem

    $$\begin{aligned} \int _{D_m}\nabla \widetilde{u}_j\cdot \nabla z=\int _{D_m}fz-\int _{\partial D_m}\nabla u_{j-1}^{(0)}\cdot n_{m}z, \text{ for } \text{ all } z\in H^1(D_m), \end{aligned}$$

    for \(m=1,\dots ,M\). The constants \(c_{j,m}\) will be chosen suitably.

  2. 2.

    Solve a Dirichlet problem in the background \(D_0\) with data \(\widetilde{u}_{j}\) in each inclusion. For \(j=1,2,\dots \), we have that \(u_j\) in \(D_m\), \(m=1,\dots ,M\), then we find \(u_j^{(0)}\) in \(D_0\) by solving the Dirichlet problem

    $$\begin{aligned} \int _{D_0}\nabla u_{j}^{(0)}\cdot \nabla z&=0,&\,&\text{ for } \text{ all } z\in H_0^1(D_0)\\ u_j^{(0)}&=u_j\, (=\widetilde{u}_j+c_{j,m}),&\,&\text{ on } \partial D_m,\, m=1,\dots ,M,\nonumber \\ u_j^{(0)}&=0,&\,&\text{ on } \partial D.\nonumber \end{aligned}$$
    (19)

    Since \(c_{j,m}\) are constants, we define their corresponding harmonic extension by \(\sum _{m=1}^{M}c_{j,m}\chi _{D_m}\). So we rewrite

    $$\begin{aligned} u_j=\widetilde{u}_j+\sum _{m=1}^{M}c_{j,m}\chi _{D_m}. \end{aligned}$$
    (20)
  3. 3.

    The \(u_{j+1}\) in \(D_m\) satisfy the following Neumann problem

    $$\begin{aligned} \int _{D_m}\nabla u_{j+1}\cdot \nabla z=-\int _{\partial D_m}\nabla u_j^{(0)}\cdot n_0z,\quad \text{ for } \text{ all } z\in H^1(D). \end{aligned}$$

    The compatibility condition is satisfied for \(\ell =1,\dots , M\), then

    $$\begin{aligned} 0 = \int _{\partial D_{\ell }}\nabla u_{j+1}\cdot n_{\ell }= & {} -\int _{\partial D_{\ell }}\nabla u_j^{(0)}\cdot n_0\\= & {} -\int _{D_{\ell }}\nabla \left( \widetilde{u}_j^{(0)}+\sum _{m=1}^{M}c_{j,m}\chi _{D_m}^{(0)}\right) \cdot n_0\\= & {} -\int _{\partial D_{\ell }}\nabla \widetilde{u}_j^{(0)}\cdot n_0-\sum _{m=1}^{M}c_{j,m}\int _{\partial D_m}\nabla \chi _{D_m}^{(0)}\cdot n_0, \end{aligned}$$

    where \(n_0,n_\ell \) with \(\ell =1,\dots , M\) are the outward pointing unit normal vector of the boundary \(\partial D_0\) and \(\partial D_\ell \), respectively. The term \(\chi _{D_m}^{(0)}\) is the restriction of \(\chi _{D_m}\) in the background \(D_0\).

A detailed description of the differential problems can be found in Calo et al. (2014). The constants \(\{c_{j,m}\}_{m=1}^{M}\) in (18) are computed solving a linear system similar to the one defined above in (15). We have that \(\mathbf {c}_j=(c_{j,1},\dots ,c_{j,M})\) is the solution of the system

$$\begin{aligned} \mathbf {A}_\mathrm{geom}\mathbf {c}_j=\mathbf {y}_j, \end{aligned}$$

where

$$\begin{aligned} \mathbf {y}_j=\left( -\int _{D_0}\nabla \widetilde{u}_{j}^{(0)}\cdot \nabla \chi _{D_1},\dots ,-\int _{D_0}\nabla \widetilde{u}_j^{(0)}\cdot \nabla \chi _{D_M}\right) . \end{aligned}$$

In Calo et al. (2014), Poveda et al. (2016) the authors prove that the expansion (3) converges absolutely in \(H^1(D)\) for \(\eta \) sufficiently large.

Theorem 1

Consider the problem (1) with coefficient (2). The corresponding expansion (3) with boundary condition (4) converges absolutely in \(H^1(D)\) for \(\eta \) sufficiently large. Moreover, there exist positive constants C and \(C_1\) such that for every \(\eta >C\), we have

$$\begin{aligned} \left\| u-\sum _{j=0}^{J}\eta ^{-j}u_j\right\| _{H^1(D)}\le C_1\left( \Vert f\Vert _{H^{-1}(D)}+\Vert g\Vert _{H^{1/2}(\partial D)}\right) \sum _{j=J+1}^{\infty }\left( \frac{C}{\eta }\right) ^{j}, \end{aligned}$$

for \(J\ge 0\).

4 An expansion

In this section, we illustrate the expansion in two dimensions. We use MatLab for the computations. In particular, a few terms are computed numerically using the finite element method, see for instance Johnson (2009), Hughes (2012). In particular, we solve the sequence of problems posed in the background subdomain and in the inclusions. Our main goal is to design efficient numerical approximations for \(u_0\) (and then for \(u_\eta \) by using Theorem 1).

We consider \(D=B(0,1)\) the circle with center (0, 0) and radius 1. We add 36 (identical) circular inclusions of radius 0.07. This is illustrated in the Fig. 1a. Then, we numerically solve the problem

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} -\text{ div }(\kappa (x)\nabla u_\eta (x))=1, &{} \text{ in } D\\ u(x)=x_1+x_2^2, &{} \text{ on } \partial D. \end{array}\right. \end{aligned}$$
(21)
Fig. 1
figure 1

Circular domain with 36 identical inclusions. (a) Geometry and mesh, (b) Finite element solution of problem (21) with \(\eta = 6\), (c) Asymptotic expansion of \(u_{0}\) in (13) (Colour on-line)

Full size image

Figure 1 shows that the solution for \(\eta =6\) against the computed \(u_0\).

Fig. 2
figure 2

Functions \(u_c=\sum _{m=1}^{M}c_m(u_0)\chi _{D_m}\) and \(u_{0,0}\) for problem (21) with \(\eta =6\). See (13) (Colour on-line)

Full size image

In Fig. 2, we show the two parts of \(u_0\) in (13), i.e., the combination of the harmonic characteristic functions \(\sum _{m=1}^{M}c_m(u_0)\chi _{D_m}\) and the boundary corrector \(u_{0,0}\). The results suggest that the boundary corrector \(u_0\) decays fast away from the boundary \(\partial D\).

Fig. 3
figure 3

Top functions \(u_1\) and \(u_2\) for the problem (21) with \(\eta =6\). Bottom functions \(u_1\) and \(u_2\) restricted to the inclusions for the problem (21) with \(\eta =6\) (Colour on-line)

Full size image

In Fig. 3, we show the second and third terms of the expansions, \(u_1\) and \(u_2\). We also show the influence of \(\eta \) on the convergence of the series in Table 1. As predicted by Theorem 1, as \(\eta \) grows convergence of the series expansion is accelerated. For example, problem (21) with \(\eta =10\) requires eight terms (i.e., \(J=8\), in Theorem 1) in the series to achieve a relative error of \(10^{-8}\) while for \(\eta =10^4\) requires only two terms.

5 Approximation with localized harmonic characteristic functions

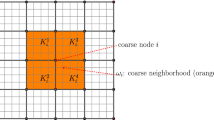
In this section, we present a computable method based on the asymptotic expansion described in Sect. 3 and the insights on the structure of the solution described in Sect. 4. We assume that D is the union of a background and multiple inclusions that are homogeneously distributed. We only approximate the leading term \(u_0\). The remaining terms can be approximated similarly. We describe \(u_0\) with localized harmonic characteristic functions. The computation of the harmonic characteristic functions is computationally expensive since these are fully global functions. That is, we approximate harmonic characteristics functions by solving a local problem (instead of a whole background problem). For instance, we pose a problem in a small neighborhood of each inclusion. The domain where the harmonic characteristic functions are computed is sketched in Fig. 4. The domain marked in Fig. 4 corresponds to the adopted neighborhood of the inclusion painted with green color. In this case, the approximated (or truncated) harmonic characteristic function is set to be zero on the boundary of the neighborhood of the selected inclusion.

Table 1 Number of terms J needed to obtain a relative error of \(10^{-8}\) for a given value of \(\eta \)
Full size table
Fig. 4
figure 4

Illustration of \(\delta \)-neighborhood of an inclusion. The selected inclusion is green. The \(\delta \)-neighborhood of this inclusion is given in blue color, while preserving the truncated harmonic characteristics function. We highlight with white color the other inclusions that are within the \(\delta \)-neighborhood of the selected inclusion (Colour on-line)

Full size image

To reduce the cost of computing the characteristic harmonic functions, we solve problem (12), but restrict it to a neighborhood of the corresponding inclusion. The exact characteristic functions are defined by (11). We define the neighborhood of the inclusion \(D_m\) by

$$\begin{aligned} D_{m,\delta }=\overline{D}_{m}\cup \left\{ x\in D_0:d(x,D_m)<\delta \right\} , \end{aligned}$$

and approximate the characteristic function for the \(\delta \)-neighborhood solving

$$\begin{aligned} \Delta \chi _m^{\delta }&=0, \quad \text{ in } D_{m,\delta }, \nonumber \\ \chi ^{\delta }_m&=0, \quad \text{ on } \partial D_{m,\delta } \text{ and } \partial D_{\ell } \cap D_{m,\delta } \text{ for } \ell \not = m, \\ \chi ^{\delta }_m&=1, \quad \text{ on } \partial D_m.\nonumber \end{aligned}$$
(22)

The exact expression for \(u_0\) is given by

$$\begin{aligned} u_0=u_{0,0}+\sum _{m=1}^{M}c_m\chi _{D_m}= u_{0,0}+u_c, \end{aligned}$$
(23)

where we have introduced \(u_c=\sum _{m=1}^{M}c_m(u_0)\chi _{D_m}\). The matrix problem for \(u_c\) with globally supported basis was given in (15). We now define \(u_0^{\delta }\), the multiscale approximation of \(u_0\), using a similar expression

$$\begin{aligned} u_0^{\delta }=u_{0,0}^{\delta }+ \sum _{m=1}^{M}c_m^{\delta }\chi _{D_m}^{\delta }= u_{0,0}^{\delta }+u_c^{\delta }, \end{aligned}$$
(24)

where \(u_c^{\delta }=\sum _{m=1}^{M}c_m^{\delta }\chi _{D_m}^{\delta }\) with each \(c_m^{\delta }\) computed similar to \(c_{m}\) using an alternative matrix problem with basis \(\chi _{D_m}^{\delta }\) instead of \(\chi _{D_m}\). This system is given by

$$\begin{aligned} \mathbf {A}^{\delta }\mathbf {c}^{\delta }=\mathbf {b}^{\delta }. \end{aligned}$$

with \(\mathbf {A}^{\delta }=[a_{m\ell }^{\delta }]\), with \(a_{m\ell }^{\delta }=\int _{D_m}\nabla \chi ^{\delta }_m \cdot \nabla \chi ^{\delta }_{\ell }\), \(\mathbf {c}=[c^{\delta }_0(u_0),\dots ,c^{\delta }_M(u_0)]\) and \(\mathbf {b}^{\delta }=[b_{\ell }^{\delta }]=\int _Df\chi _{D_{\ell }}^{\delta }\).

We also introduce \(u_{0,0}^{\delta }\), as an approximation to the boundary corrector \(u_{0,0}\), that solves the problem

$$\begin{aligned} -\Delta u_{0,0}^{\delta }&= f,\quad \text{ in } D_0^{\delta },\\ u_{0,0}^{\delta }&=g,\quad \text{ on } \partial D\\ u_{0,0}^{\delta }&=0,\quad \text{ on } \partial D_0^{\delta }\cap D, \end{aligned}$$

where \(D_0^{\delta }\) is the subdomain within a distance \(\delta \) from the boundary \(\partial D\),

$$\begin{aligned} D_0^{\delta }=\left\{ x\in D:d(x,\partial D)<\delta \right\} . \end{aligned}$$

The approximation construction hinges on the fact that \(u_{0,0}^{\delta }\) satisfies homogeneous Dirichlet boundary conditions at all neighboring inclusions. Thus, long range effects from the forcing are heavily attenuated.

Fig. 5
figure 5

Global versus localized characteristic functions. Here we use \(\delta =0.3\) and obtained maximum error of 0.016 (Colour on-line)

Full size image

6 Numerical experiments

To show the effectiveness of the numerical methodology we describe in Sect. 5, we first consider the problem configuration used in Sect. 4. See Fig. 1. We study the expansion which localizes the harmonic characteristic functions. We first compare the global and the localized harmonic characteristic functions. In Fig. 5, we plot the global characteristic function (left picture) corresponding to a randomly selected inclusion. By construction this harmonic characteristic function is zero at the boundary of all other inclusions which implies a fast decay away from the inclusion. In addition, we plot the difference between the localized characteristic function in (22) and the characteristic function in (11); see Fig. 5b. Here, we use \(\delta =0.3\) and observe that the maximum value of this absolute difference is 0.016 less than 2%.

For further comparison, we introduce the relative \(H^1\) error from \(u_0\) in (23) to its approximation \(u_0^\delta \) in (24). This is given by

$$\begin{aligned} e(u_0-u_0^{\delta })= & {} \frac{\Vert u_0-u_0^{\delta }\Vert _{H^1(D)}}{\Vert u_0\Vert _{H^1(D)}}. \end{aligned}$$

Analogously, the relative \(H^1\) error of the approximation of \(u_{0,0}\) is given by

$$\begin{aligned} e(u_{0,0}-u_{0,0}^{\delta })= & {} \frac{\Vert u_{0,0}-u_{0,0}^{\delta }\Vert _{H^1(D)}}{\Vert u_{0,0}\Vert _{H^1(D)}}. \end{aligned}$$

The error \(e\left( u_c-u_c^{\delta }\right) \) is defined in a similar way. According to Theorem 1, the error between the exact solution of problem (1) with coefficient (2) and \(u_0\) in (23) is of order \({\eta }^{-1}\).

Table 2 and Fig. 6 show the relative errors of the multiscale method. In Table 2, we observe that as the neighborhood size grows, the error is reduced. For instance, for \(\delta = 0.2\) the error between the exact solution \(u_0\) and the truncated solution \(u_0^{\delta }\) is \(8\%\). By selecting \(\delta =0.3\) we obtain a relative error of the order of 4%. Numerically, we observe that an optimal value for \(\delta \) is the smallest distance that includes one layer of inclusions away from the selected one. Therefore, this approximation is more efficient for densely packed inclusions.

We now consider an additional geometrical configuration of inclusions. We consider \(D=(0,1)\), the circle with center (0, 0) and radius 1, and 60 (identical) circular inclusions of radius 0.07. We consider the problem,

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} -\text{ div }(\kappa (x)\nabla u_\eta (x))=1, &{} \text{ in } D\\ u(x)=x_1+x_2^2, &{} \text{ on } \partial D, \end{array}\right. \end{aligned}$$
(25)

In the Fig. 7 we illustrate the geometry for problem (25). Table 3 summarizes similar results to those described above.

Table 2 Relative error in the approximation of \(u_0\) using locally computed basis functions and truncated boundary condition effect
Full size table
Fig. 6
figure 6

Relative error in the approximation of \(u_0\) given by Table 2 (Colour on-line)

Full size image
Fig. 7
figure 7

Geometry for the problem (25) (Colour on-line)

Full size image
Table 3 Relative error in the approximation of \(u_0\) when using locally computed basis functions and a truncated boundary condition effect for the problem (25) with 60 identical inclusions
Full size table
Fig. 8
figure 8

Relative error in the approximation of \(u_0\) given by Table 3 (Colour on-line)

Full size image

The problem setup and simulation of the localized harmonic characteristic functions proceeds as described in Sect. 5. In the present setup, the inclusions are clustered more tightly. This induces a faster decay of the characteristic harmonic function for each individual inclusion, see Fig. 8. Thus, as expected in Table 3 we observe a reduction in the relative error when compared to Table 2 for a fixed value of \(\delta \). For example, \(\delta =0.2\) induces a relative error of \(1 \%\) on \(u_0^{\delta }\) and of \(2 \%\) for \(u_{0,0}^{\delta }\) for the geometry show in the Fig. 7 while this value of \(\delta \) induces errors of 8 and \(26 \%\) for these two variables for the geometry shown in Fig. 1a.

7 Conclusions

We consider the solution of elliptic problems modeling properties of composite materials. Using an expansion in terms of the properties ratio presented in Calo et al. (2014), we design a multiscale method to approximate solutions. We develop procedures that effectively and accurately compute the first few terms in the expansion. In particular, we compute the asymptotic limit which is an approximation of order \(\eta ^{-1}\) to the solution (where \(\eta \) represent the ratio between lowest and highest material property values). The expansion in Calo et al. (2014) is written in terms of the harmonic characteristic functions that are globally supported functions, one for each inclusion. The main idea we propose is to approximate the harmonic characteristic functions by solving local problems around each inclusion. We use numerical examples to compute the asymptotic limit \(u_0\) with the localized harmonic characteristic functions. The analysis of the truncation error depends on decay properties of the harmonic characteristic functions and is under current investigation. This method can be used in several important engineering applications with heterogeneous coefficients such as complex flow in porous media and complex modern materials.