Maximum Penetration Level Evaluation of Hybrid Renewable DGs of Radial Distribution Networks Considering Voltage Stability

Abstract

The issues regarding generation uncertainties associated with wind energy and solar photovoltaic (PV) systems along with load demand uncertainties are considered in this paper to evaluate the maximum penetration of renewable energy resources. The nodes which are less voltage stable are considered as the most suitable locations for distributed generations (DGs) placement. For identification of these critical nodes, a voltage stability index (VSI) has been utilized. To analyze the voltage profile, power losses and system voltage stability with large penetration of the wind energy and solar PV into the distribution networks, a probabilistic-based approach has been adopted. The penetration limit depends upon the type of DG that is connected to the distribution network. Usually, the integration of DGs reduces the power losses in the network, however as penetration level increases, the power losses begins to increase. The detailed mathematical models of wind and solar PV-based renewable resources are used. The Hong’s $2m+1$ point estimation method combined with Cornish–Fisher expansion is adopted in this paper to conduct the probabilistic studies. The effectiveness of the method is validated through IEEE 33-node radial distribution test network for four different scenarios. The results obtained have been verified and compared with Monte Carlo simulation technique.

1 Introduction

Due to advancement in the renewable-based generation technologies, a rapid development for integration of these energy resources into the existing power networks has been witnessed in recent years. The energy outputs from renewable energy resources, i.e., wind and solar PV are random and stochastic in nature and depends upon weather conditions. Owing to the large penetration level (PL) of renewable-based DGs into the distribution network, the uncertainties associated with generation and loads have significantly influenced the system voltage stability (Wang et al. 2016). For studying the uncertainties associated with the power system, the probabilistic load flow (PLF) method is one of the best-known tools. Probabilistic load flow methods are broadly categorized as Monte Carlo simulation (MCS) and analytical methods. MCS is a traditional method which provides more accurate results as compared to other analytical methods. However, thousands of iterations are required to simulate that are extremely time consuming and are unsuitable for real time applications (Rubinstein 1991). To reduce the simulation time analytical methods such as point estimation method (PEM) (Su 2005; Morales and Perez-Ruiz 2007), cumulants method (Schellenberg et al. 2005), cumulants and Gram–Charlier expansion (Zhang and Lee 2004), cumulants and Cornish–Fisher expansion (Usaola 2009) are used for PLF studies. The DGs integration in the distribution network have several benefits such as reduction in system power loss, reduced emission, increase of system reliability, improved power quality and deferral of transmission upgrades. Due to the small capacity of DGs in comparison with central power plant, their impacts are minor if the penetration level (1–5%) is low. However, if the penetration level increases to the level of 30–40%, the impact of DGs will be significant (Atwa and El-Saadany 2010). In the literature, maximum penetration level of DGs in the distribution networks had been investigated by various researchers taking into account different factors at a given point of time.

One of the major factors which limit the penetration level of DGs in the distribution network is over voltages. For determining the maximum active power injected by DGs into the distribution network without violating voltage constraints, a sensitivity-based method was investigated by Ayres et al. (2010). The time-varying voltage-dependent load models were analyzed by Hung et al. (2014) in order to determine the maximum penetration level of solar PV units in the radial distribution network. The authors of Hoke et al. (2013) address the maximum PV penetration level by considering the steady state voltage limit at nodes not to be violated. Total 336 cases were simulated with various locations of PV clusters along the feeder, and it was found that in 86% cases, the maximum penetration level was at 30% of system peak load. The deterministic load flow is usually employed to assess the maximum penetration level of DGs. Howsoever, owing to uncertainty associated with the power output of DGs and system load demands, for accurate estimation of maximum penetration level in distribution network, the probabilistic-based approaches are required.

In Kolenc et al. (2015) and Zio et al. (2015), the Monte Carlo simulation (MCS)-based probabilistic approach is dealt for estimating the maximum penetration level of DGs in the low voltage (LV) distribution network. To counteract the voltage rise problem caused by the high penetration of the residential PV system, a rule-based OLTC filled transformer is used for the real UK residential LV network (Procopiou and Ochoa 2017). Lamberti et al. (2015) had applied the energy storage system (ESS) with PV systems to balance the mismatch between the generation and demand at the LV distribution network. Gaunt et al. (2017) analyzed the voltage violations in the low voltage feeder for large penetration of PV-based DGs. Liew and Strbac (2002) investigated the maximum penetration level of the wind-based DGs on the rural distribution networks. The voltage stability considerations with large penetration of DGs into the distribution network are less evaluated. In Almeida et al. (2013), the voltage collapse using P–V and Q–V curve methods into distribution networks with intermittent generation was analyzed using MCS and empirical distribution function (EDF).

Xiuhong et al. (2002) uses the probabilistic continuous power flow (CPF) with load variation for probabilistic voltage stability analysis. In Haesen et al. (2009), the stochastic response surface method (SRSM) is explored for accessing the probabilistic load margin into the power system. In Liu et al. (2015), the authors investigated the static voltage stability in distribution network using two point estimation method (2PEM) and CPF. To evaluate the probability density function (PDF) of the critical voltage stability Cornish–Fisher series is used. In Kataoka (2003), the load variation of the system was taken as hypercone. The intersection point of the transfer limit surface and the loading hypercone makes use of for detecting worst-case loading. In Hatziargyriou and Karakatsanis (1998), the assessment of voltage stability is investigated using probabilistic load flow considering random variation of loads, generation unit unavailabilities and topological variations. In Zhang et al. (2010), for determining the probabilistic voltage stability margin, maximum entropy method is adopted. Probabilistic load flow for the unbalanced distribution network has been proposed in Ran and Miao (2015) considering the uncertainties of load and wind power generation.

For investigating the maximum penetration level of DGs in the distribution network, researchers have taken either wind energy or PV-based DGs but the hybrid combination of these renewable DGs have not been applied in research work as per authors’ knowledge. The deterministic load flow is usually employed to assess the maximum penetration of DGs. Due to uncertainty associated with power output of DGs and system load, for accurate estimation of maximum penetration level, probabilistic approaches are required. Although some probabilistic studies have been investigated with MCS for determining maximum DGs penetration, but no studies have been investigated with analytical methods such as point estimation method. In probabilistic load flow with non-Gaussian input random variables, Cornish–Fisher expansion had found better performance than the Gram–Charlier expansion for obtaining PDF and CDF of output variables (Ruiz Rodriguez et al. 2012). In this paper, Hong’s $2m+1$ point estimation method is applied for probabilistic load flow study (Delgado and Dominguez Navarro 2014), whereas Cornish–Fisher expansion is incorporated to obtain the PDF and CDF of the output variables. The voltage stability index (VSI) has been utilized to obtain the suitable locations of DGs from voltage stability viewpoint. Moreover, to analyze the effect of large penetration of renewable DGs, four different scenarios have been investigated.

The rest of the paper is organized as follows: Sect. 2 elaborates modeling of renewable energy sources and system load. Section 3 explains the Hong’s $2m+1$ point estimation method coordinated with Cornish–Fisher expansion, MCS method and utilized VSI. Section 4 describes the proposed algorithm for investigation of probabilistic voltage stability for different load levels. In Sect. 5, case study is performed on 33-node radial distribution test network. Finally, Sect. 6 concludes the research work.

2 Modeling of Renewable Energy Sources and Load

2.1 Photovoltaic Modeling

Solar irradiance has a high degree of uncertainty and can be modeled as Beta PDF (Mistry and Roy 2014).

$$\begin{aligned} f_{\mathrm{b}}(s){=\!}{\left\{ \begin{array}{ll} \frac{\varGamma {(\alpha +\beta )}}{\varGamma {(\alpha )}\varGamma {(\beta )}}\times s^{\alpha -1}\times (1-s)^{\beta -1}: &{}\quad 0\le s \le 1,\\ &{}\quad \alpha \ge 0, \beta \ge 0\\ 0: &{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(1)

where s is solar irradiance in kW/m$^{2}$; $f_{\mathrm{b}}(s)$ is a Beta distribution function of s; $\alpha$, $\beta$ are parameters of the Beta distribution function. The parameters of the Beta PDF depend upon mean $(\mu )$ and standard deviation $(\sigma )$ of the random variables are calculated as following:

$$\begin{aligned} \begin{aligned} \beta&=(1-\mu )\times \left( \frac{\mu (1-\mu )}{\sigma ^{2}}-1\right) \\ \alpha&=\frac{\mu \times \beta }{1-\mu }\\ \end{aligned} \end{aligned}$$

(2)

Using the generated solar irradiance data from Beta PDF, the output power from PV module can be calculated as following:

$$\begin{aligned}&{{T}_{\mathrm{c}}}={{T}_{\mathrm{A}}}+{{s}_{\mathrm{a}}}\left( \frac{{{N}_{\mathrm{OT}}}-20}{0.8} \right) \end{aligned}$$

(3)

$$\begin{aligned}&I={{s}_{\mathrm{a}}}\left[ {{I}_\mathrm{sc}}+{{C}_{i}}({{T}_{\mathrm{c}}}-25) \right] \end{aligned}$$

(4)

$$\begin{aligned}&V={{V}_{\mathrm{oc}}}-{{C}_{\mathrm{v}}}*{{T}_{\mathrm{c}}}\end{aligned}$$

(5)

$$\begin{aligned}&{{P}_{s}}\left( s \right) =N*FF*V_{\mathrm{oc}}*I_\mathrm{sc}\end{aligned}$$

(6)

$$\begin{aligned}&FF=\frac{{{V}_{\mathrm{mpp}}}*{{{\text {I}}}_{\mathrm{mpp}}}}{{{V}_{\mathrm{oc}}}*{{I}_\mathrm{sc}}}, \end{aligned}$$

(7)

where $s_{\mathrm{a}}$ is the average solar irradiance; $C_{\mathrm{v}}$ and $C_{i}$ are voltage temperature coefficient in V/$^{\circ }$C and current temperature coefficient in A/$^{\circ }$C, respectively; $N_{\mathrm{OT}}$, $T_{\mathrm{c}}$ and $T_{\mathrm{A}}$ are nominal operating temperature of cell, cell temperature, and ambient temperature in $^{\circ }$C. $I_{\mathrm{SC}}$ and $V_{\mathrm{oc}}$ are short circuit current and open circuit voltage respectively; FF represents fill factor; $I_{\mathrm{mpp}}$ and $V_{\mathrm{mpp}}$ are current and voltage at maximum power point; $P_{s}$ is the total output power from the PV array.

2.2 Wind Energy Generator Modeling

Wind speed is unpredictable and varies with time and geographical location. A Weibull probabilistic density function is used to model wind speed behavior.

$$\begin{aligned} {{f}_{\mathrm{w}}}(v)=\frac{a}{b}{{\left( \frac{{{v}_{\mathrm{w}}}}{b} \right) }^{a-1}}\exp \left[ -{{\left( \frac{{{v}_{\mathrm{w}}}}{b} \right) }^{a}} \right] \end{aligned}$$

(8)

where $\nu _{\mathrm{w}}$ is wind speed; a and b are shape and scale index respectively. For modeling wind turbine generator’s output power, first the wind speed samples are generated through Weibull PDF and then transformed into power output using the following mathematical model.

$$\begin{aligned} {{P}_{\mathrm{WT}}}={\left\{ \begin{array}{ll} 0&{}\quad \text {for}\,\,{{\nu }_{\mathrm{w}}}\le {{V}_{i}}\text { or }{{\nu }_{\text {w}}}\ge {{V}_{0}} \\ {{{\text {P}}}_{\mathrm{r}}}\left( \frac{{{\nu }_{\mathrm{w}}}-{{V}_{i}}}{{{V}_{\mathrm{r}}}-{{V}_{i}}} \right) &{}\quad \text {for}\,\,{{V}_{i}}<{{\nu }_{\mathrm{w}}}<{{V}_{\mathrm{r}}} \\ {{{\text {P}}}_{\mathrm{r}}}&{}\quad \text {for}\,\,{{V}_{\mathrm{r}}}\le {{\nu }_{\mathrm{w}}}<{{V}_{0}} \\ \end{array}\right. } \end{aligned}$$

(9)

where $V_{i}$, $V_{\mathrm{r}}$, and $V_{\mathrm{o}}$ are cut-in speed, rated speed, and cutoff speed of wind turbine, respectively. $P_{\mathrm{WT}}$ represents the output power of a wind turbine. The power output from wind farm can be considered as negative load in the corresponding bus.

2.3 Probabilistic Load Modeling

Active and reactive power load are described by a normal distribution with the corresponding probability distribution function given by Eqs. (10) and (11), respectively.

$$\begin{aligned}&f({{P}_{Li}})=\frac{1}{\sqrt{2\pi {{\sigma }_{{{P}_{Li}}}}^{2}}}\exp \left( -\frac{{{\left( {{P}_{Li}}-{{\mu }_{{{P}_{Li}}}} \right) }^{2}}}{2\sigma _{{{P}_{Li}}}^{2}} \right) \end{aligned}$$

(10)

$$\begin{aligned}&f({{Q}_{Li}})=\frac{1}{\sqrt{2\pi {{\sigma }_{{{Q}_{Li}}}}^{2}}}\exp \left( -\frac{{{\left( {{Q}_{Li}}-{{\mu }_{{{Q}_{Li}}}} \right) }^{2}}}{2\sigma _{{{Q}_{Li}}}^{2}} \right) \end{aligned}$$

(11)

where $f(P_{L_{i}})$ and $f(Q_{L_{i}})$ are the normally distributed active and reactive power at each node. In Eqs. (10) and (11), $\mu _{P_{L_{i}}}$ and $\mu _{Q_{L_{i}}}$ represents the mean values, which are base active and reactive power demands at any node i, respectively. The standard deviation of active ($\sigma _{P_{L_{i}}}$) and reactive ($\sigma _{Q_{L_{i}}}$) power load varies between 5 and 10% of base load at any node i. In this work, standard deviation is considered 5% of base load demand.

3 Probabilistic Power Flow and Voltage Stability Index

3.1 Hong’s $2m+1$ Point Estimation Method

In Hong’s $2m+1$ point estimation method, the fitness function which is a deterministic load flow in this particular case has to be calculated k times for each input random variables. For m input random variable, fitness function should be calculated $m \times k$ times. The input vector in each evaluation process is determined as following:

$$\begin{aligned} \left( \mu _{p1},\mu _{p2},\ldots ,P_{l,k},\ldots , \mu _{pm}\right) \end{aligned}$$

(12)

where $P_{l,k}$ assigned to input random variable $P_{l}$, while the remaining $m-1$ input random variables are fixed to their corresponding mean $(\mu _{pi})$. The $P_{l,k}$ is calculated using Eq. (13).

$$\begin{aligned} P_{l,k}=\mu _{pl}+\xi _{l,k}\sigma _{pl} \end{aligned}$$

(13)

where $\mu _{pl}$ represents mean value and $\sigma _{pl}$ represents the standard deviation of input random variable $P_{l}$. $\xi _{l,k}$ is the standard location which depends upon the number of estimated points. The standard locations can be calculated as follows.

$$\begin{aligned} \xi _{l,k}= & {} \frac{\lambda _{l,3}}{2}+\left( -1\right) ^{3-k}\sqrt{ \lambda _{l,4}-\frac{3}{4}\lambda _{l,3}^{2}} \quad k=1,2 \end{aligned}$$

(14)

$$\begin{aligned} \xi _{l,3}= & {} 0 \end{aligned}$$

(15)

where $\lambda _{l,3}$ and $\lambda _{l,4}$ are the skewness and kurtosis of input random variable $P_{l}$. After estimating the sample points, the fitness function is to be evaluated for all estimated points. The expected values of outputs are determined by Eq. (16).

$$\begin{aligned} E({{Z}^{j}})=\sum \limits _{l=1}^{m}{\sum \limits _{k=1}^{3}{{{w}_{l,k}}}}Z_{l,k}^{j} \end{aligned}$$

(16)

where Z and E(Z) are output vector and expected value of output random variable, respectively. The weighting coefficients $w_{l,k}$ are calculated as following:

$$\begin{aligned} {{w}_{l,k}}= & {} \frac{{{\left( -1 \right) }^{3-k}}}{{{\xi }_{l,k}}\left( {{\xi }_{l,1}}-{{\xi }_{l,2}} \right) }\quad k=1,2 \end{aligned}$$

(17)

$$\begin{aligned} {{w}_{l,3}}= & {} \frac{1}{m}-\frac{1}{{{\lambda }_{l,4}}-\lambda _{l,3}^{2}} \end{aligned}$$

(18)

Approximate mean and moments are calculated as following:

$$\begin{aligned} \begin{aligned}&{{k}_{1}}=E(Z) \\&{{k}_{2}}=E({{Z}^{2}})-E{{(Z)}^{2}} \\&{{k}_{3}}=E({{Z}^{3}})-3E({{Z}^{2}})E(Z)+2E{{(Z)}^{3}} \\&{{k}_{4}}=E({{Z}^{4}})-4E({{Z}^{3}})E(Z)+6E({{Z}^{2}})E{{(Z)}^{2}}-3E{{(Z)}^{4}} \end{aligned} \end{aligned}$$

(19)

3.1.1 Cornish–Fisher Expansion Series

The statistical moments obtained from PEM can be used with some expansion series to obtain the PDF and CDF of the output random variable. Cornish–Fisher, Edgeworth, and Gram–Charlier expansion series are used in the literature. In this paper, Cornish–Fisher expansion is used to compute the PDF and CDF of the output random variables. It is used to obtain the quantile $\alpha$ of the probability distribution F(x). Here $\xi (\alpha ) =\varPhi ^{-1}(\alpha )$ and $\varPhi$ is the PDF of a standard normal distribution N(0, 1).

$$\begin{aligned} X\left( \alpha \right)\approx & {} \xi \left( \alpha \right) +\frac{{{\xi }^{2}}\left( \alpha \right) -1}{6}{{k}_{3}}+\frac{{{\xi }^{3}}\left( \alpha \right) -3\xi \left( \alpha \right) }{24}{{k}_{4}}\nonumber \\&-\,\frac{2{{\xi }^{3}}\left( \alpha \right) -5\xi \left( \alpha \right) }{36}k_{3}^{2} \end{aligned}$$

(20)

$$\begin{aligned} M\approx & {} \mu +\sigma *X \end{aligned}$$

(21)

where $\mu$ and $\sigma$ are mean and standard deviation of output random variable.

3.2 Monte Carlo Simulation Method

Monte Carlo simulation method (MCS) is an iterative method which utilizes PDF of input random variable to obtain the final results. To keep higher accuracy 20,000 samples are considered in the present study. Stopping criteria is based on number of samples or iterations or coefficient of variation tolerances. MCS method requires high computation efforts.

3.3 Voltage Stability Index (VSI)

With the development of economy and a sharp increase in load demand, the voltage stability has been considered as an important issue in the distribution network. The loading margin of the system is calculated from voltage instability techniques such as P–V/Q–V curve method, bifurcation analysis, modal analysis and voltage stability indices. Among various available methods, voltage stability index (VSI) has emerged as very fast and effective tool for offline voltage stability assessment. In this work, VSI proposed by Chakravorty and Das (2000) is utilized for finding weak buses in the network from voltage stability point of view.

Fig. 1

Equivalent circuit of radial distribution network

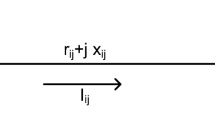
From the equivalent circuit (Fig. 1) of radial distribution network, the following expressions can be deduced.

$$\begin{aligned}&I_{ij}=\frac{V_{i}-V_{j}}{r_{ij}+jx_{ij}} \end{aligned}$$

(22)

$$\begin{aligned}&P_{j}+jQ_{j}=V_{j}I_{ij}^{*} \end{aligned}$$

(23)

where i, j are sending and receiving nodes respectively; $I_{ij}$ is branch current; $V_{i}$, $V_{j}$ are voltage at node i and j respectively; $P_{j}$, $Q_{j}$ are total real and reactive load power fed from node j. From Eqs. (22) and (23), the following expression can be written.

$$\begin{aligned}&|{V_{j}}|^{4}-\left( |{V_{i}}|^{2}-2P_{j}r_{ij}-2Q_{j}x_{ij}\right) |{V_{j}}|^{2}\nonumber \\&\quad +\left( P_{j}^{2}+Q_{j}^{2}\right) \left( r_{ij}^{2}+x_{ij}^{2}\right) \end{aligned}$$

(24)

Let,

$$\begin{aligned}&b=|V_{i} |^{2}-2P_{j}r_{ij}-2Q_{j}x_{ij} \end{aligned}$$

(25)

$$\begin{aligned}&c=\left( P_{j}^{2}+Q_{j}^{2}\right) \left( r_{ij}^{2}+x_{ij}^{2}\right) \end{aligned}$$

(26)

$$\begin{aligned}&|{V_{j}}|^{4}-b |{V_{j}}|^{2}+c=0 \end{aligned}$$

(27)

The feasible solution of Eq. (27) is unique and can be obtained as follows:

$$\begin{aligned}&|{V_{j}}|=0.707 \sqrt{b+\sqrt{b^{2}-4c}} \end{aligned}$$

(28)

$$\begin{aligned}&b^{2}-4c\ge 0 \end{aligned}$$

(29)

From Eqs. (25), (26) and (29),

$$\begin{aligned} \left( |{V_{i}}|^{2}-2P_{j}r_{ij}-2Q_{j}x_{ij}\right) ^{2}-4\left( P_{j}^{2}+Q_{j}^{2}\right) \left( r_{ij}^2+x_{ij}^2\right) {\ge }0 \end{aligned}$$

(30)

Rearranging Eq. (30),

$$\begin{aligned} |{V_{i}}|^{4}-4\left( P_{j}x_{ij}-Q_{j}r_{ij}\right) ^2-4\left( P_{j}r_{ij}+Q_{j}x_{ij}\right) |{V_{i}}|^{2}\ge 0 \end{aligned}$$

(31)

Voltage stability index (VSI) of node j can be expressed as following:

$$\begin{aligned} VSI=|{V_{i}}|^{4}-4\left( P_{j}x_{ij}-Q_{j}r_{ij}\right) ^2-4\left( P_{j}r_{ij}+Q_{j}x_{ij}\right) |{V_{i}}|^{2} \end{aligned}$$

(32)

The minimum value of the stability index at any node represents that the node is more sensitive to voltage collapse. For the stable operation of distribution network VSI value must be $\ge$ 0.

4 Proposed Algorithm

This section caters to the formulation of proposed probabilistic method for the static voltage stability analysis in the radial distribution network.

• Step 1 In a typical distribution network, the load demand is represented as the variation of load with respect to time. The load growth in distribution network is a natural phenomena. With the increase in load demand, the system power losses and voltage drop increases. To analyze the uncertainty associated with load demands, the normally distributed PDF is utilized in this study. The load demand at each node has been taken as mean value with 5 % standard deviation. To access the performance of the distribution network, three load levels: 0.5 (light), 1.0 (nominal), 1.5 (heavy) are considered.

• Step 2 In order to incorporate the uncertainty associated with generation, the Beta and Weibull PDF have been utilized to represent solar irradiance and wind speed respectively.

• Step 3 To determine the voltage stability of considered distribution network, the load connected at each node is increased in steps until VSI at any node falls to nearly zero value. The node with the lowest value of VSI is considered as the weakest node from stability viewpoint and hence, selected as the optimal location for DG placement.

• Step 4 It is assumed that the DG units are operating at unity power factor. Only one type of DG can be connected to a particular node. To study the impact of renewable-based DGs penetration into the distribution network, the following scenarios are proposed.

  • Scenario-I No DG units are integrated into the distribution network and considered as the reference scenario.

  • Scenario-II Only solar PV-based DGs are connected to distribution network.

  • Scenario-III Only wind-based DGs are connected to distribution network.

  • Scenario-IV Both wind and solar PV-based DGs (Hybrid) are connected to distribution network.

• Step 5 Using Hong’s $2m+1$ point estimation method, the expected values of output random variables are found. Also, the means and moments ($k_{1}, k_{2}, k_{3}, k_{4}$) are obtained. For deterministic load flow of the distribution network, the method proposed by Das et al. (1995) is taken into account.

• Step 6 The PDF and CDF of output random variable are determined using Cornish–Fisher expansion series.

• Step 7 The issue associated with the performance of the distribution network due to renewable-based DGs penetration such as voltage stability, network power loss reduction are analyzed for proposed scenarios and are compared with MCS method.

The flowcharts to study the impact of the hybrid DGs penetration on the radial distribution network at various load levels using 3PEM are shown in Fig. 2.

Fig. 2

Flowchart of hybrid DGs integration at different load levels using 3PEM

5 Results and Discussion

The proposed algorithm has been demonstrated and examined on 12.66 kV, 33-node radial distribution test system. The line and load data of the test system are taken from Baran and Wu (1989). The total real and reactive power load demands of the test system are 3.72 MW and 2.3 MVAr, respectively. For the test system, the substation voltage is considered as 1 pu. The selected DGs locations are limited to three, since if the selected DGs locations are more than three, the improvement in the percentage loss reduction decreases (Mistry and Roy 2014). In order to observe the impact of number of DGs locations on network power losses, a deterministic study has been performed on 33-node radial distribution network (Fig. 3). It is observed that the minimum power loss (kW) has been achieved in the distribution network with three DGs only. Moreover, further reduction in percentage power loss is insignificant with larger penetration level of DGs.

Fig. 3

Effect on network power losses due to enhancement in DGs locations

The voltage stability index (VSI) has been evaluated for each node by increasing the load demands in steps. The VSI values evaluated for the nominal and critical load demands are shown in Table 1. By observing Table 1, it is concluded that node nos. 18, 17, 16 and 33 are the critical nodes from voltage stability viewpoint. The critical nodes are referred to those nodes, which are more prone to voltage collapse. Hence, node nos. 16, 18, and 33 are selected as the optimal locations to place DGs from voltage stability viewpoint (Fig. 4). The uncertainties associated with wind speed and solar irradiance are modeled as Weibull and Beta PDF respectively.

In this study, the shape and scale index for Weibull PDF are taken as 6 m/s and 1.4, respectively, and parameters selected for Beta PDF are $\alpha = 2.57$, $\beta = 1.6$. The normal PDF is applied to demonstrate the uncertainties associated with load demands. In normal PDF, the load demand at selected node is considered as the mean value $(\mu )$ with standard deviation $(\gamma )$ of 5%. To access the performance of the test network, the three load levels: 0.5 (light), 1.0 (nominal), and 1.5 (heavy) are considered in each scenario. For analyzing the effect of DGs on voltage stability and power losses of the network, the various DGs penetration levels up to 40% have been taken into consideration. The selected solar PV modules and wind turbines are shown in Tables 2 and 3 respectively.

Table 1 Critical nodes of IEEE 33-bus distribution network

Fig. 4

IEEE 33-node distribution network with hybrid distributed generation

Table 2 Characteristics of the PV modules

Table 3 Characteristics of considered wind turbines

Fig. 5

Capacity factor for wind turbines and solar PV modules

The capacity factor for the DG unit can be defined as the ratio of the average output power from DG unit and the rated power output of the DG unit (Atwa et al. 2010). The solar PV module B has highest capacity factor (0.4264), and therefore, the module type B is selected for the study (Fig. 5a). Similarly, the wind turbine C has the highest capacity factor (0.2340), therefore selected for the study (Fig. 5b). It was observed from Table 4, at scenario-I, that the power losses at light, nominal and heavy load demand conditions are 47 kW, 202.77 kW and 496.61 kW respectively. In scenario-II, the solar PV units are placed at node 16, 18, and 33, respectively. The equal penetration level of DGs is considered at the selected locations. The percentage active power loss (APL) reduction at 10% PV penetration for light, nominal and heavy loads is 20.40, 21.57, and 22.51, respectively. Also, the minimum system voltage and VSI got improved. It is observed from Table 4 that, at 10–20% penetration level of solar PV DGs, the % APL reduction is higher compared to the high penetration level of 30–40%. The higher reduction in the power losses have been also observed up to 30% penetration level with solar PV DGs at light, nominal, and heavy load conditions. The power loss reduction at 40% penetration level is very low for nominal and heavy load demands compared to 30% penetration level. Therefore, 30% penetration should be considered as a penetration limit for solar PV type DGs.

Table 4 Results analysis of test network for scenarios I, II, and III using $2m+1$ point estimation method

Table 5 Results analysis for the test network with hybrid DGs using $2m+1$ point estimation method in scenario-IV

Table 6 Comparison between two probabilistic-based approaches for the test network

In scenario-III, the wind energy-based DGs are placed at selected locations, and it was observed that only 10% penetration is possible for test system with wind energy-based DGs. The penetration level more than 10% had a negative effect on system active power losses. It was also observed that the power losses are higher with wind energy-based DGs compared to solar PV DGs for same penetration levels in the test network. One of the reasons for this is owing to the solar PV panels being smaller in power capacity (few watt) compared to wind energy-based DGs (several kW to few MW). However, the power generated from solar PV modules are more consistent with each sample of random input (solar irradiance) compared to wind energy which generates the electrical power only when the wind speed is between cut-in and cutout wind speed. In scenario-IV, the maximum penetration study is performed with the hybrid (solar PV and wind energy) DGs in the test network. Throughout the year, the wind speed and solar irradiance are weakly anticorrelated $(-0.4\le \rho \le - 0.2)$ (Bett and Thornton 2016). In order to determine the maximum penetration level with hybrid renewable DGs, the electrical power output is taken approximately 70% from wind generators and 30% from solar PV-based DGs. The three locations (nodes 17, 18, and 33) are identified for the placements of hybrid DGs. Based on identified locations, the three case studies were further investigated. In case-I, the wind energy-based DGs are placed at node 17 and 18, whereas solar PV-based DG is placed at node 33. In case-II, the wind energy-based DGs are placed at node 17 and 33, whereas solar PV-based DG is placed at node 18. In case-III, the wind energy-based DGs are placed at node 18 and 33, whereas solar PV DG is placed at node 17. The results analysis for the test network with hybrid DGs have presented in Table 5. It is observed from Table 5, the penetration level of renewable-based DGs increases up to 20% when hybrid combinations of renewable DGs are used. It is noted that when only wind energy-based DGs are integrated into the test network, only 10% penetration level was achieved, whereas the small amount of solar PV integration has boosted the penetration level to 20%. Also, for case-II, the active power losses at various load levels are less compared to case-I and II. Hence, it can be concluded that when solar DG is placed at a most critical node (node 18) of the network, much improvement in power loss reduction is obtained.

Usually, the integration of DGs reduces the power losses in the network; however, it is observed that as the penetration level of DGs increases, the power losses begin to increase. A similar observation were found by Ogunjuyigbe et al. (2016). Finally the results obtained from the $2m+1$ point estimation method are compared with the MCS method in Table 6. The comparisons of the voltage profile for various scenarios of the test system at different load levels, i.e., light, nominal and heavy are shown in Figs. 6, 7, and 8, respectively. Similarly, comparison of active power losses for various types of DGs penetration at different load levels, i.e., light, nominal, and heavy are shown in Figs. 9, 10, and 11, respectively. The simulation has been performed on MATLAB software in Intel i7 processor 2.4 GHz, 8GB RAM computer. The simulation time for $2m+1$ point estimation method is 0.9083 s for scenario-I at nominal load whereas MCS method takes 90.528 s.

Fig. 6

Voltage profile of nodes in test network under nominal load

Fig. 7

Voltage profile of nodes in test network under light load

Fig. 8

Voltage profile of nodes in test network under heavy load

Fig. 9

Active power loss of test network with different types of DG’s penetration level under nominal load

Fig. 10

Active power loss of test network with different types of DG’s penetration level under heavy load

Fig. 11

Active power loss of test network with different types of DG’s penetration level under light load

6 Conclusions

In this paper, the static voltage stability index (VSI) is used to identify the optimal locations of DGs in the radial distribution network. The various penetration levels (10–40%) of renewable-based DGs in the radial distribution networks and their effects on power losses, voltage profiles and voltage stability have been studied through the probabilistic approach. The 33-node radial distribution test network has been utilized for the validation of the proposed approach. Owing to the uncertainty associated with the solar irradiance, wind speed and load demands, a probabilistic-based load flow method is performed in this research paper. The Hong’s $2m+1$ point estimation method (PEM) is applied and compared with the benchmark MCS method. To obtain the PDF and CDF of output random variables, the Cornish–Fisher expansion series is incorporated with PEM method. From the result analysis, it is observed that the maximum penetration level of DGs in the test network in light of voltage stability is determined by three key factors, i.e., type of DGs, the location of DGs and load level of the network. When only solar-based DGs are integrated into the test network, the maximum penetration level of 30% is achieved, whereas only 10% is attained with wind energy-based DGs.

Hence, the authors have tried to exploit those geographical locations where wind energy is abundant but also the solar irradiance has enough exposure. At such places instead of only going with wind-based PV a hybrid combination of wind and solar PV will increase the penetration level. Moreover, such locations can easily be found on wide coastal line of tropical country like India. In this paper, a hybrid combination of the power output from wind energy (70%) and solar PV (30%) is analyzed in order to enhance the penetration level of renewable-based DGs up to 20%.

The paper also highlights to adopt the probabilistic approaches over deterministic ones as former incorporates the uncertainties associated with renewable energy sources. The proposed approach based on PEM has an edge over other methods available in the literature as it requires very less iterations and hence computational time too reduces which facilitates the power engineers working on online applications in the radial distribution network. For the first time, based upon point estimation method, the power losses and voltage stability studies are conducted for hybrid-based DGs in the radial distribution network.