Design and Implementation of Feedback Resonance Compensator in Hard Disk Drive Servo System: A Mixed Passivity, Negative-Imaginary and Small-Gain Approach in Discrete Time

Abstract

This paper presents a feedback resonance compensator designed in a simple and yet efficient way to suppress the effects of resonant modes of voice coil motor actuator used in hard disk drive (HDD) servo system. A velocity feedback controller is chosen as the feedback resonance compensator. Resonant modes of the actuator prohibit bandwidth to be pushed to higher frequencies and it causes large oscillations to the closed-loop system response. Therefore, effective compensation of mechanical resonant modes is one of the design challenges in HDD servomechanism. The proposed design is based on a mixed passivity, negative-imaginary and small-gain approach in discrete time which results in a robust stable controller. Firstly, stability of discrete-time interconnected system is analyzed using mixed passivity, negative-imaginary and small-gain properties. These results are analogous to previously established continuous-time case. Nowadays most of the control design is done in discrete time. Hence, this paper provides a base for discretization of mixed system with passivity, negative-imaginary and small-gain properties. Secondly, a velocity feedback controller for resonance compensation is designed using this mixed approach. Simulation and experimental results substantiate the effectiveness of the controller.

1 Introduction

The magnetic components, i.e., the media and the head of a hard disk drive (HDD) are the major components that enable storage and writing or retrieval of binary information. Data bits are stored in concentric data tracks on a rotating disk coated with magnetic media. The read/write head (R/W head) fabricated on a single piece of slider is used for recording as well as retrieving data bits. The slider is positioned on the tracks by a head-positioning servomechanism. The head is controlled to move from one track to another track in minimum possible of time and then it is maintained as close to the center of the track as possible. Nowadays, HDD servomechanism uses dual-stage actuation which consists of a voice coil motor (VCM) and a piezoelectric secondary actuator (PSA). The VCM is used to provide coarse motion, and the PSA is used for fine positioning. Therefore, for both single stage and dual-stage HDD, resonance of VCM actuator is a issue to be solved. This problem with resonance of the VCM actuator is addressed in this paper.

The HDD industry has experienced tremendous growth in recording density over the years and presently the density is around 1 Tbits per square inch. It is projected to exceed the 10 Tbits per square inch barrier in the near future. This will require increase in both density of tracks (track density) and density of bits on a track (bit density). Increased track density means smaller track width and thus, improved accuracy in positioning the R/W head in spite of various disturbances. The high track density needs a servo controller with high bandwidth for eliminating the effects external disturbances. But resonant modes of the actuator prohibit bandwidth to be pushed to higher frequencies and it causes large oscillations to the closed-loop system response.

Open-loop design approach is a popular method of suppressing resonance by cascading notch filters with the plant (Al Mamun et al. 2006; Thum et al. 2010; Lan et al. 2010; Suthasan et al. 2004). In this approach, a pre-compensator for resonant modes is designed in such a way that the frequency response of the pre-compensated plant bears resemblance to that of a rigid-body model. However, this approach is less effective when model uncertainty is taken into consideration. If a pre-compensator notch filter is designed for finite number of resonant modes, imperfect cancelation of resonant modes may occur. On the contrary, feedback controllers can provide robustness in the presence of variations of the resonant modes. Optimal robust controller design methods such as LQG/LTR control Chang and Ho (1999) and $H_2$ optimal controller Li et al. (2004) can be used to suppress mechanical resonance. However, the order of controllers using LQG/LTR or $H_2/H_\infty$ method depends on the order of the systems. Since large number of resonant modes are found in actuators used in HDD, a high-order plant model is required to include all resonances. Therefore, LQG/LTR or $H_2/H_\infty$ method results in a controller of very high order. An adaptive notch filter is proposed in Kang and Kim (2005), comprising of a tunable finite-duration impulse response (FIR) filter. A tuner is designed to identify the resonance frequency rapidly, and the center frequency of the filter is adjusted automatically. A similar method is used in Ohno and Hara (2006), in which the center frequency follows the change in resonance frequency based on the balance of two types of frequency weighted variances of the control input signal. However, in almost all the adaptive methods, finding the adaptive law is nontrivial and choosing the adaptive law parameters is tedious. Besides, adaptive methods are often complex and computationally expensive.

In this paper, a velocity feedback controller (VFC) is designed to increase damping of the first major resonant mode of the VCM actuator. The method is simple and easy to implement. A mixed passivity, negative-imaginary and small-gain approach in discrete time is followed to achieve large damping of the resonant mode with robust finite-gain stability. To the best knowledge of the authors, the mixed negative-imaginary, passivity and small-gain theory for resonance compensator design were never analyzed and implemented before for the HDD servo systems. Besides, this paper is not a direct implementation of the mixed theory in continuous time. This paper establishes a base for the mixed system to be analyzed in discrete time and then the discrete-time approach is implemented in the HDD.

The small-gain theorem, passivity theorem and negative-imaginary theorem are important results in the theory of stability of input-output systems. The small-gain theorem confirms the finite-gain stability of the feedback interconnection of two stable systems if the product of the gain of the systems at each frequency is $<$1 (Desoer and Vidyasagar 1975). Passivity theorem states that the negative feedback interconnection between two stable linear time invariant systems is stable when both systems are passive and one of them is strictly passive with finite gain (Desoer and Vidyasagar 1975; Green and Limebeer 1996). According to negative-imaginary theorem, the positive feedback interconnection between two systems where one system is negative-imaginary and other system is strictly negative-imaginary is stable if and only if the DC loop gain is $<\!1$ (Lanzon and Petersen 2007, 2008).

However, it is often seen that many practical systems do not always belong to the specific class, i.e., only passivity or only negative-imaginary over the whole frequency range (Griggs et al. 2007, 2009; Patra and Lanzon 2011; Das et al. 2013). There are many other systems which may have mixed passivity and small-gain (Griggs et al. 2007, 2009) properties or mixed negative-imaginary and small-gain (Patra and Lanzon 2011) properties. An unconditional stability analysis for negative feedback interconnected systems with mixed passivity and small-gain properties is presented in Griggs et al. (2007), whereas Das et al. (2013) shows conditional stability between systems with mixed negative-imaginary and small-gain properties using positive feedback. Only Small-gain stability analysis can be applied and implemented to any kind of mixed system where the system does not hold only negative-imaginary or passivity property. However, the use of the small-gain theorem makes the controller gain low which leads to low level of damping of the structures resonant modes in vibration control applications. Therefore, use of mixed theorem is very essential for the controller design.

Nowadays, most of the feedback control systems are implemented digitally using microcontroller or digital signal processors. In order to implement the control design for high-speed system through some RTI tool like dSPACE, a discrete-time representation of the system is required. Thus, it is to be settled whether the discretization of continuous-time systems can preserve the fundamental properties after discretization. Several papers Pietrus and Veliov (2009), Zappavigna et al. (2012), Borrelli et al. (2006), Falcone et al. (2008), Shorten et al. (2011), Sanfelice and Teel (2010) have recently discussed on this topic of system discretization, particularly in the switched systems community. Characterization of mixed passivity and small-gain property in discrete time is discussed in Griggs et al. (2013). However, the purpose of our paper is to establish the foundation for the discretization of mixed systems with passivity, negative-imaginary and small-gain properties and establishing a stability analysis on discrete time for these types of mixed systems. These results are analogous to previously established continuous-time case (Das et al. 2013, 2015).

The rest of the paper is organized as follows. Section 2 presents the mathematical definitions of passivity, negative-imaginary and mixed properties and also highlights some preliminary results. Feedback stability analysis is presented in Sect. 3. Identification of VCM actuator model using experimental frequency response is given in Sect. 4. Section 5 presents the controller design methodology. Simulation and Experimental results are shown in Sect. 6, and finally, a conclusion is drawn in Sect. 7.

2 Mathematical Definitions and Preliminary Results

Considering $y=xe^{j\theta }$ is a complex number where $x=|y|$ and $\theta =\angle y$ and assuming that $\theta =\omega T_s$ where $T_s$ and $\omega$ are the sampling interval in seconds and signal frequency in rad/s, respectively. The largest and smallest singular values of a matrix $A$ is denoted by $\bar{\sigma }(A)$ and $\underline{\sigma }(A)$.

Finite-gain A bounded-input bounded-output (BIBO) stable, discrete-time system with square, proper, real-rational transfer function matrix $M(z)$ is said to have the finite-gain property bounded by $K>0$ over $[-m,-n]\cup [m,n]$ if

$$\begin{aligned} K:= inf\left\{ k\in \mathbb {R}_+:-M^*\left( e^{j\theta }\right) M\left( e^{j\theta }\right) +k^{2}I\right\} \ge 0 \end{aligned}$$

(1)

for all $\theta \in [-m,-n]\cup [m,n]$ where $0\le m\le n\le \pi$ and $k\ge 0$

Passivity (1) A BIBO stable system with square, proper, real-rational transfer function matrix $G(z)$ is said to be input–output strictly passive over $[-m,-n]\cup [m,n]$ if

$$\begin{aligned} -\alpha G^*\left( e^{j\theta }\right) G\left( e^{j\theta }\right) +G^*\left( e^{j\theta }\right) +G\left( e^{j\theta }\right) -\beta I\ge 0\nonumber \\ \end{aligned}$$

(2)

for all $\theta \in [-m,-n]\cup [m,n]$ where $0\le m\le n\le \pi$ and $\alpha ,\beta \ge 0$

(2) A BIBO stable system with square, proper, real-rational transfer function matrix $H(z)$ is said to be input–output strictly negative passive over $[-m,-n]\cup [m,n]$ if

$$\begin{aligned} -\alpha H^{*}\left( e^{j\theta }\right) H\left( e^{j\theta }\right) -H^{*}\left( e^{j\theta }\right) -H\left( e^{j\theta }\right) -\beta I\ge 0\nonumber \\ \end{aligned}$$

(3)

for all $\theta \in [-m,-n]\cup [m,n]$ where $0\le m\le n\le \pi$ and $\alpha ,\beta \ge 0$

The systems $G(z)$ and $H(z)$ are called input strictly passive and input strictly negative passive, respectively, if (2) and (3) are satisfied, respectively, for $\alpha =0$; output strictly passive and output strictly negative passive, respectively, if (2) and (3) are satisfied, respectively, for $\beta =0$; and passive and negative passive, respectively, if (2) and (3) are satisfied, respectively, for $\alpha =\beta =0$.

Negative-imaginary A BIBO stable system with square, proper, real-rational transfer function matrix $G(z)$ is said to be input–output strictly negative-imaginary over $[-m,-n]\cup [m,n]$ if

$$\begin{aligned} -\alpha \theta ^2 G^*\left( e^{j\theta }\right) G\left( e^{j\theta }\right) +j\theta G^*\left( j\omega \right) -j\theta G\left( j\omega \right) -\beta I \ge 0 \end{aligned}$$

(4)

for all $\theta \in [-m,-n]\cup [m,n]$ where $0\le m\le n\le \pi$ and $\alpha ,\beta \ge 0$

The systems $G(z)$ is called input strictly negative-imaginary if (4) is satisfied for $\alpha =0$; output strictly negative-imaginary if (4) is satisfied for $\beta =0$; and negative-imaginary if (4) is satisfied for $\alpha =\beta =0$.

Mixed passivity, negative-imaginary and small-gain (1) A BIBO stable, discrete-time system with square, proper, real-rational transfer function matrix $G(z)$ is said to have the mixed passivity, negative-imaginary and small-gain properties if for each frequency $\theta \in [-\pi ,\pi ]$ there exists a) $-\alpha G^*(e^{j\theta })G(e^{j\theta })+G^*(e^{j\theta })+G(e^{j\theta })-\beta I\ge 0$ or b)$-\delta \theta ^2 G^*(e^{j\theta })G(e^{j\theta })+j\theta G^*(j\omega )-j\theta G(j\omega )-\gamma I \ge 0$ and/or c) $-G^*(e^{j\theta })G(e^{j\theta })+k^{2}I \ge 0$ where $\alpha ,\beta ,\delta ,\gamma ,k\ge 0$

(2) A BIBO stable, discrete-time system with square, proper, real-rational transfer function matrix $G(z)$ is said to have the mixed negative-passivity, negative-imaginary and small-gain properties if for each frequency $\theta \in [-\pi ,\pi ]$, there exists a) $-\alpha G^*(e^{j\theta })G(e^{j\theta })-G^*(e^{j\theta })-G(e^{j\theta })-\beta I\ge 0$ or b)$-\delta \theta ^2 G^*(e^{j\theta })G(e^{j\theta })+j\theta G^*(j\omega )-j\theta G(j\omega )-\gamma I \ge 0$ and/or c) $-G^*(e^{j\theta })G(e^{j\theta })+k^{2}I \ge 0$ where $\alpha ,\beta ,\delta ,\gamma ,k\ge 0$

Let us now consider the following example from Das et al. (2013)

$$\begin{aligned} M(s)=\frac{-186.6s^2+1.348\times 10^6s-2.412\times 10^10}{s^3+1955s^2+3.452\times 10^7s+4.459\times 10^10} \end{aligned}$$

(5)

$M(s)$ is a system with mixed negative-imaginary and passivity properties (Das et al. 2013; Glad and Ljung 2000). Now using zero-order hold discretization method, $M(s)$ is discretized to $M_1(z)$ and $M_2(z)$ for sampling interval $T=0.0002$ sec and $T=0.02$ s, respectively.

$$\begin{aligned} M_1(z)=\frac{-0.03z^2-0.046z-0.066}{z^3-1.519z^2+1.458z-0.676} \end{aligned}$$

(6)

and

$$\begin{aligned} M_2(z)=\frac{-0.541z^2-0.0019z-1.88\times 10^-6}{z^3+0.0034z^2 +3.29\times 10^-6-1.045\times 10^-17} \end{aligned}$$

(7)

The nyquist plots in Fig. 1 shows that $M_1 (z)$ is a discrete-time system with mixed passivity, negative-passivity, negative-imaginary and small-gain properties where $M_2 (z)$ is a discrete-time system with mixed passivity, negative-passivity and small-gain properties. $M_1 (z)$ holds the same properties as the $M(s)$ where $M_2 (z)$ fails to preserve the same properties after discretization. Thus, discretization may change the properties of a system from its continuous-time case. This leads to the motivation of designing the controller in discrete-time approach.

Fig. 1

a Nyquist plot of $M(s)$, b Nyquist plot of $M_1(z)$, c Nyquist plot of $M_2(z)$

Now some preliminary results are presented to establish the main results

Theorem 1

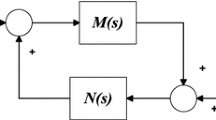
According to Zhou et al. (1996), if $M(z)$ and $N(z)$ are strictly proper, real-rational transfer function matrices, then feedback interconnection of Fig. 2 is stable if the nyquist plot of $\hbox {det}[I-M(e^{j\theta } )N(e^{j\theta } )]$ for $-\pi \le \theta \le \pi$ does not make any encirclements of the origin.

Fig. 2

Interconnection of system with positive feedback

The nyquist plot of $\hbox {det}[I-M(e^{j\theta } )N(e^{j\theta } )]$ is included in the group of nyquist plots of $\hbox {det}[I-\frac{1}{\Gamma }M(e^{j\theta } )N(e^{j\theta } )]$, where $\Gamma \in [1,\infty )$. Suppose the nyquist plot of $\hbox {det}[I-\frac{1}{\Gamma }M(e^{j\theta } )N(e^{j\theta } )]$ encircles the origin at least once which means that if $\Gamma$ is continuously decreased from a large value toward 1, then there must be at least one $\Gamma _0$ and one $\theta _0$ for which $\hbox {det}[I-\frac{1}{\Gamma _0}M(e^{j\theta _0} )N(e^{j\theta _0} )]=0$. Therefore, to avoid the encirclement of the origin, the sufficient condition is that for all $\Gamma \in [1,\infty )$ and all $\theta \in [-\pi ,\pi ]$, $\hbox {det}[I-\frac{1}{\Gamma }M(e^{j\theta } )N(e^{j\theta } )]\ne 0$.

Lemma 1

Suppose that $M(z)$ and $N(z)$ are BIBO stable, square, strictly proper, real-rational transfer function matrices. At some $\theta _0\in [-\pi ,\pi ]$, if $M^*(e^{j\theta _0})+M(e^{j\theta _0})>0$ and $-N^*(e^{j\theta _0})-N(e^{j\theta _0})\ge 0$, then $\hbox {det}[I-M(e^{j\theta _0} )N(e^{j\theta _0})]\ne 0$

Proof

: Since $M^*(e^{j\theta _0})+M(e^{j\theta _0})>0$ and $-N^*(e^{j\theta _0})-N(e^{j\theta _0})\ge 0$, hence real parts of $\lambda _i [M(e^{j\theta _0})]>0$ and real parts of $\lambda _i[-N(e^{j\theta _0})]\ge 0$, where $\lambda _i[.]$ denotes the ith eigen value (Lancaster and Tismenetsky 1985). Therefore, $M(e^{j\theta _0})$ is nonsingular.

Since $M^*(e^{j\theta _0})+M(e^{j\theta _0})$ and $M^{-*}(e^{j\theta _0})+M^{-1}(e^{j\theta _0})$ are Hermitian congruent (Noble and Daniel 1988), hence $M^{-*}(e^{j\theta _0})+M^{-1}(e^{j\theta _0})>0$ which therefore implies that $M^{-*}(e^{j\theta _0})-N^*(e^{j\theta _0})+M^{-1}(e^{j\theta _0})-N(e^{j\theta _0})>0$. Therefore, the real parts of $\lambda _i[M^{-1}(e^{j\theta _0})-N(e^{j\theta _0})]>0$ for all $\lambda _i$ and $\hbox {det}[M^{-1}(e^{j\theta _0})-N(e^{j\theta _0})]\ne 0$ which entails that $\hbox {det}[I-M(e^{j\theta _0})N(e^{j\theta _0})]\ne 0$. $\square$

Since $\hbox {det}[I-M(e^{j\theta _0})N(e^{j\theta _0})]= \hbox {det}[M(e^{j\theta _0})\hbox {det}[M^{-1}(e^{j\theta _0})-N(e^{j\theta _0})]]$, hence $M(e^{j\theta _0})$ is nonsingular.

Lemma 2

Suppose that $M(z)$ and $N(z)$ are BIBO stable, square, strictly proper, real-rational transfer function matrices. At some $\theta _0\in [-\pi ,\pi ]$, if $j(M(e^{j\theta _0})-M^*(e^{j\theta _0}))>0$ and $j(N(e^{j\theta _0})-N^*(e^{j\theta _0}))>0$ then $\hbox {det}[I-M(e^{j\theta _0})N(e^{j\theta _0})]\ge 0$.

Proof

The two suppositions can be written as $jM(e^{j\theta _0})+((jM(e^{j\theta _0}))^*>0$ and $(jN(e^{j\theta _0}))^{-1}+(jN(e^{j\theta _0}))^{-*}>0$. Hence, $\hbox {det}[I-M(e^{j\theta _0})N(e^{j\theta _0})] =\hbox {det}[I+(jM(e^{j\theta _0})(jN(e^{j\theta _0}))] =\hbox {det}[(jM(e^{j\theta _0})+(jN(e^{j\theta _0}))^{-1}]\hbox {det} [jN(e^{j\theta _0})]\ne 0$.

3 Feedback Stability

Theorem 2

Let $M(z)$ and $N(z)$ are BIBO stable, square, strictly proper, real-rational transfer function matrices where $M(z)$ and $N(z)$ are bounded by gain $k_1>\bar{\sigma }(M(z=1))$ and $k_2>\bar{\sigma }(N(z=1))$, respectively. Then, for the feedback interconnected system in Fig. 2, the interconnected system is finite-gain stable if (a)$k_1k_2<1$, (b) there exists four sets of frequency range: (1)$\phi _{NI}$, a set consists of $\theta _0\in [-\pi ,\pi ]$ over which both $M(z)$ and $N(z)$ have negative-imaginary property (2) $\phi _{P-NP}$, a set consists of $\theta _0\in [-\pi ,\pi ]$ over which $M(z)$ has passivity property and $N(z)$ has negative-passivity property (3) $\phi _{NP-P}$, a set of consists of $\theta _0\in [-\pi ,\pi ]$ over which $M(z)$ has negative-passivity property and $N(z)$ has passivity property (4) $\phi _{FG}$, a set consists of $\theta _0\in [-\pi ,\pi ]$ over which $M(z)$ is bounded by $k_1$ and $N(z)$ is bounded by $k_2$.

Proof

The proof can be divided into three parts: (a) For $M(z)$ and $N(z)$ belong to set $\phi _{NI}$, it is to be shown that $\hbox {det}[I-\frac{1}{\Gamma }M(e^{j\theta _0})N(e^{j\theta _0})\ne 0$ for all $\Gamma \in [1,\infty )$ (b) For $M(z)$ and $N(z)$ belong to set $\phi _{P-NP}$ or $\phi _{NP-P}$, it is to be shown that $\hbox {det}[I-\frac{1}{\Gamma }M(e^{j\theta _0})N(e^{j\theta _0})\ne 0$ for all $\Gamma \in [1,\infty )$ (c) For $M(z)$ and $N(z)$ belong to set $\phi _{FG}$, it is to be shown that $\hbox {det}[I-\frac{1}{\Gamma } M(e^{j\theta _0})N(e^{j\theta _0})\ne 0$ for all $\Gamma \in [1,\infty )$ if $k_1 k_2<1$.

Part (a): Since $M(z)$ and $N(z)$ belong to set $\phi _{NI}$, there exists $\alpha _i,\beta _i>0, i=1,2$ such that $-\alpha _1\theta _0^2 M^*(e^{j\theta _0})M(e^{j\theta _0})+j\theta _0 M(e^{j\theta _0})-j\theta _0 M(e^{j\theta _0})-\beta _1 I\ge 0$ and $-\alpha _2\theta _0^2 N^*(e^{j\theta _0})N(e^{j\theta _0})+j\theta _0 N(e^{j\theta _0})-j\theta _0 N(e^{j\theta _0})-\beta _2 I\ge 0$, respectively, which entails that $j\theta _0 M(e^{j\theta _0})-j\theta _0 M(e^{j\theta _0})>0$ and $j\theta _0 N(e^{j\theta _0})-j\theta _0 N(e^{j\theta _0})>0$. Therefore, $\frac{1}{\sqrt{\Gamma }} j\theta _0(M(e^{j\theta _0})-M^*(e^{j\theta _0}))>0$, for $\Gamma >0$. Hence, according to Lemma 3, $\hbox {det}[I-\frac{1}{\Gamma }M(e^{j\theta _0})N(e^{j\theta _0})\ne 0$.

Part (b): Let us consider $M(z)$ and $N(z)$ belong to set $\phi _{P-NP}$, then there exists $\alpha _i,\beta _i>0, i=1,2$ such that $-\alpha _1 M^*(e^{j\theta _0}M(e^{j\theta _0})+M^* (e^{j\theta _0} )+M(e^{j\theta _0})-\beta _1 I\ge 0$ and $-\alpha _2 N^*(e^{j\theta _0}N(e^{j\theta _0})+N^* (e^{j\theta _0} )+N(e^{j\theta _0})-\beta _2 I\ge 0$, respectively, which implies that $M^* (e^{j\theta _0})+M(e^{j\theta _0})>0$ and $-N^*(e^{j\theta _0})-N(e^{j\theta _0})\ge 0$. Therefore, $\frac{1}{\Gamma }[M^*(e^{j\theta _0})+M(e^{j\theta _0})]>0$ and $\frac{1}{\Gamma }[-N^*(e^{j\theta _0})-N(e^{j\theta _0})]>0$, for $\Gamma >0$. Hence, from Lemma 2, $\hbox {det}[I-\frac{1}{\Gamma }M(e^{j\theta _0})N(e^{j\theta _0})\ne 0$. If, $M(z)$ and $N(z)$ belong to set $\phi _{NP-P}$, the above proof is vice versa.

Part (c): Since $M(z)$ and $N(z)$ belong to set $\phi _{FG}$, hence there exists $k_1, k_2>0$ such that $-M^*(e^{j\theta _0})M(e^{j\theta _0})+k_1^2I\ge 0$ and $-N^*(e^{j\theta _0})N(e^{j\theta _0})+k_2^2I\ge 0$ . Now, since $k_1>\bar{\sigma }(M(z=1))$ and $k_2>\bar{\sigma }(N(z=1))$ and $M(z)$ and $N(z)$ are bounded by $k_1$ and $k_2$, respectively, hence $\hbox {det}[I-\frac{1}{\Gamma }M(e^{j\theta _0})N(e^{j\theta _0})\ne 0$ if and only if $k_1k_2<1$ for all $\Gamma \in [1,\infty )$.

4 Plant Model

The experimental setup used for measuring the frequency response consists of a dynamic signal analyzer (DSA), a driver for the VCM actuator and Laser Doppler Vibrometer (LDV) OFV 5001. The sweep sine excitation signal generated by the DSA is applied to the driver which provides required voltage-to-current conversion to drive the VCM actuator. Displacement is measured using the LDV. The laser beam from the LDV is focused on the tip of actuator, and the difference between frequencies of the incident beam and reflected beam is used to measure the velocity of the tip. The built-in decoder of the LDV generates displacement data from the measured velocity. The resolution of displacement measurement is set to 50 nm/V in all experiments reported in this paper. This measurement setup is illustrated in Fig. 3.

Fig. 3

a Experimental setup, b frequency response experiment, c controller implementation

The excitation signal (sweep sine) applied to the VCM driver circuit is generated by $LabVIEW^{TM}$ (National Instrument) virtual instrument. The same signal is also connected to one of the input channels of DSA. The displacement signal from the LDV is connected to the second input channel of DSA. The analyzer produces the frequency response data, and the result is saved for further processing. Modeling method used in Yamaguchi and Hirata (2011), Rahman et al. (2014), Rahman and Mamun (2014) is used to identify the resonant modes and overall linear model of the system. In general, the guidelines for constructing a $\sum$-type model are (1) begin with the modes with larger gain before proceeding to the modes with smaller gain (2) set the modal angular frequency to match the frequency of the peak gain (3) tune the modal damping ratio by using the half value method in order to fit frequency width of the peak gain at half of the maximum and shape of phase change and (4) adjust the absolute value and sign of the residue to match the peak gain and direction of phase change in the data, respectively. The frequency response data are used to identify a linear model in the form of

$$\begin{aligned} P(s)=K\times \frac{K_v}{s^2}\times \sum \limits _{i=1}^N H_{r,i} \end{aligned}$$

(8)

where $K$ and $K_v$ are the gains. $N$ is the number of resonant modes modeled as lightly damped complex conjugate poles as is

$$\begin{aligned} H_{r,i}=\frac{A_i}{s^2+2\zeta _i\omega _{r,i}s+\omega _{r,i}^2} \end{aligned}$$

(9)

The identified parameters are shown in Tables 1 and 2. Experimental frequency response and identified model response are shown in Fig. 4. Note that the high-frequency part of the identified model is not exactly matched with the experimental response which is the case of neglecting high-frequency resonant modes in the identified model. As there is always a high-frequency roll-off in the actuator response, the controller can be designed in such a way that the high-frequency region satisfies the small-gain theorem; therefore, this high-frequency mismatch between the identified model and the experimental response does not affect much in the design.

Fig. 4

Frequency response of VCM actuator

Table 1 Parameter values $P(s)$

Table 2 Parameter values for $H_{r,i}$

Remark 1

The measured frequency response relates an input signal measured in volts to an output signal also measured in volts. So the transfer function is unit-free. The output signal can be converted into displacement unit by multiplying it by the scaling factor of 50 nm/V.

5 Controller Design

Since the rigid body dynamics of the actuator is a double integrator, a lead compensator is used to stabilize it. A lag compensator is also designed to increase the low-frequency slope of the Bode (magnitude) plot which is required for better tracking. The lag–lead compensator is designed according to the bode-stability criteria (Al Mamun et al. 2006). The overall controller is,

$$\begin{aligned} C(s)=K_d \frac{\left( \frac{s}{\omega _2}+1\right) \left( \frac{s}{\omega _3}+1\right) }{\left( \frac{s}{\omega _1}+1\right) \left( \frac{s}{\omega _4}+1\right) } \end{aligned}$$

(10)

The gain $K_d$ is chosen to satisfy the following condition

$$\begin{aligned} \left| \frac{1}{C(j\omega )P(j\omega )}\right| _{\omega =\omega _v}=1 \end{aligned}$$

(11)

The design is further simplified by considering the predefined relationship between the frequency crossover points as $\omega _1=10\pi ,\omega _2=2\times \frac{\omega _v}{\Gamma },\omega _3=2\times \frac{\omega _v}{3}$ and $\omega _4=3\times \omega _v$ where $\Gamma$ can be chosen between 3 and 5. Then with these relationships, the gain $K_d$ can be obtained as

$$\begin{aligned} K_d=\left| \frac{\left( \frac{1}{10\pi }s+1\right) \left( \frac{1}{3\omega _v}s+1\right) }{\left( \frac{\omega _v}{\Gamma }s+1\right) \left( \frac{3}{\omega _v}s+1\right) }\right| \end{aligned}$$

(12)

Now, the transfer function $M(s)$ in Fig. 2 is the closed-loop transfer function of VCM with lag–lead controller (Fig. 5) where $P(s)$ is the VCM actuator and $C(s)$ is the lead–lag controller . Then $M(s)$ is discretized to $M(z)$ using the zero-order hold method and a VFC $N(z)$ is then designed based on $M(z)$.

Fig. 5

Closed-loop stabilized VCM plant, $M(s)$

Before designing $N(z)$, a VFC is designed in continuous time and then discretized using the ’tustin approximation’ method. The corresponding step responses for continuous-time controller and discretized controller are shown in Fig. 7. The figure shows the performance degradation when the controller is designed in continuous time and then discretized by using some standard approximation methods.

Fig. 6

Overall block diagram of the design for experimental implementation

Fig. 7

Comparison of step responses between system with continuous-time designed controller and system with discretized model of continuous-time designed controller

In this paper, the VFC is designed in discrete time and the controller parameters are tuned to find the best suitable resonance compensator. The general transfer function for the discrete-time resonant controller is as follows:

$$\begin{aligned} N(z)=K_r\frac{b_1z^2+b_2}{a_1z^2+a_2z+a_3} \end{aligned}$$

(13)

In this design, the parameters $a_1,a_2,a_3,b_1,b_2$ are selected in such a way that the VFC will act as the resonance compensator for the first major resonant mode and the interconnected system between $M(z)$ and $N(z)$ satisfies theorem 2. Since the bandwidth of the system is fixed by the nominal controller, the high-frequency resonant modes do not have any effects on the system response and therefore first resonant mode can be considered as the dominant one.

First of all, the frequency intervals are obtained where $M(z)$ has negative-imaginary (NI) or passivity properties. When $M(z)$ and $N(z)$ have no intersecting region where the stability is satisfied by either negative-imaginary or passivity property, the gain $k_1$ is chosen such that $M(z)$ is bounded by gain $k_1$. Then the controller gain $K_r$ is selected as large as possible and $k_2$ is selected accordingly. If $k_1k_2<1$ then the parameters $a_1,a_2,a_3,b_1,b_2$ are tuned such that (1) $N(z)$ has NI property where $M(z)$ has NI property. (2) $N(z)$ has negative-passivity property where $M(z)$ has passivity property and vice versa. (3) $N(z)$ is bounded by gain $k_2$ where $M(z)$ is bounded by $k_1$. (4) $N(z)$ is either bounded by gain $k_2$ or has negative passivity at the frequency intervals where $M(z)$ is bounded by $k_1$ and has passivity property and vice versa. (5) $N(z)$ is either bounded by gain $k_2$ or has NI property at the frequency intervals where $M(z)$ is bounded by $k_1$ and has NI property. (6) $N(z)$ is either bounded by gain $k_2$ or has NI property or has negative-passivity property at the frequency intervals where $M(z)$ is bounded by $k_1$ and has NI and passivity properties. Bode plot of the controller $N(z)$ is shown in Fig. 8.

Fig. 8

Bode plot of the velocity feedback controller $N(z)$

6 Results

6.1 Simulation Results

It is observed from the closed-loop frequency response, shown in Fig. 9, that the first major resonant mode is attenuated by almost 15 dB with the VFC in use. The aim was to increase the damping of this mode, which is achieved. Besides this mode, few other resonant modes are also attenuated. It must be mentioned that the attenuation of the resonant mode at 7.29 KHz is not significant. However, as the product $\zeta \omega _n$ for this mode is larger than that of the mode at 3.14 KHz, the high-frequency oscillation is decayed much faster than the oscillation from the major resonance. That is why it makes sense to increase the damping of the resonance at 3.14 KHz. This argument is further verified by the negligible high-frequency oscillation observed in the step response when VFC is used (Fig. 10).

Fig. 9

Simulated frequency response

Fig. 10

a Simulated step response. b Zoom-in of step response

In applications like HDD, choice of sampling frequency is restricted by the system constraint. Sampling frequency used for the HDD servo system is always a compromise between the demand for higher sampling frequency and limitations imposed by the rotational speed of the disks and the number of servo sectors used. So it varies from HDD to HDD depending on the storage capacity of the HDD and rotation speed of the spindle motor. And if the nyquist frequency of the digital resonance compensator is lower than the critical resonance frequency, then a digital resonance compensator cannot be designed using the same sampling frequency. Therefore, its not always useful in applications like HDD that controller is designed for compensating all the resonant modes. By considering this issue, in this work, the VFC is designed for compensating the first resonant mode.

It must be noted that notch filter designed by pre-compensation method will perform better than any other resonance compensator if the designer is free to choose any sampling frequency to accommodate the multiple frequency modes. However, the VFC has some advantages over the conventional approaches which can be summarized as:

• 1. VFC can be designed as a low-order controller which can perform satisfactorily.

• 2. This mixed approach of designing the VFC substantiates the robust stability of the closed-loop system which is not the case for pre-compensation method. Pre-compensator notch filter only performs better when the plant model is exactly identified. This means if the resonant modes of the plant exactly match with the designed notch filter modes, then it performs good. On the other hand, system can perform worse if the modes are not exactly matched. VFC performs better over the notch filter in such case.

• 3. Unlike the complex adaptive resonance compensator design, the proposed method of designing VFC is simple and hence easy to implement.

• 4. On the other side, if the VFC is designed by using the small-gain theorem which is also a popular method of designing feedback controller, this would result in low-gain controller. This low-gain controller would be unable to compensate the resonant mode effectively.

To test the stability robustness of the design, two perturbed plant models are considered by changing the resonance frequencies. According to benchmark model in Yamaguchi and Hirata (2011), resonant modes can be shifted by 5–10 %. Therefore, here we consider two perturbed models wherein we change the frequency of the first two major resonant modes. In perturbed model 1, the resonance frequencies are changed by 5 and 4 % for resonant mode 1 and mode 2, respectively. In perturbed model 2, resonance frequencies are changed by 7 and 10 %, respectively. The lag–lead controller and the VFC are kept same as before. The nyquist plots of the closed-loop system $M(z)$ for nominal VCM model and different models are shown in Fig. 11. Besides, nyquist plot of VFC ($N(z)$) is also shown in the same figure. Bode plots of these models and VFC are shown in Fig. 12. From these two figures, it can be observed that different frequency regions of $M(z)$ [for nominal or perturbed model] and $N(z)$ satisfy Theorem 2. Therefore, this confirms the robust stable performance of the system.

Fig. 11

Nyquist plot of a $M(z)$ for VCM nominal model, b $M(z)$ for VCM perturbed model 1, c $M(z)$ for VCM perturbed model 2, d VFC, $N(z)$

Fig. 12

Bode plot of a $M(z)$ for VCM nominal model, b $M(z)$ for VCM perturbed model 1, c $M(z)$ for VCM perturbed model 2, d VFC, $N(z)$

Two different bode plots and the step responses for different perturbed models are shown in Figs. 13 and 14, respectively. These figures affirm the stability of the closed-loop systems for both of the perturbed models. Although the design method confirms the robust stability of the closed-loop system, sufficient performance improvement is achieved as well. For each case of perturbed model (Fig. 13), significant attenuation of the first major resonant mode is observed. The step response (Fig. 14) for each case shows negligible or less oscillation with VFC than that of without VFC.

Fig. 13

Simulated frequency response for a perturbed model 1, b perturbed model 2

Fig. 14

Simulated step response for a perturbed model 1, b perturbed model 2

Remark 2

LDV resolution is set to 50 nm/V during the time of frequency response measurement and controller implementation, therefore the scaling factor from volts to nanometer (nm) is 50.

6.2 Experimental Results

For real-time implementation of controller, the setup is modified by replacing the DSA with a real-time controller card (dSPACE SD1104) (Fig. 3). The sampling interval is set to $25\,\upmu$s. The overall architecture of the system is shown in Fig. 6 which includes the lag–lead controller $C(z)$ and the feedback resonance compensator $N(z)$. The performance of the proposed controller is evaluated experimentally using two types of reference signals. Firstly, a step input of 2 V is applied. The displacements measured with and without VFC are shown in Fig. 15. Figure 16 shows the zoom-in of the measured step responses. From the figures, it is evident that the step response is less oscillatory when the feedback resonance compensator (VFC) is implemented. Besides, from the power spectrums in Fig. 17, it can be observed that first resonant mode which is considered as the dominant mode is attenuated when VFC is used. Next, a sum of sinusoids $r(t)=\hbox {sin}(2\pi \times 100t) + 0.8 \hbox {sin}(2\pi \times 200t) + 0.5 \hbox {sin}(2\pi \times 300t)$ is used as the reference input. Figure 18 shows the corresponding output with and without VFC. It is clearly evident from the results that oscillation in output becomes smaller when the VFC is used. Therefore, it can be concluded that the proposed design is able to suppress the effects of resonance.

Fig. 15

Measured step response, a with VFC, b without VFC (obtained from experimental implementation)

Fig. 16

Zoom-in of measured step response, a with VFC, b without VFC (obtained from experimental implementation)

Fig. 17

Power spectrum of the measured error signal, a With VFC, b without VFC (obtained from experimental implementation)

Fig. 18

Measured response for multiple frequency sinusoidal reference, a with VFC, b without VFC (obtained from experimental implementation)

7 Conclusion

This paper proves the stability of discrete-time interconnected systems with mixed passivity, negative-imaginary and small-gain properties. Discretization method may change the properties of the system than from its continuous-time case. Therefore, finite-gain stability theorem is presented here in discrete time for system with mixed negative-imaginary and passivity properties. Based on this mixed passivity, negative-imaginary and small-gain approach in discrete time, a VFC is designed for resonance compensation of a VCM actuator in a HDD servo system. Simulation and experimental results prove the effectiveness of the proposed method. The method is simple and easy to implement. Designed VFC effectively suppresses the resonance which are confirmed from the simulation and experimental results. Although in this paper, VCM actuator of HDD is used as the experimental platform, this simplified methodology can be applied to a wide range of applications.