Keywords

1 Introduction

The non-ideal vibrating system is characterized by its response influenced excitation in which power supply is limited. All dynamical systems are inherently non-ideal, and an additional differential equation is needed to describe the complex dynamics between drive and the system itself. The problem of passage through resonance has attracted many researchers among the mechanical engineering community for more than 150 years. But sometimes, the passage through resonance requires more input power than the driving source has available. As a result, the system cannot pass through resonance or needs a strong interaction with the non-ideal, i.e., limited source of power. In high speed rotor system, during run up/coast up operation, as the driving frequency gets closer to the critical speed, upon exceeding a critical power input, the rotor speed exhibits nonlinear jump phenomena (i.e., jumps suddenly to a much higher value, simultaneously its amplitude jumps to a much lower value) is known as Sommerfeld effect [1]. This effect may lead to catastrophic failure of the high speed rotor system.

In order to attenuate the Sommerfeld, several works have been reported based on passive, active semi-active control strategies. In 2006, a group of researchers [2] proposed tuned liquid column damper-based passive control scheme to control the structural vibration near the resonance. Afterward, Felix and Balthazar [3] employed active control technique through electromechanical vibration absorber to attenuate the non-ideal structural vibration. In 2018, Balthazar and his co-workers [4] presented an experimental method to attenuate the jump phenomena via shape memory element for a cantilever beam driven through an unbalanced DC motor. In 2019, Jha and Dasgupta [5] studied the Sommerfeld effect attenuation for an internally damped non-ideal shaft–disk system using active PD control through a linearized model of active magnetic bearings.

Active control is considered to be one of the effective methods for suppressing the Sommerfeld effect and structural vibrations. However, their energy input is typically high and may lead to the system toward instability under certain conditions. Passive vibration control, on the other hand, though relatively simple has improved stability characteristics, but the response time is very slow. Therefore, a trade-off must be made between the active and passive control toward the development of an adaptive and semi-active alternative.

In 2000, a technique based on switched-stiffness concept [6] was proposed to attenuate the structural vibrations. This method is basically a semi-active control scheme in which the energy of the system is dissipated through changing the values of spring stiffness. The spring possesses two distinct stiffness values, low and high. The switching from low to high stiffness can be implemented through either shape memory alloys (SMA) [7] or through an electrical shunt circuit of a piezoelectric patch actuator [8] in which open circuit and short circuit states represent the high and low values of stiffness, respectively. In 1976, Wauer [9] proposed the switching stiffness method for the first time a possible attenuation of non-stationary resonance vibrations for a distributed parameter rotor model. In 1998, Wauer and Suherman [10] studied the vibration suppression of a rotating shaft driven by a non-ideal source through using switching shaft stiffness. Recently, Min et al. [11] proposed a serial stiffness switch system to reduce the structural vibration without damping. In 2019, in a different study [12], Min and his co-workers developed a semi-active shock isolation based on the serial stiffness switch system and successfully showed the efficacy of this system over a passive system.

It is evident from the earlier studies [5, 13] that internal damping of rotor–shaft in addition to non-ideal source plays a crucial role to exhibit the Sommerfeld effect. However, to the best of author’s knowledge, using switched-stiffness method, study of Sommerfeld effect attenuation for an internally damped rotor has not been reported so far. In the present study, an internally damped, eccentric shaft–disk system driven through a DC motor is presented. A pair of non-conservative springs in order to implement the switching stiffness effect is incorporated into the rotor system. The switching phenomena can be physically realized either by using SMA or piezoelectric patch into the system. The equations of motion are solved numerically along with an addition equation arising out of the complex interaction between the rotor and the non-ideal DC drive. The time response characteristics as well as amplitude with rotor speed diagrams are obtained for different values of stiffness (i.e., high as well low). As a result of increased stiffness values, the Sommerfeld effect is found to be attenuated. In addition, the potential energy (P.E.) is also found to be diminished with time after passing through the critical speed which also confirms the effectiveness of switching stiffness method in attenuation of Sommerfeld effect.

2 Mathematical Modeling of Non-ideal Shaft–Disk System with Switched-Stiffness Method

2.1 Switched-Stiffness-Based Vibration Control

The switched-stiffness method is basically a semi-active vibration control technique [14] in which the energy of the system is allowed to dissipate by incorporating a spring into it such that the stiffness of the spring switches between two distinct values, referred to as high and low stiffness thus effectively increases the energy dissipation from the system. When the system attains the maximum potential energy, the spring is switched to low stiffness state and switched to high stiffness, while the system reaches minimum potential energy. As a result, the potential energy of the system gets reduced. In turn, the reduced potential energy is then transformed into kinetic energy, which is lower than the kinetic energy of the previous cycle owing to the change of spring stiffness. This dissipation technique can be applied for the vibration attenuation of any transient system. Based on the above switching characteristics, a semi-active skyhook type control scheme can be implemented heuristically based on the position of the system with respect to its equilibrium configuration. The control law can be defined as

$$F\left( {x,\dot{x}} \right) = k\left( t \right)x = k_{1} x + \left( {k_{2} {\text{sgn}}\left( {x\dot{x}} \right)} \right)x,\quad {\text{for }}k_{\text{low}} \le k \le k_{\text{high}}$$
(1)

where \(k_{1} = \left( {k_{\text{high}} + k_{\text{low}} } \right)/2,\quad k_{2} = \left( {k_{\text{high}} - k_{\text{low}} } \right)/2.\)

Therefore, the force due to switching stiffness is composed of two terms: a state feedback term (i.e., \(k_{1} x\)) and a switching term \(\left( {k_{2} {\text{sgn}}\left( {x\dot{x}} \right)x} \right)\) in which the product \(\left( {x\dot{x}} \right)\) represents a nonlinear sliding surface. This overall logic can be used as nonlinear switched-stiffness feedback. Using piezoelectric materials, the switching stiffness-based vibration control can also be achieved efficiently. Two piezoelectric patch actuators can be embedded into the rotor–shaft at a suitable distance from the supports. The piezoelectric patch is characterized with effective piezoelectric modulus of elasticity \(\left( {\bar{Y}_{\text{p}} } \right)\) which can be defined as \(\bar{Y}_{\text{p}} = Y_{\text{p}} \left( {1 - K^{2} } \right)\) where \(Y_{\text{p}}\) = modulus of elasticity of the piezoelectric material and \(K\) = electromechanical coupling coefficient of the piezoelectric circuit which acts as an indicator between electrical and mechanical fields. Using an open circuit stiffness \(\left( {k_{\text{OC}} } \right)\) and short circuit stiffness consideration \(\left( {k_{\text{SC}} } \right),\) the ratio of two stiffness can be expressed as a function of coupling coefficient, i.e., \(k_{\text{OC}} /k_{\text{SC}} = 1/\left( {1 - K^{2} } \right).\) Accordingly, to the control law given by Eq. (1), the effective piezoelectric Young’s modulus can be switched [14] as follows:

$$\bar{Y}_{\text{p}} = \left[ {\begin{array}{*{20}l} {\bar{Y}_{\text{p}}^{\text{High}} = \bar{Y}_{\text{p}} /\left( {1 - K^{2} } \right)} \hfill & {x\dot{x} \ge 0} \hfill \\ {\bar{Y}_{\text{p}}^{\text{Low}} = \bar{Y}_{\text{p}} } \hfill & {x\dot{x} < 0} \hfill \\ \end{array} } \right.$$
(2)

The optimum value of switched-stiffness can be achieved through a suitable open circuit (high stiffness) and short circuit (low stiffness) configurations. The disadvantage of this kind of control law is it induces chatter. The faster the drive dynamics the more likely chatter to occur. To suppress the chatter, suitable anti-chatter strategies need to be adopted.

2.2 Mathematical Modeling

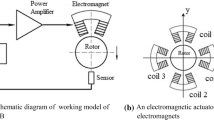
A non-ideal shaft–disk system (shown in Fig. 1) driven by a brushed DC motor (i.e., non-ideal energy source) is considered for the present study. A pair of non-conservative springs is also incorporated into the system to implement the proposed switched-stiffness method.

Fig. 1
figure 1

Schematic of DC motor-driven shaft–rotor with non-conservative springs

Full size image

The equations of motion of the shaft–disk system [15] can be represented as follows:

$$m\ddot{x} + \left( {R_{\text{e}} + R_{i} } \right)\dot{x} + R_{i} \dot{\theta }y + \left( {K + k_{w} \left( t \right)} \right)x = me\left( {\dot{\theta }^{2} \cos \left( {\theta + \varphi } \right) + \ddot{\theta }\sin \left( {\theta + \varphi } \right)} \right)$$
(3)
$$m\ddot{y} + \left( {R_{\text{e}} + R_{i} } \right)\dot{y} - R_{i} \dot{\theta }x + \left( {K + k_{w} \left( t \right)} \right)y = me\left( {\dot{\theta }^{2} \sin \left( {\theta + \varphi } \right) - \ddot{\theta }\cos \left( {\theta + \varphi } \right)} \right)$$
(4)

The complex interaction of the shaft–disk system with the non-ideal DC drive is described by the following additional equation

$$I\ddot{\theta } + R_{\text{r}} \dot{\theta } = T_{\text{m}} - T_{\text{L}} ,$$
(5)

Internal damping (also known as material damping) in rotor dynamics plays a key role in determining the stability of the system. It is considered to be a function of past history of loading, strain rate and temperature of the system [15]. The notations describing the system parameters are enlisted in the nomenclature.

A brushed DC motor is used for the present study (shown in Fig. 2). The armature current may be expressed as [5]:

Fig. 2
figure 2

Schematic representation of brushed DC motor

Full size image
$$i_{\text{m}} = \left( {V_{\text{s}} - \mu_{\text{m}} \dot{\theta }} \right)/R_{\text{m}} .$$
(6)

The supplied torque \(\left( {T_{m} } \right)\) present in Eq. (5) provided by the DC motor becomes

$$T_{\text{m}} = \mu_{\text{m}} i_{\text{m}} = \mu_{\text{m}} \left( {V_{\text{s}} - \mu_{\text{m}} \dot{\theta }} \right)/R_{\text{m}}$$
(7)

The modified source loading torque \(\left( {T_{\text{L}} } \right)\) owing to the presence of switching stiffness terms may be expressed as

$$\begin{aligned} T_{\text{L}} & = R_{i} \left( {x\dot{y} - \dot{x}y} \right) + \left[ {\left( {R_{\text{e}} + R_{i} } \right)\dot{x} + \left( {K + k_{w} \left( t \right)} \right)x} \right]e\sin \theta \\ & \quad - \left[ {\left( {R_{\text{e}} + R_{i} } \right)\dot{y} + \left( {K + k_{w} \left( t \right)} \right)y} \right]e\cos \theta \\ \end{aligned}$$
(8)

3 Simulation Study and Results

Following representative parameters of the shaft–disk system chosen from the reference [5] are considered for numerical simulations:

$$\begin{aligned} m & = 2\,{\text{kg,}}\;K = 8 \times 10^{4} \,{\text{N/m,}}\;e = 0. 0 0 1\,{\text{m,}}\;R_{\text{e}} = 50\,{\text{Ns/m, }} \\ R_{i} & = 50\,{\text{Ns/m,}}\;R_{\text{r}} = 2 \times 10^{ - 5} \,{\text{N m s/rad,}}\;R_{\text{m}} = 40\,\Omega ,\\ \mu_{\text{m}} & = 0.1\,{\text{Nm/A,}}\;I_{\text{r}} = 0.004\,{\text{kg m}}^{2} \;{\text{and }} \\ \omega_{n} & = 200\,{\text{rad/s,}}\;V_{\text{s}} = 300{\text{ V}} .\\ \end{aligned}$$

In addition, \(k_{\text{high}} = 6 \times 10^{4} \,{\text{N/m}}\;{\text{and}}\;k_{\text{low}} = 1 \times 10^{4} {\text{ N/m}} .\) Two non-dimensional quantities are introduced here to study the Sommerfeld effect. These are the non-dimensional rotor spin speed \(\left( {\omega^{*} } \right) = \dot{\theta }/\omega_{n}\) and the non-dimensional whirl amplitude \(\left( \beta \right) = \sqrt {x^{2} + y^{2} } \omega_{n}^{2} /g,\) where g, the gravitational acceleration.

The Eqs. (3), (4) and (5) are solved numerically with the help of Runge-Kutta method using ode45 solver for 10 s. with time step = 0.01 s. and initial conditions \(\left( {x = y = \dot{x} = \dot{y} = \theta = \dot{\theta } = 0} \right).\)

Figure 3 represents the three-dimensional orbital representation of an unbalanced response of the rotor system which starts at zero speed and then enlarges, taking the shape of an elliptical cross-section and tends to a circular cylindrical at high speeds. Figure 4 represents a comparison study between two time histories using with and without switching stiffness. The nature of the phase plot shown in Fig. 5 ensures the asymptotic stability of the system using switching stiffness. The variation of stiffness with time for a representative value of khigh and klow is shown in Fig. 6. The efficacy of the switching stiffness method is confirmed through Fig. 7 in which the Sommerfeld effect is found to be attenuated gradually with relatively higher values of switched-stiffness. Additionally, it is evident from Fig. 7 that the response peak tends to shift gradually toward the right as the stiffness value increases. This result signifies that the effective critical speed tends to alter as the stiffness value changes thus helping the system to attenuate the undesirable Sommerfeld effect.

Fig. 3
figure 3

Three-dimensional orbital tube representation of rotor x and y amplitudes with the rotor speed using switched-stiffness method

Full size image
Fig. 4
figure 4

a Time history of shaft–disk system along the x-direction. b Time history of shaft–disk system along the y-direction

Full size image
Fig. 5
figure 5

Phase portrait of the shaft–disk system with switching stiffness consideration

Full size image
Fig. 6
figure 6

Variation of switched-stiffness with time with representative values of \(k_{\text{high}} = 2 \times 10^{3} \,{\text{N/m, }}k_{\text{low}} = 1.5 \times 10^{3} \,{\text{N/m}}\)

Full size image
Fig. 7
figure 7

Variation of amplitude of shaft–disk system for different values of switched-stiffness

Full size image

Moreover, inset of Fig. 7 shows the magnified response with spikes. These spikes in the response of the shaft–disk system ensure the presence of chatter as a consequence of the switching technique. The undesirable effect of chattering can be attenuated by using filtering, introducing a dead band around the switching points, etc. Finally, Fig. 8 illustrates how the potential energy (P.E.) is reduced due to switching stiffness however in the presence of chattering (as shown in the inset of Fig. 8) and ensures the potential energy is diminished, and in turn, the overall energy is being reduced as a result of dissipative effect of the switching stiffness.

Fig. 8
figure 8

Variation of potential energy with time for \(k_{\text{high}} = 9 \times 10^{3} \,{\text{N/m, }}k_{\text{low}} = 2 \times 10^{3} \,{\text{N/m}}\)

Full size image

4 Conclusions

The present study aims to attenuate the Sommerfeld effect of an internally damped unbalanced flexible shaft–disk system, driven by a DC motor using switched-stiffness method. The concept of switched-stiffness-based vibration control can be implemented using piezoelectric (i.e., PZT) material or SMA that results in significant change in effective modulus of elasticity through open circuit and short circuit configurations leading to switching of stiffness between high and low values, respectively. The equations of motion of the shaft–disk system are solved numerically along with an additional equation arising out of the complex interaction between the rotor and the non-ideal DC drive. The time response characteristics as well as amplitude with rotor speed diagrams are obtained for different values of switched-stiffness. As a result of increased stiffness values, the Sommerfeld effect is also found to be attenuated. The peak of the response is also found to be shifted toward right as the critical speeds alter gradually (i.e., increase as the stiffness increases). In addition, the potential energy (P.E.) also found to be decreased with time after passing through the critical speed which also confirms the effectiveness of switching stiffness method over the attenuation of Sommerfeld effect. However, the presence of spikes in the frequency response and time varying potential energy clearly indicate the onset of induced chatter as a consequence of switching stiffness which in turn may destabilize the system if the switching becomes very fast. The future work can be envisioned as suppression of chatter of high speed non-ideal rotor through switching stiffness method using various anti-chattering strategies.