MILP Acceleration: A Survey from Perspectives of Simplex Initialization and Learning-Based Branch and Bound

Abstract

Mixed integer linear programming (MILP) is an NP-hard problem, which can be solved by the branch and bound algorithm by dividing the original problem into several subproblems and forming a search tree. For each subproblem, linear programming (LP) relaxation can be solved to find the bound for making the following decisions. Recently, with the increasing dimension of MILPs in different applications, how to accelerate the solution process becomes a huge challenge. In this survey, we summarize techniques and trends to speed up MILP solving from two perspectives. First, we present different approaches in simplex initialization, which can help to accelerate the solution of LP relaxation for each subproblem. Second, we introduce the learning-based technologies in branch and bound algorithms to improve decision making in tree search. We also propose several potential directions and extensions to further enhance the efficiency of solving different MILP problems.

1 Introduction

Mixed integer linear programming (MILP) is a minimization or maximization optimization problem with a linear objective. It includes both linear and integer constraints. A general formulation of the MILP is given as follows:

Definition 1

(MILP) Given a matrix $A\in {\mathbb {R}}^{m\times n}$, vectors $b\in {\mathbb {R}}^{m}$ and $c \in {\mathbb {R}}^{n}$, and a subset $I \subseteq \{1,\cdots , n\},$ the mixed-integer linear program $\textrm{MILP}=(A,b,c,I)$ is

$$\begin{aligned} z^{\star }= \min \{c^\textrm{T} x \mid Ax\leqslant b, x \in {\mathbb {R}}^n, x_j\in {\mathbb {Z}},\forall j\in I \}. \end{aligned}$$

(MILP)

The vectors in the feasible region $X_\textrm{MILP}=\{x\in {\mathbb {R}}^n \mid Ax\geqslant b, x\in {\mathbb {R}}^n, x_j\in {\mathbb {Z}},\forall j\in I\}$ are called feasible solution of MILP. A feasible solution $x^\star \in X_\textrm{MILP}$ of MILP is optimal if its objective value satisfies $c^\textrm{T} x^\star =z^\star$.

Owing to the integrality requirement, MILP is usually an NP-hard problem. Most modern MILP solvers, such as CPLEX[1], LINDO[2], and SCIP[3], use the branch and bound (B &B) as the framework to efficiently enumerate the candidate solution. The B &B was initially proposed by Land and Doig [4]. This method implicitly enumerates all possible solutions by iteratively dividing the original problem into a series of subproblems, organized in a tree structure, and discarding the subproblems where a global optimum cannot be found. Once the entire tree has been explored, the exact optimal solution can be achieved. It implements a divide-and-conquer algorithm, where a linear programming (LP) relaxation of the problem is computed by removing the integrality conditions. By solving the relaxed problem, a lower bound of the original MILP problem can be obtained. This bound is a crucial element for making the following decisions in the tree search. For example, if the objective value $\check{z}$ of the LP problem is larger than or equal to the value $\hat{z}=c^\textrm{T}\hat{x}$ of the current best solution $\hat{x}$, the corresponding branch can be discarded. The definition of the LP relaxation problem is shown as follows:

Definition 2

(LP relaxation of an MILP) The LP relaxation of an MILP is

$$\begin{aligned} \check{z}= \min \{c^\textrm{T} x \mid Ax\leqslant b, x\in {\mathbb {R}}^n \}. \end{aligned}$$

(LP)

Compared with the MILP problem, the LP problem only has linear constraints. The foundation of LP dates back to the work proposed by [5]. There are two commonly used methods for solving a given LP problem, namely the simplex method [6] and the interior point method (IPM) [7]. In this survey, the simplex method is considered to solve the relaxed problem of the MILP.

MILP has many applications in engineering, agriculture, transportation, food industry, and manufacturing. However, in recent years, as the dimension of MILPs becomes larger and larger, how to find an effective way to solve large-scale MILPs becomes a huge challenge. From the solving process discussed before, we can note that both the solution time of the relaxed subproblems and the choices of tree search strategies in the B &B are important factors in determining the entire efficiency. Therefore, in this survey, we investigate how to speed up the solution of a given MILP from two corresponding perspectives as follows.

The first way is to speed up the solving process of the LP relaxation for different subproblems. Specifically, for the simplex algorithm, a crucial factor for improving the solving efficiency is to find a suitable initialization method. A good starting point can lead to fewer iterations or less computation time within each iteration, thus achieving a faster solution process. In this survey, we provide an overview of the initialization methods in the simplex approach.

The second way is to improve the tree search strategies of the B &B algorithm. A recent research trend is to utilize some advanced machine learning (ML)-based techniques to improve decision making during the tree search. In this survey, we summarize the related works which focus on improving four components of the B &B algorithm, namely the branching rule, the node selection, the node pruning, and the cutting-plane selection. In general, a supervised learning method helps to generate a policy that mimics an expert but significantly improves the speed. An unsupervised learning method helps to choose different methods based on the features. Furthermore, models trained with reinforcement learning can defeat the expert policy, given enough training and a supervised initialization.

To the best of our knowledge, this is the first survey that provides these two perspectives together for accelerating the solution of the MILP. At the end of the survey, we also provide some potential future directions to further improve the existing methods. We propose several learning-based designs in simplex initialization and present some extensions of the B &B algorithm. These designs and extensions can further accelerate the solution of the MILP.

The remainder of the survey is organized as follows. In Sect. 2, we present the preliminary knowledge of the simplex method and the B &B approach. In Sect. 3, we summarize the simplex initialization methods from the perspective of the primal simplex and the dual simplex, respectively. In Sect. 4, we provide a survey of the learning techniques to deal with the four critical components in B &B algorithms for the MILP. In Sect. 5, we provide suggestions for future work to further improve the existing methods for accelerating the solution of MILPs.

Notations: For a matrix A, $A_{i\bullet }$ and $A_{\bullet j}$ denote the ith row and jth column of A, respectively, and $A_{ij}$ represents the element at ith row and jth column in A. ${A}^\textrm{T}$ and ${A}^{-1}$, respectively, denote the transpose and inverse of A. $\textrm{rank}(A)$ denotes the rank of A. For a vector b, $b_i$ denotes the ith element of b. ${\mathbb {R}}$ is the set of real numbers, and ${\mathbb {R}}^n$ is the n-dimensional Euclidean space. ${\mathbb {R}}^{m\times n}$ denotes the space of $m\times n$ real matrices. Given two sets $C_1$ and $C_2$, $C_1\backslash C_2=\{s\in C_1 \mid s\notin C_2\}$. $\cup$ denotes the intersection of sets. $\parallel \cdot \parallel _2$ and $\mid \cdot \mid$, respectively, denote the Euclidean norm of a vector and the absolute value of a scalar. ${I}_m$ denotes an $m\times m$ identity matrix.

2 Preliminary

2.1 The Simplex Method

2.1.1 Standard and Dual Forms of LPs

Given a general LP problem, it can be formulated into the standard form as

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{x} &{}\quad c^\textrm{T}x\\ \text {s.t.} &{}\quad Ax=b,\\ &{}\quad x\geqslant 0, \end{array} \end{aligned}$$

(Standard)

where $c\in {\mathbb {R}}^n$, $b\in {\mathbb {R}}^m$, and $A\in {\mathbb {R}}^{m\times n}$ are parameters and $x\in {\mathbb {R}}^n$ is the decision variable. Without loss of generality, we assume $\textrm{rank}(A)=m$. Although LP problems may appear in other forms, trivial approaches can be applied to transform them into this standard form [8]. There is an associated LP problem, called its dual, in the form of

$$\begin{aligned} \begin{array}{cl} \displaystyle \max _{y,s} &{}\quad b^\textrm{T}y\\ \text {s.t.} &{} \quad A^\textrm{T}y+s=c,\\ &{}\quad s\geqslant 0, \end{array} \end{aligned}$$

(Dual)

where $y\in {\mathbb {R}}^m$ is the dual decision variable associated with x and $s\in {\mathbb {R}}^n$ is the introduced slack variable.

The mathematical relationship between the standard and the dual problems is given in the following theorems.

Theorem 1

(Weak Duality) Given arbitrary feasible solutions x to (Standard) and (y, s) to (Dual), we have $c^\textrm{T}x\geqslant b^\textrm{T}y$.

Theorem 2

(Strong Duality) If one of the problems admits an optimal solution, the optimal solution exists for the other problem, and for any optimal solution pair $x^*$ and $(y^*,s^*)$, the duality gap is zero, i.e., $c^\textrm{T}x^*=b^\textrm{T}y^*$.

2.1.2 Basic Solutions

As $\textrm{rank}(A)=m$, A can be permuted into a partitioned matrix form, i.e., $A = [A_B,A_N]$, where $A_B\in {\mathbb {R}}^{m\times m}$ is a nonsingular submatrix of A.

Definition 3

Any column collection of $A_B$ is called a basis of (Standard).

Let B and N be the associated column indices of $A_B$ and $A_N$, respectively. (Standard) can then be rewritten in the canonical form as follows:

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{x_B, x_N} &{} \quad c_B^\textrm{T}x_B+c_N^\textrm{T}x_N\\ \mathrm{s.t}. &{} \quad A_Bx_B+A_Nx_N=b,\\ &{}\quad x_B,x_N\geqslant 0, \end{array} \end{aligned}$$

(1)

where $c^\textrm{T}=[c^\textrm{T}_B,c^\textrm{T}_N]$ and $x^\textrm{T}=[x^\textrm{T}_B, x^\textrm{T}_N]$ are permuted and partitioned, respectively. The basic solution, which satisfies the equality constraints, is obtained by setting non-basic variables to zero. Thus, the primal basic solution based on the current partition is

$$\begin{aligned} \left\{ \begin{aligned}&x_B=(A_B)^{-1}b,\\&x_N=0. \end{aligned}\right. \end{aligned}$$

(2)

Analogously, (Dual) can be written as

$$\begin{aligned} \begin{array}{cl} \displaystyle \max _{y, s_B, s_N} &{}\quad b^\textrm{T}y\\ \mathrm{s.t}. &{}\quad A_B^\textrm{T}y+s_B=c_B,\\ &{}\quad A_N^\textrm{T}y+s_N=c_N,\\ &{}\quad s_B,s_N\geqslant 0. \end{array} \end{aligned}$$

(3)

Since the primal non-basic variables are complementary to the dual basic variables, the associated dual basic solution is obtained by letting $s_B=0$, i.e.,

$$\begin{aligned} \left\{ \begin{aligned}&y=(A_B^\textrm{T})^{-1}c_B,\\&s_B=0,\\&s_N=c_N-A_N^\textrm{T}y. \end{aligned}\right. \end{aligned}$$

(4)

In the literature, $\bar{b}:= A_B^{-1}b$ is called the right-hand side (RHS) coefficient, $\pi := (A_B^\textrm{T})^{-1}c_B$ is the simplex multiplier, and $\bar{c}:= c_N-A_N^\textrm{T}\pi$ is referred to as the reduced cost. Given the basis $A_B$, the basic solution is said to achieve primal feasibility if and only if $x_B\geqslant 0$, while it achieves dual feasibility if and only if $s_N \geqslant 0$. Furthermore, if a basic solution is both primal feasible and dual feasible, then it is an optimal solution. Additionally, a basis is said to be degenerate if there exists an element in $x_B$ that is equal to 0. Degeneracy will cause cycling or stalling in practice, so as to influence the performance of the simplex.

2.1.3 The Primal and Dual Simplex Algorithms

Starting with a feasible basis, the simplex method moves from one basis to a neighboring one, i.e., a basis that differs from the previous one by only one element, while preserving the feasibility. The selection of such entering/leaving (basis) variable is called the pivot rule. Geometrically, since the feasible basic solution is associated with a vertex of the feasible region, the simplex method goes through a vertex-to-vertex path to the optimum. After the pivoting operation, the newly generated bases have three features in common:

• (1) Exactly one column of $A_B$ is changed;

• (2) The feasibility is preserved;

• (3) The objective function decreases/increases monotonically.

According to the type of feasibility preserved during the iteration, the simplex method can be categorized into two classes, i.e., the primal simplex and the dual simplex. The primal simplex method is initialized with a primal feasible basis. The feasibility remains within iterations until optimality or unboundedness is detected. Instead of starting with a primal feasible basis, the dual simplex method requires a dual feasible one.

For both the primal and dual simplex algorithms, an appropriate initialization method can lead to a better starting point, which may result in a shorter computation time. In Sect. 3, we summarize different initialization methods in the simplex algorithm to accelerate the solution of a given LP.

2.2 Branch and Bound Algorithms

Define an MILP problem as ${\mathcal {P}}=({\mathcal {D}}, f)$, where ${\mathcal {D}}$ (search space) is denoted as a set of valid solutions to the problem and $f: {\mathcal {D}} \rightarrow {\mathbb {R}}$ is denoted as the objective function. The problem ${\mathcal {P}}$ aims to find an optimal solution $x^\star \in \arg \min _{x\in {\mathcal {D}}} f(x)$. A search tree T of subproblems is built by the B &B algorithm in order to solve problem ${\mathcal {P}}$. Moreover, a feasible solution $\hat{x} \in {\mathcal {D}}$ is stored globally. At each iteration, the B &B algorithm selects a new subset of the search space ${\mathcal {S}} \subset {\mathcal {D}}$ for exploration from a queue ${\mathcal {L}}$ of unexplored subsets. Then, if a solution $\hat{x}' \in {\mathcal {S}}$ (candidate incumbent) has a better objective value than $\hat{x}$, i.e., $f(\hat{x}')<f(\hat{x})$, the incumbent solution is updated. On the other side, the subset is pruned or fathomed if there is no solution in ${\mathcal {S}}$ with a better objective value than $\hat{x}$, i.e., $f(x)\geqslant f(\hat{x}),\forall x \in {\mathcal {S}}$. Otherwise, the subset ${\mathcal {S}}$ is branched into subproblems ${\mathcal {S}}_1, {\mathcal {S}}_2, \cdots , {\mathcal {S}}_r$, which are then pushed into ${\mathcal {L}}$. Once there are no unexplored subsets in the queue ${\mathcal {L}}$, the best incumbent solution is returned, and the algorithm is terminated. The pseudocode for the generic B &B is given in Algorithm 1.

Many decisions affect the performance of the B &B by guiding the search to a promising space and improving the chance of quickly finding an exact solution. These decisions are the variable selection (i.e., which of the fractional variables to branch on), the node selection (i.e., which of the current nodes to explore next), the pruning rules (i.e., rules that prevent exploration of the suboptimal space), and the cutting rules (i.e., rules that add constraints to find cutting planes). In terms of Algorithm 1, the variable selection strategy (branching rules) affects how the subproblem is partitioned in Line 7 of Algorithm 1; the node selection strategy affects the order in which nodes are selected to explore (Line 3 of Algorithm 1), and the pruning rule in Line 6 of Algorithm 1 determines whether ${\mathcal {S}}$ is fathomed.

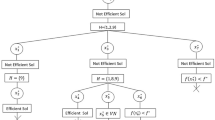
Figure 1 illustrates a concrete example of the B &B algorithm for a minimization integer linear programming. The optimization problem is shown in the upper right corner of Fig. 1. The original upper bound is 0, which is calculated at $x_1=0,x_2=0$. At each node, the local lower bound based on the LP relaxation problem is computed by the LP solver. A local upper bound is updated when an integer solution is found. At each iteration, we first solve the current LP relaxation and then compare the solution with the minimum upper bound found so far. If it is larger than the minimum upper bound for a certain subproblem, the solution cannot be improved, and the node can be fathomed. In Fig. 1, the fathomed nodes are shown in red rectangles.

Fig. 1

Adopting the B &B algorithm to solve a minimization integer linear programming

In order to enhance the above enumeration framework, MILP solvers tend to adopt cutting planes (linear inequalities), especially at the root node. By adding cuts to the original linear programming, the studied region narrows, which will reduce the solving time for the LP relaxation. More details of these four key components in the B &B are introduced as follows.

Branching Variable Selection: As a critical task in brand-and-bound, branching variable selection decides how to partition a current node into two child nodes recursively. Specifically, it decides which fractional variables (also known as candidates) to branch on. Branching on a bad variable that does not simplify subproblems doubles the size of the B &B tree, thus reducing the efficiency of the algorithm. The ultimate objective of an effective branching strategy is to minimize the number of explored nodes before the algorithm terminates. To indicate the quality of a candidate variable, the score of this variable is used to measure its effectiveness, and the candidate with the highest score is selected to branch on. The pseudocode for the generic variable selection is presented in Algorithm 2.

The difference among various branching policies is how the score is computed. Making high-quality branching decisions is usually nontrivial and time-consuming. Although a good branching method should produce trees as small as possible, the primary goal of solving large-scale optimizations is to spend as little time as possible. Therefore, great branching strategies should compromise the quality of decisions to reduce the time taken to make each decision.

Node Selection: After a subproblem has been produced by constraining some integer variables in MILP, the solving process can continue with any subproblem that is a leaf of the current search tree. We refer to the subproblems as nodes. The node selection designs which node to process in the next step. The existing literature always selects the next node based on the following two goals:

• 1. Finding good feasible MILP solutions to improve the primal (upper) bound, which helps to prune the search tree by bounding;

• 2. Improving the global dual (lower) bound.

Node Pruning: Pruning suboptimal branches is an important part of B &B algorithms since it keeps the B &B tree and the computing steps small, reducing the solving time and the required memory. In a standard B &B algorithm, the pruning policy prunes a node only if one of the following conditions is met:

• 1. Prune by bound: a lower bound on the objective value is computed at each node. If the lower bound of the node is larger than the optimal objective value obtained, the node will be pruned, i.e., $\check{z}>\hat{z}$.

• 2. Prune by infeasibility: if the relaxed problem of a node is infeasible, which means that the lower bound of this node is $\infty$, the node will be pruned. This can be viewed as a special case of prune by bound.

• 3. Prune by integrality: if the obtained solution for the relaxed problem satisfies the integer constraints, it is unnecessary to search the children of this node.

We call the nodes satisfying one of the above conditions as fathomed nodes.

Cutting-Plane Selection: Cutting planes are additional linear constraints violated by the current LP solution, but do not cut off integer feasible solutions. Specifically, cutting-plane (sometimes called valid inequalities) methods repeatedly add cuts to the LPs, excluding some part of the feasible region while conserving the integral optimal solution so that the LP relaxation can be tightened. The difference between tightening LP relaxation by branching and by cutting planes is illustrated in Fig. 2.

Fig. 2

Tightening LP relaxation by branching and cutting planes

Depending solely on cutting-plane methods is intractable for solving MILPs, and thus, they are always combined with the B &B algorithm to further tighten the bound for pruning the tree. According to where cutting planes are generated, at the root or at the subproblems in the B &B tree, there are two algorithms called cut-and-branch and branch-and-cut, respectively. The former only generates cutting planes at the root of the B &B tree, while the latter also produces cutting planes at the subproblems. The branch-and-cut is the core of state-of-the-art commercial integer programming (IP) solvers. Moreover, in branch-and-cut, globally valid cuts and locally valid cuts should be distinguished, since cuts locally generated at a particular node may be invalid for other nodes, while valid global inequalities can be used for all subproblems.

A well-designed decision strategy in the four components of B &B algorithms can help to reduce the search space and significantly speed up the search progress of the B &B algorithm. In Sect. 4, we present a survey on ML-based techniques for improving the decisions in the B &B algorithm to accelerate the solution process. Note that a family of related LPs will be solved during B &B algorithms. A warm start which allows the algorithm to make fast initial progress would also speed up the solving process. One special initialization method to accelerate the B &B algorithm is to utilize the previous optimal basis for each member of the partition to aid in obtaining the basis of the new nodes. The detailed implementation can be referred to [9]. However, in some cases, utilizing the previous node’s solution as the initial point for the LP relaxation subproblem of the current node may not be the best option. For example, if the previous node’s solution is far from optimal, it can slow down the convergence of the algorithm. Another case is when there is a difference in the objective function between the current and previous nodes, making the solution from the previous node not directly applicable to the current node’s LP relaxation subproblem. Moreover, for some learning-based MILP methods, the subproblems considered may not have a strong relationship, necessitating the use of alternative simplex initialization techniques to expedite the solving process. More initialization methods in the simplex algorithm are reviewed in Sect. 3.

3 Simplex Initialization Methods

The initialization methods in the simplex algorithm can be divided into two parts based on the form (standard or dual) of the LP problem. For accelerating the solving of MILPs, the simplex initialization is not limited to the root node and can also aid in solving nodes throughout the tree. An overview of the related simplex initialization methods summarized in this survey is illustrated in Fig. 3.

Fig. 3

Overview of the initialization methods in simplex

3.1 Initialization in Primal Simplex

The initialization methods in the primal simplex can be classified into three types. The first type concentrates on “optimality” and tries to find a near-optimal basis. The second type focuses on “computation efficiency” and attempts to construct a basis with a special structure, e.g., sparse, triangular, or near-triangular. The structure can help to speed up the computing process, such as inverse calculation. The third type, however, pays attention to “feasibility” and tries to create a feasible or near-feasible basis. To implement the primal simplex algorithm, a primal feasible basis is required. Therefore, the methods belonging to the first two types can be followed by some methods in the third type to obtain a primal feasible basis. In the following subsections, methods belonging to these three types will be investigated, respectively.

3.1.1 Generate a Basis Based on Optimality

The Cosine Criterion: The cosine criterion is inspired by the observation that the optimal vertex is usually formed by the constraints that make the minimum angle with the objective function (Fig. 4). Although a similar idea has been studied in [10, 11], these algorithms cannot be implemented efficiently due to the existence of redundant constraints. [12] and [13] proposed new algorithms that can handle the redundant constraints. In these algorithms, though the cosine criterion cannot guarantee an optimal solution, the obtained vertex turns out to be a near-optimal point. Starting from such a vertex can reduce the number of iterations required by the simplex method, thus speeding up the solution process.

Fig. 4

Illustration of the observation, plotted using Plot 2D/3D region [14]. The bold lines represent the constraints that make the minimum angle with the objective function, which is denoted by the dashed line

With a bit of abuse of notations, we initialize $B=\varnothing$ and let $N=\{1,\cdots ,n\}$ be the corresponding complementary set. At each time, one variable is moved from N to B, i.e., $B=B\cup \{q\}$ and $N=N\backslash \{q\}$, where q is selected based on the angle and the rank of $A_B$, i.e.,

$$\begin{aligned} q = \arg \max _{j\in N}\{\alpha _j \mid \left\| \bar{(N_2})_{\bullet j} \right\| _{\infty }\ne 0\}, \end{aligned}$$

(5)

where $\alpha _j=(A_{\bullet j})^\textrm{T}b\big /\left\| A_{\bullet j}\right\|$ is named the dual pivoting index, which is proportional to the cosine of the angle between $A_{\bullet j}$ (the ith constraint of (Dual)) and b (the objective function of (Dual)), and $\bar{N}_2$ is a matrix calculated based on the LU factorization. The condition $\left\| \bar{N_2} \right\| _{\infty }\ne 0$ ensures that the constructed basis $A_B$ is nonsingular. According to the feasibility of the obtained basis, either the primal simplex or the dual simplex is applied to solve the problem. Nevertheless, if the basis is infeasible, other initialization methods introduced in this section can be performed to generate a feasible one.

The advantage of the cosine criterion is that it can significantly reduce the number of iterations, up to 40% on Netlib problems. However, the calculation of $\bar{N_2}$ requires the LU factorization, which unfortunately tends to be time-consuming. Furthermore, as the obtained basis is not likely to be sparse, the computation time per iteration may increase. Therefore, the overall efficiency may not be improved much.

The Most-Obtuse-Angle Column Rule: The most-obtuse-angle column rule [15] combines, to some degree, the work of finding a feasible basis with the work of finding an optimal one [16]. In detail, this method suggests achieving primal feasibility by iteratively using a modified dual pivot rule. Geometrically, the leaving variable specifies the most obtuse angle with the uphill direction determined by the entering variable. If the uphill direction is close to the direction of the dual objective function, from Fig. 4 we can conclude that the basis constructed in this way is more favorable from the perspective of the objective function. The complete procedure for this method is shown in the following:

• (1) Select the entering index $q=\arg \min _{i\in B}x_i$. If $x_p\geqslant 0$, the basis is already feasible and go to step 4.

• (2) Compute $\Delta s_N=(A_B^{-1}A_N)^\textrm{T}e_p$. Here, $e_p$ is a unit vector whose pth element is 1 and the other elements are 0. If $\Delta s_N\geqslant 0$, the algorithm terminates with infeasibility. Otherwise, select the leaving index $p=\arg \min _{i\in N}\Delta s_i$.

• (3) Perform pivoting $B \leftarrow B\cup \{q\}\backslash \{p\}$ and go to step 1.

• (4) Apply the primal simplex to compute the optimum.

Since the feasibility of other variables cannot be maintained in this method, cycling may occur even without degeneracy. Although [17] provides a cycling example, this problem may rarely appear in practice.

Idiot Crash Algorithm (ICA): The main idea of the ICA [18] is to relax the original LP problem to an approximate problem with “soft” constraints, and then solve this relaxed problem to obtain a near-optimal point. This point is later used as the starting point of the simplex method for solving the original problem.

Recall the standard LP defined in (Standard), the ICA obtains the relaxed problem by replacing the equality constraint with two additional terms in the objective function, i.e., a linear Lagrangian term and a quadratic penalty term, as follows:

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{x} &{}\quad c^\textrm{T}x + \lambda ^\textrm{T}(Ax-b) + \frac{1}{2\mu } \Vert A x-{b}\Vert _{2}^{2} \\ \mathrm{s.t}. &{}\quad x \geqslant 0, \end{array} \end{aligned}$$

(6)

where $\lambda$ is the Lagrange multiplier and $\mu$ is a penalty weight. This relaxed problem can be easily solved by existing methods, such as IPMs. As $\lambda$ goes to infinite, the optimal solution of this relaxed problem will converge to the optimal solution of the original LP problem. To obtain a near-optimal point of the original problem, in each iteration, the ICA updates the parameters $\lambda$ and $\mu$ by some heuristic rules and then solves the corresponding relaxed problem. The total iteration number of the ICA is finite and is predefined heuristically.

As shown in the previous part, the primal simplex method begins with a basic feasible solution (a vertex of the feasible region). However, after finite iterations, the near-optimal point obtained by ICA may be an interior point of the feasible region. To obtain a basic feasible solution near the point given by ICA, a crossover procedure is added. For some LP problems with special structures, the crossover procedure can be further accelerated to improve efficiency. These methods will be discussed later.

The advantage of ICA is that it can transform the original problem into a more tractable problem without the equality constraint and obtain a near-optimal point quickly. Nevertheless, one challenge of ICA is how to design the heuristic rules for updating the parameters. If the rules are not chosen properly, the obtained point will not be a good starting point and the efficiency of the algorithm will not be improved much. In [18], the authors tested the efficiency of the ICA on a dataset with 30 public LP problems. The numerical results show that the ICA can achieve a speed-up in 28 problems. In particular, for 10 problems of the dataset, a speed-up of more than 2.5 times can be obtained.

$\varepsilon$-Optimality Search Direction: The $\varepsilon$-optimality search direction algorithm was proposed in [19]. This algorithm was motivated by the fact that the IPM can approach the neighborhood of the optimal solution faster than the simplex method. In this algorithm, an improved point is obtained by moving in a proposed direction. This point is later used as the starting point of the simplex method to calculate the optimal solution to a given LP problem. The proposed direction combines an interior direction of the feasible region with the negative direction of the objective.

This algorithm focuses on a normalized LP problem where $\Vert c\Vert ^2_2 = 1, \Vert A_{i\bullet } \Vert ^2_2 = 1, \forall i \in \{1,2,\cdots ,m\}$. Any LP problem can be easily transferred to the normalized version by choosing $c = \frac{c}{\Vert c\Vert ^2_2}, A_{i\bullet } =\frac{A_{i\bullet }}{\Vert A_{i \bullet } \Vert ^2_2}, b_i = \frac{b_i}{\Vert A_{i\bullet } \Vert ^2_2}$. This normalization process will not change the optimal solution of the original LP problem.

Definition 4

Given a feasible point x, if $\forall \,\delta >0$, the set $\{x'\mid \Vert x'-x\Vert ^2_2 < \delta \}$ does not belong to the feasible region, then x is called a boundary point.

Given a boundary point x, this algorithm defines two sets as follows:

$$\begin{aligned} \Omega _1&= \{i \mid A_{i\bullet } x =b_i\},\nonumber \\ \Omega _2&= \{ j \mid x_j=0\}. \end{aligned}$$

(7)

These two sets collect the indices of active constraints at the given boundary point x. Based on these two sets, the algorithm calculates a vector h as follows:

$$\begin{aligned} h = \frac{\sum _{i \in \Omega _{1}} {A}^\textrm{T}_{i\bullet } +\sum _{j \in \Omega _{2}} {e}_{j}}{\left\| \sum _{i \in \Omega _{1}} {A}^\textrm{T}_{i\bullet } +\sum _{j \in \Omega _{2}} {e}_{j}\right\| _2}, \end{aligned}$$

(8)

where $e_j$ is a unit vector whose jth element is 1 and the other elements are 0. The dimension of $e_j$ is consistent with $A^\textrm{T}_i$. Then, based on h, the direction for obtaining an improved point starting from the given point x is defined as

$$\begin{aligned} {g}=\left\{ \begin{array}{cl} 0, &{} \text{ if } h=c, \\ \textrm{Proj}\left( \frac{{h}-{c}}{\left\| h-c\right\| _2}\right) , &{} \text{ if } h \ne c, \end{array}\right. \end{aligned}$$

(9)

where c is the vector of the objective function. The projection operation $\textrm{Proj}(\cdot )$ is used to guarantee the feasibility of the direction, and its mathematical form can be found in [19]. Starting from the current boundary point x, the direction g points to the interior of the feasible region.

Since the LP problem attempts to minimize the objective, this algorithm also constructs a proper step size $\eta$ and proves that the objective can be reduced when moving in the direction of g with the step size $\eta$. In addition, with this specific step size, the new point obtained after one iteration, i.e., $x' = x +\eta g$, is also a boundary point of the feasible range. This iteration can then be repeated based on this new point $x'$.

An important detail in the implementation of this algorithm is that the search direction given in (9) will be replaced by $\textrm{Proj}(c)$ when the step size is less than a predefined value. This is done to improve the efficiency of the algorithm when the current point is close to the optimal point. According to the experimental results given in [19], the $\varepsilon$-optimality search direction algorithm can reduce the iteration number of the simplex method by about 40%.

An extension work of this algorithm was introduced in [20]. In this extension work, a special example is given to show that the denominator term in (8) can be zero. Therefore, to handle the anomaly where the denominator is 0, the new algorithm changes the definition of h as follows:

$$\begin{aligned} h = {\left\{ \begin{array}{ll} 0, &{} \sum _{i \in \Omega _{1}} {A}^\textrm{T}_{i\bullet } +\sum _{j \in \Omega _{2}} {e}_{j}=0, \\ \frac{\sum _{i \in \Omega _{1}} {A}^\textrm{T}_{i\bullet } +\sum _{j \in \Omega _{2}} {e}_{j}}{\left\| \sum _{i \in \Omega _{1}} {A}^\textrm{T}_{i\bullet } +\sum _{j \in \Omega _{2}} {e}_{j}\right\| _2}, &{} \sum _{i \in \Omega _{1}} {A}^\textrm{T}_{i\bullet } +\sum _{j \in \Omega _{2}} {e}_{j} \ne 0. \end{array}\right. } \end{aligned}$$

(10)

The new algorithm also shows that if the initial direction is chosen as $-c$, the algorithm efficiency can be further improved. In addition, the extension work corrects several mathematical errors in [19].

The $\varepsilon$-optimality search direction algorithm and its improved version given in [19, 20] can be regarded as auxiliary tasks before the basic simplex method. An interesting issue to be investigated is how to find the optimal number of iteration steps to reduce the total computation time.

Hybrid-LP Method: The hybrid-LP method was introduced in [21]. The idea of the hybrid-LP is similar to the $\varepsilon$-optimality search direction algorithm, but it differs in that instead of designing the iterative direction to acquire an improved starting point based on a given point, it obtains the direction according to the non-basic variables (NBVs). The hybrid-LP method experimentally shows a reduction in both the iteration number and the total computation time. The process of the hybrid-LP method can be divided into five steps:

• (1) Select k NBVs to construct the iterative direction. The value of k is chosen as

  $$\begin{aligned} k = \alpha \min (m, n-m), \end{aligned}$$

  where m is the number of constraints and $n-m$ is the number of NBVs. The variable $\alpha \in [0,1]$ is a predefined parameter.

• (2) Divide these k selected variables into two sets based on whether a change in the variable will result in an increase or decrease in the objective function. Denote these two sets by $s_I$ and $s_D$, respectively.

• (3) Construct the iterative direction as $d = \zeta d_I + (1-\zeta ) d_D$ where $d_I$ is generated by NBVs in $s_I$, while $d_D$ is given by NBVs in $s_D$. The parameter $\zeta$ is selected based on the rule that the direction can lead to an improved objective value.

• (4) Given the current point x, find the maximum step size $\theta$ such that the point $x'$ obtained after one iteration along the direction d, i.e., $x' = x + \theta d$, is still within the feasible range.

• (5) Find a nearby basic feasible solution (vertex) of $x'$ by the reduction process or some crossover methods, and treat it as the starting point of the basic simplex method to solve the original LP problem.

In the experiments, the parameters $\alpha , \zeta$, etc., are chosen heuristically. Therefore, one possible way to improve the hybrid-LP method is to optimize the parameters In [21], the hybrid-LP method was tested on some randomly generated LP problems and the standard Netlib test problems. For the former, Hybrid-LP saved 34.4% in the number of iterations and 24.9% in the total running time. For the latter, the savings in the number of iterations and the running time were 22.7% and 11.2%.

3.1.2 Generate a Basis Based on Computing Efficiency

Crash Basis: Compared with an extremely sophisticated algorithm that can provide a good initial basis, a crude algorithm that can provide a reasonably good initial basis quickly is favored. Therefore, some heuristic algorithms, called crashing, have emerged. These crash algorithms are used to quickly find a good initial basis with as many decision variables as possible. Usually, the obtained basis is a triangular basis due to some irreplaceable benefits. First, there will be no fill-in in the inverse calculation of the basis. Second, it is numerically accurate to calculate the inverse of a triangular matrix. Third, it is easy to create a triangular basis. Last but not least, operations with triangular matrices are less time-consuming. In the LP context, there are two types of triangular basis: the lower triangular basis and the upper triangular basis. Both types have zero-free diagonals.

Most triangular crash procedures are based on the same conceptual framework as follows. First, partition the coefficient matrix A into $[\hat{A},I]$, where $\hat{A}$ corresponds to the decision variables and I corresponds to the logical variables. Then, define the row and column counts, $R_i$ and $C_j$, as the number of nonzeros in the ith row of $\hat{A}$ and that in the jth column of $\hat{A}$, respectively. For the lower triangular basis, select a pivot row $i=\arg \min _k\{R_k\}$. If $R_i=1$, the pivot column is unique; otherwise, the column with the smallest column count should be selected to keep the number of nonzero elements in $A_B$ small. All the columns with nonzero in the ith row will not be considered in the subsequent selection process. Then, update the row and column counts for the remaining rows and columns of $\hat{A}$ and repeat the above procedure. The main idea for the upper triangular basis is similar.

In practice, the triangular crash procedures include more other considerations, such as feasibility (CRASH(LTSF)) and degeneracy (CRASH(ADG)). More details can be found in [22, 23]. In [23], the authors selected 30 larger problems from Netlib and observed that CRASH(LTSF) can make considerable improvements when all the constraints are equalities (iterations of Phase I can be reduced to 0) or inequalities (iterations of Phase I can be reduced by about 40%). Moreover, the performance of CRASH(LTSF) is well balanced over a wide variety of problems.

Triangular and Fill-Reducing Basis: One computation difficulty of the simplex method lies in the calculation of the basis inverse. In computational practice, the LU factorization is used. To further improve efficiency, [24] intended to find a sparse and near-triangular basis so that the factorization becomes easier. In this case, though the number of iterations may increase, the computation time per iteration is reduced, and the overall efficiency is improved.

The first step of this algorithm is to permute the matrix A and find its maximal diagonal submatrix $A_{11}$. If $\textrm{rank}(A_{11}) = m$, i.e., $A_{11}$ is large enough to form an initial basis, the algorithm stops. Otherwise, the algorithm permutes the matrix A as

$$\begin{aligned} A = \left[ \begin{matrix} A_{11} &{} A_{12}\\ 0 &{} A_{22} \end{matrix}\right] , \end{aligned}$$

(11)

where $A_{22}$ is subsequently ordered by a fill-reducing order and the first $m-\textrm{rank}(A_{11})$ columns are selected in completion of the basis.

Note that with $A_{11}$, the constructed basis will be as triangular as possible. Additionally, as $A_{22}$ is ordered based on the fill-in effect, the sparsity will be preserved during iterations. Therefore, the computation time per iteration is greatly reduced. However, since both the objective function and the constraints are completely ignored, the initial vertex may be far from optimal, thus requiring more iterations to terminate.

Compared with the cosine criterion, which aims to reduce the number of iterations by providing a near-optimal starting point, this algorithm tends to speed up the iteration process by obtaining a sparse and near-triangular basis.

CPLEX Basis: CPLEX basis was proposed by [25]. The essential purpose is to construct a sparse and well-behaved basis with as few artificial variables and as many free variables as possible. The objective of the CPLEX basis is not to find the variables in the optimal basis, but to reduce the work of removing artificial variables. To find such a CPLEX basis, a preference order of the variables should be constructed first. Consider the given LP problem in the following form:

$$\begin{aligned} \begin{array}{rl} \displaystyle \min _{x, s_1, s_2} &{}\quad c^\textrm{T}x\\ \text {s.t.} &{}\quad A_1 x + s_1 = b_1,\\ &{} \quad A_2 x - s_2 = b_2,\\ &{} \quad A_3 x = b_3,\\ &{} \quad l\leqslant x\leqslant u,\\ &{} \quad s_1\geqslant 0,\quad s_2\geqslant 0, \end{array} \end{aligned}$$

(12)

where $x=(x_1, \cdots , x_n)^\textrm{T}$ are decision variables and $s_1 =(x_{n+1}, \cdots , x_{n+m_1})^\textrm{T}$ and $s_2 = (x_{n+m_1+1}, \cdots , x_{n+m_1+m_2})^\textrm{T}$ are slack variables. All the indices of variables can be divided into four sets:

$$\begin{aligned}&C_1=\{n+1, \cdots , n+m_1+m_2 \},\\&C_2=\{j:x_j \text {{\,\,is a free variable}} \},\\&C_3=\{j\leqslant n: \text { exactly one of } l_j \text { and } u_j \text { is finite} \},\\&C_4=\{j:-\infty< l_j,u_j< +\infty \}, \end{aligned}$$

where $C_i$ will be preferred to $C_{i+1}$ $(i=1,2,3)$. Note that $C_1$ is just the set of indices of all the slack variables, which is the most preferred set due to the sparsity and numerical properties.

Then, define a penalty $\bar{q}_j$ for $j\in \{1,\cdots ,n+m_1+m_2\}$:

$$\begin{aligned} \bar{q}_j=\left\{ \begin{aligned}&0, \quad \text {if } j\in C_2,\\&l_j, \quad \text {if } j\in C_3 \text { and } u_j=+\infty ,\\&-u_j, \quad \text {if } j\in C_3 \text { and } l_j=-\infty ,\\&l_j-u_j, \quad \text {if } j\in C_4. \end{aligned}\right. \end{aligned}$$

(13)

Let $c=\max \{\mid c_j\mid :1\leqslant j \leqslant n\}$ and define

$$\begin{aligned} c_\text {max}=\left\{ \begin{aligned}&1\,000 c, \quad \text {if } c\ne 0,\\&1, \quad \text {otherwise}. \end{aligned}\right. \end{aligned}$$

(14)

Finally, for $j\in \{1,\cdots ,n\}$, define

$$\begin{aligned} q_j=\bar{q}_j+c_j/c_\text {max}. \end{aligned}$$

(15)

The indices in sets $C_2$, $C_3$, and $C_4$ are sorted in an ascending order of $q_j$. The lists are concatenated into a single ordered set $C=\{j_1,\cdots ,j_n\}$ with the most “freedom” variable in the front. Now, the basis $A_B$ can be constructed according to the steps in [25].

The construction of the CPLEX basis is quite simple and fast. It is considered as a good choice of the default initial basis. The computational results indicate that the CPLEX basis performs well in easy problems, but it is generally less effective for difficult ones. In [25], the computational results showed that the CPLEX basis leads to slower solution times in 20 of 90 cases. Of those, 12 is by 10% or less and only 1 by more than 30%. The average improvement of CPLEX over the slack basis (consisting of all available slack variables) is about 35%.

3.1.3 Generate a Basis Based on Feasibility

Two-Phase Method: The simplex method usually proceeds in two phases. Phase I ends with either a feasible basic solution or an evidence that the problem is infeasible. If in Phase I, a feasible basic solution is successfully found, then in Phase II, starting from the obtained solution, the simplex algorithm can be executed in search of the optimum.

In the two-phase method, Phase I proceeds similarly to Phase II, except that it instead deals with an auxiliary problem, i.e.,

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{x, x_a} &{} \quad \textbf{1}_m^\textrm{T}x_a\\ \mathrm{s.t}. &{} \quad Ax + x_a=b,\\ &{}\quad x,x_a\geqslant 0, \end{array} \end{aligned}$$

(16)

where $x_a\in {\mathbb {R}}^m$ is the introduced artificial variable and $\textbf{1}_m\in {\mathbb {R}}^m$ denotes the vector of ones. Since for any row with $b_i<0$, we can obtain $b_i>0$ by multiplying both sides by $-1$, without loss of generality, we can assume $b\geqslant 0$. Therefore, the auxiliary problem has a straightforward feasible basic solution, i.e., $x=0$ and $x_a=b$. Starting from this solution, we can solve (16) with the simplex algorithm and encounter two different cases at optimality:

Case A:

$x_a\ne 0$: The original problem (Standard) is infeasible;

Case B:

$x_a=0$: There are two possibilities:

Sub-case B.1:

No artificial variable remains in the basis: The basis of (16) is immediately a feasible basis of (Standard);

Sub-case B.2:

At least one artificial variable remains in the basis: Without loss of generality, assume the variable is in the ith row, where $\bar{b}_i$=0. Select a column j with $(A_B^{-1}A_N)_{ij}\ne 0$. Perform the pivoting with $x_j$ as the entering variable and the basic artificial variable in the ith row as the leaving variable. After that, go to Sub-case B.1.

Although the two-phase method can guarantee a feasible basic solution or evidence of infeasibility in Phase I, it introduces extra artificial variables, thus increasing the dimension, as well as the complexity of the problem. It has been proved that the problem of determining a feasible solution is of the same complexity degree as solving the LP problem itself. Therefore, Phase I can be very time-consuming in practice, usually even more time-consuming than Phase II. To further speed up Phase I in the two-phase method, the quick simplex method [26] can be utilized. The idea of the quick simplex method is to perform the pivoting based on multiple pairs of variables instead of only one pair.

Big-M Method: The big-M method is a well-known method to initialize the simplex algorithm. It constructs a feasible basis by introducing artificial variables into the constraints and eliminates them from the optimal basis by placing a large penalty term in the objective function. Specifically, the auxiliary problem is

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{x, x_a} &{} \quad c^\textrm{T}x+M\textbf{1}^\textrm{T}_m x_a\\ \mathrm{s.t}. &{}\quad Ax+x_a=b,\\ &{}\quad x,x_a\geqslant 0, \end{array} \end{aligned}$$

(17)

where $x_a\in {\mathbb {R}}^m$ is the introduced artificial variable and $M\gg 0$ is a very large number. Similar to the two-phase method, (17) has a trivial feasible basis, i.e., $x_a=b$ and $x=0$. With this basis, the primal simplex method can be applied to solve the problem. It should be noted that since M is large, a high cost will be paid for any $x_a\ne 0$. Therefore, though we start with the basic variable $x_a=b$, it will be removed from the basis and pushed to zero in the optimal solution. When $x_a=0$, (17) degrades to (Standard) and the obtained solution is directly an optimal solution to (Standard). If we have $x_a\ne 0$ in the solution, the original problem is infeasible.

The pivoting procedure of the big-M method is the same as that of the two-phase method. Hence, it is time-consuming as well. However, the introduction of M results in two more disadvantages. First, it is difficult to determine how large M should be to eliminate the artificial variables in practice successfully. Second, a numerical issue will occur when dealing with an extremely large M.

Logical Basis: The logical basis is the simplest initial basis [22, 27, 28]. To form such a basis, all constraints (equality and inequality) add a distinct logical variable after the decision variables. Then, the corresponding column vectors of all the logical variables form a unit matrix that can be used as an initial basis, i.e., $A_B=I$.

The logical basis has three main advantages. First, its creation is trivial. Second, the inverse of $A_B$ is just the identity matrix I, which is available without any computation. Third, the first iterations are very fast, as the LU factorization is sparse. However, the logical basis generally leads to substantially more iterations, and thus, more advanced initial bases are expected.

Algebraic Simplex Initialization: In 2015, Nabli and Chahdoura [29] developed a new initialization method based on the notion of linear algebra and Gauss pivoting (hereinafter referred to as algebraic simplex initialization). This method can find a nonsingular initial basis, i.e., $A_B$ is nonsingular, but not necessarily feasible. Therefore, the authors combined this method with NFB [30] to achieve feasibility. In addition, a new pivot rule for the NFB was proposed in this paper [29], which is advantageous in reducing the number of iterations and the computational time.

The algebraic simplex initialization consists of at most four consecutive steps. Before executing these steps, pre-processing is needed for an LP problem in the general form. Without loss of generality, the right-hand side b of the constraints is supposed to be non-negative. First of all, the constraints should be re-ordered in such a way that inequalities of type $\leqslant$ appear at first, then the inequalities of type $\geqslant$, and finally the equality constraints. Next, the problem should be transformed into the standard form by adding slack variables. The first step of the algebraic simplex initialization is to select all the slack variables as the basic variables and put their corresponding columns in the coefficient matrix into the formed matrix $A_B$, which is empty before this step. If the LP problem contains no equality constraint, then the obtained basis has been valid, i.e., the obtained $A_B$ is nonsingular; otherwise, the subsequent steps need to be executed. The second and the third steps are straightforward. Their main purpose is to continue to select variables from the decision variables as new basic variables and fill the columns of the matrix $A_B$ accordingly, so that all columns of the formed matrix $A_B$ are linearly independent. After these two steps, if the formed matrix $A_B$ is still nonsingular, the last step is required. In order to complete the basis $A_B$, some so-called pivoting variables need to be introduced in this step. Finally, the obtained matrix $A_B$ has the following form, as shown in Fig. 5.

Fig. 5

The form of the obtained matrix $A_B$. The symbol ‘$\times$’ indicates that the corresponding entry is nonzero, whereas ‘*’ means that the entry is arbitrary

Note that the pivoting variables are different from the artificial variables. The pivoting variables will be driven outside the basic variable set by some pivoting steps. Therefore, the algebraic simplex initialization is also artificial-free. Moreover, the redundant constraints and infeasibility can be detected during the pivoting steps.

Cost Modifications: The main idea of cost modifications is similar to the two-phase method. It starts with an auxiliary problem that has a straightforward feasible basis and generates a feasible basis of the original problem by solving the auxiliary one.

Recall the LP problem formulated as (Standard). Given an initial basis $A_B$ that is not necessarily feasible, the auxiliary problem is constructed by modifying the objective function, i.e.,

$$\begin{aligned} \hat{c}_{j}=\left\{ \begin{array}{ll} A_{\bullet j}^\textrm{T}(A_B^\textrm{T})^{-1}c_B+\delta _j, &{}\quad \text {if } j\in J,\\ c_j, &{}\quad \text {otherwise}, \end{array}\right. \end{aligned}$$

(18)

where $J=\{j\in N \mid s_j<0\}$ denotes the set of infeasible variables in the dual problem and $\delta _j$ is a small positive perturbation to alleviate the problem of degeneracy. It is easy to verify that the basis of (18) is dual feasible, i.e., $s_{j\in J}=\delta _j\geqslant 0$. After applying the dual simplex method, we obtain $x_B\geqslant 0$ at optimality. Therefore, the optimal basis of (18) is immediately a feasible basis to (Standard), and the primal simplex method can be applied subsequently to compute the optimal solution of the original problem. For a detailed review of this method, as well as its implementation, readers may refer to [31] and [32].

Tearing Algorithm: Gould and Reid [33] proposed a remarkable initialization algorithm for large-scale and sparse LP problems, which can find an initial basis as feasible as possible with a reasonable computational cost. This algorithm is called the tearing algorithm. Its main idea is to break the initialization problem into several smaller pieces and solve each of them. There are two main assumptions of the tearing algorithm. First, the coefficient matrix A can be transformed into a lower block triangular matrix with small blocks by permuting its rows and columns. Second, an efficient simplex solver is available to solve dense LP problems with fewer than t rows, where t is a small number. It is assumed that after some row and column permutations, the permuted matrix has the following form:

$$\begin{aligned} \begin{bmatrix} A_{11}&{} &{} &{} &{} \\ A_{21}&{}A_{22}&{} &{} &{} \\ \vdots &{}\vdots &{}\ddots &{} &{} \\ A_{r1}&{}A_{r2}&{}\cdots &{}A_{rr}&{} \\ A_{(r+1)1}&{}A_{(r+1)2}&{}\cdots &{}A_{(r+1)r}&{}0\\ \end{bmatrix}, \end{aligned}$$

(19)

where $A_{ij}\in {\mathbb {R}}^{m_i\times n_j}$. Note that $m_i$ and $n_j$ are positive integers for all $i,j\in \{1,2,\cdots ,r\}$, but $m_{r+1}$ may be zero and thus non-negative. Generally, the size $m_i$ of the blocks is very small. Such a block lower triangular form can be obtained by the algorithm proposed by [34]. Then, the following problem is considered:

$$\begin{aligned}&\min _{v,w} \quad \textbf{1}_m^\textrm{T}(v+w) \end{aligned}$$

(20a)

$$\begin{aligned}&\ \text {s.t.}\quad \begin{bmatrix} A_{11} &{} &{} &{} &{} \\ A_{21} &{} A_{22} &{} &{} &{} \\ \vdots &{} \vdots &{} \ddots &{} &{} \\ A_{r 1} &{} A_{r 2} &{} \cdots &{} A_{r r} &{} \\ A_{(r+1) 1} &{} A_{(r+1) 2} &{} \cdots &{} A_{(r+1) r} &{} 0 \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{r} \\ x_{r+1} \end{bmatrix} +\begin{bmatrix} v_{1} \\ v_{2} \\ \vdots \\ v_{r} \\ v_{r+1} \end{bmatrix} -\begin{bmatrix} w_{1} \\ w_{2} \\ \vdots \\ w_{r} \\ w_{r+1} \end{bmatrix} =\begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{r} \\ b_{r+1} \end{bmatrix}, \end{aligned}$$

(20b)

$$\begin{aligned}&\qquad l_i\leqslant x_i \leqslant u_i, \quad v_i\geqslant 0, \quad w_i\geqslant 0, \quad i=1,\cdots ,r+1, \end{aligned}$$

(20c)

where $x_i \in {\mathbb {R}}^{n_i}$, $v_i,w_i,b_i \in {\mathbb {R}}^{m_i}$, and $l_i$ and $u_i$ are the lower bound and the upper bound of $x_i$, respectively. Note that a feasible solution can be reached with $\textbf{1}_m^\textrm{T}(v+w)=0$. Although sometimes the feasibility may not be achieved, a basis near the feasible region can be obtained. It is easy to see that the first block of (20b) requires that the following conditions are satisfied:

$$\begin{aligned} A_{11}x_1+v_1-w_1=b_1, \quad l_1\leqslant x_1 \leqslant u_1,\quad v_1,w_1\geqslant 0, \end{aligned}$$

(20)

and it is expected that both $v_1$ and $w_1$ are driven to zero. Assuming that $m_i\leqslant t$ for all i, this can be achieved by minimizing $\textbf{1}^\textrm{T}_{m_1}(v_1+w_1)$ subject to (20), which produces the optimal solution $\hat{x}_1, \hat{v}_1, \hat{w}_1$ and a set of $m_1$ basic variables that probably include some of $v_1$ and $w_1$. The obtained solution $\hat{v}_1$ and $\hat{w}_1$ will be zero if the original problem is feasible.

Moving to the kth stage ($1<k\leqslant r$) of this algorithm, the optimal solution $\hat{x}_i, \hat{v}_i, \hat{w}_i, \forall 1\leqslant i <k$ and a set of $m_1+\cdots +m_{k-1}$ basic variables have been obtained. Then, the following conditions need to be satisfied:

$$\begin{aligned} A_{kk}x_k+v_k-w_k=b_k-\sum _{i=1}^{k-1}A_{ik}\hat{x}_i, \quad l_k\leqslant x_k \leqslant u_k,\quad v_k,w_k\geqslant 0, \end{aligned}$$

(21)

and $v_k$ and $w_k$ had better be zero. Similarly, this can be achieved by minimizing $\textbf{1}^\textrm{T}_{m_k}(v_k+w_k)$ subject to (21). Last, as the $(r+1)$th block is 0, $\hat{v}_{r+1}$ and $\hat{w}_{r+1}$ can be calculated as

$$\begin{aligned}&\hat{v}_{r+1}=\max \left\{ 0,b_{r+1}-\sum _{i=1}^{r} A_{(r+1)i}\hat{x}_i\right\} , \end{aligned}$$

(22)

$$\begin{aligned}&\hat{w}_{r+1}=\max \left\{ 0,-b_{r+1}+\sum _{i=1}^{r} A_{(r+1)i}\hat{x}_i\right\} , \end{aligned}$$

(23)

where the maximum is taken by elements. The variables in $\hat{v}_{r+1}$ and $\hat{w}_{r+1}$ with nonzero value are chosen to be basic. To form a full basis, some variables should be arbitrarily selected to cover the remaining rows at the end of the process.

For all $k>1$, if $\hat{v}_k\ne 0$ or $\hat{w}_k\ne 0$, the backtracking will be executed; if $m_j+m_{j+1}+\cdots +m_k\leqslant t$ holds for some j, then the subproblems in stage $j, j+1, \cdots , k$ can be integrated as one problem, which can be solved by the solver.

Non-feasible Basis Method: The so-called non-feasible basis method (NFB) was proposed by Nabli in 2009 [30]. This method is used to construct an initial feasible basis from an infeasible one. It can be easily employed without artificial variables and without any perturbation in the objective function. The feasibility of the obtained basis is achieved by modifying the selection rules of the entering and leaving variables. This method is completely new and different from the dual simplex algorithm and the criss-cross method [35]. In the same paper [30], Nabli introduced the notion of the formal tableau. By combining the NFB with the formal tableau, he proposed another new method, called the formal non-feasible basis method (FNFB).

As mentioned above, the NFB is used to handle the cases with an infeasible initial basis, i.e., the RHS vector $\bar{b}$ has at least one negative component. For such scenarios, the matrix $\beta = A_B^{-1}A_N$ is supposed to satisfy the following condition:

$$\begin{aligned} \forall i\in \{i \mid \bar{b}_i<0\}, \exists j \text { s.t. }\beta _{ij}<0. \end{aligned}$$

(24)

If this condition cannot be satisfied, then the LP problem is infeasible. Considering the standard form in (Standard), the procedure of the NFB is given as follows:

• (1) Determine $k=\arg \min \limits _i \{\bar{b}_i \mid \bar{b}_i<0\}$.

• (2) Build the set $K=\{j \mid \beta _{kj}<0\}$. If $K=\varnothing$, end the process and the original problem is infeasible.

• (3) Calculate $\bar{c} = c_N - A_N^\textrm{T}(A_B^\textrm{T})^{-1}c_B$.

• (4) Select the entering variable index $q = \arg \min _{j\in K} \{-\frac{\bar{c}_j}{\beta _{kj}}\}$.

• (5) Select the leaving variable index $p=\arg \max \limits _{i \in \{1,\cdots , m\}} \{\frac{\bar{b}_i}{\beta _{iq}} \mid \bar{b}_i<0 \text { and } \beta _{iq}<0\}$.

• (6) Repeat the process until $\bar{b}_i \geqslant 0, \forall i \in \{1,\cdots ,m\}$ (the feasible basis has been obtained).

In [30], the authors compared the NFB method with two-phase and big-M methods. In terms of the iteration number, the performance gain is about 78% and 64% in comparison with two-phase and big-M methods, respectively.

Infeasibility-Sum Method: This method is named the infeasibility-sum method because it involves an auxiliary problem that intends to minimize the infeasibility-sum [36], i.e., the negative sum of the infeasible variables. When all infeasible variables are eliminated in a certain iteration, a feasible basis is obtained.

Let $I=\{i\in B \mid x_i<0\}$ denote the set of infeasible basic variables and construct the auxiliary problem as

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{x} &{}\quad -\displaystyle \sum _{i \in I}x_i\\ \mathrm{s.t}. &{}\quad A_Bx_B+A_Nx_N=b,\\ &{}\quad x_{B \backslash I}, x_N\geqslant 0. \end{array} \end{aligned}$$

(25)

Note that here we merely impose non-negativity on the variables which already satisfy the non-negative constraints. Therefore, the basic solution (2) is feasible to (25) and the primal simplex method can be applied to minimize the infeasibility-sum, so as to compute a feasible basis of (Standard). It should be noted that, as we only impose non-negative constraints on part of the variables, the selection of leaving index is slightly different from the original algorithm.

Theorem 3

[36, Theorem 13.1.1] Let $\{\bar{y}_B,\bar{s}_B,\bar{s}_N\}$ be the dual basic solution of the auxiliary problem. The original problem is infeasible if $\bar{s}_N\geqslant 0$.

Based on the above theorem, the detailed procedure of the infeasibility-sum method is shown as follows:

• (1) If $x_B\geqslant 0$, the basis is feasible and go to step 3.

• (2) Form an auxiliary problem with respect to the current basis and compute $\bar{s}_N$. If $\bar{s}_N\geqslant 0$, stop with infeasibility. Otherwise, apply one iteration of the modified primal simplex method and go to step 1.

• (3) Apply the primal simplex to compute the optimum of the original problem.

For more details on the procedure of this method as well as the modified primal simplex algorithm, readers can refer to [36].

Smart Crossover: Most simplex methods begin with a basic feasible point (vertex) to solve the LP problem. To obtain such a starting point, the crossover operation is needed in some simplex initialization methods, such as the ICA mentioned before. However, the crossover operation can be very time-consuming. Therefore, it is necessary and meaningful to propose some smart crossover methods which are more efficient.

Ge et al. [37] introduced two network crossover methods that can deal with the minimum cost flow (MCF) problem and the optimal transport (OT) problem. These two problems are two special types of LPs. Specifically, the MCF problem can be easily transformed into an equivalent OT problem.

Column Generation Method: Given a directed graph ${\mathcal {G}}=({\mathcal {N}},{\mathcal {A}})$, ${\mathcal {N}}$ and ${\mathcal {A}}$ are the entire node set and the arc set, respectively. The node set ${\mathcal {I}}(i), \forall i\in {\mathcal {N}}$ includes all nodes that have an arc from the node i, while the node set ${\mathcal {O}}(i), \forall i\in {\mathcal {N}}$ is comprised of all nodes that have an arc pointing to the node i. The general form of the MCF problem is given as follows:

$$\begin{aligned} \begin{array}{cl} \min _{x} &{} \quad \displaystyle \sum \limits _{(i, j) \in {\mathcal {A}}} c_{i j} x_{i j} \\ \mathrm{s.t}. &{} \quad b_{i} +\displaystyle \sum \limits _{j \in {\mathcal {I}}(i)} x_{j i} =\displaystyle \sum \limits _{j \in {\mathcal {O}}(i)} x_{i j}, \forall i \in {\mathcal {N}}, \\ &{}\quad 0 \leqslant x_{i j} \leqslant u_{i j}, \forall (i, j) \in {\mathcal {A}}, \end{array} \end{aligned}$$

(26)

where $c_{ij}$ and $u_{i j}$ denote the cost and the capacity limit on the arc $(i, j)\in {\mathcal {A}}$, respectively. The variable $b_i$ represents the external supply of the node $i \in {\mathcal {N}}$.

The goal of the MCF problem is to design the amount of flow on each arc, i.e., $x_{ij}, \forall (i,j) \in {\mathcal {A}}$, to minimize the total flow cost while satisfying the node flow balance and the arc capacity constraint. Given the amount of flow on each arc, the maximal flow of a node i is defined as

$$\begin{aligned} x^f_i = \sum _{j \in {\mathcal {O}}(i)} x_{i j} +\sum _{j \in {\mathcal {I}}(i)} x_{j i}, \forall i \in {\mathcal {N}}. \end{aligned}$$

(27)

Given an arc (i, j), the flow ratio of the arc is defined as

$$\begin{aligned} f_{ij} = \max \left\{ \frac{x_{ij}}{x^f_i},\frac{x_{ij}}{x^f_j}\right\} , \forall (i, j) \in {\mathcal {A}}. \end{aligned}$$

(28)

In [37], the authors provide an important property of the MCF problem, which can help to select the basis based on an approximate solution of (26). The property claims that the arc with a larger value of the flow ratio is more likely to be included in the basis. Therefore, given an approximate solution, we can sort all the arcs according to their flow ratio values and select the first $\mid {\mathcal {N}}\mid$ arcs to create a set as $\{s_1, s_2, \cdots , s_{\mid {\mathcal {N}}\mid }\}$, where $\mid {\mathcal {N}}\mid$ is the number of elements in the set ${\mathcal {N}}$. Intuitively, this set gives the potential arcs that should be included in the basis based on the current approximate solution.

With this potential set, a column generation basis identification process is used to obtain the feasible basis of the original problem. First, the original problem should be converted into an equivalent problem in the standard form. Then, the artificial variable is added based on the big-M method mentioned before. After that, at each iteration, an index set $D_k$ is constructed as

$$\begin{aligned} {D}_{k} \leftarrow {D}_{k-1} \cup D_{\{s_{1}, s_{2}, \cdots , s_{n_{k}}\}}, \end{aligned}$$

(29)

where $n_k$ is a monotonously increasing sequence of integers. The set $D_{\{s_{1}, s_{2}, \cdots , s_{n_{k}}\}}$ includes the indices of the first $n_k$ arcs in the potential basis set. With the column generation method, the problem at each iteration has the following form:

$$\begin{aligned} \begin{array}{cl} \min _{x} &{} \quad \displaystyle \sum _{i \in {D_k}} c_{j} x_{j} \\ \mathrm{s.t}.&{} \quad \displaystyle \sum _{i \in {D_k}} A_{\bullet j} x_{j}=b,\\ &{}\quad x_{j\notin D_k} = 0,\\ &{}\quad x \geqslant 0. \end{array} \end{aligned}$$

(30)

Once there is no artificial variable in the basis at a particular iteration, the feasible basis for the original problem near the approximate solution is obtained.

This method can be further implemented to obtain an $\varepsilon$-optimal feasible solution by changing the update rule of the index set $D_k$ as follows:

$$\begin{aligned} {D}_{k} \leftarrow {D}_{k-1} \cup D_{\{s_{1}, s_{2}, \cdots , s_{n_{k}}\}} \cup \{j: \overline{c}_j < -\varepsilon \}, \end{aligned}$$

(31)

where $\overline{c}_i$ is the reduced cost.

Spanning Tree Method: Given an MCF problem, the basic feasible solution of the MCF problem is directly related to a spanning tree of the associated graph. Therefore, in the spanning tree method, the task of finding the basic feasible solution can be replaced by the task of building a spanning tree with the largest sum of flow ratios. However, if the approximate solution is not accurate, the tree solution may be infeasible. Thus, one more step to take under this condition is to push the infeasible tree solution to a feasible one. For the OT problem, this step can be easily implemented.

Considering the OT problem, the nodes in a directed graph can be divided into the supplier set ${\mathcal {S}}$ and the consumer set ${\mathcal {C}}$. Each node in ${\mathcal {S}}$ has arcs pointing to the nodes in ${\mathcal {C}}$. The target of the OT problem is to design the amount of flow on each arc to minimize the total cost under given constraints. The general form of the OT problem is given by

$$\begin{aligned} \begin{array}{cl} \min _{x} &{} \quad \displaystyle \sum _{(i,j) \in {\mathcal {S}} \times {\mathcal {C}}} c_{ij} x_{ij} \\ \mathrm{s.t}. &{} \quad \displaystyle \sum _{j \in {\mathcal {C}}} x_{ij}=s_i,\\ &{}\quad \displaystyle \sum _{i \in {\mathcal {S}}} x_{ij}=d_j,\,\\ &{}\quad x_{ij} \geqslant 0, \forall (i,j) \in {\mathcal {S}} \times {\mathcal {C}}, \end{array} \end{aligned}$$

(32)

where $c_{ij}$ is the cost of the arc (i, j). The variable $s_i$ represents the supply value of a given node $i \in {\mathcal {S}}$, while $d_j$ is the demand value of a node $j \in {\mathcal {C}}$.

For any OT problem, if the amount of flow on a given arc $(i,j)\in {\mathcal {S}} \times {\mathcal {C}}$ is out of the feasible region, there always exists a new flow design that can be feasible. The detailed method to obtain the new feasible design is given in [37] and is omitted here. After this step, the spanning tree method can be used to construct the basic feasible solution as mentioned before.

3.2 Initialization in Dual Simplex

Other than finding a primal feasible basis, we require a dual feasible point to initialize the dual simplex algorithm. The initialization method in the dual simplex can be classified into two types. Methods of the first type solve either the original problem or an auxiliary one with the conventional simplex method. The obtained solution is directly a feasible basic solution to the dual problem. Methods of the second type use a modified simplex method instead. Extra operations are implemented at each iteration of the conventional simplex method.

3.2.1 Generate a Dual Feasible Basis with Simplex

The Most-Obtuse-Angle Row Rule: The most-obtuse-angle rule was first proposed by Pan in [38] and was later analyzed in [39, 40] for its application in achieving dual feasibility. It is a dual version of the most-obtuse-angle column rule. It is inspired by the same observation illustrated in Fig. 4. In each iteration, one dual infeasible variable is moved from the non-basis into basis, while the leaving variable is selected according to the angle with the downhill edge determined by the entering variable. If the downhill direction is close to the negative direction of the objective function, the newly constructed basis is more likely to be an optimal basis. The detailed process is shown in the following:

• (1) Select the entering index $q=\arg \min _{j\in N}s_j$. If $s_q\geqslant 0$, the basis is already dual feasible and go to step 4.

• (2) Compute $\Delta x_B=A_B^{-1}A_Ne_q$. If $\Delta x_B\leqslant 0$, the algorithm terminates with (primal) unboundedness. Otherwise, select the leaving index $p=\arg \max _{i\in B}\Delta x_{i}$.

• (3) Perform pivoting $B \leftarrow B\cup \{q\}\backslash \{p\}$ and go to step 1.

• (4) Apply the dual simplex to compute the optimum.

Though the feasibility of other variables cannot be preserved and cycling may arise during iterations, due to the geometrical benefit of this method, the computational efficiency has been confirmed in [40, 41]. More specifically, Pan [40] showed that by adopting the most-obtuse-angle row pivot rule, the Phase I process is $2-3$ times faster than conditional ones on Netlib problems.

Right-Hand Side Modifications: This method was proposed by [42] and can be regarded as the dual version of the cost modification method, thus having a similar basic idea. Given a basis $A_B$, by modifying the right-hand side (RHS) coefficient $\bar{b}:= A_B^{-1}b$, or equivalently b, of the initial problem, the obtained one becomes primal feasible. After solving this modified problem and recovering the RHS coefficients, a dual feasible basis can be derived.

Recall I defined in (25), which denotes the set of primal infeasible variables. The modified RHS takes

$$\begin{aligned} \hat{\bar{b}}_i=\left\{ \begin{aligned}&\delta _i,\quad \text {if }i \in I, \\&\bar{b}_i, \quad \text {otherwise,} \end{aligned}\right. \end{aligned}$$

(33)

where $\delta _i$ is a small positive number to avoid degeneracy. In this modified problem, for all $i \in I$, we have $x_{i}=\delta _i\geqslant 0$. Therefore, the basis now becomes primal feasible. After solving the modified problem, i.e., $s_N\geqslant 0$, the original problem can be recovered by restoring the value of b. The recovered problem is clearly dual feasible.

To validate the effectiveness of the RHS modification method, Pan [42] compared it with classical two-phase simplex algorithm on four different types of problems. Computational results showed that the RHS modification method outperforms the classical one in terms of required pivot steps for all types on problems.

3.2.2 Generate a Dual Feasible Basis with Modified Simplex

Dual Infeasibility-Sum Method: Though the main idea of dual infeasibility-sum method is not new [43], its efficiency was reanalyzed in [41, 44]. Starting with a dual infeasible basis, this method aims to generate a feasible one by minimizing the infeasibility-sum. Different from the most-obtuse-angle row rule, this method can guarantee a monotonous decrease in infeasibility-sum during iterations.

Recall the dual basic solution in (4). The basis is said to be infeasible if there exists an element in $s_N$ that is less than zero. The infeasibility-sum method intends to maximize the second term in the summation of such variables, i.e.,

$$\begin{aligned} \sum _{j\in J}s_j = \sum _{j\in J}c_j -\left( \sum _{j\in J}A_{\bullet j}\right) ^\textrm{T}y, \end{aligned}$$

(34)

where the objective function is called infeasibility-sum and J is the set of dual infeasible variables defined in the cost modification method. Therefore, we can construct an auxiliary dual problem based on (4) as follows:

$$\begin{aligned} \begin{array}{rl} \max _{y, s_B, s_N} &{} \quad -\left( \displaystyle \sum _{j\in J}A_{\bullet j}\right) ^\textrm{T}y\\ \mathrm{s.t}. &{}\quad A_B^\textrm{T}y+s_B=c_B,\\ &{}\quad A_N^\textrm{T}y+s_N=c_N,\\ &{}\quad s_B,s_{N \backslash J}\geqslant 0. \end{array} \end{aligned}$$

(35)

Note that (35) is also an LP problem and its basis is exactly the same as that of the original dual problem (Dual). Nevertheless, as the constraint $s_N\geqslant 0$ becomes $s_{N \backslash J}\geqslant 0$, the basis is dual feasible. Therefore, the dual simplex method can be applied to generate a dual feasible basis for the original problem. One thing to mention is that, as the constraints are slightly different here, the selection of entering index is slightly modified as well.

Theorem 4

Let $\{\bar{x}_B,\bar{x}_N\}$ be the primal basic solution of the auxiliary problem, i.e., $\bar{x}_B=-A_B^{-1}\sum _{j\in J}A_{\bullet j}$ and $\bar{x}_N=0$. The original problem is (primal) unbounded if $\bar{x}_B\geqslant 0$.

With the above theorem, the dual infeasibility-sum method proceeds in the following steps:

• (1) If $s_N\geqslant 0$, the basis is dual feasible and go to step 3.

• (2) Form an auxiliary problem with respect to the current basis and compute $\bar{x}_B=-A_B^{-1}\sum _{j\in J}A_{\bullet j}$. If $\bar{x}_B\geqslant 0$, stop with primal unboundedness. Otherwise, apply one iteration of the modified dual simplex method and go to step 1.

• (3) Apply the dual simplex to compute the optimum of the original problem.

Artificial Bounds: The artificial bounds method is a dual version of the big-M method. Simply put, this method adds extra upper bounds to the non-basic variables so that the dual problem has a straightforward feasible basis.

Consider the following problem where there exist newly added artificial bounds for non-basic variables compared with (Standard):

$$\begin{aligned} \begin{array}{rl} \min _{x_B, x_N} &{} \quad c_B^\textrm{T}x_B+c_N^\textrm{T}x_N\\ \mathrm{s.t}. &{}\quad A_Bx_B+A_Nx_N=b,\\ &{}\quad x_B,x_N\geqslant 0,\\ &{}\quad x_N\leqslant M, \end{array} \end{aligned}$$

(36)

where $M\gg 0$ is a large number. Since the artificial bounds can be rewritten as a constraint, i.e., $x_N+x_a=M$ with $x_a\geqslant 0$, where $x_a\in {\mathbb {R}}^{n-m}$ is the introduced artificial variable, it can be easily verified that the associated dual problem of (36) is

$$\begin{aligned} \begin{array}{rl} \max _{y, y_a, s_B, s_N} &{} \quad b^\textrm{T}y+M\textbf{1}^\textrm{T}_{n-m}y_a\\ \mathrm{s.t}. &{} \quad A_B^\textrm{T}y+s_B=c_B,\\ &{}\quad A_N^\textrm{T}y+y_a+s_N=c_N,\\ &{}\quad s_B,s_N\geqslant 0,\\ &{}\quad y_a\leqslant 0, \end{array} \end{aligned}$$

(37)

where $y_a\in {\mathbb {R}}^{n-m}$ is an artificial variable, serving as the counterpart of $x_a$. Recall the basic solution of the original dual problem, where $s_N=c_N-A_N^\textrm{T}y$. We note that such a solution is infeasible if there exists $c_j-A_{\bullet j}^\textrm{T}y<0$ for any $j\in N$. Replacing such basic variable with $y_a$ in (37), we can directly obtain a feasible basis of (Dual).

In this survey, we investigate and summarize existing works related to the simplex initialization from the aspects of the primal simplex and the dual simplex, respectively. A comparison of the discussed methods for generating the initial or starting point is summarized in Table 1.

Table 1 Comparison of initialization methods in simplex

4 Learning-Based Branch and Bound Algorithms

In this section, we review the learning techniques to deal with the four key components in B &B algorithms for the MILP. The contributions and limitations of different studies are summarized in this section. In addition, we make some comparisons of different learning methods in these four key components.

4.1 Learn to Branch

With the development of ML, alleviating the computational burden in some traditional branching strategies with ML has been a hot topic. Some works have used imitation learning to approximate decisions by observing the demonstrations shown by an expert, while others capitalize on reinforcement learning to explore better branching policies.

4.1.1 Supervised Learning in Branching

Strong branching (SB) is the most efficient expert in terms of the number of expanded nodes till now [46]. However, its main disadvantage is the prohibitive computational cost. Therefore, most works study how to mimic strong branching in an efficient way. This type of method used in these works is called imitation learning, which can be regarded as supervised learning for decision making. Some early works utilize the traditional ML methods [47,48,49]. They trained different regression models to efficiently approximate SB scores. Specifically, Alvarez et al. [47, 48] utilized ExtraTree [50] to approximate the strong branching score function, while [49] chose the linear regression. The method proposed in [47, 48] consists of two phases to learn and solve MILPs. In the first phase, the SB decisions are recorded by optimally solving a set of randomly generated problems, and a regressor is learned to predict SB scores. In the second phase, the learned function is employed for the instances from MIPLIB, which is the conventional evaluation benchmark for MILP methods. On the other hand, they proposed some significant features including static problem features, dynamic problem features, and dynamic optimization features, which describe the current problem and are easy to compute. Alvarez et al. [48] emphasized the size-independence and invariance property of branching features, followed by many later works. The experimental results in [48] show that the learned branching strategy compares favorably with SB, but its performance is slightly below that of the reliability branching (RB) [46].

Inspired by the idea behind RB, Alvarez et al. [49] used online learning to imitate SB. For a candidate, if its SB score has been computed a certain number of times, it would be deemed reliable, and its SB score could be approximated by learning. Otherwise, the feature vectors and scores of unreliable candidates can be put into the training set. Hence, in contrast to [47, 48], the training data was generated during the B &B process on-the-fly, and thus, no preliminary phase is required. Khalil et al. [51] learned SB scores in an on-the-fly fashion, without an upfront offline training phase on a large set of instances, so no preliminary phase is needed to record the expert behavior, and the computing time is saved. Moreover, they used binary labels which relax the definition of “best" branching variables and allow us to consider multiple good variables that have high scores during the learning process. Thus, the learning time is further saved. The experimental results show that imitating SB by ML methods outperforms SB and pseudocost branching (PB) [52] in terms of the solved instances and the number of nodes. Although the running time of the learned policy is more than PB for easy instances, ML runs fastest when solving medium and hard MILPs. These early works reveal the potential of taking advantage of ML to speed up the solution of large-scale MILP problems.

Moreover, to tackle tedious parameter tuning, Balcan et al. [53] proposed an ML-based method to learn the optimal parameter setting for the B &B algorithm. A certain application domain can be modeled as a distribution over problem instances, and samples can be accessed by the algorithm designer so that a nearly optimal branching strategy can be learned. Here, the optimal branching policy means the optimal convex combination of different branching rules. This work theoretically proved that using a data-independent discretization of the parameters to find an empirically optimal B &B configuration is impossible, indicating its intrinsic adaptiveness.

Fig. 6

Bipartite graph presentation of MILP [54]. The bipartite graph consists of two sets of nodes, namely the variable sets $\{x_1,\cdots ,x_n\}$ and the constraint nodes $\{\delta _1,\cdots ,\delta _m\}$. The edge connecting the variable node and the constraint node denotes the coefficients of the MILP

Fig. 7

Variable selection in the B &B integer programming algorithm as an MDP. In the left figure, a state $s_t$ includes the B &B tree with a leaf node chosen by the solver to be expanded next (in pink). In the right figure, a new state $s_{t+1}$ is obtained by branching over the variable $a_t = x_1$ [54]. (Color figure online)

Nowadays, deep learning has achieved huge success in speeding up variable selections, with the power to process a large amount of data compared with machine learning. Due to the bipartite graph representing MILP (Fig. 6), it is natural to encode the branching policies into a graph convolutional neural network (GCNN), which speeds up the MILP solver by reducing the amount of manual feature engineering. Moreover, the previous statistical learning of branching strategies is only able to generalize to similar instances, whereas the GNN model has a better generalization ability since it can model problems of arbitrary size. Gasse et al. [54] adopted imitation learning to train an exclusive GCNN model for addressing the B &B variable selection problem. In this work, the problem was formulated by the task of searching for the optimal policy of a Markov decision process (MDP), as illustrated in Fig. 7. Since the graph structure is the same for all LP relaxation problems in the B &B tree represented as a bipartite graph with node and edge features, the cost of extraction is reduced to a great extent. By adopting imitation learning, a GCNN model was trained to approximate the SB policy. As shown in Fig. 8, the bipartite representation is taken as the input of the model. After two half convolutions of a single graph revolution, a probability distribution over the candidate branching strategies is finally obtained by discarding the constraints node and adopting a multi-layer perceptron and a softmax activation. Their resulting branching policy is shown to perform better than previously proposed methods for branching on several MILP problem benchmarks and generalize to larger instances.

In order to make the GNN model more competitive on CPU-only machines, Gupta et al. [55] devised a hybrid branching model that uses a GNN model only at the initial decision point, and a weak but fast predictor, such as the multi-layer perceptron, for subsequent steps. The proposed hybrid architecture improves the weak model by extracting high-level structural information at the initial point by the GNN model and preserves the original GNN model’s ability to generalize to harder problems. Nair et al. [56] adopted imitation learning to obtain an MILP brancher, where the GNN approach was improved by implementing a large amount of parallel GPU computation. By mimicking an ADMM-based expert and combining the branching rule with the primal heuristic, their work is advantageous over the SCIP [57] in terms of solving time on five benchmarks in real life.

Fig. 8

The architecture of the GCNN model in [54]

However, most of the above works specialize the branching rule to distinct classes of problems, obtaining generalization ability to larger but similar MILP instances [47,48,49, 51]. Besides, these works lack a mathematical understanding of branching. With the hypothesis that parameterizing the underlying space of B &B search trees can aid in generalization to heterogeneous MILPs, Zarpellon et al. [58] introduced new features and architectures for branching, making the branching criteria adapt to the tree evolution and generalizing across different combinatorial class problems. Specifically, $C_{t}, \mathrm{Tree_{ t}}$ are used to describe the search-based features and the state of the search tree, respectively, which are independent of the specific parameters of the problem and evolve with the search. This work first used a baseline DNN (NoTree) that only uses $C_t$ as inputs to demonstrate the significance of search-based features. The output layer equipped with the softmax produces a probability distribution over the candidate set, indicating the probability for each variable to be selected. Then, $\mathrm{Tree_{t}}$ was put in the NoTree by gating layers, called the TreeGate models. Considering that people rarely use SB in practice, this work chose the SCIP default branching scheme, relpscost [59], a reliable version of HB, as a more realistic expert. In the experiment, 27 heterogeneous MILP problems were partitioned into 19 train and 8 test problems. Both NoTree and TreeGate outperform GCNN, RB, and PC in terms of the total number of nodes explored. Since GCNN struggles to generalize across heterogeneous instances, it expands around three times as many nodes as this method. On the other hand, the test accuracy of TreeGate is 83.70%, improving 19% over the NoTree model, while the accuracy of GCNN is only 15.28%. The comparison between the mentioned methods is shown in Tables 2 and 3.

Table 2 Machine learning-based variable selection comparison

Table 3 Deep learning-based variable selection comparison

4.1.2 Reinforcement Learning in Branching

One of the main limitations of imitation learning is that the expert bounds the performance of the learned strategy. However, expert knowledge is sometimes not satisfactory. Sun et al. [61] analyzed why imitating SB for learning branching strategy is not a wise choice: SB yielding small B &B trees is a consequence of reductions from solving branch LP instead of its decision quality, and these reductions cannot be learned by imitating a branching policy. They designed experiments that eliminate the side-effect of reduction obtained in solving branch LP and found that SB has poor performance. Thus, researchers hope to propose better methods for selecting variables.

Sun et al.  [61] designed a novel primal–dual policy network over reduced LP relaxation and a novel set representation for the branching strategy. To encourage the agent to solve problems with as few steps as possible, the reward is set to $r_t = 1$ at each time step. Although the primal–dual policy is similar to GCN, it uses a dynamic reduced graph by removing redundant fixed variables and trivial constraints during the process, which gives a more precise and accurate description of the state. On the other hand, instead of edge embedding in GCN, primal–dual policy relies on simple matrix multiplication, which further saves computational time. Here, the set representation and the optimal transport distance (or Wasserstein distance) are used to define the novelty score. Given an instance Q, the collection of its subproblems under a branch policy $\pi$ can be defined as $b(\pi , Q) = \{R_1, \cdots , R_H\}$. For each subproblem, $R_i$, its feasible region is a polytope. The weight function $w(\cdot )$ represents the number of feasible points in the associated polytope. The distance between two subproblems $R_i$ and $R_j$ is defined as $d(R_i, R_j):=\Vert g_i-g_j \Vert _{1}$, where $g_i$ and $g_j$ are their mass centers. Then, the optimal transport distance between two policy representations is computed as

$$\begin{aligned} D(b_1, b_2)=\min _{\Gamma }\sum _{i,j} \Gamma _{ij}W_{ij}(b_1, b_2) \quad \text {s.t.} \quad \Gamma \varvec{1}=p(b_1), \Gamma ^\textrm{T} \varvec{1} = p(b_2), \end{aligned}$$

(38)

where $p(b) \in \Delta ^{H-1}$ is a simplex mapped from b by normalizing the weights. Therefore, given a collection of older policies M and an instance Q, the novelty score is defined as

$$\begin{aligned} N(\theta , Q, M) = \frac{1}{k}\sum _{\pi _{j} \in k\text {NN}(M, \theta )} D(b(\pi _{\theta }, Q), b(\pi _{j}, Q)), \end{aligned}$$

(39)

where kNN produces the k-nearest neighbors of $\pi _{\theta }$ in M. Equipped with this novelty score, novelty search evolution strategy was proposed to encourage exploration in reinforcement learning (RL). Their experiments compared the proposed RL method with some existing approaches, including SVM, GCN, and three SCIP’s branching rules (RPB [62], FSB [57], and VFS [57]). The RL method performs best in terms of the running time, the number of expanded nodes, and primal bounds. However, in obtaining a higher dual value, the proposed method performs worst initially, but it finally obtains the best result, indicating its non-myopic property. Different from [63], this work can further be transferred to larger instances, and its performance is significantly superior to FSB, RPB, SVM, and GCN.

Although reinforcement learning can potentially produce a better branching strategy than the expert, the performance is limited by the length of the episode, and it learns inefficiently at the beginning due to insufficient data.

4.1.3 Dynamic Approach for Switching Branching Heuristics

Based on the observation of the highly dynamic and sequential nature of the B &B algorithm, Di Liberto et al. [64] believed that there are no single branching heuristics that would perform the best on all problems, even on different subproblems induced from the same MILP. Therefore, the efficiency of the search can be greatly improved if we adopt the correct branching method at the right time during the B &B search. Motivated by portfolio algorithms that attempt to predict the best heuristic for a given instance, this work proposed an algorithm named dynamic approach for switching heuristics (DASH). Based on the defined features, a clustering of problems was learned with the g-means algorithm at the first step. Then the correct assignment of the branching methods to clusters is learned during an offline training phase with a similar method as in Kadioglu et al. [65]. As the search depth increases, the instance tends to shift to a different cluster. When such a change occurs, the heuristic would be switched to a new one that best fits the current cluster. The numerical results show that DASH outperforms the static and random switching heuristic methods in terms of the running time, indicating the benefit of dynamics and adaptiveness of the switching methods. Nevertheless, Lodi and Zarpellon [66] observed that the upfront offline clustering conflicts with the ever-changing characteristic of the tree evolution and somehow affects time efficiency.

4.2 Learn to Select

As shown in [67], the effectiveness of different selection methods depends on the type of problem. It is preferable to seek a selection strategy that adapts to different types of problems. We divide the existing learning-based literature into the following two categories, i.e., one is adaptation in evaluation criteria and the other is learning in heuristics.

4.2.1 Adaption in Evaluation Criteria

The evaluation criteria of a node during a B &B run are from the following two sides, the feasibility side and the optimality side. If the selection criteria pay more attention to the feasibility side, the selection strategy will perform more like the depth-first search strategy, while on the other side, the selection strategy would perform more like the best-first strategy.

Borrowing an RL vocabulary, some grade of adaption could be pursued in the combination of best-first and depth-first strategies to balance exploration and exploitation in the B &B run. Sabharwal et al. [68] exploited the RL framework. The score of a node N is a weighted sum of two terms,

$$\begin{aligned} \text {score}(N)=\text {estimate}(N)+\varGamma \dfrac{\text {visits}(P)}{100\text {visits}(N)}, \end{aligned}$$

(40)

where estimate(N) is some measure of the quality of node N, P is the parent node of N, and visits$(\cdot )$ counts the number of times the search algorithm has visited a node. The parameter $\varGamma$ balances the tradeoff between exploitation(first term) and exploration(second term), and nodes with a higher estimate or have been visited less time than their siblings will be pursued first. This geometric means of runtime, the number of searched nodes, and the simplex iterations are improved compared with three other selection strategies: best-first, breath-first, and CPLEX default heuristic. The improvement is gained due to a balanced usage of best-first and breath-search-like schemes. However, this work treats every node of a B &B tree equivalently, ignoring the uniqueness of each node’s feature during the B &B run. An interesting question arises about employing the node feature in the scoring system to improve the learning quality.

4.2.2 Learning in Heuristics in Selecting

The main idea of learning in heuristics is rating each node based on a weighted sum of criteria and choosing the node with the highest score. The first heuristic search procedure by learning methods was proposed by Glover and Greenberg [69, 70] which adjusts the weights offline using a learning procedure. Ansótegui et al. [71] induced the hyper-configurable reactive search to learn the parameters of a metaheuristic online with a linear regression, where the regression weights are tuned offline with the GGA++ algorithm configuration [72].

Daumé et al. [73] and Chang et al. [74] converted the solving problem into a sequential decision-making problem. The policy for that decision-making problem is then learned or improved. A fundamental limitation of their work is that there is no correction due to the greedy search at each test time. Thus, the obtained solution sequence will have deviations from the optimal one.

He et al. [75] instead proposed a method to learn the node selection strategy in a B &B run by imitation learning. They categorized their features into three groups:

• 1. Node features include bounds, estimated objective at a given node, indications of the current depth, and the (parental) relationship for the proceeded node.

• 2. Branching features represent the variable branching changes, including pseudocosts, variable’s value modifications, and bound improvement.

• 3. Tree features describe measures, i.e., the number of obtained solutions, global bounds, and gaps.

They assumed that the training time will have a small set of solved problems and will solve the problems of the same type at the test time. A learning-based node selection policy to repeatedly pick a node from the queue of the remaining unexplored nodes mimics a simple oracle that knows the optimal solution in advance and only expands nodes that contain the optimal solution. This learning-based selection method obtains better solutions with a smaller gap, using less time demonstrated on multiple datasets compared to SCIP. However, the author leaves the seek of certified optimality as the future work. In addition, this work is problem dependent, which requires the test data to have the same type of training data. Yilmaz and Smith [76] used a similar method in [75] to select the direct children at non-leaf nodes.

Hottung et al. [77] proposed a new method that integrates deep neural networks (DNNs) into a heuristic tree search to choose the next branch, namely the deep learning heuristic tree search (DLTS). DLTS is capable of achieving better performance without problem-specific knowledge. The problem-specific information is almost exclusively provided as input to the DNN that is trained offline via supervised learning on given (near-) optimal solutions. It is shown in [77] that DLTS can find solutions with smaller gaps to optimality on real-world-sized instances compared to the state-of-the-art metaheuristics proposed by Karapetyan et al. [78]. In addition, it does not require extra training data. However, as a coin has two sides, the system performance relies on the quality of the provided solutions. In addition, the policy is not adjusted in terms of the runtime and solution quality. The comparison between the above papers is shown in Table 4.

Table 4 Learning-based node selection comparison

A relatively large amount of literature focuses on embedding learning methods into primal heuristics, including but not limited to [56, 79,80,81,82,83,84,85]. Khalil et al. [79] introduced binary classification to predict the success of a primal heuristic at a given node. It is the first systematic attempt to optimize the use of heuristics in tree searching. This work boosts the performance of SCIP, even on instances for which experts already fine-tune the solver. However, the learning rules can be refined, taking into account the running time left to the solver. Hendel [80] formulated a multi-armed bandit approach to learn to switch nine primal heuristic strategies online. Hottung and Tierney [81], Addanki et al. [82] and Song et al. [83] adopted learning methods to improve the neighborhood search to improve the primal performance. The learning methods were adopted to either select the next modified variables or choose new values to a subset of variables that have been selected already. However, those methods require at least a feasible point as input. Xavier et al. [84] proposed three different learning models to extract information from previously solved instances, which can help to improve the computational performance of the MILP solvers when dealing with similar instances. The first model was designed to predict the relaxation and omitted constraints. The second model was proposed to construct a good warm start point using k-nearest neighbors. The third model develops an ML model for finding constraints to restrict the solution without affecting the optimal solution set. These three models boost the speed to find a solution with optimality guarantees. The main limitation of this work is that a large number of solved instances must be available. In addition, it requires that the problem to be solved in future is sufficiently similar to the past sample. Unlike the above learning primal heuristic works [79,80,81,82,83,84], Ding et al. [85] and Nair et al. [56] removed the similarity requirement and built a tripartite graph representation to extract the relation between variables, constraints, and objective function without human interaction. Nair et al. [56] proposed a generative modeling problem to model predicting variable assignments problem, which enables learning from all existing feasible assignments and generates partial assignments at test time in a principled way. However, this training method requires GPU. Figure 9 demonstrates the main contributions of the above literature.

Fig. 9

Main studies on learning-based primal heuristics and their main contributions

4.3 Learn to Prune

When using the B &B algorithm to solve large-scale systems, the number of non-pruning nodes by traditional pruning methods is still quite massive. As a result, it either requires a large computational cost to solve the problem, or a possible good solution cannot be obtained within the time limit. Therefore, the question arises of whether we could use some learning methods to effectively prune a large set of unexplored nodes as early as possible and achieve a solution with a guarantee of the optimality gap. There are mainly three ways to accelerate the pruning policy by learning. One is learning whether to discard or expand the selected node given the current progress of the solver once the popped node is not fathomed, such as [75]. The second is using learning methods to achieve better bounds to accelerate the pruning process, such as [77]. The last one is trimming the neural network by cutting off redundant connections between weights or neurons of adjacent layers and attaching fine-tuning subsequently to the pruned model for improving the performance, such as Han et al. [86]. Note that the third method is not a particular method for the B &B algorithm since it can be applied to simplify the problem model if it implements the neural network. In this survey, we will add more references related to the first two ways as follows. We call the first method learning-based node pruning and the second one learning-based bounds.

4.3.1 Learning-Based Node Pruning

Nowadays, learning methods are adopted to prune the non-optimal nodes to accelerate the B &B algorithm. He et al. [75] treated the node pruning policy as a binary classifier that predicts an action in $\{prune, expand\}$. The classifier takes a feature-vector description of the current state and attempts to predict the current action to mimic the expert action, which prunes a node when it does not belong to the optimal branch. Thus, it obtains a smaller gap solution using less time than SCIP. However, when the network scale is large, the computational complexity of [75] is still high since the state space is quite ample. Shen et al. [87] contributed to improving the computational efficiency over [75] by exploiting the structure of the B &B algorithm and problem data. The authors also proposed self-learning, a kind of transfer learning method without labeling, to cope with the task mismatch problem by only adding a small set of additional unlabeled training samples. As a result, this method requires few training samples and shows effectiveness on acceleration compared to the algorithm in [75]. Unfortunately, the above two methods are not required to learn to prune the fathomed nodes. To cope with this difficulty, Lee et al. [88] proposed to keep the traditional prune policy and introduce an auxiliary learning-based prune policy to reinforce the prune task. Different from only keeping the top solution and pruning the other non-optimal nodes in the above literature, Yilmaz and Smith [76] kept the best k solutions. Five MIP datasets were included to demonstrate that this policy obtains solutions more quickly than the methods precedent in the literature. In addition, with the same time limitation requirement, this algorithm can achieve a better optimality gap.

4.3.2 Learning-Based Bounds

Since the MILP is hard to solve, relaxed convex subproblems are solved as the lower bounds. More nodes can be pruned if the lower bound can be determined much closer to the original subproblem. Hottung et al. [77] used a DNN to heuristically determine the lower bounds. The authors then proposed three pruning functions to determine whether to prune certain branches or nodes based on the output. On the other hand, if the upper bound is loose, which is often much higher than the actual objective, then few branches of the search tree can be pruned. In the traditional B &B algorithm, one usually updates the upper bound along with diving the tree. However, if a tighter upper bound can be obtained faster, more subproblems can be pruned. The primal heuristics [56, 79,80,81,82,83,84,85] which aim to find a possible solution as fast as possible give a possible solution with a high-quality upper bound; thus, they will also have a significant improvement to accelerate the pruning speed. Some special learning-based upper bounds are derived for some particular MILP problems, such as decision trees [89] by Again et al. and informative path planning [90] by Binney and Sukhatme.

4.4 Learn to Cut

Existing literature on cutting-plane methods is mainly divided into two categories: cut generation and cut selection. Cut generation aims to generate valid linear inequalities to further tighten the LP relaxations. Nonetheless, adding all the generated cuts to the LP relaxation brings a huge computational burden. To improve the computation efficiency, cut selection emerges to select the valuable generated cuts. Therefore, the cut selection problem is of significance for the overall performance and thus becomes the main focus of recent works. Traditional theoretical analyses limit the understanding of cutting-plane selections, and they have so far failed to help in practical cutting-plane selection [91] directly. Applying learning to cut selection has the potential to improve the solution to MILPs and offer help in understanding and tackling related issues.

4.4.1 Score-Based Cut Selection

To reduce the total running time, Huang et al. [92] proposed a new metric, named Problem Solvability Improvement, to measure the quality of the selected cut subset. Since obtaining the problem solvability is infeasible in practice, this metric was substituted with the reduction ratio of solution time of selecting a cut subset. A score function that measures this quality was learned as a rank formulation which labels the top-ranked cuts as positive and the remaining cuts as negative because the main goal is to differentiate good cuts from poor cuts, rather than to rank all candidate cuts. Different from Khalil et al. [51], labels for individual cuts are more complicated to obtain than branching. Therefore, multiple instance learning (MIL) was capitalized on to tackle this issue. Instead of requiring instances to be labeled individually, in Babenko [93], MIL receives a set of labeled bags, each including several instances. In the binary classification, a bag would be labeled negative when all instances are negative, and positive otherwise. This technique fits the scenario of cut selection since the label assignment is determined by more than one instance, and the effect of an individual cut is very imperceptible for large-scale problems. Experimental results demonstrate the power of this ranking-based cut selection policy in terms of the quality, generalization ability, and performance on large-scale real-world tasks, and this work is the first one that applies the learning-based cut selection strategy to large-scale MILPs with more than $10^{7}$ variables and constraints. Moreover, for real-world production planning problems, this method improves the efficiency of Huawei’s industrial MILP solver and solves problems without loss of accuracy, speeding up the ratio of 14.98% and 12.42% in the offline and online settings, respectively.

Balcan et al. [94] provided the first provable guarantees for sample complexity of learning parameterized cut selection policies, and they showed that this analysis can be generalized to variable and node selection. Based on the sample complexity of learning cutting planes, the branch-and-cut (B &C) algorithm can adaptively apply cuts as it builds the search tree.

Inspired by the widely used imitation learning on the SB expert for learning to branch, Paulus et al. [95] proposed a powerful expert, called Lookahead rule, and utilized imitation learning to learn the cutting-plane selection policy. In the spirit of the SB, the Lookahead cut selector performs a Lookahead step to measure the variation of the LP bound of each available cut and then select the optimal cut greedily. Therefore, similar to the SB heuristic, the Lookahead expert is a strong rule for selecting cuts, which outperforms common heuristics in terms of the integrality gap and the number of cuts. However, it suffers from a high computational burden, since it needs to solve all LPs of all cut candidates. Therefore, the authors learn a cut selection policy that imitates the Lookahead expert. Specifically, the LP relaxation and cut candidates are formulated as a tripartite graph similar to [54], and the features are extended to fit the cut selection setup. Then a new neural architecture, NeuralCut, is developed by combining the graph convolutions and attention. Experimental results illustrate that NeuralCut outperforms manual heuristics and a competing RL approach in Tang et al. [96] with a higher average bound fulfillment and a smaller average reversed integrality gap.

The comparison between the mentioned methods is shown in Table 5.

Table 5 Score-based cut selection

4.4.2 Reinforcement Learning in Cut Selection

Tang et al. [96] first used reinforcement learning to enhance the performance of heuristics. It formulated the process of sequentially selecting cutting planes as an MDP. At iteration t, the numerical representation of the state is $s_t=\{ {\mathcal {C}}^{(t)}, c, x_\textrm{LP}^{*}(t), {\mathcal {D}}^{(t)} \}$, where ${\mathcal {C}}^{(t)} = \{a_{i}^\textrm{T} \leqslant b_{i}\}_{i=1}^{N_t}$ is the feasible region with $N_{t}$ constraints of the current LP, c is the parameter of the objective function. Solving this new LP yields an optimal solution $x_\textrm{LP}^{*}(t)$ and the set of candidate Gomory’s cuts ${\mathcal {D}}^{(t)}$. Thus, the action space at iteration t is ${\mathcal {D}}^{(t)}$. After taking an action, which is adding one inequality $e_{i}^\textrm{T}x \leqslant d_{i}$ from ${\mathcal {D}}^{(t)}$, the new feasible region becomes ${\mathcal {C}}^{(t)} = {\mathcal {C}}^{(t)} \cup \{e_{i}^\textrm{T}x \leqslant d_{i}\}$. Then $x_\textrm{LP}^{*}(t+1)$ and ${\mathcal {D}}^{(t+1)}$ can be computed, and the new state $s_{t+1}=\{ {\mathcal {C}}^{(t+1)}, c, x_\textrm{LP}^{*}(t+1), {\mathcal {D}}^{(t+1)} \}$ is determined. The gap between the objective values of these LP solutions $r_{t}=c^\textrm{T}x^{*}_\textrm{LP}(t+1) - c^\textrm{T}x^{*}_\textrm{LP}(t)$ is the reward for the RL agent at iteration t, encouraging the agent to approach the optimal integer solution as fast as possible. The trained policy specifies a distribution over the action space ${\mathcal {D}}^{(t+1)}$ at a given state $s_t$. An attention network was adopted to make the policy agnostic to the ordering among the constraints. Besides, to enable the network to handle IP instances with various sizes, LSTM with hidden states was utilized, which encoded all information in the original inequalities. Experiment results illustrate the performance of the RL agent from five perspectives: efficiency of cuts, integrality gap closed, generalization properties, impact on the efficiency of branch-and-cut, and interpretability of cuts. Compared to some commonly used human-designed heuristics, the RL agent needs the least number of cuts. For some larger-scale instances with sizes close to 5000, the agent can close the highest fraction of integrality. Although trained on smaller instances, the RL agent can still have extremely competitive performance on 10 times larger test problems. Moreover, even if the agent is trained on small packing problems, it can be applied to 10 times larger graph-based maximum-cut problems, indicating its great generation properties. Compared to the pure B &B method, this learning-based cutting-plane selection significantly reduces the number of expanded nodes. However, the running time of the RL policy is not improved substantially compared with other methods since running the policy is somehow costly.

Based on the observation that for a specific cut selection method, any finite grid search will miss all parameters values, and consequently select integer optimal inducing cuts in an infinite family of MILP instances, Turner [97] utilized RL to learn the parameters of a cut selection scoring rule and make it adaptive with the input instance. The official SCIP cut scoring rule is a convex combination of four heuristic measures. Therefore, the action in the MDP formulation corresponds to the choice of four parameters, and the state is the MILP instance represented by a bipartite graph. The policy network is parameterized as a GCNN following [54], and the parameterized is represented the weights and biases in the GCNN. Experimental results show that the learned policy outperforms the random initialized cut scoring rule. However, the learned scoring parameters are instance dependent, and consequently, the learned policy suffers some generalization loss when extended to MIPLIB 2017 as a whole.

Recently, [98] found that the order of selected cuts significantly affects the efficiency of solving MILPs from extensive empirical results. Therefore, they proposed a hierarchical sequence model (HEM) to consider the preferred cuts, the number of selected cuts, and the order of the selected cuts simultaneously from a data-driven perspective. The considered MILP solver is regarded as the environment, and the proposed HEM for policy is formulated as the agent. The MDP formulation is similar to [96]. Specifically, the high-level policy learns how many cuts should be selected by predicting an appropriate ratio, and the lower-level policy learns what order of selected cuts should be preferred. The authors’ model is a tanh-Gaussian distribution for the higher-level policy, whose mean and variance are given by a multi-layer perceptron (MLP). To embed the sequence of candidate cuts, the LSTM is used. As for the lower-level policy, it is formulated as a sequence model so that it can capture the interaction among cuts. A pointer network with attention is used to generalize across different instances. In a word, the designed NN structure in the HEM model captures the underlying order information together with the interaction among cuts, which brings new insights into learning to cut. Experimental results show that the HEM improves the efficiency of the MILP solving process compared with human-designed heuristic and learning-based baselines.

The detailed comparison among the mentioned methods is shown in Table 6.

In addition, several works have applied learning to cut generation in nonlinear programming, such as Dey et al. [99] and Baltean-Lugojan et al. [100]. This topic is beyond our scope, and here we do not investigate the related works in detail.

Table 6 RL-based cut selection

5 Future Work

5.1 Learning-Based Initial Basis Construction

In Sect. 3, we discuss many approaches to construct the initial basis from different perspectives. Choosing the appropriate initialization methods for each LP based on its features is one of the possible ways to improve the overall efficiency. With advanced ML technologies, we can design a classifier to automatically select the appropriate simplex initialization method. In addition, we can design a classifier to determine whether a variable should be included in the basis directly.

For different LPs, we first need to design some features to distinguish them. There are two types of features, namely self-designed features and graph embedding features.

Self-Designed Features: Considering the LP standard form given in (Standard), the self-designed features can be further divided into the problem-dependent and the problem-independent features. The dimension of the problem-dependent features changes when given different LPs, while the dimension of the problem-independent features does not change. The details of the features can be designed as follows:

• (1) Problem-dependent features: the matrix A, the vectors c, b, the dimensions m, n.

• (2) Problem-independent features: the sparsity of the matrix A, which is quantified by the percentage of zeros in A; the sparsity of the vector b, which is defined by the percentage of zeros in b; the triangularity of the matrix A, which is designed as:

  $$\begin{aligned} \frac{\mid z_U - z_L \mid }{\max (z_U, z_L)}, \end{aligned}$$

  (41)

  where $z_U$ and $z_L$ are the percentages of nonzero elements in the upper part and the lower part of the matrix A, respectively.

Graph Embedding Features: Motivated by [54, 85, 104], and [56], we can also represent an LP as a bipartite graph (see Fig. 6). The bipartite graph representation of LP enables feature extraction through graph embedding.

5.1.1 Initial Basis Construction with Deep Learning-Based Classification

The first possible future work is to design a deep learning-based classifier that can divide variables into basic variables and non-basic variables. The input of the classifier is the feature of each variable node. The output is the probability that the corresponding variable should be selected as a basic variable. The architecture is given in Fig. 10.

Fig. 10

Classification of initial basic variable selection

To train such a neural network, enough training data pairs are required. Each training data pair consists of the feature of a variable node and the label indicating whether its corresponding variable is a basic variable, i.e., the label is “1” if it is a basic variable, otherwise “0.” However, how to obtain the labels of variable nodes can be a tricky problem. One approach to obtain the labels is to exactly solve the LP problem, then the type (basic/non-basic) of the variable when reaching the optimality can serve as its label. Obviously, this approach is very costly. Another approach is to obtain the label by the initialization methods introduced before, but the obtained label can be inappropriate since some of these methods cannot guarantee the feasibility or the nonsingularity of the derived basis. If enough training data have been obtained, the feature and the label can serve as the input and the output of the deep neural network, respectively. The architecture of the deep neural network, including the number of layers, the activation function, the loss function, etc., should be further designed.

The trained neural network can be used to select basic variables for LPs. The main steps are as follows: first, construct the graph representation for the LP to be solved; second, learn the low-dimensional features of the variable nodes via graph embedding; third, input the derived features into the neural network to obtain probability outputs, then sort all variables in descending order of their corresponding outputs and select the first m variables as basic variables.

5.1.2 Initialization Method Selection with Deep Learning-Based Classification

Another possible future work is to design a classifier for the initialization method selection, which is illustrated in Fig. 11.

Fig. 11

Classification of initialization method selection

The input of the classifier is the designed features of different LPs. These features can be the self-designed features, the graph embedding features, or a combination of different features, depending on the classification performance. The output of the classifier is a probabilistic distribution of choosing different simplex initialization methods to construct the initial basis. Given an LP problem, the method with the highest probability will be selected as the optimal initialization method.

To train the classifier, we first collect the total computation time with different candidate methods and label the method with the shortest time as “1”. The others can be labeled as “0”. Then, these labels are regarded as the training dataset to train the classifier.

5.2 Learning-Based Starting Point Construction

In Sect. 3, we also cover some methods for finding an improved starting point for the simplex method. These methods design different interior directions to do the iteration and obtain the improved point. However, the tradeoff between the iteration steps and the total computation time has not been well studied. In future work, we can propose a RL-based method for investigating the tradeoff between the iteration steps and the total computation time in methods for finding the improved starting point.

In the RL, an action is selected based on the current state. After the action selection, a reward and the next state will be returned. This process is then repeated in the following steps. In our problem, the action selection is equivalent to designing whether the iteration will continue or stop. The state includes two parts. One is the feature of the given LP. The feature can be the self-designed one or the graph embedding one. The other part is the state related to the current improved point. For example, in the $\varepsilon$-optimality search direction method, the iteration direction is designed based on the active constraint of the current improved point. Therefore, the active constraint can be included in the state. The search direction can also be considered as part of the state. Based on the designed state, the action selection is learned by RL algorithms.

The general process of the RL-based starting point construction is given in Fig.12. The reward can be designed based on the computation time of each iteration.

Fig. 12

Learning-based starting point construction

According to the dimensionality of the designed state, different RL methods can be chosen. When the state dimension is small, we can choose a basic learning-based method such as the Q-learning algorithm. When the state space is large or continuous, we can choose some advanced algorithms like the deep Q-network algorithm or the double deep Q-network algorithm, etc.

Fig. 13

Illustration that depth-first would cost redundant effort to solve non-optimal nodes (if the optimal node belongs to the right side tree, it would cost a lot of effort but is meaningless to search the whole left side tree)

5.3 Enhanced Learning-Based B &B

As reviewed in Sect. 4, to speed up the solving time of B &B, some learning methods are used to obtain a suitable tuning parameter that balances the best-first and depth-first in the B &B runs or to develop a binary classification of whether primal heuristics will succeed at a given node. However, most of the literature in this part does not consider the uniqueness of each node during the B &B run and the time limitation for implementation. To cope with these problems, two possible enhanced ideas are proposed as follows.

• 1. Online Tuning in the B &B

  To take into account the uniqueness of each node during the B &B run, we will adopt an online tuning parameter that balances the best-first and depth-first in the B &B run taking into account the nodes’ features. For example, it should count more on the quality of the achieved solution for the root node, since achieving a solution with high quality would significantly reduce the search space. Otherwise, it should make a redundant effort to solve non-optimal nodes, as illustrated in Fig. 13. Therefore, it would be preferable for the root node to assign more weight to the best-first policy. On the other hand, satisfying the feasibility constraints would be more critical for the near-leaf nodes, since the quality can be adjusted with just a few backward exploitations. From the above analysis, it would be interesting to consider the nodes’ features (such as depth) and propose an online tuning learning method to balance the tradeoff between exploration and evaluation along with the implementation of the B &B algorithm.

  Moreover, we can improve the estimate in [68] using the evaluation criteria. Instead of using the normalized relaxed LP objective value as the estimate of this node in [68], we can take into account the feasibility quality along with the optimality quality. We can further introduce a parameter to tune the importance of the feasibility quality versus optimality quality, and we can learn this parameter online.

• 2. Extension to Nonbinary Classifications and Adapt Learning Strategies at a Given Time

  To adapt the learning strategies given quality constraints and time limitations, we could expand the binary classification to a probability of whether to conduct a primal heuristic [79] (or other problems that have binary classes) with problem features (A, b, c) or the feature extracted by GCNN [54,55,56, 85] as shown in Figs. 6 and 8. The learning task is to approximate the probability distribution. We employ an L-layer multi-layer perceptron, a type of neural network, to learn the mapping from the input feature vector to the output indicating the probability of each class. We then adopt the supervised learning, or Data Aggregation [105] to learn the model parameters by minimizing the weighted loss function. The time limitation could be considered to tune the threshold. For example, in the standard classification, if the probability is larger than 0.5 of belonging to the first class, we cluster this input to the first class; otherwise, it belongs to the second class. Suppose the first class means conducting primal heuristics, decreasing the threshold leads to a larger exploration space and obtains a feasible solution with higher quality. We could iteratively decrease the threshold to satisfy the quality constraints and time limitations and obtain the learned parameter adaptively.

Fig. 14

Demonstration of the difference between transfer learning and traditional ML

5.4 Reduce Training Samples

A common limitation of learning-based algorithms in this survey is that in order to have good predictors, a large number of solved instances must be available, and the solved instances in most literature must be of the same type as the problem we expect to solve in future. However, when the problem scale becomes quite large, generating the training data is costly, let alone training the network by the data.

In order to address this limitation, there are two possible directions. One is generating the training data along with the problem-solving progress. Dataset Aggregation (DAGGER), which was proposed by Ross et al. [105], is an iterative algorithm that trains a deterministic policy that achieves good performance guarantees under its induced distribution of states. The pseudocode for DAGGER is shown in Algorithm 3, where $\pi ^{*}$ is the presence of the expert in DAGGER and $\beta _{i} \in [0,1]$ represents the trust of the expert decisions. The other direction is using transfer learning to exploit the pre-trained neural network and train a new model with only a few additional samples. Figure 14 demonstrates the transfer learning method. The essential advantage is that with transfer learning, the new task can be trained with fewer additional training samples than the traditional one, since some information can be achieved by transferring the knowledge from the old task into the new task.

6 Conclusion

In this survey, we summarize the methods to accelerate the MILP solution process from two aspects. The first is to utilize appropriate simplex initialization approaches to speed up the solution of LPs. The second way is to improve the B &B algorithms with machine learning technologies. We also propose several possible future works that can further improve the efficiency.