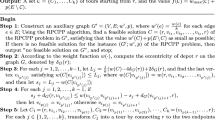1 Introduction

The problems to be discussed in this paper are all defined on undirected graphs. Arc routing problems are very active and interesting topics in operations research fields, due to their many applications in our reality, such as routings of street sweepers, mail delivery, snow plows and the inspection of electric power lines. In most arc routing problems, the objective is to determine a least-weight traversal of a set of specified edges in a graph. Guan [1] in 1960 considered the Chinese postman problem (the CP problem, for short), which is one of the arc routing problems specialized to weighted graphs, and it is defined as follows. Given a weighted graph \(G=(V,E;w)\) with a weight function \(w:E\rightarrow {\mathbb {R}}^{+}\), it is asked to find a tour C traversing each edge \(e\in E\) at least once, the objective is to minimize the total weight \(w(C)=\sum _{e\in E} t(e)w(e)\) among all possible tours mentioned above, where t(e) denotes the number of times that the edge e in G is traversed by the tour C. For the CP problem, using an algorithm to solve the maximum weighted matching problem [2], Edmonds and Johnson [3] designed an exact polynomial-time algorithm.

Frederickson et al. [4] in 1978 introduced the k-Chinese postman problem (the k-CP problem, for short), which is a generalization of the CP problem, and it is defined as follows. Given a weighted graph \(G=(V,E;w;v_{1})\) with a weight function \(w:E\rightarrow {\mathbb {R}}^{+}\), a fixed depot \(v_{1}\in V\) and an integer \(k\in {\mathbb {Z}}^{+}\), it is asked to find a set \(\mathcal{C}_{k}=\{C_{1},C_{2},\cdots , C_{k}\}\) of k tours starting and ending at the same depot \(v_{1}\), jointly traversing each edge in G at least once. The objective is to minimize the weight \(w_{\max }(\mathcal{C}_{k})=\max \{w(C_{i})\,\vert \,C_{i}\in \mathcal{C}_{k}\}\) among all k tours, where \(w(C_{i})=\sum _{e\in C_{i}}c(e)\) for each \(i=1,2,\cdots ,k\). Although the CP problem is solvable by the exact algorithm due to Edmonds and Johnson [3], Frederickson et al. [4] showed that the k-CP problem is NP-complete for the case \(k\geqslant 2\), and using a splitting technique, they designed a \((2-\frac{1}{k})\)-approximation algorithm to solve the k-CP problem. For other different arc routings and related problems, we can find considerable number of approximation algorithms in these references [5,6,7,8,9,10,11].

In network design, it is often of interest to know how sensitive a particular property of a network is with respect to changes in the graph structure, like the removal or failure of edges or vertices. One natural measure of sensitivity is to compute the maximum change of the property when some limited set of edges or vertices is being removed, which leads to a class of problems referred to as the interdiction problems. The interdiction problems have been employed in a wide variety of settings, these problems involve many practical applications in real life, such as military planning [12], hospital infection control [13], drug interdiction [14], infrastructure protection [15] and electric power grids protection [16].

Many edge interdiction problems may be formulated as follows. Given a weighted graph \(G=(V,E;w,c)\) with a weight function \(w:E\rightarrow {\mathbb {R}}^{+}\), an interdiction cost function \(c:E\rightarrow {\mathbb {Z}}^{+}\), and a budget \(B\in {\mathbb {N}}\), it is asked to determine a subset \(E'\subseteq E\) satisfying \(c(E')=\sum _{e\in E'}c(e) \leqslant B\). The objective is to maximize the change of some existing property (i.e., the optimal value of some optimization problem) between the original graph G and the residual subgraph \(G\backslash E'\), where \(G\backslash E'\) is the subgraph of G only by deleting the edges in \(E'\) from G. Similarly, the interdiction problems of vertices in undirected graphs may be formulated in the view to use a certain set of vertices to substitute for a subset of edges in the edge interdiction problems. Given many different existing properties, these interdiction problems have been studied extensively, including the minimum spanning tree interdiction problem [17,18,19,20,21], the maximum matching interdiction problem [22,23,24], the shortest path interdiction problem [25,26,27], the maximum s-t flow interdiction problem [14, 28, 29] and the connectivity interdiction (minimum cut interdiction) problem [30]. It is well known that most of these problems are NP-complete [18, 22, 26, 29, 30], even in some special versions.

In recent years, many approximation algorithms have been designed to solve some aforementioned interdiction problems. Using linear programming and rounding techniques, Dinitz and Gupta [23] in 2013 presented an O(1)-approximation algorithm to solve the maximum matching interdiction problem. Employing an algorithm for solving the budgeted minimum cut problem [31], Zenklusen [30] in 2014 gave a polynomial-time approximation scheme (PTAS) to solve the connectivity interdiction problem. Using a greedy algorithm for extracting a good interdiction set from one that exceeds the interdiction budget, Zenklusen [20] in 2015 designed a 14-approximation algorithm to solve the minimum spanning tree interdiction problem. Considering the tree knapsack problem [32] to extract a good interdiction set, Linhares and Swamy [21] in 2017 designed a 4-approximation algorithm to resolve the minimum spanning tree interdiction problem. In particular, Smith and Song [33] in 2020 presented a survey of network interdiction models and algorithms. However, as far as we know, there are no approximation algorithms with constant performance ratios to solve the interdiction versions of the arc routing problems.

In real life, it is necessary to rescue persons on some roads of a network who are about to suffer from natural disasters. Now, we may consider the question as follows. Given k vehicles that are used to rescue persons on some roads of a network, it is necessary to arrange these k vehicles starting and ending at the same depot such that they jointly traverse each road of this network at least once. In order to minimize the rescuing-time span as short as possible, we would choose a limited set of roads from this network, whose removal causes to decrease maximum of rescuing-time span, equivalently, these k vehicles do not need to jointly traverse these limited roads removed. And then, we determine k routings of these k vehicles to jointly traverse each road in this residual network, transfer persons in need to the fixed depot, avoid traversing these limited roads removed. The question must be raised in the following way: which limited roads of this network are chosen for removal?

Motivated by this interesting question, the aforementioned interdiction problems and the k-CP problem, we want to find a limited set of edges for removal so that the optimal value of the k-CP problem on the remaining graph is as small as possible, then we address the k-Chinese postman problem under interdiction budget constraints (the k-CPIBC problem, for short). Specifically, given a weighted connected graph \(G=(V, E;w,c;v_{1})\) equipped with a weight function \(w:E\rightarrow {\mathbb {R}}^{+}\) that satisfies the triangle inequality, an interdiction cost function \(c:E\rightarrow {\mathbb {Z}}^{+}\), a fixed depot \(v_{1}\in V\), an integer \(k\in \mathbb Z^{+}\) and a budget \(B\in {\mathbb {N}}\), we are asked to find a subset \(S_{k}\subseteq E\) such that \(c(S_{k})=\sum _{e\in S_{k}}c(e)\leqslant B\) and that the subgraph \(G\backslash S_{k}\) is connected, where \(G\backslash S_{k}\) is the subgraph of G only by deleting all edges in \(S_{k}\) from G. The objective is to minimize the value \(\min _{\mathcal{C}_{E\backslash S_{k}}}\max \{w(C_{i})\,\vert \,C_{i}\in \mathcal{C}_{E\backslash S_{k}}\}\) among all aforementioned subsets \(S_{k}\), i.e., \(\min _{S_{k}}\min _{\mathcal{C}_{E\backslash S_{k}}}\max \{w(C_{i})\,\vert \,C_{i}\in \mathcal{C}_{E\backslash S_{k}}\}\), where \(\mathcal{C}_{E\backslash S_{k}}\) is a set of k-tours starting and ending at the same depot \(v_{1}\), jointly traversing each edge in \(G\backslash S_{k}\) at least once, and \(w(C_{i})=\sum _{e\in C_{i}}c(e)\) for each tour \(C_{i}\in \mathcal{C}_{E\backslash S_{k}}\). For convenience, such a set of these k-tours, denoted by \(\mathcal{C}_{E\backslash S_{k}}\), is called as a k-tours covering of the subgraph \(G\backslash S_{k}\).

Now, there are three comments to be presented: (1) Whenever the budget B is less than the value \(\min \{c(e)\) \(\vert \) \(e\in E\}\), the k-CPIBC problem reduces to the k-CP problem, implying that the k-CPIBC problem is NP-complete for the case \(k\geqslant 2\). (2) We can prove that the 1-CPIBC problem is NP-complete (see Theorem 1). (3) Whenever a cost function \(c(\cdot )\) satisfies \(c(e)\equiv 1\) for each edge e in the connected graph G, we refer to this version of the k-CPIBC problem as the k-Chinese postman problem under interdiction cardinality constraints (the k-CPICC problem, for short).

As far as we know, the k-CPIBC problem and the related problems have not been considered in the literature works. We shall design some approximation algorithms to solve this new problem and its special version in the sequel. We hope that these problems will have many further practical applications in real life.

The remainder of this paper is organized into the following sections. In Sect. 2, we present some terminologies and notations to state descriptions of approximation algorithms and some fundamental lemmas to ensure the correctness of our algorithms. In Sect. 3, given an \(\alpha \)-approximation algorithm to solve the minimization knapsack problem, we design an \((\alpha +\beta )\)-approximation algorithm to solve the k-CPIBC problem, where \(\lfloor \frac{1}{k} \rfloor \) is the greatest integer less than or equal to \(\frac{1}{k}\) and \(\beta =\frac{7}{2}-\frac{1}{k}-\lfloor \frac{1}{k}\rfloor \). In Sect. 4, we present a \(\beta \)-approximation algorithm to solve the k-CPICC problem, where \(\beta \) is defined as mentioned above. In Sect. 5, we provide our conclusion and further research.

2 Preliminaries

In order to clearly present our approximation algorithms to solve the k-CPIBC problem, we provide some terminologies, notations and fundamental lemmas in the sequel, most of which are standard.

If no confusion, given a graph \(G=(V,E)\), we may denote \(n=\vert V\vert \) and \(m=\vert E\vert \) to be the numbers of vertices and edges in G, respectively. For a real number r, denote \(\lfloor r\rfloor \) to be the greatest integer less than or equal to r.

Given a graph \(G=(V,E)\), a graph \(G'=(V',E')\) is called as a subgraph of G if \(V'\subseteq V\) and \(E'\subseteq E\). In addition, if \(V'=V\), then \(G'=(V',E')\) is called a spanning subgraph of G. If \(E'=\{uv \in E\,\vert \,u,v\in V'\}\), the subgraph \(G[V']=(V',E')\) is called as the subgraph induced by \(V'\). Similarly, if \(V'=\{u,v\in V\,\vert \, uv\in E'\}\), we call \(G[E']=(V',E')\) as the subgraph induced by \(E'\). For a subset \(E'\subseteq E\) in G, denote \(G\backslash E'=(V,E\setminus E')\).

Given two vertices \(v_{i_1}\), \(v_{i_{k+1}}\) in the graph \(G=(V, E)\), a walk P connecting \(v_{i_1}\) and \(v_{i_{k+1}}\) is an alternating sequence \(\pi = v_{i_1}e_{i_1}v_{i_2}e_{i_2}v_{i_3}\cdots v_{i_{k}}e_{i_{k}}v_{i_{k+1}}\) such that, for each integer \(1\leqslant j\leqslant k\), two end-vertices of edge \(e_{i_j}\) are \(v_{i_{j}}\) and \(v_{i_{j+1}}\). A walk P is called as a tour with k edges if \(v_{i_1}=v_{i_{k+1}}\). A walk P is said to be a path if the vertices in P are all distinct. Similarly, we call a tour C a cycle if the vertices in C are all distinct. In addition, a Hamiltonian cycle C is a cycle that traverses each vertex \(v\in V\) exactly once, and an Euler tour C is a tour that traverses each edge \(e\in E\) exactly once. We call a graph G to be an Eulerian graph if G admits an Euler tour.

A graph \(G=(V, E)\) is called to be connected if, for each pair of distinct vertices \(x,y\in V\), there exists a path \(P_{xy}\) connecting x and y. For a vertex \(v\in V\), the degree \(d_{G}(v)\) of vertex v is the number of edges which are incident to v. We call v an even-degree vertex if \(d_{G}(v)\) is even, otherwise v is said to be an odd-degree vertex. In addition, a matching M is a set of vertex-disjoint edges, and M is called a perfect matching if the vertices in V are all covered by M. Moreover, for a weighted graph \(G=(V, E;w)\), M is called a minimum-weight perfect matching if M is a perfect matching and \(w(M)=\sum _{e\in M}w(e)\) is minimized among all perfect matchings in G.

Given a weighted graph \(G=(V,E;w;v_{1})\) with a fixed depot \(v_{1}\in V\) and an integer \(k\in {\mathbb {Z}}^{+}\), a k-tours covering in G is a set of k tours starting and ending at the same depot \(v_{1}\), jointly traversing each edge in G at least once. An optimal k-tours covering in G is a k-tours covering such that the maximum value of the weights of such k tours is minimized among all k-tours coverings in G. Given a set \(S\subseteq E\), we then denote \(\mathcal{C}^{k}_{S}\) as an optimal k-tours covering in the induced subgraph G[S] and \(w_{\max }(\mathcal{C}^{k}_{S})=\max \{w(C_{i})\,\vert \, C_{i}\in \mathcal{C}^{k}_{S}\}\) as the weight of such a k-tours covering \(\mathcal{C}^{k}_{S}\) for G[S]. In particular, we have \(w(\mathcal{C}^{1}_{S})= w_{\max }(\mathcal{C}^{1}_{S})\).

For convenience, we denote an instance of the k-CPIBC problem as a given weighted graph \(G=(V, E;w,c;v_{1})\) with an integer \(k\in {\mathbb {Z}}^{+}\) and a budget \(B\in {\mathbb {N}}\), where \(w:E\rightarrow {\mathbb {R}}^{+}\) is a weight function that satisfies the triangle inequality, \(c:E\rightarrow {\mathbb {Z}}^{+}\) is an interdiction cost function and \(v_{1}\in V\) is a fixed depot. If there exists a subset \(S_{k}\subseteq E\) such that \(c(S_{k})\leqslant B\) and that the subgraph \(G\setminus S_{k}\) is connected, implying that there exists a k-tours covering in \(G\setminus S_{k}\), then we call the subset \(S_{k}\subseteq E\) to be a feasible solution to the graph G for the k-CPIBC problem.

When we design approximation algorithms to solve the k-CPIBC problem, we shall use the following lemmas.

Lemma 1

Given a weighted connected graph \(G=(V, E;w,c;v_{1})\) as an instance of the k-CPIBC problem and the m-CPIBC problem, respectively, if \(k\geqslant m\), then the k-CPIBC problem is equivalent to the m-CPIBC problem, where \(m=\vert E\vert \).

Proof

Given an instance \(G=(V, E;w,c;v_{1})\) of the k-CPIBC problem and the m-CPIBC problem, respectively, we may first prove that \(S'\) is a feasible solution to G for the k-CPIBC problem with the value \(w_{\max }(\mathcal{C}^{k}_{E\setminus S'})\) if and only if \(S'\) is a feasible solution to G for the m-CPIBC problem with the value \(w_{\max }(\mathcal{C}^{m}_{E\setminus S'})\). In fact, if \(S'\) is a feasible solution to G for the k-CPIBC problem, we have \(c(S')\leqslant B\) and that the subgraph \(G{\setminus } S'\) is connected, implying that there exists an m-tours covering in \(G\setminus S'\) by the fact that there is an optimal tour to \(G\setminus S'\) for the Chinese postman problem [3], then \(S'\) is a feasible solution to the graph G for the m-CPIBC problem. And vice versa.

Secondly, we may prove that \(w_{\max }(\mathcal{C}^{k}_{E{\setminus } S'})=w_{\max }(\mathcal{C}^{m}_{E{\setminus } S'})\). For each integer \(k'\geqslant \vert E\setminus S'\vert \), since \(\mathcal{C}^{k'}_{E{\setminus } S'}\) is an optimal \(k'\)-tours covering in the subgraph \(G\setminus S'\), it is easy to conclude that \(w_{\max }(\mathcal{C}^{k'}_{E{\setminus } S'})=\max \{w(P'_{v_{1},v_{i}})+w(v_{i}v_{j})+w(P'_{v_{j},v_{1}})\mid v_{i}v_{j}\in E{\setminus } S'\}\), where \(P'_{x,y}\) is a shortest path from x to y in \(G\setminus S'\). By the assumption \(k\geqslant m= \vert E\vert \geqslant \vert E{\setminus } S'\vert \), we obtain \(w_{\max }(\mathcal{C}^{k}_{E{\setminus } S'})=w_{\max }(\mathcal{C}^{m}_{E{\setminus } S'})= \max \{w(P'_{v_{1},v_{i}})+w(v_{i}v_{j})+w(P'_{v_{j},v_{1}})\mid v_{i}v_{j}\in E{\setminus } S'\}\). Thus, the k-CPIBC problem is equivalent to the m-CPIBC problem.

This completes a proof of the lemma.

For convenience, using Lemma 1, we may assume that \(k\leqslant m\) in each instance of the k-CPIBC problem.

For a weighted connected graph \(G=(V, E;w)\) with two distinct vertices \(v_i, v_j\in V\), using the Dijkstra algorithm [34] to solve the shortest path problem, we can construct a shortest \(v_i\)-\(v_j\) path in G.

Lemma 2

[34] Given a weighted graph \(G=(V, E;w)\) with two vertices \(v_i, v_j\in V\), the Dijkstra algorithm can either produce a shortest \(v_i\)-\(v_j\) path in G or show no such a path, and this algorithm runs in time \(O(n^{2})\).

Given a weighted connected graph \(G=(V,E;w)\) and a subset \(F_{1}\subseteq E\), modifying the MST algorithm in [34, 35] to solve the minimum spanning tree problem, we can determine a minimum-weight subset \(F_{2}\subseteq E\) such that the induced subgraph \(G[F_{1}\cup F_{2}]\) is a connected spanning subgraph of G.

Lemma 3

[34, 35] Given a weighted connected graph \(G=(V,E;w)\) and a subset \(F_{1}\subseteq E\), the MST algorithm can determine a minimum-weight subset \(F_{2}\subseteq E\) such that \(G[F_{1}\cup F_{2}]\) is a connected spanning subgraph of G, and this algorithm runs in time \(O(n^{2})\).

Given a weighted connected graph \(G=(V,E;w)\), we can use the Floyd algorithm [36] to construct all shortest paths among all vertices in G.

Lemma 4

[36] The Floyd algorithm can produce all shortest paths among all vertices in G, and this algorithm runs in time \(O(n^{3})\).

Given a weighted connected graph \(G=(V,E;w)\), using a simple shrinking technique, Edmonds [2] in 1965 designed an exact algorithm in time \(O(n^{3})\) to produce a minimum-weight perfect matching in G. In addition, using a complicated data structure for blossom creation, Gabow [37] in 2018 presented an exact algorithm in lower time \(O(n(m+n\log n))\) to determine a minimum-weight perfect matching in G. It is sufficient for us to use the Edmonds algorithm [2] as a subroutine to solve the k-CPIBC problem.

Lemma 5

[2] The Edmonds algorithm can produce a minimum-weight perfect matching in G, and this algorithm runs in time \(O(n^{3})\).

Given an Eulerian graph \(G=(V, E)\), we can use the Euler algorithm [3] to determine an Euler tour in G.

Lemma 6

[3] Given an Eulerian graph \(G=(V, E)\), the Euler algorithm can produce an Euler tour in G, and this algorithm runs in time O(m).

We need the definition of K-tree in a connected graph \(G=(V,E)\) [38]. For a nonnegative integer K, a spanning K-tree in G is a connected spanning subgraph \(T_{K}=(V, E_{K})\) with \(\vert E_{K}\vert =n+K-1\) edges in G. In fact, one 0-tree is exactly a spanning tree of G. Given a weighted connected graph \(G=(V,E;w)\) with a weight function \(w:E\rightarrow {\mathbb {R}}^{+}\) and an integer \(B\in {\mathbb {N}}\), using the Fisher algorithm [38] to construct a minimum-weight spanning K-tree with \(K=\max \{m-B-(n-1),0\}\), we can determine a minimum-weight connected spanning subgraph \(T_{K}=(V, E_{K})\) with \(\vert E_{K}\vert \geqslant m-B\).

Lemma 7

[38] Given a weighted connected graph \(G=(V, E;w)\) and an integer \(B\in {\mathbb {N}}\), the Fisher algorithm can produce a minimum-weight connected spanning subgraph \(T_{K}=(V, E_{K})\) with \(\vert E_{K}\vert \geqslant m-B\) in G, and this algorithm runs in time \(O(n^{2})\).

3 The k-Chinese Postman Problem Under Interdiction Budget Constraints

In this section, we consider the k-CPIBC problem. By using the definition of the k-CPIBC problem, whenever the budget B is less than the value \(\min \{c(e)\,\vert \, e\in E\}\), the k-CPIBC problem reduces to the k-CP problem, implying that the k-CPIBC problem is NP-complete for the case \(k\geqslant 2\).

However, unlike the 1-CP problem (i.e., Chinese postman problem), which is solvable in polynomial time [3], we have the following result for the 1-CPIBC problem.

Theorem 1

The 1-CPIBC problem remains NP-complete, even if an interdiction cost function \(c:E\rightarrow {\mathbb {Z}}^{+}\) satisfies \(c(e)\equiv 1\) for each edge e in a weighted connected graph \(G=(V, E;w,\textbf{1};v_{1})\), where \(v_{1}\) is a fixed vertex in G.

Proof

The reduction is transformed from the Hamiltonian cycle (HC) problem, where the HC problem is to determine whether a given connected graph \(G=(V,E)\) would contain a cycle traversing each vertex in G exactly once. However, the HC problem is NP-complete [39].

Without loss of generality, we may assume that \(m\geqslant n\), otherwise G is a tree by our assumption, implying that G is a “NO”-instance. Given an instance \(G=(V,E)\) of the HC problem, we construct an instance \(H=(V, E;w,c;v_{1})\) of the 1-CPIBC problem by adding a weight function \(w:E\rightarrow \{1\}\), an interdiction cost function \(c:E\rightarrow \{1\}\) and a budget \(B= m-n\), where \(v_{1}\in V\) is a fixed vertex. It is straightforward to obtain the fact that G is a “YES”-instance if and only if the optimal value OPT to the instance H for the 1-CPIBC problem is exactly n, i.e., OPT\(=n\). Thus, the 1-CPIBC problem is NP-complete.

This completes a proof of the theorem.

In order to efficiently design an approximation algorithm to solve the k-CPIBC problem, we intend to consider the minimization knapsack problem (the MinKP problem, for short) [40, 41], which is defined as follows. Given a set \(X=\{x_{1},x_{2},\cdots ,x_{q}\}\) of q items with a weight function \(u:X\rightarrow {\mathbb {R}}^{+}\), a cost function \(s:X\rightarrow {\mathbb {R}}^{+}\), and a constant D, it is asked to find a subset \(X'\subseteq X\) to have \(u(X')=\sum _{x\in X'} u(x)\geqslant D\), the objective is to minimize \(s(X')=\sum _{x\in X'} s(x)\). For convenience, we always use \(I=(X;u,s)\) to denote an instance of the MinKP problem.

Given a weighted connected graph \(G=(V,E;w,c)\) with a weight function \(w:E\rightarrow {\mathbb {R}}^{+}\), an interdiction cost function \(c:E\rightarrow {\mathbb {Z}}^{+}\), and an integer \(B\in {\mathbb {N}}\), we construct an instance \(I=(X;u,s)\) of the MinKP problem in the following ways. Denote \(X=\{x_{e}\,\vert \, e\in E\}\) and a constant \(D=c(E)-B\). For each item \(x_{e}\in X\), denote \(u(x_{e})=c(e)\) and \(s(x_{e})=w(e)\), respectively. Using an \(\alpha \)-approximation algorithm \(\mathcal{A}_{\alpha }\) in [40,41,42,43] to solve the MinKP problem, we can determine a subset \(X'\subseteq X\) with \(u(X')\geqslant c(E)-B\) and \(s(X')\leqslant \alpha \cdot s(X^{*})\), where \(X^{*}\) is an optimal solution to the instance I for the MinKP problem.

Given a subset \(X'\) of the aforementioned instance \(I=(X;u,s)\) for the MinKP problem, we can construct an edge-subset \(F_{1}=\{e\,\vert \, x_{e}\in X'\}\) of the weighted connected graph \(G=(V,E;w,c)\) to have \(c(F_{1})\geqslant c(E)-B\) and \(w(F_{1})\leqslant \alpha \cdot w(F^{*}_{1})\), where \(F^{*}_{1}\) is a minimum-weight edge-subset of G such that \(c(F^{*}_{1})\geqslant c(E)-B\).

Lemma 8

Let \(G=(V,E;w,c)\) be a connected graph with a weight function \(w:E\rightarrow {\mathbb {R}}^{+}\), a cost function \(c:E\rightarrow {\mathbb {Z}}^{+}\) and an integer \(B\in {\mathbb {N}}\). Given an \(\alpha \)-approximation algorithm \(\mathcal{A}_{\alpha }\) to solve the MinKP problem, we can determine a subset \(F_{1}\subseteq E\) with \(c(F_{1})\geqslant c(E)-B\) and \(w(F_{1})\leqslant \alpha \cdot w(F^{*}_{1})\), where \(F^{*}_{1}\) is a minimum-weight edge-subset such that \(c(F^{*}_{1})\geqslant c(E)-B\).

Proof

For a weighted graph \(G=(V,E;w,c)\), we construct an instance \(I=(X;u,s)\) for the MinKP problem as mentioned above. Suppose that \(X^{*}\) is an optimal solution to the instance I for the MinKP problem and that \(F^{*}_{1}\) is a minimum-weight edge-subset of G such that \(c(F^{*}_{1})\geqslant c(E)-B\). Using the algorithm \(\mathcal{A}_{\alpha }\), we can determine a subset \(X'\subseteq X\) with \(u(X')\geqslant c(E)-B\) and \(s(X')\leqslant \alpha \cdot s(X^{*})\). Denoting \(F_{1}=\{e\,\vert \, x_{e}\in X'\}\), we obtain \(c(F_{1})=u(X')\geqslant c(E)-B\).

Since \(F^{*}_{1}\) is a minimum-weight edge-subset such that \(c(F^{*}_{1})\geqslant c(E)-B\), we obtain the fact that \(X_{1}^{*}=\{x_{e}\,\vert \, e\in F^{*}_{1}\}\) is an optimal solution to the instance I for the MinKP problem. Otherwise, we may suppose, to the contrary, that we obtain \(s(X_{1}^{*})>s(X^{*})\). Then, there exists an edge-subset \(F^{*}=\{e\,\vert \, x_{e}\in X^{*}\}\) to have the properties \(c(F^{*})=u(X^{*})\geqslant c(E)-B\); however, \(w(F^{*})=s(X^{*})<s(X_{1}^{*})=w(F^{*}_{1})\), which contradicts that \(F^{*}_{1}\) is a minimum-weight edge-subset such that \(c(F^{*}_{1})\geqslant c(E)-B\). Indeed, \(X_{1}^{*}\) is an optimal solution to the instance I for the MinKP problem, implying \(s(X_{1}^{*})=s(X^{*})\).

Since \(s(X')\leqslant \alpha \cdot s(X^{*})\) by the algorithm \(\mathcal{A}_{\alpha }\) to solve the MinKP problem, we obtain the following:

$$\begin{aligned} w(F_{1})=s(X')\leqslant \alpha \cdot s(X^{*})=\alpha \cdot s(X_{1}^{*})=\alpha \cdot w(F^{*}_{1}). \end{aligned}$$

This completes a proof of the lemma.

We now consider the tour augmentation (TA, for short) problem, which is defined as follows. Given a weighted connected graph \(G=(V, E;w;v_{1})\) with a depot \(v_{1}\in V\), a weight function \(w:E\rightarrow {\mathbb {R}}^{+}\), an integer \(k\in {\mathbb {Z}}^{+}\) and a tour \(C=v_{1} v_{i_{1}}v_{i_{2}}\cdots v_{i_{t}}v_{1}\) that traverses each vertex v in G at least once, it is asked to find a subset \(F_{4}\subseteq E\) such that the weight of the optimal k-tours covering in the induced subgraph \(G[E(C)\cup F_{4}]\) is minimized, i.e., \(\min _{F_{4}}w_{\max }(\mathcal{C}^{k}_{E(C)\cup F_{4}})\).

Using a splitting technique in [4] to solve the k-CP problem, we design an algorithm, denoted by the TA algorithm, to solve the TA problem, which is described as follows.

figure a

Executing the TA algorithm, we obtain the following.

Lemma 9

Given an instance of the tour augmentation problem, the TA algorithm can produce an edge-subset \(F_{4}\) such that there exists a k-tours covering \(\{C_{j}\,\vert \, j=1,2,\cdots , k\}\) in \(G[E(C)\cup F_{4}]\) satisfying \(w(C_{j})\leqslant \frac{1}{k}\cdot (w(C)-2w_{0})+4w_{0}\) for each integer \(j\in \{1, 2,\cdots , k\}\), where \(w_{0}\) is defined at Step 1 in the TA algorithm, and this algorithm runs in time \(O(n^{3})\).

Proof

When \(k=1\), using the TA algorithm, we have \(F_{4}=\varnothing \) and that C is still a 1-tour covering in \(G[E(C)\cup F_{4}]\), then we obtain \(w(C)\leqslant w(C)+2w_{0}= \frac{1}{1}\cdot (w(C)-2w_{0})+4w_{0}\).

When \(k\geqslant 2\), using the TA algorithm, we construct a k-tours covering \(\{C_{j}\,\vert \, j=1,2,\cdots , k\}\) in the subgraph \(G[E(C)\cup F_{4}]\) induced by \(E(C)\cup F_{4}\) as follows.

  1. (1)

    We construct k walks in the following ways: \(Q_{1}=C[v_{1},v_{i_{p(1)}}]=v_{1} v_{i_{1}}\cdots v_{i_{p(1)}}\), \(Q_{2}\) \(=C[v_{i_{p(1)}},v_{i_{p(2)}}]\) \(=v_{i_{p(1)}}\cdots v_{i_{p(2)}}\), \(\cdots \), \(Q_{k}=C[v_{i_{p(k-1)}},v_{1}]=v_{i_{p(k-1)}}\cdots v_{i_{t}}v_{1}\);

  2. (2)

    Denote \(C_1=Q_1\circ P_{v_{i_{p(1)}},v_1}\), \(C_k=P_{v_{1},v_{i_{p(k-1)}}}\circ Q_{k}\), and for each integer \(j\in \{2,\cdots , k-1\}\), we can augment \(Q_{j}\), adding two shortest paths \(P_{v_1,v_{i_{p(j-1)}}}\) and \(P_{v_1,v_{i_{p(j)}}}\) from \(\mathcal{P}=\{P_{v_{1}, u}\,\vert \, u\in V\}\) to connect \(v_{1}\) to the initial vertex \(v_{i_{p(j-1)}}\) and the terminal vertex \(v_{i_{p(j)}}\) of the walk \(Q_{j}\), to become a tour \(C_j\), i.e., \(C_j=P_{v_1,v_{i_{p(j-1)}}}\circ Q_j\circ P_{v_{i_{p(j)}},v_1}\). It is easy to verify that \(\{C_{j}\,\vert \, j=1,2,\cdots , k\}\) is a k-tours covering in \(G[E(C)\cup F_{4}]\).

Now, we first consider the tour \(C_{j}\) for each integer \(j\in \{2,\cdots , k-1\}\). Since the weight function \(w(\cdot )\) on set of edges in G satisfies the triangle inequality, depending on the definition of \(w_{0}\), which is maximum weight of paths in \(\mathcal{P}\) defined at Step 1 of the TA algorithm, we obtain the following:

$$\begin{aligned} w(v_{i_{q(j)}}v_{i_{q(j)+1}})\leqslant w\big (P_{v_{i_{q(j)}},v_{1}}\big )+w\big (P_{v_{1},v_{i_{q(j)+1}}}\big )\leqslant 2w_{0}, \end{aligned}$$

implying

$$\begin{aligned} w(P_{v_{1},v_{i_{q(j)}}})+w(v_{i_{q(j)}} v_{i_{q(j)+1}})+w(P_{v_{i_{q(j)+1}},v_{1}})\leqslant 4w_{0}. \end{aligned}$$

Then, we obtain the following:

$$\begin{aligned} \min \left\{ w(P_{v_{1},v_{i_{q(j)}}})+R_{j}, w(v_{i_{q(j)}} v_{i_{q(j)+1}})-R_{j}+w(P_{v_{i_{q(j)+1}},v_{1}})\right\} \leqslant 2w_{0}. \end{aligned}$$

Similarly, we obtain the following:

$$\begin{aligned} \min \left\{ w(P_{v_{1},v_{i_{q(j-1)}}})+R_{j-1}, w(v_{i_{q(j-1)}} v_{i_{q(j-1)+1}})-R_{j-1}+w(P_{v_{i_{q(j-1)+1}},v_{1}})\right\} \leqslant 2w_{0}. \end{aligned}$$

Using the TA algorithm, we obtain the worst case where the weight of \(C_{j}\) is maximized only when this tour \(C_{j}\) starts at the depot \(v_{1}\), reaching the vertex \(v_{i_{q(j-1)}}\) along the shortest path \(P_{v_{1}, v_{i_{q(j-1)}}}\), going to \(v_{i_{q(j)+1}}\) along C, and finally ends at the depot \(v_{1}\) along the shortest path \(P_{v_{i_{q(j)+1}}, v_{1}}\).

In the worst case, it is easy to see that \(w(P_{v_{1},v_{i_{q(j-1)}}})+R_{j-1}\leqslant 2w_{0}\) and \(w(v_{i_{q(j)}}v_{i_{q(j)+1}})-R_{j}+w(P_{v_{i_{q(j)+1}},v_{1}})\leqslant 2w_{0}\), then we obtain the following:

$$\begin{aligned} w(C_{j})\leqslant & {} 2w_{0}+\frac{1}{k}\cdot (w(C)-2w_{0})+2w_{0} \\= & {} \frac{1}{k}\cdot (w(C)-2w_{0})+4w_{0}. \end{aligned}$$

Similarly, we consider \(C_{j}\) for each \(j\in \{1, k\}\), and we obtain the following:

$$\begin{aligned} w(C_{j})\leqslant & {} w_{0}+\frac{1}{k}\cdot (w(C)-2w_{0})+2w_{0} \\\leqslant & {} \frac{1}{k}\cdot (w(C)-2w_{0})+4w_{0}. \end{aligned}$$

Combining the aforementioned arguments, for each \(j\in \{1, 2,\cdots , k\}\), we obtain the following:

$$\begin{aligned} w(C_{j})\leqslant \frac{1}{k}\cdot (w(C)-2w_{0})+4w_{0}. \end{aligned}$$

The running time of the TA algorithm can be determined as follows. (1) By Lemma 2, since it needs time \(O(n^{2})\) to execute the Dijkstra algorithm [34] per circulation, Step 1 constructs the set \(\mathcal{P}\) and the maximum weight \(w_{0}\) in time \(O(n^{3})\). (2) Since \(k\leqslant m\) by Lemma 1, Steps 2–3 execute in time O(mn). Hence, the TA algorithm needs whole time \(O(n^3)\).

This establishes the lemma.

Using the TA algorithm, we design an approximation algorithm to solve the k-CPIBC problem using the following strategies:

  1. (1)

    Find a subset \(F_{1}\subseteq E\), having \(c(F_{1})\geqslant c(E)-B\), such that \(w(F_{1})\) is minimized;

  2. (2)

    Find a minimum-weight subset \(F_{2}\subseteq E\), such that the induced subgraph \(G[F_{1}\cup F_{2}]\) is a connected spanning subgraph in G;

  3. (3)

    Determine a minimum-weight subset \(F_{3}\subseteq E\) such that the induced subgraph \(G[F_{1}\cup F_{2}\cup F_{3}]\) is an Eulerian graph;

  4. (4)

    Find a subset \(F_{4}\subseteq E\) such that the weight of the optimal k-tours covering in the induced subgraph \(G[F_{1}\cup F_{2}\cup F_{3}\cup F_{4}]\) is minimized;

  5. (5)

    Output the subset \(S_{k}=E{\setminus } (F_{1}\cup F_{2}\cup F_{3}\cup F_{4})\).

Our approximation algorithm, denoted by the k-CPIBC algorithm, to solve the k-CPIBC problem is described as follows.

figure b

Theorem 2

Given an \(\alpha \)-approximation algorithm \(\mathcal{A}_{\alpha }\) for solving the MinKP problem, the k-CPIBC algorithm is an \((\alpha +\beta )\)-approximation algorithm to solve the k-CPIBC problem, and this algorithm runs in time \(O(n^{3}+f(n,m))\), where f(n, m) is the running time of the algorithm \(\mathcal{A}_{\alpha }\) and \(\beta =\frac{7}{2}-\frac{1}{k}-\lfloor \frac{1}{k}\rfloor \).

Proof

Given an instance \(G=(V, E;w,c;v_{1})\) of the k-CPIBC problem, we may assume that \(S^{*}_{k}\) is an optimal solution with an optimal k-tours covering \(\mathcal{C}_{E\setminus S_{k}^{*}}^{k}\) in \(G\setminus S_{k}^{*}\) and the optimal value OPT\(_{k}=w_{\max }(\mathcal{C}_{E{\setminus } S_{k}^{*}}^{k})\). And let \(S_{k}\) (\(=E{\setminus } (F_{1}\cup F_{2}\cup F_{3}\cup F_{4})\)) denote the edge-subset produced by the k-CPIBC algorithm with a k-tours covering \(\mathcal{C}_{E\setminus S_{k}}^{k}\) in the subgraph \(G{\setminus } S_{k}\) and the output value OUT\(_{k}=w_{\max }(\mathcal{C}_{E{\setminus } S_{k}}^{k})\).

For each integer \(k\in {\mathbb {Z}}^{+}\), by Steps 1–4 of the k-CPIBC algorithm, we obtain the facts \(c(F_{1})\geqslant c(E)-B\) and that \(G[F_{1}\cup F_{2}]\) is a connected spanning subgraph in G, then we have \(c(S_{k})=\) \(c(E{\setminus } (F_{1}\cup F_{2}\cup F_{3}\cup F_{4}))\) \(\leqslant \) \(c(E{\setminus } F_{1})\) \(\leqslant \) \( c(E)-(c(E)-B)= B\) and \(G{\setminus } S_{k}\supseteq G[F_{1}\cup F_{2}]\), which implies that \(G\setminus S_{k}\) is connected. This shows that \(S_{k}\) produced by the k-CPIBC algorithm is a feasible solution to the instance \(G=(V, E;w,c;v_{1})\) of the k-CPIBC problem. We shall prove that \(\textrm{OUT}_{1}\leqslant (\alpha +\frac{3}{2})\cdot \textrm{OPT}_{1}\) for the case \(k=1\) and \(\textrm{OUT}_{k}\leqslant (\alpha +\frac{7}{2}-\frac{1}{k})\cdot \textrm{OPT}_{k}\) for the case \(k\geqslant 2\).

We consider the following two cases.

Case 1  \(k=1\)

For each optimal solution \(S^{*}_{1}\) to the graph G as an instance of the 1-CPIBC problem, we have the facts \(c(E{\setminus } S^{*}_{1})\geqslant c(E)-B\) and that \(G{\setminus } S^{*}_{1}\) is connected. Suppose that \(F_{1}^{*}\) is a minimum-weight edge-subset with \(c(F_{1}^{*})\geqslant c(E)-B\) in G. Since \(E{\setminus } S^{*}_{1}\) is an edge-subset with \(c(E{\setminus } S^{*}_{1})\geqslant c(E)-B\) in G, i.e., \(c(S^{*}_{1})\leqslant B\), we obtain \(w(F_{1}^{*})\leqslant w(E\setminus S^{*}_{1})\). Since the k-CPIBC algorithm executes the algorithm \(\mathcal{A}_{\alpha }\) for the MinKP problem to find a subset with \(F_{1}\subseteq E\), using Lemma 8, we obtain \(c(F_{1})\geqslant c(E)-B\) and \(w(F_{1})\leqslant \alpha \cdot w(F_{1}^{*})\), respectively. Then, we obtain the following:

$$\begin{aligned} w(F_{1})\leqslant \alpha \cdot w(F_{1}^{*})\leqslant \alpha \cdot w(E\setminus S^{*}_{1})\leqslant \alpha \cdot w(\mathcal{C}^{1}_{E\setminus S^{*}_{1}}). \end{aligned}$$

For the subgraph \(G[F_{1}]\), the MST algorithm [34, 35] at Step 4 produces a minimum-weight edge-subset \(F_{2}\) such that \(G[F_{1}\cup F_{2}]\) is a connected spanning subgraph in G. Since \(G\setminus S^{*}_{1}\) is connected, we obtain the fact \(w(F_{2})\leqslant w(E{\setminus } S^{*}_{1})\leqslant w(\mathcal{C}^{1}_{E{\setminus } S^{*}_{1}})\).

Using the similar arguments as in [44], we can use the tour \(\mathcal{C}^{1}_{E\setminus S^{*}_{1}}\) to construct a Hamiltonian cycle \(C_{o}=v_{j_{1}} v_{j_{2}} \cdots v_{j_{\vert V_{o}\vert }} v_{j_{1}}\) in \(H=(V_{o}, E_{H};\) \(w_{H})\), i.e., the Hamiltonian cycle \(C_{o}\) may be constructed by visiting each vertex in the orders of their occurrences first in the tour \(\mathcal{C}^{1}_{E{\setminus } S^{*}_{1}}\), satisfying \(w_{H}(C_{o})\leqslant w(\mathcal{C}^{1}_{E{\setminus } S^{*}_{1}})\). Knowing the fact that the Hamiltonian cycle \(C_{o}\) has even vertices, we can choose alternating edges from the even cycle \(C_{o}\) to construct two perfect matchings in H, denoted by \(M_{1}=\{v_{j_{i}}v_{j_{i+1}}\,\vert \, i=1,3,\cdots , \vert V_{o}\vert -1\}\) and \(M_{2}=\{v_{j_{i}}v_{j_{i+1}}\,\vert \, i=2,4, \cdots , \vert V_{o}\vert -2\}\cup \{v_{j_{\vert V_{o}\vert }}v_{j_{1}}\}\). Since Step 5 produces a minimum-weight perfect matching M in H, we obtain the fact \(w_{H}(M)\leqslant \min \{w_{H}(M_{1}), w_{H}(M_{2})\}\leqslant \frac{1}{2} w_{H}(C_{o})\), implying that \(w(F_{3})=w_{H}(M)\leqslant \frac{1}{2}w_{H}(C_{o})\leqslant \frac{1}{2} w(\mathcal{C}^{1}_{E{\setminus } S^{*}_{1}})\).

By Steps 3–5, we see that \(G[F_{1}\cup F_{2}\cup F_{3}]\) is an Eulerian graph. Since \(S_{1}=E{\setminus } (F_{1}\cup F_{2}\cup F_{3})\), it follows that \(\textrm{OUT}_{1}=w(\mathcal{C}^{1}_{E{\setminus } S_{1}})\leqslant w(F_{1})+w(F_{2})+w(F_{3})\). Thus, we obtain the following:

$$\begin{aligned} \textrm{OUT}_{1}\leqslant & {} w(F_{1})+w(F_{2})+w(F_{3}) \nonumber \\\leqslant & {} \alpha \cdot w(\mathcal{C}^{1}_{E\setminus S^{*}_{1}})+w(\mathcal{C}^{1}_{E\setminus S^{*}_{1}})+\frac{1}{2} w(\mathcal{C}^{1}_{E\setminus S^{*}_{1}}) \nonumber \\= & {} (\alpha +\frac{3}{2})\cdot w(\mathcal{C}^{1}_{E\setminus S^{*}_{1}}) \nonumber \\= & {} (\alpha +\frac{3}{2})\cdot \textrm{OPT}_{1}. \end{aligned}$$

Case 2  \(k\geqslant 2\)

Using the similar arguments in Case 1, we have \(F_{1}\cup F_{2}\cup F_{3}= E(C)\) and \(w(C)=w(F_{1})+w(F_{2})+w(F_{3})\leqslant (\alpha +\frac{3}{2})\cdot w(\mathcal{C}^{1}_{E{\setminus } S^{*}_{1}})\). We shall prove \(\textrm{OUT}_{k}\leqslant (\alpha +\frac{7}{2}-\frac{1}{k})\cdot \textrm{OPT}_{k}\) in the sequel.

Since \(F_{1}\cup F_{2}\cup F_{3}= E(C)\) by the k-CPIBC algorithm, we obtain \(G[F_{1}\cup F_{2}\cup F_{3}\cup F_{4}]=G[E(C)\cup F_{4}]\). Using the proof of Lemma 9, we can construct a k-tours covering \(\{C_{j}\,\vert \, j=1,2,\cdots , k\}\) in \(G[F_{1}\cup F_{2}\cup F_{3}\cup F_{4}]\), i.e., this k-tours covering is in \(G\setminus S_{k}\), and for each integer \(j\in \{1, 2,\cdots , k\}\), this k-tours covering satisfies \(w(C_{j})\leqslant \frac{1}{k}\cdot (w(C)-2w_{0})+4w_{0}\).

Since \(S^{*}_{1}\) is an optimal solution to the graph G as an instance of the 1-CPIBC problem and \(S^{*}_{k}\) is an optimal solution to the graph G as an instance for the k-CPIBC problem, implying that \(S^{*}_{k}\) is a feasible solution to the graph G as an instance for the 1-CPIBC problem, we obtain \(w(\mathcal{C}^{1}_{E{\setminus } S_{1}^{*}})\leqslant w(\mathcal{C}^{1}_{E{\setminus } S^{*}_{k}})\). Since all tours in the k-tours covering \(\mathcal{C}^{k}_{E{\setminus } S^{*}_{k}}\) start and end at the depot \(v_{1}\), we can easily transform them into 1-tour covering in \(G{\setminus } S_{k}^{*}\). Since \(\mathcal{C}^{1}_{E{\setminus } S_{k}^{*}}\) is an optimal 1-tour covering in \(G\setminus S_{k}^{*}\), we obtain \(w(\mathcal{C}^{1}_{E{\setminus } S_{k}^{*}})\leqslant w(\mathcal{C}^{k}_{E{\setminus } S^{*}_{k}})\leqslant k\cdot w_{\max }(\mathcal{C}^{k}_{E{\setminus } S^{*}_{k}})\), which shows that \(w(\mathcal{C}^{1}_{E{\setminus } S_{1}^{*}})\leqslant w(\mathcal{C}^{1}_{E{\setminus } S_{k}^{*}})\leqslant k\cdot w_{\max }(\mathcal{C}^{k}_{E{\setminus } S^{*}_{k}})\).

Since \(S^{*}_{k}\) is an optimal solution to the graph G as an instance of the k-CPIBC problem, we have the fact that \(G{\setminus } S^{*}_{k}\) is a connected spanning subgraph in G, which implies that the union of all tours in \(\mathcal{C}^{k}_{E\setminus S_{k}^{*}}\) must traverse each vertex \(v\in V\) at least once, then we have \(w_{0}\leqslant \frac{1}{2}w_{\max }(\mathcal{C}^{k}_{E{\setminus } S_{k}^{*}})\). Thus, for each \(j\in \{1, 2,\cdots , k\}\), we obtain the following:

$$\begin{aligned} w(C_{j})\leqslant & {} \frac{1}{k}\cdot (w(C)-2w_{0})+4w_{0} \\= & {} 2\cdot \bigg (2-\frac{1}{k}\bigg )\cdot w_{0}+\frac{1}{k}\cdot w(C) \\\leqslant & {} 2\cdot \bigg (2-\frac{1}{k}\bigg )\cdot w_{0}+\frac{1}{k}\cdot \bigg (\alpha +\frac{3}{2}\bigg )\cdot w(\mathcal{C}^{1}_{E\setminus S_{1}^{*}}) \\\leqslant & {} \bigg (2-\frac{1}{k}\bigg )\cdot w_{\max }(\mathcal{C}^{k}_{E\setminus S_{k}^{*}})+\bigg (\alpha +\frac{3}{2}\bigg )\cdot w_{\max }(\mathcal{C}^{k}_{E\setminus S^{*}_{k}})\\= & {} \bigg (\alpha +\frac{7}{2}-\frac{1}{k}\bigg )\cdot w_{\max }(\mathcal{C}^{k}_{E\setminus S_{k}^{*}})\\= & {} \bigg (\alpha +\frac{7}{2}-\frac{1}{k}\bigg )\cdot \textrm{OPT}_{k}, \end{aligned}$$

implying \(\textrm{OUT}_{k}=w_{\max }(\mathcal{C}^{k}_{E{\setminus } S_{k}})\leqslant \max \{w(C_{j})\,\vert \, j=1,2,\cdots ,k\}\leqslant (\alpha +\frac{7}{2}-\frac{1}{k})\cdot \textrm{OPT}_{k}\).

Combining the aforementioned arguments in Cases 1 and 2, we obtain the following:

$$\begin{aligned} \textrm{OUT}_{k}\leqslant (\alpha +\beta )\cdot \textrm{OPT}_{k}, \end{aligned}$$

where \(\beta =\frac{7}{2}-\frac{1}{k}-\lfloor \frac{1}{k}\rfloor \) for each integer \(k\in {\mathbb {Z}}^{+}\). This shows that the k-CPIBC algorithm is an \((\alpha +\beta )\)-approximation algorithm to solve the k-CPIBC problem.

The complexity of the k-CPIBC algorithm can be determined as follows: (1) Step 1 needs time \(O(m+n)\) to construct an instance \(I=(X;u,s)\) of the MinKP problem as mentioned above. (2) Step 2 executes the algorithm \(\mathcal{A}_{\alpha }\) in time f(n, m) to find a subset \(X'\subseteq X\). (3) Step 3 constructs a subset \(F_{1}=\{e\,\vert \, x_{e}\in X'\}\) (\(\subseteq E\)) in time O(m). (4) By Lemma 3, the MST algorithm [34, 35] at Step 4 needs time \(O(n^2)\) to compute a minimum-weight subset \(F_{2}\subseteq E\) such that \(G[F_{1}\cup F_{2}]\) is a connected spanning subgraph in G. (5) For the case where there exists an odd-degree vertex in \(G[F_{1}\cup F_{2}]\), using the Floyd algorithm [36], we can construct the graph H at Step 5 in time \(O(n^3)\) due to Lemma 4, and the Edmonds algorithm [2] at Step 5 needs time \(O(n^3)\) to produce a minimum-weight perfect matching M in H due to Lemma 5. (6) By Lemma 6, the Euler algorithm [3] at Step 7 needs time O(m) to construct an Euler tour C in \(G[F_{1}\cup F_{2}\cup F_{3}]\). (7) The TA algorithm at Step 8 needs at most time \(O(n^{3})\). Hence, the k-CPIBC algorithm needs whole time \(O(n^3+f(n,m))\).

This establishes the theorem.

4 The k-Chinese Postman Problem Under Interdiction Cardinality Constraints

In this section, we consider the k-CPIBC problem specialized to connected graphs with unit costs, i.e., the special version of the k-CPIBC problem where an interdiction cost function \(c(\cdot )\equiv 1\) holds. For convenience, we refer this version as the k-Chinese postman problem under interdiction cardinality constraints (the k-CPICC problem).

Given a graph \(G=(V, E;w,\textbf{1};v_{1})\) as an instance of the k-CPICC problem, we can choose \(m-B\) least-weight edges \(F'_{1}\) from E in time \(O(m\log m)\). And it is easy to verify that \(F'_{1}\) is a minimum-weight edge-subset with \(\vert F'_{1}\vert \geqslant m-B\) in E, implying that we may choose \(\alpha =1\) in the k-CPIBC algorithm for an interdiction cost function \(c(\cdot )\equiv 1\). Using Theorem 2, we obtain the fact that there exists a \((\beta +1)\)-approximation algorithm in running time \(O(n^{3})\) to solve the k-CPICC problem, where \(\beta =\frac{7}{2}-\frac{1}{k}-\lfloor \frac{1}{k}\rfloor \).

In addition, we use the Fisher algorithm [38] to solve the minimum-weight spanning K-tree problem, then we design a better approximation algorithm to solve the k-CPICC problem using the following strategies: (1) Determine a minimum-weight subset \(F_{1,2}\subseteq E\), such that \(\vert F_{1,2}\vert \geqslant m-B\) and that \(G[F_{1,2}]\) is a connected spanning subgraph in G; (2) find a minimum-weight subset \(F_{3}\subseteq E\), such that \(G[F_{1,2}\cup F_{3}]\) is an Eulerian graph; (3) compute a subset \(F_{4}\subseteq E\), such that the weight of the optimal k-tours covering in \(G[F_{1,2}\cup F_{3}\cup F_{4}]\) is as small as possible; and (4) output the subset \(S_{k}=E{\setminus } (F_{1,2}\cup F_{3}\cup F_{4})\).

Our approximation algorithm, denoted by the k-CPICC algorithm, for the k-CPICC problem is described as follows.

figure c

Theorem 3

The k-CPICC algorithm is a \(\beta \)-approximation algorithm to solve the k-CPICC problem, and this algorithm runs in time \(O(n^{3})\), where \(\beta =\frac{7}{2}-\frac{1}{k}-\lfloor \frac{1}{k}\rfloor \).

Proof

Given an instance \(G=(V, E;w,\textbf{1};v_{1})\) of the k-CPICC problem, we may assume that \(S^{*}_{k}\) is an optimal solution with an optimal k-tours covering \(\mathcal{C}_{E\setminus S_{k}^{*}}^{k}\) in \(G\setminus S_{k}^{*}\) and the optimal value \(\textrm{OPT}_{k}=w_{\max }(\mathcal{C}_{E\setminus S_{k}^{*}}^{k})\). And let \(S_{k}\) (\(=E\setminus (F_{1,2}\cup F_{3}\cup F_{4})\)) denote the edge-subset produced by the k-CPICC algorithm with a k-tours covering \(\mathcal{C}_{E\setminus S_{k}}^{k}\) in the subgraph \(G\setminus S_{k}\) and the output value \(\textrm{OUT}_{k}=w_{\max }(\mathcal{C}_{E{\setminus } S_{k}}^{k})\).

For each integer \(k\in {\mathbb {Z}}^{+}\), executing Step 1, we have that \(\vert S_{k}\vert =\vert E{\setminus } (F_{1,2}\cup F_{3}\cup F_{4})\vert \leqslant \vert E{\setminus } F_{1,2}\vert \leqslant m-(m-B)=B\) and \(G{\setminus } S_{k}\supseteq G[F_{1,2}]\), implying that \(G\setminus S_{k}\) is connected. This shows that \(S_{k}\) is a feasible solution to the instance G of the k-CPICC problem. We shall prove \(\textrm{OUT}_{1}\leqslant \frac{3}{2}\cdot \textrm{OPT}_{1}\) for the case \(k=1\) and \(\textrm{OUT}_{k}\leqslant (\frac{7}{2}-\frac{1}{k})\cdot \textrm{OPT}_{k}\) for the case \(k\geqslant 2\), respectively.

Case 1  \(k=1\)

For each optimal solution \(S^{*}_{1}\) to the graph G as an instance of the 1-CPICC problem, we have that \(G\setminus S^{*}_{1}\) is a connected spanning subgraph in G with \(\vert E{\setminus } S^{*}_{1}\vert \geqslant m-B\). Since \(G[F_{1,2}]\) produced at Step 1 is a minimum-weight connected spanning subgraph with \(\vert F_{1,2}\vert \geqslant m-B\) in G, we obtain the following:

$$\begin{aligned} w(F_{1,2})\leqslant w(E\setminus S^{*}_{1})\leqslant w(\mathcal{C}^{1}_{E\setminus S^{*}_{1}}). \end{aligned}$$

Using the similar arguments as in [44] and in the proof of Theorem 2, we can use \(\mathcal{C}^{1}_{E{\setminus } S^{*}_{1}}\) to construct a Hamiltonian cycle \(C_{o}=v_{j_{1}} v_{j_{2}} \cdots \) \(v_{j_{\vert V_{o}\vert }} v_{j_{1}}\) in \(H=(V_{o}, E_{H}; w_{H})\) satisfying \(w_{H}(C_{o})\leqslant w(\mathcal{C}^{1}_{E{\setminus } S^{*}_{1}})\). In addition, we can construct two perfect matchings in H, denoted by \(M_{1}=\{v_{j_{i}}v_{j_{i+1}}\,\vert \, i=1,3,\cdots , \vert V_{o}\vert -1\}\) and \(M_{2}=\{v_{j_{\vert V_{o}\vert }}v_{j_{1}}\}\cup \{v_{j_{i}}v_{j_{i+1}}\,\vert \, i=2,4, \cdots , \vert V_{o}\vert -2\} \). Since M produced at Step 2 is a minimum-weight perfect matching in H, we have \(w_{H}(M)\leqslant \min \{w_{H}(M_{1}), w_{H}(M_{2})\}\leqslant \frac{1}{2} w_{H}(C_{o})\). This implies \(w(F_{3})=w_{H}(M)\leqslant \frac{1}{2}w_{H}(C_{o})\) \(\leqslant \frac{1}{2} w(\mathcal{C}^{1}_{E{\setminus } S^{*}_{1}})\).

Using Steps 1–2, we have that \(G[F_{1,2}\cup F_{3}]\) is an Eulerian graph. And by the fact \(S_{1}=E\setminus (F_{1,2}\cup F_{3})\) produced by the k-CPICC algorithm, we have that \(\textrm{OUT}_{1}=w(\mathcal{C}^{1}_{E{\setminus } S_{1}})\leqslant w(F_{1,2})+w(F_{3})\). Thus, we obtain the following:

$$\begin{aligned} \textrm{OUT}_{1}\leqslant w(F_{1,2})+w(F_{3})\leqslant w(\mathcal{C}^{1}_{E\setminus S^{*}_{1}})+\frac{1}{2} w(\mathcal{C}^{1}_{E\setminus S^{*}_{1}})=\frac{3}{2}\cdot w(\mathcal{C}^{1}_{E\setminus S^{*}_{1}})= \frac{3}{2}\cdot \textrm{OPT}_{1}. \end{aligned}$$

Case 2  \(k\geqslant 2\)

Using the similar arguments in Case 1, we obtain \(F_{1,2}\cup F_{3}= E(C)\), and \(w(C)=w(F_{1,2})+w(F_{3})\leqslant \frac{3}{2}\cdot w(\mathcal{C}^{1}_{E{\setminus } S^{*}_{1}})\). We shall prove \(\textrm{OUT}_{k}\leqslant (\frac{7}{2}-\frac{1}{k})\cdot \textrm{OPT}_{k}\).

Since \(F_{1,2}\cup F_{3}= E(C)\) produced by the k-CPICC algorithm, we have \(G[F_{1,2}\cup F_{3}\cup F_{4}]=G[E(C)\cup F_{4}]\). Using Lemma 9, we can construct a k-tours covering \(\{C_{j}\,\vert \, j=1,2,\cdots , k\}\) in \(G[F_{1,2}\cup F_{3}\cup F_{4}]\), i.e., this k-tours covering is in \(G{\setminus } S_{k}\), and for each integer \(j\in \{1, 2,\cdots , k\}\), this k-tours covering satisfies \(w(C_{j})\leqslant \frac{1}{k}\cdot (w(C)-2w_{0})+4w_{0}\).

Using the similar arguments in the proof of Case 2 of Theorem 2, we have that \(w(\mathcal{C}^{1}_{E{\setminus } S_{1}^{*}})\leqslant w(\mathcal{C}^{1}_{E{\setminus } S_{k}^{*}})\leqslant k\cdot w_{\max }(\mathcal{C}^{k}_{E{\setminus } S^{*}_{k}})\) and \(w_{0}\leqslant \frac{1}{2}w_{\max }(\mathcal{C}^{k}_{E{\setminus } S_{k}^{*}})\). Thus, for each \(j\in \{1, 2,\cdots , k\}\), we obtain the following:

$$\begin{aligned} w(C_{j})\leqslant & {} \frac{1}{k}\cdot (w(C)-2w_{0})+4w_{0} \\= & {} 2\cdot \bigg (2-\frac{1}{k}\bigg )\cdot w_{0}+\frac{1}{k}\cdot w(C) \\\leqslant & {} 2\cdot \bigg (2-\frac{1}{k}\bigg )\cdot w_{0}+\frac{1}{k}\cdot \frac{3}{2}\cdot w(\mathcal{C}^{1}_{E\setminus S_{1}^{*}}) \\\leqslant & {} \bigg (2-\frac{1}{k}\bigg )\cdot w_{\max }(\mathcal{C}^{k}_{E\setminus S_{k}^{*}})+\frac{3}{2}\cdot w_{\max }(\mathcal{C}^{k}_{E\setminus S^{*}_{k}})\\= & {} \bigg (\frac{7}{2}-\frac{1}{k}\bigg )\cdot w_{\max }(\mathcal{C}^{k}_{E\setminus S_{k}^{*}})\\= & {} \bigg (\frac{7}{2}-\frac{1}{k}\bigg )\cdot \textrm{OPT}_{k}, \end{aligned}$$

implying \(\textrm{OUT}_{k}=w_{\max }(\mathcal{C}^{k}_{E{\setminus } S_{k}})\leqslant \max \{w(C_{j})\,\vert \, j=1,2,\cdots ,k\}\leqslant (\frac{7}{2}-\frac{1}{k})\cdot \textrm{OPT}_{k}\).

Combining the aforementioned arguments in Cases 1 and 2, we obtain the following:

$$\begin{aligned} \textrm{OUT}_{k}\leqslant \beta \cdot \textrm{OPT}_{k}, \end{aligned}$$

where \(\beta =\frac{7}{2}-\frac{1}{k}-\lfloor \frac{1}{k} \rfloor \) for each integer \(k\in {\mathbb {Z}}^{+}\).

The complexity of the k-CPICC algorithm can be determined as follows: (1) By Lemma 7, the Fisher algorithm [38] at Step 1 needs time \(O(n^2)\) to compute a minimum-weight connected spanning subgraph \(G[F_{1,2}]\) with \(\vert F_{1,2}\vert \geqslant m-B\). (2) By the similar arguments of the complexity of the k-CPIBC algorithm in Theorem 2, Steps 2–5 need at most time \(O(n^{3})\) to obtain \(F_{3}\) and \(F_{4}\), respectively. Hence, the k-CPICC algorithm needs the whole time \(O(n^{3})\).

This establishes the theorem.

5 Conclusion and Further Research

In this paper, we consider the k-Chinese postman problem under interdiction budget constraints (the k-CPIBC problem) and its special version (the k-CPICC problem) and obtain the following two main results:

  1. (1)

    Given an \(\alpha \)-approximation algorithm \(\mathcal{A}_{\alpha }\) for solving the minimization knapsack problem, we design an \((\alpha +\beta )\)-approximation algorithm to solve the k-CPIBC problem, where \(\beta =\frac{7}{2}-\frac{1}{k}-\lfloor \frac{1}{k}\rfloor \);

  2. (2)

    We present a \(\beta \)-approximation algorithm to solve the k-CPICC problem, where \(c(e)\equiv 1\) for each edge e in \(G=(V, E;w,\textbf{1};v_{1})\) and \(\beta \) is defined in (1).

In further research, we shall consider some interdiction versions of other arc routing problems.