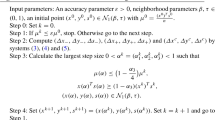A Wide-Neighborhood Predictor-Corrector Interior-Point Algorithm for Linear Complementarity Problems

Abstract

In this paper, a wide-neighborhood predictor-corrector feasible interior-point algorithm for linear complementarity problems is proposed. The algorithm is based on using the classical affine scaling direction as a part in a corrector step, not in a predictor step. The convergence analysis of the algorithm is shown, and it is proved that the algorithm has the polynomial complexity $O\left(\sqrt{n}\log \varepsilon ^{-1}\right)$ which coincides with the best known iteration bound for this class of mathematical problems. The numerical results indicate the efficiency of the algorithm.

1 Introduction

Linear complementarity problem (LCP) consists of finding a vector in a finite-dimensional real space that satisfies a certain system of inequalities. LCP is a fundamental problem in mathematical programming which includes some well-known and well-studied mathematical programming problems such as linear optimization (LO) problems and convex quadratic optimization (CQO) problems. Due to wide applications of LCPs in engineering, economics, management science, bimatrix games and other fields, LCPs have received lots of attention in recent years.

There are many approaches for solving LCPs. The book by Cottle et al. [1] is a good reference for pivoting methods to solve LCPs. Interior-point methods (IPMs) are the most efficient and powerful numerical algorithms for solving the LCPs. They have been well known as the most effective methods for solving wide classes of mathematical problems due to both theoretical and practical aspects.

After the seminal work of Karmarkar [2], IPMs for LCPs have been studied extensively. Many strong results in IPMs are obtained by using the prima-dual IPMs that are reliable both in theory and in practice. Kojima et al. [3] proposed a polynomial time algorithm for LCPs. The existence and uniqueness of the central path for LCPs were first proved by Kojima et al. [4]. Peng et al. [5] introduced a class of primal-dual IPMs based on so-called self-regular functions for LCPs.

Based on a new class of search directions, Achache [6] proposed a short-step primal-dual interior-point algorithm for monotone LCPs. Mansouri et al. [7] presented the first full-Newton step infeasible IPM for LCPs. Wang et al. [8] proposed a new full-Newton step feasible interior-point algorithm for $P_{*}(\kappa )$-LCPs and derived the currently best known iteration bound for this class of mathematical problems. Zangiabadi and Mansouri [9] improved the proposed algorithm in [7] and suggested a modified interior-point algorithm for LCPs. Mansouri and Pirhaji [10], based on a new technique for finding the search direction and the strategy of the central path, suggested a full-Newton feasible IPM for monotone LCPs.

The theoretical study of complexity is one of the key points in IPMs. The search for variant of interior-point algorithms with better complexity results led to a powerful class of IPMs. Predictor-corrector interior-point algorithms are a special class of iterative algorithms that play a key role in IPMs since they are the most efficient and applicable iterative approach among primal-dual IPMs.

The first algorithm that has divided the Newton’s directions into the affine and centering search directions is due to Mehrotra [11]. Mizuno et al. [12] presented a predictor-corrector interior-point algorithm for LO problems such that the complexity bound of their algorithm coincides with the best known one in the literature. This algorithm was first extended to $P_{*}(\kappa )$-LCPs by Miao [13]. Gurtuna et al. [14] presented a corrector-predictor interior-point algorithm for sufficient LCPs. Their algorithm is quadratically convergent, and it has the same computational complexity as Miao’s algorithm for $P_{*}(\kappa )$-LCPs.

The most of above predictor-corrector interior-point algorithms keep the iterates in the small neighborhoods of the central path. Although the use of small neighborhoods of the central path leads to the efficient theoretical algorithms, it affects actually their implementation on real problems and concludes the poor numerical results. On the other hand, it is well known that the algorithms with large neighborhoods of the central path have better performance in practice, but more poor polynomial complexity in theory.

Potra [15], using a wide neighborhood of the central path, presented two corrector-predictor interior-point algorithms for LCPs. Introducing a new wide neighborhood of the central path, Ai and Zhang [16] proposed a primal-dual path-following interior-point algorithm with $O\left(\sqrt{n}L\right)$ complexity for LCPs. This algorithm is the first wide-neighborhood algorithm that gains the same theoretical complexity as the small neighborhood algorithms for LCPs. A modified version of Ai–Zhang’s path-following algorithm [16] has been proposed by Liu et al. [17] to gain a class of Mehrotra-type predictor-corrector algorithm for LCPs. Their algorithm is based on computing a corrector direction in addition to Ai–Zhang’s direction in an attempt to improve performance.

In this paper, motivated by [18] and using the Ai–Zhang’s wide neighborhood, we propose a wide-neighborhood predictor-corrector interior-point algorithm for LCPs. In order to improve optimality, the algorithm first takes a predictor step by using the predictor search directions and moves to a larger neighborhood of the central path. Then, using the corrector directions, in an attempt for more improvement in the centrality and the optimality, the algorithm brings the iterate toward the central path, back to the smaller neighborhood of the central path from the predictor point. Different from other algorithms in the same wide neighborhood and similar to [18], we use the classical affine scaling direction as a part in a corrector step, not in a predictor step. This simplifies our analysis, contributes the complexity result and concludes the complexity $O\left(\sqrt{n}L\right)$ for the algorithm.

The reminder of the paper is organized as follows. In Sect. 2, after introducing the LCPs, we recall the Ai–Zhang’s wide neighborhood which is required in our algorithm. In Sect. 3, we describe how the predictor-corrector algorithm works in the wide neighborhood of central path. Section 4 devotes to prove the convergence analysis and polynomial complexity of the algorithm. The computational performance of the algorithm is tested in Sect. 5. Finally, the paper ends with some concluding remarks in Sect. 6.

The notations used throughout the paper are rather standard. Capital letters denote matrices, lower case letters denote vectors, script capital letters denote sets, and Greek letters denote scalars. All vectors are considered to be column vectors. The components of a vector $u\in \mathbb {R}^{n}$ are denoted by $u_i,\,i=1,\,\cdots ,\,n$. The relation $u>0$ is equivalent to $u_i>0$, for $i=1,\,\cdots ,\,n,\,$ while $u\geqslant 0$ means $u_i\geqslant 0$, for $i=1,\,\cdots ,\,n$.

For $u\in \mathbb {R}^{n}$, we use the notation $\min (u)=\min _{i}u_{i}$. If $u\in \mathbb {R}^{n}$, the notation $U:=\mathrm{diag}\,\left(u\right)$ denotes the diagonal matrix having the components of u as diagonal entries. If $u,\,v\in \mathbb {R}^{n},\,$ then uv denotes the componentwise (Hadamard) product of the vectors u and v. Furthermore, e denotes the all-one vector of length n. The positive and negative parts of a vector $u\in \mathbb {R}^{n}$ are denoted by $u^{+}:=\max \{u,0\}$ and $u^{-}:=\min \{u,0\}$ such that $u=u^{+}+u^{-}$. Finally, the 2-norm for vectors are denoted by $\left\Vert \cdot \right\Vert$.

2 The Preliminary

The monotone LCP requires to find a pair of nonnegative vectors $(x,s)\in \mathbb {R}_{+}^{2n}$ such that

$$\begin{aligned} s= Mx+q,\,~~xs=0,\,~~ \end{aligned}$$

(2.1)

where $q\in \mathbb {R}^{n}$ and M is a positive semidefinite matrix, that is, $u^\mathrm{T}Mu\geqslant 0$, for $u\in \mathbb {R}^{n}$. Denoting the feasible set of problem 2.1 by

$$\begin{aligned} \mathcal {F}:=\left\{ {\left(x,s\right)\in \mathbb {R}^{2n}_+: \quad s=Mx+q}\right\} , \end{aligned}$$

we assume that the interior feasible set

$$\begin{aligned} \mathcal {F}^{0}:=\left\{ {\left(x,s\right)\in \mathbb {R}^{2n}_{++}: \quad s=Mx+q}\right\} \end{aligned}$$

is nonempty, that is, problem 2.1 satisfies the interior-point condition (IPC).

The basic idea of feasible IPMs is based on replacing the complementarity condition $xs=0$ in 2.1 by the perturbed equation $xs=\mu e$, to get the following parameterized system

$$\begin{aligned} Mx-s+q=0,\,~~~xs=\mu e,\,~~ x,s\geqslant 0, \end{aligned}$$

(2.2)

where $\mu >0$. Kojima et al. [4] established that under IPC, system 2.2 has a unique solution for each $\mu >0$. The set of all such solutions constructs a homotopy path which is called the central path of the LCP and it is used as a guideline to the solution of LCP. Therefore, the central path of LCP is defined as

$$\begin{aligned} \mathcal {H}:=\Big \{ \left(x,s\right)\in \mathcal {F}^{0}:~ xs=\mu e\Big \}. \end{aligned}$$

(2.3)

Interior-point algorithms generate a sequence of iterates in some neighborhoods of the central path. Short-step interior-point algorithms use a small neighborhood of the central path while large-step ones work in the negative infinity neighborhood of the central path, defined by

$$\begin{aligned} \mathcal {N}_{-}^{\infty }(1-\gamma ):=\Big \{(x,s)\in \mathcal {F}^{0}: x_{i}s_{i}\geqslant \gamma \mu \Big \}, \end{aligned}$$

(2.4)

where $\gamma \in (0,1]$. The short-step methods have the best theoretical complexity in comparison with the large-step methods. The large-step methods, unlike their poor theoretical complexity, lead to the efficient algorithms in practice.

In 2005, Ai and Zhang [16] introduced a new wide neighborhood of the central path for LCPs and proved that the new wide neighborhood is larger than the neighborhood $\mathcal {N}_{-}^{\infty }(1-\gamma )$ (see [16]). Motivated by Ai and Zhang [16], we use the following neighborhood of the central path:

$$\begin{aligned} \mathcal {N}(\tau ,\beta ):=\Big \{(x,s)\in \mathcal {F}^{0}: \left\Vert \left(\tau \mu e-xs\right)^{+} \right\Vert \leqslant \beta \tau \mu \Big \}, \end{aligned}$$

(2.5)

where $\mu =\frac{x^\mathrm{T}s}{n}$ and $\beta ,\tau \in [0,1]$.

3 The Wide-Neighborhood Predictor-Corrector Algorithm

In this section, we present a predictor-corrector algorithm for LCPs. Since the algorithm is feasible, it needs an initial feasible point $(x^{0},s^{0})\in \mathcal {N}(\tau ,\beta )$. It is well known we can obtain such a starting point by using the homogeneous embedding method for monotone LCP [19].

Let $(x,s)\in \mathcal {N}(\tau ,\beta )$ be the current iterate of the algorithm. Furthermore, suppose that $\left(\tau \mu e-xs\right)^{+}$ and $\left(\tau \mu e-xs\right)^{-}$ denote the positive and negative parts of the vector $\tau \mu e-xs$, respectively. In order to improve optimality, the algorithm first moves to the larger neighborhood $\mathcal {N}(\tau ,2\beta )$ from $(x,s)\in \mathcal {N}(\tau ,\beta )$. To this end, it takes a predictor step using the following search direction system:

$$\begin{aligned} \left[ \begin{array}{cc} M &{} -I \\ S &{} X\\ \end{array} \right] \left[ \begin{array}{c} {\Delta {x}}^{-} \\ {\Delta {s}}^{-}\\ \end{array} \right] =\left[ \begin{array}{c} 0 \\ \left(\tau \mu e-xs\right)^{-}\\ \end{array} \right] . \end{aligned}$$

(3.1)

Computing the predictor search directions ${\Delta {x}}^{-}$ and ${\Delta {s}}^{-}$ by (3.1), we obtain the predictor iterate $\left(x(\alpha _{1}), s(\alpha _{1})\right)$ as follows:

$$\begin{aligned} \left(x(\alpha _{1}), s(\alpha _{1})\right):=(x,s)+\alpha _{1}({\Delta {x}}^{-},{\Delta {s}}^{-}), \end{aligned}$$

(3.2)

where $\alpha _{1}>0$ is the step size taken along the predictor directions. The best value for the step size $\alpha _{1}$ can be obtained by solving the following optimization problem:

$$\begin{aligned} \begin{array}{llllll} \text{ min }~ &{} x(\alpha _{1})^\mathrm{T}s(\alpha _{1}) \\ ~~~\text{ s.t. }~ &{} \left(x(\alpha _{1}), s(\alpha _{1})\right)\in \mathcal {N}(\tau ,2\beta ), &{}\\ &{}0< \alpha _{1} \leqslant 1.&{} \end{array} \end{aligned}$$

(3.3)

After the predictor step, assuming $\hat{\alpha }_{1}$ as the optimal solution of problem 3.3 and

$$\begin{aligned} \hat{x}=x(\hat{\alpha }_{1}), ~~\hat{s}=s(\hat{\alpha }_{1}),~~ \hat{\mu }:=\frac{\hat{x}^\mathrm{T}\hat{s}}{n}~~ \text{ and } ~~ \left(\hat{x}, \hat{s}\right)\in \mathcal {N}(\tau ,2\beta ), \end{aligned}$$

the algorithm moves back toward the slightly smaller neighborhood of the central path from the predictor point $\left(\hat{x}, \hat{s}\right)$ to improve the centrality and the optimality. To this end, the algorithm takes a corrector step using the search direction systems

$$\begin{aligned} \left[ \begin{array}{cc} M &{} -I \\ \hat{S} &{} \hat{X}\\ \end{array} \right] \left[ \begin{array}{c} {\Delta {x}}^{+} \\ {\Delta {s}}^{+}\\ \end{array} \right] =\left[ \begin{array}{c} 0 \\ \left(\tau \hat{\mu } e-\hat{x}\hat{s}\right)^{+}\\ \end{array} \right] , \end{aligned}$$

(3.4)

and

$$\begin{aligned} \left[ \begin{array}{cc} M &{} -I \\ \hat{S} &{} \hat{X}\\ \end{array} \right] \left[ \begin{array}{c} {\Delta {x}}^{a} \\ {\Delta {s}}^{a}\\ \end{array} \right] =\left[ \begin{array}{c} 0 \\ -\hat{x}\hat{s}\\ \end{array} \right] . \end{aligned}$$

(3.5)

Clearly, the above two systems have the same coefficient matrix and in spite of the fact that two linear systems have to be solved, the additional cost is very marginal. Moreover, different from other predictor-corrector algorithms, the classical affine search direction $\left({\Delta {x}}^{a},{\Delta {s}}^{a}\right)$ has been considered as a part of the corrector step not in the predictor step. This makes the reduction in duality gap even in corrector steps. However, considering $\alpha _{2}>0$ as the step size taken along the direction $\left({\Delta {x}}^{a}, {\Delta {s}}^{a}\right)$, we define

$$\begin{aligned} \left(\hat{x}(\alpha _{2}), {\hat{s}}(\alpha _{2})\right)=({\hat{x}},{\hat{s}})+({\Delta {x}}^{+},{\Delta {s}}^{+})+\alpha _{2}({\Delta {x}}^{a},{\Delta {s}}^{a}), \end{aligned}$$

(3.6)

as the corrector point with $\hat{\mu }(\alpha _{2}):=\frac{\hat{x}(\alpha _{2})^\mathrm{T} \hat{s}(\alpha _{2})}{n}$. Similar to the predictor step, the best value for the step size $\alpha _{2}$ can be obtained by the following optimization problem:

$$\begin{aligned} \begin{array}{llllll} \text{ min }~ &{} \hat{x}(\alpha _{2})^\mathrm{T}\hat{s}(\alpha _{2}) \\ ~~~\text{ s.t. }~ &{} \left(\hat{x}(\alpha _{2}), \hat{s}(\alpha _{2})\right)\in \mathcal {N}(\tau ,\beta ), &{}\\ &{}0< \alpha _{2} \leqslant 1.&{} \end{array} \end{aligned}$$

(3.7)

Let $\bar{\alpha }_{2}$ be the optimal solution of the above optimization problem. Thus,

$$\begin{aligned} \left(\bar{x},\bar{s}\right):=\left(\hat{x}(\bar{\alpha }_{2}), \hat{s}(\bar{\alpha }_{2})\right)=(\hat{x},\hat{s})+({\Delta {x}}^{+},{\Delta {s}}^{+})+\bar{\alpha }_{2}({\Delta {x}}^{a},{\Delta {s}}^{a}), \end{aligned}$$

(3.8)

and $\bar{\mu }=\frac{\bar{x}^\mathrm{T}\bar{s}}{n}$. The algorithm uses the new iterate $\left(\bar{x},\bar{s}\right)\in \mathcal {N}(\tau ,\beta )$ as a starting point in the next iteration and repeats the above procedure until an $\varepsilon$-approximate solution of the problem 2.1 is found.

Due to the monotonicity, the objective functions $x(\alpha _{1})^\mathrm{T}s(\alpha _{1})$ and $\hat{x}(\alpha _{2})^\mathrm{T}\hat{s}(\alpha _{2})$ of the optimization problems 3.3 and 3.7 are convex and monotonically decreasing in $\alpha _{1}$ and $\alpha _{2}$ (see [16]). Moreover, solving these optimization problems may be expensive from the computational point of view. Therefore, a sufficient reduction in duality gap can be considered against the maximal one. However, without loss of polynomial complexity, the plane search procedures 3.3 and 3.7 can be replaced by some line search procedures, such as the bisection method (see [17]).

Below, the generic form of the predictor-corrector interior-point algorithm is described.

4 Convergence Analysis

In this section, we prove the proposed Algorithm 1 and obtain an $\varepsilon$-approximate solution of the LCP in polynomial time complexity. To this end, we first recall some lemmas in [16] which are necessary in our analysis.

Lemma 4.1

(Proposition 3.1 in [16]) For any $u,v\in \mathbb {R}^{n}$ and $p\geqslant 1$, we have

$$\begin{aligned} \left\Vert (u+v)^{+} \right\Vert _{p}\leqslant & {} \left\Vert u^{+} \right\Vert _{p}+\left\Vert v^{+} \right\Vert _{p},\\ \left\Vert (u+v)^{-} \right\Vert _{p}\leqslant & {} \left\Vert u^{-} \right\Vert _{p}+\left\Vert v^{-} \right\Vert _{p}. \end{aligned}$$

Lemma 4.2

(Proposition 3.2 in [16]) Suppose that $(x,s)\in \mathcal {F}^{0}$ and $z+xs\geqslant 0$. Let $(\Delta x,\Delta s)$ be the solution of

$$\begin{aligned} \left[ \begin{array}{cc} M &{} -I \\ {S} &{} {X}\\ \end{array} \right] \left[ \begin{array}{c} {\Delta {x}} \\ {\Delta {s}}\\ \end{array} \right] =\left[ \begin{array}{c} 0 \\ z\\ \end{array} \right] . \end{aligned}$$

(4.1)

If $(x+t_{0}\Delta x)(s+t_{0}\Delta s)>0$ for some $0<t_{0}\leqslant 1$, then $x+t\Delta x>0$ and $s+t\Delta s>0$ for all $0\leqslant t\leqslant t_{0}$.

Lemma 4.3

(Proposition 3.5 in [16]) Let $u,v\in \mathbb {R}^{n}$ such that $u^\mathrm{T}v\geqslant 0$, and moreover, assume that $u+v=r$. Then, we have

$$\begin{aligned} \left\Vert (uv)^{-} \right\Vert _{1}\leqslant \left\Vert (uv)^{+} \right\Vert _{1}\leqslant \frac{1}{4}\left\Vert r \right\Vert ^{2}. \end{aligned}$$

By some simple calculations, we can easily obtain the following useful relationship:

$$\begin{aligned} \left\Vert (\tau \mu e-xs)^{-} \right\Vert _{1}=(1-\tau )x^\mathrm{T}s+e^\mathrm{T}(\tau \mu e-xs)^{+}. \end{aligned}$$

(4.2)

Moreover, using the second equation of system (3.1), we easily derive

$$\begin{aligned} (\tau \mu e-xs)^{-}+xs= & {} (\tau \mu e-xs)^{-}-(\tau \mu e-xs)+\tau \mu e\nonumber \\= & {} \tau \mu e-(\tau \mu e-xs)^{+}\geqslant 0. \end{aligned}$$

(4.3)

Using (3.2), the fact $e^\mathrm{T}\left({\Delta {x}^{-}}\Delta {s}^{-}\right)\geqslant 0$ and (4.3), we have for $\alpha _{1}\in (0,1]$

$$\begin{aligned} \mu (\alpha _{1})=\frac{x(\alpha _{1})^\mathrm{T}s(\alpha _{1})}{n}= & {} \frac{e^\mathrm{T}\left(xs+\alpha _{1}(x\Delta {s}^{-}+s\Delta {x}^{-})+\alpha _{1}^{2}{\Delta {x}^{-}}\Delta {s}^{-}\right)}{n}\\= & {} \frac{e^\mathrm{T}\left(xs+\alpha _{1}(\tau \mu e-xs)^{-}+\alpha _{1}^{2}{\Delta {x}^{-}}\Delta {s}^{-}\right)}{n}\\\geqslant & {} \frac{x^\mathrm{T}s+\alpha _{1}e^\mathrm{T}(\tau \mu e-xs)^{-}}{n}>0. \end{aligned}$$

Lemma 4.4

Let $\left(\Delta {x}^{-}, \Delta {s}^{-}\right)$ be the solution of system (3.1). Then,

$$\begin{aligned} \left\Vert \left(\Delta {x}^{-}\Delta {s}^{-}\right)^{-} \right\Vert \leqslant \frac{1}{4}n\mu . \end{aligned}$$

(4.4)

Proof

Using the fact $e^\mathrm{T}\left(\Delta {x}^{-}\Delta {s}^{-}\right)\geqslant 0$ and Lemma 4.3 and defining $D:=\left(XS^{-1}\right)^{\frac{1}{2}}$, we derive

$$\begin{aligned} \left\Vert \left(\Delta {x}^{-}\Delta {s}^{-}\right)^{-} \right\Vert\leqslant & {} \left\Vert \left(\Delta {x}^{-}\Delta {s}^{-}\right)^{-} \right\Vert _{1} \leqslant \left\Vert \left(\Delta {x}^{-}\Delta {s}^{-}\right)^{+} \right\Vert _{1}\\\leqslant & {} \left\Vert \left(\left(D^{-1}\Delta {x}^{-}\right)\left(D\Delta {s}^{-}\right)\right)^{+} \right\Vert _{1} \leqslant \frac{1}{4}\left\Vert {{D^{-1}\Delta {x}^{-}}+{D\Delta {s}^{-}}} \right\Vert ^{2}\\= & {} \frac{1}{4}\left\Vert \left(XS\right)^{-\frac{1}{2}}\left(S\Delta {x}^{-}+X\Delta {s}^{-}\right) \right\Vert ^{2} =\frac{1}{4}\left\Vert \left(XS\right)^{-\frac{1}{2}}\left(\tau \mu e-xs\right)^{-} \right\Vert ^{2}\\= & {} \frac{1}{4}\left\Vert \left(XS\right)^{-\frac{1}{2}}\left(xs-\tau \mu e\right)^{+} \right\Vert ^{2}\\\leqslant & {} \frac{1}{4}\left\Vert \left(XS\right)^{\frac{1}{2}} \right\Vert ^{2}=\frac{1}{4}x^\mathrm{T}s=\frac{1}{4}n\mu . \end{aligned}$$

The proof is completed.

The following lemma presents some upper and lower bounds for the parameter $\mu (\alpha _{1})$ in the predictor step.

Lemma 4.5

Let $\mu (\alpha _{1}):=\frac{x(\alpha _{1})^\mathrm{T}s(\alpha _{1})}{n}$ and $\tau \leqslant \frac{1}{8}$. Then,

$$\begin{aligned} (1-\alpha _{1})\mu \leqslant \mu (\alpha _{1})\leqslant \left( 1-\frac{5}{8}\alpha _{1}\right) \mu . \end{aligned}$$

Proof

Using (3.2), the second equation of (3.1), (4.2), the fact $a^\mathrm{T}b\leqslant \left\Vert (ab)^{+} \right\Vert _{1}$ for any $a,b\in \mathbb {R}^{n}$ and Lemma 4.4, we have

$$\begin{aligned} \mu (\alpha _{1})=\frac{x(\alpha _{1})^\mathrm{T}s(\alpha _{1})}{n}= & {} \frac{1}{n}\left(x^\mathrm{T}s+\alpha _{1}e^\mathrm{T}(\tau \mu e-xs)^{-}+\alpha _{1}^{2}e^\mathrm{T}(\Delta {x}^{-}\Delta {s}^{-})\right)\\= & {} \mu +\frac{\alpha _{1}}{n}e^\mathrm{T}(\tau \mu e-xs)^{-}+\frac{\alpha _{1}^{2}}{n}{e^\mathrm{T}(\Delta {x}^{-}\Delta {s}^{-})}\\\leqslant & {} \mu -\frac{\alpha _{1}}{n}(1-\tau )x^\mathrm{T}s+\frac{\alpha _{1}^{2}}{n}\left\Vert (\Delta {x}^{-}\Delta {s}^{-})^{+} \right\Vert _{1}\\\leqslant & {} \mu -\alpha _{1}(1-\tau )\mu +\frac{1}{4}\alpha _{1}^{2} \mu \\= & {} (1-[1-\tau -\frac{1}{4}\alpha _{1}]\alpha _{1})\mu \leqslant \left( 1-\frac{5}{8}\alpha _{1}\right) \mu , \end{aligned}$$

where the last inequality is due to assumption $\tau \leqslant \frac{1}{8}$. On the other hand, due to the fact $e^\mathrm{T}(\Delta {x}^{-}\Delta {s}^{-})\geqslant 0$, we consequently derive

$$\begin{aligned} \mu (\alpha _{1})= & {} \frac{1}{n}\left(x^\mathrm{T}s+\alpha _{1}e^\mathrm{T}(\tau \mu e-xs)^{-}+\alpha _{1}^{2}e^\mathrm{T}(\Delta {x}^{-}\Delta {s}^{-})\right)\\\geqslant & {} \frac{1}{n}\left(x^\mathrm{T}s+\alpha _{1}e^\mathrm{T}(\tau \mu e-xs)^{-}\right)\geqslant \frac{1}{n}\left(x^\mathrm{T}s+\alpha _{1}e^\mathrm{T}(-xs)\right)=(1-\alpha _{1})\mu . \end{aligned}$$

This completes the proof.

The following lemma gives a lower bound for the step size $\alpha _{1}$ satisfying (3.3).

Lemma 4.6

Let $(x,s)\in \mathcal {N}(\tau ,\beta )$ and $\beta <\frac{1}{2}$. If $\alpha _{1}=\frac{\beta \tau }{8n}$, then after a predictor step $(x(\alpha _{1}),s(\alpha _{1}))\in \mathcal {N}(\tau ,2\beta )$.

Proof

To prove the result, using the definition of wide neighborhood $\mathcal {N}(\tau ,\beta )$, we should demonstrate $\left\Vert (\tau \mu (\alpha _{1})e-x(\alpha _{1})s(\alpha _{1}))^{+} \right\Vert \leqslant 2\beta \tau \mu (\alpha _{1})$ and $(x(\alpha _{1}),s(\alpha _{1}))\in \mathcal {F}^{0}$. To this end, using (3.2), we obtain

$$\begin{aligned} \tau \mu (\alpha _{1})e-x(\alpha _{1})s(\alpha _{1})=\tau \mu (\alpha _{1})e-xs-\alpha _{1}(\tau \mu e-xs)^{-}-{\alpha _{1}^{2}}\Delta {x}^{-}\Delta {s}^{-}. \end{aligned}$$

Therefore, by Lemma 4.1, we conclude

$$\begin{aligned} \left\Vert (\tau \mu (\alpha _{1})e-x(\alpha _{1})s(\alpha _{1}))^{+} \right\Vert\leqslant & {} \left\Vert (\tau \mu (\alpha _{1})e-xs)^{+} \right\Vert +\alpha _{1}\left\Vert (\tau \mu e-xs)^{-} \right\Vert \nonumber \\&+\,\, \alpha _{1}^{2}\left\Vert \left(\Delta {x}^{-}\Delta {s}^{-}\right)^{-} \right\Vert . \end{aligned}$$

(4.5)

Using the assumption $(x,s)\in \mathcal {N}(\tau ,\beta )$ and the fact $\mu (\alpha _{1})\leqslant \mu$, we easily obtain an upper bound for the term $\left\Vert (\tau \mu (\alpha _{1})e-xs)^{+} \right\Vert$ as follows:

$$\begin{aligned} \left\Vert (\tau \mu (\alpha _{1})e-xs)^{+} \right\Vert \leqslant \left\Vert \frac{\mu (\alpha _{1})}{\mu }(\tau \mu e-xs)^{+} \right\Vert \leqslant \beta \tau \mu (\alpha _{1}). \end{aligned}$$

(4.6)

On the other hand, using (4.2), the fact $\mu (\alpha _{1})\geqslant \frac{1}{2}\mu$ for $\beta <\frac{1}{2}$ and $\alpha _{1}=\frac{\beta \tau }{8n}$, one has

$$\begin{aligned} \alpha _{1}\left\Vert (\tau \mu e-xs)^{-} \right\Vert\leqslant & {} \alpha _{1}\left\Vert (\tau \mu e-xs)^{-} \right\Vert _{1}=\alpha _{1}\left[ (1-\tau )x^\mathrm{T}s+e^\mathrm{T}(\tau \mu e-xs)^{+}\right] \nonumber \\\leqslant & {} \alpha _{1}[(1-\tau )n\mu +\sqrt{n}\beta \tau \mu ]\leqslant 2\alpha _{1}n\mu \nonumber \\\leqslant & {} 2\alpha _{1}n(2\mu (\alpha _{1}))\leqslant \frac{1}{2}\beta \tau \mu (\alpha _{1}), \end{aligned}$$

(4.7)

where the last inequality is due to $\alpha _{1}=\frac{\beta \tau }{8n}$. Finally, using Lemma 4.4, we obtain

$$\begin{aligned} \alpha _{1}^{2}\left\Vert \left(\Delta {x}^{-}\Delta {s}^{-}\right)^{-} \right\Vert \leqslant \frac{1}{4}\alpha _{1}^{2}n\mu \leqslant \frac{1}{4}\left(\frac{\beta \tau }{8n}\right)^{2}n(2\mu (\alpha _{1}))\leqslant \frac{1}{2}\beta \tau \mu (\alpha _{1}). \end{aligned}$$

(4.8)

Substituting (4.6), (4.7) and (4.8) into (4.5), we consequently derive

$$\begin{aligned} \left\Vert (\tau \mu (\alpha _{1})e-xs)^{+} \right\Vert \leqslant 2\beta \tau \mu (\alpha _{1}). \end{aligned}$$

(4.9)

To complete the proof, we need to prove $(x(\alpha _{1}),s(\alpha _{1}))\in \mathcal {F}^{0}$. The feasibility of $(x(\alpha _{1}),s(\alpha _{1}))$ is clearly concluded by system (3.1). On the other hand, due to inequality (4.9), we have $x(\alpha _{1})s(\alpha _{1})\geqslant (1-2\beta )\tau \mu (\alpha _{1})$, which means $x(\alpha _{1})s(\alpha _{1})>0$ for $\beta <\frac{1}{2}$. Therefore, due to Lemma 4.2, it can be obtained that $x(\alpha _{1})>0$ and $s(\alpha _{1})>0$. This concludes the result and ends the proof.

In following, we proceed to prove some fundamental results in corrector step and find a lower bound for the step size $\alpha _{2}$ satisfying 3.7. Consider the predictor point $\left(\hat{x},\hat{s}\right)$, and define

$$\begin{aligned} \Delta x:=\Delta x^{+}+\alpha _{2}\Delta x^{a}~~~\text{ and }~~~\Delta s:=\Delta s^{+}+\alpha _{2}\Delta s^{a}. \end{aligned}$$

(4.10)

Then,

$$\begin{aligned} \Delta x^\mathrm{T}\Delta s\geqslant 0~~~\text{ and }~~~\hat{x}\Delta s+\hat{s}\Delta x=\left(\tau \hat{\mu } e-\hat{x}\hat{s}\right)^{+}-\alpha _{2}\hat{x}\hat{s}. \end{aligned}$$

(4.11)

Lemma 4.7

Let $\left(\Delta {x}, \Delta {s}\right)$ be defined as (4.10). Then, for $\beta \leqslant \frac{1}{6}$

$$\begin{aligned} \left\Vert \left(\Delta {x}\Delta {s}\right)^{-} \right\Vert \leqslant \frac{1}{4}\beta \tau \hat{\mu }+\frac{1}{4}n\alpha _{2}^{2}\hat{\mu }. \end{aligned}$$

(4.12)

Proof

Defining $\hat{D}:=\left(\hat{X}\hat{S}^{-1}\right)^{\frac{1}{2}}$ and using (4.11) and Lemma 4.3, we have

$$\begin{aligned} \left\Vert \left(\Delta {x}\Delta {s}\right)^{-} \right\Vert\leqslant & {} \left\Vert \left(\Delta {x}\Delta {s}\right)^{-} \right\Vert _{1} \leqslant \left\Vert \left(\Delta {x}\Delta {s}\right)^{+} \right\Vert _{1}\\\leqslant & {} \left\Vert \left(\left(\hat{D}^{-1}\Delta {x}\right)\left(\hat{D}\Delta {s}\right)\right)^{+} \right\Vert _{1} \leqslant \frac{1}{4}\left\Vert {{\hat{D}^{-1}\Delta {x}}+{\hat{D}\Delta {s}}} \right\Vert ^{2}\\= & {} \frac{1}{4}\left\Vert \left(\hat{X}\hat{S}\right)^{-\frac{1}{2}}\left(\hat{S}\Delta {x}+\hat{X}\Delta {s}\right) \right\Vert ^{2}\\= & {} \frac{1}{4}\left\Vert \left(\hat{X}\hat{S}\right)^{-\frac{1}{2}}\left(\left(\tau \hat{\mu } e-\hat{x}\hat{s}\right)^{+}-\alpha _{2}\hat{x}\hat{s}\right) \right\Vert ^{2}\\\leqslant & {} \frac{1}{4}\left(\left\Vert \left(\hat{X}\hat{S}\right)^{-\frac{1}{2}}\left(\tau \hat{\mu } e-\hat{x}\hat{s}\right)^{+} \right\Vert ^{2}+\alpha _{2}^{2}\left\Vert \left(\hat{x}\hat{s}\right)^{\frac{1}{2}} \right\Vert ^{2}\right)\\\leqslant & {} \frac{1}{4}\left(\frac{\left(2\beta \tau \hat{\mu }\right)^{2}}{(1-2\beta )\tau \hat{\mu }}+\alpha _{2}^{2}n\hat{\mu }\right)\\= & {} \frac{\beta }{(1-2\beta )}\beta \tau \hat{\mu }+\frac{n}{4}\alpha _{2}^{2}n\hat{\mu }\\= & {} \frac{1}{4}\beta \tau \hat{\mu }+\frac{1}{4}n\alpha _{2}^{2}\hat{\mu }, \end{aligned}$$

where the last inequality is due to assumption $({\hat{x}},{\hat{s}})\in \mathcal {N}(\tau ,2\beta )$ and last equality follows from $\beta \leqslant \frac{1}{6}$. The result is derived.

Lemma 4.8

Let ${\hat{\mu }}(\alpha _{2}):=\frac{{\hat{x}}(\alpha _{2})^\mathrm{T}{\hat{s}}(\alpha _{2})}{n}$ and $\beta \leqslant \frac{1}{6}$. If $\alpha _{2}=\frac{3\beta \tau }{\sqrt{n}}$, then

$$\begin{aligned} (1-\alpha _{2})\hat{\mu }\leqslant \hat{\mu }(\alpha _{2})\leqslant \left( 1-\frac{\beta \tau }{4\sqrt{n}}\right) \hat{\mu }. \end{aligned}$$

Proof

Using (3.6), (4.10), (4.11) and Lemma 4.7, we have

$$\begin{aligned} \hat{\mu }(\alpha _{2})=\frac{1}{n}{\hat{x}(\alpha _{2})^\mathrm{T}\hat{s}(\alpha _{2})}= & {} \frac{1}{n}{(\hat{x}+\Delta x)^\mathrm{T}(\hat{s}+\Delta s)}\\= & {} \frac{1}{n}\left(\hat{x}^\mathrm{T}\hat{s}+(\hat{x}^\mathrm{T}\Delta s+\hat{s}^\mathrm{T}\Delta x)+\Delta x^\mathrm{T}\Delta s\right)\\= & {} \frac{1}{n}\left(\hat{x}^\mathrm{T}\hat{s}+e^\mathrm{T}\left[ \left(\tau \hat{\mu } e-\hat{x}\hat{s}\right)^{+}-\alpha _{2}\hat{x}\hat{s}\right] +\Delta x^\mathrm{T}\Delta s\right)\\\leqslant & {} \frac{1}{n}\left(\hat{x}^\mathrm{T}\hat{s}+\sqrt{n}\left\Vert \left(\tau \hat{\mu } e-\hat{x}\hat{s}\right)^{+} \right\Vert -\alpha _{2}\hat{x}^\mathrm{T}\hat{s}+\left\Vert \left(\Delta x\Delta s\right)^{+} \right\Vert _{1}\right)\\\leqslant & {} \frac{1}{n}\left((1-\alpha _{2})n\hat{\mu }+2\sqrt{n}\beta \tau \hat{\mu }+\frac{1}{4}\beta \tau \hat{\mu }+\frac{1}{4}n\alpha _{2}^{2}\hat{\mu }\right)\\= & {} {(1-\alpha _{2})\hat{\mu }+\frac{2}{\sqrt{n}}\beta \tau \hat{\mu }+\frac{1}{4n}\beta \tau \hat{\mu }+\frac{1}{4}\alpha _{2}^{2}\hat{\mu }}\\\leqslant & {} {(1-\frac{\beta \tau }{\sqrt{n}})\hat{\mu }+\frac{1}{4n}\beta \tau \hat{\mu }+\frac{3}{64n}\beta \tau \hat{\mu }}\\\leqslant & {} (1-\frac{19}{64\sqrt{n}}\beta \tau )\hat{\mu }\leqslant (1-\frac{\beta \tau }{4\sqrt{n}})\hat{\mu }, \end{aligned}$$

where the third inequality is due to $\alpha _{2}=\frac{3\beta \tau }{\sqrt{n}}$. On the other hand, using the nonnegativity of the terms $e^\mathrm{T}\left(\tau \hat{\mu } e-\hat{x}\hat{s}\right)^{+}$ and $\Delta {x}^\mathrm{T}\Delta {s}$, we easily derive $\mu (\alpha _{2})\geqslant (1-\alpha _{2})\hat{\mu }$. This concludes the result and ends the proof.

Lemma 4.9

Let $(\hat{x}(\alpha _{2}),\hat{s}(\alpha _{2}))$ be the generated corrector point by the algorithm. If $\beta <\frac{1}{6}$ and $\alpha _{2}=\frac{3\beta \tau }{\sqrt{n}}$, then after a corrector step $(\hat{x}(\alpha _{2}),\hat{s}(\alpha _{2}))\in \mathcal {N}(\tau ,\beta )$.

Proof

Using the definition of the wide neighborhood $\mathcal {N}(\tau ,\beta )$, in the same way as Lemma 4.6, we need to prove $\left\Vert (\tau \hat{\mu }(\alpha _{2})e-\hat{x}(\alpha _{2})\hat{s}(\alpha _{2}))^{+} \right\Vert \leqslant \beta \tau \hat{{\mu }}(\alpha _{2})$ and $(\hat{x}(\alpha _{2}),\hat{s}(\alpha _{2}))\in \mathcal {F}^{0}$. By (3.6), (4.10), (4.11) and the fact $\hat{\mu }(\alpha _{2})\leqslant \hat{\mu }$, we consequently derive

$$\begin{aligned} \tau \hat{\mu }(\alpha _{2})e-\hat{x}(\alpha _{2})\hat{s}(\alpha _{2})= & {} \tau \hat{\mu }(\alpha _{2})e-(\hat{x}+\Delta x)(\hat{s}+\Delta s)\\= & {} \tau \hat{\mu }(\alpha _{2})e-\hat{x}\hat{s}-(\hat{x}\Delta s+\hat{s}\Delta x)-\Delta x\Delta s\\= & {} \tau \hat{\mu }(\alpha _{2})e-(1-\alpha _{2})\hat{x}\hat{s}-\left(\tau \hat{\mu } e-\hat{x}\hat{s}\right)^{+}-\Delta x\Delta s\\= & {} (1-\alpha _{2})(\tau \hat{\mu }(\alpha _{2})e-\hat{x}\hat{s})+\alpha _{2}\tau \hat{\mu }(\alpha _{2})e\\&-\left(\tau \hat{\mu } e-\hat{x}\hat{s}\right)^{+}-\Delta x\Delta s\\\leqslant & {} (1-\alpha _{2})\frac{\hat{\mu }(\alpha _{2})}{\hat{\mu }}(\tau \hat{\mu }e-\hat{x}\hat{s})+\alpha _{2}\tau \hat{\mu }(\alpha _{2})e\\&-\frac{\hat{\mu }(\alpha _{2})}{\hat{\mu }}\left(\tau \hat{\mu } e-\hat{x}\hat{s}\right)^{+}-\Delta x\Delta s\\\leqslant & {} \alpha _{2}\tau \hat{\mu }(\alpha _{2})e-\Delta x\Delta s. \end{aligned}$$

Thus, using Lemma 4.7, we have

$$\begin{aligned} \left\Vert \left(\tau \hat{\mu }(\alpha _{2})e-\hat{x}(\alpha _{2})\hat{s}(\alpha _{2})\right)^{+} \right\Vert\leqslant & {} \sqrt{n}\alpha _{2}\tau \hat{\mu }(\alpha _{2}) +\left\Vert \left(\Delta x\Delta s\right)^{-} \right\Vert \nonumber \\\leqslant & {} \sqrt{n}\alpha _{2}\tau \hat{\mu }(\alpha _{2})+\frac{1}{4}\beta \tau \hat{\mu }+\frac{1}{4}n\alpha _{2}^{2}\hat{\mu }\nonumber \\\leqslant & {} \left( 3\tau +\frac{1}{2}+\frac{3}{32}\right) \beta \tau \hat{\mu }(\alpha _{2})\leqslant \beta \tau \hat{\mu }(\alpha _{2}),\qquad \end{aligned}$$

(4.13)

where the third inequality is due to assumptions $\beta \leqslant \frac{1}{6}$, $\tau \leqslant \frac{1}{8}$, $\alpha _{2}=\frac{3\beta \tau }{\sqrt{n}}$ and the fact that $\hat{\mu }(\alpha _{2})\geqslant \frac{1}{2}\hat{\mu }$.

Furthermore, we need to prove $(\hat{x}(\alpha _{2}),\hat{s}(\alpha _{2}))\in \mathcal {F}^{0}$. The feasibility of $(\hat{x}(\alpha _{2}),\hat{s}(\alpha _{2}))$ is clearly concluded by systems (3.4) and (3.5). Due to inequality (4.13), we have $\hat{x}(\alpha _{2})\hat{s}(\alpha _{2})\geqslant (1-\beta )\tau \hat{\mu }(\alpha _{2})$ which means $\hat{x}(\alpha _{2})\hat{s}(\alpha _{2})>0$ for $\beta <\frac{1}{6}$. Therefore, due to Lemma 4.2, we get $\hat{x}(\alpha _{2})>0$ and $\hat{s}(\alpha _{2})>0$. The result is derived.

4.1 Complexity Analysis

We are ready to state the main result of the paper. We prove the proposed Algorithm 1 has good global convergence and it will be terminated in at most $O\left(\sqrt{n}L\right)$ iterations.

Lemma 4.10

Let $\beta \leqslant \frac{1}{6}$ and $\tau \leqslant \frac{1}{8}$. The predictor-corrector Algorithm 1 has $O\left(\sqrt{n}L\right)$ complexity.

Proof

By Lemmas 4.6 and 4.9, in each iteration, we have $(\hat{x},\hat{s})\in \mathcal {N}(\tau ,2\beta )$ after a predictor step and $(\bar{{x}},\bar{{s}})\in \mathcal {N}(\tau ,\beta )$ after a corrector step. Moreover,

$$\begin{aligned} \bar{\mu }\leqslant \hat{\mu }(\alpha _{2})\leqslant \left(1-\frac{\beta \tau }{4\sqrt{n}}\right)\hat{\mu }\leqslant \left(1-\frac{\beta \tau }{4\sqrt{n}}\right) \mu (\alpha _{1})\leqslant \left(1-\frac{\beta \tau }{4\sqrt{n}}\right){\mu }. \end{aligned}$$

This implies that after k iterations the relations $\bar{\mu }^{k}\leqslant \varepsilon \mu ^{0}$ hold if $\left(1-\frac{\beta \tau }{4\sqrt{n}}\right)^{k}\leqslant \varepsilon$. Taking logarithms and using $-\log (1-t)\geqslant t$ for $t\in (0,1)$, we get $k\geqslant \frac{4\sqrt{n}}{\beta \tau }\log \varepsilon ^{-1}$. This implies that after at most $O\left(\sqrt{n}\log \varepsilon ^{-1}\right)$ iterations, we have $\bar{\mu }^{k}\leqslant \varepsilon \mu ^{0}$. We finish the proof.

5 Simulation Experiments

In this section, we test the presented Algorithm 1 by some numerical examples of monotone LCPs [20, 21]. Numerical results were obtained by using MATLAB R2007a (Version: 7.4.0.287) on Windows XP Enterprise 32-bit operating system. The algorithm starts with the initial starting points $x^{0}=s^{0}=e$. Also, considering $q=e-Me$ and $\varepsilon =10^{-5}$ as the accuracy parameter, the algorithm terminates after the relative duality gap $\frac{x^\mathrm{T}s}{1\,+\,{x^{0}}^\mathrm{T}s^{0}}$ is less than $\varepsilon$.

Example5.1

Consider the monotone LCPs with the positive semidefinite matrices $M_{1}$ and $M_{2}$ as follows:

$$\begin{aligned} M_{1}:=\left[ \begin{array}{cccccccc} 1 &{} 2 &{} 2 &{} \cdots &{} 2\\ 0 &{} 1 &{} 2 &{} \cdots &{} 2\\ 0 &{} 0 &{} 1 &{} \cdots &{} 2\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 1\\ \end{array} \right] ,~~M_{2}:=\left[ \begin{array}{cccccccc} 1 &{} 2 &{} 2 &{} \cdots &{}2\\ 2 &{} 5 &{} 6 &{} \cdots &{}6 \\ 2 &{} 6 &{} 9 &{} \cdots &{}10\\ \vdots &{} \vdots &{} \vdots &{} &{}\vdots \\ 2 &{} 6 &{} 10 &{}\cdots &{}4(n-1)+1\\ \end{array} \right] . \end{aligned}$$

Example5.2

We shall test the algorithm on some randomly generated instances.

The numerical results related to these examples are summarized in Tables 1 and 2, where “Iter.” denotes the required iteration numbers, “R.D.G” denotes the value of relative duality gap as the stopping criteria and “CPU(s)” denotes the CPU time (in seconds) required to obtain an $\varepsilon$-approximate solution of the underlying problem.

Table 1 Numerical results for Example 5.1

Table 2 Numerical results for Example 5.2

The obtained numerical results show that the algorithm practically is simple and efficient.

6 Concluding Remarks

Among various classes of primal-dual IPMs, predictor-corrector interior-point algorithms are the most efficient and applicable iterative approaches. They divide the Newton directions into the affine and centering search directions. In this paper, we proposed a predictor-corrector interior-point algorithm for LCPs which usees the classical affine scaling direction as a part in a corrector step, not in a predictor step. This led to the reduction in duality gap in both predictor and corrector steps and moreover concluded the complexity $O\left(\sqrt{n}\log \varepsilon ^{-1}\right)$ for the algorithm. The numerical results showed the efficiency of the proposed algorithm.