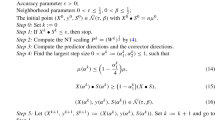A new wide-neighborhood predictor-corrector interior-point method for semidefinite optimization

Abstract

In this paper, we present a new predictor-corrector interior-point algorithm based on a wide neighborhood for semidefinite optimization. The proposed algorithm is a Mizuno-Todd-Ye predictor-corrector type and uses the Nesterov-Todd (NT) search direction in predictor step and a commutative class of search directions involving Helmberg-Kojima-Monteiro and NT directions in corrector step. We show that the proposed algorithm at every both predictor and corrector steps reduces the duality gap. The method enjoys the iteration complexity of ${\mathcal {O}}(\sqrt{n\kappa _{\infty }}L)$, which matching to the currently best known iteration bound for wide neighborhood algorithms. Numerical results also confirm the algorithm is reliable and promising.

1 Introduction

Semidefinite optimization (SDO) is concerned with finding a symmetric positive semidefinite matrix that optimizes a linear function subject to linear constraints. In recent decades, due to the widespread applications of semidefinite optimization in areas such as system and control theory [4], combinatorial optimization [1], and engineering [23] have attracted the attention of many researchers. These applications led researchers to look for efficient methods to solve SDO. It is obvious that due to the close connection between linear optimization (LO) and SDO, interior-point methods (IPMs) have been successfully developed from LO to SDO. The first all on, Nesterov and Nemirovski [17] introduced the theoretical base for solving SDO with IPMs by studying LO over closed convex cones. Of course, Alizadeh [2] simultaneously generalized Ye’s projective potential reduction algorithm from LO to SDO and discussed that many IPMs could be extended to SDO.

Predictor-corrector methods play an important role among primal-dual path-following IPMs. A popular representative of such methods is the Mizuno-Todd-Ye (MTY) algorithm [15] for solving LO that has ${\mathcal {O}}(\sqrt{n}L)$ iteration-complexity bound in the worst case, where L is the size of the problem. Later on, this algorithm was extended to monotone linear complementarity problem (MLCP) by Ji et. al [9] and proved which the resulting algorithm has ${\mathcal {O}}(\sqrt{n}L)$-iteration complexity bound and superlinear convergence. It is proved by Ye and Anstreicher [27] that MTY algorithm converges quadratically assuming that the LCP is nondegenerate. In [20], Potra proposed a predictor-corrector method based on a ${\mathcal {N}}_{\infty }^-$ neighborhood of the central path and proved that this algorithm has ${\mathcal {O}}(nL)$ iteration complexity bound under general condition and quadratically converges when the LCP is nondegenerate. Then by using a higher order predictor reduces the iteration complexity to ${\mathcal {O}}(\sqrt{n}L)$ and proves superlinear convergence even in the degenerate case. Zhang and Zhang [29] developed the MTY predictor-corrector algorithm to convex quadratic optimization (CQO) and obtained superlinear convergence result.

In [3], Ai and Zhang introduced a new wide neighborhood of the central path for MLCP, and proposed an IPM for solving MLCP. Their algorithm has ${\mathcal {O}}(\sqrt{n}L)$-iteration complexity coinciding with the same theoretical complexity as a small neighborhood algorithm. Li and Terlaky [14] extended the Ai-Zhang directions to the class of SDOs. Kheirfam [12] proposed a predictor-corrector infeasible IPM for SDO based on the wide neighborhood. Feng and Fang [6] extended the Ai-Zhang predictor-corrector path-following IPM introduced in [3] to the class of SDO and proved that the algorithm has ${\mathcal {O}}(\sqrt{n}L)$ iteration complexity bound. In accordance with good performance the neighborhood introduced in [3] in the proof of polynomial complexity, many researchers have been interested to extend of this neighborhood and study algorithms in other optimization problems and obtained good results in recent years [10, 11, 19, 26].

Although the development of algorithms with the same iteration complexity as the best known iteration bound and with a different structure and analysis from existing algorithms is important, but their computational efficiency is a very important issue now. The paper is motivated by this idea. We propose a new predictor-corrector interior-point algorithm for SDO based on the wide neighborhood which is an extension of the presented technique in [21] from LO to SDO. We show that the algorithm has ${\mathcal {O}}(\sqrt{n\kappa _{\infty }}L)$ iteration complexity bound which matches the best known iteration bound for SDO. The proposed algorithm is different from the other ones because it utilizes a new corrector step. Especially, there are some major differences between our algorithm and the proposed algorithm in [6]. The first is the generated iterate by the predictor step; the second is the neighborhood as well as the search directions in the corrector step which is based on the iterate and the search directions obtained at the predictor stage; the third is the update rule of the new iterate. Moreover, we provide some numerical results, which indicates our new algorithm may also perform well in practice.

The organization of the paper is as follows. In Sect. 2, we review the notation of the central path and its associated neighborhood. In Sect. 3, we introduce the search directions and then present a theoretical framework of our algorithm. Section 4 is devoted to the analysis of the algorithm. Section 5 deals with some numerical results. Section 6 provides some concluding remarks.

2 SDO problem, the central path and its wide neighborhood

In this section, we first recall the pair of SDO problems. After that, we describe the central path and its corresponding wide neighborhood the symmetrization scheme. We finally state the corresponding wide neighborhood of the central path and its scaled system.

Consider the primal SDO problem and its associated dual in the following standard form:

$$\begin{aligned} \min \big \{\mathrm{Tr}(CX):\ \mathrm{Tr}(A_iX)=b_i,\ i=1,\ldots , m,\ X\succeq 0\big \},\quad \quad \quad \quad \quad (P) \\ \max \big \{b^Ty: \ \sum ^m_{i=1}y_iA_i+S=C, \ \ S\succeq 0\big \}, \quad \quad \quad \quad \quad \quad \quad (D) \end{aligned}$$

where $C\in {{\mathcal {S}}}^n$, $b\in {{\mathbb {R}}}^m$ and $A_i\in {{\mathcal {S}}^n} (i=1, \ldots , m)$ are linearly independent. Here ${{\mathbb {R}}}^m$ and ${{\mathcal {S}}}^n$ denote, respectively, the n-dimensional Euclidean space and the space of symmetric $n\times n$ matrices. Let

$$\begin{aligned} {\mathcal {F}}^0:=\big \{(X, y, S):\ \mathrm{Tr}(A_iX)=b_i,\ \sum ^m_{i=1}y_iA_i+S=C, \ \ X, S\succ 0\big \} \end{aligned}$$

denotes the relative interior set of the problem pair (P) and (D). By the assumption that ${\mathcal {F}}^0$ is nonempty, both problems (P) and (D) are solvable and the optimal conditions for them can be written as follows [5]:

$$\begin{aligned} \begin{array}{ccc} \mathrm{Tr}(A_iX)=b_i,&{}&{} X\succeq 0,~ i=1, \ldots , m\\ \displaystyle \sum ^m_{i=1}y_iA_i+S=C, &{}&{} S\succeq 0, \\ XS=0, &{}&{} \end{array} \end{aligned}$$

(1)

where the last equality is said to be the complementarity condition. The key idea of primal-dual path-following IPMs is to replace the complementarity condition $XS=0$ by the perturbed equation $XS=\tau \mu I$ with $\mu >0$ and $\tau \in (0, 1)$, where I is the identity matrix. Under this assumption, we have the following perturbed system

$$\begin{aligned} \begin{array}{ccc} \mathrm{Tr}(A_iX)=b_i,&{}&{} X\succeq 0,~ i=1, \ldots , m\\ \displaystyle \sum ^m_{i=1}y_iA_i+S=C, &{}&{} S\succeq 0,\\ XS=\tau \mu I.&{}&{} \end{array} \end{aligned}$$

(2)

It has been proven that system (2) has a unique solution $(X(\mu ), y(\mu ), S(\mu ))$ for every $\mu >0$, assuming that ${\mathcal {F}}^0\ne \emptyset$ (see, e.g., [13]). The set of all such solutions form the central path, which converges to the optimal solution of the problem, when $\mu \downarrow 0$ [7]. As can be seen from the system (2) that its left-hand side maps ${\mathcal {S}}^n\times {\mathbb {R}}^m\times {\mathcal {S}}^n$ to ${\mathbb {R}}^{n\times n}\times {\mathbb {R}}^m\times {\mathcal {S}}^n$, where ${\mathbb {R}}^{n\times n}$ denotes the set of all $n\times n$ matrices with real entries. It follows that system (2) is not a square system when X and S are restricted to ${\mathcal {S}}^n$. Assuming $P\in {\mathbb {R}}^{n\times n}$ as a non-singular matrix and using the symmetrization operator $H_P:{\mathbb {R}}^{n\times n}\rightarrow {\mathcal {S}}^n$

$$\begin{aligned} H_P(M)=\frac{1}{2}\big (PMP^{-1}+(PMP^{-1})^T\big ),~~M\in {\mathbb {R}}^{n\times n}, \end{aligned}$$

proposed by Zhang [28], we replace the parameterized equation $XS=\tau \mu I$ by $H_P(XS)=\tau \mu I$, where the matrix P belongs to the specific class

$$\begin{aligned} {\mathcal {C}}(X, S):=\{P\in {\mathcal {S}}^n_{++}: PXSP^{-1}\in {\mathcal {S}}^n\}, \end{aligned}$$

where $X, S\in {\mathcal {S}}^n_{++}$. The most common choices for the scaling matrix P are $P=S^{\frac{1}{2}}, P=X^{-\frac{1}{2}}$ and $P=W^{\frac{1}{2}}$ which respectively lead to the H.K.M. search directions [8, 13] and the NT search direction [18], where

$$\begin{aligned} W=X^{-\frac{1}{2}}(X^{\frac{1}{2}}SX^{\frac{1}{2}})^{\frac{1}{2}}X^{-\frac{1}{2}} =S^{\frac{1}{2}}(S^{\frac{1}{2}}XS^{\frac{1}{2}})^{-\frac{1}{2}}S^{\frac{1}{2}}. \end{aligned}$$

(3)

Thus, system (2) can be rewritten in equivalent form as follows:

$$\begin{aligned} \begin{array}{ccc} \mathrm{Tr}(A_iX)=b_i,&{}&{} X\succeq 0,~ i=1, \ldots , m\\ \displaystyle \sum ^m_{i=1}y_iA_i+S=C, &{}&{} S\succeq 0, \\ H_P(XS)=\tau \mu I. &{}&{} \end{array} \end{aligned}$$

(4)

For the scaling matrix $P\in {\mathcal {C}}(X, S)$, we scale the matrices X and S and the other data as follows: ${\widetilde{X}}=PXP, {\widetilde{S}}=P^{-1}SP^{-1}, {\widetilde{A}}_i=P^{-1}A_iP^{-1}$ and ${\widetilde{C}}=P^{-1}CP^{-1}$. In this way, we have ${\widetilde{X}}{\widetilde{S}}={\widetilde{S}}{\widetilde{X}}$ and $H_P(XS)=H_I({\widetilde{X}}{\widetilde{S}})={\widetilde{X}}{\widetilde{S}}$. In the scale-aforementioned, system (4) becomes the following system

$$\begin{aligned} \begin{array}{ccc} \mathrm{Tr}({\widetilde{A}}_i{\widetilde{X}})=b_i,&{}&{} i=1, \ldots , m \\ \displaystyle \sum ^m_{i=1}y_i{{\widetilde{A}}}_i+{\widetilde{S}}={\widetilde{C}}, &{}&{}\\ H_I({\widetilde{X}}{\widetilde{S}})=\tau \mu I.&{}&{} \end{array} \end{aligned}$$

(5)

Applying Newton’s method for the system (5) leads to the following system

$$\begin{aligned}&\mathrm{Tr}({{\widetilde{A}}}_i\varDelta {\widetilde{X}})=0,\quad \quad i=1, \ldots , m \nonumber \\&\displaystyle \sum ^m_{i=1}\varDelta {y}_i{{\widetilde{A}}}_i+\varDelta {\widetilde{S}}=0, \nonumber \\&H_I(\widetilde{X}\varDelta \widetilde{S}+\varDelta \widetilde{X}\widetilde{S})=\tau \mu I-\widetilde{X}\widetilde{S}, \end{aligned}$$

(6)

where the scaled directions $\varDelta {\widetilde{X}}=P\varDelta XP$ and $\varDelta {\widetilde{S}}=P^{-1}\varDelta SP^{-1}.$

In the primal-dual IPMs, it is needed that all the iterates to be in within a certain neighborhood of the central path. One of the popular neighborhoods is the so-called negative infinity neighborhood that is a wide neighborhood, defined as

$$\begin{aligned} {\mathcal {N}}^-_{\infty }(1-\gamma ):=\{(X, y, S)\in {\mathcal {F}}^0: \lambda _{\min }(XS)\ge \gamma \mu \}, \end{aligned}$$

where $\gamma \in (0, 1)$. Another popular wide neighborhood of the central path introduced by Ai and Zhang [3] for LCP and generalized to SDO by Feng and Fang [6] which is defined as

$$\begin{aligned} {\mathcal {N}}(\tau , \beta )=\big \{(X, y, S)\in {\mathcal {F}}^0: \big \Vert \big (\tau \mu I-X^{1/2}SX^{1/2}\big )^+\big \Vert _F\le {\tau \beta \mu }\big \}, \end{aligned}$$

where $\beta \in (0, 1)$ is given constant. One can easily verify that

$$\begin{aligned} {\mathcal {N}}^-_{\infty }(1-\tau )\subseteq {\mathcal {N}}(\tau , \beta ). \end{aligned}$$

Note that the neighborhood ${\mathcal {N}}(\tau , \beta )$ is scaling invariant, that is (X, y, S) is in the neighborhood if and only if $({\widetilde{X}}, y, {\widetilde{S}})$ is.

3 Search directions and algorithm

In this section, we present a new predictor-corrector wide neighborhood interior point algorithm for SDO. The predictor step uses only the NT search direction when the used direction in the corrector step can belong to the class ${\mathcal {C}}(X, S)$. This is one of the differences of our algorithm with the existing algorithms in the literature.

In accordance with the Ai-Zhang’s original idea, we decompose the Newton direction into two separate parts corresponding to the positive and negative parts of the right-hand side of the third equality of the system (6); i.e, $\tau \mu I-\widetilde{X}\widetilde{S}$. Given an iterate $({\widetilde{X}}, y, {\widetilde{S}})\in {\mathcal {N}}(\tau , \frac{\beta }{2})$, we compute the predictor direction by solving the following system

$$\begin{aligned}&\mathrm{Tr}({{\widetilde{A}}}_i\varDelta {\widetilde{X}}^p_-)=0,\quad \quad i=1, \ldots , m \nonumber \\&\displaystyle \sum ^m_{i=1}(\varDelta {y}^p_i)_-{{\widetilde{A}}}_i+\varDelta {\widetilde{S}}^p_-=0, \nonumber \\&H_I(\widetilde{X}\varDelta \widetilde{S}^p_-+\varDelta \widetilde{X}^p_-\widetilde{S})=(-\widetilde{X}\widetilde{S})^-. \end{aligned}$$

(7)

Then, the largest step size ${\bar{\alpha }}_p$ is computed such that for every $\alpha _p\in [0, {\bar{\alpha }}_p]$

$$\begin{aligned} \big ({\widetilde{X}}(\alpha _p), y(\alpha _p), \widetilde{S}(\alpha _p)\big )=({\widetilde{X}}, y, \widetilde{S})+\alpha _p(\varDelta {\widetilde{X}}^p_-, \varDelta {y}^p_-, \varDelta \widetilde{S}^p_-)\in {\mathcal {N}}(\tau , \beta ). \end{aligned}$$

(8)

We use the iterate $({\widetilde{X}}(\alpha _p), y(\alpha _p), \widetilde{S}(\alpha _p))$ and the direction $(\varDelta {\widetilde{X}}^p_-, \varDelta {y}^p_-, \varDelta {\widetilde{S}}^p_-)$ obtained from the predictor step to compute the corrector directions given by the following systems:

$$\begin{aligned}&\mathrm{Tr}({{\widetilde{A}}}_i\varDelta {\widetilde{X}}^c_-)=0,\quad \quad i=1, \ldots , m \nonumber \\&\displaystyle \sum ^m_{i=1}(\varDelta {y}^c_i)_-{{\widetilde{A}}}_i+\varDelta {\widetilde{S}}^c_-=0, \nonumber \\&H_I(\widetilde{X}(\alpha _p)\varDelta \widetilde{S}^c_-+\varDelta \widetilde{X}^c_-\widetilde{S}(\alpha _p))= [\tau \mu (\alpha _p) I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^- \nonumber \\&\quad -\,\alpha _pH_I(\varDelta \widetilde{X}^p_-\varDelta {\widetilde{S}}^p_-), \end{aligned}$$

(9)

and

$$\begin{aligned}&\mathrm{Tr}({{\widetilde{A}}}_i\varDelta {\widetilde{X}}^c_+)=0,\quad \quad i=1, \ldots , m \nonumber \\&\displaystyle \sum ^m_{i=1}(\varDelta {y}^c_i)_+{{\widetilde{A}}}_i+\varDelta {\widetilde{S}}^c_+=0, \nonumber \\&H_I(\widetilde{X}(\alpha _p)\varDelta \widetilde{S}^c_++\varDelta \widetilde{X}^c_+\widetilde{S}(\alpha _p))= [\tau \mu (\alpha _p) I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^+. \end{aligned}$$

(10)

In terms of Kronecker product, the third equations of (7), (9) and (10) can be expressed, respectively, as follows:

$$\begin{aligned}&\mathcal {\widetilde{E}}vec(\varDelta \widetilde{X}^p_{-})+\mathcal {\widetilde{F}}vec(\varDelta \widetilde{S}^p_{-}) =vec\big ((-\widetilde{X}\widetilde{S})^{-}\big ), \end{aligned}$$

(11)

$$\begin{aligned}&\mathcal {\widetilde{E}}(\alpha _p)vec(\varDelta \widetilde{X}^c_{-})+\mathcal {\widetilde{F}}(\alpha _p)vec(\varDelta \widetilde{S}^c_{-}) \nonumber \\&\quad =vec\big ([\tau \mu (\alpha _p) I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^-\big )-\alpha _p vec H_I\big (\varDelta {\widetilde{X}}^p_-\varDelta \widetilde{S}^p_-\big ), \end{aligned}$$

(12)

$$\begin{aligned}&\mathcal {\widetilde{E}}(\alpha _p)vec(\varDelta \widetilde{X}^c_{+})+\mathcal {\widetilde{F}}(\alpha _p)vec(\varDelta \widetilde{S}^c_{+}) =vec\big ([\tau \mu (\alpha _p) I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^+\big ),\nonumber \\ \end{aligned}$$

(13)

where

$$\begin{aligned}&\mathcal {\widetilde{E}}=\frac{1}{2}(\widetilde{S}\otimes I+I\otimes \widetilde{S}),\ \ \mathcal {\widetilde{F}}=\frac{1}{2}(\widetilde{X}\otimes I+I\otimes \widetilde{X}),\nonumber \\&\mathcal {\widetilde{E}}(\alpha _p)=\frac{1}{2}(\widetilde{S}(\alpha _p)\otimes I+I\otimes \widetilde{S}(\alpha _p)),\ \ \mathcal {\widetilde{F}}(\alpha _p)=\frac{1}{2}(\widetilde{X}(\alpha _p)\otimes I+I\otimes \widetilde{X}(\alpha _p)).~~\nonumber \\ \end{aligned}$$

(14)

Furthermore, one easily checks that the following equations hold as $P=W^{\frac{1}{2}}$ [6]:

$$\begin{aligned} {\widetilde{X}}={\widetilde{S}},\quad \mathrm{and}\quad {\widetilde{\mathcal {E}}}={\widetilde{\mathcal {F}}}. \end{aligned}$$

Finally, the step size $\alpha =(\alpha _1, \alpha _2)\in [0, 1]^2$ should be computed such that

$$\begin{aligned}&({\widetilde{X}}(\alpha ), y(\alpha ), {\widetilde{S}}(\alpha )):= ({\widetilde{X}}(\alpha _p), y(\alpha _p), \widetilde{S}(\alpha _p))\nonumber \\&\quad +(\varDelta {\widetilde{X}}(\alpha ), \varDelta y(\alpha ), \varDelta \widetilde{S}(\alpha ))\in {\mathcal {N}}\big (\tau , \frac{\beta }{2}\big ), \end{aligned}$$

(15)

where

$$\begin{aligned} (\varDelta \widetilde{X}(\alpha ), \varDelta y(\alpha ), \varDelta \widetilde{S}(\alpha ))=\alpha _1(\varDelta \widetilde{X}^c_-, \varDelta y^c_-, \varDelta \widetilde{S}^c_-)+\alpha _2(\varDelta \widetilde{X}^c_+, \varDelta y^c_+, \varDelta \widetilde{S}^c_+). \end{aligned}$$

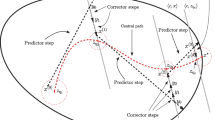
Here, we present a theoretical framework of our algorithm. Let $0<\beta <1$ be parameter measuring the size of neighborhood of the central path. Then an MTY type algorithm moves the iterates forward to a neighborhood of size $\beta$ and then back to the smaller one of size $\beta /2$ by alternately using the NT and a general commutative class of directions.

Algorithm 1: Predictor-corrector algorithm for SDO
Input: accuracy parameter $\varepsilon >0$; neighborhood parameters $0<\beta \le \frac{1}{3}$ and $0<\tau \le \frac{1}{3}$;
the initial point $(X^0, y^0, S^0)\in {\mathcal {N}}(\tau , \beta /2).$
Set $k=0$;
If $\mathrm{Tr}(X^0S^0)\le \varepsilon$, then stop; otherwise, go to next step.
Predictor step
Compute the scaling matrix $P^k=(W^k)^{\frac{1}{2}}$ where $W^k$ is defined by (3).
Compute the search direction $(\varDelta {\widetilde{X}}^{p,k}_-, \varDelta y^{p,k}_-, \varDelta {\widetilde{S}}^{p,k}_-)$ by (7);
Set $\alpha ^k_p=\frac{1}{4}\sqrt{\frac{\beta \tau }{2n}}$;
Compute $({\widetilde{X}}(\alpha ^k_p), y(\alpha ^k_p), \widetilde{S}(\alpha ^k_p))$ from (8);
Corrector step
Compute the scaling matrix $P^k\in {\mathcal {C}}(X(\alpha ^k_p), S(\alpha ^k_p))$;
Compute the directions $(\varDelta {\widetilde{X}}^{c,k}_-, \varDelta y^{c,k}_-, \varDelta {\widetilde{S}}^{c,k}_-)$ and $(\varDelta \widetilde{X}^{c,k}_+, \varDelta y^{c,k}_+, \varDelta {\widetilde{S}}^{c,k}_+)$ by (9) and (10);
Set $\alpha _2^k=\frac{1}{2\sqrt{{\mathrm{cond}}({\overline{G}})}}$ and $\alpha _1^k=\alpha ^k_2\sqrt{\frac{\tau \beta }{2n}}$;
Compute $({\widetilde{X}}(\alpha ^k), y(\alpha ^k), \widetilde{S}(\alpha ^k))$ from (15);
Set $({\widetilde{X}}^{k+1}, y^{k+1}, {\widetilde{S}}^{k+1})=(\widetilde{X}(\alpha ^k), y(\alpha ^k), \widetilde{S}(\alpha ^k))$;
If $\mathrm{Tr}(X^{k+1}S^{k+1})\le \varepsilon$, then stop; otherwise, go to predictor step.

4 Analysis of the algorithm

In this section, we discuss the convergence analysis of the proposed algorithm and also present our main convergence result which establishes the iteration-complexity bound for Algorithm 1. To this do, we analyze the steps of predictor and corrector separately.

4.1 Analysis of the predictor step

From (8) and the third equation of system (7), we obtain

$$\begin{aligned} H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))= & {} H_I\big ((\widetilde{X}+\alpha _p\varDelta {\widetilde{X}}^p_-)(\widetilde{S}+\alpha _p\varDelta {\widetilde{S}}^p_-)\big )\nonumber \\= & {} {\widetilde{X}}{\widetilde{S}}+\alpha _pH_I({\widetilde{X}}\varDelta \widetilde{S}_-^p+{\widetilde{S}}\varDelta \widetilde{X}^p_-)+\alpha _p^2H_I(\varDelta {\widetilde{X}}_-^p\varDelta \widetilde{S}_-^p)\nonumber \\= & {} (1-\alpha _p){\widetilde{X}}{\widetilde{S}}+\alpha _p^2H_I(\varDelta \widetilde{X}_-^p\varDelta {\widetilde{S}}_-^p), \end{aligned}$$

(16)

and using $\mathrm{Tr}\big (H_I(\varDelta {\widetilde{X}}_-^p\varDelta \widetilde{S}_-^p)\big )=\mathrm{Tr}(\varDelta {\widetilde{X}}_-^p\varDelta \widetilde{S}_-^p)=0$, we have

$$\begin{aligned} \mu (\alpha _p)=\frac{1}{n}\mathrm{Tr}\big (\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p)\big )=\frac{1-\alpha _p}{n}\mathrm{Tr}({\widetilde{X}}{\widetilde{S}})=(1-\alpha _p)\mu . \end{aligned}$$

(17)

Lemma 1

Let $({\widetilde{X}}, y, {\widetilde{S}})\in {\mathcal {N}}(\tau , \beta /2)$ and $(\varDelta {\widetilde{X}}_-^p, \varDelta y^p_-, \varDelta {\widetilde{S}}_-^p)$ be the solution of system (7). Then

(i) $H_I(\varDelta \widetilde{X}_-^p\varDelta {\widetilde{S}}_-^p)\preceq \frac{1}{2}{\widetilde{X}}\widetilde{S}$.    (ii) $\Vert H_I(\varDelta {\widetilde{X}}_-^p\varDelta \widetilde{S}_-^p)\Vert _F\le \frac{1}{2}n\mu .$

Proof

Using ${\widetilde{X}}={\widetilde{S}}$ and the following inequalities

$$\begin{aligned} {\widetilde{X}}\varDelta \widetilde{S}_-^p\varDelta {\widetilde{X}}_-^p\widetilde{S}\preceq \frac{1}{4}\big ({\widetilde{X}}\varDelta \widetilde{S}_-^p+\varDelta {\widetilde{X}}_-^p{\widetilde{S}}\big )^2 \end{aligned}$$

and

$$\begin{aligned} \widetilde{S}(\varDelta {\widetilde{S}}_-^p\varDelta {\widetilde{X}}_-^p)^T\widetilde{X}\preceq \frac{1}{4}\big ([{\widetilde{X}}\varDelta \widetilde{S}_-^p+\varDelta {\widetilde{X}}_-^p{\widetilde{S}}]^T\big )^2, \end{aligned}$$

we obtain

$$\begin{aligned}&\frac{\varDelta {\widetilde{S}}_-^p\varDelta {\widetilde{X}}_-^p+(\varDelta \widetilde{S}_-^p\varDelta {\widetilde{X}}_-^p)^T}{2}\\&\quad \preceq \frac{1}{8}\widetilde{X}^{-1}\Big (\big ({\widetilde{X}}\varDelta {\widetilde{S}}_-^p+\varDelta \widetilde{X}_-^p{\widetilde{S}}\big )^2+\big ([{\widetilde{X}}\varDelta \widetilde{S}_-^p+\varDelta {\widetilde{X}}_-^p{\widetilde{S}}]^T\big )^2\Big )\widetilde{S}^{-1}\\&\quad \preceq \frac{1}{8}{\widetilde{X}}^{-1}\Big ({\widetilde{X}}\varDelta \widetilde{S}_-^p+\varDelta {\widetilde{X}}_-^p{\widetilde{S}}+[\widetilde{X}\varDelta {\widetilde{S}}_-^p+\varDelta {\widetilde{X}}_-^p\widetilde{S}]^T\Big )^2{\widetilde{S}}^{-1}, \end{aligned}$$

which implies

$$\begin{aligned} H_I(\varDelta {\widetilde{S}}_-^p\varDelta \widetilde{X}_-^p)\preceq \frac{1}{2}{\widetilde{X}}^{-1}H_I\big (\widetilde{X}\varDelta {\widetilde{S}}_-^p+\varDelta {\widetilde{X}}_-^p\widetilde{S}\big )^2{\widetilde{S}}^{-1}. \end{aligned}$$

From the above inequality and the third equation of (7) we can find

$$\begin{aligned} H_I(\varDelta {\widetilde{S}}_-^p\varDelta \widetilde{X}_-^p)\preceq \frac{1}{2}{\widetilde{X}}^{-1}(-{\widetilde{X}}\widetilde{S})^2{\widetilde{S}}^{-1}=\frac{1}{2}{\widetilde{X}}{\widetilde{S}}, \end{aligned}$$

which proves part (i).

Multiplying both sides of (11) by $\mathcal {\widetilde{E}}^{-1}$ and using $\mathcal {{\widetilde{E}}}=\mathcal {{\widetilde{F}}}$, we obtain

$$\begin{aligned} vec(\varDelta \widetilde{X}^p_{-})+vec(\varDelta \widetilde{S}^p_{-})=\mathcal {\widetilde{E}}^{-1}vec\big ((-\widetilde{X}\widetilde{S})^{-}\big ). \end{aligned}$$

Taking 2-norm squared on both sides of the above equation and using $0=\mathrm{Tr}(\varDelta \widetilde{X}^p_{-}\varDelta \widetilde{S}^p_{-})=vec(\varDelta \widetilde{X}^p_{-})^Tvec(\varDelta \widetilde{S}^p_{-}),$ we can get

$$\begin{aligned}&\big \Vert vec(\varDelta \widetilde{X}^p_{-})\big \Vert ^2+\big \Vert vec(\varDelta \widetilde{S}^p_{-})\big \Vert ^2 =\big \Vert \mathcal {{\widetilde{E}}}^{-1}vec\big ((-\widetilde{X}\widetilde{S})^{-}\big )\big \Vert ^2 \nonumber \\&\quad =\Big (vec\big ((-\widetilde{X}\widetilde{S})^{-}\big )\Big )^T\mathcal {\widetilde{E}}^{-2}vec\big ((-\widetilde{X}\widetilde{S})^{-}\big ) \nonumber \\&\quad =\sum _{i=1}^n([-\lambda _i]^-)^2/\lambda _i=\sum _{i=1}^n\lambda _i=\mathrm{Tr}({\widetilde{X}}{\widetilde{S}})=n\mu . \end{aligned}$$

(18)

On the other hand, we have

$$\begin{aligned}&\Vert H_I(\varDelta {\widetilde{X}}_-^p\varDelta \widetilde{S}_-^p)\Vert _F\le \Vert \varDelta {\widetilde{X}}_-^p\varDelta \widetilde{S}_-^p\Vert _F\le \Vert \varDelta {\widetilde{X}}_-^p\Vert _F\Vert \varDelta \widetilde{S}_-^p\Vert _F \\&\quad =\big \Vert vec\big (\varDelta \widetilde{X}_-^p\big )\big \Vert \big \Vert vec\big (\varDelta \widetilde{S}_-^p\big )\big \Vert \\&\quad \le \frac{1}{2}\Big (\big \Vert vec(\varDelta \widetilde{X}^p_{-})\big \Vert ^2+\big \Vert vec(\varDelta \widetilde{S}^p_{-})\big \Vert ^2\Big ) \le \frac{n\mu }{2}, \end{aligned}$$

where the last inequality follows from (18). Thus we have completed the proof. $\square$

Lemma 2

Let ${\bar{\alpha }}_p$ be the largest possible step size such that (8) holds. Then

$$\begin{aligned} {\bar{\alpha }}_p\ge \frac{2}{1+\sqrt{1+\frac{4n}{\tau \beta }}}. \end{aligned}$$

Proof

We have

$$\begin{aligned}&\big \Vert \big [\tau \mu (\alpha _p)I-\widetilde{X}(\alpha _p)^{\frac{1}{2}}{\widetilde{S}}(\alpha _p)\widetilde{X}(\alpha _p)^{\frac{1}{2}}\big ]^+\big \Vert _F \\&\quad \le \big \Vert \big [H_{\widetilde{X}(\alpha _p)^{\frac{1}{2}}}\big (\tau \mu (\alpha _p)I-\widetilde{X}(\alpha _p)^{\frac{1}{2}}{\widetilde{S}}(\alpha _p)\widetilde{X}(\alpha _p)^{\frac{1}{2}}\big )\big ]^+\big \Vert _F \\&\quad =\big \Vert \big [\tau \mu (\alpha _p)I-H_I\big (\widetilde{X}(\alpha _p){\widetilde{S}}(\alpha _p)\big )\big ]^+\big \Vert _F \\&\quad =\big \Vert \big [(1-\alpha _p)\big (\tau \mu I-{\widetilde{X}}\widetilde{S}\big )-\alpha _p^2H_I(\varDelta {\widetilde{X}}_-^p\varDelta \widetilde{S}_-^p)\big ]^+\big \Vert _F \\&\quad \le (1-\alpha _p)\big \Vert [\tau \mu I-{\widetilde{X}}\widetilde{S}]^+\big \Vert _F+\alpha _p^2\big \Vert [-H_I(\varDelta \widetilde{X}_-^p\varDelta {\widetilde{S}}_-^p)\big ]^+\big \Vert _F\\&\quad =(1-\alpha _p)\big \Vert \big [\tau \mu I-{\widetilde{X}}\widetilde{S}\big ]^+\big \Vert _F+\alpha _p^2\big \Vert \big [H_I(\varDelta \widetilde{X}_-^p\varDelta {\widetilde{S}}_-^p)\big ]^-\big \Vert _F,\\&\quad \le (1-\alpha _p)\frac{\tau \beta \mu }{2}+\alpha _p^2\big \Vert H_I(\varDelta \widetilde{X}_-^p\varDelta {\widetilde{S}}_-^p)\big \Vert _F \\&\quad \le (1-\alpha _p)\frac{\tau \beta \mu }{2}+\frac{n\mu }{2}\alpha _p^2, \end{aligned}$$

where the first inequality is due to [14, Lemma 3.3], the second equality follows with equations (16) and (17), the second inequality used [14, Proposition 3.1], the third inequality follows from the fact that $\Vert [H_I(\varDelta {\widetilde{X}}_-^p\varDelta \widetilde{S}_-^p)]^-\Vert _F\le \Vert H_I(\varDelta {\widetilde{X}}_-^p\varDelta \widetilde{S}_-^p)\Vert _F$ and $({\widetilde{X}}, y, {\widetilde{S}})\in {\mathcal {N}}(\tau , \frac{\beta }{2})$ and the last inequality is concluded from Lemma 1 (ii).

Thus $({\widetilde{X}}(\alpha _p), y(\alpha _p), \widetilde{S}(\alpha _p))\in {\mathcal {N}}(\tau , \beta )$ if

$$\begin{aligned} (1-\alpha _p)\frac{\tau \beta \mu }{2}+\frac{n\mu }{2}\alpha _p^2\le \tau \beta \mu (\alpha _p)=\tau \beta (1-\alpha _p)\mu , \end{aligned}$$

or by rearranging,

$$\begin{aligned} f(\alpha _p):=\frac{n}{2}\alpha _p^2+\frac{\tau \beta }{2}\alpha _p-\frac{\tau \beta }{2}\le 0. \end{aligned}$$

Therefore, the largest $\alpha _p$ satisfying the above inequality is the largest positive root of $f(\alpha _p)=0$, which is $\frac{2}{1+\sqrt{1+\frac{4n}{\tau \beta }}}$. Therefore, for all $0\le \alpha _p\le \frac{2}{1+\sqrt{1+\frac{4n}{\tau \beta }}}$, we have $f(\alpha _p)\le 0$. Thus we have completed the proof. $\square$

4.2 Analysis of the corrector step

From (15), together with (9) and (10), we obtain

$$\begin{aligned} H_I\big ({\widetilde{X}}(\alpha ){\widetilde{S}}(\alpha )\big )=&H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p)) \nonumber \\&+\,\alpha _1\big ([\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p){\widetilde{S}}(\alpha _p))]^--\alpha _pH_I(\varDelta \widetilde{X}^p_-\varDelta {\widetilde{S}}^p_-)\big ) \nonumber \\&+\,\alpha _2[\tau \mu (\alpha _p)I-H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))]^++H_I\big (\varDelta {\widetilde{X}}(\alpha )\varDelta \widetilde{S}(\alpha )\big ),\nonumber \\ \end{aligned}$$

(19)

and the duality gap corresponding to the corrector step is as follows

$$\begin{aligned} \mu (\alpha )=&\frac{1}{n}\mathrm{Tr}\big (H_I\big (\widetilde{X}(\alpha ){\widetilde{S}}(\alpha )\big )\big ) =\mu (\alpha _p) \nonumber \\&+\,\frac{\alpha _1}{n}\mathrm{Tr}\big ([\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^-\big ) \nonumber \\&+\,\frac{\alpha _2}{n}\mathrm{Tr}\big ([\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p){\widetilde{S}}(\alpha _p))]^+\big ). \end{aligned}$$

(20)

Furthermore, using $\mathrm{Tr}(H_I(M))=\mathrm{Tr}(M)$, it is easy to see that

$$\begin{aligned} \mathrm{Tr}\big ([\tau \mu (\alpha _p)I-H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))]^-\big )\le -(1-\tau )n\mu (\alpha _p) \end{aligned}$$

and

$$\begin{aligned}&\mathrm{Tr}\big ([\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^+\big )\le \sqrt{n}\big \Vert [\tau \mu (\alpha _p)I-\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p)]^+\big \Vert _F\\&\quad \le \sqrt{n}\tau \beta \mu (\alpha _p). \end{aligned}$$

From these inequalities and (20) it follows that

$$\begin{aligned} \mu (\alpha )\le \big (1-(1-\tau )\alpha _1+\alpha _2\tau \beta /\sqrt{n}\big )\mu (\alpha _p), \end{aligned}$$

(21)

and

$$\begin{aligned} \mu (\alpha )\ge \mu (\alpha _p)+\frac{\alpha _1}{n}\mathrm{Tr}\big (-{\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p)\big )=(1-\alpha _1)\mu (\alpha _p). \end{aligned}$$

(22)

Lemma 3

Let ${\overline{G}}=\mathcal {\widetilde{E}}(\alpha _p)^{-1}\mathcal {{\widetilde{F}}}(\alpha _p), \alpha _p\le \frac{\alpha _2}{2}\sqrt{\frac{\tau \beta }{2n}}, \alpha _1\le \alpha _2\sqrt{\frac{\tau \beta }{2n}}, \beta \le \frac{1}{3}$ and $\tau \le \frac{1}{3}$. If $(\widetilde{X}(\alpha _p), y(\alpha _p), \widetilde{S}(\alpha _p))\in {\mathcal {N}}(\tau , \beta )$, then we have

$$\begin{aligned} \big \Vert H_I\big (\varDelta \widetilde{X}(\alpha )\varDelta \widetilde{S}(\alpha )\big )\big \Vert _F\le \frac{6}{10}\alpha _2^2\tau \beta \mu {\sqrt{\mathrm{cond}}({\overline{G}})}. \end{aligned}$$

Proof

Notifying the definition $H_I(\cdot )$ and the properties of $\Vert \cdot \Vert _F$ and $\Vert \cdot \Vert$, we have

$$\begin{aligned}&\big \Vert H_I\big (\varDelta {\widetilde{X}}(\alpha )\varDelta \widetilde{S}(\alpha )\big )\big \Vert _F\le \big \Vert \varDelta \widetilde{X}(\alpha )\varDelta \widetilde{S}(\alpha )\big \Vert _F\le \big \Vert \varDelta \widetilde{X}(\alpha )\big \Vert _F\big \Vert \varDelta {\widetilde{S}}(\alpha )\big \Vert _F~~\nonumber \\&\quad =\big \Vert vec\big (\varDelta \widetilde{X}(\alpha )\big )\big \Vert \big \Vert vec\big (\varDelta \widetilde{S}(\alpha )\big )\big \Vert \nonumber \\&\quad \le \frac{\sqrt{\mathrm{cond}}({\overline{G}})}{2}\Big (\big \Vert \overline{G}^{-\frac{1}{2}}vec\big (\varDelta \widetilde{X}(\alpha )\big )\big \Vert ^2+\big \Vert \overline{G}^{\frac{1}{2}}vec\big (\varDelta {\widetilde{S}}(\alpha )\big )\big \Vert ^2\Big ), \end{aligned}$$

(23)

where the last inequality is due to [16, Lemma 4.6]. From (12) and (13), we have

$$\begin{aligned}&\mathcal {{\widetilde{E}}}(\alpha _p)vec\big (\varDelta \widetilde{X}(\alpha )\big )+\mathcal {\widetilde{F}}(\alpha _p)vec\big (\varDelta \widetilde{S}(\alpha )\big ) \\&\quad =\alpha _1vec\big ([\tau \mu (\alpha _p) I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^-\big ) -\alpha _1\alpha _p vec H_I\big (\varDelta {\widetilde{X}}^p_-\varDelta \widetilde{S}^p_-\big )\\&\qquad +\,\alpha _2vec\big ([\tau \mu (\alpha _p) I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^+\big ). \end{aligned}$$

Multiplying both sides of the above equation by $(\mathcal {{\widetilde{E}}}(\alpha _p)\mathcal {\widetilde{F}}(\alpha _p))^{-\frac{1}{2}}$ and taking norm-squared on both side of the resulting equation, we obtain

$$\begin{aligned}&\big \Vert {{\overline{G}}}^{-\frac{1}{2}}vec\big (\varDelta \widetilde{X}(\alpha )\big )\big \Vert ^2+\big \Vert \overline{G}^{\frac{1}{2}}vec\big (\varDelta \widetilde{S}(\alpha )\big )\big \Vert ^2 \\&\quad \le \Big (\alpha _1\big \Vert (\mathcal {\widetilde{E}}(\alpha _p)\mathcal {\widetilde{F}}(\alpha _p))^{-\frac{1}{2}}vec\big ([\tau \mu (\alpha _p) I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^-\big )\big \Vert \\&\qquad +\alpha _1\alpha _p\big \Vert (\mathcal {\widetilde{E}}(\alpha _p)\mathcal {{\widetilde{F}}}(\alpha _p))^{-\frac{1}{2}}vec H_I\big (\varDelta {\widetilde{X}}^p_-\varDelta \widetilde{S}^p_-\big )\big \Vert \\&\qquad +\,\alpha _2\big \Vert (\mathcal {{\widetilde{E}}}(\alpha _p)\mathcal {\widetilde{F}}(\alpha _p))^{-\frac{1}{2}}vec\big ([\tau \mu (\alpha _p) I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^+\big )\big \Vert \Big )^2\\&\quad \le \Big (\alpha _1\sqrt{\mathrm{Tr}\big (\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p)\big )}+\frac{\alpha _1\alpha _p}{\sqrt{\lambda _{\min }\big (\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p)\big )}}\big \Vert vec H_I\big (\varDelta {\widetilde{X}}^p_-\varDelta \widetilde{S}^p_-\big )\big \Vert \\&\qquad +\,\alpha _2\big \Vert (\mathcal {{\widetilde{E}}}(\alpha _p)\mathcal {\widetilde{F}}(\alpha _p))^{-\frac{1}{2}}\big \Vert \big \Vert vec\big ([\tau \mu (\alpha _p) I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^+\big )\big \Vert \Big )^2\\&\quad \le \Big (\alpha _1\sqrt{n\mu (\alpha _p)}+\frac{\alpha _1\alpha _p}{\sqrt{(1-\beta )\tau \mu (\alpha _p)}}\big \Vert H_I\big (\varDelta \widetilde{X}^p_-\varDelta \widetilde{S}^p_-\big )\big \Vert _F\\&\qquad +\,\frac{\alpha _2}{\sqrt{(1-\beta )\tau \mu (\alpha _p)}}\big \Vert [\tau \mu (\alpha _p) I-\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p)]^+\big \Vert _F\Big )^2\\&\quad \le \Big (\alpha _1\sqrt{n\mu (\alpha _p)}+\frac{n\mu \alpha _1\alpha _p}{2\sqrt{(1-\beta )\tau \mu (\alpha _p)}} +\frac{\alpha _2}{\sqrt{(1-\beta )\tau \mu (\alpha _p)}}\tau \beta \mu (\alpha _p)\Big )^2~~~\\&\quad =\left( \Big (\alpha _1\sqrt{n}+\frac{\alpha _2\sqrt{\tau }\beta }{\sqrt{1-\beta }}\Big )\sqrt{\mu (\alpha _p)} +\frac{n\alpha _1\alpha _p}{2\sqrt{(1-\alpha _p)(1-\beta )\tau }}\sqrt{\mu }\right) ^2, \\&\quad \le \left( \Big (\frac{1}{\sqrt{2}}+\frac{\sqrt{\beta }}{\sqrt{1-\beta }}\Big )\alpha _2\sqrt{\tau \beta \mu (\alpha _p)} +\frac{\alpha _2\sqrt{\beta }}{8\sqrt{(1-\alpha _p)(1-\beta )}}\alpha _2\sqrt{\tau \beta \mu }\right) ^2\\&\quad \le \left( \alpha _2\sqrt{\tau \beta \mu (\alpha _p)} +\frac{1}{8\sqrt{3}}\sqrt{\frac{9\sqrt{2}}{6\sqrt{2}-1}}\alpha _2\sqrt{\tau \beta \mu }\right) ^2\\&\quad \le \Big (1+\frac{19}{202}\Big )^2\alpha _2^2\tau \beta \mu =\Big (\frac{221}{202}\Big )^2 \alpha _2^2\tau \beta \mu \le \frac{6}{5}\alpha _2^2\tau \beta \mu , \end{aligned}$$

where the argument for the second inequality is similar to the one given for the proof of [14, Lemma 5.10] and noticing that $\lambda _{\min }(\mathcal {{\widetilde{E}}}(\alpha _p)\mathcal {\widetilde{F}}(\alpha _p))=\lambda _{\min }({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))\ge (1-\beta )\tau \mu (\alpha _p)$, the four inequality follows from Lemma 1 and $({\widetilde{X}}(\alpha _p), y(\alpha _p), {\widetilde{S}}(\alpha _p))\in {\mathcal {N}}(\tau , \beta )$ and the last equality is due to (17). Substituting this bound into (23), we obtain the inequality in the lemma. $\square$

Lemma 4

Let

$$\begin{aligned}&\varGamma (\alpha ):=H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))+\alpha _1\big ([\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^-\\&\quad -\alpha _pH_I(\varDelta \widetilde{X}^p_-\varDelta \widetilde{S}^p_-)\big )+\alpha _2[\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p){\widetilde{S}}(\alpha _p))]^+. \end{aligned}$$

If $({\widetilde{X}}(\alpha _p), y(\alpha _p), \widetilde{S}(\alpha _p))\in {\mathcal {N}}(\tau , \beta ),$ then

$$\begin{aligned} \lambda _{\min }(\varGamma (\alpha ))\ge (1-\beta )\tau \mu (\alpha _p)+\alpha _2\beta \tau \mu (\alpha _p)-\frac{\alpha _1\alpha _p n\mu }{2}. \end{aligned}$$

Proof

We first consider the position of $\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p){\widetilde{S}}(\alpha _p))\succeq 0$. In this case, we have

$$\begin{aligned} \lambda _{\min }(\varGamma (\alpha ))=&\lambda _{\min }\Big (H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))-\alpha _1\alpha _pH_I(\varDelta \widetilde{X}^p_-\varDelta \widetilde{S}^p_-)\\&\qquad +\alpha _2[\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p){\widetilde{S}}(\alpha _p))]^+\Big )\\&\quad =\lambda _{\min }\Big (H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))-\alpha _1\alpha _pH_I(\varDelta \widetilde{X}^p_-\varDelta \widetilde{S}^p_-)\\&\qquad +\,\alpha _2[\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p){\widetilde{S}}(\alpha _p))]\Big )~~\\&\quad =\lambda _{\min }\Big ((1-\alpha _2)H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))+\alpha _2\tau \mu (\alpha _p)I\\&\qquad -\,\alpha _1\alpha _pH_I(\varDelta \widetilde{X}^p_-\varDelta {\widetilde{S}}^p_-)\Big )\\&\quad \ge \lambda _{\min }\Big ((1-\alpha _2)H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))+\alpha _2\tau \mu (\alpha _p)I\Big ) \\&\qquad -\,\alpha _1\alpha _p\big \Vert H_I(\varDelta \widetilde{X}^p_-\varDelta {\widetilde{S}}^p_-)\big \Vert _F\\&\quad =(1-\alpha _2)\lambda _{\min }\big (H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))\big )+\alpha _2\tau \mu (\alpha _p)\\&\qquad -\alpha _1\alpha _p\big \Vert H_I(\varDelta \widetilde{X}^p_-\varDelta {\widetilde{S}}^p_-)\big \Vert _F\\&\quad \ge (1-\alpha _2)\lambda _{\min }\big ({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p)\big )+\alpha _2\tau \mu (\alpha _p)\\&\qquad -\alpha _1\alpha _p\big \Vert H_I(\varDelta \widetilde{X}^p_-\varDelta {\widetilde{S}}^p_-)\big \Vert _F\\&\quad \ge (1-\alpha _2)(1-\beta )\tau \mu (\alpha _p)+\alpha _2\tau \mu (\alpha _p)-\frac{\alpha _1\alpha _p n\mu }{2} \\&\quad =(1-\beta )\tau \mu (\alpha _p)+\alpha _2\beta \tau \mu (\alpha _p)-\frac{\alpha _1\alpha _p n\mu }{2}, \end{aligned}$$

where the second inequality is due to Lemma 1.

Now, let us consider the case that $\tau \mu ({\bar{\alpha }}_p)I-H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))\preceq 0$. In this way, we have

$$\begin{aligned} \lambda _{\min }(\varGamma (\alpha ))=&\lambda _{\min }\Big (H_I(\widetilde{X}({\bar{\alpha }}_p)\widetilde{S}({\bar{\alpha }}_p))+\alpha _1[\tau \mu (\alpha _p)I-H_I(\widetilde{X}({\bar{\alpha }}_p)\widetilde{S}({\bar{\alpha }}_p))]^-\\&\qquad -\alpha _1\alpha _pH_I(\varDelta {\widetilde{X}}^p_-\varDelta {\widetilde{S}}^p_-)\Big )\\&=\lambda _{\min }\Big (H_I({\widetilde{X}}(\alpha _p)\widetilde{S}({\bar{\alpha }}_p))+\alpha _1[\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]~~\\&\qquad -\alpha _1\alpha _pH_I(\varDelta {\widetilde{X}}^p_-\varDelta \widetilde{S}^p_-)\Big )~~ \\&\ge \lambda _{\min }\Big (H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))+\alpha _1[\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]\big )\\&\qquad -\,\alpha _1\alpha _p\big \Vert H_I(\varDelta {\widetilde{X}}^p_-\varDelta \widetilde{S}^p_-)\Big \Vert _F \\&\ge \lambda _{\min }\Big (H_I(\widetilde{X}(\alpha _p){\widetilde{S}}(\alpha _p))+\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))\Big ) \\&\qquad -\,\alpha _1\alpha _p\big \Vert H_I(\varDelta {\widetilde{X}}^p_-\varDelta \widetilde{S}^p_-)\big \Vert _F\\&\ge \tau \mu (\alpha _p)-\frac{\alpha _1\alpha _p n\mu }{2}-\beta \tau \mu (\alpha _p)+\beta \tau \mu (\alpha _p)\\&\ge (1-\beta )\tau \mu (\alpha _p)+\alpha _2\beta \tau \mu (\alpha _p)-\frac{\alpha _1\alpha _p n\mu }{2}. \end{aligned}$$

Thus we have completed the proof. $\square$

Lemma 5

Let $\alpha _p\le \frac{\alpha _2}{2}\sqrt{\frac{\tau \beta }{2n}}, \alpha _1\le \alpha _2\sqrt{\frac{\tau \beta }{2n}}, \beta \le \frac{1}{3}, \tau \le \frac{1}{3}$ and $\alpha _2\le \frac{1}{\sqrt{{\mathrm{cond}}({\overline{G}})}}$. If $({\widetilde{X}}(\alpha _p), y(\alpha _p), \widetilde{S}(\alpha _p))\in {\mathcal {N}}(\tau , \beta )$, then $\widetilde{X}(\alpha )$ and ${\widetilde{S}}(\alpha )$ are in ${\mathcal {S}}^n_{++}$.

Proof

Using (19) and the fact that $\lambda _{\min }(\cdot )$ is a homogeneous concave function on the space of symmetric matrices, we have

$$\begin{aligned}&\lambda _{\min }\Big (H_I\big ({\widetilde{X}}(\alpha )\widetilde{S}(\alpha )\big )\Big )=\lambda _{\min }\Big (\varGamma (\alpha )+H_I\big (\varDelta \widetilde{X}(\alpha )\varDelta {\widetilde{S}}(\alpha )\big )\Big ) \\&\ge \lambda _{\min }\big (\varGamma (\alpha )\big )-\big \Vert H_I\big (\varDelta \widetilde{X}(\alpha )\varDelta {\widetilde{S}}(\alpha )\big )\big \Vert _F \\&\quad \ge \Big ((1-\beta )\tau +\alpha _2\beta \tau -\frac{\alpha _1\alpha _p n}{2(1-\alpha _p)}\Big )\mu (\alpha _p) -\frac{6}{10}\alpha _2^2\tau \beta \mu {\sqrt{\mathrm{cond}}({\overline{G}})}\\&\ge \Big (1-\beta +\alpha _2\beta -\frac{3\sqrt{2}\beta \alpha _2}{4(6\sqrt{2}-1)} -\frac{36\sqrt{2}\beta \alpha _2}{10(6\sqrt{2}-1)}\Big )\tau \mu (\alpha _p)\\&\quad \ge \Big (1-\beta -\frac{3\sqrt{2}\beta \alpha _2}{4(6\sqrt{2}-1)} -\frac{36\sqrt{2}\beta \alpha _2}{10(6\sqrt{2}-1)}\Big )\tau \mu (\alpha _p)\\&\ge \Big (\frac{2}{3}-\frac{1}{2\sqrt{2}(6\sqrt{2}-1)}-\frac{6\sqrt{2}}{5(6\sqrt{2}-1)}\Big )\tau \mu (\alpha _p)>0, \end{aligned}$$

where the second inequality is due to Lemmas 3 and 4 and (17). By using continuity, it follows that ${\widetilde{X}}(\alpha )$ and ${\widetilde{S}}(\alpha )$ are in ${\mathcal {S}}^n_{++}$ since ${\widetilde{X}}(\alpha _p)$ and $\widetilde{S}(\alpha _p)$ are. The proof is completed. $\square$

Lemma 6

Suppose $({\widetilde{X}}, y, {\widetilde{S}})\in {\mathcal {N}}(\tau , \beta /2)$ and $\varGamma (\alpha )$ is defined as in Lemma 4. If $({\widetilde{X}}(\alpha _p), y(\alpha _p), \widetilde{S}(\alpha _p))\in {\mathcal {N}}(\tau , \beta )$, then we have

$$\begin{aligned} \big \Vert \big [\tau \mu (\alpha )I-\varGamma (\alpha )\big ]^+\big \Vert _F\le (1-\alpha _2)(1-\alpha _p)\frac{\beta }{2}\tau \mu . \end{aligned}$$

Proof

Assume that the eigenvalues of $\lambda _i(\alpha _p):=\lambda _i(H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p)))$ are ordered so that $\tau \mu (\alpha _p)-\lambda _i(\alpha _p)>0$ for each $i=1, \ldots , k-1$ and $\tau \mu (\alpha _p)-\lambda _i(\alpha _p)\le 0$ for $i=k, \ldots , n$. Now, let us consider the diagonal elements of $\varLambda (\alpha _p)+\alpha _1[\tau \mu (\alpha _p)I-\varLambda (\alpha _p)]^--\frac{1}{2}\alpha _1 \alpha _p\lambda _i+\alpha _2[\tau \mu (\alpha _p)I-\varLambda (\alpha _p)]^+$, where $\varLambda (\alpha _p)=\mathrm{diag}(\lambda (\alpha _p))$. In this way, for $i=1, \ldots , k-1, \lambda _i(\alpha _p)-\frac{1}{2}\alpha _1\alpha _p\lambda _i+\alpha _2\big (\tau \mu (\alpha _p)-\lambda _i(\alpha _p)\big ) =(1-\alpha _2)\lambda _i(\alpha _p)-\frac{1}{2}\alpha _1\alpha _p\lambda _i+\alpha _2\tau \mu (\alpha _p)$, together with (21), we obtain

$$\begin{aligned}&\tau \mu (\alpha )-\big ((1-\alpha _2)\lambda _i(\alpha _p)-\frac{1}{2}\alpha _1\alpha _p\lambda _i+\alpha _2\tau \mu (\alpha _p)\big ) \\&\quad \le \tau \big (1-(1-\tau )\alpha _1+\alpha _2\tau \beta /\sqrt{n}\big )\mu (\alpha _p)\\&\qquad -\big ((1-\alpha _2)(1-\alpha _p+\frac{1}{2}\alpha _p^2)\lambda _i-\frac{1}{2}\alpha _1\alpha _p\lambda _i+\alpha _2\tau \mu (\alpha _p)\big )\\&\quad =\tau \big (1-(1-\tau )\alpha _1+\alpha _2\tau \beta /\sqrt{n}\big )\mu (\alpha _p) \\&\qquad -\big (1-\alpha _2-\alpha _p+\alpha _2\alpha _p+\frac{1}{2}\alpha _p^2- \frac{1}{2}\alpha _2\alpha _p^2-\frac{1}{2}\alpha _1\alpha _p\big )\lambda _i-\alpha _2\tau \mu (\alpha _p)\\&\quad =\tau \mu (1-\alpha _p-\alpha _1+\alpha _1\alpha _p)+\tau ^2\mu (1-\alpha _p)\big (\alpha _1+\alpha _2\beta /\sqrt{n}\big )\\&\qquad -\big (1-\alpha _2-\alpha _p+\alpha _2\alpha _p+\frac{1}{2}\alpha _p^2- \frac{1}{2}\alpha _2\alpha _p^2-\frac{1}{2}\alpha _1\alpha _p\big )\lambda _i-\alpha _2\tau \mu +\alpha _2\alpha _p\tau \mu \\&\quad \le \big (1-\alpha _2-\alpha _p+\alpha _2\alpha _p+\frac{1}{2}\alpha _p^2- \frac{1}{2}\alpha _2\alpha _p^2-\frac{1}{2}\alpha _1\alpha _p\big )(\tau \mu -\lambda _i)\\&\qquad +\Big (-1+\frac{1}{2}\sqrt{\frac{\beta \tau }{2n}}+\tau +\sqrt{2\beta \tau }+\frac{1}{4}\sqrt{\frac{\beta \tau }{2n}}\Big )\alpha _1\tau \mu -\tau ^2\mu \alpha _p\big (\alpha _1+\alpha _2\beta /\sqrt{n}\big )\\&\qquad -\frac{1}{2}(1-\alpha _2)\tau \mu {\bar{\alpha }}_p^2\\&\quad \le \big (1-\alpha _2-\alpha _p+\alpha _2\alpha _p+\frac{1}{2}\alpha _p^2- \frac{1}{2}\alpha _2\alpha _p^2-\frac{1}{2}\alpha _1\alpha _p\big )(\tau \mu -\lambda _i)\\&\quad \le \Big ((1-\alpha _2)(1-\alpha _p)+\frac{1}{2}\alpha _p(\alpha _p-\alpha _1)\Big )(\tau \mu -\lambda _i) \\&\quad \le (1-\alpha _2)(1-\alpha _p)(\tau \mu -\lambda _i), \end{aligned}$$

where the last inequality follows if $\tau \mu -\lambda _i>0$ for $i\in \{1, \ldots , k-1\}$. Now, we consider the case $\tau \mu -\lambda _i\le 0$ for $i\in \{1, \ldots , k-1\}$. Using (16) and (17), we derive that

$$\begin{aligned} 0\prec \tau \mu (\alpha _p)I-H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))=(1-\alpha _p)(\tau \mu I-{\widetilde{X}}\widetilde{S})-\alpha _p^2H_I(\varDelta {{\widetilde{X}}}_-^p\varDelta {\widetilde{S}}_-^p), \end{aligned}$$

which implies $H_I(\varDelta {\widetilde{X}}_-^p\varDelta {{\widetilde{S}}}_-^p)\prec 0$. Therefore, from (16), one has

$$\begin{aligned}&H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))-\alpha _1\alpha _pH_I(\varDelta \widetilde{X}^p_-\varDelta \widetilde{S}^p_-)+\alpha _2[\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p){\widetilde{S}}(\alpha _p))]\\&\quad =(1-\alpha _2)(1-\alpha _p){\widetilde{X}}\widetilde{S}+((1-\alpha _2)\alpha _p^2-\alpha _1\alpha _p)H_I\big (\varDelta \widetilde{X}^p_-\varDelta {\widetilde{S}}^p_-\big )+\alpha _2\tau \mu (\alpha _p)I\\&\quad \succeq (1-\alpha _2)(1-\alpha _p)\tau \mu I+\alpha _2(1-\alpha _p)\tau \mu I=(1-\alpha _p)\tau \mu I, \end{aligned}$$

where the inequality is due to $\tau \mu -\lambda _i\le 0$ and (17).

From the last inequality and (21) we deduce that

$$\begin{aligned}&\tau \mu (\alpha )-\lambda _i\Big (H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))-\alpha _1\alpha _pH_I(\varDelta \widetilde{X}^p_-\varDelta \widetilde{S}^p_-)+\alpha _2[\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p){\widetilde{S}}(\alpha _p))]\Big )\\&\quad \le \tau \big (1-(1-\tau )\alpha _1+\alpha _2\tau \beta /\sqrt{n}\big )\mu (\alpha _p)-(1-\alpha _p)\tau \mu \\&\quad =\Big (-\frac{1-\tau }{\sqrt{2}}+\sqrt{\tau \beta }\Big )\alpha _2\tau \mu (\alpha _p)\sqrt{\frac{\beta \tau }{n}} \le \Big (\frac{1-\sqrt{2}}{3}\Big )\alpha _2\tau \mu (\alpha _p)\sqrt{\frac{\beta \tau }{n}}\le 0, \end{aligned}$$

where the equality is due to (17). For $i=k, \ldots , n,$ by (16), we have

$$\begin{aligned}&\varGamma (\alpha )=(1-\alpha _1)H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))+\alpha _1\tau \mu (\alpha _p)I-\alpha _1\alpha _pH_I(\varDelta \widetilde{X}^p_-\varDelta {\widetilde{S}}^p_-)\\&\quad =(1-\alpha _1)(1-\alpha _p){\widetilde{X}}\widetilde{S}+\big ((1-\alpha _1)\alpha _p^2-\alpha _1\alpha _p\big )H_I(\varDelta \widetilde{X}^p_-\varDelta {\widetilde{S}}^p_-)+\alpha _1\tau \mu (\alpha _p)I\\&\quad \succeq \Big (1-\alpha _p-\alpha _1+\alpha _1\alpha _p+\frac{1}{2}\alpha _p^2- \frac{1}{2}\alpha _p^2\alpha _1-\frac{1}{2}\alpha _1\alpha _p\Big )\widetilde{X}{\widetilde{S}}+\alpha _1\tau \mu (\alpha _p)I, \end{aligned}$$

where the inequality follows from Lemma 1 (i). Therefore, we have

$$\begin{aligned}&\tau \mu (\alpha )-\Big (1-\alpha _p-\alpha _1+\alpha _1\alpha _p+\frac{1}{2}\alpha _p^2- \frac{1}{2}\alpha _p^2\alpha _1-\frac{1}{2}\alpha _1\alpha _p\Big )\lambda _i-\alpha _1\tau \mu (\alpha _p)\\&\quad \le \tau \big (1-(1-\tau )\alpha _1+\alpha _2\tau \beta /\sqrt{n}\big )\mu (\alpha _p)-\alpha _1\tau \mu (\alpha _p)\\&\qquad -\Big (1-\alpha _p-\alpha _1+\alpha _1\alpha _p+\frac{1}{2}\alpha _p^2- \frac{1}{2}\alpha _p^2\alpha _1-\frac{1}{2}\alpha _1\alpha _p\Big )\lambda _i\\&\quad \le \big (1-2\alpha _1+\tau \alpha _1+\alpha _1\sqrt{2\tau \beta }\big )\lambda _i(\alpha _p) \\&\qquad -\Big (1-\alpha _p-\alpha _1+\alpha _1\alpha _p+\frac{1}{2}\alpha _p^2- \frac{1}{2}\alpha _p^2\alpha _1-\frac{1}{2}\alpha _1\alpha _p\Big )\lambda _i\\&\quad \le \big (1-2\alpha _1+\tau \alpha _1+\alpha _1\sqrt{2\tau \beta }\big )\big (1-\alpha _p+\frac{1}{2}\alpha _p^2\big )\lambda _i\\&\qquad -\Big (1-\alpha _p-\alpha _1+\alpha _1\alpha _p+\frac{1}{2}\alpha _p^2- \frac{1}{2}\alpha _p^2\alpha _1-\frac{1}{2}\alpha _1\alpha _p\Big )\lambda _i\\&\quad \le \Big (-1+\tau +\sqrt{2\tau \beta }+\frac{3}{4}\sqrt{\frac{\beta \tau }{2n}}\Big )\alpha _1\lambda _i \le \Big (-\frac{2}{3}+\frac{11}{12\sqrt{2}}\Big )\alpha _1\lambda _i\\&\quad \le 0. \end{aligned}$$

Therefore, we can find

$$\begin{aligned}&\big \Vert \big [\tau \mu (\alpha )I-\varGamma (\alpha )\big ]^+\big \Vert _F \\&\quad =\big \Vert \big [\tau \mu (\alpha )I-\big (H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))+\alpha _1\big ([\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^-\\&\qquad -\alpha _pH_I(\varDelta {\widetilde{X}}^p_-\varDelta \widetilde{S}^p_-)\big )+\alpha _2[\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p){\widetilde{S}}(\alpha _p))]^+\big )\big ]^+\big \Vert _F\\&\quad \le \big \Vert \big [\tau \mu (\alpha )I-\big (H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))+\alpha _1[\tau \mu (\alpha _p)I-H_I(\widetilde{X}(\alpha _p)\widetilde{S}(\alpha _p))]^-\\&\qquad -\frac{1}{2}\alpha _1\alpha _p{\widetilde{X}}\widetilde{S}+\alpha _2[\tau \mu (\alpha _p)I-H_I({\widetilde{X}}(\alpha _p)\widetilde{S}(\alpha _p))]^+\big )\big ]^+\big \Vert _F\\&\quad =\big \Vert \big [Q\big (\tau \mu (\alpha )I-\big (\varLambda (\alpha _p)+\alpha _1[\tau \mu (\alpha _p)I-\varLambda (\alpha _p)]^- -\frac{1}{2}\alpha _1\alpha _p\varLambda \\&\qquad +\alpha _2[\tau \mu (\alpha _p)I-\varLambda (\alpha _p)]^+\big )\big )Q^T\big ]^+\big \Vert _F \\&\quad =\big \Vert \big [\tau \mu (\alpha )I-\big (\varLambda (\alpha _p)+\alpha _1[\tau \mu (\alpha _p)I -\varLambda (\alpha _p)]^--\frac{1}{2}\alpha _1\alpha _p\varLambda \\&\qquad +\alpha _2[\tau \mu (\alpha _p)I-\varLambda (\alpha _p)]^+\big )\big ]^+\big \Vert _F\\&\quad \le (1-\alpha _2)(1-\alpha _p)\big \Vert \big [\tau \mu I-\varLambda \big ]^+\big \Vert _F \\&\quad =(1-\alpha _2)(1-\alpha _p)\big \Vert Q\big [\tau \mu I-\varLambda \big ]^+Q^T\big \Vert _F\\&\quad =(1-\alpha _2)(1-\alpha _p)\big \Vert \big [\tau \mu I-{\widetilde{X}}\widetilde{S}\big ]^+\big \Vert _F\le (1-\alpha _2)(1-\alpha _p)\frac{\beta }{2}\tau \mu , \end{aligned}$$

where the first inequality is followed by Lemma 1 (i), the second equality used [14, Lemma 3.2] and the last inequality is due to the fact that $({\widetilde{X}}, y, \widetilde{S})\in {\mathcal {N}}(\tau , \beta /2)$. The proof is completed. $\square$

Proposition 1

Suppose $\alpha _p\le \frac{\alpha _2}{2}\sqrt{\frac{\tau \beta }{2n}}, \alpha _1=\alpha _2\sqrt{\frac{\tau \beta }{2n}}, \beta \le \frac{1}{3}, \tau \le \frac{1}{3}$ and $\alpha _2\le \frac{1}{2\sqrt{\mathrm{cond}({\overline{G}})}}$, where $\overline{G}={\mathcal {E}}(\alpha _p)^{-1}{\mathcal {F}}(\alpha _p)$. If the current iterate $({\widetilde{X}}, y, {\widetilde{S}})\in {\mathcal {N}}(\tau , \beta /2)$ , then

$$\begin{aligned} ({\widetilde{X}}(\alpha ), y(\alpha ), \widetilde{S}(\alpha ))\in {\mathcal {N}}(\tau , \beta /2). \end{aligned}$$

Proof

We have

$$\begin{aligned}&\big \Vert \big [\tau \mu (\alpha )I-{\widetilde{X}}(\alpha )^{1/2}\widetilde{S}(\alpha ){\widetilde{X}}(\alpha )^{1/2}\big ]^+ \big \Vert _F \\&\quad \le \big \Vert \big [H_{\widetilde{X}(\alpha )^{1/2}}\big (\tau \mu (\alpha )I-\widetilde{X}(\alpha )^{1/2}{\widetilde{S}}(\alpha )\widetilde{X}(\alpha )^{1/2}\big )\big ]^+\big \Vert _F \\&\quad =\big \Vert \big [\tau \mu (\alpha )I-H_I\big ({\widetilde{X}}(\alpha )\widetilde{S}(\alpha )\big )\big ]^+\big \Vert _F \\&\quad =\big \Vert \big [\tau \mu (\alpha )I-\varGamma (\alpha )-H_I\big (\varDelta \widetilde{X}(\alpha )\varDelta {\widetilde{S}}(\alpha )\big )\big ]^+\big \Vert _F \\&\quad \le \big \Vert \big [\tau \mu (\alpha )I-\varGamma (\alpha )\big ]^+\big \Vert _F+\big \Vert \big [-H_I\big (\varDelta \widetilde{X}(\alpha )\varDelta {\widetilde{S}}(\alpha )\big )\big ]^+\big \Vert _F\\&\quad =\big \Vert \big [\tau \mu (\alpha )I-\varGamma (\alpha )\big ]^+\big \Vert _F+\big \Vert \big [H_I\big (\varDelta \widetilde{X}(\alpha )\varDelta {\widetilde{S}}(\alpha )\big )\big ]^-\big \Vert _F \\&\quad \le \big \Vert \big [\tau \mu (\alpha )I-\varGamma (\alpha )\big ]^+\big \Vert _F+\big \Vert H_I\big (\varDelta \widetilde{X}(\alpha )\varDelta {\widetilde{S}}(\alpha )\big )\big \Vert _F \\&\quad \le (1-\alpha _2)(1-\alpha _p)\frac{\beta }{2}\tau \mu +\frac{6}{10}\alpha _2^2\tau \beta \mu {\sqrt{\mathrm{cond}}(\overline{G})} \\&\quad =(1-\alpha _1)(1-\alpha _p)\frac{\beta }{2}\tau \mu \\&\qquad +\Big (\alpha _1-\alpha _2-\alpha _1\alpha _p+\alpha _2\alpha _p+\frac{6}{5}\alpha _2^2{\sqrt{\mathrm{cond}}({\overline{G}})}\Big )\frac{\beta }{2}\tau \mu \\&\quad \le (1-\alpha _1)(1-\alpha _p)\frac{\beta }{2}\tau \mu \\&\qquad +\Big (\sqrt{\frac{\beta \tau }{2n}}-1+\frac{\alpha _2}{2}\sqrt{\frac{\beta \tau }{2n}}+\frac{6}{5}\alpha _2{\sqrt{\mathrm{cond}}({\overline{G}})}\Big )\frac{\beta }{2}\alpha _2\tau \mu \\&\quad \le (1-\alpha _1)(1-\alpha _p)\frac{\beta }{2}\tau \mu +\Big ({\frac{1}{3\sqrt{2}}}-1+\frac{1}{12\sqrt{2}}+\frac{3}{5}\Big )\frac{\beta }{2}\alpha _2\tau \mu \\&\quad \le (1-\alpha _1)(1-\alpha _p)\frac{\beta }{2}\tau \mu =(1-\alpha _1)\frac{\beta }{2}\tau \mu (\alpha _p)\le \frac{\beta }{2}\tau \mu (\alpha ) \end{aligned}$$

where the first inequality is followed from [14, Lemma 3.3], the second equality is from (19) and the definition $\varGamma (\alpha )$. The fourth step used from [14, Proposition 3.1] and the fourth inequality is due to Lemmas 3 and 6. The last equality is due to (17) and the last inequality follows from (22). We have completed the proof. $\square$

We end this section by stating the main result of this paper, which establishes an iteration-complexity bound for the proposed algorithm.

Theorem 1

Suppose $\alpha _p\le \frac{\alpha _1}{2}=\frac{\alpha _2}{2}\sqrt{\frac{\beta \tau }{2n}}, \alpha _2=\frac{1}{2\sqrt{\mathrm{cond}}({\overline{G}})}, \beta \le \frac{1}{3}$ and $\tau \le \frac{1}{3}$ . Then the algorithm will terminate in ${\mathcal {O}}(\sqrt{n\kappa _{\infty }}\log \frac{\mathrm{Tr}(X^0S^0)}{\varepsilon })$ iterations with a solution such that $\mathrm{Tr}(XS)\le \varepsilon$, where $\kappa _{\infty }=\sup \{\mathrm{cond}({\overline{G}})^k, k=0,1, \ldots \}<\infty .$

Proof

By Lemma 2 and Proposition 1, we have

$$\begin{aligned} ({\widetilde{X}}(\alpha _p), y(\alpha _p), {\widetilde{S}}(\alpha _p))\in {\mathcal {N}}(\tau , \beta ), ({\widetilde{X}}(\alpha ), y(\alpha ), \widetilde{S}(\alpha ))\in {\mathcal {N}}(\tau , \beta /2). \end{aligned}$$

Using (21), we can find

$$\begin{aligned}&\mu (\alpha )\le \Big (1-(1-\tau )\alpha _1+\alpha _2\frac{\tau \beta }{\sqrt{n}}\Big )\mu (\alpha _p)\\&\quad =\Big (1-\alpha _2\big (1-\tau -\sqrt{2\beta \tau }\big )\sqrt{\frac{\beta \tau }{2n}}\Big )\mu (\alpha _p)\\&\quad \le \Big (1-\alpha _2\Big (1-\frac{1}{3}-\frac{\sqrt{2}}{3}\Big )\sqrt{\frac{\beta \tau }{2n}}\Big )\mu (\alpha _p)~~\\&\quad \le \left( 1-\frac{5}{52}\sqrt{\frac{\beta \tau }{2n\mathrm{cond}({\overline{G}})}}\right) \mu (\alpha _p) \\&\quad \le \left( 1-\frac{5}{52}\sqrt{\frac{\beta \tau }{2n\kappa _{\infty }}}\right) \mu (\alpha _p). \end{aligned}$$

By [24, Theorem 3.2] the lemma follows. $\square$

Table 1 Number of iterations and CPU time on SDO problems

5 Numerical results

In this section, we compare our algorithm (Algor.1) with the algorithms by Yang et al. in [25] (Algor.2) and Feng and Fang in [6] (Algor. 3) to test some SDO problems from [22]: Max-cut problem(Mc); Norm-min problem(Nm); Control problem(C); Graph partitioning problem (Gp); Lovasz theta number problem(Ltn); Random feasible SDP problem(Rfs); Education testing problem (Etp); Ideal GMRES polynomial problem (Igmres); logarithmic Chebyshev approximation problem(Logcheby); for the NT directions and give the results in Table 1. Numerical results were obtained by using MATLAB R2017a on an Intel Core i7 PC with 8GB RAM under Windows 10. The algorithms are stopped when $\mu \le \varepsilon \mu _0$ with $\varepsilon =10^{-5}$. In Table 1, we present the names of the test problems, the dimension of the blocks and the number of the constraint equations (denoted by (n, m)), the number of iterations (iter) and the total CPU time (time) for each algorithms. Also the notation “—” means that the algorithm is not able to solve the problem in less than 500s. We run 10 times for the same m and n and obtain the average results which presented in Table 1. From Table 1, it can be seen that not only is Algorithm 1 faster than the other two algorithms, but it is also better in terms of number of iterations.

6 Concluding remarks

In this paper, we presented a predictor-corrector path-following interior-point algorithm for SDO based on the large neighborhood. We proved that the algorithm has ${\mathcal {O}}(\sqrt{n\kappa _{\infty }}\log \frac{\mathrm{Tr}(X^0S^0)}{\varepsilon })$ iteration complexity bound which coincides with the currently best known theoretical complexity bound so far. Our algorithm was different from the existing wide neighborhood algorithms because it applied a new corrector strategy. Moreover, the numerical results show that our algorithm performs efficiently.