Spatial Autologistic Model with Generalized Dependent Parameter

Abstract

In the spatial autologistic model, the dependence parameter is often assumed to be a single value. To construct a spatial autologistic model with spatial heterogeneity, we introduce additional covariance in the dependence parameter, and the proposed model is suitable for the data with binary responses where the spatial dependency pattern varies with space. Both the maximum pseudo-likelihood (MPL) method for parameter estimation and the Bayesian information criterion (BIC) for model selection are provided. The exponential consistency between the maximum likelihood estimator and the maximum block independent likelihood estimator (MBILE) is proved for a particular case. Simulation results show that the MPL algorithm achieves satisfactory performance in most cases, and the BIC algorithm is more suitable for model selection. We illustrate the application of our proposed model by fitting the Bur Oak presence data within the driftless area in the midwestern USA.

1 Introduction

Spatial data with discrete responses appear very frequently in research on the distribution of species [14, 16, 23], the transmission of diseases [5, 10, 21], and land-use change [22]. For instance, binary response data can be used to describe the occurrence of certain wildlife species (e.g., one if present and zero if absent) [23]. For binary data, the spatial autologistic covariance model is one of the most well-known [4, 13]. Besag [4] proposed the spatial autologistic covariance model by modeling the conditional probability of the spatial observations with respect to their neighbors. In this model, the log-odds of the conditional probability have a linear form relating to the neighboring observations, where the dependency is described by spatial dependence parameters. Caragea and Kaiser [8] found that when the spatial dependence parameters in Besag’s model are large, the observed values will be very close to 1, which makes it difficult to interpret the practical meaning of the explanatory variable term in applications. To resolve this problem, Caragea and Kaiser [8] proposed the centered autologistic model by transforming the neighboring observations.

In a spatial autologistic model, the spatial dependence parameter $\eta _{ij}$ describes the influence of $Y_j$ on the conditional probability of $Y_i$. This parameter is often assumed to be invariant with locations, that is, $\eta _{ij} = \eta \cdot I \{ i \sim j \}$, where $I \{ \cdot \}$ is the indicator function, and $i\sim j$ means that the observation location $\varvec{s}_i$ corresponding to $Y_i$ is the neighborhood of the location $\varvec{s}_j$ corresponding to $Y_j$. For extensions on the dependence parameter, Augustin et al. [1] assumed that $\eta _{ij}$ is inversely proportional to the distance between these two locations. They fitted the data on the spatial distribution of wildlife by introducing an extra covariate. Bo et al. [5] used the same method to fit the record data on hand-foot-and-mouth disease in Mainland China. To fit a product recommendation model using the past purchase behavior data of customers, Moon and Russell [17] assumed that $\eta _{ij}$ has an exponential distribution structure, e.g., $\eta _{ij} = \sigma ^2 \exp (-\lambda \Vert \varvec{s}_i - \varvec{s}_j \Vert )$, where $\sigma ^2$ and $\lambda$ are unknown parameters. For anisotropy structure, Bardos [2] considered a spatial anisotropic neighboring structure, where $\eta _{ij}$ can have two different values, relating to the horizontal and vertical autocorrelation, respectively, within the set of neighbors. Caragea and Berg [7] introduced the spatial anisotropy structure by allowing $\eta _{ij}$ to be dependent on the direction of $\varvec{s}_i - \varvec{s}_j$. However, these extensions of $\eta _{ij}$ are only dependent on $\varvec{s}_i - \varvec{s}_j$, not on separate $\varvec{s}_i$ and $\varvec{s}_j$. In other words, the spatial autologistic models considered in these works are only those with spatial autocovariance structures invariant with spatial observation locations. Bo et al. [5] pointed out that this assumption of stationarity may not be suitable when the range of observations is extensive. For instance, let $Y_i$ be a binary response to the occurrence of a specific disease. The covariate representing the speed of spread may be related to the climate and socio-economic factors. In a heavily polluted area, the disease may be more likely to spread due to residents’ lack of immunity. A stationary spatial model may not fit the data when these factors vary in different locations.

When the observed values come from a continuous random variable, the data with spatial heterogeneity can be fitted by various non-stationary models. In the literature, the kernel convolution model is intuitive, which can be considered a Matérn covariance model with spatially variant parameters [19, 20]. Parker et al. [20] constructed the non-stationary model by dividing the observation region into small subregions and assigning parameters for each subregion with various values. The spatial autoregressive model is also a popular non-stationary model, including simultaneous and conditional autoregressive models. These two models are suitable for the cases where the data are observed from certain predetermined regions, e.g., the administrative divisions [12]. The construction of the conditional autoregressive model is similar to that of the spatial autologistic model. Let $Z_1, \ldots , Z_n$ be continuous variables. Disregarding the covariates and the observation errors, the conditional distribution of $Z_i$ satisfies

$$\begin{aligned} Z_i \mid \{ Z_j, j \ne i \} \sim \mathcal {N} \left( \sum _{j \sim i} c_{ij} Z_j, m_{ii} \right) , \end{aligned}$$

(1.1)

where the notation $j \sim i$ is defined before, $c_{ij}$ is the spatial autocovariance part, and $m_{ii}$ is the variance part. Hoef et al. [12] pointed out that one can include a covariate term in $c_{ij}$, such as the ecological covariate and connectivity structure for each observation location, which helps make the model suitable for more delicate autocovariance structures. However, this inclusion is not popular in the literature. Hanks and Hooten [11] introduced the landscape characteristic covariate $\varvec{x}_i$ and assumed that when $i \sim j$,

$$\begin{aligned} c_{ij} = \exp \left\{ \frac{1}{\Vert \varvec{s}_i - \varvec{s}_j \Vert }\left( \frac{\varvec{x}_i^\top + \varvec{x}_j^{\top }}{2} \right) \varvec{\beta } \right\} , \end{aligned}$$

(1.2)

where $\varvec{\beta }$ is the vector of the unknown parameter. For the simultaneous autoregressive model, Bera et al. [3] assumed that the element of the weight matrix $\varvec{W}$ comes from extra spatial data satisfying a linear model. However, to our best knowledge, no previous work provides a spatial model with binary observations capable of fitting data with spatial heterogeneity.

Inspired by the work stated above, such as Hanks and Hooten’s work [11] for the continuous case, we propose in this article a non-stationary model for binary responses, the spatial autologistic covariance model with spatial heterogeneity by generalizing the autocorrelation parameter $\eta _{ij}$. The Gibbs sampling method for data generation, the maximum likelihood estimation (MLE), two kinds of maximum pseudolikelihood estimation (MPL) for parameter estimation, and the Akaike information criterion (AIC) and Bayesian information criterion (BIC) for parameter selection are all included. For the maximum block independent likelihood estimation (MBILE), an estimation similar to the MPL, we prove the exponential consistency for a particular case where the explanatory variable term is an unknown constant. It is shown from numerical simulations that our proposed model can characterize the binary response data with spatial heterogeneity well. The performance of the MPL estimator and the criteria of variable selection for the simulation are also investigated. To illustrate the application of our proposed model, we also fit the Bur Oak presence dataset in the driftless area of the midwestern USA. Results show that, compared to Caragea and Kaiser’s [8] model, our proposed model is more capable of describing the spatial varying autocorrelation relationships and can provide better prediction results for this dataset.

The rest of the article is organized as follows. In Sect. 2, we define the spatial autologistic model with spatial heterogeneity. In Sect. 3, we give the methods of data generation, estimation, and variable selection for our proposed model. In Sect. 4, we prove the exponential consistency of the MBILE estimation. In Sect. 5, we provide the simulation results. In Sect. 6, we provide the applications for fitting the Bur Oak presence dataset. Conclusions and discussions are given in Sect. 7.

2 Definition of Our Proposed Model

In this section, for the spatial dataset with binary responses, we propose our model by generating the spatial autologistic model of Besag [4] and Caragea and Kaiser [8]. In real applications, the spatial dataset may have spatially varying autocorrelation structures. For instance, consider a disease with infectivity in the epidemic area stronger than in the non-epidemic area. Then assume that the autocovariance within the epidemic area is stronger. However, the autocorrelation parameter in the spatial autologistic covariance model is usually irrelevant to the spatial locations [24]. We propose the spatial autologistic model with spatial heterogeneity by introducing the correlation covariate. We extend Caragea and Kaiser [8]’s model by allowing the autocorrelation parameter to be dependent on the spatial locations. The methods of data generation, estimation, and selection are also provided for our proposed model.

Consider the binary-valued response $Y_i = Y(\varvec{s}_i),\ i\in \{1, \ldots , n\}$ observed on $\varvec{s}_1, \ldots , \varvec{s}_n \in \mathbb {R}^2$, where the value of $Y_i$ can be zero or one. Besag [4] first proposed the spatial autologistic model, but the covariate may not reflect the mean value of the response. To tackle this problem, Caragea and Kaiser [8] proposed the following centered spatial autologistic model:

$$\begin{aligned} \text { logit} \{ \text { Pr} (Y_i = 1 \mid Y_j, j \ne i) \} = \varvec{x}_i^\top \varvec{\beta } + \eta \sum _{i \sim j}\left\{ Y_j - \frac{\exp (\varvec{x}_j^\top \varvec{\beta })}{1+\exp (\varvec{x}_j^\top \varvec{\beta })} \right\} , \end{aligned}$$

(2.1)

where $\varvec{x}_i^\top \varvec{\beta }$ is the covariate term or the explanatory variable term, $\varvec{\beta }$ is an unknown p-dimensional vector of covariate parameters, $\eta$ is the spatial autologistic parameter, $i \sim j$ means that $i \in A_j$ and $j \in A_i$, where $A_i \subset \{1, \ldots , n\}$ is the set of neighbors for the location $\varvec{s}_i$. This model assumes that the conditional distribution of $Y_i$ with respect to the other observed values is only related to the responses observed in the locations within $A_i$; in other words, $\text { Pr} (Y_i = 1 \mid Y_j, j \ne i) = \text { Pr} (Y_i = 1 \mid Y_j, j \in A_i)$. Thus $A_i$ is called the set of neighbors. One can set that $A_i = \{ \varvec{s}_j: 0 < \Vert \varvec{s}_i - \varvec{s}_j \Vert \le h \}$, where h is the radius of the neighbor. For instance, when the data are observed on a regular grid, Besag [4] would set h as the distance between two locations, so there can be at most four locations for $A_i$. Such a setting is called the nearest neighborhood setting. Note that the set of neighbor $A_i$ for location $\varvec{s}_i$ does not include $\varvec{s}_i$ itself.

As we have mentioned in Introduction, although this condition allows the spatial autologistic parameter to change with space, this parameter is usually assumed to be a constant or has a simple form with respect to $\varvec{s}_i - \varvec{s}_j$ in the literature. To introduce the heterogeneity to this model, we allow that $\eta$ is dependent on i and j and propose the following spatial autologistic model with spatial heterogeneity:

$$\begin{aligned}{} & {} \text { logit} \{ \text { Pr} (Y_i = 1 \mid Y_j, j \ne i) \} = \varvec{x}_i^\top \varvec{\beta } + \sum _{i \sim j} \eta _{ij} \left\{ Y_j - \frac{\exp (\varvec{x}_j^\top \varvec{\beta })}{1+\exp (\varvec{x}_j^\top \varvec{\beta })} \right\} , \end{aligned}$$

(2.2)

$$\begin{aligned}{} & {} \eta _{ij} = \frac{1}{2} \varvec{\gamma }^\top (\varvec{z}_{i} + \varvec{z}_j) I \{ i \sim j\}, \end{aligned}$$

(2.3)

where $\varvec{x}_i^\top \varvec{\beta }$ is the covariate term, $i \sim j$ means that $i \in A_j$ and $j \in A_i$, $A_i$ is the set of neighbors for location $\varvec{s}_i$, $\varvec{z}_{i}$ is a predetermined q-dimensional vector, called the correlation covariate, $\varvec{\gamma }$ is an unknown q-dimensional vector of parameters, called the intrinsic correlation parameter. Here $\varvec{z}_i$ describes how the autocovariance term $\eta _{ij}$ relates to space. Besag [4] proved that the joint distribution of $(Y_1, \ldots , Y_n)$ exists if and only if:

• $i \in A_j$ if and only if $j \in A_i$;

• $\eta _{ij} = \eta _{ji}$, and $\eta _{ij} = 0$ when $i \notin A_j$.

For the simulation, we consider the case of $q=2$, where $\varvec{z}_i = (1, z_i)^\top$. Now every location corresponds to a one-dimensional correlation covariate $z_i = z(\varvec{s}_i) \in \mathbb {R}$. For instance, if the response means the occurrence of a certain disease, then $z_i$ can represent whether the location lies within the epidemic area; if the response means the existence of a certain wild animal, then $z_i$ can represent the land type, such as whether the observation located in woodland. In this case,

$$\begin{aligned} \eta _{ij} = \{ \gamma _0 + \gamma _1 (z_i + z_j) / 2 \} \cdot I \{ i \sim j\}, \end{aligned}$$

(2.4)

where $\varvec{\gamma } = (\gamma _0, \gamma _1)^\top$. In this setting, $\gamma _1$ represents the difference in autocorrelation in different spatial locations.

In applications, one can choose the correlation covariate $\varvec{z}_i$ by application backgrounds and the information of the dataset, such as the observation locations and the covariate $\varvec{x}_i$. For instance, in Sect. 6, we will fit the Bur Oak presence data using our proposed model, where $\varvec{z}_i$ includes the spatial coordinates and the White Oak presence information. More precisely, we will choose $\varvec{z}_i = (1, s_{i, 1}, s_{i, 2}, W_i)$, where $(s_{i,1}, s_{i, 2})$ is the coordinate of observation locations, and $W_i$ is the White Oak presence data. To remove possibly redundant correlation covariate terms in $\varvec{z}_i$, one can perform the model selection by computing the BIC criterion for models with different $\varvec{z}_i$, which will be introduced in Sect. 3. The model with the smallest BIC value is the model selection result.

3 Data Generation, Estimation, and Model Selection Methods

Next, we will provide the methods of data generation, estimation, and model selection for our proposed spatial autologistic model.

Since model (2.2) is defined by conditional probability, we can use Gibbs sampling to get a sample of $(Y_1, \ldots , Y_n)$. The algorithm can be stated as follows:

Input: Covariates $\varvec{x}_i, i \in \{i, \ldots , n \}$, correlation covariates $\varvec{z}_i, i \in \{ 1, \ldots , n \}$, parameters $\varvec{\beta }$, $\varvec{\gamma }$.

• 1. First generate a suitable initial sample $\varvec{y}^{(0)} = (y_1^{(0)}, \ldots , y_n^{(0)})$, where $y_i^{(0)} \in \{ 0, 1 \}$, $i \in \{ 1, \ldots , n \}$.

• 2. When $\varvec{y}^{(i)} = (y_1^{(i)}, \ldots , y_n^{(i)})$, $i \ge 0$ is generated, generate $\varvec{y}^{(i+1)} = (y_1^{(i+1)}, \ldots , y_n^{(i+1)})$ by the following steps:

  • Generate $y_1^{(i+1)} \sim \text { Binom}(1, p_1^{(i+1)})$, where $p_1^{(i+1)} = \text { Pr} (Y_1=1 \mid Y_2 = y_2^{(i)}, \ldots , Y_n = y_n^{(i)})$ is computed by (2.2);

  • Generate $y_2^{(i+1)} \sim \text { Binom}(1, p_2^{(i+1)})$, where $p_2^{(i+1)} = \text { Pr} (Y_2=1 \mid Y_1 = y_1^{(i+1)}, Y_3 = y_3^{(i)}, \ldots , Y_n = y_n^{(i)})$ is generated by (2.2); $\ldots$

  • Generate $y_n^{(i+1)} \sim \text { Binom}(1, p_n^{(i+1)})$, where $p_n^{(i+1)} = \text { Pr} (Y_n=1 \mid Y_1 = y_1^{(i+1)}, \ldots , Y_{n-1} = y_{n-1}^{(i+1)})$ is generated by (2.2).

• 3. Repeat step 2 until the number of generations i reaches a sufficiently large number M.

Output: A generated sample $\varvec{y}^{(M)}$.

In the simulation, the initial sample $y_1^{(0)}, \ldots , y_n^{(0)}$ is generated from a random sample of size n from Bernoulli distribution $\text { Binom}(1, 0.5)$, and we set $M=1000$.

The unknown parameters of our proposed model can be estimated by the maximum pseudolikelihood (MPL) proposed by Hughes et al. [13]. This method approximates the logarithm of the probability mass function $\log \{ \text { Pr} (Y_1, \ldots , Y_n) \}$ by the sum of the logarithm of the conditional probability mass function on each location, e.g.,

$$\begin{aligned} \log \{ \text { Pr} (Y_1, \ldots , Y_n) \} \approx \sum _{i=1}^n \log \{ \text { Pr} (Y_i \mid Y_j, j \ne i) \}. \end{aligned}$$

(3.1)

For spatial autologistic model (2.2), the log-pseudolikelihood function is

$$\begin{aligned} \begin{aligned} \ell (\varvec{\theta }\mid Y_1, \ldots , Y_n)&= \sum _{i=1}^n \left[ Y_i \text { logit} \{ \text { Pr} (Y_i \mid Y_j, j \ne i) \} \right. \\&\quad \left. - \log \left[ 1 + \exp \left[ \text { logit} \{ \text { Pr} (Y_i \mid Y_j, j \ne i) \} \right] \right] \right] \\&= \sum _{i=1}^n \left[ Y_i \left[ \varvec{x}_i^\top \varvec{\beta } + \sum _{i \sim j} \eta _{ij} \left\{ Y_j - \frac{\exp (\varvec{x}_j^\top \varvec{\beta })}{1+\exp (\varvec{x}_j^\top \varvec{\beta })} \right\} \right] \right. \\&\quad \left. - \log \left[ 1 + \exp \left[ \varvec{x}_i^\top \varvec{\beta } + \sum _{i \sim j} \eta _{ij} \left\{ Y_j - \frac{\exp (\varvec{x}_j^\top \varvec{\beta })}{1+\exp (\varvec{x}_j^\top \varvec{\beta })} \right\} \right] \right] \right] . \\ \end{aligned} \end{aligned}$$

(3.2)

The maximum point of this function is defined as the MPL estimate of the parameter. The MPL can be computed by iterative optimization algorithms, such as the Nelder-Mead algorithm [18]. In Sects. 5 and 6, we will adopt the $\texttt {R}$ function $\texttt {optim()}$ (version 4.1.1) for implementing the Nelder-Mead algorithm. The iteration stops when the improvement of one iteration is smaller than $\epsilon _r (|\ell |+ \epsilon _r)$, where $\ell$ is the log-pseudolikelihood function value, and $\epsilon _r$ is the relative convergence tolerance, for which the default value is $\epsilon _r = 1.49\times 10^{-8}$, or the square root of the machine epsilon in double precision.

We can use the following Akaike information criterion (AIC) or Bayesian information criterion (BIC) to deal with the variable selection problem for our proposed model:

$$\begin{aligned} \text { AIC} = -2 \ell (\varvec{\hat{\theta }}\mid Y_1, \ldots , Y_n) + 2 p; \quad \text { BIC} = -2 \ell (\varvec{\hat{\theta }}\mid Y_1, \ldots , Y_n) + \log (n) p, \end{aligned}$$

(3.3)

where $\ell$ is the log-pseudolikelihood function, $\hat{\theta }$ is the MPL estimate, p is the number of unknown parameters, and n is the number of observations. The selection procedure prefers the model with the smallest AIC or BIC value. In Sect. 5, we will show by numerical simulations that the BIC criterion is more suitable for variable selection.

For the variable selection procedure, we adopt the forward selection algorithm. Denote the unknown parameters of our proposed model by $\varvec{\theta } = (\varvec{\beta }, \varvec{\gamma }) = (\theta _1, \ldots , \theta _{p+q})$ and the feature set $F \subset \{1, \ldots , p+q\}$, which represents the indices of selected parameters. We define the model with feature F as our proposed model which $\theta _j$ is unknown if $j \in F$ and $\theta _j$ is fixed at zero if $j \notin F$. The algorithm is as follows:

• 1. Let $F = \emptyset$ and $\text {BIC}_{F} = +\infty$.

• 2. For i in $\{1, \ldots , p+q\} \backslash F$:

  • Let $F_{\text {new}} = F$.

  • Fit the proposed model with feature $F \cup \{i\}$ and compute the corresponding BIC value $\text {BIC}_{F \cup \{i\}}$;

  • If $\text {BIC}_{F \cup \{i\}} < \text {BIC}_{F}$, then let $F_{\text {new}} = F \cup \{i\}$ and $\text {BIC}_{F} = \text {BIC}_{F \cup \{i\}}$.

• 3. If $F_{\text {new}} = F$ still holds or $F_{\text {new}} = \{1, \ldots , p+q\}$, then stop the algorithm. The model with feature $F_{\text {new}}$ is the final selected model. If not, let $F = F_{\text {new}}$ and continue running Step 2 until the algorithm stops.

4 Exponential Consistency of the MPL Estimator

With the results of Comets [9], for the spatial autologistic model without centering, the exponential consistency of the maximum likelihood estimation (MLE) and the maximum block independent likelihood estimation (MBILE) can be proved under a specific setting. Here the MBILE is an estimator similar to the MPL, which splits the observation region into several squares and ignores the correlation between different squares. We assume that the covariate term is a single parameter $\beta _0$ and the covariate $z_i$ in (2.4) has periodicity.

Assume that the data are observed on $\varvec{i} \in \mathbb {Z}^d$ and the neighborhood structure is the nearest neighborhood. We further assume that the observations $Y_{\varvec{i}}$ follow

$$\begin{aligned}{} & {} \text { logit} \left( \text { Pr} \{ Y_{\varvec{i}}=1 \mid Y_{\varvec{j}}: \varvec{j} \ne \varvec{i} \} \right) = \beta _0 + \sum _{\varvec{i} \sim \varvec{j}} \eta _{\varvec{i} \varvec{j}} Y_{\varvec{j}}; \end{aligned}$$

(4.1)

$$\begin{aligned}{} & {} \eta _{\varvec{i} \varvec{j}} = \left\{ \gamma _0 + \gamma _1 (z_{\varvec{i}} + z_{\varvec{j}}) / 2 \right\} \cdot I\{ \varvec{i} \sim \varvec{j} \}, \end{aligned}$$

(4.2)

where $\varvec{\theta } = (\beta _0, \gamma _0, \gamma _1)$ is the unknown parameter, $\varvec{i} \sim \varvec{j}$ means that the observed locations $\varvec{i}$ and $\varvec{j}$ are adjacent to the nearest neighborhood definition.

We consider the consistency under increasing domain regime, and the observation region can be divided into several squares. Without loss of generality, we set $d=2$. In this case, for any $\varvec{i} = (i_1, i_2) \in \mathbb {Z}^2$, we denote the square by

$$\begin{aligned} R(\varvec{i}) = \{ (K_1 i_1 + j_1, K_2 i_2 + j_2) \mid j_1 = 0, \ldots , K_1-1, j_2 = 0, \ldots , K_2-1 \}, \end{aligned}$$

(4.3)

and denote $R(\varvec{0}) = R$. Note that the square is a regular lattice with $K_1 \times K_2$ locations. The observed value in each square is denoted by

$$\begin{aligned} \varvec{Y}_{\varvec{i}}^{[R]} := Y_{R(\varvec{i})} = \{ Y_{(K_1 i_1 + j_1, K_2 i_2 + j_2)} \mid j_1 = 0, \ldots , K_1-1, j_2 = 0, \ldots , K_2-1 \}, \end{aligned}$$

(4.4)

and we denote $[\varvec{Y}_{\varvec{i}}^{[R]}]_{(j_1, j_2)} = Y_{(K_1 i_1 + j_1, K_2 i_2 + j_2)}$. Similarly, we define

$$\begin{aligned} \varvec{z}_{\varvec{i}}^{[R]} := z_{R(\varvec{i})} = \{ z_{(K_1 i_1 + j_1, K_2 i_2 + j_2)} \mid j_1 = 0, \ldots , K_1-1, j_2 = 0, \ldots , K_2-1 \}. \end{aligned}$$

(4.5)

When $\varvec{z}_{\varvec{i}}^{[R]}$ is not dependent on $\varvec{i}$ for all $\varvec{i}$, the correlation covariate has periodicity with respect to the squares. In this case, $\varvec{Y}_{\varvec{i}}^{[R]}$ can be regarded as a stationary process with the observed values relying on $\mathcal {X} = \{ 0, 1 \}^R$. Thus, we can prove the consistency using the results in Comets [9]. Note that we denote $\{0, 1\}^A$ as the set of mappings from A to $\{0, 1\}$ for a countable set A.

We set the observed region as $\Lambda _n = \cup _{\varvec{i} = (i_1, i_2): \mid i_1\mid \le n, \mid i_2\mid \le n} R(\varvec{i}) = [-K_1 n, (K_1+1)n-1] \times [-K_2 n, (K_2+1) n-1]$, where $n \in \mathbb {N}$, and denote $\varvec{Y}_n$ as the response variable in this region. We set the observed values outside this region by $\varvec{y}_b \in \{0, 1\}^{\Lambda _n^C}$. In this case, the conditional log-likelihood function for the observed values is

$$\begin{aligned} l_{\Lambda _n, \varvec{y}_b}(\varvec{\theta }, \varvec{Y}_n) = f_{\Lambda _n} (\varvec{\theta }, \varvec{Y}_n; \varvec{y}_b) - \log \left[ \sum _{\tilde{\varvec{Y}}_n \in \{0, 1\}^{\Lambda _n} } \exp \{ f_{\Lambda _n} (\varvec{\theta }, \tilde{\varvec{Y}}_n; \varvec{y}_b ) \} \right] , \end{aligned}$$

(4.6)

where

$$\begin{aligned} f_{\Lambda _n} (\varvec{\theta }, \varvec{Y}_n; \varvec{y}_b) = \beta _0 \sum _{\varvec{i} \in \Lambda _n} \tilde{Y}_{\varvec{i}} + \sum _{\varvec{i} \sim \varvec{j}, \{\varvec{i}, \varvec{j}\} \cap \Lambda _n \ne \emptyset } \eta _{\varvec{i} \varvec{j}} \tilde{Y}_{\varvec{i}} \tilde{Y}_{\varvec{j}}, \end{aligned}$$

$\tilde{\varvec{Y}} = \{ \tilde{Y}_{\varvec{i}}: \varvec{i} \in \mathbb {Z}^2 \}$ is the vector consisting of $\varvec{Y}_n$ and $\varvec{y}_b$, where the elements are

$$\begin{aligned} \tilde{Y}_{\varvec{i}} = {\left\{ \begin{array}{ll} Y_{\varvec{i}} &{} \varvec{i} \in \Lambda _n, \\ {[}\varvec{y}_b]_{\varvec{i}} &{} \varvec{i} \notin \Lambda _n. \end{array}\right. } \end{aligned}$$

Thus, the value of $l_{\Lambda _n, \varvec{y}_b}(\varvec{\theta }, \varvec{Y}_n)$ is only related to $\varvec{\theta }, \varvec{Y}_n$, and the value of $\varvec{y}_b$ on $\partial \Lambda _n:= \{ \varvec{i} \in \Lambda _n^C \mid \exists \varvec{j} \in \Lambda _n, \varvec{i} \sim \varvec{j} \}$. Here $\partial \Lambda _n$ is called the boundary of $\Lambda _n$.

The maximum block independent likelihood estimation (MBILE) is proposed by Lim et al. [15]. The main idea is to approximate the conditional log-likelihood function $l_{\Lambda _n, \varvec{y}_b}(\varvec{\theta }, \varvec{Y}_n)$ by the sum of conditional log-likelihood functions on different blocks, e.g.,

$$\begin{aligned} pl_{\Lambda _n, \varvec{y}_b}(\varvec{\theta }, \varvec{Y}_n) = \sum _{\varvec{i} = (i_1, i_2): \mid i_1\mid \le n, \mid i_2\mid \le n} l_{R(\varvec{i}), \varvec{y}_b^{[R]}(\varvec{i})}(\varvec{\theta }, \varvec{Y}_{\varvec{i}}^{[R]}), \end{aligned}$$

where $\varvec{y}_b^{[R]}(\varvec{i})$ is the vector of $\varvec{Y}_n$ and $\varvec{y}_b$, restricted in the region $R(\varvec{i})^C$. For the MLE and MBILE, we have the following result of exponential consistency.

Theorem 4.1

Consider the spatial autologistic model with spatially dependent autocorrelation parameters defined by (4.1) and (4.2), where the autocovariance covariate $z_i$ is periodic with respect to the square R, e.g., $\varvec{z}_{\varvec{i}}^{[R]}$ defined by (4.5) is not related to $\varvec{i}$. Assume that the model is identifiable, denote

$$\begin{aligned} \hat{\varvec{\theta }}_{n, y_b} = \underset{\varvec{\theta }}{\text { argmax}}\ l_{\Lambda _n, \varvec{y}_b}(\varvec{\theta }, \varvec{Y}_n), \quad \tilde{\varvec{\theta }}_{n, y_b} = \underset{\varvec{\theta }}{\text { argmax}}\ pl_{\Lambda _n, \varvec{y}_b}(\varvec{\theta }, \varvec{Y}_n), \end{aligned}$$

are the MLE and MBILE of the parameter $\varvec{\theta }$, respectively. Then $\forall \epsilon >0,$ there exists $c> 0\textrm{,} \delta > 0$, which are not related to $\varvec{y}_b$, such that

$$\begin{aligned} \begin{aligned}&\text { Pr}_{n, \varvec{\theta }_0} \left( \Vert \hat{\varvec{\theta }}_{n, \varvec{y}_b} - \varvec{\theta }_0 \Vert> \epsilon \right) \le c \exp \left( -\mid \Lambda _n\mid \delta \right) ; \\&\text { Pr}_{n, \varvec{\theta }_0} \left( \Vert \tilde{\varvec{\theta }}_{n, \varvec{y}_b} - \varvec{\theta }_0 \Vert > \epsilon \right) \le c \exp \left( -\mid \Lambda _n\mid \delta \right) , \end{aligned} \end{aligned}$$

where $\varvec{\theta }_0$ is the true value of the parameter, $\text { Pr}_{n, \varvec{\theta }_0}$ is the probability distribution of $\varvec{Y}_n$, $\mid \Lambda _n\mid$ is the number of observations when the observation region is $\Lambda _n$.

Proof

Let $\mathcal {X} = \{0, 1\}^R$, where $R=R(\varvec{0})$ is defined by (4.3). For all $\varvec{i} = (i_1, i_2) \in \mathbb {Z}^2$, the observations on the square $R(\varvec{i})$ are denoted by $\varvec{Y}_{\varvec{i}}^{[R]} \in \mathcal {X}$, see (4.4). For all $\Lambda \subset \mathbb {Z}^2$, denote by $\varvec{Y}_{\Lambda }^{[R]} = \{ \varvec{Y}_{\varvec{i}}^{[R]}: \varvec{i} \in \Lambda \} \in \mathcal {X}^\Lambda$ the observations on the region $\cup _{\varvec{i} \in \Lambda } R(\varvec{i})$, $\varvec{y}_b^{[R]} = \{ \varvec{Y}_{\varvec{i}}^{[R]}: \varvec{i} \notin \Lambda \} \in \mathcal {X}^{\Lambda ^C}$ the response value outside the region, and $\varvec{Y}^{[R]} \in \mathcal {X}^{\mathbb {Z}^2}$ the combinations of the observations $\varvec{Y}_{\Lambda }^{[R]}$ and $\varvec{y}_b^{[R]}$. Due to the periodicity of $z_{\varvec{i}}$, let

$$\begin{aligned}{} & {} I_{\{ \varvec{i} \}}^{(1)}(\varvec{Y}^{[R]}) = \sum _{\varvec{j} \in R} \left[ \varvec{Y}_{\varvec{i}}^{[R]} \right] _{\varvec{j}}, \\{} & {} I_{\{ \varvec{i} \}}^{(2)}(\varvec{Y}^{[R]}) = \sum _{\varvec{j}, \varvec{\ell } \in R} \left[ \varvec{Y}_{\varvec{i}}^{[R]} \right] _{\varvec{j}} \left[ \varvec{Y}_{\varvec{i}}^{[R]} \right] _{\varvec{\ell }}, \\{} & {} I_{\{ \varvec{i}, \varvec{i} + (1, 0) \}}^{(2)}(\varvec{Y}^{[R]}) = \sum _{j=0}^{K_2-1} \left[ \varvec{Y}_{\varvec{i}}^{[R]} \right] _{(K_1-1, j)} \left[ \varvec{Y}_{\varvec{i} + (1, 0)}^{[R]} \right] _{(0, j)}, \\{} & {} I_{\{ \varvec{i}, \varvec{i} + (0, 1) \}}^{(2)}(\varvec{Y}^{[R]}) = \sum _{j=0}^{K_1-1} \left[ \varvec{Y}_{\varvec{i}}^{[R]} \right] _{(j, K_2-1)} \left[ \varvec{Y}_{\varvec{i} + (0, 1)}^{[R]} \right] _{(j, 0)}, \\{} & {} I_{\{ \varvec{i} \}}^{(3)}(\varvec{Y}^{[R]}) = \frac{1}{2} \sum _{\varvec{j}, \varvec{\ell } \in R} (z_{\varvec{j}} + z_{\varvec{\ell }}) \left[ \varvec{Y}_{\varvec{i}}^{[R]} \right] _{\varvec{j}} \left[ \varvec{Y}_{\varvec{i}}^{[R]} \right] _{\varvec{\ell }}, \\{} & {} I_{\{ \varvec{i}, \varvec{i} + (1, 0) \}}^{(3)}(\varvec{Y}^{[R]}) = \frac{1}{2} \sum _{j=0}^{K_2-1} (z_{(K_1-1, j)} + z_{(0, j)}) \left[ \varvec{Y}_{\varvec{i}}^{[R]} \right] _{(K_1-1, j)} \left[ \varvec{Y}_{\varvec{i} + (1, 0)}^{[R]} \right] _{(0, j)}, \\{} & {} I_{\{ \varvec{i}, \varvec{i} + (0, 1) \}}^{(3)}(\varvec{Y}^{[R]}) = \frac{1}{2} \sum _{j=0}^{K_1-1} (z_{(j, K_2-1)} + z_{(j, 0)}) \left[ \varvec{Y}_{\varvec{i}}^{[R]} \right] _{(j, K_2-1)} \left[ \varvec{Y}_{\varvec{i} + (0, 1)}^{[R]} \right] _{(j, 0)}, \end{aligned}$$

then the log-likelihood function $l_{\Lambda _n, \varvec{y}_b}(\varvec{\theta }, \varvec{Y}_n)$ of the model satisfies (4.6), where

$$\begin{aligned}{} & {} \begin{aligned} f_{\Lambda _n} (\varvec{\theta }, \varvec{Y}_n; \varvec{y}_b)&= \beta _0 \sum _{\varvec{i} \in I} I_{\{ \varvec{i} \}}^{(1)}(\varvec{Y}^{[R]}) \\&\quad +\gamma _0 \bigg [ \sum _{\varvec{i} \in I} I_{\{ \varvec{i} \}}^{(2)}(\varvec{Y}^{[R]}) + \sum _{\varvec{i} \in I \text { or } \varvec{i}+(1, 0) \in I} I_{\{ \varvec{i}, \varvec{i} + (1, 0) \}}^{(2)}(\varvec{Y}^{[R]}) \\&\quad + \sum _{\varvec{i} \in I \text { or } \varvec{i}+(0, 1) \in I} I_{\{ \varvec{i}, \varvec{i} + (0, 1) \}}^{(2)}(\varvec{Y}^{[R]}) \bigg ] \\&\quad + \gamma _1 \bigg [ \sum _{\varvec{i} \in I} I_{\{ \varvec{i} \}}^{(3)}(\varvec{Y}^{[R]}) + \sum _{\varvec{i} \in I \text { or } \varvec{i}+(1, 0) \in I} I_{\{ \varvec{i}, \varvec{i} + (1, 0) \}}^{(3)}(\varvec{Y}^{[R]}) \\&\quad + \sum _{\varvec{i} \in I \text { or } \varvec{i}+(0, 1) \in I} I_{\{ \varvec{i}, \varvec{i} + (0, 1) \}}^{(3)}(\varvec{Y}^{[R]}) \bigg ], \\ \end{aligned} \\{} & {} I = \{ \varvec{i} = (i_1, i_2) \in \mathbb {Z}^2: \mid i_1\mid \le n, \mid i_2\mid \le n\}. \end{aligned}$$

Next, we verify that our model meets the assumptions of Theorem 2.1 of Comets [9]. Define the following distance on $\mathcal {X}$:

$$\begin{aligned} d(\varvec{a}, \varvec{b}) = {\left\{ \begin{array}{ll} 0, &{} \varvec{a} \text { is the same as } \varvec{b}; \\ 1, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

then $\mathcal {X}$ and this distance constitute a Polish space. One can verify that $I_{ \{ \varvec{i} \} }^{(1)}$, $I_{\{ \varvec{i} \}}^{(2)}$, $I_{\{ \varvec{i}, \varvec{i} + (1, 0) \}}^{(2)}$, $I_{\{ \varvec{i}, \varvec{i} + (0, 1) \}}^{(2)}$, $I_{\{ \varvec{i} \}}^{(3)}$, $I_{\{ \varvec{i}, \varvec{i} + (1, 0) \}}^{(3)}$, $I_{\{ \varvec{i}, \varvec{i} + (0, 1) \}}^{(3)}$ are all bounded continuous functions on $\Omega = \mathcal {X}^{\mathbb {Z}^2}$, and $I_{ \{ \varvec{i} \} }^{(1)}$, $I_{ \{ \varvec{i} \} }^{(2)}$, $I_{ \{ \varvec{i} \} }^{(3)}$ are only dependent on $\varvec{Y}_{\varvec{i}}^{[R]}$; $I_{\{ \varvec{i}, \varvec{i} + (0, 1) \}}^{(2)}$, $I_{\{ \varvec{i}, \varvec{i} + (0, 1) \}}^{(3)}$ are only dependent on $\varvec{Y}_{\varvec{i}}^{[R]}$ and $\varvec{Y}_{\varvec{i} + (1, 0)}^{[R]}$; $I_{\{ \varvec{i}, \varvec{i} + (1, 0) \}}^{(2)}$, $I_{\{ \varvec{i}, \varvec{i} + (1, 0) \}}^{(3)}$ are only dependent on $\varvec{Y}_{\varvec{i}}^{[R]}$ and $\varvec{Y}_{\varvec{i} + (1, 0)}^{[R]}$. Moreover, define the shift operator

$$\begin{aligned} \tau _{\varvec{i}}: \Omega \rightarrow \Omega , (\tau _{\varvec{i}} \varvec{Y}^{[R]})_{\varvec{j}} = \varvec{Y}_{\varvec{i}+\varvec{j}}^{[R]}, \end{aligned}$$

then for the $I_{V}^{(l)}$, $l=1, 2, 3$ defined before, one can verify the following properties of shifting invariance and additivity:

$$\begin{aligned}{} & {} I_{V}^{(l)} \circ \tau _{\varvec{i}} = I_{\varvec{i}+V}^{(l)} \text { for all } \varvec{i}, V, l; \\{} & {} \quad \left[ \sum _{m=1}^3 \left\{ \sum _{V: (0, 0) \in V} \Vert I_V^{(l)} \Vert _{\infty } \right\} \right] < \infty . \end{aligned}$$

Finally, the model is identifiable. Then the theorem is proved, since the assumptions of Theorem 2.1 in Comets [9] hold. $\square$

5 Numerical Simulations

In this section, numerical simulations will be performed to compare the cases where the autocorrelation parameter in the spatial logistic model is independent or dependent on spatial locations. We will consider two settings of the autocorrelation parameter for the dependent cases, linearly dependent on spatial locations or related to a circular area. The properties of the MPL estimation and model selection methods will also be investigated.

5.1 The Case Where the Autocorrelation Parameter is Linearly Dependent

Here we set the autocorrelation parameter as being linearly dependent, e.g., the $z_i$’s in (2.4) have a linear trend with spatial location $\varvec{s}_i = (s_{i, 1}, s_{i, 2})^\top$ with locations $s_{i, 1}, s_{i, 2} \in \{ 1, \ldots , 30 \}$, and the number of observations is $n=30^2=900$. The observed values follow the autocovariance model

$$\begin{aligned} \text { logit} \{ \text { Pr} (Y_i = 1 \mid Y_j, j \ne i) \} = \beta _0 + \beta _1 x_i + \sum _{i \sim j} \eta _{ij} \left\{ Y_j - \mu _j \right\} , \end{aligned}$$

(5.1)

where

$$\begin{aligned} \mu _j = \frac{\exp (\beta _0 + \beta _1 x_j)}{1+\exp (\beta _0 + \beta _1 x_j)}, \end{aligned}$$

(5.2)

and the neighborhood structure is the nearest-neighbor scheme. We generate each $x_i$ from independent samples assuming the distribution $\mathcal {N}(s_{i, 1}+s_{i, 2}+4, 1)$, $i \in \{ 1, 2, \ldots , n \}$ and choose $\beta _0=-2$, $\beta _1 = 0.1$. The values of the covariate $x_i$’s and the approximated mean $\mu _i$’s are shown in Fig. 1.

Fig. 1

Illustrations of the covariate $x_i$’s and the approximated mean $\mu _i$’s of the observations in the case of linearly dependent autocorrelation parameter cases

In this simulation, we have the following two choices of $\eta _{ij}$:

• 1. The autocorrelation parameter is independent of spatial locations:

  $$\begin{aligned} \eta _{ij} = \gamma _0 \cdot I \{ i \sim j\}, \end{aligned}$$

  (5.3)

  where $\gamma _0$ can be 0.5, 1, 1.5.

• 2. The autocorrelation parameter is linearly dependent on spatial locations:

  $$\begin{aligned} \eta _{ij} = \gamma _1 (z_i + z_j) / 2 \cdot I \{ i \sim j\}, \end{aligned}$$

  (5.4)

  where $z_i = (s_{i, 1}-s_{i, 2}+29)/58$. Here, $z_i$ has a linear relationship with spatial locations, ranging from 0 to 1. The values of $z_i$ are shown in Fig. 2, indicating that this model has a smaller spatial autocovariance in the upper left corner and a larger autocovariance in the bottom right corner. We choose $\gamma _1 \in \{ 0.5, 1, 1.5 \}$.

Fig. 2

Illustration of the covariate $z_i$ in (5.4) in the simulation of linearly dependent autocorrelation parameter cases

In summary, we consider six parameter combinations. For each combination, we use the MPL estimation to fit model (5.1), where the autocorrelation parameter can be (5.3), (5.4), or more generally, (2.4). The estimation properties are investigated in terms of the sample mean and the standard deviation. For model selection, we compute the AIC and BIC for these models, select the model with the smallest criterion values, and explore their accuracy via the frequency of correct selections.

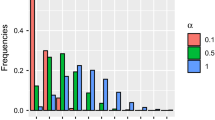
First, we show a randomly generated sample for each parameter combination, shown in Fig. 3. The first row is model (5.3), where the autocorrelation parameter does not change with space, with $\gamma _0 \in \{ 0.5, 1.0, 1.5 \}$; the second row is model (5.4), where the autocorrelation parameter is linearly related to the locations, with $\gamma _1 \in \{ 0.5, 1.0, 1.5 \}$. One can find that when the autocorrelation parameter does not change with space, the samples have different patterns for different $\gamma _0$’s. For instance, when $\gamma _0=0.5$, the white parts in the figure are small, but they become larger when $\gamma _0=1.0$ and $\gamma _0=1.5$. This indicates that the samples are smoother for larger $\gamma _0$’s. In these figures, for a sample with a larger autocorrelation parameter, the block of the same color is larger and has a smoother boundary. When the autocorrelation parameter is linearly related to the locations, one can inspect different smoothness only for $\gamma _1=1.5$. Figures of samples from different spatial logistic models with large autocorrelation parameters are distinct. However, if the autocorrelation parameter is small, it is difficult to tell whether the autocorrelation parameter is related to locations. In this case, one may need to adopt statistical methods such as model selection to inspect it.

Fig. 3

Illustrations of a generated sample for each parameter combination in the simulation, where the autocorrelation parameter is linearly dependent with observation locations

Next, we compare the performance of the maximum pseudolikelihood (MPL) estimates, where the autocorrelation parameter can be: irrelevant to locations (5.3), linearly correlated with locations (5.4), or linearly correlated with locations with unknown intercept   (2.4), respectively. Results are shown in Table 1. In Table 1, $\gamma _0$ and $\gamma _1$ in the true model are the values of $\gamma _0$ and $\gamma _1$ in models (5.3) and (5.4), respectively. The estimation results under the correct model are in bold. The number of replicates for the simulation is 500. Results show that, if the model is correctly specified, then the estimates of $\beta _0$, $\beta _1$, and $\gamma _0$ have no apparent biases for the actual model determined by (5.3). When the autocorrelation increases, the standard deviations of the estimates for $\beta _0$ and $\beta _1$ first increase and then decrease, whereas the standard deviation of the estimates for $\gamma _0$ decreases. If the autocorrelation structure is misspecified as (5.4), then the estimates of $\beta _0$ and $\beta _1$ are biased when the autocorrelation is large. The estimates are unbiased if the autocorrelation structure is set as (2.4). However, the standard deviation of the estimates for $\gamma _0$ is significantly larger than that of the model determined by (5.3). For the true model determined by (5.4), the estimates of $\beta _0$, $\beta _1$, and $\gamma _1$ are also unbiased. When the autocorrelation increases, the estimates for $\beta _0$ and $\beta _1$ increase, whereas the standard deviation of the estimates for $\gamma _1$ decreases. If the autocorrelation structure is misspecified as (5.3), then the estimate of $\beta _0$ is biased when the autocorrelation is large. If the autocorrelation structure is set as (2.4), then the parameter estimates are also unbiased and have a larger variance than the correct model. In conclusion, the estimation behaves well when the model is correctly specified. If one adopts more general autocorrelation structure (2.4), the estimates may have a larger standard deviation. Therefore, removing redundant parameters in the model by a model selection procedure can be helpful.

The data generation and estimation are computationally efficient in our simulation settings. We adopt the 64-bit 20-core Intel Xeon Gold 6248 CPU running at 2.50 GHz for our computation. The time for generating one sample from the model considered in this section ranges from 12.62 to 19.84 s. The MPL estimation times for models (5.3) and (5.4) range from 1.21 to 5.09 s; and 1.21 to 5.75 s, respectively, whereas the MPL estimation time for model (2.4) ranges from 2.41 to 9.75 s. Therefore, removing redundant parameters can also cut the computational time.

Table 1 Sample mean and standard deviation (in brackets) of the MPL estimation in the simulation, where the autocorrelation parameters are linearly correlated with locations

Finally, we investigate the model selection performance of the AIC and BIC procedures defined by (3.3). For each parameter combination, we compute the AIC and BIC for the data, where the autocorrelation parameters in the model can be (5.3), (5.4), or (2.4). Results on the frequency of determined models are shown in Table 2. In this table, the “Constant," “Linear," and “General" mean that the autocorrelation parameter is irrelevant to locations (5.3), linearly correlated with locations (5.4), and linearly correlated with locations with unknown intercept (2.4). The frequency corresponding to the correct model is in bold. For the true model, $\gamma _0$ and $\gamma _1$ represent the true parameter values in the model determined by (5.3) and (5.4), respectively. Table 2 shows that the model selection works better when the autocorrelation parameter is larger. Moreover, the BIC procedure is more likely to choose the correct model than the AIC because the BIC procedure tends to select the model with fewer parameters. In conclusion, the AIC and BIC both perform well in model selection, where the BIC is recommended as the better choice.

Table 2 Frequency of the model selection results by the AIC and BIC in the simulation, where the autocorrelation is linearly related to the locations

5.2 The Case Where the Autocorrelation Parameter is Dependent with a Circle

Next, we consider the case where the autocorrelation parameter depends on a circular region. The covariance $z_i$ in (2.4) is an indicator function of a circular region. In this case, if $\gamma _1>0$, then the autocovariance within the circle is stronger than that outside.

Assume that the observation region is $[0, 1]^2$, and the observation locations are $((k_1-0.5)/\sqrt{n}, (k_2-0.5)/\sqrt{n})^\top$, $k_1, k_2 \in \{ 1, \ldots , \sqrt{n} \}$, which is denoted by $\varvec{s}_i = (s_{i, 1}, s_{i, 2})^\top$, $i \in \{ 1, \ldots , n \}$. Choose the number of locations as $n \in \{ 30^2, 40^2, 50^2 \}$, and the observations follow the following autologistic model:

$$\begin{aligned} \text { logit} \{ \text { Pr} (Y_i = 1 \mid Y_j, j \ne i) \} = \beta _0 + \sum _{i \sim j} \eta _{ij} \left\{ Y_j - \mu _j \right\} , \end{aligned}$$

(5.5)

where

$$\begin{aligned} \mu _j = \frac{\exp (\beta _0)}{1+\exp (\beta _0)}, \end{aligned}$$

(5.6)

with the neighborhood being the nearest neighborhood structure. The autocorrelation parameter in this model follows (2.3), where $z_i = I \{ (s_{i, 1}-0.5)^2+(s_{i, 2}-0.5)^2 \le 0.3^2 \}$. Thus, the autocorrelation parameters in the circle with center (0.5, 0.5) and radius 0.3 are larger than that outside the circle. Set $\beta _0 = \log (0.6/0.4) \approx 0.4055$, $\gamma _0 \in \{0.5, 1.0\}$, $\gamma _1 \in \{ 0, 0.5 \}$, where $\text { E} \{ Y_i \} \approx 0.6$. Note that when $\gamma _1=0$, the autocorrelation parameter is independent of space. We also take simulations for the case where $\text { E} \{ Y_i \} \approx 0.4$ or $\beta _0 = \log (0.4/0.6) \approx -0.4055$. The results are omitted here due to the resemblance of $\text { E} \{ Y_i \} \approx 0.6$.

Similar to the previous simulation, we first generate one sample and inspect the properties of the generated data. Then we perform maximum pseudolikelihood estimation to the models with different settings of autocorrelation parameters, using AIC and BIC (3.3) for model selection, and investigate the results. Consider eight models in Table 3, where the model for data generation can be model O1 (when $\gamma _1=0.5$) or model O2 ($\gamma _1=0$), $\mu _j = e^{\beta _0}/(1+e^{\beta _0})$, $\tilde{\mu }_j = e^{\beta _0 + \beta _1 z_j}/(1+e^{\beta _0 + \beta _1 z_j})$. Besides the correct settings, for the autocorrelation parameters in Table 3, we also consider the case where the parameter is zero if outside the circle and the case where the parameter is always zero. For the covariance term, we also consider the case where $z_i$ is included. The number of replicates is 200 here in this simulation.

Table 3 List of models for the simulation where the autocorrelation parameter is dependent on a circular region

First, we inspect one generated data for each case where $n=50^2$, $\beta _0 = \log (0.6/0.4)$, $\gamma _0 \in \{0.5, 1.0\}$, $\gamma _1 \in \{ 0, 0.5 \}$. The results are shown in Fig. 4, where the first row represents the case with the autocorrelation parameter being independent of space (Model O2) and $\gamma _0$ being 0.5 or 1.0; the second row represents the case with the autocorrelation parameter being dependent on a circular region (Model O1), $\gamma _0$ being 0.5 or 1.0 and $\gamma _1=0.5$. Red curves show the circular region. Figure 4 shows that when the autocorrelation parameter is independent of the space, the white or black parts are more concentrated when the autocorrelation parameter is larger. When the autocorrelation parameter depends on a circular region, the patterns inside and outside the circle differ. The difference can be more drastic when $\gamma _0$ is large. Also, note that the data have more zero-valued observations inside the circle when $\gamma _0=1$. Thus we add an extra $z_i$, rendering Models E1–E4 in Table 3.

Fig. 4

Illustration of four generated data in simulations where the autocorrelation parameter is dependent on a circular region

Next, we investigate the performance of the maximum pseudolikelihood estimation when $\beta _0 = \log (0.6/0.4)$. The results are shown in Tables 4 and 5, where the correct models are in bold. The bias of $\beta _0$ is calculated as the sample means of the estimates of $\beta _0$ minus its true value, and n is the number of observations. Table 4 shows that when the autocorrelation parameter is dependent on a circular region (the correct model is Model O1 in Table 3), the maximum pseudolikelihood estimation performs well, for it is unbiased with a small standard deviation for a large number of observations. When we fit the misspecified model (Model O2 in Table 3), $\beta _0$ has a larger bias, and $\gamma _0$ is overestimated. When the autocorrelation parameter is independent of the space (Model O2), the maximum pseudolikelihood estimation of $\gamma _0$ for the correct model works well. The estimation for $\beta _0$ in this case also performs well if $\gamma _0=0.5$ but can be underestimated if $\gamma _0=1$. When we fit Model O1, which has an excessive parameter, the estimation of $\beta _0$ and $\gamma _0$ is similar to that of Model O2, and the estimation of $\beta _1$ is close to zero with a small standard deviation for a large number of observations. Thus, if the model we fit is correct, the maximum pseudolikelihood estimation performs well unless for Model O2 and $\gamma _0=1.0$.

Table 4 Sample mean and standard deviation (in parentheses) of the MPL estimates for fitting Models O1 and O2 in the simulation when the autocorrelation parameter is dependent on a circular region

Then, we investigate the performance of the maximum pseudolikelihood estimation for the model with an excessive covariance term $\beta _1 z_i$. Table 5 shows that when the true model is Model O1. The fitted model is Model E1; the estimation results of $\beta _0$, $\gamma _0$ and $\gamma _1$ are similar to the case of fitting the correct model, whereas the estimation results of $\beta _1$ are close to zero with a large variance. When the fitted model is Model E2, the estimation of $\beta _0$ is slightly larger than that of Model O2 when the autocorrelation parameter is small; and smaller when the autocorrelation parameter is large. The estimation of $\beta _1$ is likely to be smaller than zero, with a large standard deviation. The estimation of $\gamma _0$ behaves similarly to the case of fitting Model O2, with a large standard deviation when the autocorrelation parameter is large. When the true model is Model O2, and the fitted model is Model E2, the estimation results of $\beta _0$ and $\gamma _0$ are similar to the case of fitting the correct model. The mean value of the estimates of $\beta _1$ is close to zero, but the standard deviation is larger when $\gamma _0=1.0$. When fitting Model E1, the estimation results of $\beta _0$, $\gamma _0,$ and $\gamma _1$ are similar to the case of fitting Model O1; the mean value of the estimates for $\beta _1$ is slightly smaller than zero, with the standard deviation larger when $\gamma _0=1.0$. Thus, if the covariance term has an excessive parameter, such as $\beta _1$ in Models E1 and E2, then the estimates of this excessive parameter may have a large variance, making the model selection necessary for fitting.

For the case when $\beta _0 = \log (0.4/0.6) \approx -0.4055$, the estimation results are similar to the case stated above, except for the true model being Model O2 and $\gamma _0=1.0$. In this latter case, $\beta _0$ is overestimated.

Note that the data generation and MPL estimation are also computationally efficient in the simulation in this section. The maximum generation time for the $50\times 50$ non-stationary dataset is 52.82 s, and the maximum MPL estimation time for all cases is 31.85 s. The model with lesser parameters also has a shorter computational time.

Table 5 Sample mean and standard deviation (in parentheses) of the MPL estimates for fitting Models E1 and E2 in the simulation when the autocorrelation parameter is dependent on a circular region

Finally, we investigate how AIC and BIC (3.3) perform the model selection. The results are shown in Tables 6 and 7. Here n is the number of observations, and the correct selection results are in bold. Tables 6 and 7 show that if the correct model is Model O1, then the frequencies of correct selections are large for a large n. If the correct model is Model O2, then such frequencies are nearly invariant to n. Since the frequency of choosing the correct model via the BIC is larger than that of the AIC, we recommend the BIC for model selection. When $\beta _0 = \log (0.4/0.6) \approx -0.4055$, the AIC and BIC simulation results are similar to the case of $\beta _0 \approx 0.4055$.

Table 6 The frequencies of model selection results obtained via the AIC in the simulation where the autocorrelation parameter is dependent on a circular region

Table 7 The frequencies of model selection results obtained via the BIC in the simulation where the autocorrelation parameter is dependent on a circular region

In conclusion, simulation results show that the distribution of the generated data from our proposed model significantly differs from the standard autologistic model, where the autocorrelation parameter is a constant. Thus, for the data with the spatial autocorrelation being spatially dependent, we recommend fitting our proposed spatial autologistic model with generalized dependence parameters (2.2) and (2.3). The maximum pseudolikelihood estimation performs well for most cases in our simulation. For model selection, we recommend the BIC in (3.3).

6 Spatial Distribution of the Bur Oak Presence Within the Driftless Area

In this section, we fit the Bur Oak (Quercus macrocarpa) presence data within the Driftless Area of the Mississippi River, Midwestern USA, introduced by Caragea and Berg [7]. The data are collected from the Public Land Survey System (PLSS) dataset [6], which includes the forest competition information in an area of about 2500 square mile. In this section, we investigate the data within a $40\times 40$ regular grid, where the area of one grid is one square mile. Figure 5 illustrates the observed data of two oak species, where black indicates presence and white indicates absence. We aim to fit the presence of the Bur Oak using the information of the White Oak (Quercus alba) and the locations.

Fig. 5

Illustrations of the Bur Oak and White Oak species’ existence data

6.1 Fitting the Model with Spatial Heterogeneity

Let $Y_i$ and $W_i$ be the presence data of the Bur Oak and the White Oak, respectively, observed on a regular grid within $[0, 1]^2$. More precisely, the observation locations are $((i_1-0.5)/40, (i_2-0.5)/40)$, $i_1, i_2 \in \{1, \ldots , 40\}$, which are ordered lexicographically. Denote $\varvec{s}_i = (s_{i, 1}, s_{i, 2})$ as the observation location of $Y_i$. We will fit the following spatial autologistic model with spatial heterogeneity:

$$\begin{aligned}{} & {} \text { logit} \{ \text { Pr} (Y_i = 1 \mid Y_j, j \ne i) \} = \varvec{x}_j^\top \varvec{\beta } + \sum _{i \sim j} \eta _{ij} \left\{ Y_j - \frac{\exp (\varvec{x}_j^\top \varvec{\beta })}{1+\exp (\varvec{x}_j^\top \varvec{\beta })} \right\} , \end{aligned}$$

(6.1)

$$\begin{aligned}{} & {} \eta _{ij} = \frac{1}{2} \varvec{\gamma }^\top (\varvec{z}_{i} + \varvec{z}_j) I \{ i \sim j\}, \end{aligned}$$

(6.2)

where $\varvec{\beta } = (\beta _0, \beta _1, \beta _2, \beta _3)$, $\varvec{\gamma } = (\gamma _0, \gamma _1, \gamma _2, \gamma _3)$,

$$\begin{aligned} \varvec{x}_i^\top \varvec{\beta } = \beta _0 + \beta _1 s_{i, 1} + \beta _2 s_{i, 2} + \beta _3 W_i, \quad \varvec{\gamma }^\top \varvec{z}_{i} = \gamma _0 + \gamma _1 s_{i, 1} + \gamma _2 s_{i, 2} + \gamma _3 W_i, \end{aligned}$$

$W_i$ is the White Oak presence data, and $i \sim j$ means that $i \in A_j$ and $j \in A_i$, where $A_i$ is the set of neighbors defined in Sect. 2, following the nearest neighborhood setting. The MPL estimation result of this model is $\hat{\varvec{\beta }} = (-0.2092, -2.4866, 0.5768, -0.6805)$, $\hat{\varvec{\gamma }} = (0.2119, 0.6474, 0.2294, 0.1838)$, and the computational time of this fitting is 57.45 s.

We also adopt the BIC criterion and the forward selection to reduce redundant parameters in our proposed autologistic model. The fitted model is also defined by (6.1) and (6.2), where

$$\begin{aligned} \varvec{x}_i^\top \varvec{\beta } = \beta _1 s_{i, 1} + \beta _3 W_i, \quad \varvec{\gamma }^\top \varvec{z}_{i} = \gamma _1 s_{i, 1} + \gamma _2 s_{i, 2}. \end{aligned}$$

The estimation values are $(\hat{\beta }_1, \hat{\beta }_3) = (-2.4448, -0.6518)$, $(\hat{\gamma }_1, \hat{\gamma }_2) = (0.9076, 0.5244)$. The computational time of the forward selection procedure is 109.34 seconds.

Figure 6 illustrates the fitted approximated mean $\hat{\beta }_1 s_{i, 1} + \hat{\beta }_3 W_i$ and the fitted autocovariance $\hat{\gamma }_1 s_{i, 1} + \hat{\gamma }_2 s_{i, 2}$. Results show that the approximated mean of the Bur Oak presence is larger when $s_{i, 1}$ is small, and the presence of the White Oak has a negative impact on the mean. The Bur Oak presence is more closely related to its neighborhood when $s_{i, 1}$ is large.

Fig. 6

Illustrations of the fitted approximated mean and the autocovariance term of the Bur Oak presence data

6.2 Comparison of Caragea and Kaiser’s Model

Next, we fit the data to Caragea and Kaiser’s [8] centered model (CK model) and compare the corresponding BIC value and the prediction performance, assessed by the Brier skill score. Let $\hat{p}_i$ be the estimated conditional probability of $Y_i=1$ with respect to its neighbors. The Brier score is defined by

$$\begin{aligned} \text {BS} = \frac{1}{n} \sum _{i=1}^n (Y_i - \hat{p}_i)^2, \end{aligned}$$

whereas the Brier skill score is defined by comparing BS to the Brier score for a constant mean model, or more precisely,

$$\begin{aligned} \text {BSS} := 1 - \text {BS}/\{\bar{Y}(1 - \bar{Y})\}, \end{aligned}$$

where $\bar{Y}$ is the mean value of $Y_1, \ldots , Y_n$. A larger BSS indicates a better model prediction performance.

In this section, the fitted CK model is

$$\begin{aligned} \text { logit} \{ \text { Pr} (Y_i = 1 \mid Y_j, j \ne i) \} = \varvec{x}_i^\top \varvec{\beta } + \eta \sum _{i \sim j}\left\{ Y_j - \frac{\exp (\varvec{x}_j^\top \varvec{\beta })}{1+\exp (\varvec{x}_j^\top \varvec{\beta })} \right\} , \end{aligned}$$

where

$$\begin{aligned} \varvec{x}_i^\top \varvec{\beta } = \beta _0 + \beta _1 s_{i, 1} + \beta _2 s_{i, 2} + \beta _3 W_i, \end{aligned}$$

and $i\sim j$ is defined similarly to model (6.1). The MPL estimate of this model is $\hat{\varvec{\beta }} = (-0.3898, -2.5096, 1.1114, -0.6196)$ and $\hat{\eta } = 0.6778$, and the computational time is 21.04 s. We also use the BIC criterion and the forward selection procedure to reduce the number of parameters of this model. The reduced $\varvec{x}_i^\top \varvec{\beta }$ is

$$\begin{aligned} \varvec{x}_i^\top \varvec{\beta } = \beta _1 s_{i, 1} + \beta _3 W_i, \end{aligned}$$

where the parameter estimates are $(\hat{\beta }_1, \hat{\beta }_3) = (-2.1983, -0.5974)$, $\hat{\eta } = 0.6847$. The computational time of this selection procedure is 43.67 s.

Table 8 shows the BIC and the Brier skill score of different fitted models for the Bur Oak presence data, where “BIC selected" and “full" mean the model fitting results with and without the forward selection, respectively. Results show that our proposed model outperforms the CK model counterparts in the BIC and the Brier skill score, indicating that our model has a better prediction performance compared to the CK model in this dataset.

Table 8 BIC and Brier skill scores of the fitted models for the Bur Oak presence data

In conclusion, our proposed spatial autologistic model is suitable for fitting the data in which the spatial dependency varies with space. Our model provides a better prediction performance in the sense of the Brier skill score compared to Caragea and Kaiser’s [8] model for the Bur Oak dataset. The final fitting model of this dataset is model (6.1), where

$$\begin{aligned} \varvec{x}_i^\top \varvec{\beta } = -2.4448 s_{i, 1} -0.6518 W_i, \quad \varvec{\gamma }^\top \varvec{z}_{i} = 0.9076 s_{i, 1} + 0.5244 s_{i, 2}. \end{aligned}$$

7 Conclusion and Discussion

In this article, we have generalized the centered spatial autologistic model by allowing the autocorrelation parameter to vary with space. This model can be used to fit the spatial binary dataset where the dependency varies with space. Simulation shows that whether the autocorrelation parameter varies with space can significantly affect the pattern of the generated spatial dataset. The maximum pseudolikelihood estimation performs well in estimating unknown parameters in most cases. Our suggested BIC can select the correct spatial autologistic models, verifying whether the autocorrelation parameter is dependent on space.

The results of stochastic simulations reveal the excellent properties of maximum pseudo-likelihood estimation. In the future, we could derive some asymptotic properties of the estimation, such as asymptotic normality, to provide further theoretical support for estimating spatial logistic models with spatial heterogeneity. Moreover, the maximum pseudolikelihood estimation may be biased when the autocorrelation parameter is large and independent of space, so an estimation method with a smaller bias may be called for. Future studies can also extend the model to fit observations with respect to time and space and spatial data with an unknown correlation structure of observed locations.