Systematic Design of Optimal Low-Thrust Transfers for the Three-Body Problem

Abstract

We develop a computational approach for the design of continuous low thrust transfers in the planar circular restricted three-body problem. The use of low thrust propulsion allows the spacecraft to depart from the natural dynamics and enables a wider range of transfers. We generate the reachable set of the spacecraft and use this to determine transfer opportunities, analogous to the intersection of control-free invariant manifolds. The reachable set is developed on a lower dimensional Poincaré section and used to design transfer trajectories. This is solved numerically as a discrete optimal control problem using a variational integrator, which preserves the geometric structure of the motion in the three-body problem. We demonstrate our approach with two numerical simulations of transfers in the Earth-Moon three-body system.

Introduction

Designing spacecraft trajectories is a classic and ongoing topic of research. There has been significant research into the design of orbital transfers for space vehicles. Optimal expenditure of onboard propellant is critical to allowing a mission to continue for a longer period of time or to enable the launch of a less massive spacecraft. Electric propulsion systems offer a much greater specific impulse than chemical systems. As a result, the greatly increased efficiency allows for greater payload mass or extended duration missions. However, these electric propulsion systems typically have much less thrust than their chemical counterparts and therefore orbital maneuvers have a much longer time of flight. In spite of this drawback, a wide variety of missions, such as communication and deep space probes, have utilized the unique benefits of low thrust electric propulsion to great effect [3].

Recent developments in miniature electric propulsion and small satellites now offer the potential for new research opportunities [6, 9]. The potential for more demanding missions places an even greater importance on the mission design to ensure that optimal trajectories satisfy mission requirements [6, 7, 14, 25]. There has been extensive research focused on the optimal control of spacecraft orbital transfers in the three-body problem [8, 14, 22, 25]. Within the three-body problem, a spacecrafts feasible region of motion is constrained by its energy, or Jacobi integral. The addition of low-thrust propulsion offers the potential of reduced transfer transit times and the ability to depart from the free motion trajectory to allow for increased transfer opportunities. Frequently, insight into the problem or intuition on the part of the designer is required to determine initial conditions that will converge to the desired solution due to the inherent nonlinear and chaotic behavior of the three-body system [28]. Conventional general-purpose Runge-Kutta integration techniques, such as those implemented in [8, 22], may fail to preserve geometric properties of the dynamic system numerically. Variational integrators can allow for reduced computational effort without any loss of numerical stability or energy drift which exist in conventional integration schemes.

Objective and Contribution

In this paper, we propose a systematic design method which enables low-thrust transfers in the planar circular restricted three-body problem. We utilize the concept of the reachability set to enable a simple methodology of selecting initial conditions to achieve general orbital transfers. The reachable set, defined as the set of all attainable states subject to the system constraints, allows for the extension of the previous control-free methods based on invariant manifolds. Defining the reachable set on a Poincaré section reduces the dimensionality of the system dynamics to the study of a related discrete update map. Through the use of low-thrust control input, the reachable set on the Poincaré section is enlarged and enables a larger space of potential transfers. By iteratively computing the reachable set, and minimizing the distance to the target on the Poincaré section, we generate general transfer trajectories. With this proposed method, the previous research on control-free trajectories will be generalized with the addition of low thrust propulsion systems.

In short, the authors present a systematic method of generating optimal transfer orbits in the three-body problem. This paper provides a discrete optimal control formulation to generate the reachability set on a Poincaré section.

In addition, the use of a geometric integrators ensures numerical stability for long-duration orbit transfers and maintains this behavior with the addition of small magnitude control inputs. Our computation of the reachable set allows for a simple metric of defining optimal trajectories. We avoid the issues inherent in selecting a valid initial condition for optimization. Rather, we choose a state on the reachability set which minimizes the distance toward the desired target. We demonstrate these capabilities via two numerical examples simulating transfer trajectories in the Earth-Moon system.

Problem Formulation and Mathematical Background

We utilize the planar circular restricted three body problem (PCRTBP) as the basis of our system definition. It is a popular model in the preliminary analysis of multibody spacecraft trajectories. In the context of Earth based mission, the PCRTBP affords a relatively simple dynamic model while still capturing the major third body perturbation of the Moon. In addition, this model allows for a systematic process to define and exploit Poincaré sections. Furthermore, the 2D solutions afforded by the PCRTBP are frequently used to gain a qualitative understanding of the trade space of transfers in the Earth-Moon system. The PCRTBP approach offers insight into the fundamental dynamical structure while capturing the major dynamic properties of the planar motion. As a result, this approach is best suited for preliminary trajectories which do not require large plane changes.

The research in this work utilizes a variety of disparate concepts in dynamics, control theory, and astrodynamics. As a result, we briefly present some key concepts in the system model as well as established tools in the three body problem, such as invariant manifolds and Poincaré sections. In addition, we summarize the derivation of a variational integrator for the PCRTBP which is used in the subsequent geometric optimal control formulation.

Planar Circular Restricted Three Body Problem

The Earth is assumed to be the more massive primary, m₁, while the Moon is the second, smaller primary m₂. The equations of motion are developed in a rotating reference frame which allows for much greater insight into the structure of the dynamics. Following convention, the system is also non-dimensionalized by the characteristic units of length, mass, and time [14]. As a result, the system can be characterized by a single mass ratio parameter μ,

$$ \mu = \frac{m_{2}}{m_{1}+m_{2}} . $$

(1)

In the rotating reference frame the Lagrangian is given by

$$ L = \frac{1}{2} \left( {\left( {\dot{x} - y}\right)^{2} + \left( {\dot{y} + x}\right)^{2}}\right) + \frac{1 - \mu}{r_{1}} + \frac{\mu}{r_{2}}, $$

(2)

where the distances r₁,r₂ ∈ ℝ define the distance from the spacecraft to each primary and are defined as

$$\begin{array}{@{}rcl@{}} r_{1} &= \sqrt{\left( {x + \mu}\right)^{2} + y^{2}}, \end{array} $$

(3)

$$\begin{array}{@{}rcl@{}} r_{2} &= \sqrt{\left( {x -1 + \mu}\right)^{2} + y^{2}} . \end{array} $$

(4)

Following a straightforward application of the Euler-Lagrange equations, a more detailed derivation is provided in [28], results in the following equations of motion defined in the rotating reference frame

$$ \left[\begin{array}{c} \dot{\boldsymbol{r}} \\ \dot{\boldsymbol{v}} \end{array} \right] = \left[ \begin{array}{c} \boldsymbol{v} \\ A \boldsymbol{v} + \nabla U + \boldsymbol{u} \end{array} \right] = f\left( t,\boldsymbol{x}, \boldsymbol{u}\right) , $$

(5)

where the matrix A and pseudo gravitational potential gradient ∇U are

$$\begin{array}{@{}rcl@{}} A &=& \left[ \begin{array}{ccc} 0 & 2 & 0 \\ -2 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right], \end{array} $$

(6)

$$\begin{array}{@{}rcl@{}} \nabla U &=& \left[ \begin{array}{c} x - \frac{ \left( 1 - \mu\right) \left( x + \mu\right)}{{r_{1}^{3}}} - \frac{\mu \left( x - 1 + \mu \right)}{{r_{2}^{3}}} \\ y - \frac{ \left( 1 - \mu\right) y}{{r_{1}^{3}}} - \frac{\mu y}{{r_{2}^{3}}} \\ - \frac{ \left( 1 - \mu\right) z}{{r_{1}^{3}}} - \frac{\mu z}{{r_{2}^{3}}} \end{array}\right] = \left[\begin{array}{c} U_{x} \\ U_{y} \\ U_{z} \end{array} \right] , \end{array} $$

(7)

and the control input is defined as u = [ u_xu_y ]^T ∈ ℝ^2×1 and assumed to be continuously variable but bounded in magnitude, i.e. $\boldsymbol {u}^{T} \boldsymbol {u} \leq u_{max}^{2}$. The state is defined as x = [ rv ]^T with r = [ xy ]^T ∈ ℝ^2×1 and v = [ ẋ ẏ ]^T ∈ ℝ^2×1 representing the position and velocity with respect to the system barycenter, respectively.

Jacobi Integral

There exists a single integral, or constant of motion for the three-body problem [16, 28]. This energy constant is analogous to the total mechanical energy, however it is a non-physical quantity arising from the problem formulation [28]. Also known as the Jacobi constant, it is defined as a function of the position and velocity in the rotating frame and given by

$$ E\left( \boldsymbol{r} , \boldsymbol{v} \right) = \frac{1}{2}\left( \dot{x}^{2} + \dot{y}^{2}\right) - U\left( x,y \right) . $$

(8)

Equation 8 divides the phase space into distinct regions of allowable motion based on the energy level of the spacecraft. Fixing the Jacobi integral to a constant defines zero velocity curves, which are the locus of points where the kinetic energy, and hence velocity vanishes. As seen in Fig. 1, the phase space is divided into distinct realms based on the energy level. In the vicinity of m₁ or m₂ there exists a potential well. As the energy level increases there are five critical points of the effective potential where the slope is zero. Three collinear saddle points on the ê₁ axis and two equilateral points. These equilibrium, or Lagrange points, are labeled L_i,i = 1,…,5 and are shown in Fig. 1. The Jacobi integral is a valuable invariant property of the three-body system that allows for greater insight into the motion of the spacecraft.

Fig. 1

Contour plot of Jacobi integral: Zero velocity curves of constant Jacobi integral. A particle with fixed energy level cannot cross the contour lines and is therefore limited to specific regions of the phase space

Invariant Manifolds and Poincaré Map

Dynamics systems theory has been applied to the design of control-free maneuvers in the restricted three-body problem [14]. As previously introduced in Section “Jacobi Integral”, there exist five equilibrium points in the equations of motion for the three-body problem. It has been shown that the local orbit structure near the Lagrange points gives rise to families of periodic orbits as well as the stable and unstable manifolds of these periodic orbits. This rich structure is globally connected and gives rise to a dynamical chain which allows trajectories to pass through the phase space [4, 14]. The manifold structure associated with periodic orbits about the L₁ and L₂ Lagrange points are critical to the understanding of the motion of spacecraft as well as comets/asteroids. In addition, the stable and unstable manifolds serve as the boundaries of the phase space region that allow for the transport between realms in a single three-body system or between multiple three-body systems. These invariant manifolds only exist as a result of the dynamic formulation of the three-body problem in a rotating reference frame. Invariant manifolds serve as a higher dimensional generalization of the concept of seperatrices from linear systems as applied to the case of nonlinear systems.

Poincaré maps are a useful tool in the analysis of the flow near periodic orbits in the three-body problem. We let Σ define a hypersurface of section chosen such that all trajectories in the vicinity of a state q ∈Σ cross Σ transversely and in the same direction. A Poincaré map, P(q) = ϕ(T;q), maps the state of a trajectory from one intersection to the next. Choosing a section in this manner results in a Poincaré section as shown in Fig. 2. In Fig. 2 we show two examples of periodic trajectories intersecting the Poincaré section. Periodic solutions will appear as fixed points on the section, such as q₀,q₁ in Fig. 2, while stable or unstable trajectories become clearly visible by viewing successive intersections of the section. This allows for greater insight into the stability and dynamics of periodic solutions of a dynamic system as a fixed point on the Poincaré section corresponds to a periodic orbit while movement on the section is associate with the stability of neighboring trajectories. For example, Poincaré maps have been used to prove the existence of homoclinic orbits, which are orbits both forward and backward asymptotic to a single unstable periodic orbit, and heteroclinic orbits, which join different periodic orbits [4, 13]. These dynamic features have been shown to play a vital role in the movement of natural bodies as well as critical for spacecraft missions [7, 18].

Fig. 2

Diagram of the Poincaré map: Periodic orbits will appear as fixed points on the Poincaré section Σ. Stability of periodic orbits is clearly visible on the section as successive intersections approach or depart a fixed point

Combining invariant manifolds and an appropriate Poincaré section provides a conceptually simple manner to determine trajectories which connect wide regions of the phase space. However, the results previously developed are highly case specific and difficult to generalize to arbitrary transfers. Also, these results are based on control-free trajectories which rely on the underlying structure of the three-body system. In addition, transfer orbits along an invariant manifold require large time of flights which may be undesirable for time critical missions. The addition of low-thrust propulsion offers the potential of reduced transit times and the ability to depart from the free motion trajectory to allow for increased transfer opportunities. In this paper, we formulate an optimal control problem to generate the reachable set of the spacecraft. We compute the reachable set on an appropriate Poincaré section and use this to design a transfer trajectory.

Variational Integrator for PCRTBP

Geometric numerical integration deals with numerical integration methods which preserve the geometric properties of the flow of a differential equation, such as invariant properties and symplecticity. Variational integrators are constructed by discretizing Hamilton’s principle rather than the continuous Euler-Lagrange equations. As a result, integrators developed in this manner have the desirable properties that they are symplectic and momentum preserving. In addition, they exhibit improved energy behavior over long integration periods. A thorough discussion of variational integrators is provided in [21, 30]. We use this approach to construct a variational integrator for the PCRTBP with the inclusion of low-thrust propulsion.

Consider the autonomous mechanical system described by the Lagrangian, L(q,q̇), for the generalized coordinates, q and velocities q̇. The integration of the continuous Lagrangian along a path, q(t), followed by the system must satisfy Hamilton’s principle, which results in the well-known Euler-Lagrange equations [16]. In the discrete time scenario, the continuous path q(t),q̇(t), is replaced by a finite difference approximation over a fixed time step, e.g. $q_{0}, \frac {q_{1} - q_{0}}{h}$, which converges to the true velocity as h tends towards zero. In this manner, we define a discrete Lagrangian, L_d(q₀,q₁,h) which approximates the integral of the true Lagrangian over the time interval h between q₀ and q₁ [21].

The discrete equations of motion for the PCRTBP are derived by choosing an appropriate quadrature rule to discretize the continuous Lagrangian in Eq. 2 [21]. In this work, we apply the trapezoidal rule to approximate the action integral over a fixed time interval. The trapezoidal rule allows for a second order accurate approximation and alleviates the difficulties in applying implicit quadrature schemes. The discrete Lagrangian for the PCRTBP is given by

$$\begin{array}{@{}rcl@{}} L_{d} & = &\frac{h}{2} \left( \frac{1}{2} {\left[ \left( \frac{{x_{k + 1}} - {x_k}}{h} -{y_{k}} \right)^{2} + \left( \frac{{y_{k + 1}} - {y_{k}}}{h} + {x_k} \right)^{2} \right]} + \frac{1 - \mu}{r_{1_{k}}} + \frac{\mu}{r_{2_{k}}} \right. \\ && + \left. \frac{1}{2} {\left[ \left( \frac{{x_{k + 1}} - {x_k}}{h} - {y_{k + 1}} \right)^{2} + \left( \frac{{y_{k + 1}} - {y_{k}}}{h} + {x_{k + 1}} \right)^{2} \right]} + \frac{1 - \mu}{r_{1_{k + 1}}} + \frac{\mu}{r_{2_{k + 1}}} \right) . \end{array} $$

(9)

Applying a discrete version of the Lagrange-d’Alembert principle allows for inclusion of an external control force on the system [21]. Using Eq. 9 and some manipulation, gives the discrete equations of motion as

$$\begin{array}{@{}rcl@{}} {x_{k + 1}} & = & \frac{1}{1+ h^{2}} {\left[ h \dot{x}_{k} + h^{2} \dot{y}_{k} + {x_k} \left( {1 + \frac{3h^{2}}{2}}\right) + \frac{h^{3}}{2} {y_{k}} - \frac{h^{3}}{2} U_{y_{k}} - \frac{h^{2}}{2} U_{x_{k}} \right]} , \end{array} $$

(10a)

$$\begin{array}{@{}rcl@{}} {y_{k + 1}} &=& h \dot{y}_{k} + h {x_k} - h {x_{k + 1}} + {y_{k}} + \frac{h^{2} {y_{k}}}{2} - \frac{h^{2} }{2} U_{y_{k}} , \end{array} $$

(10b)

$$\begin{array}{@{}rcl@{}} \dot{x}_{k + 1} &=& \dot{x}_{k} - 2 {y_{k}} + 2 {y_{k + 1}} + \frac{h}{2} \left( {{x_{k + 1}} + {x_k}}\right) - \frac{h}{2} U_{{x_{k + 1}}} - \frac{h}{2} U_{{x_k}} + h u_{x} , \end{array} $$

(10c)

$$\begin{array}{@{}rcl@{}} \dot{y}_{k + 1} &=& \dot{y}_{k} + 2 {x_k} - 2 {x_{k + 1}} + \frac{h}{2} \left( {{y_{k + 1}} + {y_{k}}}\right) - \frac{h}{2} U_{{y_{k + 1}}} - \frac{h}{2} U_{{y_{k}}} + h u_{y} . \end{array} $$

(10d)

The discrete equations of motion are given in the Lagrangian form after applying the discrete fiber derivative as $p_{{x_k}} = \dot {x}_{k} - {y_{k}}$ and $p_{{y_{k}}} = \dot {y}_{k} + {x_k}$. The state is defined as x_k = [ x_ky_kẋ_kẏ_k ]^T and the control input is u = [ u_xu_y ]^T. This results in a discrete update map f_k : x_k →x_k+ 1 which preserves the same properties of the continuous-time dynamics in Eq. 5 such as invariants, symplecticity, and the configuration manifold. The discrete potential gradients are given by

$$\begin{array}{@{}rcl@{}} U_{{x_k}} &= &\frac{{\left( 1 -\mu \right)} {\left( {x_k} + \mu \right)}}{{r_{1_k}}^{3}} + \frac{ \mu {\left( {x_k} -1 + \mu \right)}}{{r_{2_{k}}}^{3}} , \end{array} $$

(11a)

$$\begin{array}{@{}rcl@{}} U_{{y_{k}}} &=& \frac{{\left( 1 -\mu \right)} {y_{k}}}{{r_{2_{k}}}^{3}} + \frac{ \mu {y_{k}}}{{r_{2_{k}}}^{3}} , \end{array} $$

(11b)

$$\begin{array}{@{}rcl@{}} U_{{x_{k + 1}}} &=& \frac{{\left( 1 -\mu \right)} {\left( {x_{k + 1}} + \mu \right)}}{{r_{1_{k + 1}}}^{3}} + \frac{ \mu {\left( {x_{k + 1}} -1 + \mu \right)}}{{r_{2_{k + 1}}}^{3}} , \end{array} $$

(11c)

$$\begin{array}{@{}rcl@{}} U_{{y_{k + 1}}} &= \frac{{\left( 1 -\mu \right)} {y_{k + 1}}}{{r_{1_{k + 1}}}^{3}} + \frac{ \mu {y_{k + 1}}}{{r_{2_{k + 1}}}^{3}} . \end{array} $$

(11d)

The distances to each primary are defined as

$$\begin{array}{@{}rcl@{}} {r_{1_k}} &=& \sqrt{\left( {x_k} + \mu\right)^{2} + {y_{k}}^{2}} , \end{array} $$

(12a)

$$\begin{array}{@{}rcl@{}} {r_{2_{k}}} &=& \sqrt{\left( {x_k} - 1 + \mu\right)^{2} + {y_{k}}^{2}} , \end{array} $$

(12b)

$$\begin{array}{@{}rcl@{}} {r_{1_{k + 1}}} &=& \sqrt{\left( {x_{k + 1}} + \mu\right)^{2} + {y_{k + 1}}^{2}} , \end{array} $$

(12c)

$$\begin{array}{@{}rcl@{}} {r_{2_{k + 1}}} &= &\sqrt{\left( {x_{k + 1}} - 1 + \mu\right)^{2} + {y_{k + 1}}^{2}} . \end{array} $$

(12d)

Care must be taken during the implementation of Eq. 10a–d. As Eqs. 11a–d, and 12a–d are defined at both step k and k + 1 they must be evaluated at both time instances. Equation 10a–d is implemented by first defining an initial state x_k and control u_k. The distances and gravitational potential at step k are evaluated from Eqs. 11a, 11b, 12a and 12b. The discrete update steps in Eqs. 10a, and 10b are evaluated to generate x_k+ 1 and y_k+ 1. Next, the distances and gravitational potential at step k + 1 are evaluated from Eqs. 11c, 11d, 12c and 12d. Finally, the update steps in Eqs. 10c and 10d are evaluated. This results in the complete discrete update map x_k →x_k+ 1 given u_k.

Numerical Example

A simulation comparing the variational integrator to a conventional Runge-Kutta method is presented in this section. A particle is simulated from an initial condition of x₀ = [ 0.75 0 0.2 0 ]^T for t_f = 200 ≈ 15 years in the Earth-Moon system. The variational integrator uses a range of step sizes between 47.2–4720 s while the Runge-Kutta method uses a variable step size implemented via ODE45 in Matlab. The step size of the variational integrator is varied to approximately match the run time required by the conventional ODE45 integrator. Figure 3a shows the trajectory of the spacecraft in the rotating reference for this comparison. Both integration schemes result in trajectories that are initially nearly identical.

Fig. 3

a Earth-Moon three-body trajectory used for integrator comparison: A stable trajectory is used to test the variational and conventional integrators. The energy level is high enough to enter the vicinity of the Moon but not escape the three body system. b Mean Jacobi integral deviation between variational integrator and Matlab ODE45: A range of fixed step sizes are used for the variational integrator to approximately match the computational time of ODE45

Figure 3b shows the mean Jacobi integral deviation over the entire simulation time as a function of computation time. For a given computational effort, in the form of simulation run time, the variational integrator will provide a smaller energy deviation as compared to the conventional integration scheme. Over long simulation horizons or with the addition of small control inputs the inability of conventional integration schemes to accurately track the system energy limits the applicability of conventional techniques in which energy conservation is mandatory for characterizing the solution space. In spite of this improved energy behavior, the order and design of the variational integrator still play an important role in the accuracy of the state vector.

This work uses a second order integrator which has improved energy behavior in comparison to first order integration techniques without a significant increase in computational demand. The variational integrator is constructed according to a discrete version of Hamilton’s principle, specifically for the given dynamic system, and it provides long-term structural stability in capturing the effects of low-thrust propulsion systems. General purpose numerical integrators, such as adaptive stepsize Runge-Kutta methods may yield a more accurate state trajectory depending on the choice of integration parameters, but at the expense of additional computational demand and total energy deviations. However, for this preliminary analysis the variational integrator provides reduced computational demands, as compared with general-purpose numerical integrators with a similar level of numerical error, and is useful to characterize and explore the trade space in preliminary mission design scenarios. In addition, it has been shown that variable step integrators, such as ODE45 in Matlab, tend to degrade first-order gradient based methods, such as those used in Section “Optimal Control Formulation” [24]. The presented results are based on the variational integrator with a fixed time step for numerical simulation and gradient computation. In summary, this paper utilizes the variational integrator to capture the long-term effects of low-thrust devices accurately and efficiently. The structural stability during numerical integration is critical for numerical optimization in the subsequent developments.

Optimal Control Formulation for Reachability Set

In this section, an optimal control formulation is presented to determine and design transfers within the three-body problem. The application of variational integrators to optimal control problems is referred to as computational geometric optimal control. Our formulation is based on the concept of the reachability set on a Poincaré section. This method allows one to easily determine potential transfer opportunities by finding set intersections on a lower dimensional space and greatly reduces the design process. The addition of continuous low thrust propulsion extends the control free design process developed previously and allows for a greater range of potential transfers with a reduced time of flight.

The numerical examples presented in this section are designed in the context of the PCRTBP. The dynamic environment has a four dimensional state space and offers a convenient integration constant in the form of the Jacobi integral. As a result, there are well defined methods to define and exploit Poincaré sections, which result in straightforward two-dimensional subspaces of the system. Our approach uses the Poincaré section to approximate the reachability set on this reduced subspace. As a result, this approach is more difficult to apply to three-dimensional transfers in the general three body problem. Poincaré sections in the case of the general six dimensional state space are significantly more challenging and typically require more complicated visualization techniques. However, this is an area of active research and some of the authors future research is aimed at implementing this approach for non-planar transfer trajectories [15].

Reachability Set

Reachability theory provides a framework to evaluate control capability and safety. The reachable set contains all possible trajectories that are achievable over a fixed time horizon from a defined initial condition, subject to the operational constraints of the system. Reachability theory has been applied to aerospace systems such as collision avoidance, safety planning, and performance characterization. The theory formally supporting reachability has been extensively developed and is directly derivable from optimal control theory [19, 20, 29]. More recently, reachability theory has recently been applied to space systems [5, 10, 12]. Computation of the reachable set for a system involves solving the Hamilton-Jacobi partial differential equation or satisfying a dynamic programming principle. Analytical computation of reachable sets is an ongoing problem and is only possible for certain classes of systems. Typically, numerical methods are used to generate approximations of the reachability set, but are generally limited by the dimensionality of the problem.

Computation of reachable sets is critical to space situational awareness, rendezvous and proximity operations, and orbit determination operations. Specifically, maintaining accurate estimates of a spacecraft state over extended periods is not trivial. The challenge is increased for multiple spacecraft operating in close proximity or when there are long periods of time between measurements. Coupling the ability for continuous low-thrust propulsion between measurements increases the measurement association complexity. Computing the reachability set given estimated states and control authorities allows one to better correlate subsequent measurements or determine sensor pointing regions in the event of a lost spacecraft.

Optimal Control Formulation

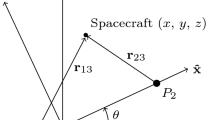
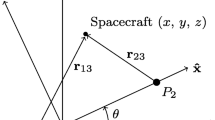
In this paper, we seek to approximate the reachability set on a Poincaré section by solving a related optimal control problem. We choose our Poincaré section in a similar manner to those used previously for the design of transfers via invariant manifolds. The Poincaré section is chosen to intersect transversally with trajectories emanating from the initial orbit. In the case of a periodic orbit the trajectories will cross the Poincaré section at two distinct fixed points every half period. The main idea is that the addition of low thrust propulsion allows us to enlarge the set of trajectories achievable in the Poincaré section. Figure 4 illustrates how, without any control input, trajectories will intersect with the Poincaré section at x_n. However, the addition of low thrust propulsion allows the spacecraft to depart from the natural dynamics and intersect the Poincaré section at a different location. We use a cost function to define a distance metric on the Poincaré section from the control-free intersection to an intersection under the influence of the control input. Maximization of this distance along varying directions enables us to generate the largest reachability set under the bounded control input. In Fig. 4 the reachable set is shown as a circular region on the Poincaré section. In practice, the reachable set will be of a general shape and also higher dimensional in the nonplanar case.

Fig. 4

Reachability set on a Poincaré section: Pictorial representation of the reachability set (blue circle) on the Poincaré section, Σ. The terminal state, x_n, is the intersection without any control input. Adding a control input allows for the terminal state, x_f, to be displaced by some distance/cost J as measured on the section. We parameterize a specific direction on the section with the angles 𝜃_d and seek to maximize the distance between x_f and x_n. Computation of the maximum distance, or reachability, for a variety angles gives a discrete approximation of the reachability set. In general, the reachable set can be an arbitrary shape on the section rather than the circular set depicted

We define the Poincaré section along the horizontal axis, which is equivalent to the surface y = 0, and given by

$$\begin{array}{@{}rcl@{}} {\Sigma} = {\left\{ (x, \dot{x}) | y = 0 \right\}} . \end{array} $$

(13)

This is similar to the previous work in determining homoclinic orbits in the three-body problem [14, 17]. Previous analytical results have shown that homoclinic orbits intersect transversally in the (x,ẋ) space on the plane y = 0. We seek to compliment these results with the addition of low thrust propulsion to maximize the reachable set on the Poincaré section. Placing our section at y = 0 ensures that all trajectories will intersect our section. An optimal control problem is defined by a cost function

$$ J = -\frac{1}{2} \left( \boldsymbol{x}(N) - \boldsymbol{x}_{n}(N)\right)^{T} \left[ \begin{array}{cccc} 1 & 0& 0& 0 \\ 0& 0& 0& 0\\ 0 & 0 & 1 &0\\ 0 & 0& 0& 0 \end{array} \right] \left( \boldsymbol{x}(N) - \boldsymbol{x}_{n}(N)\right) = \phi(\boldsymbol{x}(N),\boldsymbol{x}_{n}(N)) . $$

(14)

The term x_n(N) is the final state of a control-free trajectory while the term x(N) is the final state under the influence of the control input. Maximization of the distance between x_n and x, on the Poincaré section defined in Eq. 13 at the terminal time t_f = N, is equivalent to the minimization of J defined in Eq. 14. The Poincaré section is defined through the use of appropriate terminal constraints given by

$$\begin{array}{@{}rcl@{}} v_{1}(\boldsymbol{x}(N) ) &=& y(N) = 0 , \end{array} $$

(15a)

$$\begin{array}{@{}rcl@{}} v_{2} (\boldsymbol{x}(N) )&=& \frac{\dot{x}(N) - \dot{x}_{n}(N) }{x(N) -x_{n}(N) } - \tan{\theta_{d}} = 0, \end{array} $$

(15b)

$$\begin{array}{@{}rcl@{}} 0 &\geq&\boldsymbol{u}^{T} \boldsymbol{u} - u_{max}^{2} , \end{array} $$

(15c)

where the angle 𝜃_d defines a direction in which we wish to maximize the reachability set on the Poincaré section. The maximum control thrust magnitude is defined by u_max and is non-dimensionalized by the characteristic units of length, mass, and time. The goal is to determine the control input u_k such that the cost function (14) is minimized subject to the state equations of motion (10a–d) and constraints (15a–c).

Application of the Euler-Lagrange equations allows us to derive the necessary conditions for optimality [1]. The discrete variational integrator in Eq. 10a–d is used rather than the continuous time counterpart. This results in a discrete optimal control problem and the discrete necessary conditions are given as

$$\begin{array}{@{}rcl@{}} \boldsymbol{\lambda}_{k + 1}^{T} &=& \boldsymbol{\lambda}_{k}^{T} {\left( {\frac{\partial \boldsymbol{f}_{k}}{\partial \boldsymbol{x}_{k}}} \right)}^{-1} , \end{array} $$

(16a)

$$\begin{array}{@{}rcl@{}} 0 &=& {\frac{\partial H_{k}}{\partial \boldsymbol{u}_{k}}} , \end{array} $$

(16b)

$$\begin{array}{@{}rcl@{}} 0 &=& {\frac{\partial \phi}{\partial \boldsymbol{x}_{k}}}^{T} + {\frac{\partial \boldsymbol{v}}{\partial \boldsymbol{x}_{k}}}^{T} \boldsymbol{\beta} - \boldsymbol{\lambda}^{T}(N) , \end{array} $$

(16c)

where the Hamiltonian H is defined as

$$ H_{k} = \boldsymbol{\lambda}_{k}^{T} \boldsymbol{f}(\boldsymbol{x}_{k}, \boldsymbol{u}_{k}) , $$

(17)

and λ ∈ ℝ^4×1 is the costate and β ∈ ℝ^2×1 are the additional Lagrange multipliers associated with the terminal constraints in Eq. 15a–c. The state dynamics are represented by f(x_k,λ_k) after substituting (16b) into Eq. 10a–d. This indirect optimal control formulation leads to a two point boundary value problem with split boundary conditions. By sweeping the angle 𝜃_d one can approximate the reachable set on the Poincaré section subject to the bounded control input.

The costate equation of motion requires the Jacobian of Eq. 10a–d and is given by

$$\begin{array}{@{}rcl@{}} \boldsymbol{\lambda}_{k + 1}^{T} = \boldsymbol{\lambda}_{k}^{T} \left[\begin{array}{lllllllll} f_{1_{x}} & f_{1_{y}} & f_{1_{\dot{x}}} & f_{1_{\dot{y}}} \\ f_{2_{x}} & f_{2_{y}} & f_{2_{\dot{x}}} & f_{2_{\dot{y}}} \\ f_{3_{x}} & f_{3_{y}} & f_{3_{\dot{x}}} & f_{3_{\dot{y}}} \\ f_{4_{x}} & f_{4_{y}} & f_{4_{\dot{x}}} & f_{4_{\dot{y}}} \end{array}\right]^{-1} . \end{array} $$

(18)

The derivation of Eq. 18 is given in Appendix. In addition, the computation of Eq. 18 requires inversion of the Jacobian matrix. This is a computationally expensive operation that is prone to numerical error and instability. We use Gauss-Jordan elimination to avoid this inversion in Eq. 18 and determine an explicit update map λ_k →λ_k+ 1.

The optimal control formulation presented in this section results in a two point boundary value problem (TPBVP). There exist many methods to solve TPBVPs such as gradient, quasilinearization, and shooting methods [1, 11]. Shooting methods are common in astrodynamic trajectory design problems and relatively simple to implement. In the shooting method, initial conditions are varied such that a terminal constraint is satisfied, similar to the way an archer modifies the bow in order to more accurately strike a target. Consider the vector of initial conditions, χ = {x₀,λ₀}, which is varied to satisfy some terminal constraints of the form G(χ) = {x_t −x_n} = 0. The free variables at the terminal time are computed by propagation of χ over the selected time horizon. At the terminal time, the constraint vector is calculated and if not satisfied χ is varied. Rather than numerical integration over the entire time interval, multiple shooting segments the interval into several smaller sub-arcs [27]. This multiple shooting approach incorporates additional interior constraints but reduces the sensitivity of the costates along each sub-arc. The use of the multiple shooting method reduces the sensitivity of changes in the initial costate at the expense of additional design variables, but has been shown to provide more stable and robust solutions [23].

In Fig. 5, we show a schematic representation of the multiple shooting procedure. We split the optimal control horizon into equal length subsegments such that the length of each segment is kn, where k,n are the total number of steps and number of stages, respectively. Similarly, we divide the state and costate trajectories into n equal segments. To ensure continuity, additional interior constraints are incorporated as

$$\begin{array}{@{}rcl@{}} \boldsymbol{x}_{1}^{-} - \boldsymbol{x}_{1}^{+} &=& 0 , \end{array} $$

(19a)

$$\begin{array}{@{}rcl@{}} \boldsymbol{\lambda}_{1}^{-} - \boldsymbol{\lambda}_{1}^{+} &=& 0 , \end{array} $$

(19b)

$$\begin{array}{@{}rcl@{}} \boldsymbol{x}_{2}^{-} - \boldsymbol{x}_{2}^{+} &=& 0 , \end{array} $$

(19c)

$$\begin{array}{@{}rcl@{}} \boldsymbol{\lambda}_{2}^{-} - \boldsymbol{\lambda}_{2}^{+} &= &0 , \end{array} $$

(19d)

$$\begin{array}{@{}rcl@{}} &{\vdots} \\ \boldsymbol{x}_{n-1}^{-} - \boldsymbol{x}_{n-1}^{+} &=& 0 , \end{array} $$

(19e)

$$\begin{array}{@{}rcl@{}} \boldsymbol{\lambda}_{n-1}^{-} - \boldsymbol{\lambda}_{n-1}^{+} &=& 0. \end{array} $$

(19f)

Fig. 5

Schematic diagram of the multiple shooting method: The complete trajectory is split into a number of sub-segments, and additional interior constraints are included to ensure state and costate continuity. Splitting the optimal trajectory into short segments reduces the sensitivity of terminal states to variations of the initial states

Using the multiple shooting method reduces the sensitivity of the terminal states, xi+,λi+, to variations of the initial states, xi− 1−,λi− 1−. As a result, the design vector χ is augmented with the additional interior initial conditions, xi−,λ⁻. Similarly, the constraint vector is augmented with the additional interior constraints defined in Eq. 19a. Based on experimentation, we use four stages in our multiple shooting method. This provided the best performance and convergence stability while minimizing the difficulties in additional interior constraints. The multiple shooting algorithm now varies the design vector χ to ensure that the constraints in G(χ) are satisfied. In this work, we use the Matlab nonlinear solver fsolve to solve the system of nonlinear equations defined by the multiple shooting algorithm with a convergence tolerance of 1 × 10^− 5. Within fsolve, we use the trust-region dogleg solver which makes use of the Powell dogleg procedure for computing a step direction and magnitude to minimize successive iterations of the solver. All numerical integration is performed using the discrete variational integrator described in Section “Variational Integrator for PCRTBP”. The numerical results are specific to the choice of nonlinear solver, and different tolerances or software tools may result in slight changes.

Numerical Example

We present two numerical simulations in the Earth-Moon system to demonstrate the transfer procedure. These simulations enable the spacecraft to depart from the natural dynamics through the use of low-thrust propulsion. The reachability set on the Poincaré section allows for a straightforward method of determining transfer opportunities. The first example is a transfer from a periodic orbit of the L₁ Lagrange point to a fixed orbit of the moon. This example uses a single iteration of the reachable set computation in the design of the transfer. The second example is a transfer from geostationary orbit of the Earth to a period orbit of L₁. This examples demonstrates the ability to extend the reachability process to multiple iterations, to allow for a much larger and more general transfer. With both examples it is possible to depart from the vicinity of the Earth to a Moon orbit via a series of reachable sets defined on Poincaré sections. The numerical examples presented in this section satisfy the necessary conditions for local optimality and obtaining a globally optimal solution is considered beyond the scope of this paper.

Periodic Orbit transfer

The first objective is to design a transfer trajectory from a planar periodic orbit about the L₁ Lagrange point to a bounded orbit in the vicinity of the Moon. The target region is created by choosing an initial condition of x₀ = [ 1.05 0 0 0.35 ]^Twith μ = 0.0125. The target set is propagated over a period of t = 20 in non-dimensional units which corresponds to approximately 1.5 years.

Figure 6 shows that the target set remains in the vicinity of the Moon, or m₂, in the rotating reference frame. This type of orbit would be useful for a variety of mission scenarios. For example, a series of communication satellites could be placed in this type of orbit. The bounded trajectories of the vehicles and constant line of sight to both the Moon and the Earth would allow for constant communication for future manned missions and potential habitats. The initial set is a planar periodic orbit about L₁, which is generated using the process of differential correction of a linear approximation [14].

Fig. 6

L₁ periodic orbit transfer to orbit of the Moon: Example scenario demonstrating the initial and target orbit. Without the low-thrust propulsion, the spacecraft is constrained to the initial periodic orbit. We determine the reachability set to find a transfer trajectory to the target orbit about the moon

As a source for comparison, the method of using invariant manifolds, introduced in [14], is implemented. As described in Section “Invariant Manifolds and Poincaré Map”, these invariant manifolds are the set of trajectories that either asymptotically arrive or depart the periodic orbit. We generate the unstable manifold associated with the initial planar periodic orbit. We numerically propagate the unstable manifold forward in time until the trajectories intersect the Poincaré section y = 0. Figure 7a shows the unstable invariant manifold generated from the initial L₁ periodic orbit. The blue points in Fig. 7b are the intersections of the target Moon orbit and the Poincaré section. The two circular regions are the ascending (right) and descending (left) intersections of the target orbit and Poincaré section. The green points in Fig. 7b are intersections of the unstable manifold from Fig. 7a with the Poincaré section y = 0. Only a single branch of the invariant manifold intersects with the ascending region of the target orbit. There are no intersections of the invariant manifold with the descending region of the target orbit. The numerical values associated with the green points denote the required time of flight along the invariant manifold in non-dimensional units. The required travel time for a transfer using the unstable invariant manifold is approximately t_f ≈ 3.1 non-dimensional time units.

Fig. 7

Invariant manifold transfer: An example transfer using the invariant manifolds is shown in both the position and Poincaré spaces. The control free transfer from the initial periodic orbit to the target orbit result in a long time of flight. In addition, the manifold only intersects the target orbit on the ascending or far side of the moon

Next, we determine the reachability set with addition of a low-thrust control input over a fixed time horizon. In Section “Reachability Set on the Poincaré Section”, we demonstrate the effect of variations in the choice of maximum control bound and terminal time. While Section “Transfer to Periodic Orbit” show a specific example of a transfer design process using the intersection of the reachability set on the Poincaré section. The analysis presented in the following sections define a maximum magnitude of the thrust as u_m and assume that the trust can be directed arbitrarily within the plane. This model is representative of many spacecraft which have a body fixed thruster and attitude control system. Assuming a fully actuated spacecraft model allows us to decouple the translation and rotational dynamics of the spacecraft.

Reachability Set on the Poincaré Section

From the initial state on the periodic orbit, a series of optimal trajectories are generated to determine the reachable set. The multiple shooting approach is implemented to solve the optimal control problem. We divide the time horizon into two equal length segments. The state trajectory is initialized using the free trajectory of the periodic orbit. Similarly, the costate trajectory is initialized from an initial guess of λ₀ = [ − 1 − 1 − 1 − 1 ]^Tand propagated using the discrete equations of motion in Eq. 18. This results in the initial guess of the design vector χ = [ λ₀x1−λ1−β ]^T. This design vector is then varied to ensure that the necessary conditions of optimality and the interior point constraints are satisfied. Table 1 shows the range of terminal times, t_f, and maximum control bound, u_m, which are used to investigate their effect on the subsequent reachable set on the Poincaré section.

Table 1 Combinations for t_f and u_m used to generate the reachability sets in Fig. 8

The angle 𝜃_d in Eq. 15a–c is varied to select a different direction along the Poincaré section to maximize. We discretely vary the angle over the range 0^∘≤ 𝜃_d < 360^∘ to approximate the reachability set of the spacecraft. Choosing a new angle 𝜃_d corresponds to a different direction as well as a new optimal control problem which is again solved using the multiple shooting approach laid out previously. Each optimal control solution, corresponding to a discrete value of 𝜃_d, is solved using fsolve as described earlier. Each solution on the reachability set is computed in approximately 2 min on a desktop computer using an 3.4 GHz Intel i7-3700. The intersection of the optimal trajectories as well as those of the target Moon orbit with the Poincaré section are shown in Fig. 8.

Fig. 8

Variation of t_f and u_m on the reachability set. Colors, {red}, blue, green, yellow}, are used note increasing t_f while markers, {circle, square, cross}, are used to denote increasing u_m. Increasing the maximum control bound has a large effect and enables the reachability set to intersect the target manifold. Increases in t_f are less critical and have minimal impact on the distribution of the reachability set on the Poincaré section

Figure 8 shows the reachabilty set for twelve combinations of t_f and u_m listed in Table 1. With a small maximum control bound, u_m = 0.05 shown using square markers, the reachable set is not dramatically changed from that of the no control solution. The reachable set is denoted using square markers on the left most portion of Fig. 8b. Variations of t_f are indicated using different colors and also demonstrate that this parameters has a smaller impact than changes in u_m. Increasing the control bound to u_m = 0.25 and u_m = 0.5 shows that the reachable set progressively approaches the target set.

The reachable sets presented in Fig. 8 are highly dependent on the initial condition, terminal time, and maximum control bound. This example demonstrates that increasing the u_m results in a larger displacement between the controlled and uncontrolled trajectories. The reachable set is enlarged from a single point, as shown in Fig. 7b by the black point, to a larger region as shown in Fig. 8b. The choice of u_m, t_f and initial condition all combine to change the resulting reachability set.

Transfer to Periodic Orbit

Here we use the results of the preceding section to demonstrate one specific example of a transfer designed using the reachability set. The acceleration limit is chosen as u_max = 0.75 ≈ 2mm s^− 2 in the Earth-Moon system. Assuming a fixed spacecraft mass of 500 kg, this model defines a maximum thrust of approximately 1 N. Currently, the NASA NEXT xenon thruster is able to provide approximately 0.25 N of thrust, and a cluster of such engines could be used to provide the desired thrust used in this work [26]. The trajectories are generated from a fixed initial state of x₀ = [ 0.8156 0 0 0.1922 ]^Tover a fixed time span of t_f = 1.4. This initial state lies on the initial periodic orbit and the time of flight is equivalent to one half period of the initial periodic orbit.

The optimal trajectories, under the influence of the control input u, are plotted in red in Fig. 9a. Initially, the spacecraft is assumed to lie on the periodic orbit. As a result, the intersection of this periodic orbit with the Poincaré section are two points corresponding to the two crossing of the orbit. We show the control-free intersection, x_n, of the periodic orbit on the Poincaré section in Figs. 7b and 9b The use of the continuous low thrust propulsion expands the reachable set to region bounded by the red markers in Fig. 9b. The reachable set is an ellipsoidal region with a major axis aligned along 𝜃 ≈ 70^∘ as compared to a fixed point without any control input.

Fig. 9

L₁ Reachability set transfer: The low thrust propulsion is used to approximate the reachability set starting from the initial periodic orbit over a fixed time horizon. The reachability set is shown in Fig. 9a and b in both the position and Poincaré space respectively. From this reachability set we chose a trajectory which intersects the target orbit and it is shown in Fig. 9c. The optimal control to achieve this transfer is shown in Fig. 9d

Figure 9b shows that the reachable set and those of the descending target region intersect. As both regions are discretely approximated a linear interpolation is used to determine the exact intersection state on the Poincaré section. This intersection generates a partial target state of x_t,ẋ_t and y = 0 from the Poincaré section. Using the energy level of the target region, defined by Eq. 8, and the intersection state we can calculate the final component ẏ. This results in a complete target state x_t which lies on the reachable set and on the target orbit. Due to the use of low-thrust propulsion, there is a change in Jacobi energy during the transfer as the vehicle transitions between the initial and final periodic orbits. This behavior is demonstrated in Fig. 9e as the vehicles experiences an increase in energy transitioning towards the target followed by a decrease to arrive at the target.

A final optimal trajectory is generated such that the x(N) = x_t. This transfer serves to satisfy a required boundary condition to ensure a continous trajectory to the target. The reachability set, and the intersection on the Poincaré section, are used to generate a partial target state for the transfer. Due to the difference in Jacobi energy, a final optimal transfer is computed to satisfy the desired target state. This transfer trajectory is denoted by the green path in Fig. 9c. The optimal control input is shown in Fig. 9d. The spacecraft achieves the desired target while satisfying the bounded control input. The Jacobi energy integral, computed using Eq. 8, is shown in Fig. 9e. Figure 9e shows that the vehicle begins with an energy level equal to the periodic orbit and arrives at the target orbit with the appropriate energy. The first half of the transfer is associated with and increase in energy as the control is used to transition towards the target orbit which is followed by a energy decrease to the target orbit. This roughly corresponds with the expected optimal solution of a bang-coast-bang type orbital transfer [11]. Convergence statistics associated for this transfer are shown in Table 2.

Table 2 Convergence statistics for the periodic orbit transfer

A transfer along the invariant manifold requires on average t_f ≈ 3.1 as compared to t_f ≈ 1.4 for a transfer using low thrust propulsion and the reachable set. This long time of flight is typical of transfers using invariant manifolds. The unstable invariant manifold traverses a large region of the phase space and is dependent on the system dynamics. In addition, the invariant manifolds asymptotically arrive and depart from the periodic orbit. As a result, it may take an arbitrarily long period of time to depart from the vicinity of the periodic orbit. In addition, only a small portion of the invariant manifold intersects with the target Moon orbit. In contrast, the low thrust control input we are able to enlarge the reachability set from a single point, x_n associated with the periodic orbit, to a larger ellipsoidal region shown in red in Fig. 9b. This achieves an intersection with the target orbit with a much lower time of flight as compared to the invariant manifold method. In addition, by generating the reachability set we are able to compute the required control input to exactly intersect the target orbit. This avoids having to compute and accomplish a secondary impulsive maneuver to transition from the invariant manifold to the target orbit.

Geostationary Transfer

There are many situations where a more complicated and extensive orbital transfer is desired. In this section, we present a simulation of transferring from a geostationary orbit to a periodic orbit about the L₁ Lagrange point. From this location, it is possible to transition to the Moon, as shown in Section “Periodic Orbit transfer”, or beyond the Earth-Moon system through the use of invariant manifolds [14]. This type of low energy transfer would be most suitable for unmanned spacecraft transitioning from the Earth to the Moon. The long time of flight would make such a transfer unsuitable for manned missions due to life support constraints. Future proposals for permanent lunar spacecraft and bases will require frequent supply missions to remain viable. Transfers from the Earth to the Lagrange points, through the use of low-thrust electric propulsion, offer an additional and potentially shorter time of flight in comparison to the low-energy transfers which utilize solar perturbations.

Section “Periodic Orbit transfer” demonstrated the capability of determining an orbital transfer after locating the intersection of the reachability set and a target orbit. However, it may not be possible to achieve an intersection on the Poincaré section after a single iteration. Since the spacecraft has an upper bounded control input and time of flight the reachability set is finite in size. As a result, we present a method of performing several iterations of the reachability set computation. A straightforward method is presented which allows for a series of reachability sets to be computed which progressively move the trajectory towards the target. In this manner, it is possible to determine more complicated transfers by a simple selection of states from the reachability set. This affords a systematic method of determining general transfer trajectories in the three body problem.

It is possible to design arbitrary transfers using either a direct optimization or invariant manifold based approach. The direct optimization method transforms the optimal control problem into a nonlinear programming problem. Instead of solving the Euler-Lagrange equations the state and control histories are parameterized and solved through any number of mathematical programming methods. However, due to this parameterization only an approximate solution, which approximates the true optimal solution in the limit, is feasible. On the other hand, our method applies an indirect optimization method. The necessary conditions for optimality are computed and directly solved in generating the reachability set. The use of the reachability set also avoids the issues of selecting a valid initial condition. We select a state on the maximum reachability set which minimizes the distance toward the target. This straightforward approach achieves an optimal trajectory and is used to generate general transfers.

The invariant manifold method is difficult to apply to general orbital transfers. The manifolds are associated with periodic orbits in the three-body system. In this case, an appropriate periodic orbit must first be determined prior to generating the invariant manifold. Furthermore, there is no guarantee that the invariant manifold will pass through a desired region of space. For example, in the Earth-Moon system the unstable manifolds of periodic orbits about L₁ do not pass close to the Earth, but rather are beyond the geostationary orbit altitude. In addition, determining the intersections between various invariant manifolds is not trivial. It requires an appropriate Poincaré section and the generation of several invariant manifolds. There is no clear method of selecting the periodic orbits required based on the type of transfer desired. Determining an intersection between these invariant manifolds generally requires extended flight times, involving several orbits of the primaries, before an appropriate intersection is found. As a result, it is difficult to generalize this method to arbitrary transfers in the three-body problem.

This numerical simulation demonstrates the ability of the our approach to determine more general transfer trajectories in the PCRTBP. We use multiple iterations of the reachability set to achieve a more complicated transfer. In this manner, it is possible to design arbitrary transfers which are not possible using a single reachability computation. Initially, it is assumed that the spacecraft lies on a circular geostationary orbit in the non-dimensional Earth-Moon three-body system. While the geostationary orbit is not a typical “parking orbit” for most spacecraft missions it serves as a convenient altitude to demonstrate our approach. The geostationary orbit about the Earth is transformed into the rotating reference frame of the Earth-Moon three body problem. In addition, we non-dimensionalize the initial state to find x₀ = [ 0.0972 0 0 3.0010 ]^Tas the initial condition of the spacecraft on the geostationary orbit. It is desired to transfer to a periodic orbit about the L₁ Lagrange point. The periodic orbit is defined by the initial condition [ 0.8057 0 0 0.2982 ]^T. The initial and target orbits are illustrated in Fig. 10.

In Fig. 10, the initial orbit is located in the center of the figure and centered about m₁ while the target periodic orbit is determined about the L₁ Lagrange point. Instead of determining a transfer directly between the geostationary orbit and the periodic orbit, we seek to instead transfer to the stable manifold of the periodic orbit. This stable manifold will then asymptotically approach the target orbit without any further control input. Once on the manifold, the spacecraft will coast in an uncontrolled fashion and asymptotically arrive at the desired periodic orbit.

Fig. 10

Geostationary to L₁ transfer: Representation of the initial and target orbits for the reachability transfer. Vehicle is assumed to begin on the geostationary orbit about m₁ and will transfer to the periodic orbit about L₁

We first generate the stable invariant manifold associated with the periodic orbit in order to determine our target set. The stable manifold is propagated to the Poincaré section at y = 0, which is denoted by the horizontal black line in the position space visualizations given in Figs. 11, 12 and 13a. The stable manifold is denoted by the green trajectories which span the majority of the phase space. In addition, we plot the intersection of the stable manifold with the Poincaré section with green markers. The initial orbit and the stable invariant manifold do not intersect and the transfer objective is to enlarge the reachability set to include the stable manifold.

Fig. 11

Stage 1-4 reachability sets: The first four reachability sets visualized in both the position (left) and Poincaré space (right). The minimum trajectories from the preceding stages are shown in red, while the next stage is shown in blue. The transfer goal is to generate a complete trajectory from the initial geostationary orbit to the L₁ stable manifold, with an eventual arrival at the L₁ periodic orbit

Fig. 12

Stage 5-8 reachability sets: The last four reachability sets visualized in both the position (left) and Poincaré space (right). The minimum trajectories from the preceding stages are shown in red, while the next stage is shown in blue. The transfer goal is to generate a complete trajectory from the initial geostationary orbit to the L₁ stable manifold, with an eventual arrival at the L₁ periodic orbit

Fig. 13

Geostationary to L₁ periodic orbit transfer: Complete transfer from the geostationary orbit to the stable manifold

Next, we compute the reachable sets originating on the geo-stationary orbit and subject to the maximum control constraint. The multiple shooting approach is used to solve the optimal control problem with two segments. For the first reachability set computation, the initial geostationary orbit is used to initialize the multiple shooting algorithm. We use the same initial guess of λ₀ as in Section “Periodic Orbit transfer” and propagate over the fixed time horizon of the period of the geostationary orbit to initialize λi−.

The first reachable set is computed beginning on the geostationary orbit at it’s intersection with the Poincaré section and we again assume a upper bound on the thrust magnitude of u_max = 0.75. The reachable set is generated by varying the angle 0^∘≤ 𝜃 < 360^∘ in Eq. 15a–c defined on the Poincaré section. This allows us to approximate the set of states that are achievable in the (x,ẋ) space. The intersection of the first reachable set with the Poincaré section is shown in Fig. 11b in red. While the reachable set does not intersect the stable manifold, it does reduce some of the distance in the ẋ dimension. From this reachable set, we chose a trajectory which minimizes the distance towards the stable manifold, which is shown in Fig. 11b by the black marker. The distance on the Poincaré section between the reachable set and the stable manifolds is defined as the function d,

$$d(\boldsymbol{x}(N)) = \sqrt{{\left( x - x_{t} \right)}^{2} + {\left( \dot{x} - \dot{x}_{t} \right)}^{2}}. $$

From the reachable set, the trajectory which minimizes d is used to initialize the next iteration. The minimum trajectory is also shown in Fig. 11a and is used to initialize the following stage. Over the relatively short time horizon of the geostationary orbital period, the reachability set remains quite close to the initial orbit. However, the addition of the control input has increased the velocity component of the trajectory. It is this velocity change that is subsequently exploited to generate the transfer trajectory.

The minimum trajectory from the first iteration of the reachability set is used to initialize the following stage. From the terminal state of the first iteration, the second reachability set is computed and displayed in Fig. 11c and d. The second reachability set is shown on the Poincaré section in Fig. 11d. This iteration greatly decreases the distance in the x component between the trajectory and the target, at the expense of a small deviation in the ẋ component. In Fig. 11c, the first stage trajectory is shown in red while the additional stage is shown in blue, which demonstrates the decrease in the x component.

With each reachable set we move the controlled trajectory closer to the target stable manifold. Figures 11 and 12 shows all of the intermediate reachability iterations to transfer between the initial orbit and the stable invariant manifold. The final reachable set intersects the stable manifold of the periodic orbit. A final fixed terminal time and terminal state optimal transfer is finally used to arrive at the stable manifold. The optimization statistics for the final transfer are shown in Table 3.

The complete transfer trajectory, after eight iterations, is shown in Fig. 13. Combining these trajectories results in the powered portion of the transfer from the geostationary orbit to the stable manifold. Each iteration systematically moves the reachable set towards the stable manifold. Furthermore, the optimal control formulation is simplified as each iteration is initialized using a simple distance metric on the Poincaré section. Figure 13a and b shows the resulting trajectory, with the final trajectory shown in red which ensures the intersection with the stable invariant manifold. Figure 13c shows the Poincaré section with the minimum reachable state from each iteration. Each iteration seeks to decrease the distance to the stable manifold on the Poincaré section. Furthermore, these minimum states serve to initialize each subsequent stage of the transfer. This method provides a systematic and simple methodology to determine transfer trajectories. Instead of relying purely on numerical optimization to find an appropriate trajectory, our method instead utilizes the reachability set to determine suitable trajectories. Once at the stable manifold, no further control input is required and the vehicle will coast towards the target periodic orbit. Figure 13d shows the control input during the powered portion of the transfer. We utilize the same spacecraft assumption of 500 kg from Section “Periodic Orbit transfer” which gives a maximum thrust of approximately 1 N. The spacecraft maintains a bounded control magnitude during the transfer to the stable manifold. Figure 13e shows the evolution of the Jacobi energy over the transfer. Each stage of the transfer serves to raise the energy level of the vehicle. After eight stages the reachability set intersects the stable manifold and a demonstrates that a transfer is achievable. The final optimal control drives the vehicle towards the target manifold with the appropriate energy level.

Table 3 Convergence statistics for the geostationary orbit transfer

This numerical example demonstrates the ability to link several computations of the reachability set to enable a more general transfer. We use eight iterations of computing the reachability set in order to transfer from the geostationary orbit to the stable manifold. The example shows a transfer between an initial geostationary orbit and the stable manifold associated with a periodic orbit. This approach allows for a larger class of potential transfers which leverage the capabilities of low-thrust propulsion systems. However, the presented approach does not offer a optimal solution in terms of energy/fuel usage. The reachability sets are computed on the lower dimensional Poincaré section. As a result, the repeated intersections of the trajectory with the Poincaré section results in a fuel inefficient transfer. Furthermore, the issue of discrepancy in the Jacobi integral may become more serious when multiple reachability sets are interconnected. Nonetheless, we are able to apply the proposed approach for the challenging case where the reachability set is not sufficiently close to the invariant manifold of the target orbit. Consequently, this example illustrates a straightforward method to depart from the natural dynamics and transfer to a large region of the phase space that is not accessible via invariant manifolds alone. The presented idea of connecting reachability sets can be further studied to address the aforementioned issues of optimality and mismatch of the Jacobi integral.

Conclusions

In this paper, we construct a systematic approach which combines the concepts of reachability sets and Poincaré sections to generate orbital transfers between planar periodic orbits in the three-body problem using low-thrust propulsion systems. The Poincaré section allows for trajectory design on a lower dimensional phase space thereby reducing the complexity and search space. The approximation of the reachability set enables a simple methodology for the selection of good initial parameters which will allow for convergence of the optimal control formulation. The combination of these two concepts allows the engineer to capture the characteristics inherent in the three-body problem. Additionally, we utilize geometric integrators to efficiently capture the long-term effects of low-thrust on the system dynamics. Our approach enables the computation of orbital transfers within the three-body problem but does not guarantee optimality of the resulting transfer. Instead, the resulting transfers will require no excessive control inputs as it is formulated as a deviation from the control-free trajectory. The presented approach allows for a systematic method to determine and generate orbital transfers in the three-body problem using low-thrust propulsion.

There is additional research to extend these results to more general transfer scenarios in future work. The incorporation of fourth body perturbations, such as the Sun in the Earth-Moon system, offers an additional method of increasing the reachable set with the combined use of the solar perturbation and low-thrust propulsion. In addition, the assumed acceleration magnitude is currently beyond the capabilities of current electric propulsion systems and future research is aimed at investigating smaller magnitude control inputs. Furthermore, this analysis did not consider the effect of variable mass on the optimal control solution. This will result in a more complicated optimal control problem and is a focus of future research. Finally, Lyapunov control theory, which has previously been applied to the two-body problem, is being investigated in the hope of designing closed loop control schemes for this three-body scenario [2]. The addition of attitude dynamics and realistic pointing constraints would also significantly improve the applicability of this work.

Appendix: Costate Equations of Motion

The development of the costate equations of motions begins with determining the second order partial derivatives of the gravitational potential. Due to the symmetry of partial derivatives only three terms are required and are given by

$$\begin{array}{@{}rcl@{}} U_{xx_k} &=& \left( {1-\mu}\right) \left[{\frac{1}{r_{1_k}^{3}} - \frac{3 \left( {x_k +\mu}\right)^{2}}{r_{1_k}^{5}}}\right] + \mu \left[{\frac{1}{r_{2_{k}}^{3}} - \frac{3 \left( {x_k -1 + \mu}\right)^{2}}{r_{2_{k}}^{5}}}\right] , \end{array} $$

(20)

$$\begin{array}{@{}rcl@{}} U_{yy_{k}} &=& \left( {1-\mu}\right) \left[{\frac{1}{r_{1_k}^{3}} - \frac{3 y_{k}^{2}}{r_{1_k}^{5}}}\right] + \mu \left[{\frac{1}{r_{2_{k}}^{3}} - \frac{3 y_{k}^{2}}{r_{2_{k}}^{5}}}\right] , \end{array} $$

(21)

$$\begin{array}{@{}rcl@{}} U_{xy_{k}} &=& U_{yx_k} = \frac{-3 \left( {1-\mu}\right) \left( {x_k +\mu}\right) y_{k}}{r_{1_k}^{3}} - \frac{3\mu y_{k}\left( {x_k-1+\mu}\right)}{r_{2_{k}}^{5}} . \end{array} $$

(22)

The gradient of Eq. 10a is given as

$$\begin{array}{@{}rcl@{}} f_{1_{x}} &=& \frac{1}{1+h^{2}} \left[{h^{2} + 1 + \frac{h^{2}}{2} -\frac{h^{3}}{2} U_{yx_k} - \frac{h^{2}}{2}U_{xx_k}}\right] , \end{array} $$

(23a)

$$\begin{array}{@{}rcl@{}} f_{1_{y}} &=& \frac{1}{1+h^{2}} \left[{ \frac{h^{3}}{2} -\frac{h^{3}}{2} U_{yy_{k}} - \frac{h^{2}}{2}U_{xy_{k}}}\right] , \end{array} $$

(23b)

$$\begin{array}{@{}rcl@{}} f_{1_{\dot{x}}} &= &\frac{h}{1+h^{2}} , \end{array} $$

(23c)

$$\begin{array}{@{}rcl@{}} f_{1_{\dot{y}}} &= &\frac{h^{2}}{1+h^{2}} . \end{array} $$

(23d)

The gradient of Eq. 10b is given as

$$\begin{array}{@{}rcl@{}} f_{2_{x}} &=& h -h f_{1_{x}} - \frac{h^{2}}{2} U_{yx_k} , \end{array} $$

(24a)

$$\begin{array}{@{}rcl@{}} f_{2_{y}} &=& -h f_{1_{y}} + 1 + \frac{h^{2}}{2} - \frac{h^{2}}{2} U_{yy_{k}} , \end{array} $$

(24b)

$$\begin{array}{@{}rcl@{}} f_{2_{\dot{x}}} &=& -h f_{1_{\dot{x}}} ,\end{array} $$

(24c)

$$\begin{array}{@{}rcl@{}} f_{2_{\dot{y}}} &=& h - h f_{1_{\dot{y}}} . \end{array} $$

(24d)

The gradients of Eqs. 12c and 12d are given as

$$\begin{array}{@{}rcl@{}} \frac{\partial {r_{1_k}p}}{\partial {\bar{x}}} &= &\left( {\left( x_{k + 1} + \mu\right)^{2} + y_{k}p^{2}}\right)^{-\frac{1}{2}} \left[{\left( {x_{k + 1} + \mu}\right) f_{1_{\bar{x}}} + y_{k}p f_{2_{\bar{x}}}}\right] , \end{array} $$

(25a)

$$\begin{array}{@{}rcl@{}} \frac{\partial {r_{2_{k}}p}}{\partial {\bar{x}}} & = & \left( {\left( x_{k + 1} - 1 + \mu\right)^{2} + y_{k}p^{2}}\right)^{-\frac{1}{2}} \left[{\left( {x_{k + 1} - 1 + \mu}\right) f_{1_{\bar{x}}} + y_{k}p f_{2_{\bar{x}}}}\right] . \end{array} $$

(25b)

The second order partial derivatives of the gravitational potential at k + 1 are given as

$$\begin{array}{@{}rcl@{}} \frac{\partial {U_{xx_{k + 1}}}}{\partial {\bar{x}}} &=& \left( {1-\mu}\right)\left[{\frac{1}{r_{1_k}p^{3}} f_{1_{\bar{x}}} - \frac{3 \left( {x_{k + 1} +mu}\right)}{r_{1_k}p^{4}} \frac{\partial {r_{1_k}p}}{\partial {\bar{x}}}}\right] \\&&+ \mu \left[{\frac{1}{r_{2_{k}}p^{3}} f_{1_{\bar{x}}} - \frac{-3 \left( {x_{k + 1} -1 + \mu}\right)}{r_{2_{k}}p^{4}} \frac{\partial {r_{2_{k}}p}}{\partial {\bar{x}}}}\right] , \end{array} $$

(26a)

$$\begin{array}{@{}rcl@{}} \frac{\partial {U_{yx_{k + 1}}}}{\partial {\bar{x}}} &=& \left( {1-\mu}\right)\left[{\frac{1}{r_{1_k}p^{3}} f_{2_{\bar{x}}} - \frac{3 y_{k}p}{r_{1_k}p^{4}} \frac{\partial {r_{1_k}p}}{\partial {\bar{x}}}}\right] \\&&+ \mu \left[{\frac{1}{r_{2_{k}}p^{3}} f_{2_{\bar{x}}} - \frac{-3 y_{k}p}{r_{2_{k}}p^{4}} \frac{\partial {r_{2_{k}}p}}{\partial {\bar{x}}}}\right] . \end{array} $$

(26b)

The gradient of Eqs. 10c and 10d are given as

$$\begin{array}{@{}rcl@{}} f_{3_{x}} &= &2 f_{2_{x}} + \frac{h}{2} \left( {f_{1_{x}} + 1}\right) - \frac{h}{2} U_{xx_{k + 1}} - \frac{h}{2} U_{xx_k} , \end{array} $$

(27a)

$$\begin{array}{@{}rcl@{}} f_{3_{y}} &= &-2 + 2 f_{2_{y}} + \frac{h}{2} f_{1_{y}} - \frac{h}{2} U_{xy_{k}p} -\frac{h}{2} U_{xy_{k}} , \end{array} $$

(27b)

$$\begin{array}{@{}rcl@{}} f_{3_{\dot{x}}} &=& 1 + 2 f_{2_{\dot{x}}} + \frac{h}{2} f_{1_{\dot{x}}} - \frac{h}{2} U_{x\dot{x}_{k + 1}} , \end{array} $$

(27c)

$$\begin{array}{@{}rcl@{}} f_{3_{\dot{y}}} &=& 2 f_{2_{\dot{y}}} , \end{array} $$

(27d)

$$\begin{array}{@{}rcl@{}} f_{4_{x}} &=& 2 - 2 f_{1_{x}} + \frac{h}{2} f_{2_{x}} - \frac{h}{2} U_{yx_{k + 1}} - \frac{h}{2} U_{yx_k} , \end{array} $$

(28a)

$$\begin{array}{@{}rcl@{}} f_{4_{y}} &=& -2f_{1_{y}} - \frac{h}{2} \left( {f_{2_{y}} + 1}\right) - \frac{h}{2} U_{yy_{k}p} -\frac{h}{2} U_{yy_{k}} , \end{array} $$

(28b)

$$\begin{array}{@{}rcl@{}} f_{4_{\dot{x}}} &=& - 2 f_{1_{\dot{x}}} + \frac{h}{2} f_{2_{\dot{x}}} - \frac{h}{2} U_{y\dot{x}_{k + 1}} , \end{array} $$

(28c)

$$\begin{array}{@{}rcl@{}} f_{4_{\dot{y}}} &=& 1 - 2 f_{1_{\dot{y}}} + \frac{h}{2} f_{2_{\dot{y}}} - \frac{h}{2} U_{y\dot{y}_{k + 1}} . \end{array} $$

(28d)

These gradient equations are in a cascade type structure. Equations 27a–d and 28a–d are functions of Eqs. 10c and 10d. As a result, the accuracy of the Jacobian will tend to decrease as the first order approximation errors accumulate.