A new Chelyshkov matrix method to solve linear and nonlinear fractional delay differential equations with error analysis

Abstract

In this paper, we investigate the possible treatment of a class of fractional-order delay differential equations. In delay differential equations, the evolution of the state depends on the past time, which increases the complexity of the model. The fractional term is defined in the Caputo sense, and to find its solution we discretize the unknown solution using a truncated series based on orthogonal Chelyshkov functions. Then, the resulting system in terms of the unknown coefficients is solved that guarantees to produce highly accurate solutions. A detailed error analysis for the proposed technique is studied to give some insight into the error bound of the proposed technique. The method is then tested on some examples to verify the efficiency of the proposed technique. The method proves the ability to provide accurate solutions in terms of error and computational cost and through some comparisons with other related techniques. Thus, the method is considered a promising technique to encounter such problems and can be considered as an efficient candidate to simulate such problems with applications in science.

Introduction

Fractional calculus has become a rapidly increasing branch of science that gained an increasing interest in recent years with various areas of applications ranging from physical attainments and engineering to natural phenomena and financial viewpoints. A regularly expanding number of fractional frameworks show up typically in disciplines such as viscoplasticity, the vibration of earthquake motions, circuits in electrical engineering, and so on. The use of fractional operator extended in simulating these problems or phenomena in the form of differential equations, especially with a delayed part which may refer to memory terms. While trying to describe any physical process, one may assume that the process depends only on the present state which is verified for a large of dynamical processes. This assumption is not verified for all the physical processes which may lead to some drawbacks on the performance while analyzing the system. In this situation, the assumption may be better changed to consider that the behavior of the system may also depend on the previous information of the previous state which may provide better simulation but may increase the complexity of the model. These modified systems can be called the delay problem that has many applications in different areas of science and engineering. For example, Ockendon et al. [1] described the behavior and dynamics of a current collection system for an electric locomotive through some delayed systems. Also, Ajello et al. [2] introduced a delay model describing the stage-structured population growth with density dependent on time delay. In addition, some other applications of delayed models in science [3] and biology can be found in [4, 5].

In recent years, there have been several attempts to solve integer and non-integer real-life models of different types. For example, Sedaghat et al. [6] adapted a colocation method based on Chebyshev polynomials for solving a delay pantograph differential equations. Also, Bernoulli polynomials have been used to solve the pantograph delay differential equations as in [7]. In addition, Adel et al. [8] adapted a collocation method based on Bernoulli polynomials for solving pantograph-type equations of Lane–Emden type with applications in astrophysics. Also, in [9] a delayed version of the famous Ambartsumian model has been solved using Bernoulli functions. Yüzbaşı et al. have used various basis functions to solve generalized and multi-pantograph differential equations through collocation approaches in [10,11,12,13]. Izadi et al. in [14,15,16,17,18,19,20,21] employed some novel techniques for solving different types of equations using various polynomials acquiring good results. Other methods and models include neural network method for solving single delay differential equation [22], Zhou method [23], fractional-order Boubaker polynomials [24], Taylor wavelet method [25], spectral collocation methods [26, 27], variational iteration method [28], one-leg θ-method [29], hybrid of block-pulse functions and Taylor series [30], Hermite wavelet method [31], and Legendre pseudospectral method [32].

Orthogonal functions play an important role in finding numerical solutions to differential equations. These functions play the role of converting the solution of the model into solving an algebraic system of equations. For example, Saadatmandi et al. [33] adapted the Legendre operational matrix of fractional derivative defined in the Caputo sense for solving the class of fractional-order differential equations. Also, Maleknejad et al. [34] provided a novel wavelet approach based on Müntz–Legendre polynomials for solving distributed order fractional differential equations in the time domain. Chebyshev polynomials have also been used to solve differential equations of different types. Li et al. [35] employed the Chebyshev wavelet method for solving nonlinear fractional differential equations. In addition, the second kind Chebyshev wavelet has been used by Rashidinia et al. [36] to simulate the result of a general form of a distributed order fractional differential equations. A similar approach can be found by Li et al. in [35], and also the (shifted) Chebyshev polynomials have been utilized by Bhrawy et al. [37] for solving the linear fractional differential equations. In addition, the (shifted) Jacobi polynomials have been used to solve the fractional differential equations by Behroozifar et al. [38]. The block pulse polynomials have been used several times for solving different problems of the fractional type including Li et al. [39] for solving the fractional differential equations and Maleknejad et al. [40] for solving the nonlinear two-dimensional fractional integro-differential equations.

Additionally, among these functions is the orthogonal Chelyshkov polynomials which were presented by Chelyshkov in [41] for the first time and have been used for solving differential equations. Using these polynomials, some numerical solutions have been found to some models including linear functional integro-differential equations with variable coefficients [42], weakly singular integral equations in [43], Volterra–Fredholm integral equations in [44] and two-variable distributed order fractional differential equations in [45]. Moreover, the operational matrix of fractional derivatives utilizing Chelyshkov polynomials to solve multi-order fractional differential equations has been considered by Talaei et al. [46]. The technique of operational matrix of fractional integration for solving a class of nonlinear fractional differential equations has been proposed by Meng et al. [47] for finding the solution of nonlinear fractional differential equations and by Al-Sharif et al. [48] introducing the integral operational matrix of fractional order.

The main subject of this work is to solve the fractional delay differential equations (FDDEs) numerically with the approximation algorithm based on the Chelyshkov functions. Some novel aspects of the designed algorithm are as follows:

• A wide class of delay fractional differential equations are being considered with the fractional derivative defined in terms of the Caputo fractional derivative.

• A new method based on the Chelyshkov functions and their differentiation matrix is used to solve this type of equation dealing with different complexities of the problem.

• The comparison of the proposed results from the used technique is presented to check the correctness of the models proving the superiority of the proposed technique over other methods even for some examples with the exact solution depending on the fractional order.

• The error bound for the proposed technique is examined in details ensuring that the provided technique provides convergent solutions.

It is worth mentioning that to the best of our knowledge, this is the first time the proposed technique relying on Chelyshkov functions is being considered for solving this wide class of fractional delay problems. In this paper, we consider the following FDDEs

$${}^C {D}_t^{(\gamma )}\chi (t)=G\Big (t,\chi (t),{}^C {D}^{(\mu )}_{t}\chi (t),\chi (\omega \,t-\tau (t)),{}^C {D}^{(\nu )}_{t}\chi (\omega \,t-\tau (t))\Big ),\quad 0< t\le 1,$$

(1)

where $\gamma \ge \mu >0$, and $\nu >0$ are some known constants as the orders of the fractional derivatives interpreting in the Caputo’s sense. Also, the parameters $\omega$, $\tau (t)$ and $(\omega \,t-\tau (t))$ are the constant and variable delay arguments of the model, and G is a given function. The FADEs in (1) are dealt with the initial conditions

$$\begin{aligned} \chi ^{(k)}(0)=\pi _k,\quad k=0,1,\ldots ,n-1,\quad n-1<\gamma \le n. \end{aligned}$$

(2)

Some researchers have studied on existence and uniqueness of delay fractional differential equations and fractional pantograph equations. We refer the readers to [49,50,51].

The outline of this study is organized as follows. In Sect. 2, first, some preliminary facts regarding the fractional operators are illustrated. Then, some definitions for the Chelyshkov functions are given from a different perspective. In Sect. 3, the steps of the proposed technique are illustrated in detail to obtain the approximate solution of (1). The error bounds in the $L^2$ weighted and $L_{\infty }$ norms are obtained for the present method in Sect. 4. The numerical examples are solved by the suggested method in Sec. 5. In Sect. 6, we give a conclusion for the study.

Some preliminary facts

A review of fractional calculus

In this part, some fundamental information related to fractional calculus will be given. The fractional derivative of f(t) in the Caputo sense is defined as follows [52]:

$$\begin{aligned} {}^C {D}^{(\alpha )}_{t}f(t)&=J^{m-\alpha }D^{m}f(t)\\&=\frac{1}{\Gamma {(m-\alpha )}}\int _{0}^{t}(t-x)^{m-\alpha -1}f^{(m)}(x){\text {d}}x, \end{aligned}$$

being $m-1<\alpha <m$, $m\in \mathbb {N}$, $t>0$, $f\in C_{-1}^{m}$, and $D=\frac{{\text {d}}}{{\text {d}}x}$. When c is a constant, we have

$$\begin{aligned} {}^C {D}^{(\alpha )}_{t}c=0. \end{aligned}$$

(3)

Moreover, if it is $f(t)=t^{\beta }$, then the Caputo fractional derivative of f becomes as follows [53]:

$$\begin{aligned} {}^C {D}^{(\alpha )}_{t}t^{\beta }=\left\{ \begin{array}{ll} 0, &{} \text {for}\; \beta \in \mathbb {N}_{0}\; \text{and}\; \beta < {\left\lceil \!\lceil \alpha \right\rceil \!\rceil },\\ \frac{\Gamma {(\beta +1)}}{\Gamma {(\beta +1-\alpha )}}t^{\beta - \alpha }, &{} \text {for}\; \beta \in \mathbb {N}_{0}\; \text {and}\; \beta \ge {\left\lceil \!\lceil \alpha \right\rceil \!\rceil }\; \text {or}\; \beta \notin \mathbb {N}_0\; \text {and}\; \beta > \left\lfloor \!\lfloor \alpha \right\rfloor \!\rfloor . \end{array} \right. \end{aligned}$$

(4)

A review of Chelyshkov functions

In 2006 year, Chelyshkov defined a new polynomial via Jacobi polynomials $P_m^{\alpha ,\beta }(t)$ in [41] and named them as Chelyshkov polynomials. These polynomials are defined by

$$\begin{aligned} \rho _{\ell ,L}(z)=(-1)^{L-\ell }\,z^{\ell }\,P_{L-\ell }^{0,2\ell +1}(2z-1),\quad \ell =0,1,\ldots ,L. \end{aligned}$$

It is also shown in [41] that $y(z)=z\,\rho _{\ell ,L}(z)$ satisfies the following second-order differential equation

$$\begin{aligned} z^2(1-z)y''-z^2y'+\big [(L+1)^2z-\ell (\ell +1)\big ]y=0. \end{aligned}$$

This implies that these polynomials are the solutions of the following differential equation in the Sturm-Liouville form

$$\begin{aligned} \frac{{\text {d}}}{{\text {d}}z}\big [z^2(1-z)\frac{{\text {d}}}{{\text {d}}z}\rho _{\ell ,L}(z)\big ]+\big [L(L+2)z-\ell (\ell +1)\big ]\rho _{\ell ,L}(z)=0. \end{aligned}$$

(5)

Chelyshkov polynomials were expressed more explicity in [41, 42] as follows:

$$\begin{aligned} \rho _{\ell ,L}(z)=\sum _{m=0}^{L-\ell }(-1)^m\,\left( {\begin{array}{c}L+\ell +m+1\\ L-\ell \end{array}}\right) \left( {\begin{array}{c}L-\ell m\end{array}}\right) \,z^{\ell +m},\quad \ell =0,1,\ldots ,L. \end{aligned}$$

(6)

The set of Chelyshkov polynomials $\{\rho _{\ell ,L}(z)\}_{\ell =0}^L$ for $L=0,1,\ldots$ forms an orthogonal system on [0, 1] with respect to the weight function $w(z) = 1$, namely

$$\begin{aligned} \int _0^1 \rho _{\ell ,L}(z)\,\rho _{k,L}(z)dz=\frac{\delta _{\ell k}}{\ell +k+1},\quad \ell ,k\ge 0. \end{aligned}$$

We now use of substitution $z=t^{\alpha }$ with $\alpha >0$ in (5) to get fractional-order Chelyshkov differential equation. In the singular Sturm–Liouville form, it can be written as follows

$$\begin{aligned}&\frac{{\text {d}}}{{\text {d}}t}\big [(t^{\alpha +1}-t^{2\alpha +1})\frac{{\text {d}}}{{\text {d}}t}\rho ^{\alpha }_{\ell ,L}(t)\big ]\nonumber \\& \quad +\big [L(L+2)t^{2\alpha -1}-\ell (\ell +1)t^{\alpha -1}\big ]\rho ^{\alpha }_{\ell ,L}(t)=0. \end{aligned}$$

(7)

where $\rho ^{\alpha }_{\ell ,L}(t):=\rho _{\ell ,L}(t^{\alpha })$. Note that by setting $\alpha =1$ in (7) we will recover (5). Thus, after some manipulations in (6), the explicit expression of the solution of (7) becomes as follows

$$\begin{aligned}& \rho ^{\alpha }_{\ell ,L}(t)=\sum _{m=\ell }^{L}(-1)^{m-\ell }\, \left( {\begin{array}{c}L+m+1\\ L-\ell \end{array}}\right) \left( {\begin{array}{c}L-\ell \\ m-\ell \end{array}}\right) \,t^{m\alpha },\quad \ell =0,1,\ldots ,L. \end{aligned}$$

(8)

In here, the set $\{\rho ^{\alpha }_{\ell ,L}(t)\}_{\ell =0}^L$ for $L=0,1,\ldots$ are orthogonal with respect to $w_{\alpha }(t)\equiv t^{\alpha -1}$ for $0\le t\le 1$ in the sense that

$$\begin{aligned}&\int _0^1 \rho ^{\alpha }_{\ell ,L}(t)\,\rho ^{\alpha }_{k,L}(t)\,w_{\alpha}(t){\text {d}}t =\frac{\delta _{\ell k}}{\alpha (2\ell +1)},\quad \ell ,k\ge 0. \end{aligned}$$

In order to devise the Chelyshkov matrix approach, we constitute the vector of Chelyshkov bases as

$$\begin{aligned} \pmb {\Psi }^{\alpha }_{L}(t)=\left[ \rho ^{\alpha }_{0,L}(t)\quad \rho ^{\alpha }_{1,L}(t)\quad \ldots \quad \rho ^{\alpha }_{L,L}(t)\right] =\pmb {M}^{\alpha }_{L}(t)\,\pmb {E}_L. \end{aligned}$$

(9)

Here, $\pmb {M}^{\alpha }_{L}(t)=\left[ 1\quad t^{\alpha }\quad t^{2\alpha }\quad \ldots \quad t^{L\alpha }\right]$ denotes the monomial basis and $\pmb {E}_L$ is a lower triangular matrix of size $(L+1)\times (L+1)$ defined as follows. According to the case of being an odd number and even number of L, respectively, the matrix $\pmb {E}_L$ becomes as follows:

$$\begin{aligned} \pmb {E}_L= \left[ \begin{array}{ccccc} \displaystyle {\left( {\begin{array}{c}L+1\\ L\end{array}}\right) \left( {\begin{array}{c}L\\ 0\end{array}}\right) } &{} 0 &{} \ldots &{} 0 &{} 0\\ \displaystyle {-\left( {\begin{array}{c}L+2\\ L\end{array}}\right) \left( {\begin{array}{c}L\\ 1\end{array}}\right) } &{} \displaystyle {\left( {\begin{array}{c}L+2\\ L-1\end{array}}\right) \left( {\begin{array}{c}L-1\\ 0\end{array}}\right) } &{} \ldots &{} 0 &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ \displaystyle {\left( {\begin{array}{c}2L\\ L\end{array}}\right) \left( {\begin{array}{c}L\\ L-1\end{array}}\right) } &{} -\displaystyle {\left( {\begin{array}{c}2L\\ L-1\end{array}}\right) \left( {\begin{array}{c}L-1\\ L-2\end{array}}\right) } &{} \ldots &{} \displaystyle {\left( {\begin{array}{c}2L\\ 1\end{array}}\right) \left( {\begin{array}{c}1\\ 0\end{array}}\right) } &{} 0\\ -\displaystyle {\left( {\begin{array}{c}2L+1\\ L\end{array}}\right) \left( {\begin{array}{c}L\\ L\end{array}}\right) } &{} \displaystyle {\left( {\begin{array}{c}2L+1\\ L-1\end{array}}\right) \left( {\begin{array}{c}L-1\\ L-1\end{array}}\right) } &{} \ldots &{} \displaystyle {\left( {\begin{array}{c}2L+1\\ 1\end{array}}\right) \left( {\begin{array}{c}1\\ 1\end{array}}\right) }&1 \end{array}\right] , \end{aligned}$$

and

$$\begin{aligned} \pmb {E}_L=\left[ \begin{array}{ccccc} \displaystyle {\left( {\begin{array}{c}L+1\\ L\end{array}}\right) \left( {\begin{array}{c}L\\ 0\end{array}}\right) } &{} 0 &{} \ldots &{} 0 &{} 0\\ \displaystyle {-\left( {\begin{array}{c}L+2\\ L\end{array}}\right) \left( {\begin{array}{c}L\\ 1\end{array}}\right) } &{} \displaystyle {\left( {\begin{array}{c}L+2\\ L-1\end{array}}\right) \left( {\begin{array}{c}L-1\\ 0\end{array}}\right) } &{} \ldots &{} 0 &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ -\displaystyle {\left( {\begin{array}{c}2L\\ L\end{array}}\right) \left( {\begin{array}{c}L\\ L-1\end{array}}\right) } &{} \displaystyle {\left( {\begin{array}{c}2L\\ L-1\end{array}}\right) \left( {\begin{array}{c}L-1\\ L-2\end{array}}\right) } &{} \ldots &{} \displaystyle {\left( {\begin{array}{c}2L\\ 1\end{array}}\right) \left( {\begin{array}{c}1\\ 0\end{array}}\right) } &{} 0\\ \displaystyle {}\left( {\begin{array}{c}2L+1\\ L\end{array}}\right) \left( {\begin{array}{c}L\\ L\end{array}}\right) &{} -\displaystyle {\left( {\begin{array}{c}2L+1\\ L-1\end{array}}\right) \left( {\begin{array}{c}L-1\\ L-1\end{array}}\right) } &{} \ldots &{} -\displaystyle {\left( {\begin{array}{c}2L+1\\ 1\end{array}}\right) \left( {\begin{array}{c}1\\ 1\end{array}}\right) }&1 \end{array}\right] . \end{aligned}$$

Clearly, the determinant of $\pmb {E}_L$ as the product of the diagonal elements in both cases is nonzero, since the product of the diagonal elements is not zero.

By utilizing our method, we will aim to obtain the approximate solutions of (1) in terms of Chelyshkov functions with fractional powers in the form

$$\begin{aligned} {\chi }_{L,\alpha }(t)=\sum _{\ell =0}^L a_{\ell }\,\rho ^{\alpha }_{\ell ,L}(t). \end{aligned}$$

(10)

Thus, we use the Chelyshkov matrix technique to determine $(L+1)$ unknown coefficients $a_{\ell }$. In this respect, let us define the vector $\pmb {A}_L=[a_0\quad a_1\quad \ldots \quad a_L]^t$. With the aid of (9), we are able to rewrite ${\chi }_{L,\alpha }(t)$ in (10)

$$\begin{aligned} {\chi }_{L,\alpha }(t)=\pmb {\Psi }^{\alpha }_L(t)\,\pmb {A}_L. \end{aligned}$$

(11)

The Chelyshkov Matrix Technique

Firstly, we constitute the matrix representations of all unknowns functions in (1) by utilizing the solution form (11). By using (9), let us rewrite the solution form as

$$\begin{aligned} {\chi }_{L,\alpha }(t)=\pmb {\Psi }^{\alpha }_L(t)\,\pmb {A}_L=\pmb {M}^{\alpha }_L(t)\,\pmb {E}_L\,\pmb {A}_L. \end{aligned}$$

(12)

To our approximation algorithm, we associate a set of $(L+1)$ collocation points $\{t_r\}_{r=0}^L$ on [0, 1]. To this end, we employ

$$\begin{aligned} t_r=\frac{r}{L},\quad r=0,1,\ldots ,L. \end{aligned}$$

(13)

By evaluating the relation (12) at the collocation points (13) gives us the following matrix expression for the solution $\chi (t)$ as

$$\begin{aligned} \pmb {X}=\pmb {M}\,\pmb {E}_L\,\pmb {A}_L,\qquad \pmb {X}= \begin{pmatrix} {\chi }_{L,\alpha }(t_0)\\ {\chi }_{L,\alpha }(t_1)\\ \vdots \\ {\chi }_{L,\alpha }(t_L) \end{pmatrix},\quad \pmb {M}= \begin{pmatrix} \pmb {M}^{\alpha }_L((t_0)\\ \pmb {M}^{\alpha }_L(t_1)\\ \vdots \\ \pmb {M}^{\alpha }_L(t_L) \end{pmatrix}. \end{aligned}$$

(14)

Next, our goal is to obtain the matrix representations for ${}^C {D}^{(s)}_{t}{\chi }_{L,\alpha }(t)$ for $s=\gamma$, $\mu$. According to (12), we require to compute the s-order fractional derivatives denoted by $\pmb {M}^{(s)}_{\alpha }(t)$ for $s=\gamma ,\mu$. In  these cases, we get

$$\begin{aligned} {}^C {D}^{(s)}_{t}{\chi }_{L,\alpha }(t)=\pmb {M}^{(s)}_{\alpha }(t)\,\pmb {E}_L\,\pmb {A}_L. \end{aligned}$$

(15)

Mathematically, the calculation of $\pmb {M}^{(s)}_{\alpha }(t)$ is carried out through using properties (3)–(4). Practically, we utilize the Algorithm (3.1) to compute it efficiently. One can easily seen that the complexity of this algorithm not more than $\mathcal {O}(L+1)$ [14, 54].

After evaluating the Eq. (15) at the collocation points, we have proved the following results

Theorem 3.1

The matrix forms of ${}^C {D}^{(s)}_{t}{\chi }_{L,\alpha }(t)$, $s=\gamma ,\mu$, evaluated at the collocation points (13) are represented by

$$\begin{aligned} \pmb {X}^{(s)}=\pmb {M}^{(s)}\,\pmb {E}_L\,\pmb {A}_L, \end{aligned}$$

(16)

where

$$\begin{aligned} \pmb {X}^{(s)}= \begin{pmatrix} {}^C {D}^{(s)}_{t} {\chi }_{L,\alpha }(t_0)\\ {}^C {D}^{(s)}_{t} {\chi }_{L,\alpha }(t_1)\\ \vdots \\ {}^C {D}^{(s)}_{t} {\chi }_{L,\alpha }(t_L) \end{pmatrix}, \quad \pmb {M}^{(s)}= \begin{pmatrix} \pmb {M}^{(s)}_{\alpha }(t_0)\\ \pmb {M}^{(s)}_{\alpha }(t_1)\\ \vdots \\ \pmb {M}^{(s)}_{\alpha }(t_L) \end{pmatrix}. \end{aligned}$$

To express $\chi (\omega \,t-\tau (t))$ in a matrix form, the next theorem will be established.

Theorem 3.2

For any function $\tau (t)$ and constant $\omega$, the matrix form of ${\chi }_{L,\alpha }(\omega \,t-\tau (t))$ evaluated at the collocation points (13) has the matrix representation

$$\begin{aligned} \pmb {X}_{\omega ,\tau }=\widehat{\pmb {M}}\,\widehat{\pmb {F}}_{\omega ,\tau }\,\widehat{\pmb {E}}_L\,\widehat{\pmb {A}}_L. \end{aligned}$$

(17)

Here, the matrices $\widehat{\pmb {M}},~\widehat{\pmb {F}}_{\omega ,\tau },~\widehat{\pmb {E}}_L$, $\widehat{\pmb {A}}_L$ are as in (20) and the vector $\pmb {X}_{\omega ,\tau }$ is given by

$$\begin{aligned} \pmb {X}_{\omega ,\tau }= \begin{pmatrix} {\chi }_{L,\alpha }(\omega \,t_0-\tau (t_0))\\ {\chi }_{L,\alpha }(\omega \,t_1-\tau (t_1))\\ \vdots \\ {\chi }_{L,\alpha }(\omega \,t_L-\tau (t_L)) \end{pmatrix}. \end{aligned}$$

Proof

Let us prove the result when $\alpha =1$. Due to (12), we obtain

$$\begin{aligned} {\chi }_{L,\alpha }(\omega \,t-\tau (t))=\pmb {M}^{1}_L(\omega \,t-\tau (t))\,\pmb {E}_L\,\pmb {A}_L. \end{aligned}$$

(18)

Our attempt is to write $\pmb {M}^{1}_L(\omega \,t-\tau (t))$ in terms of $\pmb {M}^{1}_L(t)$, which is already defined in (9). Using of binomial formula reveals that

$$\begin{aligned} (\omega \,t-\tau (t))^n=\sum _{k=0}^n \left( {\begin{array}{c}n\\ k\end{array}}\right) \omega ^k(-\tau (t))^{n-k}\,t^k. \end{aligned}$$

Now, we introduce the matrix $\pmb {F}_{\omega ,\tau ,L}(t)$ depends on the parameters $\omega$, $\tau (t)$, and L as follows:

$$\begin{aligned} \pmb {F}_{\omega ,\tau ,L}(t)=\begin{pmatrix} \left( {\begin{array}{c}0\\ 0\end{array}}\right) \omega ^0\,\tau ^0(t) &{} -\left( {\begin{array}{c}1\\ 0\end{array}}\right) \omega ^0\,\tau ^1(t) &{} \left( {\begin{array}{c}2\\ 0\end{array}}\right) \omega ^0\,\tau ^2(t) &{}\ldots &{} (-1)^L\left( {\begin{array}{c}L\\ 0\end{array}}\right) \omega ^0\,\tau ^L(t)\\ 0 &{} \left( {\begin{array}{c}1\\ 1\end{array}}\right) \omega ^1\,\tau ^0(t) &{} -\left( {\begin{array}{c}2\\ 1\end{array}}\right) \omega ^1\,\tau ^1(t)&{}\ldots &{} (-1)^{L-1}\left( {\begin{array}{c}L\\ 1\end{array}}\right) \omega ^1\,\tau ^{L-1}(t)\\ 0 &{} 0 &{} \left( {\begin{array}{c}2\\ 2\end{array}}\right) \omega ^2\,\tau ^0(t)&{}\ldots &{} (-1)^{L-1}\left( {\begin{array}{c}L\\ 2\end{array}}\right) \omega ^2\,\tau ^{L-2}(t)\\ \vdots &{} \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0 &{} 0 &{} 0 &{} \ldots &{} \left( {\begin{array}{c}L\\ L\end{array}}\right) \omega ^L\,\tau ^{0}(t)\\ \end{pmatrix}. \end{aligned}$$

This enables us to express the vector $\pmb {M}^{1}_L(\omega \,t-\tau (t))$ in the form

$$\begin{aligned} \pmb {M}^{1}_L(\omega \,t-\tau (t))=\pmb {M}^{1}_L(t)\,\pmb {F}_{\omega,\tau,L}(t). \end{aligned}$$

(19)

After inserting the former relation (19) into (18), we have

$$\begin{aligned} {\chi }_{L,1}(\omega \,t-\tau (t))=\pmb {M}^{1}_L(t)\,\pmb {F}_{\omega ,\tau ,L}(t)\,\pmb {E}_L\,\pmb {A}_L. \end{aligned}$$

We then insert the collocation points (13) into the preceding equation and obtain the following block diagonal matrices

$$\begin{aligned} \begin{aligned}&\widehat{\pmb {M}}= \begin{pmatrix} \pmb {M}^{1}_L(t_0)&{}\pmb {0}&{}\ldots &{}\pmb {0}\\ \pmb {0}&{}\pmb {M}^{1}_L(t_1)&{}\ldots &{}\pmb {0}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ \pmb {0}&{}\pmb {0}&{}\ldots &{}\pmb {M}^{1}_L(t_L) \end{pmatrix},\quad \widehat{\pmb {E}}= \begin{pmatrix} \pmb {E}_L&{}\pmb {0}&{}\ldots &{}\pmb {0}\\ \pmb {0}&{}\pmb {E}_L&{}\ldots &{}\pmb {0}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ \pmb {0}&{}\pmb {0}&{}\ldots &{}\pmb {E}_L \end{pmatrix},\\&\widehat{\pmb {F}}_{\omega ,\tau }= \begin{pmatrix} \pmb {F}_{\omega ,\tau ,L}(t_0)&{}\pmb {0}&{}\ldots &{}\pmb {0}\\ \pmb {0}&{}\pmb {F}_{\omega ,\tau ,L}(t_1)&{}\ldots &{}\pmb {0}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ \pmb {0}&{}\pmb {0}&{}\ldots &{}\pmb {F}_{\omega ,\tau ,L}(t_L) \end{pmatrix},\quad \widehat{\pmb {A}}_L= \begin{pmatrix} \pmb {A}_L\\ \pmb {A}_L\\ \vdots \\ \pmb {A}_L \end{pmatrix}. \end{aligned} \end{aligned}$$

(20)

By considering the definition of $\pmb {X}_{\omega ,\tau }$ the proof is complete for $\alpha =1$. For other values of $\alpha$, see the following Remark.$\square$

Remark 3.3

Let us remark that the complexity of computing $\pmb {X}_{\omega ,\tau }(\omega \,t-\tau (t))$ via Theorem (3.2) is $\mathcal {O}((L+1)^3)$. However, in practice, we calculate it through using the symbolic toolbox in MATALB. In this case, the corresponding cost is of order $\mathcal {O}((L+1)^2)$. In this respect, we first compute the monomial vector $\pmb {M}^{\alpha }_L(t)$ with the aid of symbolic notations. Once the vector $\pmb {M}^{\alpha }_L(t)$ is created, we substitute $(\omega \,t-\tau (t))$ into it to get

$$\begin{aligned} \pmb {M}^{\alpha }_L(\omega \,t-\tau (t))\approx \pmb {M}^{\alpha }_L(t)\Big |_{t\rightarrow (\omega \,t-\tau (t))}. \end{aligned}$$

By placing the collocation points (13) in the last equation, we get the matrix

$$\begin{aligned} \pmb {M}_{\omega ,\tau }= \begin{pmatrix} \pmb {M}^{\alpha }_L(\omega \,t_0-\tau (t_0))\\ \pmb {M}^{\alpha }_L(\omega \,t_1-\tau (t_1))\\ \vdots \\ \pmb {M}^{\alpha }_L(\omega \,t_L-\tau (t_L)) \end{pmatrix}. \end{aligned}$$

Thus, the matrix $\pmb {X}_{\omega ,\tau }$ in Theorem (3.2) with lower efforts can be expressed as

$$\begin{aligned} \pmb {X}_{\omega ,\tau }=\pmb {M}_{\omega ,\tau }\,\pmb {E}_L\,\pmb {A}_L. \end{aligned}$$

(21)

The same conclusion can be drawn for $\alpha =1$ as well.

Now, let us construct an explicit expression for ${}^C {D}^{(\nu )}_{t}{\chi }_{L,\alpha }(\omega \,t-\tau (t))$ at the collocation points (13). By differentiating (12) with regard to the fractional derivative $\nu$ and then substituting $(\omega \,t-\tau (t))$ into the resultant equation, we get

$$\begin{aligned} {}^C {D}^{(\nu )}_{t}{\chi }_{L,\alpha }(\omega \,t-\tau (t))={}^C {D}^{(\nu )}_{t}\,\pmb {M}^{\alpha }_L(\omega \,t-\tau (t))\,\pmb {E}_L\,\pmb {A}_L. \end{aligned}$$

(22)

Thus, we use the collocation points (13) in (22) to get

$$\begin{aligned} \pmb {X}^{(\nu )}_{\omega ,\tau }=\pmb {M}^{(\nu )}_{\omega ,\tau }\,\pmb {E}_L\,\pmb {A}_L, \end{aligned}$$

(23)

where

$$\begin{aligned} \pmb {X}^{(\nu )}_{\omega ,\tau }= \begin{pmatrix} {}^C {D}^{(\nu )}_{t}\,{\chi }_{L,\alpha }(\omega \,t_0-\tau (t_0))\\ {}^C {D}^{(\nu )}_{t}\,{\chi }_{L,\alpha }(\omega \,t_1-\tau (t_1))\\ \vdots \\ {}^C {D}^{(\nu )}_{t}\,{\chi }_{L,\alpha }(\omega \,t_L-\tau (t_L)) \end{pmatrix},\quad \pmb {M}^{(\nu )}_{\omega ,\tau }= \begin{pmatrix} {}^C {D}^{(\nu )}_{t}\,\pmb {M}^{\alpha }_L(\omega \,t_0-\tau (t_0))\\ {}^C {D}^{(\nu )}_{t}\,\pmb {M}^{\alpha }_L(\omega \,t_1-\tau (t_1))\\ \vdots \\ {}^C {D}^{(\nu )}_{t}\,\pmb {M}^{\alpha }_L(\omega \,t_L-\tau (t_L)) \end{pmatrix}. \end{aligned}$$

Now let us collocate the FDDEs model problem (1) at the set of collocation points (13) as follows:

$$\begin{aligned} {}^C {D}_t^{(\gamma )}\chi (t_r)-G\Big (t_r,\chi (t_r),{}^C {D}^{(\mu )}_{t}\chi (t_r),\chi (\omega \,t_r-\tau (t_r)),{}^C {D}^{(\nu )}_{t}\chi (\omega \,t_r-\tau (t_r))\Big ), \end{aligned}$$

(24)

for $r=0,1,\ldots ,L$. We put the matrix forms (14), (16),  (17) or (21), and (23) into (24) and thus get a fundamental nonlinear matrix equation.

In the linear case, we assume that

$$\begin{aligned} G:=\theta _0(t)\,\chi (t)+\theta _1(t)\,{}^C {D}^{(\mu )}_{t}\chi (t)+\theta _2(t)\,\chi (\omega \,t-\tau (t))+\theta _3(t)\,{}^C {D}^{(\nu )}_{t}\chi (\omega \,t-\tau (t))+q(t), \end{aligned}$$

where $\theta _j(t)$, $j=0,1,2,3$ and q(t) are some known functions. By collocating the preceding equation at the collocation points and then utilizing (14)-(23), we have

$$\begin{aligned} \pmb {X}^{(\gamma )}=\Theta _0\,\pmb {X}+\Theta _1\,\pmb {X}^{(\mu )}+\Theta _2\,\pmb {X}_{\omega ,\tau }+\Theta _3\,\pmb {X}^{(\nu )}_{\omega ,\tau }+\pmb {Q}. \end{aligned}$$

(25)

In (25), we have used the coefficient matrices as well as the vector $\pmb {Q}$ as

$$\begin{aligned} \Theta _p=\begin{pmatrix} \theta_p (t_0) &{} 0 &{}\ldots &{} 0\\ 0 &{} \theta_p (t_1)&{}\ldots &{} 0\\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} \theta_p (t_L) \end{pmatrix},\quad p=0,1,2,3,\quad \pmb {Q}=\begin{pmatrix} q(t_0) \\ q(t_1)\\ \vdots \\ q(t_L) \end{pmatrix}. \end{aligned}$$

We ultimately obtain the fundamental linear matrix equation for the underlying model problem (1).

Proposition 3.4

Suppose that the solution of (1) can be obtained in the form based on Chelyshkov functions (12). Then, we get

$$\begin{aligned} \underbrace{ \left( \pmb {M}^{(\gamma )}-\Theta _0\,\pmb {M}-\Theta _1\,\pmb {M}^{(\mu )}-\Theta _2\,\pmb {M}_{\omega ,\tau }-\Theta _3\,\pmb {M}^{(\nu )}_{\omega ,\tau }\right) \pmb {E}_L}_{\pmb {Y}}\,\pmb {A}_L=\pmb {Q},\quad \text{ or }\quad [\pmb {Y}; \pmb {Q}]. \end{aligned}$$

(26)

Proof

The proof of the fundamental matrix equation (26) is straightforward just by placing (14), (16), (21), and (23) into (25).$\square$

Note that in the case of $\alpha =1$ and using Theorem 3.1, we get the following modified matrix equation instead of (26) as

$$\begin{aligned} \pmb {Y}:=\left( \pmb {M}^{(\gamma )}-\Theta _0\,\pmb {M}-\Theta _1\,\pmb {M}^{(\mu )}-\Theta _3\,\pmb {M}^{(\nu )}_{\omega ,\tau }\right) \pmb {E}_L\,\pmb {A}_L-\Theta _2\,\widehat{\pmb {M}}\,\widehat{\pmb {F}}_{\omega ,\tau }\,\widehat{\pmb {E}}_L\,\widehat{\pmb {A}}_L=\pmb {Q}. \end{aligned}$$

(27)

It is worth pointing out that the matrix equation (26) or (27) is linear in terms of unknown coefficient $\pmb {A}_L$ to be calculated. However, what is left to implement the initial conditions (2) so that they take part in the fundamental matrix equation (26). This task is the subject of the next part.

Initial conditions in the matrix form

Our main concern is to express the initial conditions (2) in the matrix formats. This enables us to determine the solution of (1) through solving the linear or nonlinear fundamental matrix equation as described above.

Let us first transform $\chi (0)=\pi _0$ into a matrix format. For this purpose, let us approach $t\rightarrow 0$ in (12) yielding

$$\begin{aligned} \widetilde{\pmb {Y}}_0:=\pmb {M}^{\alpha }_{L}(0)\,\pmb {E}_L\pmb {A}_L=\pi _0,\qquad \text{ or }\qquad [\widehat{\pmb {Y}}_0; \pi _0]. \end{aligned}$$

For the remaining initial conditions, we require to compute $\frac{{\text {d}}^k}{{\text {d}}t^k}\pmb {M}^{\alpha }_{L}(t)$ for $k=1,2,\ldots ,n-1$ due to (12). This task is performed by calling Algorithm 3.1 utilizing integer values $s=1,\ldots ,n-1$. Upon defining $\pmb {M}^{(k)}_{L,\alpha }(t):=\frac{{\text {d}}^k}{{\text {d}}t^k}\pmb {M}^{\alpha }_{L}(t)$ and letting $t\rightarrow 0$, we arrive at the following matrix relations

$$\begin{aligned} \widetilde{\pmb {Y}}_k:=\pmb {M}^{(k)}_{L,\alpha }(0)\,\pmb {E}_L\pmb {A}_L=\pi _k,\qquad \text{ or }\qquad [\widehat{\pmb {Y}}_k; \pi _k], \end{aligned}$$

for $k=1,2,\ldots ,n-1$.

Remark 3.5

For $\alpha =1$, an alternative approach has been used in the literature, see cf. [14]. In this approach, one may find a relationship between $\pmb {M}^{1}_{L}(t)$ and its k-order derivatives $\frac{{\text {d}}^k}{{\text {d}}x^k}\pmb {M}^{1}_{L}(t)$ through an differentiation matrix $\pmb {D}$ for $k\ge 1$ as

$$\begin{aligned} \frac{{\text {d}}^k}{{\text {d}}t^k}\pmb {M}^{1}_{L}(t)=\pmb {M}^{1}_{L}(t)\,\pmb {D}^k,\quad \pmb {D}=\begin{pmatrix} 0 &{} 1 &{} 0 &{}\ldots &{} 0\\ 0 &{} 0 &{} 2 &{}\ldots &{} 0\\ \vdots &{} \vdots &{} 0 &{}\vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{}\ddots &{} L\\ 0 &{} 0 &{} 0 &{} \ldots &{} 0 \end{pmatrix}_{(L+1)\times (L+1)}. \end{aligned}$$

(28)

Therefore, after differentiating (12) k times with respect to t, we find

$$\begin{aligned} \frac{{\text {d}}^k}{{\text {d}}t^k}\chi _{L,1}(t)=\frac{{\text {d}}^k}{{\text {d}}t^k}\pmb {M}^{1}_{L}(t)\,\pmb {E}_L\,\pmb {A}_L=\pmb {M}^{1}_{L}(t)\,\pmb {D}^k\,\pmb {E}_L\,\pmb {A}_L. \end{aligned}$$

It now suffices to let $t\rightarrow 0$ to get

$$\begin{aligned} \widetilde{\pmb {Y}}_k:=\pmb {M}^{1}_{L}(0)\,\pmb {D}^k\,\pmb {E}_L\,\pmb {A}_L=\pi _k,\qquad \text{ or }\qquad [\widehat{\pmb {Y}}_k; \pi _k], \end{aligned}$$

for $k=1,2,\ldots ,n-1$.

We finally combine the fundamental matrix equation (26) or (27), and the matrix forms of the initial conditions (2). To do so, the replacements of the first n rows of the matrix $[\pmb {Y}; \pmb {Q}]$ are carried out by the row matrices $[\widetilde{\pmb {Y}}_k; \pi _k]$ for $k=0,1,\ldots ,n-1$. Let us denoted $[{\widetilde{\pmb {Y}}}; \widetilde{\pmb {Q}}]$ to be the modified fundamental matrix equation. Once this linear or nonlinear algebraic matrix equation is solved, the unknown coefficients $a_{\ell }$, $\ell =0,1,\ldots ,L$ are determined and thus the desired approximation ${\chi }_{L,\alpha }(t)$ of FDDEs (1) is computed.

Approximation results for Chelyshkov functions

An error bound in the $L^2_{w}$ norm

Let us consider the convergence properties of the Chelyshkov functions in the weighted $L^2_w[0,1]$ norm. We recall that the norm of an arbitrary function h(t) with respect to the weight function w(t) is given by

$$\begin{aligned} \Vert h(t)\Vert _w=\sqrt{\int _0^1 |h(t)|^2\,w(t){\text {d}}t}. \end{aligned}$$

By defining the space spanned by the Chelyshkov basis functions

$$\begin{aligned} \mathcal {S}_{L}^{\alpha }=\text{ Span }\langle \rho ^{\alpha }_{0,L}(t),\rho ^{\alpha }_{1,L}(t),\ldots ,\rho ^{\alpha }_{L,L}(t)\rangle , \end{aligned}$$

we have the following theorem.

Theorem 4.1

Suppose that for $s=0,1,\ldots , L$ we have ${}^C {D}^{(s\alpha )}_{t}\chi (t)\in C(0,1]$. Let us denoted $\chi _{L-1,\alpha }(t)=\pmb {\Psi }^{\alpha }_{L-1}(t)\,\pmb {A}_{L-1}$ to be the best approximation out of $\mathcal {S}_{L-1}^{\alpha }$ to $\chi (t)$. Then, we get an error bound as:

$$\begin{aligned} \Vert \chi (t)-\chi _{L-1,\alpha }(t)\Vert _{w_{\alpha }}\le \frac{1}{\sqrt{(2L+1)\alpha }}\,\frac{{M^{\infty }_{\alpha }}}{\Gamma (L\alpha +1)}, \end{aligned}$$

where $|{}^C {D}^{(L\alpha )}_{t}\chi (t)|\le M^{\infty }_{\alpha }$, for $t\in (0,1]$.

Proof

For a similar proof, we refer the readers to [55, Theorem 2.]. $\square$

An error bound in the $L_{\infty }$ norm

We now aimed to obtain an error bound for the suggested method in the $L_{\infty }$ norm. In the following theorem, we will construct an upper boundary of errors.

Theorem 4.2

(Upper Boundary of Errors) Let us assume that $\chi (t)$ and $\chi _{L,\alpha }(t)=\pmb {\Psi }^{\alpha }_{L}(t)\,\pmb {A}_{L}$ are the exact solution and the Chelyshkov series solution with $\alpha L$-th degree of Eq. (1) in interval $0\le t\le 1$. Let $\chi _{L,\alpha }^{Mac}(t)=\pmb {M}^{\alpha }_{L}(t)\,\widetilde{\pmb {A}_L}$ be the expansion of the generalized Maclaurin series [56] by $\alpha L$-th degree of $\chi _{}(t)$. Then, the errors of the Chelyshkov series solution $\chi _{L,\alpha }(t)$ are bounded as follows:

$$\begin{aligned} \Vert \chi _{}(t)-\chi _{L,\alpha }(t)\Vert _{\infty } & \le \frac{1}{\Gamma (\alpha (L+1)+1)} \\ & \qquad \Vert \chi _{}^{(\alpha (L+1))}(c_{t})\Vert _{\infty }+\Vert \widetilde{\pmb {A}_L}\Vert _{\infty }+\Vert \pmb {E}_L\Vert _{\infty }\Vert \pmb {A}_{L}\Vert _{\infty }, \end{aligned}$$

(29)

for some $c_t\in (0,1)$. Here, $\pmb {M}^{\alpha }_{L}(t)$, $\pmb {\Psi }^{\alpha }_{L}(t)$, and the matrix $\pmb {E}_L$ are defined in Sect. 2, relation (9).

Proof

Firstly, by utilizing the triangle inequality and the generalized Maclaurin expansion $\chi _{L,\alpha }^{Mac}(t)$ by $\alpha L$-th degree, we can arrange the error $\Vert \chi _{}(t)-\chi _{L,\alpha }(t)\Vert _{\infty }$ as follows:

$$\begin{aligned} \Vert \chi _{}(t)-\chi _{L,\alpha }(t)\Vert _{\infty }&=\Vert \chi _{}(t)-\chi _{L,\alpha }^{Mac}(t)+\chi _{L,\alpha }^{Mac}(t)-\chi _{L,\alpha }(t)\Vert _{\infty }\nonumber \\&\le \Vert \chi _{}(t)-\chi _{L,\alpha }^{Mac}(t)\Vert _{\infty }+\Vert \chi _{L,\alpha }^{Mac}(t)-\chi _{L,\alpha }(t)\Vert _{\infty }. \end{aligned}$$

(30)

According to (12), the Chelyshkov series solution $\chi _{L,\alpha }(t)=\pmb {\Psi }^{\alpha }_{L}(t)\pmb {A}_{L}$ can be written in the matrix form $\chi _{L,\alpha }(t)=\pmb {M}^{\alpha }_{L}(t)\pmb {E}_L \pmb {A}_{L}$. Also, we know that the expansion of the generalized Maclaurin series by $\alpha L$-th degree of $\chi _{}(t)$ is $\chi _{L,\alpha }^{Mac}(t)=\pmb {M}^{\alpha }_{L}(t)\,\widetilde{\pmb {A}_L}$. Hence, by using this information, we can write the following inequality

$$\begin{aligned} \Vert \chi _{L,\alpha }^{Mac}(t)-\chi _{L,\alpha }(t)\Vert _{\infty }&=\Vert \pmb {M}^{\alpha }_{L}(t)\,\widetilde{\pmb {A}_L}-\pmb {M}^{\alpha }_{L}(t)\pmb {E}_L \pmb {A}_{L}\Vert _{\infty }\nonumber \\&\le \Vert \pmb {M}^{\alpha }_{L}(t)(\widetilde{\pmb {A}_L}-\pmb {E}_L \pmb {A}_{L})\Vert _{\infty }\nonumber \\&\le \Vert \pmb {M}^{\alpha }_{L}(t)\Vert _{\infty }\big (\Vert \widetilde{\pmb {A}_L}\Vert _{\infty }+\Vert \pmb {E}_L\Vert _{\infty }\Vert \pmb {A}_L\Vert _{\infty }),\\& \quad 0\le t\le 1. \end{aligned}$$

(31)

The norm $\Vert \pmb {M}_L^\alpha (t)\Vert$ in [0, 1] is bounded as $\Vert \pmb {M}_L^\alpha (t)\Vert _{\infty }\le 1$. Then, Eq. (31) can be arranged as follows:

$$\begin{aligned} \Vert \chi _{L,\alpha }^{Mac}(t)-\chi _{L,\alpha }(t)\Vert _{\infty }\le \Vert \widetilde{\pmb {A}_L}\Vert _{\infty }+\Vert \pmb {E}_L\Vert _{\infty }\Vert \pmb {A}_L\Vert _{\infty }. \end{aligned}$$

(32)

On the other hand, by utilizing that the reminder term of the generalized Maclaurin series [56] $\chi _{L,\alpha }^{Mac}(t)$ by $\alpha L$-th degree is

$$\begin{aligned} \frac{t^{\alpha (L+1)}}{\Gamma (\alpha (L+1)+1)}\chi _{}^{(\alpha (L+1))}(c_{t}), \quad 0\le t\le 1, \end{aligned}$$

where $c_t$ is some constant in (0, 1). Therefore, we get the following error bound

$$\begin{aligned} \Vert \chi (t)-\chi _{L,\alpha }^{Mac}(t)\Vert _{\infty } \le \frac{1}{\Gamma (\alpha (L+1)+1)}\Vert \chi _{}^{(\alpha (L+1))}(c_{t})\Vert _{\infty }. \end{aligned}$$

(33)

Lastly, by combining Eqs. (30),  (32) and  (33), we have proved the desired result.$\square$

Simulation examples

In this part, the applications of novel Chelyshkov matrix algorithm for the considered delay model (1) are demonstrated through numerical simulations. We validate our numerical results by developing diverse test examples as well as a comparison with available computational and experimental results has been performed. For implementation and visualization, we utilize MATLAB software version 2017a. In order to evaluate the accuracy as well as the convergence of the proposed Chelyshkov matrix technique, we define

$$\begin{aligned} \mathcal {E}_{L,\alpha }(t):=|{\chi }_{L,\alpha }(t)-\chi (t)|, \qquad t\in [0,1]. \end{aligned}$$

However, the exact solutions are usually not at hand for some examples or at various values of fractional orders $\gamma ,\mu ,\nu$. In these cases, we define the residual error function to testify the accuracy of the presented approach

$$\begin{aligned} \mathcal {R}_{L,\alpha }(t):=\Big |{}^C {D}_t^{(\gamma )}{\chi }_{L,\alpha }(t)-G\Big (t,{\chi }_{L,\alpha }(t),{}^C {D}^{(\mu )}_{t}{\chi }_{L,\alpha }(t),{\chi }_{L,\alpha }(\omega \,t-\tau (t)),{}^C {D}^{(\nu )}_{t}{\chi }_{L,\alpha }(\omega \,t-\tau (t))\Big )\Big |, \end{aligned}$$

(34)

for $t\in [0,1]$.

Test case 5.1 We firstly consider the FDDEs model problem of the form [57,58,59,60]

$$\begin{aligned} & {}^C {D}^{(\gamma )}_{t}\chi (t)+\chi (t)-\chi (t-\tau (t))\\ & \quad =2t\tau (t)-\tau ^2(t)-\tau (t)+\frac{2}{\Gamma (3-\gamma )}t^{2-\gamma }-\frac{1}{\Gamma (2-\gamma )}t^{1-\gamma }, \end{aligned}$$

being $\gamma \in (0,1]$ and initial condition is $\chi (0)=0$. A straightforward calculation shows that true exact solution is given by $\chi (t)=t^2-t$ for all values of $\gamma \in (0,1]$.

Let’s begin computations by setting $\tau (t)=ce^{-t}$, $c=0.01$ and using $L=2$. Taking this value of L would be sufficient to get an accurate solution. Using $\gamma$ and $\alpha$ both equal to unity, the approximate solution is

$$\begin{aligned} \chi _{2,1}(t)&=1.0\,t^2 - 1.0\,t,\quad t\in [0,1], \end{aligned}$$

which is exactly the true solution. The aforesaid approximation along with the related absolute error is shown in Fig. 1.

Fig. 1

Graphs of the exact and computed solutions (left) and the resulting absolute errors (right) utilizing $L=2$, $\gamma ,\alpha =1$ in Example 5.1

Note, using diverse values of $0<\gamma <1$ will also lead to the same exact solution as for $\gamma =1$. In the next experiments, the results of absolute errors utilizing diverse values of $\gamma =0.25,0.5,075$ are reported. Table 1 tabulates the results of $\mathcal {E}_{L,\alpha }(t)$, which are calculated at some points $t_i=2i/10$ while i varies from 0 to 5. A comparison with the outcomes of operational-based methods with constant $\tau =0.01$ are presented in Table 1 to testify the validity of our numerical results. These methods are the Bernoulli wavelet method (BWM) [57], the Chebyshev spectral collocation method (CSCM) [59], and the Chebyshev functions of third kind (CFTK) [60] Looking at Table 1 reveals that our numerical model results are more accurate in comparison to other existing computational results.

Table 1 The comparison of absolute errors in Chelyshkov matrix approach in Example 5.1 using $L=2$, $\alpha =1$, and diverse $\gamma =0.25,0.5,0.75,1.0$ and $t\in [0,1]$

Next, we investigate the influence of utilizing diverse delayed functions $\tau (t)$ on the computed solutions. We take $\tau (t)=e^t,e^{-t},\sin (t),\sqrt{t}$, $\tau (t)=t^{10}$. In all cases, the obtained approximate solutions by the Chelyshkov matrix approach are the same and coincide with the exact true solution. In Fig. 2, we depict the related absolute errors, which are obtained using $\gamma =0.5$, $\alpha =1$, and $L=2$.

Fig. 2

Graphs of the absolute errors utilizing $L=2$, $\gamma =0.5,\alpha =1$, and diverse delayed functions $\tau (t)$ in Example 5.1

Test case 5.2 As the second test problem, let us consider the FDDEs of the form

$$\begin{aligned} {}^C {D}^{(\gamma )}_{t}\chi (t)-\frac{1}{2}\chi (t)=\frac{1}{2}\,e^{\frac{t}{2}}\chi \left( \frac{t}{2}\right) ,\quad 0< \gamma \le 1, \end{aligned}$$

with initial condition $\chi (0)=1$. It is not a difficult task to show that the exact solution of (5.2) for $\gamma =1$ is $\chi (t)=e^t$.

Firstly, $N=3,5$ being used for this example. Considering $\gamma ,\alpha =1$, the resulting approximative solutions via Chelyshkov matrix technique for $t\in [0,1]$ are as follows:

$$\begin{aligned} \chi _{3,1}(t)&= 0.330827997\,t^3 + 0.3380024642\,t^2 + 1.070786443\,t + 1.0,\\ \chi _{5,1}(t)&=0.01535493092\,t^5 + 0.03061950307\,t^4 + 0.1749117548\,t^3 + 0.4968973814\,t^2\\& \quad + 1.000599604\,t + 1.0. \end{aligned}$$

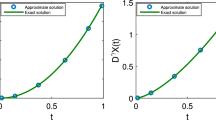
The obtained approximations along with the exact solution are visualized in Fig. 3. In addition to $L=3,5$, the resulting absolute errors for $L=7,9$ are also depicted in this figure, but on the right plot. Clearly, the exponential convergence of the proposed algorithm can be visible when the number of bases getting large.

Fig. 3

Graphs of the exact and computed solutions using $L=3,5$ (left) and the resulting absolute errors (right) for $L=3,5,7,9$ for $\gamma ,\alpha =1$ in Example 5.2

Moreover, for $\gamma =1$, the results of absolute errors ${\mathcal {E}}_{{L},{1}}(t)$ utilizing diverse values of $L=5,7,9$, and $L=11$ are reported in Table 2. Comparisons are further made in this table between the outcomes of the present technique and the other existing methods, i.e., the Chebyshev wavelet method (CWM) [61] and the CFTK [60].

Table 2 The comparison of absolute errors in Chelyshkov matrix approach in Example 5.2 utilizing $L=5,7,9,11$, $\gamma ,\alpha =1$, and diverse $t\in [0,1]$

Let us consider the behavior of solutions when the fractional order $0<\gamma <1$ is used. In this respect, we take $\gamma =0.5,0.75$. Additionally, we utilize $\gamma ,\alpha =1$. Fig. 4 displays the solutions $\chi _{10,\alpha }(t)$, where both $\alpha =1$ and $\alpha =\gamma$ are used for comparisons. In the right graph, the residual errors ${\mathcal {R}}_{{10},{\alpha }}(t)$ for $t\in [0,1]$ are also depicted. It can be readily observed that a smaller magnitude of error is achieved when the degrees of local basis functions $\alpha$ are taken as the fractional order of model $\gamma$.

Fig. 4

Graphs of computed solutions (left) and the resulting residual errors (right) utilizing $\gamma =0.5,0.75$, $\alpha =1,\gamma$ for $L=10$ in Example 5.2

Test case 5.3 The third test case is devoted to the following nonlinear FDDEs defined on $0\le t\le 1$ as

$$\begin{aligned} {}^C {D}^{(\gamma )}_{t}\chi (t)=1-2\chi ^2\left( \frac{t}{2}\right) ,\quad 1< \gamma \le 2. \end{aligned}$$

The initial conditions are $\chi (0)=1$, $\chi '(0)=0$. For $\gamma =2$, an easy calculation shows that $\chi (t)=\cos t$ is the exact solution of this model problem.

First, we set $\gamma =2,\alpha =1$. Utilizing $L=5,10$ in the Chelyshkov matrix procedure, we get the following polynomial forms for the approximate solutions for $t\in [0,1]$ as follows:

$$\begin{aligned} \chi _{5,1}(t)&=-0.005332031785\,t^5 + 0.05030385241\,t^4 - 0.007577193623\,t^3\\&- 0.496492205\,t^2 + 1.0, \end{aligned}$$

and

$$\begin{aligned} \chi _{10,1}(t)&=-2.2608\times 10^{-7}\,t^{10} -1.9315\times 10^{-7}\,t^9 + 2.5175\times 10^{-5}\,t^8- 4.4477\times 10^{-7}\,t^7\\&- 0.00138853644\,t^6 - 1.9113\times 10^{-7}\,t^5 + 0.04166673776\,t^4 - 1.7846\times 10^{-8}\,t^3\\&- 0.4999999971\,t^2 + 1.0. \end{aligned}$$

Let us consider the series form of the exact solution, i.e., $\cos t\approx 1-\frac{t^2}{2!}+\frac{t^4}{4!}-\cdots +\frac{t^{10}}{10!}$. A comparison between the achieved approximations and the exact one indicates the good alignment between them, especially when L is increased. Moreover, the absolute errors ${\mathcal {E}}_{{L},{1}}(t)$ utilizing diverse values of $L=5,8,10,15$ in the approximate solutions are presented in Table 3. The outcomes of the BWM [57] with $k=2$ and various $M=7,9$ as well as the modified Laguerre wavelet method MLWM [62] with $k=1$ and different $M=10,20$ are also reported in Table 3. We observe that the proposed method using a lower number of bases produces more accurate results than the BWM method does.

Table 3 The comparison of absolute errors in Chelyshkov matrix approach in Example 5.3 using $\gamma =2$, $\alpha =1$, and diverse $L=5,8,10,15$ and $t\in [0,1]$

Figure 5 displays the numerical solutions corresponding to diverse fractional orders $\gamma =1.5,1.6,1.7,1.8$, and 1.9. Besides, Fig. 5 shows the results related to $\gamma =2$ at which the exact solution is available. In all plots, we use $\alpha =1$ and $L=10$ is taken. On the right panel, the behavior of residual errors ${\mathcal {R}}_{{10},{1}}(t)$, $t\in [0,1]$ at different values of $\gamma$ are visualized.

Fig. 5

Graphs of computed solutions using $L=10,\alpha =1$ (left) and the resulting residual errors (right) for diverse $\gamma =1.5,1.6,\ldots ,2$ in Example 5.3

Precisely speaking, in Table 4, the computed values of numerical solutions $\chi _{10,1}(t)$ for various $\gamma =1.5,1.6,\ldots ,1.9$ at some points $t\in [0,1]$ for Example 5.3 are shown.

Table 4 The computed solutions in Chelyshkov matrix method in Example 5.3 utilizing $L=10$, $\alpha =1$, and diverse $\gamma =1.5,1.6,\ldots ,1.9$ for some $t\in [0,1]$

Test case 5.4 We consider the following FDDEs

$$\begin{aligned} {}^C {D}^{(\gamma )}_{t}\chi (t)=-\chi (t)-\chi (t-0.3)+e^{0.3-t},\quad 2< \gamma \le 3. \end{aligned}$$

The given initial conditions are $\chi (0)=1$, $\chi '(0)=-1$, and $\chi ''(0)=1$. If $\gamma =3$, one can show that $\chi (t)=e^{-t}$ is the exact solution of (5.4).

First, we take $\gamma =3$ and $\alpha =1$. We get the following polynomial solutions when using $L=5,10$ in the Chelyshkov matrix approach on [0, 1] as follows:

$$\begin{aligned} \chi _{5,1}(t)&=- 0.0046134994\,t^5 + 0.036777943\,t^4 - 0.16319738\,t^3 + 0.5\,t^2 - 1.0\,t + 1.0,\\ \chi _{10,1}(t)&=1.5868\times 10^{-7}\,t^{10} - 2.4685\times 10^{-6}\,t^9 + 2.4368\times 10^{-5}\,t^8 - 1.9798\times 10^{-4}\,t^7\\&+ 0.0013885928\,t^6 - 0.00833319237\,t^5 + 0.04166662023\,t^4 - 0.1666666563\,t^3 \\&+ 0.5\,t^2 - 1.0\,t + 1.0. \end{aligned}$$

Furthermore, the numerical evaluations of the latter approximate solution are presented in Table 5. The resulting absolute errors at some points $t\in [0,1]$ are also shown. The numerical results of two existing schemes, namely the MLWM [62] with $k=1,M=20$ and the BWM [57] utilizing $k=2,M=7$, are reported in this table for comparison.

Table 5 The comparison of numerical solutions in Chelyshkov matrix method in Example 5.3 utilizing $L=10$, $\alpha =1$, and $\gamma =3$ for some $t\in [0,1]$

In the next study, we examine the impact of using non-integer order values on the obtained numerical solutions. Let us consider $L=10$ and $\alpha =1$. The numerical evaluations at $\gamma =2.5,2.7,2.9$ are seen in Table 6. The associated residual errors are further presented in Fig. 6. This figure also shows the errors for other values of $\gamma =2.6,2.8,3$.

Table 6 Numerical solutions in Chelyshkov matrix method in Example 5.4 utilizing $L=10$, $\alpha =1$, and diverse $\gamma =2.5,2.7,2.9$ for some $t\in [0,1]$

Fig. 6

Plots of residual errors in Example 5.4 utilizing $L=10$, $\alpha =1$ and diverse $\gamma =2.5,2.6,\ldots ,3$

Our further goal is to examine the benefits of utilizing fractional-order Chelyshkov functions in the presented matrix technique.

Test case 5.5 Let us consider the nonlinear FDDEs of the form

$$\begin{aligned} {}^C {D}^{(\gamma )}_{t}\chi (t)=\chi (t)+\chi ^2\left( \frac{t}{4}\right) +g(t),\quad 0< \gamma \le 1, \end{aligned}$$

where $g(t)=\frac{3\sqrt{\pi }}{\Gamma (\frac{5}{2}-\gamma )}t^{\frac{3}{2}-\gamma }-t^{\frac{3}{2}}-t$ and with the initial condition $\chi (0)=0$. It can be seen that the exact solution is given by $\chi (t)=t\sqrt{t}$.

Let us first consider $\gamma =\frac{1}{2}$ and $L=5$. To highlight the discrepancy between integer and non-integer order of basis functions, we set $\alpha =1$ and $\alpha =\frac{1}{2}$ in the experiments. For $\alpha =1$, the following approximate solution via Chelyshkov matrix technique is gotten on [0, 1]

$$\begin{aligned} \chi _{5,1}(t)&=- 0.1592325852\,t^5 + 0.6061142788\,t^4 - 1.005116759\,t^3 + 1.329574057\,t^2\\&+ 0.2365275176\,t + 2.005042339\times 10^{-22}, \end{aligned}$$

which is obviously far from the exact solution. Even using a larger number of L cannot lead to a significant change in the accuracy of approximate solutions due to appearance of the fractional power in the exact solution. One remedy is to utilize a set of fractional bases so that the exact solution is written in terms of them. In this case, we set $\alpha =\frac{1}{2}$. Thus, we get $\pmb {M}_{5}^{\frac{1}{2}}=[ 1\quad t^{1/2}\quad t\quad t^{3/2}\quad t^2\quad t^{5/2}]$. The corresponding approximation is

$$\begin{aligned} \chi _{5,\frac{1}{2}}(t)&=1.692665537\times 10^{-14}\,t + 1.396525139\times 10^{-13}\,t^2 + 1.124313168\times 10^{-15}\,t^{1/2} \\& \quad + 1.0\,t^{3/2} - 9.409720268\times 10^{-14}\,t^{5/2} - 3.597072825\times 10^{-23}, \end{aligned}$$

which is in excellent agreement with the exact solution. Note that one obtains also the same accurate solutions using a smaller number of bases. For instances, taking $L=3$ with $\alpha =\frac{1}{2}$ gives us

$$\begin{aligned} \chi _{3,\frac{1}{2}}(t)= 1.0071\times 10^{-10}\,t - 5.0401\times 10^{-11}\,t^{1/2}+ 0.9999999999\,t^{3/2} - 1.1571\times 10^{-22}. \end{aligned}$$

The same approximation result is obtained with $L=2$ and $\alpha =\frac{3}{2}$ as

$$\begin{aligned} \chi _{2,\frac{3}{2}}(t)&=1.000000152\,t^{3/2} - 0.0000004120797475\,t^{3} - 8.056246369\times 10^{-20}. \end{aligned}$$

All the above approximations together with related absolute errors are depicted in Fig. 7.

Fig. 7

Graphs of the exact and computed solutions (left) and the resulting absolute error (right) using $\gamma =\frac{1}{2}$ and different L for $\alpha =1,\frac{1}{2},\frac{3}{2}$ in Example 5.5

We further utilize diverse $\gamma =\frac{1}{4},\frac{1}{2}$, and $\gamma =\frac{3}{4}$ in the computations. Correspondingly, the values of $\alpha =\frac{1}{2},\frac{3}{4}$ are used. The numerical results are presented in Table 7 with $L=3$. By looking at the numerical results we can see that employing the fractional-order Chelyshkov functions gives rise to a considerable achievement of accuracy in the approximate solutions and even with a small number of bases.

Table 7 The comparison of numerical solutions in Chelyshkov matrix method in Example 5.5 utilizing $L=3$, $\alpha =\frac{1}{2},\frac{3}{4}$, and $\gamma =\frac{1}{4},\frac{1}{2},\frac{3}{4}$ for some $t\in [0,1]$

Test case 5.6 We consider the following FDDEs as

$$\begin{aligned} {}^C {D}^{(\gamma )}_{t}\chi (t)+\chi (t)=\frac{1}{10}\chi \left( \frac{8t}{10}\right) +\frac{1}{2}{}^C {D}^{(\gamma )}_{t}\chi \left( \frac{8t}{10}\right) +g(t),\quad 0< \gamma \le 1, \end{aligned}$$

where $g(t)=e^{-t}+(0.32t-0.5)e^{-0.8t}$ and with the initial condition $\chi (0)=0$. It can be seen that for $\gamma =1$, the exact analytical solution is $\chi (t)=te^{-t}$.

As for the previous examples, we consider first $\gamma ,\alpha =1$ and $L=5$ as well as $L=10$. Employing the Chelyshkov matrix technique, the following polynomial solutions are obtained on [0, 1] as

$$\begin{aligned} \chi _{5,1}(t)&= \, 0.01943184902\,t^5 - 0.1368955319\,t^4 + 0.4782339744\,t^3 - 0.991309991\,t^2 \\& \quad + 0.9983985365\,t,\\ \chi _{10,1}(t)&=-1.4884\times 10^{-6}\,t^{10} +2.1687\times 10^{-5}\,t^9 - 1.9370\times 10^{-4}\,t^8 + 0.001384157975\,t^7\\& \quad - 0.008330076157\,t^6 +0.04166510579\,t^5 - 0.166666148\,t^4 + 0.4999998831\,t^3 \\& \quad - 0.999999983\,t^2 + 0.9999999986\,t. \end{aligned}$$

In comparison with the series expansion of $te^{-t}$, we find that the obtained solutions are in good alignment especially when L getting larger. The exponential convergence of the proposed technique is presented in Table 8, in which we have used $L=5,7,9,11$, and $L=15$. A comparison with the scheme CFTK [60] is further presented in Table 8.

Table 8 The comparison of absolute errors in Chelyshkov matrix approach in Example 5.6 utilizing $L=5,7,9,11,15$, $\gamma ,\alpha =1$, and diverse $t\in [0,1]$

Finally, we take $L=10$ and see the effect of fractional order of differential equation as well as basis functions. The numerical solutions $\chi _{10,\alpha }(x)$ utilizing diverse values of $\gamma =0.25,0.5,0.75$ are depicted in Fig. 8. To show the discrepancy between integer and non-integer basis functions, the graphical representations of the solutions using two different $\alpha =1$ and $\alpha =\gamma$ are shown in Fig. 8. As previously observed in the former examples and in our former experiences with other polynomial bases [55], utilizing $\alpha =\gamma$ leads to more accurate results. Based on this fact, we report numerical results for different values of $\gamma =0.25,0.5,0.75$ in Table 9 while considering $\alpha =\gamma$. The related residual errors are shown in Fig. 9.

Fig. 8

The computed solutions using $L=10$, diverse $\gamma =0.25,0.5,0.75,1$, and $\alpha =1,\gamma$ in Example 5.6

Table 9 Numerical solutions in Chelyshkov matrix method in Example 5.6 utilizing $L=10$, $\alpha =\gamma$, and diverse $\gamma =0.25,0.5,0.75$ for some $t\in [0,1]$

Fig. 9

Plots of residual errors in Example 5.6 utilizing $L=10$, $\alpha =\gamma$ and diverse $\gamma =0.25,0.5,0.75$

Test case 5.7 Lastly, we consider the following nonlinear FDDEs

$$\begin{aligned} {}^C {D}^{(\gamma )}_{t}\chi (t)=\chi \left( \frac{t}{3}\right) +\chi ^2(t)+g(t),\quad 0< \gamma \le 1, \end{aligned}$$

whose exact solution $\chi _{\gamma }(t)=t^{\gamma +\frac{3}{2}}-t$ depending on the parameter $\gamma$ and with the initial condition $\chi (0)=0$. This model for $\gamma =\frac{1}{2}$ considered in [63].

We take $\gamma =1/2$ and $\alpha =1$. We then utilize $L=2$ and the collocation points $\{0,\frac{1}{2},1\}$. After solving the nonlinear fundamental matrix equation $[{\widetilde{\pmb {Y}}}; \widetilde{\pmb {Q}}]$ described in Section 4, we get the coefficient matrix $\pmb {A}_2$ as

$$\begin{aligned} \pmb {A}_2=\begin{pmatrix} 0\quad -\frac{1}{4}\quad -\frac{1}{4} \end{pmatrix}^t. \end{aligned}$$

Therefore, the resulting approximate solution obtained via our algorithm is

$$\begin{aligned} \chi _{2,1}(t)=\pmb {\Psi }^{1}_{2}(t)\,\pmb {A}_2= \begin{pmatrix} 10t^2-12t+3\quad -5t^2+4t\quad t^2 \end{pmatrix}\,\pmb {A}_2=t^2-t, \end{aligned}$$

which clearly coincides with the exact solution excellently. Similarly, using $L=3$, we get

$$\begin{aligned} \chi _{3,1}(t)=-1.466850252\times 10^{-11}\,t^3 + 1.0\,t^2 - 1.0\,t + 5.30426519\times 10^{-23}. \end{aligned}$$

To validate our results and to make a comparison with the outcomes obtained via the Jacobi spectral Galerkin method (JSGM) [63], we calculate the $L_2$ and $L_{\infty }$ error norms. In this respect, we compute

$$\begin{aligned} E_{L,\infty }:=\max _{0\le t\le 1} \mathcal {E}_{L,\alpha }(t),\quad E_{L,2}:=\Big (\int _0^1[\chi (t)-\chi _{L,\alpha }(t)]^2{\text {d}}t\Big )^{\frac{1}{2}}. \end{aligned}$$

The results are tabulated in Table 10. Obviously, our results using less number of bases and less computational efforts are more accurate than those reported by the JSGM.

Table 10 A comparison of $L_{\infty }/L_2$ error norms for Example 5.7

Finally, we examine the behavior of approximate solutions when the fractional order $\gamma$ is varied on (0, 1]. To this end, we consider $\gamma =0.1,0.25,0.5,0.75$ and $\gamma =1$ while the values of $\alpha$ are chosen appropriately as $\alpha =\frac{1}{5},\frac{1}{4},1,\frac{1}{2}$ accordingly. Moreover, we take $L=8,7,2,10,5$, respectively, for each $\gamma$. Graphical representations of the aforesaid approximations together with achieved absolute errors are shown in Fig. 10.

Fig. 10

Graphs of the exact and computed solutions (left) and the resulting absolute errors (right) using $\gamma =\frac{1}{10},\frac{1}{4},\frac{1}{2},\frac{3}{4},1$ and different L and $\alpha$ in Example 5.7

Conclusions

In this research, a class of linear and nonlinear fractional delay differential equations is being investigated. The solution to such models is found through a novel collocation method named the Chelyshkov collocation approach depending on the use of Chelyshkov functions. The fractional derivative is defined in the Caputo type, and the fractional differentiation matrices for the Chelyshkov functions are being derived. These matrices along with the collocation points are then used to convert the designed models into a system of algebraic equations and thus this system is then solved to find the unknown coefficients that are used to represent the required solution. A detailed error analysis is being performed for the presented technique provide that the proposed approach ensures sufficient convergence. The method is tested for several examples of different types including some with the exact solution depending on the fractional order. The satisfactory absolute error results for all the examples ensure that the provided technique is better than other related methods in terms of absolute error and computational cost. One can determine based on these accessible observers that the designed technique is accurate and fast. This may provide a future insight to some applications to this technique as to consider more complex models with applications.