New sampling theorem and multiplicative filtering in the FRFT domain

Abstract

Having in consideration a fractional convolution associated with the fractional Fourier transform (FRFT), we propose a novel reconstruction formula for bandlimited signals in the FRFT domain without using the classical Shannon theorem. This may be considered the main contribution of this work, and numerical experiments are implemented to demonstrate the effectiveness of the proposed sampling theorem. As a second goal, we also look for the designing of multiplicative filters. Indeed, we also convert the multiplicative filtering in FRFT domain to the time domain, which can be realized by fast Fourier transform. Two concrete examples are included where the use of the present results is illustrated.

1 Introduction

The fractional Fourier transform (FRFT) was first introduced by Wiener and Condon in the 1920s. After a period without attention, it was reinvented in 1980 by Namias in order to solve certain classes of quadratic Hamiltonians in quantum mechanics (cf. [9]). Later on, McBride and Kerr [8] improved the former studies to develop operational calculus and other properties of the fractional Fourier transform. In recent years, the FRFT has become the focus of many research papers in optics, optical systems and optical signal processing, time–frequency representation, quantum mechanics, filter design, pattern recognition, and many other applied sciences.

In very simple terms, the FRFT can be considered as a generalization of the Fourier transform with one additional parameter. For any real angle $\alpha$, let

$$\begin{aligned} K_\alpha (x,p) = {\left\{ \begin{array}{ll} { {\frac{c(\alpha )}{\sqrt{2\pi }}} \exp \left\{ {i a(\alpha )\left( {x^2 + p^2 - 2b( \alpha )xp } \right) } \right\} ,} \\ \text {if }{\alpha }\text { is not a multiple of }{\pi } \\ {\delta \left( {x - p} \right) },\\ \text {if }{\alpha }\text { is a multiple of }{2\pi } \\ {\delta \left( {x + p} \right) }, \\ \text {if }{\alpha +\pi }\text { is a multiple of }{2\pi }, \end{array}\right. } \end{aligned}$$

with

$$\begin{aligned} a(\alpha ) = \frac{{\cot \alpha }}{2},\quad b(\alpha ) = \sec \alpha ,\quad c(\alpha ) = \sqrt{1 - i\cot \alpha } \end{aligned}$$

(where the square root is defined such that the argument of the result lies in the interval $(-\pi /2, \pi /2]$). With the help of this transformation kernel, the FRFT with angle $\alpha$ is usually defined as

$$\begin{aligned} {\mathcal {F}}_\alpha \left[ f \right] (p) = \int _{ - \infty }^\infty {f(x)K_\alpha (x,p)\mathrm{d}x}. \end{aligned}$$

(1)

For $\alpha =0$ and $\alpha = {\pi }/{2}$, the FRFT domain becomes time domain and frequency domain, respectively. Since the FRFT can be interpreted as an anticlockwise rotation by the $\alpha$ angle in the time–frequency plane, it is more flexible than the Fourier transform in many applications.

As a generalization of the Fourier transform, the relevant theory of the FRFT (such as convolution theorems and sampling theory) has been developed in a growing manner through the years by several authors (cf., without being exhaustive, Almeida [1, 2], Zayed [20], Deng et al. [6]). As far as it concerns convolutions and their consequences, a huge amount of works could also be pointed out due to both theoretical and practical perspectives. Anyway, for this purpose, as examples, we simply refer the interested reader to [4, 5, 11,12,13, 16] and to the references therein.

Signal reconstruction from some sample is an important signal processing operation, which can provide a suitable model of sampling and reconstruction in many applications. For example, in [15] sampling formulae were derived to reconstruct a bandlimited signal in the FRFT domain. By a similar technique, the sampling theorem of bandlimited signals was obtained in [6] for the linear canonical transform domain.

In [3], we have introduced two new convolutions for the FRFT. Namely, one of such convolutions was defined by

$$\begin{aligned} x(t) \odot y(t)= & {} \frac{c}{{\sqrt{2\pi } }}e^{ - iat^2 } \nonumber \\&\times \, \left[ {x(t)e^{ iat^2 } * y\left( {t + \frac{1}{{2ab}}} \right) e^{ia(t^2 + t/ab)} } \right] \nonumber \\ \end{aligned}$$

(2)

and has the factorization property

$$\begin{aligned} {\mathcal {F}}_\alpha \left[ {x(t) \odot y(t)} \right] (u) =X_\alpha (u) {\hat{Y}}_\alpha (u), \end{aligned}$$

(3)

where $X_\alpha (u)={\mathcal {F}}_\alpha \left[ x \right] ,\,{\hat{Y}}_\alpha (u) ={\mathcal {F}}_\alpha \left[ y \right] e^{ - iau^2 + iu}$.

The main purpose of this paper is to obtain a new fractional sampling theorem by using the fractional convolution (2) without using the classical Shannon theorem. At the same time, the paper also gives the design of multiplicative filters in the FRFT domain via this convolution.

The paper is divided into four main sections and a final conclusion, and organized as follows. In the next section, we define the bandlimited signal in the FRFT domain, and recall Xia’s sampling theorem, which can be considered as a Shannon-type sampling theorem for the FRFT. In Sect. 3, by using the fractional convolution (2), we establish the sampling theorem for bandlimited signals in the FRFT domain and give numerical experiments to demonstrate the effectiveness of the proposed sampling theorem. In Sect. 4, we design the multiplicative filters in the FRFT domain from the point of view of the convolution (2) in the time domain and the product in the FRFT domain. Examples are then considered and, to finalize the paper, a conclusion is provided.

2 Known sampling theory

To start this section, we recall at first the definition of the bandlimited signals in the FRFT sense.

Definition 1

If the $\alpha$ angle FRFT of the signal x(t) satisfies the following condition

$$\begin{aligned} X_\alpha \left( u \right) = 0,\,\,\left| u \right| > {\varOmega }_h , \end{aligned}$$

then x(t) is called the bandlimited signal in the FRFT $\alpha$ angle or $\alpha$ angle fractional bandlimited signal, whose bandwidth is defined as ${\varOmega }_h$.

If a signal x(t) is ${\varOmega }_h$ bandlimited with angle $\alpha$ and $\alpha \ne n\pi$ for any integer n, then by the inverse FRFT

$$\begin{aligned} x(t)= & {} \sqrt{\frac{{1 + i\cot \alpha }}{{2\pi }}} e^{ - iat^2 }\\&\times \, \int _{ - {\varOmega }_h }^{{\varOmega }_h } {{\mathcal {F}}_\alpha \left[ x \right] \left( u \right) e^{ - iau^2 } e^{iut\csc \alpha } \mathrm{d}u}. \end{aligned}$$

Let

$$\begin{aligned} g(t) = \int _{ - {\varOmega }_h }^{{\varOmega }_h } {{\mathcal {F}}_\alpha \left[ x \right] \left( u \right) e^{ - iau^2 } e^{iut\csc \alpha } \mathrm{d}u} . \end{aligned}$$

It is easily seen that g is ${\varOmega }_h \csc \alpha$ bandlimited in the conventional sense. Based on this, Xia [19] applied the Shannon sampling theorem to g in the following way

$$\begin{aligned} g(t) = \sum \limits _n {g(n{\varDelta }_\alpha )\frac{{\sin \left[ {{\varOmega }_h \csc \alpha \left( {t - n{\varDelta }_\alpha } \right) } \right] }}{{{\varOmega }_h \csc \alpha \left( {t - n{\varDelta }_\alpha } \right) }}} \end{aligned}$$

(4)

where ${\varDelta }_\alpha = \frac{{\pi \sin \alpha }}{{{\varOmega }_h }}$. Substituting (4) into the representation

$$\begin{aligned} x(t) = g(t)\sqrt{\frac{{1 + i\cot \alpha }}{{2\pi }}} e^{ - iat^2 }, \end{aligned}$$

the author derived a sampling formula for the bandlimited signal in the $\alpha$ angle FRFT domain

$$\begin{aligned} x(t)= & {} e^{ - iat^2 } \sum \limits _n {x(n{\varDelta }_\alpha )e^{ - ia{\varDelta }_\alpha ^2 } \frac{{\sin \left[ {{\varOmega }_h \csc \alpha \left( {t - n{\varDelta }_\alpha } \right) } \right] }}{{{\varOmega }_h \csc \alpha \left( {t - n{\varDelta }_\alpha } \right) }}}.\nonumber \\ \end{aligned}$$

(5)

In fact, this is the uniform sampling formula which has been generalized to many other forms. In 1999, Zayed and Garcia [21] derived a new sampling theorem using samples of the signal and its Hilbert transform. In [15], Tao et al. utilized the product theorem (cf. [2]) for the FRFT to obtain the FRFT of the sampled signal and then derived the reconstructed signal through a bandpass filter in the FRFT domain. The authors also discussed sampling and sampling rate conversion of bandlimited signals in the FRFT domain. Based on the fractional Fourier series (FRFS), Wei at al. [17] proposed another proof for Xias sampling theorem, and showed that this sampling expansion for fractional bandlimited signal is a special case of Parseval’s relation for complex FRFS. Furthermore, Stern [14] extended Xia’s result to the linear canonical transform (which is a generalization of the FRFT).

3 A new sampling procedure

In this section, we prove the reconstruction formula for bandlimited signals from uniform samples associated with the FRFT, and give a numerical experiment to demonstrate the usefulness of the sampling theorem presented in this work.

3.1 A new sampling theorem

Theorem 1

Let x(t) be a bandlimited signal to $[-{\varOmega }_h,{\varOmega }_h]$ in the FRFT sense. Then, the following sampling formula for x(t) holds:

$$\begin{aligned} x(t)= & {} \frac{{Te^{\frac{{ - i\sin 2\alpha }}{4}} }}{{2\pi \sin \alpha }}e^{ - iat^2 }\nonumber \\&\times \, \sum \limits _{n = - \infty }^{ + \infty } {x\left( {nT} \right) e^{ia\left( {nT} \right) ^2 } \frac{{\sin \left[ {2ab\left( {t - nT} \right) {\varOmega }_\alpha } \right] }}{{ab\left( {t - nT} \right) }}} ,\nonumber \\ \end{aligned}$$

(6)

where $n \in {\mathbb {Z}}$, $T \le \dfrac{\pi }{{{\varOmega }_h \left| {\csc \alpha } \right| }}$ is the sampling period and ${\varOmega }_\alpha \in [{\varOmega }_h,\omega _s /|\csc \alpha |-{\varOmega }_h]$ is the cutoff frequency.

Proof

The uniform sampled signal is described as

$$\begin{aligned} {\hat{x}} = x(t) \; s_\delta (t) = x(t)\sum \limits _{n = - \infty }^{ + \infty } {\delta (t - nT)} , \end{aligned}$$

(7)

where T is the sampling period and $s_\delta (t)$ is the uniform impulse train having its Fourier transform given by

$$\begin{aligned} S_\delta (u) = \frac{{2\sqrt{\pi } }}{T}\sum \limits _{n = - \infty }^{ + \infty } {\delta \left( {u - n\frac{{2\pi }}{T}} \right) } . \end{aligned}$$

(8)

According to the product theorem for the FRFT, we have

$$\begin{aligned} {\hat{X}}_\alpha (u)= & {} \frac{{\left| {\csc \alpha } \right| }}{{\sqrt{2\pi } }}e^{iau^2 }\\&\times \, \left( {X_\alpha (u) e^{-iau^2 } * \frac{{2\sqrt{\pi } }}{T}\sum \limits _{n = - \infty }^{ + \infty } {\delta \left( {u\csc \alpha - n\frac{{2\pi }}{T}} \right) } } \right) , \end{aligned}$$

where “$*$” denotes the classical convolution defined by

$$\begin{aligned} f(t) * g(t) = \int \limits _{ - \infty }^{ + \infty } {f(\tau )g(t - \tau )\mathrm{d}\tau } . \end{aligned}$$

Since

$$\begin{aligned} \frac{1}{|a|}\delta \left( {u - b/a} \right) = \delta (au - b), \end{aligned}$$

we have

$$\begin{aligned} {\hat{X}}_\alpha (u)= & {} \frac{{1} }{T}e^{iau^2 } \nonumber \\&\times \, \left( {X_\alpha (u) e^{ - iau^2 } * \sum \limits _{n = - \infty }^{ + \infty } {\delta \left( {u - \frac{{2\pi }}{{T\csc \alpha }}n} \right) } } \right) .\nonumber \\ \end{aligned}$$

(9)

From (9), we find that $X_\alpha (u)$ is replicated with a period of ${{1}}/({{T\csc \alpha }})$ after being sampled, and the nth component of ${\hat{X}}_\alpha (u)$ differs from $X_\alpha (u)$ only by a magnitude factor 1 / T when $n=0$, while for $n \ne 0$ it modulates both the amplitude by 1 / T and the phase of $X_\alpha (u)$.

If x(t) is a bandlimited signal in the FRFT sense, or, in another words, the support interval of $X_\alpha (u)$ is $(-{\varOmega }_h, {\varOmega }_h)$, then no overlapping occurs in ${\hat{X}}_\alpha (u)$ after sampling only if

$$\begin{aligned} \frac{{2\pi }}{{T\left| {\csc \alpha } \right| }} \ge 2{\varOmega }_h , \end{aligned}$$

i.e., we have the sampling frequency

$$\begin{aligned} \omega _{\mathrm{s}} = \frac{{2\pi }}{T} \ge 2{\varOmega }_h \left| {\csc \alpha } \right| . \end{aligned}$$

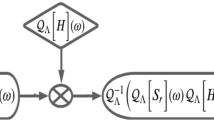
Thus, $X_\alpha (u)$ can be recovered, and the other replicated spectra are filtered out through a low-pass filter having the gain T and the cutoff frequency ${\varOmega }_\alpha$ (${\varOmega }_\alpha \in [{\varOmega }_h,\omega _s /|\csc \alpha |-{\varOmega }_h]$) in the FRFT domain, whose transfer function is given by

$$\begin{aligned} H_\alpha (u)= {\left\{ \begin{array}{ll} T&{}\quad |u| < {\varOmega }_\alpha \\ 0&{}\quad |u| \ge {\varOmega }_\alpha \end{array}\right. }. \end{aligned}$$

The original signal x(t) can be reconstructed without any distortion by the inverse FRFT of the recovered $X_\alpha (u)$. Limiting the cutoff frequency of a low-pass filter within the interval $[{\varOmega }_h,\omega _s /|\csc \alpha |-{\varOmega }_h]$ is to pick out only the zeroth component for ${\hat{X}}_\alpha (u)$.

The expression of the above-mentioned reconstructed signal can be obtained by (3). Assume ${\hat{Y}}_\alpha (u) = H_\alpha (u)$. Then,

$$\begin{aligned} y(t)&= {\mathcal {F}}_{ - \alpha } \left[ {{\hat{Y}}_\alpha (u)e^{iau^2 - iu} } \right] \\&= \frac{{\sqrt{1 + i\cot \alpha } }}{{\sqrt{2\pi } }} \!\! \int \limits _{ - {\varOmega }_\alpha }^{{\varOmega }_\alpha } \!\!\! {e^{ - ia(t^2 + u^2 - 2btu)} {\hat{Y}}_\alpha (u)e^{iau^2 - iu} \mathrm{d}u} \\&= \frac{{\sqrt{1 + i\cot \alpha } }}{{\sqrt{2\pi } }}Te^{ - iat^2 } \int \limits _{ - {\varOmega }_\alpha }^{{\varOmega }_\alpha } {e^{2iabtu - iu} \mathrm{d}u} \\&= \frac{{\sqrt{1 + i\cot \alpha } }}{{\sqrt{2\pi } }}Te^{ - iat^2 } \frac{{2\sin \left[ {\left( {2abt - 1} \right) {\varOmega }_\alpha } \right] }}{{2abt - 1}}. \end{aligned}$$

Since

$$\begin{aligned} {\hat{X}}_\alpha (u){\hat{Y}}_\alpha (u) = {\mathcal {F}}_\alpha \left[ {{\hat{x}}(t) \odot y(t)} \right] (u), \end{aligned}$$

the output of the low-pass filter is as follows

$$\begin{aligned} x(t)&= {\hat{x}}(t) \odot y(t)\\&= \frac{c}{{\sqrt{2\pi } }} e^{ - iat^2 } \left[ {{\hat{x}}(t)e^{iat^2 } *y\left( {t + \frac{1}{{2ab}}} \right) e^{ia(t^2 + t/ab)} } \right] \\&= \frac{c}{{\sqrt{2\pi } }} e^{ - iat^2 } \sum \limits _{n = - \infty }^\infty \int \limits _{ - \infty }^{ + \infty } x\left( \tau \right) \delta \left( {\tau - nT} \right) e^{ia\tau ^2 }\\&\quad \times \, \frac{{\sqrt{1 + i\cot \alpha } }}{{\sqrt{2\pi } }} Te^{ - ia\left( {t - \tau + 1/2ab} \right) ^2 } \\&\quad \times \, \frac{{2\sin \left[ {\left( {2ab\left( {t - \tau } \right) } \right) {\varOmega }_\alpha } \right] }}{{2ab\left( {t - \tau } \right) }} e^{ia\left[ {\left( {t - \tau } \right) ^2 + \frac{{t - \tau }}{{ab}}} \right] } \mathrm{d}\tau \\&= \frac{{Te^{\frac{{ - i}}{{4ab^2 }}} }}{{2\pi \sin \alpha }}e^{ - iat^2 } \sum \limits _{n = - \infty }^{ + \infty } \int _{ - \infty }^{ + \infty }x\left( \tau \right) \delta \left( {\tau - nT} \right) e^{ia\tau ^2 }\\&\quad \times \, \frac{{2\sin \left[ {2ab\left( {t - \tau } \right) {\varOmega }_\alpha } \right] }}{{2ab\left( {t - \tau } \right) }}\mathrm{d}\tau , \end{aligned}$$

which is equivalent to

$$\begin{aligned} x(t)= & {} \frac{{Te^{\frac{{ - i\sin 2\alpha }}{4}} }}{{2\pi \sin \alpha }}e^{ - iat^2} \nonumber \\&\times \, \sum \limits _{n = - \infty }^{ + \infty } {x\left( {nT} \right) e^{ia\left( {nT} \right) ^2 } \frac{{\sin \left[ {2ab\left( {t - nT} \right) {\varOmega }_\alpha } \right] }}{{ab\left( {t - nT} \right) }}}.\nonumber \\ \end{aligned}$$

(10)

Note that (10) is the reconstruction formula of the bandlimited signal in the FRFT domain. $\square$

We would like to stress that both Xia’s formula and the new sampling formula provide exact representations by the uniformly sampled signal. However, those two theorems for the bandlimited signal in the FRFT have been derived from different perspectives. Namely, while formula (5) can be found from the Shannon sampling theorem and viewed as a Shannon-type sampling theorem for the FRFT, our new sampling theorem is obtained just by using the new convolution for the FRFT. Moreover, for the ${\varOmega }_h$ bandlimited signal in the $\alpha$ angle FRFT domain, in the expression (5) the cutoff frequency is ${\varOmega }_h$, while in the expression (6) it can be chosen arbitrarily in the interval $[{\varOmega }_h,\omega _s /|\csc \alpha |-{\varOmega }_h]$. Thus, our formula presents an extra flexibility for practical use.

3.2 Simulation

For the illustration of the just obtained result, we observe a signal given by

$$\begin{aligned} x(t) = \sin \left( {0.6\pi t} \right) e^{ - it^2 }. \end{aligned}$$

Since the signal $\sin \left( {0.6\pi t} \right)$ is $0.6\pi$ bandlimited in the Fourier transform domain, from the analysis in Sect. 2, we know that the signal x(t) is $0.6\pi \sin \alpha$ bandlimited in the FRFT domain with $\cot \alpha = 2$. In this example, we have

$$\begin{aligned} \cos \alpha = \frac{2}{{\sqrt{5} }},\,\sin \alpha = \frac{1}{{\sqrt{5} }},\,{\varOmega }_h = \frac{{0.6\pi }}{{\sqrt{5} }}. \end{aligned}$$

According to Theorem 1, the sampling period T should satisfy $T \le \dfrac{5}{3}$. We choose $T=\dfrac{1}{2}$. Thus, no overlapping occurs after sampling if the cutoff frequency belongs to the interval

$$\begin{aligned} I = \left[ {\frac{{0.6\pi }}{{\sqrt{5} }},\frac{{4\pi }}{{\sqrt{5} }} - \frac{{0.6\pi }}{{\sqrt{5} }}} \right] . \end{aligned}$$

We determine

$$\begin{aligned} {\varOmega }_\alpha =\frac{\pi }{\sqrt{5}}. \end{aligned}$$

The reconstruction expression of the original signal with the sampling frequency $f_s=2$ Hz, and the sampling interval [0s, 5s] is given by

$$\begin{aligned} x_\alpha (t) = \frac{{e^{ - \frac{i}{5}} }}{\pi }e^{ - it^2 } \sum \limits _{n = - 200}^{200} {\sin \left( {0.3\pi n} \right) } \frac{{\sin \left[ {\pi \left( {t - \frac{n}{2}} \right) } \right] }}{{t - \frac{n}{2}}}. \end{aligned}$$

Figures 1 and 2 present the partial plots of the original signal. Figures 3 and 4 present those of the reconstructed signal. The reconstructed signal exhibits a very near approach to the original signal.

4 Multiplicative filtering in the FRFT domain

In this section, we mainly discuss the application of the fractional convolution (2) for the designing of multiplicative filters.

Fig. 1

The real part the original signal

Fig. 2

The imaginary part of the original signal

Fig. 3

The real part of the reconstructed signal

Fig. 4

The imaginary part of the reconstructed signal

4.1 Multiplicative filtering in the FRFT domain

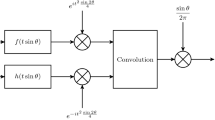
The simple model of a multiplicative filtering in the FRFT domain is shown in Fig. 5. In this configuration, the multiplicative filters can be achieved through the product in the FRFT domain. First, the FRFT with angle $\alpha$ of the input $r_\mathrm{in}(t)$ is obtained, and then, it is multiplied by a transfer function $H_\alpha (u)$ in this domain. Finally, the result is transformed with angle $-\alpha$ to obtain the output signal $r_\mathrm{out}(t)$ in the time domain. The effect of this filter can be mathematically written as the formula

$$\begin{aligned} {r_\mathrm{out}}(t) = {{\mathcal {F}}_{ - \alpha }}\left[ {H_{\alpha } \times {{\mathcal {F}}_\alpha }[{r_\mathrm{in}}]} \right] (t). \end{aligned}$$

There are many possible types of multiplicative filters in the FRFT domain. We can achieve a low-pass filter, a high-pass filter, a bandpass filter and so on, depending on the designed transfer function $H_{\alpha }(u)$.

Fig. 5

Multiplicative filtering in the FRFT domain

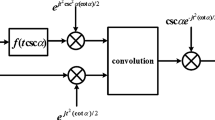
The above multiplicative filter in the FRFT domain can also be achieved through a convolution in the time domain. From (3), with the assumption that function ${\hat{Y}}_\alpha (u)$ acts as the transfer function of the multiplicative filter, $H_{\alpha }(u)$ is given by

$$\begin{aligned} H_{\alpha }(u)=Y_\alpha (u)e^{ - iau^2 + iu}. \end{aligned}$$

From (2) and (3), the output signal can be expressed as

$$\begin{aligned} r_\mathrm{out}(t)= & {} r_\mathrm{in}(t) \odot y(t)\\= & {} \frac{c}{{\sqrt{2\pi } }}e^{ - iat^2 } \\&\times \, \left[ {r_\mathrm{in}(t)e^{ iat^2 } *y\left( {t + \frac{1}{{2ab}}} \right) e^{ia(t^2 + t/ab)} } \right] . \end{aligned}$$

Figure 6 illustrates the latter method.

Fig. 6

Multiplicative filtering in the FRFT domain through the new convolution in the time domain

The simple model of a multiplicative filtering in the FRFT domain is shown in Fig. 5, which is used to eliminate the chirp noise [7]. The reason is that the major computation load of the multiplicative filtering through the new convolution is equal to the conventional convolution, while the fractional domain filtering needs to calculate FRFT twice. Since the convolution $*$ can be computed by the fast Fourier transform algorithm, the filtering model through convolution can be more useful in practical problems. The computational complexity of the method based on the new convolution for samples of length n is $O(n \log n)$.

The new convolution expression in the time domain is a simple one-dimensional integral, and therefore, it is easier to achieve filter design through the convolution in the time domain than the generalized convolution introduced in [18], where the proposed convolution cannot be expressed by a single integral form.

4.2 Simulation

For the purpose of illustration, an example of pass-stopband filter will be considered in this subsection.

Fig. 7

Using WD to filter out the undesired signal by pass-stopband fractional filter (cf. [10])

The value of the fractional angle for filtering is calculated by using the time–frequency distribution. In Fig. 7, the Wigner distribution (WD) is applied to the observed signal in order to locate the signal and noise components in the time–frequency plane. It is important to mention that the Wigner distribution of $X_{\alpha }(u)$ is a rotated version of the Wigner distribution of the signal x(t) by an angle $-\,\alpha$:

$$\begin{aligned} {W_{{X_\alpha }}}\left( {u,v} \right) = {W_x}\left( {u\cos \alpha - v\sin \alpha ,u\sin \alpha + v\cos \alpha } \right) . \end{aligned}$$

Thus, two parallel cutoff lines can separate the undesired noises from the desired signal. In this case (cf. also [10]), the transfer function is

$$\begin{aligned} H\left( u \right) = \prod {\left( {\left( {u - {u_0}} \right) /B} \right) } \end{aligned}$$

which can be rewritten in the following form

$$\begin{aligned} H\left( u \right) = {\left\{ \begin{array}{ll} 1&{}\quad \text {for } u_0 - B/2< u < {u_0} + B/2\\ 0&{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

The fractional angle and the cutoff frequency can be calculated as follows (cf. Fig. 7)

$$\begin{aligned} \alpha= & {} {\cot ^{ - 1}}\left( {\frac{{{\omega _1}}}{{{t_1}}}} \right) , \;\; {u_0} = \cos \alpha \left( {{t_0} + {t_1}} \right) /2,\\ B= & {} \left| {\cos \alpha \left( {{t_0} - {t_1}} \right) } \right| . \end{aligned}$$

Here, we use $x(t) = {e^{ - {t^2}}}$ as the original input signal. The original Gaussian signal and its WD are plotted in Fig. 8a, b, respectively. We suppose that the signal x(t) is interfered by a chirp signal

$$\begin{aligned} n(t) = {e^{i{{(t + 10)}^2}}}. \end{aligned}$$

The received signal $r_\mathrm{in}(t)$ and its WD are plotted in Fig. 8c, d, respectively.

Fig. 8

The original and the received signal

Fig. 9

The real part of the output signal of multiplicative filter achieved by using the new convolution

In the current example, we have

$$\begin{aligned} \alpha = {\cot ^{ - 1}}\left( -2 \right) ,\,B = \frac{{12}}{{\sqrt{5} }},\,{u_0} = 0. \end{aligned}$$

Hence,

$$\begin{aligned} H\left( u \right) = {\left\{ \begin{array}{ll} 1&{}\quad \text {for } - \frac{{6}}{{\sqrt{5} }}< u < \frac{{6}}{{\sqrt{5} }}\\ 0&{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

Figure 9 shows the output signal of the multiplicative filter achieved by using the new convolution with MSE equal to $1.4236 \times 10^{-4}$.

To conclude, we present a quantitative comparison between the computational loads of multiplicative filters in the time domain through the new convolution and that in the FRFT domain through the product. The comparison is carried out by using MATLAB language (version R2013a) on a system having configuration Intel (R) Core(TM)2 Duo CPU 2.13 GHz processor having 4 GB RAM (Table 1).

Table 1 Quantitative comparison of the computation times of two multiplicative filters

5 Conclusion

In this paper, having in mind the convolution (2) associated with the FRFT, we introduced a new sampling theorem for fractional bandlimited signals and a multiplicative filter in the FRFT domain. This allowed us to obtain better performances in filtering processes when compared with conventional methods. Simulations and comparative examples were included to illustrate the proposed method.