Introduction

Heat transfer is very important phenomena in equipment, like turbine blades, engine block, combustors etc. It has a significant role in design of buildings and structures and its optimization is important and critical phenomena. Estimation of convective heat transfer plays an important role in the design of heat exchangers. In particular a situation where high heat transfer surface area to volume ratio is required and hence, the role of compact heat exchanger with triangular cross-sectional passage or duct comes into existence. Many researchers have studied numerically and experimentally the laminar and turbulent flow heat transfer through ducts of arbitrary cross-sectional considering different boundary conditions, such as, constant heat flux and constant wall temperature.

Laminar Convective Heat Transfer

Shah [1] studied the heat transfer in fully developed laminar flow through the ducts of arbitrary cross-section using least squares matching technique under both constant wall heat flux and arbitrary thermal boundary conditions. Chen et al. [2] numerically investigated the effect of apex angle on laminar forced convective heat transfer in triangular duct under both constant wall flux and constant wall temperature boundary conditions using unstructured triangular grid method. They concluded that 60° apex angle gives maximum heat transfer under the laminar flow conditions. Talukdar et al. [3] numerically simulated the forced and natural heat transfer in Laminar, Hydro-dynamically and thermally developed flow through triangular ducts under constant wall temperature and also analysed the effect of apex angle on Nusselt number and bulk mean temperature. Zhang et al. [4] investigated the heat transfer in plate fin isosceles triangular duct under fully developed hydro-dynamically but thermally developing flow using uniform temperature conditions at the entrance region of the duct, which is encountered in compact heat exchanger. They emphesised the importance of apex angle and fin material on the design of compact heat exchanger. Uzun et al. [5] numerically studied the convective heat transfer inside the irregular cross-sectional ducts using both uniform wall heat flux and uniform wall temperature boundary condition, by employing elliptic grid generation technique. Yilmaz et al. [6] derived general equation for heat transfer in ducts of arbitrary cross-sections under constant wall temperature for laminar flow. Gupta et al. [7] simulated the thermo-hydraulic performance for Reynolds number less than 200 of a trapezoidal channel with triangular cross-section and analysed the effect of apex, rounding of corners and the path shape. They observed that the heat transfer performance was optimum for the apex angle ranges from 40° to 60° for such channel. Sasmito et al. [8] analysed the laminar heat transfer characteristics of various in-plane spiral ducts of various cross-sections for both constant heat flux and constant wall temperature conditions and find out the advantages and limitations of such geometries. Schmidt et al. [9] investigated the heat transfer in fully developed flow of air through rectangular and isosceles triangular duct with various aspect ratios under the influence of both constant heat flux and constant wall temperature conditions. Daschiel et al. [10] reinvestigated the experimental work of Eckert and Irvine [11] using direct numerical simulations (DNS) and analysed the impact of laminar and turbulent flow on small apex angle of 11.5° and 4°.

Convective–Radiative Heat Transfer

Yang et al. [12] numerically studied the combined effect of convection and radiation on heat transfer, using an explicit finite-difference algorithm and solved discretized algebraic equations by fourth order Runge–Kutta method in the hydrodynamically and thermally developed region of rectangular and equilateral –triangular cross-sectional ducts. Chiu et al. [13] numerically simulated the effect of radiation on convective heat transfer by solving Energy and Navier–Stokes equation using Vorticity and Velocity method, in horizontal and inclined rectangular [14] cross-sectional duct. From the results, they found that radiations have significant influence on the heat transfer and helps in reducing effect of thermal buoyancy. Zheng et al. [15] used P1 radiations model to study the combined effect of convection and radiation in helical pipes and they observed that, in fully developed region, flow and temperature fields were not influenced by the thermal radiations but enhanced total heat transfer. Yan et al. [16] numerically studied the influence of thermal radiations on convective heat transfer for a gray fluid through the vertical square duct by using vorticity–velocity method for solving Navier–Stokes equations and discrete ordinates method for solving radiation heat transfer equations.

Even though many research work, both experimental and numerical, have already been done to study the forced convection heat transfer through non-circular cross-sectional ducts for laminar and turbulent flow. In most of studies, constant heat flux is applied on all sides of the duct. In the present study, an attempt is made to analyse the effect of different wall flux configurations on the heat transfer and the friction factor under the influence of different Reynolds number values ranging from 100 to 2000. The analysis was carried out numerically using computational fluid dynamics (CFD) for a laminar flow and effect of radiations is also considered. The study was divided in two steps, initially, numerical simulation for equilateral duct with constant heat flux on all three walls was performed and results were compared with the available results in the open literature to validate the mathematical modelling. Afterwards, the validated methodology was employed for predicting the effect of the different wall heat flux configurations on the Nusselt number and friction factor, in laminar flow conditions.

Mathematical Modelling and Assumptions

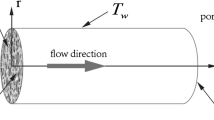
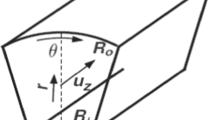
The computational domain of equilateral triangular duct with side length ‘a’ and height ‘h’ is shown in Fig. 1a and geometric parameters are given in Table 1. Three different combinations of constant heat flux boundary conditions were investigated in the present study; in Case 1, all the walls of the triangular duct were at constant heat flux boundary conditions; in Case 2, constant heat flux condition exists for right and left wall and the bottom wall is insulated, and in Case 3; only bottom wall with constant heat flux other two insulated. The schematic diagram of problem is shown in Fig. 1b. The unstructured grid were generated within the computational domain by using multi-block technique [3] and shown in Fig. 2. For all the three cases, variation of Nusselt number and friction factor for different configurations were analysed.

Fig. 1
figure 1

a Equilateral triangular duct cross-section. b Schematic detail of different configurations of conducting and adiabatic wall configuration

Full size image
Table 1 Geometry parameters
Full size table
Fig. 2
figure 2

Computational domain of the equilateral triangular duct for inlet triangular cross-section where; B1, B2, and B3 represent the Block 1, Block 2 and Block 3 respectively

Full size image

Assumptions:

Following are the assumptions for the present study:

  1. 1.

    Fluid is incompressible and flow is steady.

  2. 2.

    Fluid properties are constant through the duct.

  3. 3.

    Fluid under study is air and it enters the computational domain at ambient conditions.

  4. 4.

    The material properties of aluminium and wood are considered for conducting and adiabatic walls, respectively.

  5. 5.

    The flow is developed by hydrodyanmically and thermally developing condition coexists with developed conditions based on Reynolds number value.

  6. 6.

    No-slip conditions are valid at interface of fluid and wall.

Governing Equations

The governing equations for a steady, laminar flow through the triangular cross-sectional duct could be written in Cartesian coordinates system as:

Continuity equation:

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 $$
(1)

x-direction momentum equation:

$$ \left[ {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z}} \right] = - \frac{1}{\rho }\frac{\partial p}{\partial x} + \nu \left[ {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right] $$
(2)

y-direction momentum equation:

$$ \left[ {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z}} \right] = - \frac{1}{\rho }\frac{\partial p}{\partial y} + \nu \left[ {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{{\partial^{2} v}}{{\partial z^{2} }}} \right] $$
(3)

z-direction momentum equation:

$$ \left[ {u\frac{\partial w}{\partial x} + v\frac{\partial w}{\partial y} + w\frac{\partial w}{\partial z}} \right] = - \frac{1}{\rho }\frac{\partial p}{\partial z} + \nu \left[ {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right] $$
(4)

These momentum Eqs. (2) to (4) are the results from Newton’s second law of motions in x, y and z directions, respectively.

Energy equation:

$$ \left[ {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + w\frac{\partial T}{\partial z}} \right] = \alpha \left[ {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right] - \frac{1}{{\rho C_{p} }} \left[ {\frac{{\partial q_{r} }}{\partial x} + \frac{{\partial q_{r} }}{\partial y} + \frac{{\partial q_{r} }}{\partial z}} \right] $$
(5)

where p, T, \( \nu \),\( \alpha , \) \( q_{r} \) are the pressure, temperature, kinematic viscosity, density, thermal conductivity, thermal radiations and u, v, and w are the velocity components in x, y, and z directions, respectively.

The transport equation for radiation model is a function of incident radiations and diffusion coefficient and mathematically given as:

$$ \frac{1}{{\tau_{0} }} \frac{dI}{dS} + I = \frac{{(1 - \omega_{0} )}}{\pi }\Theta ^{4} + \frac{{\upomega_{0} }}{{4\uppi}}\mathop \smallint \limits_{{4\uppi}}^{.} {\text{I d}}\Omega $$
(6)

and radiative heat flux is calculated by using the incidence radiations which finally get added into the energy equation as heat source because of radiations [17].

$$ \left[ {\frac{{\partial q_{r} }}{\partial x} + \frac{{\partial q_{r} }}{\partial y} + \frac{{\partial q_{r} }}{\partial z}} \right] + 4\alpha \sigma T^{4} = - \alpha G $$
(7)

Calculation of Local and Average Nusselt Number

Under constant heat flux boundary conditions, constant amount of heat is applied per unit area of the equilateral duct. As air flows through the duct, it carries some amount of heat from walls and it results in increase in mean temperature of air. The convective heat transfer is calculated in terms of non-dimensional Nusselt number.

Because of constant heat flux on the wall, the heat carried by the working medium (air) is given by:

$$ Q = mc_{p} (T_{fo} - T_{fi} ) $$
(8)

where m is the mass flow rate of air, \( c_{p} \) is the specific heat at constant pressure of air, \( T_{fo} \) is the temperature of fluid at the outlet of duct, and \( T_{fi} \) is the atmospheric air temperature which is entering the duct (assumed to be 300 K).

The convective heat transfer at the triangular duct wall is;

$$ Q = \bar{h}A_{s} (T_{w} - T_{m} ) $$
(9)

where Q is the heat carried by the air, \( \bar{h} \) is the local heat transfer coefficient, \( A_{s} \) is surface area of the duct and, \( T_{w} \) and \( T_{m} \) are wall and mean temperature along the direction of flow.

Local Nusselt number is defined as:

$$ Nu_{l} = \frac{{\bar{h}}}{k}* D_{h} $$
(10)

where \( \bar{h} \) is local heat transfer coefficient, k is the thermal conductivity of the medium and \( D_{h} \) is the hydraulic diameter of the equilateral triangular duct.

Mean/Average Nusselt number is

$$ Nu_{m} = \frac{1}{x}\int_{0}^{x} {Nu_{x} dx} . $$
(11)

The friction factor can be calculated by:

$$ f = \frac{\Delta P}{L}*\frac{2\rho }{{4\dot{m}^{2} }}*D_{h} $$
(12)

Another parameter, mean/bulk temperature is also considered in the study. The mean/bulk temperature is defined as the ratio of rate of flow of energy through a cross section and rate of flow of heat-capacity through a cross-section and mathematically expressed as:

$$ T_{m} = \frac{{\mathop {\iint }\nolimits \rho uc_{p} TdA}}{{\mathop {\iint }\nolimits \rho uc_{p} dA}} $$
(13)

Solution Procedure

Finite volume approach is used for the analysis with the help of ANSYS Fluent software. The governing Eqs. (1) to (7) were employed to non-staggered grid and solved using the SIMPLE algorithm [18]. Equations were discretized by second order unwind scheme. Geometric complexibilities are handled with the help of multi-blocking technique. For predicting accurate results near the wall, refined grids are ensured increasing exponentially from the wall to the centre. A convergence criterion for energy, momentum and radiation equations is set to be of order of 10e−06.

Boundary Conditions

Following boundary conditions are employed for the fluid flow through the duct;

  • Inlet: Fluid is flowing through the duct with constant velocity and at atmospheric temperature.

  • Outlet: Pressure at outlet is specified as the outlet boundary condition with constant pressure of \( 1.013 \times 10^{5} {\text{Pa}} \)

  • Walls: Constant heat flux of 1000 W m2.

The radiation is modeled by using P1 model which is available in Fluent software.

The properties of the working air at 300 K shown in Table 2.

Table 2 Operating conditions of air [19]
Full size table

Grid Independence Test

Grid independence test has been done for air outlet temperature and pressure drop by varying the number of grids points from 20 to 35 along y, z direction with constant number of grid points of 500 were considered along the direction of flow i.e., x direction. It was also ensured that the computational domain fit better into the physical domain. For different set of grid points, the values of air outlet temperature and pressure drop are shown in the Table 3. Based on the grid independent test, 25 × 25 grid point arrangement was used for the analysis.

Table 3 Grid independence study at Reynolds number 1000
Full size table

Validation

Laminar convective heat transfer for different configuration of constant wall heat flux wall to air in the equilateral triangular cross-sectional duct was studied under the laminar flow. The numerical simulations are carried out with all the walls at constant heat flux and the results are validated with the reported work. Table 4, shows comparison of the Nusselt number and (f × Re) value with the R. K. Shah’s results [1]. The predicted Nusselt number and f × Re values shown are close match with Shah [1]. The deviation between predicted and experimental results for Nusselt number and f × Re is less than 5 %. Hence, developed numerical methodology is found valid for analysing convective heat transfer in different configurations of constant heat flux wall.

Table 4 Comparision of average Nusselt number and friction factor
Full size table

Results and Discussion

The forced convective heat transfer in an equilateral triangular duct with different combination of heat flux boundary conditions were numerically studied using finite volume method.

Mean/Bulk Temperature

The mean/bulk temperature is defined as the ratio of rate of flow of energy through a cross-section and rate of flow of heat-capacity through a cross-section (Eq. 13). It is a key parameter that signifies the rate of heat transfer as seen from Eq. (10). The variation of bulk temperature with the rise of Reynolds number is shown in Fig. 3 for different cases. It was observed from the figure that constant wall heat flux boundary condition has great influence on bulk temperature and its value was observed increasing with the Reynolds number from 100 to 2000. The bulk temperature has higher values in case of low Reynolds number because of the fact that air gets more time to extract heat from the heated constant flux wall as compared to higher Reynolds number values (Fig. 4).

Fig. 3
figure 3

3D view of computational domain for the geometry

Full size image
Fig. 4
figure 4

a Bulk temperature variation long the flow direction for Case 1. b Bulk temperature variation long the flow direction for Case 2. c Bulk temperature variation long the flow direction for Case 3

Full size image

Table 5, shows the value of average bulk temperature and pressure drop for different Cases. The maximum value of average bulk temperature and pressure drop was highlighted. Maximum value of bulk temperature was observed for Case 1 because of uniform heating of air from all the three sides of the equilateral triangular duct and it was noted that, with the decrease of number of heat conducting walls, the value of average bulk temperature gets decreased. As the number of walls with constant heat flux decreases, the value of average bulk temperature also decreases. The minimum value of bulk temperature was observed for Case 3, because of only single conducting wall. Moreover, Reynolds number was also a key parameter to decide the value of average bulk temperature. Lower the Reynolds number higher the average bulk temperature in the duct. The temperature contours at the outlet of the duct are shown in Figs. 5, 6 and 7, for different Reynolds number value. It is concluded that the mean/bulk temperature is a function of both Reynolds number and the number of heat conducting walls.

Table 5 Bulk temperature variation and Pressure drop for different Reynolds number value
Full size table
Fig. 5
figure 5

a Temperature contour at the outlet of duct for Case 1 (Re = 100). b Temperature contour at the outlet of duct for Case 1 (Re = 500). c Temperature contour at the outlet of duct for Case 1 (Re = 1000). d Temperature contour at the outlet of duct for Case 1 (Re = 1500). e Temperature contour at the outlet of duct for Case 1 (Re = 2000)

Full size image
Fig. 6
figure 6

a Temperature contour at the outlet of duct for Case 2 (Re = 100). b Temperature contour at the outlet of duct for Case 2 (Re = 500). c Temperature contour at the outlet of duct for Case 2 (Re = 1000). d Temperature contour at the outlet of duct for Case 2 (Re = 1500). e Temperature contour at the outlet of duct for Case 2 (Re = 2000)

Full size image
Fig. 7
figure 7

a Temperature contour at the outlet of duct for Case 3 (Re = 100). b Temperature contour at the outlet of duct for Case 3 (Re = 500). c Temperature contour at the outlet of duct for Case 3 (Re = 1000). d Temperature contour at the outlet of duct for Case 3 (Re = 1500). e Temperature contour at the outlet of duct for Case 3 (Re = 2000)

Full size image

Nusselt Number and Friction Factor

Nusselt number is a dimensionless number which measures the convective heat transfer rate on the walls of the duct. The Nusselt number variations under different Reynolds number were calculated and are shown in Table 6. The Nusselt number is found to be increasing with Reynolds number because of the fact that as Reynolds number increases, mass flow rate of the air through the duct increases and larger amount of heat was carried by the air while it flows through the duct. Although, the average outlet temperature of the air leaving the duct, falls with the rise of Reynolds number because flowing air lasted for lesser time in the duct. It is quite interesting to see from table that Nusselt number found to be almost similar in all the configurations regardless of number of conducting and adiabatic walls. This means the value of Nusselt number does not depend on the number of heating and adiabatic walls and constant value of Nusselt number is observed in all cases whether three wall conducting or two or one. However, with more walls conducting the net rate of heat transfer increases resulting in higher bulk temperature.

Table 6 Average Nusselt number and friction factor values for different configurations
Full size table

The friction factor is measured in order to estimate external power (pumping power) which is required to pump fluid through the duct. From Table 6, it is observed that friction factor has higher value for lower Reynolds number and it decreases with the increase of Reynolds number. The friction factor values are not influenced by conducting and adiabatic walls configurations. Such that, friction factor has constant values in all the cases.

Conclusions

A numerical study was carried out to analyse forced convective heat transfer from the constant heat fluxed walls to air flowing under laminar conditions through the equilateral cross-sectional triangular duct. Three different cases were taken into consideration. The effect of different configurations of constant heat flux boundary condition on mean temperature, local heat transfer coefficient and Nusselt number was examined. The following conclusions were drawn from the study:

  1. 1.

    Mean/Bulk temperature was found to be a function of both Reynolds number and the configuration of constant wall heat flux. The maximum mean bulk temperature is observed in Case 1 (all conducting walls), whereas, minimum mean bulk temperature is calculated in third configuration (only bottom wall is conducting).

  2. 2.

    The pressure drop is influenced by the Reynolds number and wall heat flux configuration does not affect it significantly. Such that, constant value of pressure drop is observed in all cases. Similarly, friction factor is also observed constant in all studied configurations.

  3. 3.

    The value of Nusselt number increases with the increase of the Reynolds number from 100 to 2000 but it is surprising to see that in all cases almost similar Nusselt number is observed.