1 Introduction

Devices with micro-geometry have been finding a wide range of work interest in recent years by researchers. The fact that the heat transfer mechanism that occurs in micrometer-sized devices differs from the conventional heat transfer reveals serious problems that must be resolved by researchers. The high heat fluxes that occur in these systems cause serious problems to design of micro electro-mechanical (MEM) systems in terms of heat transfer. As seen in the literature, the difficulties of conducting experimental studies on this field have led researchers to work theoretically. Despite that, these theoretical works make a serious infrastructure for the design of micro electromechanical systems. The problem is solved here numerically by developing a new solution code in Delphi that is based on Patankar’s [1] control volume method.

In systems with micro-geometry, fluid motion and heat transfer differs from macro systems. Therefore, the approach to be used in the analysis of the system differs according to the type of fluid and dimensions of geometry. In the case of micro-systems where the fluid is gas phase, the size of the system is comparable to the intermolecular distance of the fluid and this is called Knudsen number (Kn). With an increase in Kn, rarefaction effect weakens the momentum and energy transfer at the interface. Knudsen based flow regimes are seen in table 1.

Table 1 Knudsen based flow regimes [2].
Full size table

Another issue that needs to be considered in the analysis of micro systems is the axial conduction and viscous effects. The thickness to diameter ratio of the pipe is much larger than that of the conventional pipes, which also increases the influence of the axial conduction in the analysis of such systems. So the analysis in micro pipes should certainly examine the effect of wall axial conduction especially on low peclet numbers [3,4,5]. The very small flow area in the micro-piping causes the velocity gradient in the fluid to be large, thus causing the viscous effects to become more important for this kind of analysis.

Gas slip flow in micro geometries and heat transfer analyses are studied intensively in the recent years [6,7,8]. Various studies examining the rarefied gas flow and conjugate heat transfer in mini and micro dimensions in the literature can be summarized as follows.:

Le and Roohi [9] asymptotically and numerically examined the conjugate heat transfer with rarefied gas flow in their work. They stated that Navier-Stokes-Fourier simulation results can be compatible with the Burnett data at \( n = 0.1 \) . Kushwaha and Sahu [10] investigated the second order slip boundary conditions in a micro pipe in steady state. They indicated that the difference of Nu between continuum flow with slip flow models are nearly 35%. Dongari and Agrawal [11] have solved the slip flow analytically for a long microchannel with slip boundary condition and in their runs they showed that obtained Reynolds numbers are compatibile with the slip models in the literature. Xiao et al [12] have investigated the second order slip boundary conditions to solve for both momentum and energy equation and they stated that the result is a 15% change in Nusselt number over the continuum flow. Aubert and Colin [13] put forward an analytical model for gas flows in rectangular micro-ducts to conside the effect of second order slip flow. They presented that second order terms become more affected that the cross section is square-shaped. Cercignani and Lorenzani [14] provided an analytical equal for the higher order slip velocity values. They evaluated that flow velocities are much compatible with near-continuum limits in their expression. Duan [15] has worked on a transient second order slip flow problem that differs from previous slip flow studies. In this work, obtained results are given by Po numbers for different parameters. Lelea and Cioabla [16] numerically investigated a conjugate heat transfer problem with viscous dissipation in micro-tubes. They compare the effects of viscous heating on Nu and Po numbers. Investigation of micro- geometry conjugate heat transfer problem with axial conduction is made by Rahimi and Mehryar [17] and with the similar problem in slip flow regime is made by Aziz and Niedbalski [18]. Barron et al [19, 20] conducted a numerical study to analyze the Graetz problem for various parameters in micro tube slip-flow regime. Kabar et al [21], conducted a study for axial conduction and gas rarefaction in a micro geometry of parallel plate flow. They showed that, for all values of thermal conductivity, axial conduction is negligible for their system. Beside these studies, extended Graetz problem solutions involving both axial fluid and wall conduction can also be seen in the Bilir [22, 23] and Bilir and Ateş [24]. And also, several works for mini and micro pipe flows in transient regime and conjugate heat transfer for different boundary conditions have been conducted extensively in the past [25,26,27,28,29,30,31].

In this study, a heat transfer problem with constant heat flux surface boundary condition is numerically solved for a micro pipe with the effects of axial conduction, fluid rarefaction, and viscous heating. According to the author’s knowledge, the heat and flow analysis has not been done before for showing the simultaneous effects of axial conduction, viscous heating, and rarefaction in micro pipes in transient regime. In order to make the analysis more realistic, quadratic equations are used for describing the slip flow. Such analysis must be taken into consideration in micro electro-mechanical systems during start-up, shut-down and change in operating conditions with high frequencies.

2 Problem description and analysis

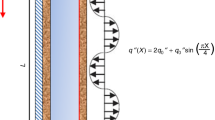
In this work, a circular pipe belongs to a micro-sized electro-mechanical system as given in figure 1 is investigated. The pipe has two infinite regions. At the beginning of the pipe, system temperature is \( T_{0} \). The gas flow is laminar and velocity profile is developed before the heated side. At the beginning of the time, a constant heat flux is applied to the outer pipe surface in the downstream region. The pipe is insulated at the upstream region. Thermal analysis was carried out to cover the whole system. It was considered that fluid and pipe-wall properties did not change for analysis.

Figure 1
figure 1

Micro-pipe geometry and boundary conditions.

Full size image

This kind of engineering problem according to shown micro-geometry and the noted boundaries, can be encountered in micro electro mechanical systems, that has constant heat flux conditions to be cooled.

The following assumptions are made for the analysis.

  • The flow is assumed to be laminar, and incompressible.

  • The flow is assumed to be hydrodynamically fully developed and thermally developing.

  • The thermal conductivity and thermal diffusitivity of the fluid are considered to be independent of temperature.

  • Body forces and heat transfer by radiation is neglected.

  • The continuum approach is coupled with the second order velocity slip and temperature jump conditions.

The temperature and velocity values of fluid molecules at the wall to fluid interface are different from those of the interface wall due to the decrease in momentum and energy transfer in rarefied gas flows. The temperature and velocity boundary conditions at the wall to fluid interface can be expressed by the second-order equations to make the analysis more realistic. These equations given below in Eqs. (1) and (2), respectively [10, 32, 33].

$$ u_{s} = - \frac{{2 - \sigma_{m} }}{{\sigma_{m} }}\left[ {\lambda \frac{\partial u}{\partial r} - \frac{{\lambda^{2} }}{2}\frac{{\partial^{2} u}}{{\partial r^{2} }}} \right] $$
(1)
$$ T_{s} - T_{w} = - \frac{{2 - \sigma_{T} }}{{\sigma_{T} }}\frac{2\gamma }{\Pr (\gamma + 1)}\left[ {\lambda \frac{\partial T}{\partial r} - \frac{{\lambda^{2} }}{2}\frac{{\partial^{2} T}}{{\partial r^{2} }}} \right] $$
(2)

Momentum (σm) and thermal (σT) accommodation coefficients vary between 0.87 and 0.99 relative to the fluid and wall material type. From the analysis, the accommodation coefficients are taken 1.0 with assumption that fluid to wall momentum and energy transfer are exact [2, 34].

Dimensionless velocity profiles can be obtained analytically by applying first and second order boundary conditions to the momentum equation [32, 33]:

$$ u' = \frac{{2(1 - (r/r_{wi} )^{2} ) + 8Kn}}{1 + 8Kn} $$
(3a)
$$ u' = \frac{{2(1 - (r/r_{wi} )^{2} ) + 8Kn - 8Kn^{2} }}{{1 + 8Kn - 8Kn^{2} }} $$
(3b)

The axial velocity values obtained according to Knudsen number by using Eq. (3a) for first order and Eq. (3b) for second order are given in table 2, and dimensionless velocity profiles for second order slip velocity are shown in figure 2. With the increase in rarefaction effect, the fluid’s slip velocity at the interface increases. However, the maximum velocity value in the pipe axis decreases. And the local velocity value is equal to the average velocity regardless of Knudsen at r′ = 0.7.

Table 2 Dimensionless axial velocities for different values of Kn (1st and 2nd order).
Full size table
Figure 2
figure 2

Velocity profiles according to Knudsen number.

Full size image

2.1 Governing equations and boundary conditions

The following dimensionless expressions are used to formulate the problem: \( T^{\prime} = \tfrac{{T - T_{0} }}{{T_{1} - T_{0} }} \), \( x^{\prime} = \tfrac{x}{{r_{wi} Pe}} \), \( r^{\prime} = \tfrac{r}{{r_{wi} }} \), \( d^{\prime} = \tfrac{d}{{r_{wi} }} \), \( \alpha_{wf} = \tfrac{{\alpha_{w} }}{{\alpha_{f} }} \), \( t^{\prime} = \tfrac{{t\alpha_{f} }}{{r_{wi}^{2} }} \), \( u' = \frac{u}{{u_{m} }} \), \( Pe = \text{Re} \Pr = \tfrac{{2r_{wi} u_{m} \rho_{f} c_{pf} }}{{k_{f} }} \), \( \Pr = \tfrac{{c_{{p_{f} }} \mu_{f} }}{{k_{f} }} \), \( Br = \frac{{\mu_{f} u_{m}^{2} }}{{k\left( {T_{1} - T_{0} } \right)}} \), \( Kn = \frac{\lambda }{D} = \frac{\lambda }{{2r_{wi} }} \)

The energy equation applicable in the wall region is as follows:

$$ \tfrac{1}{{\alpha_{wf} }}\tfrac{{\partial T^{\prime}_{w} }}{{\partial t^{\prime}}} = \tfrac{1}{{r^{\prime}}}\tfrac{\partial }{{\partial r^{\prime}}}\left( {r^{\prime}\tfrac{{\partial T^{\prime}_{w} }}{{\partial r^{\prime}}}} \right) + \tfrac{1}{{Pe^{2} }}\tfrac{{\partial^{2} T^{\prime}_{w} }}{{\partial x^{\prime 2} }} $$
(4a)

The boundary conditions for wall energy equations are as follows:

$$ {\text{At}}\;\;t^{\prime} = 0\quad T^{\prime}_{w} = 0; $$
(4b)
$$ {\text{At}}\;\;x^{\prime} = - \infty \quad T^{\prime}_{w} = 0; $$
(4c)
$$ {\text{At}}\;\;x^{\prime} = + \infty \quad \frac{{\partial T^{\prime}_{w} }}{{\partial x^{\prime}}} = 4\left( {1 + d^{\prime}} \right); $$
(4d)
$$ {\text{At}}\;\;r^{\prime} = 1\quad T^{\prime}_{wi} = T^{\prime}_{s} + 2\kappa Kn\left. {\frac{{\partial T^{\prime}}}{{\partial r^{\prime}}} - \kappa Kn^{2} \frac{{\partial^{2} T^{\prime}}}{{\partial r^{\prime 2} }}} \right)_{{r^{\prime} = 1}} ; $$
(4e)
$$ {\text{At}}\;\;r^{\prime} = 1 + d^{\prime},\quad x^{\prime} < 0\quad \frac{{\partial T^{\prime}_{w} }}{{\partial r^{\prime}}} = 0; $$
(4f)
$$ {\text{At}}\;\;r^{\prime} = 1 + d^{\prime},\quad x^{\prime} \ge 0\quad \frac{{\partial T^{\prime}_{w} }}{{\partial r^{\prime}}} = \frac{1}{{k_{wf} }}. $$
(4g)

The energy equation applicable in the fluid region is as follows:

$$ \tfrac{{\partial T^{\prime}_{f} }}{{\partial t^{\prime}}} + \frac{{\left( {1 - r^{\prime 2} + 4Kn - 4Kn^{2} } \right)}}{{1 + 8Kn - 8Kn^{2} }}\tfrac{{\partial T^{\prime}_{f} }}{{\partial x^{\prime}}} = \tfrac{1}{{r^{\prime}}}\tfrac{\partial }{{\partial r^{\prime}}}\left( {r^{\prime}\tfrac{{\partial T^{\prime}_{f} }}{{\partial r^{\prime}}}} \right) + \left( {\tfrac{1}{{Pe^{2} }}\tfrac{{\partial^{2} T^{\prime}_{f} }}{{\partial x^{\prime 2} }}} \right) + \frac{{16Br\left( {r^{\prime}} \right)^{2} }}{{\left( {1 + 8Kn - 8Kn^{2} } \right)^{2} }} $$
(5a)

The boundary conditions for fluid energy equations are as follows:

$$ {\text{At}}\;\;t^{\prime} = 0\quad T^{\prime}_{f} = 0; $$
(5b)
$$ {\text{At}}\;\;x^{\prime} = - \infty \quad T^{\prime}_{f} = 0; $$
(5c)
$$ {\text{At}}\;\;x^{\prime} = + \infty \quad \frac{{\partial T^{\prime}_{f} }}{{\partial x^{\prime}}} = 4\left( {1 + d^{\prime}} \right) $$
(5d)
$$ {\text{At}}\;\;r^{\prime} = 0\quad \frac{{\partial T^{\prime}_{f} }}{{\partial r^{\prime}}} = 0; $$
(5e)
$$ {\text{At}}\;\;r^{\prime} = 1\quad T^{\prime}_{s} = T^{\prime}_{wi} - 2\kappa Kn\left. {\frac{{\partial T^{\prime}}}{{\partial r^{\prime}}} + \kappa Kn^{2} \frac{{\partial^{2} T^{\prime}}}{{\partial r^{\prime 2} }}} \right)_{{r^{\prime} = 1}} . $$
(5f)

The other calculated thermal quantities can also be given in dimensionless form which are as follows:

$$ T^{\prime}_{b} = 4\int\limits_{0}^{1} {\frac{{(1 - r^{\prime 2} ) + 4Kn - 4Kn^{2} }}{{1 + 8Kn - 8Kn^{2} }}r^{\prime}T^{\prime}_{f} dr^{\prime}} ; $$
(6)
$$ q^{\prime}_{wi} = - \left( {\tfrac{{\partial T^{\prime}_{f} }}{{\partial r^{\prime}}}} \right)_{{r^{\prime} = 1}} ; $$
(7)
$$ Nu = \frac{{2q^{\prime}_{wi} }}{{T^{\prime}_{wi} - T^{\prime}_{b} }}. $$
(8)

2.2 Solution methodology

The wall and fluid energy equations discussed in the problem are numerically solved for suitable boundary conditions by finite difference method. Three different methods were used for discretizing the equations. These are; full implicit method, two-dimensional cylindrical system discretizing method that defined by Bilir [35], and central difference method. These discretizing methods used for time dependent, convection and conduction terms, respectively. An exemplary discretization process on fluid energy equation for a non-boundary grid point can be given as:

$$ a_{i,j} T^{\prime}_{i,j} = a_{i + 1,j} T^{\prime}_{i + 1,j} + a_{i - 1,j} T^{\prime}_{i - 1,j} + a_{i,j + 1} T^{\prime}_{i,j + 1} + a_{i,j - 1} T^{\prime}_{i,j - 1} + a_{i,j}^{0} T_{i,j}^{\prime 0} + b $$
(9a)

where;

$$ a_{i + 1,j} = \frac{{\left( {\frac{{r^{\prime}_{j} - r_{j}^{\prime 3} + 4Knr^{\prime}_{j} - 4Kn^{2} r^{\prime}_{j} }}{{1 + 8Kn - 8Kn^{2} }}} \right)}}{{\exp \left[ {\left( {\frac{{Pe^{2} \left( {1 - r_{j}^{\prime 2} + 4Kn - 4Kn^{2} } \right)}}{{1 + 8Kn - 8Kn^{2} }}} \right)(\delta x^{\prime})_{i + 1} } \right] - 1}}(\Delta r^{\prime})_{j} $$
(9b)
$$ a_{i - 1,j} = \left( {\frac{{r^{\prime}_{j} - r_{j}^{\prime 3} + 4Knr^{\prime}_{j} - 4Kn^{2} r^{\prime}_{j} }}{{1 + 8Kn - 8Kn^{2} }}} \right)\left[ {\frac{{\exp \left[ {\left( {\frac{{Pe^{2} \left( {1 - r_{j}^{\prime 2} + 4Kn - 4Kn^{2} } \right)}}{{1 + 8Kn - 8Kn^{2} }}} \right)(\delta x^{\prime})_{i - 1} } \right]}}{{\exp \left[ {\left( {\frac{{Pe^{2} \left( {1 - r_{j}^{\prime 2} + 4Kn - 4Kn^{2} } \right)}}{{1 + 8Kn - 8Kn^{2} }}} \right)(\delta x^{\prime})_{i - 1} } \right] - 1}}} \right](\Delta r^{\prime})_{j} $$
(9c)
$$ a_{i,j + 1} = \left( {\frac{{r^{\prime}_{j} }}{{(\delta r^{\prime})_{j + 1} }} + 0.5} \right)(\Delta x^{\prime})_{i} $$
(9d)
$$ a_{i,j - 1} = \left( {\frac{{r^{\prime}_{j} }}{{(\delta r^{\prime})_{j - 1} }} - 0.5} \right)(\Delta x^{\prime})_{i} $$
(9e)
$$ a_{i,j}^{0} = \tfrac{{r^{\prime}_{j} (\Delta x^{\prime})_{i} (\Delta r^{\prime})_{j} }}{{\Delta t^{\prime}}} $$
(9f)
$$ b = \frac{{16Br\left( {r^{\prime}} \right)_{j}^{3} }}{{\left( {1 + 8Kn - 8Kn} \right)^{2} }}(\Delta x^{\prime})_{i} (\Delta r^{\prime})_{j} $$
(9g)
$$ a_{i,j} = a_{i + 1,j} + a_{i - 1,j} + a_{i,j + 1} + a_{i,j - 1} + a_{i,j}^{0} . $$
(9h)

Gauss-Siedel iteration technique was used for the solution of discreted energy equations and figure 3 shows the solution algorithm of the program code.

Figure 3
figure 3

Solution algorithm of the program code.

Full size image

The temperatures at different time steps obtained by the point-by-point method of Patankar [1]. Due to the cylindrical pipe structure, the solution area is taken between the pipe surface and the axis.

2.3 Grid generation

Grid network structure was radial and axial formed to have a control volume of 16 and 40 for wall and fluid side, respectively and 56 control volume both up and down flow regions. Equal grid spacing used in radial direction of wall and fluid side taken as \( d^{\prime}/16 \) and \( 1/40 \), respectively. In the up and downstream regions, the starting grid spacing in the axial direction were taken as \( \Delta x^{\prime} = 0.001 \) and the grid size were stretched 1.4241 times as before to obtain a more precise solution. Unequal time steps were used during the iterations and the first time step was taken as \( \Delta t^{\prime} = 0.0001 \) and each new time step is increased by 10% compared to the previous one. Convergence limit was taken as \( 10^{ - 7} \) and when the number of iterations drops below two, it is assumed that the system has reached the steady state at that time.

2.4 Grid independency analysis

Grid independency analysis was realized to show that the numerical solution is independent of the grid structure. In the analysis, tests were performed for three different grid sizes: 56x28, 112x56 and 224x112. The comparison is made for bulk temperatures, \( T_{b}^{'} \), and heat flux, \( q_{wi}^{'} \) at \( x^{\prime} = 0 \) for steady heat transfer. The parameter values used in the analysis are taken as to reflect the rarefaction, axial conduction and viscous heating from defined problem. The results from the grid independence test are shown in table 3. When the results were examined, it was decided that the 112x56 grid structure was convenient in terms of stability and solution time.

Table 3 Effect of grid size on \( T_{b}^{'} \) and \( q_{wi}^{'} \).
Full size table

To see the temporal effects, 5%, 10%, and 20% time step increments are used for test runs. The runs were carried out for the same parameter values as before and the results are given in table 4.

Table 4 Effects of temporal discretization on \( T_{b}^{'} \) and \( q_{wi}^{'} \).
Full size table

As seen in the table, the difference between the calculated \( T^{\prime}_{b} \) and \( q^{\prime}_{wi} \) are almost zero. According to these results, 10% time step increment was sufficient for the stability and duration of the solution.

3 Results and discussion

The effects of four different parameters have been investigated for the numerical analysis of micro-pipe flow. In order to see the effect of each parameter in the analyses, the other parameters are fixed, and the effect parameter value is changed according to the physical conditions. In case of conjugate heat transfer problems, it is better to give the results in terms of the interfacial heat fluxes [36].

To verify the numerical solution, for slip flow, and under viscous effects, \( (Br = 0.01) \), steady state Nusselt numbers were compared with the similar study of Kushwaha and Sahu [10] in the literature and given in table 5 and plot in figure 4. The table is made for first and second order slip boundary conditions.

Table 5 Comparison of the steady Nusselt number values with the Kushwaha and Sahu [10].
Full size table
Figure 4
figure 4

Comparison of Nusselt numbers with the Kushwaha and Sahu [10].

Full size image

From figure 4, it is seen that the fully developed Nusselt numbers are highly compatible with the work of Kushwaha and Sahu [10] and the maximum deviation is 1.45 % for the obtained Nusselt number with reference results.

Figure 5a, b and c indicate the variation of the interfacial heat fluxes with the Peclet number at three different time steps. Parameters other than the Peclet number are kept constant for this runs. From figures, decreasing the Peclet number causes to increase of fluid axial conduction and the heat diffuses to the insulated side, so that the heat flux curves extend backward. As the effect of convection decreases with the increase of axial conduction, the thermal development in the downstream region takes place at a longer axial distance. As the number of Peclet increases, the peak values of the interfacial heat flux curves increase. This is due to the higher convection heat transfer than axial conduction. As shown in figure 5c, in steady state, for low Peclet numbers, the system reaches to the steady state takes a long time. However, for Peclet greater then 10, the system reaches to the steady decrease and duration of reaching the steady state does not change due to the decreasing of axial conduction.

Figure 5
figure 5

The interfacial heat flux values according to the Peclet number: (a) t′ = 2.99, (b) t′ = 76.61, (c) steady state.

Full size image

The interfacial heat flux varies to the Knudsen numbers are given in figure 6a, b and c for three different time steps. In these runs all the parameters without Knudsen are kept constant again. From figures, it is shown that at all-time steps, ıncreasing Knudsen number brings the weakening effect to the heat fluxes. This is due to the weakening of the fluid rarefaction (“\( \lambda \)” increase in molecular free path), that is caused due to the weakening of the heat transfer mechanism at the molecular level.

Figure 6
figure 6

The interfacial heat flux values according to the Knudsen number: (a) t′ = 2.99, (b) t′ = 76.61, (c) steady state.

Full size image

The heat flux profiles in the steady state being formed and the interfacial heat flux peaked at Kn = 0.001 (nearly continuum flow). In the steady state, according to Knudsen value (molecular rarefaction) the heat flux values changed but remained constant at a certain value for all Knudsen numbers in the axial direction due to the thermally developed flow.

To see the time-dependent viscous effects, values of interfacial heat fluxes due to the Brinkman number for three time steps are presented in figure 7a, b and c. In the first and second time steps, at low Brinkman numbers, the wall temperature increases more then fluid in the insulated side due to the axial conduction, and the heat transfers from wall to the fluid. With the increase of the Brinkman number (viscous heating), the temperature of the fluid increases and the interfacial heat flux is decreased. Viscous heating can be seen for both insulated and constant heat flux pipe area.

Figure 7
figure 7

The interfacial heat flux values according to the Brinkman number: (a) t′ = 2.99, (b) t′ = 76.61, (c) steady state.

Full size image

The effect of viscous heating is decreased when the system reached to the steady state and the total time of reaching to steady state is nearly the same. The heat fluxes from wall to the fluid is a bit lower for high Brinkman numbers.

Figure 8a, b and c are plotted to show the effects of micro-pipe thickness. The interfacial heat flux values according to the wall thickness, for three time steps are plotted, where the all parameters except wall thickness are kept constant. When the interim time steps are examined, the thermal resistance and the thermal capacity for \( d^{\prime} = 0.2 \) are low, hereby the heat flux values increase very rapidly, so that the axial conduction becomes dominant in the insulated side of the pipe. For this reason, reverse heat flux (fluid to wall) in the insulated side is much more effective in thin-walled pipes and ducts. For \( d^{\prime} \ge 0.5 \), this effect is weakened and as the wall thickness increases due to the micro pipe geometry, the wall axial conduction becomes dominant and the heat transfers from wall to fluid in the insulated side. Looking at the constant heat flux side of the pipe, the peak values of the interfacial heat fluxes at the thin wall thickness are higher for both time steps.

Figure 8
figure 8

The interfacial heat flux values according to the wall thickness ratio: (a) t′ = 2.99, (b) t′ = 76.61 and (c) steady state.

Full size image

At steady state, peak heat flux is seen for the thickness of \( d^{\prime} = 1.1 \) unlike transient time steps, and this situation is explained by the axial conduction in positive infinite direction of the pipe. And also to reach the steady state gets more time in thick walled pipes like micro pipe geometry (\( d^{\prime} = 1.1 \)).

4 Conclusions

The transient regime wall to fluid conjugation heat transfer problem for a sample micro-pipe in accordance with the micro-geometry structure in electro-mechanical systems is investigated by considering the viscous heating effects, axial conduction, and second order rarefied gas flow conditions on the wall-fluid interface. The effects of four defining dimensionless parameters on the interfacial heat flux are numerically investigated.

The conclusions drawn from the results can be summarized as follows.

  • For micro pipes with low Peclet flows, axial heat conduction is dominant on the insulated side due to wall thickness. As the Peclet decreases, fluid and wall axial conduction is effective in transient regimes during start-up, shut-down of the micro system. Because of backward heat transfer, axial heat conduction must be taken into account for micro pipe design.

  • With high Knudsen numbers, rarefaction effect from gas molecules has affected more heat transfer because of the weakening molecular heat transfer mechanism. With high rarefaction, the molecules at the interface cannot perform the momentum and energy transfer for desired extent. So, in micro-pipes, the rarefaction effect must certainly be included in the analysis for the gas phase fluids like air.

  • Fluid temperatures increase with increasing of Brinkman number by the viscous heating that occurs in the fluid and the interfacial heat flux is decreased. This effect is more dominant for transient time steps. This can be explained by heated gas molecules due to fluid friction.

  • Increase in wall thickness caused the decreasing on interfacial heat fluxes in transient time steps. On the other hand, in steady state interfacial heat flux is getting increased with the increase of thickness, because of the axial conduction through the positive infinite length wall temperature gets higher. This makes the wall thickness as an important parameter in designs.

  • The obtained results for second order rarefied gas flow conditions, we have to get more realistic analysis to have practical application of microscale electro-mechanical systems such as micro pumps, fuel cells, micro-chips. For example, if the Kn = 0.001 for fluid of air the diameter is being 30 micrometer and the fluid velocity for Pe = 5 is being 4.11 m/s. This combination of actual physical dimension and velocities that may correspond to the range of various modeling parameters.

  • Microchannel dimensions are of great importance as the systems are very small in size while micro-electromechanical systems are designed to cool the electronic systems, especially constant surface heat flux. In order to provide the desired heat flux, to reveal the rarefaction effect of the fluid and considering attenuating of the heat flux requires that the channel to be 2–3 times larger for dimensioning of micro geometries.