Introduction

The cantilever beams (members) under small deflection are used as structural members. These members when subjected to a concentrated tip load undergo a large deflection beyond a certain load limit. They undergo large deflection in applications where they are used as linear or torsional springs in machines, mechanisms, vehicles, instruments, etc. Plate springs in the form of cantilever undergoing large deflections are finding a wide application in general and precision engineering. In many systems, it eliminates the use of complicated mechanism for operation. Common examples are files and folder locking mechanism, window closing mechanism in fuel port of cars, hatch door mechanism in flight vehicles, etc. In all these mechanisms, a simple plate spring satisfies the functionality and eliminates the need for a torsional spring. Furthermore, cantilever plates/beams used in sports and recreations such as pole vault, board jumps and fishing rod are subjected to large deflections. There are numerous examples of such cases which call for study of large deflection behavior of cantilever beams for engineering design.

The classic example in day-to-day non-engineering application for large deflection is the loaded fishing rod. In its undeflected state, when the rod is lightly loaded, a small amount of force will cause a certain downward deflection at the tip. When the rod is heavily loaded however, a much larger amount of force will be needed to cause the tip to deflect downward by the same amount. This change in the magnitude of force required to achieve the same change in displacement implies that there is no linear relationship between force and displacement at the tip. In a cantilever undergoing small deformation, doubling the force results in doubling the displacement. In the fishing rod case, there exists a nonlinear system, i.e., a large deflection. One might need to triple the force to double the displacement, depending on how much the rod is loaded relative to its size and other properties [1, 2]. Therefore, in cantilever beams undergoing large deformation, one can observe an increase in stiffness (stress-stiffening) of the beam with an increase in geometric nonlinearity caused by progress of large deflection.

Under this large deflection, the geometrically linear or small deflection theory predicts unrealistic results because the predicted tip deflection of the member may exceed its length. In small deflection theory, the transverse (or vertical) deflection of the tip of the cantilever member is linear and is significant whereas the longitudinal (or horizontal) deflection of the tip is negligible. On the other hand, large deflection analysis predicts realistic and a nonlinear transverse and longitudinal deflections. Predicting the behavior of this cantilever member under small deflection is well established using small deflection theory of structural mechanics where certain assumptions are made in Euler–Bernoulli flexural equations and higher-order terms are neglected. In large deflections, the higher-order terms cannot be neglected. Few mathematical solutions exist for large deflections but are rather very complex for design applications.

Solutions for large deflection of an initially straight cantilever beam under a tip load have been studied theoretically by many researchers and reported in few literatures. Gross and Lehr [1] were the pioneers in providing an approximate theoretical solution for large deflection. Bishop and Drucker [2] provided a classical mathematical solution for the geometrically nonlinear large deflection of elastic cantilever beam under tip vertical load. This theoretical solution was subsequently extended by many researchers. Wang [3, 4] proposed numerical methods for analyzing nonlinear bending of beam under tip and uniformly distributed loads, respectively. Love [5], Frisch-Fay [6], Gere and Timoshenko [7] and Howell [8] considered similar case of the elastica problem in their famous text books. Other researchers such as Mattiasson [9], Bona and Zelenika [10], Su [11], Tari [12] and Tari et al. [13] provided closed-form solutions of similar problem derived in terms of elliptic integrals or Jacobi elliptical functions. Belendez et al. [14, 15] elaborated the mathematical solution of Bishop and Drucker [2] for ease of understanding and also studied experimentally. Zakharov [16] and Batista [17] gave analytical solutions for equilibrium configurations of a cantilever rod subjected to inclined force and moment acting on its free end. Kumar et al. [18] suggested genetic algorithm-based search strategies for direct numerical solution of governing differential equation and applied the principle of stationarity of the energy functional in the equilibrium state. Dado and Al-Sadder [19] developed an approach that approximates the angle of rotation by a polynomial function and applied this method effectively for complex load on non-prismatic beam with very large deflection. Shvartsman [20] studied the large deflections of a cantilever beam subjected to a follower force, and Mutyalarao et al. [21] studied the uniqueness of this large deflection under tip rotational load.

Rahman et al. [22] carried out nonlinear geometric analysis of parabolic leaf spring. Banerjee et al. [23] proposed nonlinear shooting and domain decomposition methods to determine the large deflection of a cantilever beam under arbitrary loading conditions. Chen [24] proposed an integral approach for large deflection study of a cantilever beam with complex load and varying beam properties. Roy and Saha [25] provided a nonlinear analysis of leaf springs of functionally graded material using variational method to find out deflection profiles. Large deflection of beams made of functionally graded material had been studied by different numerical approaches by Almeida et al. [26], Sitar et al. [27] and Kien [28]. Few others have studied the large deflection behavior of initially curved beams. He et al. [29] proposed a new perturbation method with two small parameters describing the effect of load and geometry of the problem, to solve nonlinear large deflection of initially curved beams under two different boundary conditions. Nallathambi et al. [30] and Shvartsman [31] studied large deflection of a curved cantilever beam under follower force, respectively, by direct numerical method and fourth-order R–K method. Ghuku and Saha [32] numerically solved the governing equations involving the geometric nonlinearity of initially curved cantilever beams and compared the results with experiments.

The differential equation governing the behavior of large deflection problem contains nonlinear term which is difficult to solve. Therefore, invariably all existing theoretical studies [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] involve a complex mathematical procedure with elliptic integral formulation for a closed-form solution to predict the behavior when subjected to geometrically nonlinear large deflection. These solutions are highly difficult to understand and apply for practical engineering problems. Remaining studies rely on different numerical approaches based on R–K method with shooting technique, finite difference method and finite element method (FEM) for solving the large deflection problems. But none have given any solution or an approach that can be adopted readily for engineering design. Further, the results of Bishop and Drucker [2] are only adopted in engineering design texts and handbooks (Wahl [33] and Shigley [34]) and are available in the form of graphs for ready use. This solution is limited to calculating the coordinates and the slope for the end point. But do not convey complete design guidelines, limitations and constraints. It is found that the cantilever members designed under these limited guidelines fail in large deflection when that exceeds elastic limit. Rather, they do not caution its applications based on strain limits. These complexities and limitations in existing solutions call for a thorough step-by-step theoretical and numerical analysis of cantilever members under large deflection that convey the practical applicability of both theoretical and numerical solutions.

In this paper, initially, the theoretical solution for large deflection is provided and compared with finite element analysis (FEA) based on beam and shell elements to assess the accuracy of element selection in FEA. The large deflections thus predicted are compared with corresponding predictions based on small deflection theory to show the extent of applicability of small deflection theory. Further, the effect of parametric variation in geometry and stiffness of beam on large deflection and resulting reactions are analyzed and discussed.

Research Objective

The objectives of this research on cantilever members are summarized below.

  • To provide a step-by-step theoretical solution for large deflection analysis;

  • To develop an appropriate FE model that matches well with theoretical predictions;

  • To compare the above predictions with well-established small deflection theory and assess its extent of applicability;

  • To study the effect of parametric variation in geometry and stiffness of cantilever member under large deflection; and

  • To provide a clear understanding for engineering design for large deflection.

Theoretical Solution for Large Deflection

Assumptions

  • The material of cantilever beam is linear elastic, homogeneous and isotropic;

  • Bending of the beam do not alter its length;

  • Although the deflection of cantilever beam is essentially a three-dimensional problem where an elastic stretching in one direction is accompanied by a compression in two other perpendicular directions due to Poisson’s effect, this effect can be ignored as the length of cantilever beam is more than the thickness of perpendicular cross section;

  • The beam is non-extensible, and strains remain small within elastic limit; and

  • Plane cross sections normal to neutral axis remain plane and perpendicular to the neutral axis before and after deformation.

Formulation of Governing Differential Equation

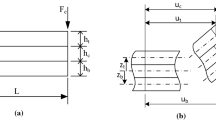
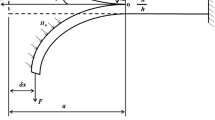
The differential equation governing the behavior of large deflection is derived based on the fundamental Euler–Bernoulli theory which states that the curvature is proportional to the bending moment. The small deflection theory neglects the square of the first derivative in the moment–curvature relation and provides no correction for the shortening of moment arm as the plate deflects. Further, under large finite loads, it gives deflection more than that of the plate length which is impossible. Therefore, in large deflection analysis, the square of the first derivative and hence correction factor for shortening of the moment arm must be considered. The nonlinear governing differential equation is solved step by step using elliptical integrals, i.e., by the use of change of variables. Let us consider a thin cantilever beam of length L with prismatic or rectangular cross section and constant modulus of elasticity E subjected to a vertical point load P at the free end. The small and large tip deflection of this beam is shown in Fig. 1a, b.

Fig. 1
figure 1

Cantilever beam under a tip load. a Small deflection. b Large deflection

Full size image

The Hooke’s law for the behavior of material is represented by the linear relation

$$ \sigma = \varepsilon E $$
(1)

where σ is the normal stress and ε is the normal strain.

Let ux and uy be the horizontal and vertical component of displacement at the loaded end, respectively. Taking the fixed end (x = 0, y = 0) as origin of Cartesian coordinate system, let (x, y) be the coordinate of an arbitrary point A, s be the arc length along the deflected beam between the fixed end and point A, and ϕ be the slope at point A.

The Euler–Bernoulli bending moment–curvature relationship for this beam is given by

$$ EI\frac{{{\text{d}}\phi }}{{{\text{d}}s}} = M $$
(2)

where M and \( \frac{{{\text{d}}\phi }}{{{\text{d}}s}} \) are the bending moment and curvature at any point in the beam, respectively, and I is the second moment of area of the cross section about the neutral axis.

Differentiating Eq. (2) with respect to s, we have

$$ EI\frac{{{\text{d}}^{2} \emptyset }}{{{\text{d}}s^{2} }} = \frac{{{\text{d}}M}}{{{\text{d}}s}} $$
(3)

where bending moment M at point A is

$$ M = P(L - u_{x} - x) $$
(4)

From the geometry of deflected beam shown in Fig. 1, for an infinitesimal arc length ds, we get

$$ \cos \emptyset = \frac{{{\text{d}}x}}{{{\text{d}}s}};\quad {\text{and}}\quad \sin \emptyset = \frac{{{\text{d}}y}}{{{\text{d}}s}} $$
(5)

Differentiating Eq. (4) w.r.t. s and substituting Eq. (5) into the resulting expression give the nonlinear differential equation that governs the deflection of this cantilever beam under tip load, as

$$ EI\frac{{{\text{d}}^{2} \emptyset }}{{{\text{d}}s^{2} }} + P\cos \emptyset = 0 $$
(6)

Solution for Slope and Deflections

Slope ϕ 0

Equation (6) is difficult to solve due to nonlinearity introduced by \( \cos \emptyset \) term. This needs to be simplified to an appropriate form that can be solved in closed form or by numerical methods. Therefore, multiplying Eq. (6) by \( \frac{{{\text{d}}\emptyset }}{{{\text{d}}s}} \) and rewriting the resulting expression give

$$ \frac{\text{d}}{{{\text{d}}s}}\left( {\frac{1}{2}EI\left( {\frac{{{\text{d}}\emptyset }}{{{\text{d}}s}}} \right)^{2} + P\sin \emptyset } \right) = 0 $$
(7)

The boundary conditions at the free end are

$$ \emptyset (x)_{x = L} = \emptyset_{0} ; \quad \left( {\frac{{{\text{d}}\emptyset }}{{{\text{d}}s}}} \right)_{x = L} = 0 $$
(8)

Integrating Eq. (7) w.r.t. s and substituting Eq. (8), we get

$$ \frac{ 1}{2}EI\left( {\frac{{{\text{d}}\emptyset }}{{{\text{d}}s}}} \right)^{2} + P\sin \emptyset = P\sin \emptyset_{0} $$
(9)

Rewriting Eq. (9) gives

$$ \frac{{{\text{d}}\emptyset }}{{{\text{d}}s}} = \sqrt {\frac{2P}{EI }} \left( {\sin \emptyset_{0} - \sin \emptyset } \right) ^{{\frac{1}{2}}} $$
(10)

Cross-multiplying the terms and integrating ds from 0 to s, we get the equation for the arc length of beam s as a function of slope ϕ as

$$ s = \sqrt {\frac{EI }{2P }} \int\limits_{0}^{\emptyset } {\left( {\frac{1}{{\sqrt {\sin \emptyset_{0} - \sin \emptyset } }}} \right)} {\text{d}}\emptyset $$
(11)

Cross-multiplying the terms in Eq. (10) and integrating ds from 0 to L (due to the inextensibility of the beam) provide

$$ \sqrt {\frac{2P}{EI }} \int\limits_{0}^{L} {{\text{d}}s} = \int\limits_{0}^{{\emptyset_{0} }} {\left( {\frac{1}{{\sqrt {\sin \emptyset_{0} - \sin \emptyset } }}} \right){\text{d}}\emptyset } $$
(12)

Equation (12) helps to find maximum slope ϕ0 at free end of the beam as a function of parameters P, L, E and I. In order to evaluate this elliptical integral on RHS, a non-dimensional load parameter α is introduced where \( \alpha^{2} = PL^{2} /EI \). This leads to

$$ \alpha = \frac{1}{\sqrt 2 }\int\limits_{0}^{{\emptyset_{0} }} {\left( {\frac{1}{{\sqrt {\sin \emptyset_{0} - \sin \emptyset } }}} \right){\text{d}}\emptyset } $$
(13)

Let

$$ 1 + \sin \emptyset = 2k^{2} \sin^{2} \theta $$
(14)

where k is given by

$$ k = \sqrt {\frac{{1 + \sin \emptyset_{0} }}{2}} ;\quad {\text{or}}\quad \sin \emptyset_{0} = 2k^{2} - 1 $$
(15)

In order to apply change of limits of integration between 0 and ϕ0 in Eq. (13) to θ1 and θ2, let us substitute ϕ = 0 and ϕ = ϕ0 in Eq. (14) to obtain θ = θ1 and θ = θ2, respectively, where θ1 and θ2 are given by

$$ \theta_{1} = \sin^{ - 1} \frac{1}{\sqrt 2 k};\quad {\text{and}}\quad \theta_{2} = \frac{\pi }{2} $$
(16)

Therefore, substituting Eqs. (14 and 16) into Eq. (13) gives

$$ \alpha = \frac{1}{\sqrt 2 }\int\limits_{0}^{{\emptyset_{0} }} {\left( {\frac{1}{{\sqrt {\sin \emptyset_{0} - \sin \emptyset } }}} \right) {\text{d}}\emptyset } = \int\limits_{{\theta_{1} }}^{{\frac{\pi }{2}}} {\frac{{{\text{d}}\theta }}{{\sqrt {\left( {1 - k^{2} \sin^{2} \theta } \right)} }}} $$
(17)

Vertical or Transverse Deflection u y

In order to arrive at a solution for the vertical deflection, let us start with Eq. (5), which gives

$$ \sin \emptyset = \frac{{{\text{d}}y}}{{{\text{d}}s}} = \frac{{{\text{d}}y}}{{{\text{d}}\emptyset }}\frac{{{\text{d}}\emptyset }}{{{\text{d}}s}} $$
(18)

Substituting Eqs. (10) into (18), we get

$$ \frac{{{\text{d}}y}}{{{\text{d}}\emptyset }}\sqrt {\frac{2P}{EI }} \left( {\sin \emptyset_{0} - \sin \emptyset } \right) ^{{\frac{1}{2}}} = \sin \emptyset $$
(19)

Cross-multiplying the terms in Eq. (19) and integrating dy from 0 to y provide

$$ u_{y} = \int\limits_{0}^{y} {{\text{d}}y} = \sqrt {\frac{EI}{ 2P }} \int\limits_{0}^{\emptyset } {\left( {\frac{\sin \emptyset }{{\sqrt {\sin \emptyset_{0} - \sin \emptyset } }}} \right) {\text{d}}\emptyset } $$
(20)

Simplifying Eq. (20), we further obtain

$$ \frac{{u_{y} }}{L} = \sqrt {\frac{EI}{{ 2PL^{2} }}} \int\limits_{0}^{{\emptyset_{0} }} {\left( {\frac{\sin \emptyset }{{\sqrt {\sin \emptyset_{0} - \sin \emptyset } }}} \right) {\text{d}}\emptyset } = \frac{1}{\sqrt 2 \alpha }\int\limits_{0}^{{\emptyset_{0} }} {\left( {\frac{\sin \emptyset }{{\sqrt {\sin \emptyset_{0} - \sin \emptyset } }}} \right) {\text{d}}\emptyset } $$
(21)

Using Eqs. (14 and 17) in Eq. (21), we get

$$ \frac{{u_{y} }}{L} = \frac{1}{\alpha }\int\limits_{{\theta_{1} }}^{{\frac{\pi }{2}}} {\frac{{\left( {2k^{2} \sin^{2} \theta - 1 } \right){\text{d}}\theta }}{{\sqrt {\left( {1 - k^{2} \sin^{2} \theta } \right)} }}} $$
(22)

Now RHS of Eq. (22) can be split up into complete and incomplete elliptical integrals of the first and second kinds. In the notation of Jahnke and Emde [35] and short tables of Peirce’s [36], this can be written as

$$ \frac{{u_{y} }}{L} = \frac{1}{\alpha }\left[ {F(k) - F(k, \theta_{1} ) - 2E(k) + 2E(k, \theta_{1} )} \right] $$
(23)

where

$$ F(k) = \int\limits_{0}^{{\frac{\pi }{2}}} {\frac{{{\text{d}}\theta }}{{\sqrt {\left( {1 - k^{2} \sin^{2} \theta } \right)} }}} $$
(24)
$$ F(k,\theta_{1} ) = \int\limits_{0}^{{\theta_{1} }} {\frac{{{\text{d}}\theta }}{{\sqrt {\left( {1 - k^{2} { \sin }^{2} \theta } \right)} }}} $$
(25)
$$ E(k) = \int\limits_{0}^{{\frac{\pi }{2}}} {\sqrt {\left( {1 - k^{2} { \sin }^{2} \theta } \right)} {\text{d}}\theta } $$
(26)
$$ E(k,\theta_{1} ) = \int\limits_{0}^{{\theta_{1} }} {\sqrt {\left( {1 - k^{2} \sin^{2} \theta } \right)} {\text{d}}\theta } $$
(27)

in which F(k) and F(k, θ1) are the complete and incomplete elliptical integrals of the first kind and E(k) and E(k, θ1) are the complete and incomplete elliptical integrals of the second kind. Further, it can be shown that

$$ F(k) - F(k, \theta_{1} ) = \int\limits_{{\theta_{1} }}^{{\frac{\pi }{2}}} {\frac{{{\text{d}}\theta }}{{\sqrt {\left( {1 - k^{2} \sin^{2} \theta } \right)} }} = \alpha } $$
(28)

Therefore, Eq. (23) becomes

$$ \frac{{u_{y} }}{L} = 1 - \frac{2}{\alpha }\left[ {E(k) - E(k, \theta_{1} )} \right] $$
(29)

From Eq. (15), it can be seen that the value of k is dependent on sin ϕ0 which in turn can range from 0 to 1. Slope at free end ϕ0 = 0 refers to fully unloaded beam and ϕ0 = π/2 refers to very large deflection indicating uy = L that is impractical. Therefore, k is bounded by the limits

$$ \frac{1}{\sqrt 2 } < k \le 1 $$
(30)

Therefore by assigning values of k from 0.71 to 1 in uniform steps and referring to short tables of Peirce’s [36] given in “Appendix 1,” we can readily obtain the corresponding values of elliptic integrals F(k), F(k, θ1), E(k) and E(k, θ1). Substituting these values in Eq. (29), we can get the complete variation of uy/L from 0 to 1 and hence the vertical deflection. The parameters used in computing the vertical deflection are given in “Appendix 2.”

Horizontal or Longitudinal Deflection u x

In order to arrive at a solution for the horizontal deflection, let us combine Eqs. (2, 4 and 10) and apply the boundary condition that at x = 0, ϕ = 0. This gives

$$ P\left( {L - u_{x} } \right) = EI\left. {\frac{{{\text{d}}\emptyset }}{{{\text{d}}s}}} \right|_{\emptyset = 0} = EI\sqrt {\frac{2P}{EI }} \left( {\sin \emptyset_{0} } \right)^{{\frac{1}{2}}} $$
(31)

This can be written as

$$ \frac{{L - u_{x} }}{L} = \frac{\sqrt 2 }{\alpha }\left( {\sin \emptyset_{0} } \right)^{{\frac{1}{2}}} $$
(32)

Substituting Eqs. (15) into (32) gives

$$ \frac{{L - u_{x} }}{L} = \frac{{\sqrt {2(2k^{2} - 1)} }}{\alpha } $$
(33)

Therefore by assigning values of k from 0.71 to 1 in uniform steps and referring to short tables of Peirce’s [36] given in “Appendix 1,” we can readily obtain the corresponding values α, and substituting these values in Eq. (33), we can get the complete variation of (L − ux)/L from 1 to 0 and hence the horizontal deflection. The parameters used in computing the horizontal deflection are given in “Appendix 2.”

Numerical Illustration: Horizontal and Vertical Deflections

Let us consider a thin cantilever steel plate with L = 100 mm, breadth b = 30 mm, thickness t = 1 mm and E = 200 GPa which gives I = bt3/12 = 2.5 mm4. The variation of α2 can be plotted against the variation of both vertical uy and horizontal ux deflections calculated from Eqs. (29 and 33) to get a complete representation of large deflections of an elastic cantilever beam as shown in Fig. 2. Further, the variation of α2 can be plotted against the variation of end slope ϕ0 calculated from Eq. (15) as shown in Fig. 3.

Fig. 2
figure 2

Comparison of deflections from (1) theory and (2) FEA with two element types (under both large and small deflection approaches)

Full size image
Fig. 3
figure 3

Comparison of end slope from (1) theory and (2) FEA with beam elements (under both large and small deflection approaches)

Full size image

Numerical Modeling and Analysis

The cantilever beam is further studied through numerical simulations using finite element analysis (FEA) in ANSYS 15.0 [37]. This FEA helps to finalize the type of modeling approach that predicts the behavior of large deflections agreeing closely with that of theoretical solutions given in Eqs. (29 and 33). The material and geometry described above in numerical illustration are adopted. This cantilever beam is modeled using Beam188 elements. This element has two nodes each having three displacements and three rotational degrees of freedom. An element size of 1 mm is adopted to model the beam after a mesh convergence study with varying element sizes. The left extreme node of the model is constrained in all degrees of freedom to represent a true cantilever. The beam is loaded with displacement control by applying a vertical tip deflection of uy = − 80 mm gradually in 1000 sub-steps. The FEA solver could provide a converged numerical solution only up to 80 mm of tip deflection. Initially, the problem is solved as small deformation in FEA, and the corresponding tip forces (reactions) are extracted. These results exactly matched with the results calculated using popular theoretical small deflection approach, i.e., P = 3EIuy/l3 and P = 2EI ϕ0/l2, as shown in Figs. 2 and 3.

Subsequently, the elements’ large deflection capability is turned on to initiate a nonlinear solution involving multiple passes through the solver using Newton–Raphson method instead of single pass needed for a linear problem. This takes care of an increase in stiffness (stress-stiffening) of the beam with an increase in nonlinearity caused by progress of large deflection. Further, it can be noted that turning on large deflection in FEA in ANSYS [37] activates four different behaviors associated with large deflection which includes large rotation, large strain, stress-stiffening and spin softening. In one way or another, all these behaviors involve change in stiffness due to deformation. In the beginning, the tip has less stiffness and even a small tip force would cause large deformation but as the plate deflects more and more, its stiffness increases, and therefore, to cause an additional small deformation, a large amount of force is needed. The small deflection theory or approach does not take care of this behavior, and stiffness remains same throughout the loading, hence does not provide an accurate result. In a linear or small deformation, doubling the force results in double the displacement, but in a nonlinear or large deformation, one needs to triple the force to double the displacement, depending on how much the beam is loaded relative to its size and other properties.

After completion of simulation with Beam188 elements, the problem is again solved by modeling the cantilever with shell elements using Shell181 in ANSYS 15.0 [37]. Shell181 is a four-node element with six degrees of freedom at each node: translations in the x, y and z directions, and rotations about the x, y and z-axes. It is well suited for linear, large rotation and large deformation nonlinear applications, and it accounts for stress-stiffening (follower effects) under load. This FEA with shell elements helps to identify the right type of element (among beam and shell elements) that best describes the large deflection behavior very closely with that predicted by theoretical results, i.e., from Eqs. (29 and 33). This shell element modeling in FEA is attempted because in many instances, plates having width equal to 30–50 times of their thickness are also used as beams in practical applications where spring back effects are needed. Although they are called as plates, their characteristics can easily be predicted appropriately using beam formulations and FEA with beam elements.

Comparison of Theory and FEA Solutions

The results of vertical and horizontal large deflections predicted from (1) large deflection theory (Eqs. 29 and 33), (2) FEA with beam elements and (3) FEA with shell elements are compared with each other in a single graph as shown in Fig. 2. Further, the predictions of small deflection approach from (1) FEA with beam elements and (2) small deflection theory are additionally plotted in same Fig. 2 to know the extent of their applicability in comparison with solutions of large deflection. Both small and large deflection results show the same trend that is initially the load varies linearly with displacement but after some time the curve of large deflection starts showing nonlinear behavior, and hence, large load is needed to additionally deform the beam even by a very little amount. It can be seen from Fig. 2 that the results of FEA with beam elements match very closely with the theoretical results as compared to that of shell elements. This reveals the suitability of beam elements in truly representing large deflection behavior of cantilever plates under transverse loadings or beams. It can be understood that this matching results are due to matching approaches in large deflection theory and beam element formulations of FEA. Similar match can be observed between the results of small deflection approach from FEA with beam elements and theory.

This comparison demonstrates that up to a limit of 0 < (uy/L) < − 0.275 for the present cantilever beam, the predictions from both small and large deflection approaches are one and the same and one can adopt the simple small deflection approach itself for design applications provided the induced longitudinal normal strains are within the elastic limit. Notwithstanding this conclusion, one needs to resort to large deflection approach only to get the horizontal deflection however small it may be within this limit, if needed, because small deflection approach cannot predict it. Even FEA predictions with shell elements provide accurate results that match FEA predictions with beam elements and theory only up to this limit of (uy/L) ≤ 0.275, beyond this limit shell element predictions drift from that of predictions from theory and FEA with beam elements as shown in Fig. 2. This limit for horizontal deflections predicted from FEA with shell elements to match with predictions from theory and FEA with beam elements is − 1.0 < 1 − (ux/L) < − 0.9.

Further, the results of end slope predicted from (1) large deflection theory (Eq. 15), (2) FEA with beam elements with large deflection turned on, (3) small deflection theory and (4) FEA with beam elements with small deflection are compared with each other in a single graph as shown in Fig. 3. The predictions and end slope behaviors shown in Fig. 3 are almost similar to that described above for vertical deflections in Fig. 2. This comparison demonstrates that up to a limit of 0 < (ϕ0) < 30° for the present cantilever plate, the predictions from both small and large deflection approaches are one and the same. The variation of elastic longitudinal strain with respect to (1) vertical (i.e., transverse) and horizontal (i.e., longitudinal) large deflections and (2) vertical deflection from small deflection approach is shown in Fig. 4. The elastic limit of 0.2% for typical engineering metallic materials is also shown in this figure. This comparison of elastic strains from small and large deflection approaches vis-à-vis typical elastic limit of common engineering metals reveals that one can readily adopt simplistic small deflection approach itself for engineering design involving metals because within this elastic design limit both results from small deflection and large deflection approaches are same, instead of resorting to complex large deflection approach.

Fig. 4
figure 4

Comparison of elastic strains with respect to large and small deflections against typical elastic limit for engineering metals

Full size image

Parametric Study and Discussion of Results

The parametric studies involving variation of beam lengths, elastic strains and flexural rigidity of cantilever beam and their effects on dependent parameters such as elastic strain, vertical deflection, tip load with respect to normalized vertical and horizontal deflections and length-to-thickness ratios are examined. This study brings out the effect of one important parameter on the other and is conducted by changing only one parameter in a given study. It provides a deeper understanding of the behavior of cantilever beam under large deflections, its characteristics and applications.

Variation of elastic strain with respect to normalized vertical large deflection for beam lengths varying from 100 to 300 mm is shown in Fig. 5. This figure also shows a typical elastic limit (permissible limit) for engineering metals. This demonstrates that the permissible vertical deflection increases with the increase in beam length at the elastic strain limit. Further, the induced maximum strain at the fixed end increases with the decrease in beam length for a given vertical deflection. Similar behavior is reflected in Fig. 6 wherein the increase in beam length-to-thickness ratio increases the vertical deflection for a given elastic strain value. Therefore, the increase in vertical deflection is directly proportional to induced elastic strain and L/t ratio.

Fig. 5
figure 5

Elastic strain versus normalized vertical large deflection for different beam lengths; and a typical elastic limit for engineering metals

Full size image
Fig. 6
figure 6

Vertical large deflection versus normalized length for different elastic strains

Full size image

Figure 7 shows the variation of bending stress with respect to normalized vertical large deflection for different beam lengths. This exhibits an increase in vertical deflection with the increase in beam length for a given induced bending stress at the fixed end of cantilever. This study also shows that the induced bending stress increases with the decrease in beam length for a given vertical deflection. The variation of tip load (i.e., tip reaction for an applied tip displacement) with respect to normalized vertical large deflection for different beam lengths is shown in Fig. 8. This demonstrates that the tip load increases with the increase in vertical deflection. This increase in tip load is inversely proportional to the beam length. The tip load required to achieve a given uy/L ratio in a shorter beam is more than that for a longer beam. This observation is due to the effect of stress-stiffening under large deformation. Similarly, the variation of tip load with respect to normalized horizontal large deflection for different beam lengths is shown in Fig. 9. The tip load is inversely proportional to the beam length for a given ux/L ratio, and the observations are very similar to that of vertical deflection shown in Fig. 8.

Fig. 7
figure 7

Bending stress versus normalized vertical large deflection for different beam lengths

Full size image
Fig. 8
figure 8

Variation of tip load versus normalized vertical large deflection for different beam lengths

Full size image
Fig. 9
figure 9

Variation of tip load versus normalized horizontal large deflection for different beam lengths

Full size image

The variation of tip load with respect to normalized vertical large deflection and normalized horizontal large deflections is shown in Figs. 10 and 11, respectively, for different flexural rigidity EI of the beam. The variations in EI range from 0.56 × 105 to 16.67 × 105 N mm2. The minimum to maximum values are obtained by varying width of the beam from 10 to 100 mm and keeping the thickness constant at 1 mm for a cantilever beam made of steel. This parametric study demonstrates that the tip load increases with the increase in vertical and horizontal deflection. The tip load required to achieve a given uy/L or ux/L ratio in a flexurally stiffer beam is more than that required for a flexurally weak beam. The increase in tip load is directly proportional to the flexural stiffness of the beam because the stiffer beam offers more resistance to deformation in addition to the stress-stiffening effect experienced in large deflections.

Fig. 10
figure 10

Variation of tip load with respect to normalized vertical large deflection for different flexural rigidity of beam

Full size image
Fig. 11
figure 11

Variation of tip load with respect to normalized horizontal large deflection for different flexural rigidity of beam

Full size image

Conclusion

This paper presented a detailed step-by-step derivation of theoretical solutions for prediction of large deflection characteristics of a cantilever beam subjected to a tip load. The problem is modeled and simulated in finite element analysis (FEA) based on beam and shell elements. The comparison of numerical results with theoretical solutions has shown that the large deflections predicted by FEA using beam elements accurately capture the theoretical results as compared to shell elements. Both the above theoretical and numerical solutions for large deflections are compared with theoretical and numerical approaches based on small deflection theory. Parametric studies with variations in beam geometry and flexural stiffness provided a deeper understanding on the behavior of beam under large deflection. Furthermore, the following conclusions can be drawn from this research work.

  1. 1.

    Beam elements can capture the theoretical results more accurately as compared to shell elements in FEA.

  2. 2.

    Within a limit of 0 < (uy/L) < 0.275 and 0 < (ϕ0) < 30° for the cantilever beam, both small and large deflection results are one and the same and one can adopt the simple small deflection approach itself for design applications provided the induced longitudinal normal strains are within the elastic limit.

  3. 3.

    Only large deflection analysis can provide the horizontal deflection, however small it may be within this elastic limit because small deflection approach cannot predict it.

  4. 4.

    The vertical deflection increases with the increase in beam length at the given elastic strain limit; and this increase is directly proportional to induced elastic strain and L/t ratio.

  5. 5.

    The induced maximum strain and bending stress at the fixed end increase with the decrease in beam length for a given vertical deflection.

  6. 6.

    The tip load increases with the increase in vertical and horizontal deflection.

  7. 7.

    The increase in tip load is inversely proportional to the beam length. The tip load required to achieve a given uy/L or ux/L ratio in a shorter beam is more than that for a longer beam due to the effect of stress-stiffening under large deformation.

  8. 8.

    The increase in tip load is directly proportional to the flexural stiffness of the beam because the stiffer beam offers more resistance to deformation.