1 Introduction

Redesigned mixed mode bending (MMB) apparatus, based on geometrical nonlinearity, reduces the error from 30 to 3% in determining its bending behavior [1, 2]. The cantilever beam is one of the essential building blocks used in micro and nanoelectromechanical (MEMS and NEMS) devices and often undergoes geometrical nonlinearity. Generally, the geometrical nonlinearity associated with cantilever beam is due to the nonlinear curvature, effect of which is highly substantial [3] (due to the insignificance of Von Karman strain [4, 5]). The DCB specimen is widely used to determine the critical stress intensity factors (or strain energy release rate) of homogenous, as well as non-homogenous materials under mode I loading configuration. Furthermore, a double cantilever beam is generally analyzed by examining the bending behavior of a cantilever beam [6, 7], since it is considered to be made of two cantilevers attached with an uncracked part. Moreover, the consideration of geometric nonlinearity in the mode I fracture toughness of non-homogenous materials is sufficed for long cracks as shown by Devitt et al. [8] and Williams [9].

Contrary to the classical continuum elasticity theories, the non-classical theories assume that stress at a material point is not entirely depended on the strain at that point but also on all other points in the body [10, 11]. This process in literature is referred as the strain gradient effect, and it is more evident when the external and the internal dimensions of the structure become comparable such as in micro-electromechanical systems (MEMS) and nanoelectromechanical systems (NEMS). In that case, microstructural length scales of a particular material become comparable to the length scale of the deformation field that eventually leads to a non-homogenous and size-dependent structural behavior [6]. The strain gradient model employed in this work was introduced by Aifantis [12], Ru and Aifantis [13], and Vardoulakis & Sulem [14], which is considered more convenient in applications [6, 15]. The Cauchy stress (\(\tau _\mathrm{xx}\)) and double stress (\(\mu _\mathrm{xxx}\)) for the 1-D case are given as: \(\tau _\mathrm{xx} =E\varepsilon _\mathrm{xx}\) and \(\mu _\mathrm{xxx} =l^{2}E\frac{\hbox {d}\varepsilon _\mathrm{xx}}{\hbox {d}x}\) respectively [7]. Here, E is Young’s Modulus; \(\varepsilon _\mathrm{xx} \) is the axial strain in the beam due to bending, l is the material microstructural length constants related to the bulk strain energy. The total stresses (\(\sigma _\mathrm{xx}\)) for the beam bending can be evaluated as: \(\sigma _\mathrm{xx} =\tau _\mathrm{xx} -\frac{\hbox {d}\mu _\mathrm{xxx} }{\hbox {d}x}=E({\varepsilon _\mathrm{xx} -l^{2}\frac{\hbox {d}^{2} \varepsilon _\mathrm{xx} }{\hbox {d}x^{2}}} )\). The application and validation of this simpler strain gradient theory are presented by Vardoulakis & Sulem [14] and Giannakopoulos et al. [6], respectively. A comprehensive review of this gradient theory along with the applications of internal length gradient across various scales is provided by Aifantis [16, 17].

There are certain molecular effects that are fascinatingly obvious when the structural dimensions are in micro and nanometer range. Effect of the surface stresses is one of those effects that have thoroughly been explained [18, 19]. The atoms on or near the free surface have different equilibrium requirements as compared to the ones in bulk. This difference causes an excess energy at the surface which is understood as a layer to which that energy is attached [20]. Accordingly, the thermodynamic theory of solid surface revealed that the relationship between the surface stress and surface free energy is obtainable [21,22,23,24]. Meanwhile, when the size of the structure is reduced to micro/nanoscale, the ratio of the surface area to bulk volume may become enormous. Therefore, the influence of surface effect on the mechanical behavior of the micro/nanomaterials becomes prominent and hence cannot be neglected [25]. Surface effects on micro/nanostructures may be characterized by two major types, i.e., the surface elasticity and the surface residual stress [26]. Gurtin and Murdoch [27] firstly considered the effect of surface stress in their theoretical framework based on continuum elasticity. In their work, the surface is considered as a mathematical layer of zero thickness with different material properties as compared to an underlying bulk. This theory has shown an excellent capability to successfully cater the surface effect on the mechanical behavior of the micro/nanostructures and is widely employed by the researchers throughout [28,29,30,31,32,33]. The general expression for the surface stress–strain relation is given as: \(\sigma _{\alpha \beta }^s =\tau _{\mathrm{o}} \delta _{\alpha \beta } +(\tau _{\mathrm{o}} +\lambda ^{s})\varepsilon _\mathrm{yy} \delta _{\alpha \beta } +2(\mu ^{s}-\tau ^{s})\varepsilon _{\alpha \beta } +\tau _{\mathrm{o}} u_{\alpha ,\beta }^s \), where \(\lambda ^{s}\) and \(\mu ^{s}\) are the surface Lame constants, \(\delta \) is Kronecker delta, and \(\tau _{\mathrm{o}}\) is the surface residual stress in the unconstrained condition. In general, the surface properties usually have anisotropic stress [34,35,36] depending upon the crystallographic direction of the surface. However, it is shown in the literature that a surface may assume anisotropic nature and it is still meaningful to use an appropriate average of the surface stresses [37,38,39].

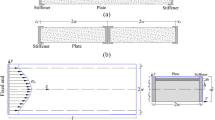
The surface elastic model is effectively employed by the researchers with both surface residual stress and surface elasticity effects in the continuum model [34, 40]. Moreover, the surface elastic model along with the generalized Young-Laplace equation has also been widely used to investigate the influence of surface effects on the mechanical response of nanostructures such as nanobeams/wires [26, 41, 42], nanoplates [43,44,45] and electrostatically actuated nanobeams [46,47,48,49]. However, the contribution of surface residual stress to the total surface stresses is considerably more noticeable than the surface elasticity [33, 50]. As mentioned before that the DCB is a widely used specimen for the determination of fracture toughness of a particular material. However, very few efforts have been devoted to study its fracture behavior with the consideration of surface effect [25]. For precise fracture analysis, the future application of micro/nanomaterials demands an inclusion of surface effects in the crack tip field quantities such as strain energy release rate or stress intensity factor. This paper establishes the numerical analysis of a DCB specimen, subjected to large deformation, for the characterization of micro/nanomaterials, with the simultaneous consideration of surface effects and strain gradients. The schematic diagram of a DCB with surface residual stress is shown in Fig. 1a. Size-dependent fracture analysis of a DCB in terms of stress intensity factors with various beam configurations is presented. Finally, the role of uncracked part of the DCB (root effect) is elaborated to conclude this study.

Fig. 1
figure 1

Schematic diagram of a a double cantilever beam with surface residual stress; b the uncracked part

Full size image

2 Theoretical formulations of the size-dependent bending of a cantilever beam

Classical beam theory is inadequate to correctly evaluate the solution of a cantilever beam under large deformation (at enhanced loads in particular), primarily as it ignores the shortening of moment arm as the free end of the beam deflects. Due to this reason, the classical results deviate from the actual observations at elevated loads. The correction for this shortening of moment arm plays a key role in solving large deformation problems. For one dimension structure, the stress–strain relation for the bulk material (in case of large deformation) is given as: \(Ez\frac{\hbox {d}\varphi }{\hbox {d}s}=\sigma _\mathrm{xx} \), where \(\varphi \) is the slope of beam and E is the Young’s Modulus. For surface layer, the stress (\(\tau ^{\mathrm{s}}\)) can be expressed as [51];

$$\begin{aligned} \tau ^{\mathrm{s}}=\tau _{\mathrm{o}}+E_{\mathrm{s}} \varepsilon _\mathrm{xx}^{\mathrm{s}} \end{aligned}$$
(1)

where \(\tau _{\mathrm{o}}\) is the surface residual stress, \(E_{\mathrm{s}}\) and \(\varepsilon _\mathrm{xx}^{\mathrm{s}}\) are Young’s modulus and surface strain, respectively. Accordingly, the bending moment of a beam is given as:

$$\begin{aligned} M=\int \limits _b {z\sigma _\mathrm{xx} \hbox {d}A+\int \limits _C {E_{\mathrm{s}} \varepsilon _\mathrm{xx}^{\mathrm{s}} dC=EI_{\mathrm{eff}} \frac{\hbox {d}\varphi }{\hbox {d}s}}} \end{aligned}$$
(2)

where C is the perimeter of the beam’s cross-section, \(EI_{\mathrm{eff}} =\frac{Ebh^{3}}{12}+\frac{E_{\mathrm{s}} h^{3}}{6}+\frac{E_{\mathrm{s}} bh^{2}}{2}\) [26, 42]. At any specified point P(x, y) along a curved beam, moment is given as: \(M=F\). (a– \(\delta x\) - x) (where a is the length of a beam and \(\delta x\) is the horizontal deflection), which if differentiated (d(\(a- \delta x - x)/\hbox {d}s = - \cos \varphi \)) gives;

$$\begin{aligned} EI_{\mathrm{eff}} \frac{\hbox {d}^{2}\varphi }{\hbox {d}s^{2}}+F\cos \varphi =0 \end{aligned}$$
(3)

Vertical deflection Y and arc length s (along with the beam axis) may be evaluated as:

$$\begin{aligned} s= & {} \sqrt{\frac{EI_{\mathrm{eff}} }{2F}}\int \limits _0^\varphi {\frac{\hbox {d}\varphi }{\sqrt{\sin \varphi _{\mathrm{o}} -\sin \varphi }}} \end{aligned}$$
(4)
$$\begin{aligned} \frac{Y}{a}= & {} \frac{1}{\sqrt{2}\alpha }\int \limits _0^{\varphi _o } {\frac{\sin \varphi \hbox {d}\varphi }{\sqrt{\sin \varphi _{\mathrm{o}} -\sin \varphi }}} ;\ \hbox {here}\ \alpha =\sqrt{\frac{Fa^{2}}{EI_{\mathrm{eff}}}}\ \hbox {and}\ a= \hbox {length of the beam} \end{aligned}$$
(5)

Here, \(\varphi _{\mathrm{o}}\) depicts an unknown slope at the free end. Eqs. (4) and (5) are usually solved numerically to evaluate Y. Alternatively, numerical techniques are applied to Eq. (3) to get \(\varphi \) and deflection Y by the following relation;

$$\begin{aligned} Y=\int \limits _0^a {\sin (\varphi )\hbox {d}s} \end{aligned}$$
(6)

These straightforward formulations may not be precisely applied at micro/nanoscale due to the predominant size effect. In order to cater this, several strain gradient theories are available in the literature (mostly dealing with second-order strain gradients). The constitutive equation for the one-dimensional case in combination with the linear elastic material behavior is written as [15, 52, 53];

$$\begin{aligned} \sigma =E(\varepsilon -l^{2}\nabla ^{2}\varepsilon ) \end{aligned}$$
(7)

where \(\sigma \) and \(\varepsilon \) are the axial stress and strain respectively, E is Young’s modulus, l is the material characteristic length and \(\nabla ^{2}=\partial ^{2}/\partial x^{2}+\partial ^{2}/\partial y^{2}+\partial ^{2}/\partial z^{2}\) is the Laplacian operator. Strain for the Euler–Bernoulli beam is given as: \(\varepsilon =z\kappa =z\frac{\hbox {d}\varphi }{\hbox {d}s}\), where \(\kappa \) is the curvature and \(\varphi \) is the deformed angle. The \(\nabla ^{2}\) operator is reduced to cater only 1D gradient since the deformation is entirely the function of “s” (although a beam is defined in 2D geometrical space, i.e., xy-plane). For 1D cantilever beam, i.e., \(\sigma _\mathrm{yy} =\sigma _\mathrm{zz} =\sigma _\mathrm{yz} =\sigma _\mathrm{xz} =\sigma _\mathrm{xy} =0\) (the beam length should at least 10 times of its height [54]), according to Eq. (7), the total stress (\(\sigma _\mathrm{xx}\)) may be written as:

$$\begin{aligned} \sigma _\mathrm{xx} =Ez\left[ {\frac{\hbox {d}\varphi }{\hbox {d}s}-l^{2}\frac{\hbox {d}^{3}\varphi }{\hbox {d}s^{3}}} \right] \end{aligned}$$
(8)

Bending moment at x is given as: \(M=\int \limits _A {\sigma _\mathrm{xx} z\hbox {d}A} \). Using Eq. (8) in the bending moment (for the bulk) equation and upon integration over the cross-section area A, one gets:

$$\begin{aligned} M=EI\left[ \frac{\hbox {d}\varphi }{\hbox {d}s}-l^{2} \frac{\hbox {d}^{\hbox {3}}\varphi }{\hbox {d}s^{3}}\right] \end{aligned}$$
(9)

here l is the material characteristics length. Here, \(I=\int \limits _A {z^{2}\hbox {d}A} \) is the second moment of cross-sectional area. Now, the governing equation and the corresponding boundary conditions of a strain gradient elastic cantilever beam are evaluated through a variational principle given as: \(\delta (U_{\mathrm{b}} +U_{\mathrm{s}} )-\delta W=0\), where W is the work done by the external forces, \(U_{\mathrm{b}}\) and \(U_{\mathrm{s}}\) are the strain energy of the bulk and surface, respectively. For one-dimensional case, the bulk strain energy \(U_{\mathrm{b}}\) may be written as:

$$\begin{aligned} U_b =\frac{1}{2}\int \limits _A {\int \limits _0^a {\left[ {\tau _\mathrm{xx} \varepsilon _\mathrm{xx} +\mu _\mathrm{xxx} .\nabla \varepsilon _\mathrm{xx} } \right] \hbox {d}s\hbox {d}A} } \end{aligned}$$
(10)

where \(\tau _\mathrm{xx} =E\varepsilon _\mathrm{xx} \) and \(\mu _\mathrm{xxx} =l^{2}E({\hbox {d}\varepsilon _\mathrm{xx} /\hbox {d}s})\) are the Cauchy and double stress, respectively, \(\varepsilon _\mathrm{xx} \) is the axial strain and \(\nabla \varepsilon _\mathrm{xx} =\hbox {d}\varepsilon _\mathrm{xx} /\hbox {d}s\) denotes the strain gradient. Accordingly, Eq. (10) may be written as: \(U_b =(EI/2)\int \limits {[(\hbox {d}\varphi /\hbox {d}s)^{2}+l^{2}(\hbox {d}^{2}\varphi /\hbox {d}s^{2})^{2}]\hbox {d}s} \), where \(\hbox {I} = bh^{3}/12\) is the moment of inertia. The variation of the integral of the type \(U=\int \limits _0^a {F(\varphi ^{{\prime }},\varphi ^{{\prime }{\prime }})\hbox {d}s} \) (where \(\varphi ^{{\prime }}=\hbox {d}\varphi /\hbox {d}s\) and \(\varphi ^{{\prime }{\prime }}=\hbox {d}^{\mathrm{2}}\varphi /\hbox {d}s^{2})\) is given as:

$$\begin{aligned} \delta U= & {} \int \limits _0^a {\left[ {\left\{ {-\frac{\hbox {d}}{\hbox {d}s}\left( {\frac{\partial F}{\partial \varphi ^{{\prime }}}} \right) +\frac{\hbox {d}^{\mathrm{2}}}{\hbox {d}s^{2}}\left( {\frac{\partial F}{\partial \varphi ^{{\prime }{\prime }}}} \right) } \right\} \delta \varphi } \right] } \hbox {d}s+\left[ {\left\{ {\left( {\frac{\partial F}{\partial \varphi ^{{\prime }}}} \right) -\frac{\hbox {d}}{\hbox {d}s}\left( {\frac{\partial F}{\partial \varphi ^{{\prime }{\prime }}}} \right) } \right\} \delta \varphi ^{{\prime }}} \right] _0^a \nonumber \\&+\left[ {\left\{ {\left( {\frac{\partial F}{\partial \varphi ^{{\prime }{\prime }}}} \right) } \right\} \delta \varphi ^{{\prime }{\prime }}} \right] _0^a \end{aligned}$$
(11)

From Eqs. (10) and (11) one gets:

$$\begin{aligned} \delta U_b= & {} \int \limits _0^a {\left[ {-EI\left\{ {\left( {\frac{\partial ^{2}\varphi }{\partial s^{2}}-l^{2}\frac{\partial ^{4}\varphi }{\partial s^{4}}} \right) } \right\} \delta \varphi } \right] } \hbox {d}s+\left[ {\left\{ {EI\left\{ {\left( {\frac{\partial \varphi }{\partial s}-l^{2}\frac{\partial ^{3}\varphi }{\partial s^{3}}} \right) } \right\} \delta \varphi } \right\} \delta \varphi ^{{\prime }}} \right] _0^a \nonumber \\&+\left[ {EIl^{2}\left\{ {\frac{\partial ^{2}\varphi }{\partial s^{2}}} \right\} \delta \varphi ^{{\prime }{\prime }}} \right] _0^a \end{aligned}$$
(12)

Similarly, the surface strain energy is written as:

$$\begin{aligned} U_s =\frac{1}{2}\int \limits _A {[\tau _\mathrm{xx}^s \varepsilon _\mathrm{xx}^s +\mu _\mathrm{xxx}^s .\nabla \varepsilon _\mathrm{xx}^s +\tau _{\mathrm{o}} \varepsilon _\mathrm{xx}^s ]\hbox {d}A} \end{aligned}$$
(13)

From Eqs. (11) and (13), one gets:

$$\begin{aligned} \delta U_{\mathrm{s}}= & {} \int \limits _0^a {\left[ {\left[ {-EI_{\mathrm{s}} \left\{ {\left( {\frac{\partial ^{2}\varphi }{\partial s^{2}}-l^{2}\frac{\partial ^{4}\varphi }{\partial s^{4}}} \right) } \right\} } \right] \delta \varphi } \right] } \hbox {d}s+\left[ {\left[ {EI_{\mathrm{s}} \left\{ {\left( {\frac{\partial \varphi }{\partial s}-l^{2}\frac{\partial ^{3}\varphi }{\partial s^{3}}} \right) } \right\} } \right] \delta \varphi ^{{\prime }}} \right] _0^a \nonumber \\&+\left[ {\left[ {EI_{\mathrm{s}} l^{2}\left\{ {\frac{\partial ^{2}\varphi }{\partial s^{2}}} \right\} } \right] \delta \varphi ^{{\prime }{\prime }}} \right] _0^a -\int \limits _0^a {T^{s}\delta \varphi \hbox {d}s} \end{aligned}$$
(14)

where \(I_{\mathrm{s}}=({ bh}^{2}/2+h^{3}/\hbox {6}\)) and \(T^{s}=\int \limits _0^a {q\hbox {d}s} \), with q(s) is the vertical load induced by the residual stress. According to the Young-Laplace equation [34, 40], stress jump across each surface depends on the surface curvature that can be expressed as [34, 40]; \(\langle {\sigma _\mathrm{ij}^+ -{\sigma _\mathrm{ij}^- } \rangle } n_i n_j =\tau _{\alpha \beta }^s \kappa _{\alpha \beta } \), where \(n_\mathrm{i}\) denotes the unit vector normal to the surface, \(\sigma _\mathrm{ij}^+ \) and \(\sigma _\mathrm{ij}^-\) are, respectively, the stresses above and below the surface, \(\kappa _{\alpha \beta }\) is the surface curvature. Therefore, equivalent vertical load q(x) induced by the residual stress is expressed as [26, 42];

$$\begin{aligned} q=H\kappa =H\frac{\hbox {d}\varphi }{\hbox {d}s} \end{aligned}$$
(15)

with \(H=2\tau _{\mathrm{o}} b\) [26, 42, 55] where b is the width of the beam. The total force along the beam axis “s” is given as: \(T^{s}=\int \limits _0^a {H\frac{\partial \varphi }{\partial s}} \hbox {d}s\). The variation of the work done by the external forces is written as: \(\delta W=\int \limits _0^a F \cos \varphi (s)\delta \varphi \hbox {d}s\). So, the variational principle \(\delta (U_{\mathrm{b}} +U_{\mathrm{s}} )-\delta W=0\) gives:

$$\begin{aligned}&\int \limits _0^a {\left[ {\left[ {-EI_{\mathrm{eff}} \left\{ {\left( {\frac{\partial ^{2}\varphi }{\partial s^{2}}-l^{2}\frac{\partial ^{4}\varphi }{\partial s^{4}}} \right) } \right\} +H\varphi -H\varphi _{(a)} -F{\cos \varphi } } \right] \delta \varphi } \right] } \hbox {d}s-\nonumber \\&\left[ {\left[ {EI_{\mathrm{eff}} \left\{ {\left( {\frac{\partial \varphi }{\partial s}-l^{2}\frac{\partial ^{3}\varphi }{\partial s^{3}}} \right) } \right\} } \right] \delta \varphi ^{{\prime }}} \right] _0^a +\left[ {\left[ {EI_{\mathrm{eff}} \left\{ {\left( {\frac{\partial ^{2}\varphi }{\partial s^{2}}} \right) } \right\} } \right] \delta \varphi ^{{\prime }{\prime }}} \right] _0^a =0 \end{aligned}$$
(16)

The governing equation can be written as:

$$\begin{aligned} EI_{\mathrm{eff}} \left[ {\frac{\hbox {d}^{\mathrm{2}}\varphi }{\hbox {d}s^{2}}-l^{2}\frac{\hbox {d}^{\mathrm{4}}\varphi }{\hbox {d}s^{4}}} \right] =-F\cos \varphi +H\varphi -H\varphi _{(a)} \end{aligned}$$
(17)

where \(EI_{\mathrm{eff}} =E\frac{bh^{3}}{12}+E_s ({\frac{h^{3}}{6}+\frac{bh^{2}}{2}})\). It is necessary to mention for simplification that the size dependence of E is not considered, as previously done in these references [56, 57]. Our model applies to those materials that do not show the significant dependence of E on size. The boundary conditions evaluated from the variational principle require \(EI_{\mathrm{eff}} [(\partial \varphi /\partial s)-l^{2}(\partial ^{3}\varphi /\partial s^{3})]\) (moment) and \(EI_{\mathrm{eff}} (\partial ^{2}\varphi /\partial s^{2})\) (higher order moment) to be specified at \(s = 0\) and \(s=a\). So, one of the possible set of boundary conditions considered in this work is as follows; At clamped end, i.e., \(s = 0\), slope, i.e., rotation of the beam is zero \(\varphi =0\), and the non-classical terms (from variational principle) are written as: \(\frac{\hbox {d}^{\mathrm{2}}\varphi }{\hbox {d}s^{2}}=0\). Meanwhile, at the free end, i.e., \(s = a\), the classical moment (without strain gradient) would be zero which eventually gives;\(\frac{\hbox {d}\varphi }{\hbox {d}s}=0\). On the other hand, the moment (with strain gradient effect) would also be zero that further gives;\(\frac{\hbox {d}\varphi }{\hbox {d}s}-l^{2} \frac{\hbox {d}^{3}\varphi }{\hbox {d}s^{3}}=0\). In a nutshell, the boundary conditions considered in this work are written as:

$$\begin{aligned} \hbox {At}\ s= & {} 0; \varphi =0, \frac{\hbox {d}^{\mathrm{2}}\varphi }{\hbox {d}s^{2}}=0 \end{aligned}$$
(18a)
$$\begin{aligned} \hbox {At}\ s= & {} a; \frac{\hbox {d}\varphi }{\hbox {d}s}=0 , \frac{\hbox {d}\varphi }{\hbox {d}s}-l^{2}\frac{\hbox {d}^{3}\varphi }{\hbox {d}s^{3}}=0\ \hbox {or} \frac{\hbox {d}\varphi }{\hbox {d}s}=0, \frac{\hbox {d}^{3}\varphi }{\hbox {d}s^{3}}=0 \end{aligned}$$
(18b)

The nonlinear fourth-order differential equation (Eq. 17) with the respective boundary conditions (Eq. 18a) is solved using a three-stage Lobatto IIIa collocation formula. It is one of a widely used finite difference method to solve the boundary value problems. Details of this and some other relevant methods are provided by Shampine et al. [58].

3 Numerical results for the cantilever beam bending

For results, the material characteristic length (l) of epoxy, i.e., \(17.6\ \upmu \hbox {m}\) [57] is taken to numerically evaluate the large deformation bending behavior of a cantilever beam. The concentrated vertical force F and height h are chosen in such a way that the beam remains elastic everywhere. In this study, the contribution of the surface residual stress toward the total surface stresses is found more noticeable than the surface elasticity, as shown by other researchers [33, 50]. The end tip deflection for gradient model \(Y_{\mathrm{g}}\), non-gradient (large deformation) model \(Y_{\mathrm{l}}\) and the classical model \(Y_{\mathrm{o}}\) (\(FL^{3}/3EI\)) are plotted in Fig. 2. It is shown that when \(t_{1}< < h\), where \(t_{1}\) is the ratio of the layer’s thickness to the height of the beam, the effect of surface elasticity is negligible and all three models give similar results. Surface elasticity modulus is taken to be as: \(E_{\mathrm{s}}=E_{1} t_{1}\) and \(E_{1}=E = 1.44\ \hbox {GPa}\) [26, 42]. The similar conclusion is drawn in the references [33, 50]. Therefore, for further study, \(E_{\mathrm{s}}\) and \(\tau _{\mathrm{o}}\) are assumed to be zero [59] and \(0.2\ \upmu \hbox {N}/\upmu \hbox {m}\), respectively. The effect of the large deformation with increased load factor \(F_{\mathrm{o}}\) (\(F_{\mathrm{o}}=Fa^{2}/2(EI)\)) is shown by Joseph et al. [15], demonstrating its pronounced effect at the enhanced loads. The surface residual stress constant may be positive or negative [2]; therefore, results for both positive and negative residual stresses are presented. The vertical deflection of a cantilever beam along its axis, normalized with \(Y_{\mathrm{o}}\) (\(FL^{3}/3EI\)) (classical endpoint vertical deflection), is presented in Fig. 3a. It can be seen, for smaller h / l ratios, that the gradient beam models are stiffer than the classical ones. The normalized deflections are shown to increase with increasing h / l, while the maximum deflection (at \(s/a = 1\)) of the strain gradient and classical model become comparable when \(h/l \approx 1\) onwards. It is important to note that the effect of strain gradient is more prominent when \(h/l \le 0.2\); therefore, the subsequent results are primarily presented with \(h/l \le 0.2\). In Fig. 3b for \(h/l \le 0.2\), the results are obtained with strain gradient model with no surface effects, strain gradient model with positive surface residual stress and strain gradient model with negative surface residual stress. All effects have shown a significant contribution to the bending behavior of a cantilever beam. For instance, with the positive surface residual stress, the beam exhibits less stiff behavior and vice versa. This phenomenon is explained due to the sign of curvature associated with surface residual stress that causes an additional distributed load and change beam [26, 51, 59]. In the case of a positive surface residual stress, a positive curvature results in a positive distributed transverse force. This positive force increases the rotation of bending cantilever and thus beam behaves like a softer material. Meanwhile, this behavior is totally opposite when \(\tau _{\mathrm{o}} < 0\) and hence, the cantilever beam may exhibit a stiffer response comparatively.

Fig. 2
figure 2

Maximum tip deflection of the strain gradient model (\(Y_{\mathrm{g}}\)) and the non-gradient model (\(Y_{\mathrm{l}}\)), normalized with the classical results (\(Y_{\mathrm{o}}\)) vs layer thickness to beam’s height ratio (\(t_{1}=t/h\))

Full size image
Fig. 3
figure 3

a The vertical deflection along the beam axis (normalization with the classical result at the tip) for strain gradient models b The vertical deflection along the beam axis (normalization with the classical result at the tip) for the strain gradient models with surface residual effect

Full size image

The normalized maximum deflections (maximum tip deflection) for various beams configurations are numerically obtained using Eq. (6) and are shown in Fig. 4. Here, \(Y_{\mathrm{g}}\), \(Y_{\mathrm{l}}\) and \(Y_{\mathrm{o}}\) (\(Fa^{3}/(3EI)\)) represent the deflection obtained with strain gradient model, non-gradient model and using the classical formulations (small deformation). Additionally, for comparison, the maximum tip deflections for positive and negative residual stresses are also included. The non-dimensional parameter (\(\alpha = 3Fa^{2}/(Eh^{4})\)) as abscissa is defined for convenience. The normalized maximum deflection \(Y_{\mathrm{g}}/Y_\mathrm{l}\) against \(\alpha \) is plotted in Fig. 4a. From Fig. 4a, the strain gradient effect seems more pronounced for smaller (a / h), presenting smaller deflections and hence exhibiting stiffer response for the gradient beams. The effect of the surface residual stress on the tip deflections is shown to be more prominent for slender beams irrespective of h / l ratio. For a certain beam height, the effect of surface residual stress tends to increase with increasing beam length. Moreover, this behavior is also evident for increasing h / l ratio. It is clear that the positive surface residual stress induces larger tip transverse displacement while the opposite holds true for the negative surface residual stress. Figure 4b compares the strain gradient results with the classical model (without strain gradient & small deformation). It is shown for the smaller beam lengths that \(Y_{\mathrm{g}}/Y_\mathrm{l}\) and \(Y_{\mathrm{g}}/Y_{\mathrm{o}}\) are identical, indicating similar results for large as well as the small deformation theory. However, with an increase in beam slenderness (a / h ratio), the beam will undergo large deformation and hence the small deformation theory would over-estimate an endpoint vertical deflection. This is evident from a peak point (in each curve) in Fig. 4b, indicating classical model inadequacy to accurately predict the large deformation. Moreover, from Fig. 4b, it is quite evident that the pattern of maximum tip deflections, for the model with cumulative effects of strain gradient and surface residual stress, is similar to that of the model without surface residual stress (only strain gradient effect), apart from the fact that for positive surface residual stress the beam tends to exhibit softer behavior and vice versa. Nevertheless, from Fig. 4a, b, it may fairly be concluded that the effect of surface residual stress is more prominent for slender beams.

Fig. 4
figure 4

a End point vertical deflection of the strain gradient model, normalization with the end point non-gradient vertical deflections (large deformation) b End point vertical deflection of the strain gradient model, normalization with the end point classical vertical deflections

Full size image

4 Fracture of a double cantilever beam with surface residual effect

Significant developments in the advance numerical methods have been made not only to accurately predict the fracture of various complex geometries [60, 61] but also to cater the size effect on the fracture properties at smaller scale [6, 7, 62, 63]. Adopting one of such numerical methods, in this section, the fracture property of a DCB, i.e., the stress intensity factor is evaluated numerically by taking the crack length to be the length of a beam as a and width b, the stress intensity factor (K) of a DCB may be written as \(K=\sqrt{EG}\), where \(G =F(\hbox {d}Y_\mathrm{max}/b\hbox {d}a\)) and it is defined as the strain energy release rate of a DCB. Meanwhile, the classical result is given by \(G_{\mathrm{o}}=12F^{2}a^{2}/(Eh^{3}b^{2})\) (Wang & Wang, 2013). Figure 5 displays the normalized stress intensity factors versus \(\alpha \). For comparison, as in Fig. 4, the results for the strain gradient model \(K_{\mathrm{g}}\), non-gradient model \(K_{\mathrm{l}}\) and classical theory \(K_{\mathrm{o}}\) are given. Additionally, for further illustration, the stress intensity factors for the model with the positive and negative residual stresses are also included. Evidently, from Fig. 5, the effect of the surface residual stress is more prominent when \(h/l \ge 0.075\) and for slender beams. It is clear that the positive residual stress enhances the stress intensity factors and vice versa. Furthermore, the effect of the negative surface residual stress is more noticeable as compared to the positive residual stress. For instance, in Fig. 5a, for \(h/l \ge 0.1\) beyond certain peak point the normalized stress intensity factor shows a swift decline, signifying a stiffer beam response. However, this prompt observation is completely absent in the case of positive surface residual stress. Moreover, the normalizations of strain gradient results with the classical ones are shown in Fig. 5b. From Fig. 5b, apart from the strain gradient effects, it may clearly be seen that effect of negative surface residual stress is more noticeable than that of the positive surface residual stress. On the other hand, the overestimation in the fracture characteristics is also evident following the trend as shown in Fig. 4.

Fig. 5
figure 5

a Stress intensity factors of the strain gradient model, normalization with the non-gradient stress intensity factors (large deformation) b Stress intensity factors of the strain gradient model, normalization with the classical stress intensity factors

Full size image
Fig. 6
figure 6

Comparison of \(R_{\mathrm{K}}\) and \(R_{\mathrm{G}}\) plotted against a / h

Full size image
Fig. 7
figure 7

Stress intensity factors with the consideration of uncracked part of DCB, normalization with the non-gradient stress intensity factors (large deformation)

Full size image

5 Effect of the uncracked part

The strain gradient effect of the uncracked part of DCB is neglected (since strains in the uncracked part would be much lower than that in the cracked part). The schematic of uncracked part of a DCB is shown in Fig. 1b. The governing equation and respective boundary conditions of an uncracked part are provided by Wang & Wang [25] and Joseph et al. [15]. Here, it is necessary to mention the prominence of shear stresses at the uncracked part that must be incorporated in the constitutive equations. Therefore, Timoshenko beam model is more suitable to study the uncracked part of the DCB. Accordingly, the potential energy of an uncracked part (\(U_{2}\)) of DCB is given as:

$$\begin{aligned} U_2 =2\int \limits _{-\infty }^0 {\frac{M^{2}}{2EI_{\mathrm{eff}}} \hbox {d}x+2\int \limits _{-\infty }^{0}{\frac{Q^{2}}{2G^{s}A}}}\hbox {d}x \end{aligned}$$
(19)

Here E is the Young’s Modulus, \(G^{\mathrm{s}}\) is the shear modulus, A is the area of cross-section and \(I_{\mathrm{eff}}\) is the effective moment of inertia. Following the rectangular coordinate system, the integrals vary from negative infinity to zero. From the references [15, 25] and using \(M_{(\mathrm{o})} =F.X_{(\varphi _{\mathrm{o}})}\) we get:

$$\begin{aligned} U_2 =\frac{1}{\sqrt{EI_{\mathrm{eff}} GA}}\left[ {F^{2}X_{(\varphi _{\mathrm{o}} )}^2 +\left[ {\int \limits _0^a {sH\frac{\hbox {d}\varphi }{\hbox {d}s}\hbox {d}s} } \right] ^{2}} \right] \end{aligned}$$
(20)

Now, the influence of the root part of DCB is investigated numerically. Here, \(R_\mathrm{K}\) and \(R_\mathrm{G}\) are defined, where \(R_\mathrm{K}\) is the ratio of the stress intensity factor associated with the uncracked part to that of the cracked part of DCB, while \(R_\mathrm{G}\) is the ratio of the strain energy release rate of an uncracked part to the cracked part. Variations of \(R_\mathrm{K}\) and \(R_\mathrm{G}\) versus a / h for different h / l ratios are plotted in Fig. 6. The results are plotted for strain gradient model without surface residual stress, strain gradient model with positive surface residual stress and strain gradient model with negative surface residual stress. It can be seen in Fig. 6 that, for a particular h / l, all models show the identical results. Thus, it may be stated that ratios \(R_\mathrm{K}\) and \(R_\mathrm{G}\) depend on the DCB geometry and it is independent of the surface residual stress. Moreover, it may equally be concluded that for smaller DCBs, i.e., for \(h/l \le 0.2\), the value of \(R_\mathrm{K}\) and \(R_\mathrm{G}\) may not be neglected even though the beam length to thickness ratio is higher (\(a/h \approx 20\)) (which was the case in classical studies).

The comparison of two strain gradient models, i.e., with root effect and without root effect in terms of stress intensity factors is shown in Fig. 7. The results are plotted for models incorporating strain gradient effect without surface residual stress, strain gradient effect with positive surface residual stress and strain gradient effect with negative surface residual stress. In general, results show that even with the incorporation of root effect, the positive surface residual stress causes DCB to exhibit softer response by enhancing the normalized stress intensity factor and vice versa. Again, this phenomenon may be explained due to the sign of curvature associated with negative surface residual stress that causes an additional distributed load (opposite to the direction of endpoint force), which in return cause the DCB to exhibit stiffer response. Hence, the influence of the root effect of DCB must be considered in mathematical modeling for accurate prediction of its fracture properties. It seems true even for the slender beams (\(a/h > 20\)), lest an underestimated fracture behavior would be expected.

6 Conclusion

The cumulative effects of the strain gradient and surface stress on the large deformation bending behavior of a cantilever beam are investigated. Both surface elasticity and surface residual stress are incorporated in the mathematical modeling. Due to the negligible influence of surface elasticity, most of the results are depicted only with the consideration of surface residual stress. The results are obtained for the strain gradient model with no surface effects, strain gradient model with positive surface residual stress and negative surface residual stress individually. Due to the positive surface residual stress, the beam exhibits less stiff behavior. This softening behavior may be attributed to the sign of curvature that causes an additional distributed load and change beam stiffness. Meanwhile, this behavior is totally opposite in the case when \(\tau _{\mathrm{o}} < 0\); hence, a cantilever beam may exhibit a stiffer response comparatively. For the fracture property of DCB, i.e., stress intensity factor, the effect of the surface residual stress is shown to be increasing with increasing beam dimensions. In general, the influence of surface residual stress is more prominent when \(h/l \ge 0.075\) and for slender beams. Moreover, the effect of negative surface residual stress was shown to be more noticeable than the positive surface residual stress. The root effect also enhances the normalized stress intensity factors. It was shown that the root effect on the ratios \(R_\mathrm{K}\) and \(R_\mathrm{G}\) for all three models remain same and thus it may be stated that \(R_\mathrm{K}\) and \(R_\mathrm{G}\) depend on the DCB geometry and are independent of the surface residual stress. It is observed for \(h/l \le 0.2\) that the significance of root effect must not be ignored.