Generalized Intuitionistic Fuzzy Entropy-Based Approach for Solving Multi-attribute Decision-Making Problems with Unknown Attribute Weights

Abstract

A new strategy for solving multi-attribute decision-making problem has been presented by using different entropies and unknown attribute weights, where preferences related to the attributes are in the form of interval-valued intuitionistic fuzzy sets. Some generalized properties have also been proved for justification. An illustrative example has been provided to demonstrate and effectiveness the approach along with the sensitivity analysis on the decision-maker parameter.

1 Introduction

Decision making is one of the most important topics in various fields to make a right decision so as to reach the final goal. However, the key issue in the decision-making process is to find the suitable attribute weights and the process to aggregate the decision makers’(DM) preferences. In a classical multi-attribute decision-making (MADM), the rating, as well as attribute weights, are assumed to be a precise number. But due to growing complexities of the systems day-by-day, it is not possible to give preferences towards the alternative under the different attribute in terms of a single or exact number. Although, intuitionistic fuzzy set(IFS) theory [1] has been successfully applied by the researchers [2,3,4,5] in different fields for handling the uncertainties. But, in some situations, it is difficult to give the preference of an object in terms of a point value and hence Atanassov and Gargov [6] extended IFS theory to interval-valued IFSs (IVIFSs). In recent years, the researchers are highly active in IVIFSs by including the investigations on their basic operations, their corresponding properties, similarity measure, aggregation operators etc. For instance, Xu [7] presented different methods for aggregating the interval-valued intuitionistic fuzzy numbers (IVIFNs). Later on, Wang and Liu [8] extended these operators by using Einstein norm operations under IFS environment. Garg [9] presented a generalized intuitionistic fuzzy interactive geometric interaction operators using Einstein norm operations for aggregating the different intuitionistic fuzzy information. Garg [10], further, proposed some series of interactive aggregations operators for IFNs. Hung and Chen [11] presented a fuzzy Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method with entropy weight for solving the decision-making problems under the intuitionistic fuzzy environment. Garg [12] presented a new generalized score function for ranking the different interval-valued IFSs. Garg [13] presented a generalized intuitionistic fuzzy aggregation operator under the intuitionistic multiplicative preference relation instead of intuitionistic fuzzy preference relations. Ye [14] presented an accuracy function for ranking the interval-valued intuitionistic fuzzy numbers (IVIFNs). Garg [15, 16] extended the theory of the IFS to the Pythagorean fuzzy set environment in which sum of their membership function is less than one has been relaxed to the square sum of its membership functions and presented a generalized geometric as well as averaging aggregation operators. Apart from that, many authors [17,18,19,20,21,22,23,24,25,26,27] have been showing growing interest in the study of the decision-making problems under the different environments by using these above theories.

However, it has been analyzed that the final ranking order of alternatives highly depends on the attribute weights and hence these particular weights play a significant role during the aggregation process. According to the attribute weight information, the considered decision-making situations can be mainly classified into the following three types: (a) the decision-making situation where the attribute weights are completely known; (b) the decision-making situation where the attribute weights are completely unknown; (c) the decision-making situation where the attribute weights are partially known. Based on the information acquisition, the attribute weights in MADM are classified as both subjective and objective. The former one is determined by preference information on the attributes as given by the decision-maker while the latter one is determined by the decision-making matrix. The Shannon entropy [28] method, used for determining the objective attribute weights, which express the relative intensities of attribute importance to signify the average intrinsic information transmitted to the decision maker. Thus, it is an important task to determine the proper attribute weights which will help the decision maker for obtaining the efficient decision in a reasonable time.

Therefore, this paper studies the multi-attribute fuzzy group decision-making problems with complete unknown attribute weight information under IVIFSs environment. The weight vector has been given by using intuitionistic fuzzy entropy measure. Although, the different preferences are aggregated by using an averaging aggregation operator for rating the alternatives. Furthermore, an effect of the various parameters of entropies functions on the ranking of the system has been accessed.

2 Preliminaries

In this section, a brief introduction about the IFS, IVIFS and their corresponding entropies have been presented over the universal set X.

2.1 Intuitionistic Fuzzy Set

An IFS [1] A over X is defined by

$$\begin{aligned} A=\{\langle x,\mu _{A}(x), \nu _{A}(x)\rangle \mid x \in X \} \end{aligned}$$

(1)

where $\mu _A$ and $\nu _A$ represent the degrees of membership and non-membership of A. For convenience, this pair $\langle \mu _A, \nu _A \rangle$ is called as intuitionistic fuzzy number (IFN), where $\mu _A, \nu _A \in [0, 1]\,\text{and}\,\mu _A+\nu _A\in [0, 1]$.

2.2 Entropy on IFSs

An entropy $E:\text {IFS}(X)\longrightarrow R^+$ on IFS(X) is a real-valued functional which satisfying the following four axioms for $A,B\in \text {IFS}(X)$ [29]

• (P1) $E(A)=0$ if and only if A is a crisp set, i.e., either $\mu _{A}(x)=1, \nu _A(x)=0$ or $\mu _{A}(x)=0, \nu _A(x)=1$ for all $x \in X$.

• (P2) $E(A)=1$ if and only if $\mu _A(x)=\nu _A(x)$ for all $x\in X$.

• (P3) $E(A)=E(A^c)$

• (P4) If $A \le B$, that is, if $\mu _{A}(x) \le \mu _B(x)$ and $\nu _{A}(x) \ge \nu _B(x)$ for any $x \in X$ then $E(A) \ge E(B)$.

2.3 Interval-Valued Intuitionistic Fuzzy Sets (IVIFS)

An IVIFS A in X is defined as [6]

$$\begin{aligned} A=\{\langle x,[\mu _{A}^L(x), \mu _A^U(x)], [\nu _{A}^L(x), \nu _A^U(x)] \rangle \mid x \in X \} \end{aligned}$$

where $\mu _A^L(x), \mu _A^U(x)$ and $\nu _A^L(x), \nu _A^U(x)$ represents the lower and upper bound of the membership and non-membership degrees such that $\mu _A^L(x), \mu _A^U(x)\in [0,1]$, $\nu _A^L(x), \nu _A^U(x)\in [0,1]$ and $\mu _A^U(x) + \nu _A^U(x) \le 1$ for each $x\in X$.

2.4 Entropy on IVIFSs

A real function $E: \text {IVIFSs}(X) \longrightarrow R^+$ is called an entropy if it satisfies the following properties $A,B\in \text {IVIFS}(X)$ [21]:

• (P1) $E(A)=0$ if and only if A is a crisp set i.e., $\mu _{A}^{L}(x)=\mu _{A}^{U}(x)$ and $\nu _{A}^{L}(x)=\nu _{A}^{U}(x)$ and $\mu _{A}^{L}(x)+\nu _{A}^{L}(x)=1$ and $\mu _{A}^{U}(x)+\nu _{A}^{U}(x)=1$.

• (P2) $E(A)=1$ if and only if $\mu _A(x)=\nu _A(x)$ for all $x\in X$.

• (P3) $E(A)=E(A^c)$

• (P4) If $A \le B$, then $E(A) \ge E(B)$.

3 Construction of New Entropy Measure for IVIFS

In this section, we have presented a method for the construction of the new entropies measure under an IVIFS environment.

Consider an IVIFS A which can be converted into an IFS with membership function

$$\begin{aligned} \mu _A(x)=\mu _{A}^{L}(x)+p\triangle \mu _A(x) \end{aligned}$$

(2)

and non-membership function

$$\begin{aligned} \nu _A(x)=\nu _{A}^{L}(x)+p\triangle \nu _A(x) \end{aligned}$$

(3)

where $\triangle \mu _A(x)=\mu _{A}^{U}(x)-\mu _{A}^{L}(x), \quad \triangle \nu _A(x)=\nu _{A}^{U}(x)-\nu _{A}^{L}(x)$ and $p \in (0,1)$ for all $x \in X$. Then based on it, we have presented a generalized entropy measure for IVIFSs as follows.

Theorem 1

Let X be a universe of discourse consisting of N elements, say $\{x_1,x_2,\ldots ,x_N\}$, then a real-valued functional $E: {\text {IVIFS}}(X) \longrightarrow R^+$ defined as

$$\begin{aligned} E(A)=\frac{1}{N}\sum \limits _{i=1}^N \left[ 1-\varPhi (\xi _A(x_i), \varphi _A(x_i)) \right] ; \xi _A(x_i), \varphi _A(x_i) \in \text {IFS}(X) \end{aligned}$$

(4)

is an entropy measure for IVIFSs, where $\varPhi$ satisfies the following conditions for $x,y\in \text {IVIFS}(X)$

• (a) $\varPhi (x,y)=1$ if and only if $x+y =1$.

• (b) $\varPhi (x,y)=0$ if and only if $x=y$.

• (c) $\varPhi (x,y)=\varPhi (y,x)$.

• (d) If $x \le x'$ and $y \ge y'$, then $\varPhi (x,y) \le \varPhi (x', y')$.

Proof

Consider an IVIFS $A = \{\langle x$, $[\mu _{A}^L(x)$, $\mu _{A}^U(x)]$, $[\nu _{A}^{L}(x)$, $\nu _{A}^{U}(x)]\rangle \mid x \in X\}$ which can be converted into the IFS$A=\{\langle x, \xi _A(x), \varphi _A(x)\rangle \mid x \in X\}$ where $\xi (x) = \mu _{A}^L(x)+p\triangle \mu _{A}(x)$ and $\varphi (x) = \nu _{A}^L(x)+p\triangle \nu _{A}(x)$ such that $\triangle \mu _A(x) = \mu _A^U(x) - \mu _A^L(x)$ and $\triangle \nu _A(x)=\nu _A^U(x) - \nu _A^L(x)$ for all $x\in X$ and $p\in (0,1)$. Now, in order to prove the valid entropy measure, the properties (P1)-(P4) as described in above section have been proved here.

• (P1) To show $E(A)=0$ if and only if A is a crisp set i.e., $\mu _{A}^{L}(x)=\mu _{A}^{U}(x)$ and $\nu _{A}^{L}(x)=\nu _{A}^{U}(x)$ and $\mu _{A}^{L}(x)+\nu _{A}^{L}(x)=1$ and $\mu _{A}^{U}(x)+\nu _{A}^{U}(x)=1$. Firstly, assume that

  $$\begin{aligned} E(A)= 0\Rightarrow & {} \frac{1}{N}\sum \limits _{i=1}^N[1-\varPhi (\xi (x_i),\varphi (x_i))]=0 \\\Rightarrow & {} \varPhi (\xi (x_i),\varphi (x_i))= 1 \\\Rightarrow & {} \xi (x_i) + \varphi (x_i)=1 \\\Rightarrow & {} (1-p)(\mu _{A}^{L}(x_i)+\nu _{A}^{L}(x_i)) \\ &+ p(\mu _{A}^{U}(x_i)+\nu _{A}^{U}(x_i)) = 1 \end{aligned}$$

  Then, the only possible solution of above is $\mu _{A}^{L}(x) + \nu _{A}^{L}(x) = 1$ and $\mu _{A}^{U}(x) + \nu _{A}^{U}(x) = 1$. Because if $\mu _{A}^{L}(x) + \nu _{A}^{L}(x) < 1$ then from $\xi (x) + \varphi (x)=1$ becomes $\mu _{A}^{U}(x) + \nu _{A}^{U}(x) > 1$ which is contradict to the definition of degree of membership and non-membership. Thus, $\mu _{A}^{L}(x) + \nu _{A}^{L}(x) = 1$ and hence A is fuzzy set.

  Conversely, assume that A is fuzzy set, then $\mu _{A}^{L}(x)=\mu _{A}^{U}(x)$, $\nu _{A}^{L}(x)=\nu _{A}^{U}(x)$ and $\mu _{A}^{L}(x) + \nu _{A}^{L}(x) = 1$ for all $x \in X$. Then by using the condition (a) of $\varPhi$, we get $\varPhi (\xi (x), \varphi (x))=1$ and hence $E(A)=0$.

• (P2) To show $E(A)=1$ if and only if $\mu _A(x)=\nu _A(x)$ for all $x\in X$.

  Assume that $\mu _{A}(x)=[0,0]$ and $\nu _A(x)=[0,0]$ for all $x \in X$ which implies that $\xi (x)=0$, $\varphi (x)=0$, $(i=1,2,\ldots ,N)$ for any $p\in (0,1)$. Thus, by condition (b) of $\varPhi$, we get $\varPhi (\xi ,\varphi )=0$ and hence $E(A)=1$.

  Conversely, assume that $E(A)=1$ which implies that $\varPhi (\xi (x_i),\varphi (x_i))=0$, $(i=1,2,\ldots ,N)$ for any $p\in (0,1)$ and hence $\xi (x_i)=0$ and $\varphi (x_i)=0$. Thus, $(1-p)\mu _{A}^{L}(x_i)+p\mu _{A}^{U}(x_i)=0$ and $(1-p)\nu _{A}^{L}(x_i)+p\nu _{A}^{U}(x_i)=0$ for any $p \in (0,1)$. Therefore, $\mu _{A}^{L}=0$ and $\mu _{A}^{U}=0$ for all x. Similarly, $\nu _{A}^{L}=0$ and $\nu _{A}^{U}=0$ for all x. Hence, $\mu _A(x)=[0, 0]$ and $\nu _A(x)=[0, 0]$ for all $x\in X$.

• (P3) To show $E(A)=E(A^c)$ for all $A \in IVIFS(X)$

  As $A^c=\{\langle x,\nu _A(x),\mu _A(x)\rangle \mid x \in X\}$ and by condition of (c) of $\varPhi$, we get $E(A)=E(A^c)$.

• (P4) To show, if $A \le B$, then $E(A) \ge E(B)$.

  If $A \le B$ then for all $x\in X$, we have $\mu _{A}^{L}(x) \le \mu _{B}^{L}(x)$, $\mu _{A}^{U}(x) \le \mu _{B}^{U}(x)$, $\nu _{A}^{L}(x) \ge \nu _{B}^{L}(x)$, and $\nu _{A}^{U}(x) \ge \nu _{B}^{U}(x)$. Thus, for any $p\in (0,1)$ we have

  $$\begin{aligned}&p(\mu _{B}^{U}(x)-\mu _{A}^{U}(x)) + (1-p)(\mu _{B}^{L}(x)-\mu _{A}^{L}(x)) \ge 0 \\ &\quad \Rightarrow p \mu _B^U + (1-p)\mu _B^L \ge p \mu _A^L + (1-p)\mu _A^L \\ &\quad \Rightarrow \mu _B^L + p(\mu _B^U -\mu _B^L) \ge \mu _A^L + p(\mu _A^U - \mu _A^L) \\ &\quad \Rightarrow \mu _{B}^{L}(x)+p\triangle \mu _B(x) \ge \mu _{A}^{L}(x) + p\triangle \mu _A(x) \\ &\quad \text{ or } \xi _A(x) \le \xi _B(x) \end{aligned}$$

  Similarly, we have $\varphi _A(x) \ge \varphi _B(x)$. Thus, by the condition (d) of $\varPhi$, we get

  $$\begin{aligned}&\varPhi (\xi _A(x_i),\varphi _A(x_i)) \le \varPhi (\xi _B(x_i), \varphi _B(x_i)) \\ &\quad \Rightarrow 1-\varPhi (\xi _A(x_i),\varphi _A(x_i)) \ge 1-\varPhi (\xi _B(x_i), \varphi _B(x_i)) \\ &\quad \Rightarrow E(A) \ge E(B) \end{aligned}$$

Hence, $E(A)=\dfrac{1}{N}\sum \nolimits _{i=1}^N \left[ 1-\varPhi (\xi _{A}(x_i),\varphi _A(x_i))\right]$, is a valid entropy measure on A. $\square$

Further, from the above measure, it has been observed that the proposed entropy measure also satisfies the following additional properties:

Theorem 2

Let $A=\{\langle x,[\mu _A^L(x), \mu _A^U(x)]$, $[\nu _A^L(x), \nu _A^U(x)]\rangle \mid x\in X \}$ and $B=\{\langle x$, $[\mu _B^L(x)$, $\mu _B^U(x)]$, $[\nu _B^L(x)$, $\nu _B^U(x)]\rangle \mid x\in X \}$ be two IVIFSs, such that for any $x \in X$ either $A \subseteq B$ or $A\supseteq B$; then

$$\begin{aligned} E(A\cup B)+ E(A\cap B) = E(A) + E(B) \end{aligned}$$

Proof

Since A and B are two IVIFSs then their equivalent IFSs are obtained for all $p\in (0,1)$ as

$$\begin{aligned} \xi _A(x)& = \mu _{A}^L(x)+p(\mu _{A}^U(x) - \mu _A^L(x)), \\ \varphi _A(x)& = \nu _{A}^{L}(x)+p(\nu _{A}^U(x) - \nu _A^L(x)), \\ \xi _B(x)& = \mu _{B}^L(x)+p(\mu _{B}^U(x) - \mu _B^L(x)), \\ \varphi _B(x)& = \nu _{B}^{L}(x)+p(\nu _{B}^U(x) - \nu _B^L(x)) \end{aligned}$$

Divide the universe X into two parts $X_1$ and $X_2$, where

$$\begin{aligned} X_1 = \{x \in X \mid A \subseteq B\}\quad ;\quad X_2 = \{x \in X \mid A \supseteq B\} \end{aligned}$$

That is for all $x \in X_1$

$$\begin{aligned} \xi _A(x) \le \xi _B(x),\quad \varphi _A(x) \ge \varphi _B(x) \end{aligned}$$

and, for all $x \in X_2$

$$\begin{aligned} \xi _A(x) \ge \xi _B(x),\quad \varphi _A(x) \le \varphi _B(x) \end{aligned}$$

Thus, by definition of $E(A\cup B)$, we have

$$\begin{aligned} E(A \cup B)& = \frac{1}{N} \sum \limits _{i=1}^N[1-\varPhi (\xi _{A\cup B}(x_i), \varphi _{A\cup B}(x_i))] \\ & = \frac{1}{N} \left[ \sum \limits _{x_i \in X_1}[1-\varPhi (\xi _{B}(x_i), \varphi _{B}(x_i))] \right. \\ &\left. + \sum \limits _{x_i \in X_2}[1-\varPhi (\xi _{A}(x_i), \varphi _{A}(x_i))] \right] \end{aligned}$$

Similarly,

$$\begin{aligned} E(A \cap B)& = \frac{1}{N} \sum \limits _{i=1}^N[1-\varPhi (\xi _{A\cap B}(x_i), \varphi _{A\cap B}(x_i))] \\ & = \frac{1}{N} \left[ \sum \limits _{x_i \in X_1}[1-\varPhi (\xi _{A}(x_i), \varphi _{A}(x_i))]\right. \\ &\left. + \sum \limits _{x_i \in X_2}[1-\varPhi (\xi _{B}(x_i), \varphi _{B}(x_i))] \right] \end{aligned}$$

Therefore,

$$\begin{aligned}&E(A \cup B) + E(A\cap B) \\ &\quad = \frac{1}{N} \left\{ \sum \limits _{x_i \in X_1}[2-\varPhi (\xi _{A}(x_i), \varphi _{A}(x_i))-\varPhi (\xi _{B}(x_i), \varphi _{B}(x_i))]\right. \\ &\quad \left. + \sum \limits _{x_i \in X_2}[2-\varPhi (\xi _{A}(x_i), \varphi _{A}(x_i)-\varPhi (\xi _{B}(x_i), \varphi _{B}(x_i))] \right\} \\ &\quad = \frac{1}{N} \sum \limits _{i=1}^n \left[ 2-\varPhi (\xi _A(x_i),\varphi _A(x_i))-\varPhi (\xi _B(x_i),\varphi _B(x_i))\right] \\ &\quad = \frac{1}{N} \sum \limits _{i=1}^n \left[ \left\{ 1-\varPhi (\xi _A(x_i),\varphi _A(x_i))\right\} \right. \\ &\left.\quad + \left\{ 1-\varPhi (\xi _B(x_i),\varphi _B(x_i))\right\} \right] \\ &\quad = E(A) + E(B) \end{aligned}$$

This prove the result. $\square$

Corollary 1

For any IVIFS A and $A^c$ is the complement of A, we have

$$\begin{aligned} E(A)=E(A^c)=E(A\cup A^c)=E(A\cap A^c) \end{aligned}$$

Theorem 3

The maximum and minimum value of E(A) are independent of its parameters i.e., p and n.

Proof

It has been proved in the Theorem 1 that the E(A) is maximum if and only if A is most IVIFS i.e., $\mu _A(x)=\nu _A(x),\,\, \forall \,x \in X$ and minimum when A is crisp set. Therefore, in order to prove the above result, it is sufficient to show that the maximum and minimum value is constant. Let A be the most IVIFS i.e., $\mu _A(x)=\nu _A(x),\,\, \forall \quad x \in X$, then we get $\mu _A^L(x)=\nu _A^L(x)$ and $\mu _A^U(x)=\nu _A^U(x)$ and hence

$$\begin{aligned} \xi (x)=\mu _A^L(x)+p(\triangle \mu _A(x)) = \nu _A^L(x)+p(\triangle \nu _A(x)) = \varphi (x) \end{aligned}$$

Therefore, by the condition (b) of $\varPhi$, we get $\varPhi (\xi ,\varphi )=0 \Rightarrow \quad E(A)=1$.

If A is crisp set i.e., $\mu _{A}^{L}(x)=\mu _{A}^{U}(x)$ ; $\nu _{A}^{L}(x)=\nu _{A}^{U}(x)$ and $\mu _{A}^{L}(x)+\nu _{A}^{L}(x)=1$, $\mu _{A}^{U}(x)+\nu _{A}^{U}(x)=1$$\forall \,\,x\in X$ then by the condition (a) of $\varPhi$, we get $\varPhi =1$ and hence $E(A)=0$. Thus, maximum and minimum value of E(A) is independent of p and n. $\square$

Here, in the present paper, we have analyzed the effect of different entropy functions on the decision-making process. For it, we have taken the different function of $\varPhi (x,y)$ which are stated as follows:

$$\begin{aligned}&\varPhi _{n,\exp }(x,y)=(x+y)^n e^{1-(x+y)^n} \end{aligned}$$

(5)

$$\begin{aligned}&\varPhi _{n,\sin }(x,y)=(x+y)^n \sin \left( \frac{\pi }{2}(x+y)^n\right) \end{aligned}$$

(6)

$$\begin{aligned}&\varPhi _{n,\log }(x,y)=(x+y)^n \log (2-(x+y)^n) \end{aligned}$$

(7)

$$\begin{aligned}&\varPhi _{n,\log 2}(x,y)=1 - \frac{1}{n}\log \left( (x+y)^n+ 2^{n}(1-(x+y)^n)\right) \end{aligned}$$

(8)

These above defined functions have been explained with a suitable numerical example, which can be read as:

Consider six IVIFNs, namely $A_1=\langle [0,0],[0,0]\rangle$, $A_2=\langle [1,1]$, $[0,0]\rangle$, $A_3=\langle [0.4,0.4]$, $[0.6,0.6]\rangle$, $A_4=\langle [0.1,0.2]$, $[0.3,0.4]\rangle$, $A_5=\langle [0.3,0.4]$, $[0.1,0.2]\rangle$ and $A_6=\langle [0.3, 0.4]$, $[0.5,0.6]\rangle$ defined on $X=\{x\}$. In order to show the effect of the various entropy function by these IVIFNs $A_i (i=1,2,\ldots ,6)$, an analysis has been conducted by taking different values of p and n. The results corresponding to it have been summarized in Table 1 and 2 respectively, and the following conclusions have been drawn.

• (i) The effect of the variation of p on the different entropies $E_{\varPhi _{n,\exp }}$, $E_{\varPhi _{n,\sin }}$, $E_{\varPhi _{n,\log }}$, $E_{\varPhi _{n,\log 2}}$ have been analyzed by taking $n=1$ and their corresponding results are summarized in Table 1. From this table, it has been concluded that by increasing the value of p, the corresponding entropy values are decreasing.

• (ii) On the other hand, the effect of the variation of n on the different entropies is analyzed for a specified value of $p=0.4$ (say) and are summarized in Table 2. From this table, it has been analyzed that for increasing the value of n, the corresponding entropy values are increasing.

Table 1 Effect of p on IVIF Entropy functions values

Table 2 Effect of n on IVIF Entropy functions values

4 Proposed Entropy Based MADM Approach

In this section, a decision-making method by using above defined entropy measure for IVIFSs have been presented followed by an illustrative example for demonstrating the approach.

4.1 Proposed Approach

Let $A=\{A_1,A_2,\ldots ,A_m\}$ be a set of alternatives and $G=\{G_1,G_2,\ldots ,G_n\}$ be set of attributes with completely unknown weights. Assume that these different alternatives $A_i (i=1,2,\ldots ,m)$ are evaluated by the decision makers with respect to the criteria and give their preferences in terms of IVIFNs $\alpha _{ij}=\langle [a_{ij},b_{ij}], [c_{ij},d_{ij}]\rangle$, where $[a_{ij}, b_{ij}] \subset [0,1]$, $[c_{ij}, d_{ij}] \subset [0,1]$ and $b_{ij}+d_{ij} \le 1$, $i=1,2,\ldots ,m; \, j=1,2,\ldots , n$ such that $[a_{ij}, b_{ij}]$ indicates the degree that the alternative $A_i$ satisfies the attribute $G_j$, $[c_{ij},d_{ij}]$ indicates the degree that the alternative $A_i$ doesn’t satisfy the criteria $G_j$ given by the decision maker. Therefore, an interval-valued intuitionistic fuzzy decision matrix is expressed as

Then, the procedure for solving the MADM problem based on entropy measure has been summarized in the following steps:

• (Step 1:) Set $p \in (0,1)$ and then the above defined decision matrix is converted into its entropy matrix by using Eq. (4) corresponding to different functions of $\varPhi$ as defined in the Eqs. (5)-(8) for different values of n. Therefore, the IVIFS entropy matrix E of $A_i$ on $G_j$ can be written as under

  $$\begin{aligned} E(\alpha _{ij})= \begin{pmatrix} E_{11}(\alpha _{11}) &{} E_{12}(\alpha _{12}) &{} \ldots &{} E_{1n}(\alpha _{1n}) \\ E_{21}(\alpha _{21}) &{} E_{22}(\alpha _{22}) &{} \ldots &{} E_{2n}(\alpha _{2n}) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ E_{m1}(\alpha _{m1}) &{} E_{m2}(\alpha _{m2}) &{} \ldots &{} E_{mn}(\alpha _{mn}) \\ \end{pmatrix} \qquad \end{aligned}$$

  (9)

• (Step 2:) Based on the entropy matrix, $E(\alpha _{ij})$ defined in Eq. (9), the degree of divergence $(d_j)$ of the average intrinsic information provided by the correspondence

  on the attribute $G_j$ can be defined as $d_j = 1-\kappa _j$ where $\kappa _j = \sum \nolimits _{i=1}^m E(\alpha _{ij}), j=1,2,\ldots ,n$. Here, the value of $d_j$ represents the inherent contrast intensity of attribute $G_j$, and hence based on it, the attributes weight $\omega _j (j=1,2,\ldots ,n)$ is given as:

  $$\begin{aligned} \omega _j = \frac{d_j}{\sum \nolimits _{j=1}^n d_j} = \frac{1-\kappa _j}{\sum \nolimits _{j=1}^n (1-\kappa _j)} = \frac{1-\kappa _j}{n-\sum \nolimits _{j=1}^n \kappa _j} \end{aligned}$$

  (10)

• (Step 3:) By using the decision matrix D and the attribute weights $\omega =(\omega _1,\omega _2,\ldots ,\omega _n)^T$, the different preferences of each alternative is aggregated into $\vartheta _i$ by using an averaging aggregation operator termed as generalized IVIF weighted averaging (GIVIFWA) operator and is defined as

  $$\begin{aligned} \vartheta _i& = \text {GIVIFWA}(\vartheta _{i1},\vartheta _{i2},\ldots ,\vartheta _{in}) \\ & = \left\langle \omega _1 \vartheta _{i1}^\lambda \oplus \omega _2 \vartheta _{i2}^\lambda \oplus \ldots \oplus \omega _n \vartheta _{in}^\lambda \right\rangle ^{1/\lambda } \\ & = \left\langle \left[ \left( 1-\prod \limits _{j=1}^n (1-a_{ij}^\lambda )^{w_j}\right) ^{1/\lambda }, \left( 1-\prod \limits _{j=1}^n (1-b_{ij}^\lambda )^{w_j}\right) ^{1/\lambda } \right] , \right. \\ &\left[ 1-\left( 1-\prod \limits _{j=1}^{n}(1-(1-c_{ij})^\lambda )^{w_j}\right) ^{1/\lambda },\right. \\ &\left. \left. 1-\left( 1-\prod \limits _{j=1}^{n}(1-(1-d_{ij})^\lambda )^{w_j}\right) ^{1/\lambda } \right] \right\rangle \end{aligned}$$

• (Step 4:) Compute the score value of $\vartheta _i=\langle [a_i,b_i]$, $[c_i,d_i]\rangle$ by score formula: $S(\vartheta _i)=\frac{a_i+b_i-c_i-d_i}{2}$ and hence the best alternative has been selected in accordance with descending values of $S(\vartheta _i)$.

4.2 Numerical Example

The above mentioned approach has been illustrated with a practical example of the decision-maker which can be read as:

An example adapted from Zhang et al [21] has been discussed here from the field of supplier selection problem which contain five alternatives denoted by $A_i(i=1,2,\ldots ,5)$ exist on the six attributes denoted by $G_j (j=1,2,\ldots ,6)$. The rating of these alternatives are measured in the form of interval-valued decision matrix which are shown in Table 3.

Table 3 IVIF decision matrix

Based on this information matrix and by using the different entropies functions of $\varPhi$ as given in Eqs. (5)-(8), the entropy value $E_{ij}$ of each alternative with respect to each criteria are calculated. Hence, the attribute weights corresponding to these entropy functions $E_{\varPhi _{n,\exp }}$, $E_{\varPhi _{n,\sin }}$, $E_{\varPhi _{n,\log }}$ and $E_{\varPhi _{n,\log 2}}$ are computed by using the step 2 of the proposed approach for the different values of $n=1,5,10,100$ and $p=0.1,0.5,0.9$ and are summarized in Table 4. From these weights, it has been concluded that

• (i) For a fixed value of n, the weight vectors corresponding to each attribute are increasing with the increasing of the value of p. On that other hand, by varying the value of n from 1 to 100 correspond to a fixed value of p implies that the value of attribute weights are firstly increasing and then becomes stationary for larger value of n. In other words, the attribute weights are independent w.r.t. the entropy functions as well as for the value of n.

• (ii) It has also been observed from the table that the values of attributes weight corresponding to different types of entropies functions are conservative in nature.

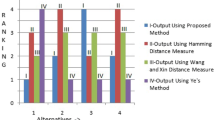
Based on these weights corresponding to different values of n and p, the weighted arithmetic average values for different alternatives $A_i, i=1,2,\ldots ,5$ are computed using GIVIFWA operator corresponding to $\lambda =1$. Finally, the score values of it for the different entropy functions are summarized in Table 5. From this, it has been concluded that corresponding to different values of n and p, the score values lie between -1 and 1. Also, from these scores values, we conclude that the most desirable attributes is $A_4$ corresponding to each value of p and n. On the other hand, the ranking order for the decision maker are shown in the table as (45321) which indicates the order of the different attributes is of form $A_4 \succ A_5 \succ A_3 \succ A_2 \succ A_1$ where $``\succ$” means “preferred to”. Hence, $A_4$ is the most desirable one while $A_1$ is the least one.

Table 4 Attributes weights based on $E_{\varPhi }$

Table 5 Score values $S(A_i)$ corresponding to $\lambda =1$

4.3 Comparison with the Existing Methodologies

In order to compare the performance of the proposed approach with some existing approaches under the IVIFS environment, we conducted a comparison analysis based on the different approaches as given by the authors in [7, 14, 21, 22]. The results corresponding to these are summarized as follows.

4.3.1 Xu [7] Approach

If we take Xu [7] approach for aggregating the different preferences then, the aggregated values by their operator, denoted by $\vartheta _i$, $(i=1,2,3,4,5)$ are summarized as $\vartheta _1 = \langle [0.2665, 0.4319]$, $[0.4019, 0.5260]\rangle$, $\vartheta _2 = \langle [0.4744, 0.6179]$, $[0.1872, 0.3580]\rangle$, $\vartheta _3 = \langle [0.5343$, 0.6399], $[0, 0.2570]\rangle$, $\vartheta _4 = \langle [0.6455, 1.000]$, $[0.00, 0.00]\rangle$ and $\vartheta _5 =\langle [0.5993, 0.7242]$, $[0, 0.1966]\rangle$. Thus, their corresponding score values are $S(\vartheta _1) = -0.1147$, $S(\vartheta _2) = 0.2735$, $S(\vartheta _3) = 0.4586$, $S(\vartheta _4) = 0.8227$ and $S(\vartheta _5) =0.5634$. Hence, the ranking of the alternative is $A_4 \succ A_5 \succ A_3 \succ A_2 \succ A_1$ and the best alternative is $A_4$.

Similarly, if we utilize geometric aggregation operator as proposed by Xu [7], then their overall score values of each alternative is $S(\vartheta _1) = -0.1267$, $S(\vartheta _2) = 0.2273$, $S(\vartheta _3) = 0.3207$, $S(\vartheta _4) = 0.5753$, $S(\vartheta _5) = 0.4249$. Thus, the best alternative is $A_4$.

4.3.2 Ye [14] Approach

If we utilize Ye [14] approach to the considered problem then, the aggregating value corresponding to each alternative is obtained as $\vartheta _1 = \langle [0.2603, 0.4277]$, [0.4071, $0.5343]\rangle$, $\vartheta _2 = \langle [0.4528$, 0.5872], [0.2091, $0.3764]\rangle$, $\vartheta _3 = \langle [0.4958, 0.5993]$, [0.1641, $0.2896]\rangle$, $\vartheta _4 = \langle [0.5782$, 0.7899], [0.0531, $0.1644]\rangle$ and $\vartheta _5 = \langle [0.5379$, 0.6690], [0.1177, $0.2394]\rangle$. Now, by using their proposed novel accuracy function $M(\vartheta _i)=a_i+b_i-1+\frac{c_i+d_i}{2}$ corresponding to alternative $\vartheta _i=\langle [a_i,b_i],[c_i,d_i]\rangle$ (for more detail, we refer to Ye [14]), we get $M(\vartheta _1) = 0.1587$, $M(\vartheta _2) = 0.3328$, $M(\vartheta _3) = 0.3219$, $M(\vartheta _4) = 0.4769$ and $M(\vartheta _5) = 0.3855$. Therefore, the best alternative is $A_4$.

4.3.3 Bai [22] Approach

If we apply Bai [22] approach to the considered problem then, based on their approach, firstly the decision matrix is converted into the score matrix R by using $I(\alpha _{ij})=\frac{a_{ij}+a_{ij}(1-a_{ij}-c_{ij})+b_{ij}+b_{ij}(1-b_{ij}-d_{ij})}{2}$ (for more detail, we refer to Bai [22]), and hence their corresponding score matrix, denoted by R, is given as

$$\begin{aligned} R = \left( \begin{array}{ccccccccccc} 0.3900 &{}&{} 0.4500 &{}&{} 0.3950 &{}&{} 0.4450 &{}&{} 0.3300 &{}&{} 0.4150 \\ 0.4300 &{}&{} 0.7500 &{}&{} 0.6250 &{}&{} 0.6550 &{}&{} 0.5600 &{}&{} 0.7400 \\ 0.5800 &{}&{} 0.8950 &{}&{} 0.7400 &{}&{} 0.8200 &{}&{} 0.4150 &{}&{} 0.7100 \\ 0.7050 &{}&{} 0.9950 &{}&{} 0.8950 &{}&{} 0.9300 &{}&{} 0.6750 &{}&{} 0.7500 \\ 0.7400 &{}&{} 0.6600 &{}&{} 0.8950 &{}&{} 0.5250 &{}&{} 0.9300 &{}&{} 0.5350 \\ \end{array} \right) \end{aligned}$$

Based on this score matrix, if we apply their approach to rank the alternative, then we obtained the relative closeness coefficient of each alternative $A_i$, $(i=1,2,\ldots ,5)$ as $C(A_1) = 0.3964$; $C(A_2) = 0.6029$; $C(A_3) = 0.6608$; $C(A_4) = 0.7850$; $C(A_5) = 0.7267$. Thus, ranking order of the alternative is $A_4\succ A_5 \succ A_3\succ A_2 \succ A_1$ and hence the best alternative is $A_4$.

4.3.4 Zhang et al. [21] Approach

If we analyzed Zhang et al. [21] approach to the considered data corresponding to entropy function $\varPhi _n(x,y)=(x+y)^n$ then the score values $S(A_i)$ corresponding to alternative $A_i (i=1,2,\ldots ,5)$ for $n=1,10, 100; p=0.1, 0.5, 0.9$ are summarized as below

(n, p)	Score values of the alternative					Ranking
	$A_1$	$A_2$	$A_3$	$A_4$	$A_5$
(1, 0.1)	−0.1168	0.2872	0.4647	0.8408	0.5785	$A_4\succ A_5 \succ A_3 \succ A_2 \succ A_1$
(1, 0.5)	−0.1139	0.2817	0.4643	0.8398	0.5754	$A_4\succ A_5 \succ A_3 \succ A_2 \succ A_1$
(1, 0.9)	−0.0968	0.3042	0.4965	0.8526	0.5412	$A_4\succ A_5 \succ A_3 \succ A_2 \succ A_1$
(10, 0.1)	−0.1044	0.2922	0.4855	0.8472	0.5399	$A_4\succ A_5 \succ A_3 \succ A_2 \succ A_1$
(10, 0.5)	−0.1050	0.2905	0.4829	0.8459	0.5429	$A_4\succ A_5 \succ A_3 \succ A_2 \succ A_1$
(10, 0.9)	−0.0951	0.3024	0.4977	0.8510	0.5213	$A_4\succ A_5 \succ A_3 \succ A_2 \succ A_1$
(100, 0.1)	−0.1021	0.2968	0.4917	0.8503	0.5349	$A_4\succ A_5 \succ A_3 \succ A_2 \succ A_1$
(100, 0.5)	−0.1021	0.2967	0.4916	0.8503	0.5349	$A_4\succ A_5 \succ A_3 \succ A_2 \succ A_1$
(100, 0.9)	−0.1029	0.2941	0.4883	0.8481	0.5351	$A_4\succ A_5 \succ A_3 \succ A_2 \succ A_1$

From their results, it has been seen that for these different pairs, the ranking order remains same and hence the best alternative is $A_4$.

4.4 Sensitivity Analysis

In order to analyze the impact of the parameter $\lambda$ during the aggregation phase by the GIVIFWA operator as described in step 3, an experiment has been conducted in which the effect of the the parameter $\lambda$ on to the ranking of the alternative have been analyzed. For it, the different values of $\lambda$’s, ($\lambda \rightarrow 0, \lambda = 0.4, 0.8$, 1, 2, 10, 15, 25, 50) have been taken and by varying the value of n from 1 to 100 corresponding to $p=0.5$. Based on these values, the proposed approach steps have been performed for each pairs of n and $\lambda$ and the score values corresponding to each entropy functions $E_{\varPhi _{n,\exp }}$, $E_{\varPhi _{n,\sin }}$, $E_{\varPhi _{n,\log }}$ and $E_{\varPhi _{n,\log 2}}$ are computed and are summarized in Table 6. From this analysis, it has been observed that the best alternative is remain same i.e., $A_4$ which shows that the proposed approach is more stable and can be effectively used to solve the decision-making problems in a more efficient ways.

Table 6 Score values and ranking by taking different values of $\lambda$ and $p=0.5$

5 Conclusion

In this manuscript, multi-attribute decision making method based on entropy weights has been proposed under IVIFSs environment. Different entropy functions have been proposed for accessing the impact of the decision-making parameters and hence the weight vector corresponding to each attribute is computing by using entropy measures. Based on it, different preferences are aggregated by using generalized averaging aggregation operator under IVIFS environment. Further, the impact of the different decision makers’ parameters on the ranking of the alternative has been done. The approach has been illustrated with a numerical example for showing their effectiveness as well as stability. From their computed results, it has been observed that the proposed approach can be equivalently utilize to solve the MADM problems. In the future, we may extend this technique to other domains such as multi-objective programming, clustering, uncertain system and pattern recognition.