Theoretical Study on Vibration of Non-homogeneous Tapered Visco-Elastic Rectangular Plate

Abstract

A temperature-thickness coupling problem of non-homogeneous rectangular plate is analyzed. Here authors considered bi-parabolic variation in temperature i.e. parabolic in x-direction and parabolic in y-direction while variation in plate’s thickness is assumed bi-linear i.e. linear in x-direction and linear in y-direction. To characterize the non-homogeneity present in plate’s material, authors considered that poisson ratio and density of the plate’s material vary exponentially and linearly in one direction respectively. Along with, material of the plate is considered isotropic and visco-elastic. Rayleigh Ritz approach has been applied to find the time period and deflection for first two modes of vibration for diverse values of non-homogeneity constant, taper constant, density parameter, aspect ratio and thermal gradient. Results for both modes of vibration are shown in tabular form.

1 Introduction

In-depth knowledge of the plate’s behaviour under vibration helps to see their potential in several areas i.e. machine designs, acoustical components, naval structures etc. The consideration of non-homogeneous plate’s material together with variation in thickness of the structural components not only ensures the reduction in weight and size but also meet the desirability of high strength in various technological situation of aerospace industry, ocean engineering and optical equipments.

In the available literature, appreciable work has been done on thermally induced vibrations of homogeneous rectangular plate of variable thickness as compared to non-homogeneous plate. Therefore authors investigated the vibrational behaviour of tapered non-homogeneous rectangular plate in which non homogeneity occurs in varying poisson ratio and density of the plate’s material.

In this paper, our endeavor is to provide a mathematical model for analyzing the vibrational behaviour of visco-elastic non-homogeneous isotropic rectangular plate with bi-linearly varying thickness and bi-parabolic temperature variation. Rayleigh Ritz method is used to calculate time period and deflection for first two modes of vibration at various values of density parameter, taper constant, thermal gradient, aspect ratio and non-homogeneity constant. It is also assumed that rectangular plate is clamped on all the four edges. All the material constants used in numerical calculation have been taken for ‘DURALIUM’, an alloy of aluminium. Findings of the present paper are given in tabular form.

2 Literature Survey

A collection of research papers published in journals, monographs, books etc. in last six decades is presented as follows:

Abu et al. [1] discussed two dimensional transient wave propagation in visco-elastic layered media. Avalos and Laura [2] reported about the transverse vibrations of a simply supported plate of generalized anisotropy with an oblique cut out. Bambill et al. [3] carried out an experiment on transverse vibrations of an orthotropic rectangular plate of linearly varying thickness with free edges. Chyanbin et al. [4] gave results on vibration suppression of composite sandwich beams. Gutirrez et al. [5] investigated vibrations of rectangular plates of bi-linearly varying thickness with general boundary conditions. Gupta and Singhal [6] presented an investigation on free vibration of non-homogeneous orthotropic visco-elastic rectangular plate having parabolic thickness variation. Here, authors discussed linear temperature variation as well as linear density variation. Gupta et al. [7] studied the vibrations of non-homogeneous rectangular plate with bi-directional thickness variation and linear density variation along with linear temperature variation. Recently, Khanna and Kaur [8] obtained first two modes of frequencies of non-homogeneous rectangular plate with exponential thickness and temperature variation. Lal et al. [9] used boundary characteristic orthogonal polynomials to analyze transverse vibrations of non-homogeneous rectangular plates with uniform thickness. Lal and Kumar [10] used characteristic orthogonal polynomials in the study of transverse vibrations of nonhomogeneous rectangular orthotropic plates with bi-linear thickness variation. Liessa [11] discussed vibrations of rectangular plate with general elastic boundary supports. Leissa [12] provided excellent data for vibration of plates of different shapes with different boundary conditions in his monograph. Patel et al. [13] discussed the inflence of stiffeners on natural frequencies of rectangular plate with simply supported edges. Sharma et al. [14] observed the effect of pasternak foundation on axisymmetric vibration of polar orthotropic annular plates of varying thickness. Wang and Chen [15] discussed the axisymmetric vibration and damping analysis of rotating annular plates with constrained damping layer treatments.

3 Materials and Methods

3.1 Fourth Order Differential Equation of Motion

Differential equation of an isotropic visco-elastic rectangular plate is [16]:

$$ {M_{x,xx}} + 2{M_{xy,xy}} + {M_{y,yy}} = \rho h{w_{,tt}} $$

(1)

where

$$\begin{aligned} {M_{x}}& =- \tilde{D}{D_1}[{w_{,xx}} + \nu {w_{,yy}}] \\ {M_{y}} & =- \tilde{D}{D_1}[{w_{,yy}} + \nu {w_{,xx}}] \quad \text {and} \\ \quad {M_{xy}} & =- \tilde{D}{D_1}(1 - \nu ){w_{,xy}} \end{aligned}$$

(2)

A comma in the suffix denotes partial differentiation of that variable with respect to suffix variable. On using Eq. (2) in Eq. (1), one obtains:

$$\begin{aligned} & \tilde{D}\left[ {{D_1}({w_{,xxxx}} + 2{w_{,xxyy}} + {w_{,yyyy}}) + 2{D_{1,x}}({w_{,xxx}} + {w_{,xyy}})} \right. \\ & \quad +2{D_{1,y}}({w_{,yyy}} + {w_{,yxx}}) + {D_{1,xx}}({w_{,xx}} + \nu {w_{,yy}}) \\ & \quad \left. {+ {D_{1,yy}}({w_{,yy}} + \nu {w_{,xx}}) + 2(1 - \nu ){D_{1,xy}}{w_{,xy}}} \right] + \rho h{w_{,tt}}= 0 \end{aligned}$$

(3)

Solution of Eq. (3) can be taken in the form of the product of two functions by using seperation of variables method [16]:

$$w(x,y,t) = W(x,y)T(t)$$

(4)

After using Eq. (4) in Eq. (3), one gets

$$\begin{aligned} & \left[ {{D_1}({W_{,xxxx}}+ 2{W_{,xxyy}} + {W_{,yyyy}})} \right. \\ &\quad +2{D_{1,x}}({W_{,xxx}}+{W_{,xyy}}) + 2{D_{1,y}}({W_{,yyy}} + {W_{,yxx}}) \\ & \quad + {D_{1,xx}}({W_{,xx}} + \nu {W_{,yy}}) + {D_{1,yy}}({W_{,yy}} + \nu {W_{,xx}}) \\ & \quad \left. { + 2(1 - \nu ){D_{1,xy}}{W_{,xy}}} \right] /\rho hW= - \frac{{\ddot{T}}}{{\tilde{D}T}} \end{aligned}$$

(5)

Here dot denotes differentiation with respect to t.

Equation (5) will exist iff both of its sides are equal to a positive constant, say $\omega ^2$. Therefore one can obtain :

$$\begin{aligned} & \left[ {{D_1}({W_{,xxxx}} + 2{W_{,xxyy}} + {W_{,yyyy}})} \right.\\ & \quad + 2{D_{1,x}}({W_{,xxx}} + {W_{,xyy}}) + 2{D_{1,y}}({W_{,yyy}} + {W_{,yxx}}) \\ & \quad + {D_{1,xx}}({W_{,xx}} + \nu {W_{,yy}}) + {D_{1,yy}}({W_{,yy}} + \nu {W_{,xx}}) \\ & \quad \left. { + 2(1 - \nu ){D_{1,xy}}{W_{,xy}}}\right] - \rho {\omega ^2}hW=0 \end{aligned}$$

(6)

and

$$\begin{aligned} \ddot{T} + {\omega ^2} \tilde{D}T = 0 \end{aligned}$$

(7)

Equations (6) and (7) represent the differential equations of motion and time function for non-homogeneous rectangular plate respectively. Here, $D_1$ is flexural rigidity of rectangular plate i.e.

$$\begin{aligned} {D_1}= \frac{{E{h^3}}}{{12(1 - {\nu ^2})}} \end{aligned}$$

(8)

3.2 Formulation of Frequency Equation

Rayleigh Ritz technique is applied to solve the frequency equation. This method is completely depends upon the law of conservation of energy according to which maximum strain energy $(E_s)$ must be equal to the maximum kinetic energy $(E_k)$. So it is necessary for the problem under consideration that [17]:

$$\begin{aligned} \delta ({E_s} - {E_k})=0 \end{aligned}$$

(9)

where,

$$\begin{aligned} E_k=\frac{1}{2}\rho \omega ^2\int _0^a\int _0^b hW^2 dydx \end{aligned}$$

(10)

and

$$\begin{aligned} {E_s} & = \frac{1}{2}\int _0^a {\int _0^b {{D_1}\left\{ {{{({W_{,xx}})}^2} + {{({W_{,yy}})}^2}} \right. } } \\ & \left.{ \quad 2\nu {W_{,xx}}{W_{,yy}} + 2(1 - \nu )(W_{,xy})^2} \right\} dydx \end{aligned}$$

(11)

3.3 Assumptions Required

3.3.1 Temperature Variation

Since most of machines or mechanical structures work under the influence of high temperature variations, it becomes necessary to investigate the effect of variation in temperature on vibrational behaviour of the structure or system. In present study, authors assumed bi-parabolic temperature variation as:

$$\begin{aligned} \tau = {\tau _0}\left( {1-\frac{x^2}{a^2}} \right) \left( {1 - \frac{y^2}{b^2}} \right) \end{aligned}$$

(12)

For most of the engineering materials, the temperature dependence on the modulus of elasticity can be expressed as [18]:

$$\begin{aligned} E = {E_0}(1 - \gamma \tau ) \end{aligned}$$

(13)

where $E_0$ is the value of the Young’s modulus at reference temperature i.e. $\tau =0$ and $\gamma$ is the slope of the variation of E with $\tau$. After using Eq. (12) in Eq. (13), one gets

$$\begin{aligned} E = {E_0}\left\{ {1 - \alpha \left( {1 - \frac{x^2}{a^2}} \right) \left( {1 - \frac{y^2}{b^2}} \right) } \right\} \end{aligned}$$

(14)

where $\alpha =\gamma \tau _0 (0\le \alpha <1)$ is thermal gradient.

3.3.2 Thickness Variation

Since plates of variable thickness are vigorously used in mechanical structures and designs, it becomes the need of the hour to investigate that how varying thickness affects the vibration of any structure or design. Hence authors studied bi-linear variation in thickness as:

$$\begin{aligned} h = {h_0}\left(1+\beta \left(\frac{x}{a}+\frac{y}{b}\right)\right) \end{aligned}$$

(15)

where $h_0$ is thickness of the plate at $x=y=0$ and $\beta(0\le \beta <1)$ is taper constant.

3.3.3 Variation in poisson ratio and density

Non-homogeneous plates have wide applications in engineering designs and structures and also, non-homogeneity directly affects the physical properties of the material. Here authors emphasized to study the non-homogeneity of the material by taking exponential variation in poisson ratio along with linear variation in density of the material as:

$$\begin{aligned} \nu = {\nu _0}{e^{{\alpha _1}x/a}} \end{aligned}$$

(16)

where $\nu _0$ denotes poisson ratio at reference temperature i.e. $\tau = 0$ and $\alpha _1 (0\le \alpha _1<1$) is non-homogeneity constant.

and

$$\begin{aligned} \rho ={\rho _0} \left (1+{\alpha _2}\frac{x}{a}\right) \end{aligned}$$

(17)

where $\rho _0$ is density at $x = 0$ and $\alpha _2$($0\le \alpha _2\le 1$) is density parameter.

After using Eq. (14), Eq. (15) and Eq. (16) in Eq. (8), one obtains:

$$\begin{aligned} {D_1} = \frac{{{E_0}\left\{ {1 - \alpha \left( {1 - \frac{x^2}{a^2}} \right) \left( {1-\frac{y^2}{b^2}} \right) } \right\} {{\left\{ {{h_0}\left( {1 + \beta (\frac{{ x}}{a}} +\frac{y}{b}) \right) } \right\} }^3}}}{{12\left( {1 - {\nu _0}^2{e^{\frac{{2{\alpha _1}x}}{a}}}} \right) }} \end{aligned}$$

(18)

3.3.4 Boundary Conditions

Rectangular plate is assumed clamped at the boundary. A set of algebric and partial differential equations for clamped boundary condition is given as follows:

$$ \left. \begin{aligned} W = {W_{,x}} = 0, \; x = 0,a \\ W = {W_{,y}} = 0, \; y = 0,b \\ \end{aligned} \right\} $$

(19)

To satisfy Eq. (19), the corresponding two-term deflection function is taken as [9]:

$$\begin{aligned} W =&\ {\left[ {\left( {\frac{x}{a}} \right) \left( {\frac{y}{b}} \right) \left( {1 - \frac{x}{a}} \right) \left( {1 - \frac{y}{b}} \right) } \right] ^2} \nonumber \\&\, \left[ {{F_1} + {F_2}\left( {\frac{x}{a}} \right) \left( {\frac{y}{b}} \right) \left( {1 - \frac{x}{a}} \right) \left( {1 - \frac{y}{b}} \right) } \right] \end{aligned}$$

(20)

where $F_1$ and $F_2$ are two arbitrary constants.

3.4 Solution of Frequency Equation

To simplify and parameterize the present problem, non-dimensionalization is introduced as:

$$\begin{aligned} X = \frac{x}{a}, \quad Y = \frac{y}{a} \end{aligned}$$

(21)

With the help of Eq. (21); Eqs. (10) and (11) become:

$$\begin{aligned} {E_k}^* = \frac{1}{2}\rho _0 {\omega ^2}{a^2}{h_0}\int _0^1 {\int _0^{b/a} {(1 + \beta (X+\frac{a}{b}Y))(1+\alpha _2X){W^2}dYdX} } \end{aligned}$$

(22)

and

$$\begin{aligned} {E_s}^* & =\phi \int _0^1 {\int _0^{b/a} {\left\{ {\frac{{\left( {1 - \alpha (1 - X^2)\left( {1 - \frac{a^2}{b^2}Y^2} \right) } \right) {{\left( {1 + \beta (X+\frac{a}{b}Y)} \right) }^3}}}{{\left( {1 - {\nu _0}^2{e^{2{\alpha _1}X}}} \right) }}} \right\} } } \\ & \quad \{ {({W_{,XX}})^2} + {({W_{,YY}})^2} + 2{\nu _0}{e^{{\alpha _1}X}}{W_{,XX}}{W_{,YY}} \\ & \quad + 2(1 - {\nu _0}{e^{{\alpha _1}X}}){({W_{,XY}})^2}\} dYdX \end{aligned}$$

(23)

where $\phi = \frac{E_0h_0^3}{24a^2}$.

After substituting $E_k^*$ and $E_s^*$ from Eqs. (22) and (23) in Eq. (9), one obtains

$$\begin{aligned} \delta ({E_s}^*-{\lambda ^2}{E_k}^*) = 0 \end{aligned}$$

(24)

Here ${\lambda ^2} = \frac{{12\rho _0 {\omega ^2}{a^4}}}{{{E_0}{h_0}^2}}$ is frequency parameter.

Equation (24) consists two unknown constants i.e. $F_1$ and $F_2$. These two constants are to be determined as follows

$$\frac{{\delta ({E_s}^*-{\lambda ^2}{E_k}^*)}}{{\delta {F_n}}} = 0, \quad n = 1,2$$

(25)

From Eq. (25), one obtains

$${Q_{{n_1}}}{F_1} + {Q_{{n_2}}}{F_2} = 0, \quad n = 1,2$$

(26)

On assuming $F_1=1$, one can get $F_2$ from Eq. (26) as $( {\frac{-Q_{11}}{Q_{12}}})$ for $n=1$.

For a non-trivial solution, the determinant of the coefficient of Eq. (26) must be zero. Therefore one gets

$$\begin{aligned} \left| {\begin{array}{ll} {{Q_{11}}} & {{Q_{12}}} \\ {{Q_{21}}} & {{Q_{22}}} \\ \end{array} } \right| = 0 \end{aligned}$$

(27)

Equation (27) gives a quadratic equation in $\lambda ^2$ which can provide desired values of $\lambda ^2$ .

On using $F_1$ and $F_2$ in Eq. (20), one gets:

$$\begin{aligned} W=&{\left[ {XY\left( {\frac{a}{b}} \right) (1 - X)\left( {1 - \left( {\frac{{aY}}{b}} \right) } \right) } \right] ^2} \nonumber \\&\, \left[ {1 + \left( {\frac{{ - {Q_{11}}}}{{{Q_{12}}}}} \right) XY\left( {\frac{a}{b}} \right) (1 - X)\left( {1 - \left( {\frac{{aY}}{b}} \right) } \right) } \right] \end{aligned}$$

(28)

Time period of the vibration of visco-elastic plate is given by

$$\begin{aligned} K=\frac{2\times \pi }{\omega } \end{aligned}$$

(29)

3.5 Solution of Differential Equation for Time Function

For Kelvin’s model, visco-elastic operator $\tilde{D}$ is defined as [18]:

$$\begin{aligned} \tilde{D}\equiv \left\{ {1 + \left( {\frac{\eta }{G}} \right) \left( {\frac{d}{{dt}}} \right) } \right\} \end{aligned}$$

(30)

Using Eq. (30) in Eq. (7), one get

$$\begin{aligned} \ddot{T} + {\omega ^2}\left( {\frac{\eta }{G}} \right) \dot{T} + {\omega ^2}T = 0 \end{aligned}$$

(31)

Solution of Eq. (31) comes out as:

$$\begin{aligned} T(t) = {e^{{a_1}t}}[{B_1}\cos {b_1}t + {B_2}\sin {b_1}t] \end{aligned}$$

(32)

where

$$\begin{aligned} {a_1} = \frac{{ - {\omega ^2}\eta }}{{2G}} \end{aligned}$$

(33)

and

$$\begin{aligned} {b_1} = \omega \sqrt{1 - {{\left( {\frac{{\omega \eta }}{{2G}}} \right) }^2}} \end{aligned}$$

(34)

where $B_1$ and $B_2$ are constants which can be determined easily from initial conditions of the plate.

Let us consider the initial conditions of the plate as follows:

$$ T = 1\quad {\text{and}} \quad {\dot{T}} = 0 \quad {\text{at}} \quad t = 0 $$

(35)

On using Eq. (35) in Eq. (32), one obtains

$$\begin{aligned} {B_1}=1 \quad {\text { and }}\quad {B_2}=\frac{\frac{\omega ^2\eta }{G}}{2{b_1}}=\frac{-{a_1}}{b_1} \end{aligned}$$

(36)

Using Eq. (36) in Eq. (32), one obtains

$$\begin{aligned} T(t)={e^{{a_1}t}}\left[ {\cos {b_1}t + \left( { - \frac{{{a_1}}}{{{b_1}}}} \right) \sin {b_1}t} \right] \end{aligned}$$

(37)

After using Eqs. (37) and (28) in Eq. (4), deflection w can be expressed as

$$\begin{aligned} w & =\left[ {XY\left( {\frac{a}{b}} \right)({1 - X} ) \left( {1 - \left( {\frac{{aY}}{b}} \right) } \right) }\right] ^2\\& \quad \left[ {1 + \left( {\frac{{ - {Q_{11}}}}{{{Q_{12}}}}} \right)XY\left( {\frac{a}{b}} \right) (1 - X)\left( {1 - \left( {\frac{{aY}}{b}} \right) } \right) } \right] \\&\quad \times \left[ {{e^{{a_1}t}}\left\{ {\cos {b_1}t +\left( {\frac{{ - {a_1}}}{{{b_1}}}} \right) \sin {b_1}t} \right\} } \right]\end{aligned}$$

(38)

4 Results and Discussion

In calculation, the following parameters are used for duralium [6] i.e.

$$\begin{aligned} E &= 7.08 \times {10^{10}}\frac{\rm N}{{{\rm M}^{2}}} ,\\ G &=\ 2.632 \times {10^{10}}\frac{\rm N}{{{{\rm M}^{2}}}} ,\\ \eta & = 14.612 \times {10^5}\frac{{\rm Ns}}{{{{\rm M}^{2}}}} , \\ \rho _0 &= 2.80 \times {10^3}\frac{{\rm Kg}}{{{{\rm M}^{3}}}} ,\\ \nu _0 & = 0.345, h_0=0.01{\rm M}. \end{aligned}$$

First two modes of time period at fixed aspect ratio $(a/b=1.5)$ with increasing values of density parameter $(\alpha _2)$ are tabulated in Table 1 for the following cases:

(i) $\alpha =\alpha _1=\beta =0.0$, (ii) $\alpha =\alpha _1=\beta =0.2$, (iii) $\alpha =\alpha _1=\beta =0.6$.

A continuous increment in time period for both modes of vibration is found as $\alpha _2$ increases from 0.0 to 1.0 for case (i) to case (iii). Also authors noticed that time period for both modes of vibration decreases as combined values of $\alpha ,\alpha _1$ and $\beta$ increase from case (i) to case (iii) for all values of $\alpha _2$.

In Table 2; time period for first two modes of vibration with increasing values of aspect ratio $(\frac{a}{b})$ are given at fixed $\beta =\alpha =0.2$ for the following cases:

(iv) $\alpha _1=\alpha _2=0.0$, (v) $\alpha _1=\alpha _2=0.2$, (vi) $\alpha _1=\alpha _2=0.6$

From Table 2; it is found that as aspect ratio increases from 0.25 to 1.5, time period for both modes of vibration decreases continuously for case (iv) to case (vi). Also time period increases as combined values of $\alpha _1$ and $\alpha _2$ increase from case (iv) to case (vi) for all values of aspect ratio.

Authors calculated first two modes of deflection for various values of plate parameters at $T=0\,\hbox{K}$ and 5K in Tables 3, 4, 5, 6, and 7. Further expression of W i.e. W(X, Y) is symmetrical about X in its domain (0,1) i.e.

$$W(X,Y,t)=W(1-X,Y,t) \quad \text{for}\, \text{all} \quad X, Y \quad \text{in}\, \text{the}\, \text{domain}\, \text{of} \, \text{plate} $$

Authors tabulated deflection for both modes of vibration at $Y=0.2$ and $Y=0.6$ in Tables 3, 4, 5 and 6. In Table 7, authors tabulated deflection for both modes of vibration at $Y=0.2$ only.

Different combinations and values of plate parameters in Tables 3, 4, 5, 6 and 7 are summaried as follows:

• Table 3: $\alpha = \beta = \alpha _2 = 0.0;\frac{a}{b} = 1.5;{\alpha _1} = 0.0,0.4,0.8$

• Table 4: $\alpha = \beta = \alpha _1 = 0.2;\frac{a}{b} = 1.5;{\alpha _2} = 0.0,0.4,0.8$

• Table 5: $\beta = \alpha _1 = \alpha _2 = 0.0;\frac{a}{b} = 1.5;{\alpha } = 0.0,0.4,0.8$

• Table 6: $\alpha = \alpha _1 = \alpha _2 = 0.0;\frac{a}{b} = 1.5;{\beta } = 0.0,0.4,0.8$

• Table 7: $\alpha = \beta = \alpha _1 = \alpha _2 = 0.2;\frac{a}{b} = 0.5,1.0,1.5$

In Tables 3, 4, 5 and 6; at $Y=0.2$; first mode of deflection increases from 0 up to a maximum value and then decreases to 0 as X increases from 0.0 to 1.0 for $T=0\,\hbox{K}$ and $T=5\,\hbox{K}$. But second mode of deflection increases from 0 and then starts decreasing up to a minimum value and further increases and finally decreases to 0 as X increases from 0.0 to 1.0 for $T=0\,\hbox{K}$ and $T=5\,\hbox{K}$.

At $Y=0.6$, deflection for both modes of vibration first increases from 0 up to maximum value and then decreases to 0 with increasing values of X for $T=0\,\hbox{K}$ and $T=5\,\hbox{K}$.

Here, variations in deflection for both modes of vibration with respect to corresponding plate parameters in Tables 3, 4, 5 and 6 are analyzed for all values of X and Y as follows:

Table 3: At $T=0\,\hbox{K}$, deflection for both the modes of vibration increases continuously as $\alpha _1$ increases from 0.0 to 0.8.

At $T=5\,\hbox{K}$, first mode of deflection decreases while second mode of deflection increases as $\alpha _1$ increases from 0.0 to 0.8.

Table 4: At $T=0\,\hbox{K}$, an acute decrement is noticed in deflection for both modes of vibration as $\alpha _2$ increases from 0.0 to 0.8.

At $T=5\,\hbox{K}$, first mode of deflection increases rapidly while second mode of deflection decreases as $\alpha _2$ increases from 0.0 to 0.8.

Table 5: It is interesting to note that deflection for both modes of vibration continuously increases as $\alpha$ increases from 0.0 to 0.8 at $T=0\,\hbox{K}$ and $T=5\,\hbox{K}$.

Table 6: At $T=0\,\hbox{K}$, values of deflection for both modes of vibration increase very slowly with increasing values of $\beta$ from 0.0 to 0.8.

At $T=5\,\hbox{K}$, first mode of deflection decreases while second mode of deflection increases very rapidly as $\beta$ increases from 0.0 to 0.8.

In Table 7, deflection for both the modes of vibration first increases from 0 up to a maximum value and then decreases to 0 as X increases from 0.0 to 1.0 at $\frac{a}{b}=0.5,1.0$ for $T=0\,\hbox{K}$ and $T=5\,\hbox{K}$. For $\frac{a}{b}=1.5$, variation in first mode of deflection remains same but second mode starts from 0 and increases up to a certain value after that decreases and again increases and finally decreases to 0 as X varies from 0.0 to 1.0 for $T=0\,\hbox{K}$ and $T=5\,\hbox{K}$.

Table 1 Time period $(\times 10^{-5})$ versus density parameter for fixed aspect ratio (a/b = 1.5)

Table 2 Time period $(\times 10^{-5})$ versus aspect ratio for fixed taper constant $(\beta =0.2)$ and thermal gradient $(\alpha =0.2)$

Table 3 Deflection $(\times 10^{-5})$ versus non-homogeneity constant for $\alpha = \beta =\alpha _2= 0.0; \frac{a}{b} = 1.5$ at T = 0 K and T = 5 K

Table 4 Deflection $(\times 10^{-5})$versus density parameter for $\alpha = \beta =\alpha _1= 0.2; \frac{a}{b} = 1.5$ at T = 0 K and T = 5 K

Table 5 Deflection $(\times 10^{-5})$ versus thermal gradient for $\beta =\alpha _1 = \alpha _2= 0.0; \frac{a}{b} = 1.5$ at T = 0 K and T = 5 K

Table 6 Deflection $(\times 10^{-5})$ versus taper constant for $\alpha =\alpha _1 = \alpha _2= 0.0; \frac{a}{b} = 1.5$ at T = 0 K and T = 5 K

Table 7 Deflection $(\times 10^{-5})$ versus aspect ratio for $\alpha = \beta =\alpha _1 =\alpha _2=0.2$; at T = 0 K and T = 5 K

5 Conclusions

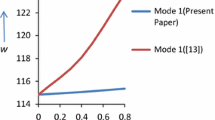
In Table 8, authors compared the frequency for first two modes of vibration of present paper with [8] at $\alpha _1=0.8,\alpha _2=0.0,\frac{a}{b}=1.5$ for various values of $\alpha$ and $\beta$. Here authors found that frequency for both modes of vibration in this paper is greater than [8] at corresponding values of plate’s parameters. Therefore, authors conclude the following:

• 1. Consideration of varying poisson ratio due to non-homogeneous nature of plate’s material affects the vibrational characteristics of the plate.

• 2. Frequency, in case of bi-parabolic temperature variations i.e. present paper, is more than as linear temperature variation i.e. [8].

• 3. By appropriate tapering and considering suitable values of plate’s parameters, desired values of time period and deflection can be obtained.

Table 8 Comparison of the frequencies of present problem with [8]* at $\alpha _1=0.8$ , $\alpha _2=0.0$, $\frac{a}{b}=1.5$