Generalized integral transform solution for free vibration of orthotropic rectangular plates with free edges

Abstract

Free vibration of orthotropic rectangular thin plates of constant thickness with two opposite edges clamped and one or two edges free is analyzed by generalized integral transform technique. Numerically stable eigenfunctions in exponential function forms of Euler–Bernoulli beams with appropriate boundary conditions are adopted for each direction of the plate. The governing fourth-order partial differential equation for the mode function of free vibration is transformed into a system of linear equations, by integral transform in both directions of the rectangular plate. The boundary conditions at free edges are satisfied exactly by considering the terms generated in the transformed equations by integration by parts, which are absent in the equations by traditional Rayleigh–Ritz method. The natural frequencies of free vibration of orthotropic rectangular thin plates obtained by the proposed integral transform solution are compared with available results in the literature and numerical solutions by finite element analysis, showing excellent agreement and high convergence rate.

1 Introduction

The present work addresses the free vibration of rectangular plate with one or two free edges, which has received continual attention in the literature [1,2,3,4,5,6,7,8,9,10,11]. It is well known that exact Levy’s solutions exist for free vibration of rectangular plates when there is a pair of simply supported opposite edges. The Rayleigh–Ritz method has been used widely to determine free vibration frequency for other combinations of boundary conditions. Leissa [1] presented a comprehensive study of free vibration of rectangular plates and pointed out that among 21 combinations of simply supported, clamped and free boundary conditions at the four edges of a rectangular plate, exact solutions exist for six combinations with at least a pair of simply supported opposite edges (SSSS, SCSC, SCSS, SCSF, SSSF, SFSF), with the four letters indicating the boundary conditions at the edges in counterclockwise order starting from the left edge. Among the remaining 15 combinations of boundary conditions, three combinations do not involve a free edge (CCCC, CCCS, CCSS). For these three cases, the Rayleigh–Ritz method based on corresponding beam functions for the pair of opposite boundary conditions of the rectangular plate generates accurate results for the free vibration as the plate boundary conditions on all edges are exactly satisfied by the trial functions used in the Rayleigh–Ritz method. There are still 12 combinations of boundary conditions that involve at least one free edge. For rectangular plates with at least a free edge, the Rayleigh–Ritz method based on beam functions can only generate approximate results for the natural frequencies of free vibration, as the beam functions do not satisfy the plate boundary conditions at a free edge.

The difficulty with rectangular plate with at least one free edge has received special attention in the literature. A number of methods have been applied to tackle the problem. Bhat and Liew et al. [2, 12] used a set of beam characteristic orthogonal polynomials in the Rayleigh–Ritz method to obtain natural frequencies of rectangular plates. The orthogonal polynomials are generated by using a Gram–Schmidt process recursively from the first function that is constructed to satisfy all boundary conditions of the corresponding beam problem associated with the pair of opposite boundary conditions of the plate problem. Dickson and Di Blasio [3] showed that the orthogonal polynomials approach generated excellent results, with simpler first functions compared with Bhat [2] who used order four or five polynomial for the first function. Mizusawa [4] used B-Spline functions in the Rayleigh–Ritz method for isotropic rectangular plates with free edges. Shu and Du [5] proposed a generalized approach to implement general boundary conditions in the GDQ method for free vibration analysis of rectangular plates. Rossi et al. [6] used an optimized Rayleigh–Ritz method and a pseudo-Fourier expansion containing a number of optimization parameters. Kshirsagar and Bhaskar [7] showed that Levy solutions could be used in untruncated infinite series superposition method (UISSM) for any combination of boundary conditions of rectangular plates. Khov et al. [8] presented an exact series method for static and dynamic analyses of orthotropic plates with general boundary conditions, based on the expansion of the displacement function in a 2-D Fourier cosine series supplemented by several 1-D series. Eftekhari and Jafari [9, 10] proposed an alternative Ritz formulation for free vibration of rectangular plates with free edges, based on orthonormal trial functions [2, 3]. Integrations by parts are carried out in both edge directions to implement all general equations on each edge. Xing and Liu [13] obtained exact solutions for free vibrations of orthotropic rectangular thin plates using separation of variables method and presented exact solutions of three configurations (G-G-C-C, S-G-C-C and C-C-C-G) for the first time (where G stands for guided boundary condition). Recently, Banerjee et al. [11] developed the dynamic stiffness matrix of a rectangular plate for general cases to solve the free vibration problem of rectangular plates. Liang et al. [14, 15] proposed a semi-analytical method for the transient response of functionally graded material (FGM) rectangular plates under various boundary conditions, combining the state space method, differential quadrature method and numerical inversion of Laplace transform.

Recently, generalized integral transform technique (GITT) has been applied to obtain analytical solution of bending problem of orthotropic rectangular thin plate with two opposite edges clamped [16]. Among five sets of boundary conditions treated, three sets involve one or two free edges. The boundary conditions at free edges of the rectangular plate were treated exactly by carrying out integral transform of the boundary conditions along the free edge direction. Generalized integral transform technique is a hybrid analytical–numerical method that has been applied successfully in a wide range of flow and heat transfer problems [17,18,19,20], as well as in static and dynamic structural analyses [21,22,23,24,25,26,27,28,29,30,31,32,33,34]. In this work, the free vibration of orthotropic thin rectangular plates with a pair of opposite edges clamped and one or two free edges (CSCF, CCCF, CFCF) is studied analytically by using generalized integral transform technique. As the traditional expressions for eigenfunctions of Euler–Bernoulli beams in combinations of hyperbolic functions and trigonometric functions are not suitable for numerical implementations involving high-order modes [35,36,37,38], numerically stable expressions for eigenfunctions of Euler–Bernoulli beams with corresponding boundary conditions, in exponential function forms, are adopted as base functions for integral transform. Additional terms due to the difference between the boundary conditions of beam and plate at free edges of the rectangular plate are represented exactly by integral transform. The governing equation and all boundary conditions are integral-transformed into an infinite system of linear algebraic equations for the transformed coefficients. The infinite system of equations is truncated at a sufficiently high order to a finite size linear system of homogeneous equations. The eigenvalues and eigenvectors of the linear system are obtained by using a subroutine in Mathematica [39], thus yielding natural frequencies and mode functions of the free vibration of the rectangular plates. To our best knowledge, it is the first time that integral transform solutions for free vibration of orthotropic rectangular thin plates with free edges are obtained with numerically stable beam functions as base functions, large number of terms in series expansion and exact treatment of the boundary conditions at free edges. The calculated natural frequencies are compared with available results in the literature and a reference finite element solution, showing excellent convergence and agreement with the finite element solution.

Fig. 1

Orthotropic thin rectangular plates with a CSCF, b CCCF and c CFCF boundary conditions

2 Mathematical formulation

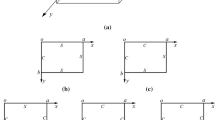
Let us consider free vibration of an orthotropic rectangular thin plate with a pair of opposite edges clamped and one or two free edges (CSCF, CCCF, CFCF). The plate has length a, width b, constant thickness h and lies in the (x, y) plane when no deflection occurs, as presented in Fig. 1. The notation for the combination of boundary conditions follows that proposed by Leissa [1]. For example, CSCF stands for a rectangular plate with clamped, simply supported, clamped and free boundary conditions at x = 0, y = 0, x = a and y = b edges, respectively. The governing equation for the free vibration of the orthotropic rectangular thin plate can be written as follows:

$$\begin{aligned} D_x\frac{\partial ^4 w}{\partial x^4}+2H\frac{\partial ^4 w}{\partial x^2 \partial y^2}+D_y\frac{\partial ^4 w}{\partial y^4} + \rho \frac{\partial ^2 w}{\partial ^2 t}=0 , \end{aligned}$$

(1)

where w(x, y, t) is the dynamic transverse deflection, $\rho$ is the mass density per unit area, and $D_x$ and $D_y$ are the flexural rigidities in the y and x directions, respectively. $H=D_1+2D_{xy}$ is the effective torsional rigidity, in which $D_{xy}$ is called the torsional rigidity and $D_1=\nu _y D_x=\nu _x D_y$ in terms of the Poisson’s ratios $\nu _x$ and $\nu _y$. The flexural and torsional rigidities of the plate are defined by

$$\begin{aligned} D_x=\frac{E_x h^3}{12(1-{\nu _x} {\nu _y})},\quad D_y=\frac{E_y h^3}{12(1-{\nu _x} {\nu _y})},\quad D_{xy}=\frac{G h^3}{12}, \end{aligned}$$

(2)

where $E_x$ and $E_y$ are the Young’s moduli for the principal directions, respectively, and G is the shear modulus.

The following dimensionless variables and parameters are defined:

$$\begin{aligned} w^*=\frac{w}{w_0}, \quad x^*=\frac{x}{a}, \quad y^*=\frac{y}{b},\quad t^*=\frac{t}{a^2\sqrt{\rho/D_x}}, \end{aligned}$$

(3a-d)

$$\begin{aligned} \xi=\frac{b}{a}, \quad \alpha=\frac{H}{D_x}, \quad \beta=\frac{D_y}{D_x},\quad \eta=\frac{D_{xy}}{D_x}, \end{aligned}$$

(3e-h)

where $w_0$ is a reference deflection.

The governing equation (1) is cast in the following dimensionless form (dropping the superposed asterisks for simplicity):

$$\begin{aligned} \frac{\partial ^4 w}{\partial x^4}+\frac{2\alpha }{\xi ^2}\frac{\partial ^4 w}{\partial x^2 \partial y^2}+\frac{\beta }{\xi ^4}\frac{\partial ^4 w}{\partial y^4} +\frac{\partial ^2 w}{\partial ^2 t}=0. \end{aligned}$$

(4)

We consider that a pair of left and right edges is clamped, with the following dimensionless boundary conditions:

$$\begin{aligned} w=0 \quad {\text{and}}\quad \frac{\partial w}{\partial x}=0, \quad {\hbox{at}}\quad x=0 \quad {\text{and}}\quad 1. \end{aligned}$$

(5a-b)

For the boundary conditions at the bottom and top edges, the following three sets of dimensionless boundary conditions are considered:

(a) Simply supported and free (CSCF):

$$\begin{aligned} w=0 \quad {\text{and}}\quad \frac{\partial^2 w}{\partial y^2}=0, \quad{\hbox{at}}\quad y=0, \end{aligned}$$

(6a-b)

$$\begin{aligned} \frac{1}{\xi^2}\frac{\partial^2 w}{\partial y^2}+\nu_x \frac{\partial^2 w}{\partial x^2}=0, \quad {\text{at}}\quad y=1,\end{aligned}$$

(6c)

$$\begin{aligned} \frac{\beta}{\xi^2}\frac{\partial^3 w}{\partial y^3}+(\alpha+2\eta)\frac{\partial^3 w}{\partial x^2\partial y}=0 , \quad{\hbox{at}}\quad y=1;\end{aligned}$$

(6d)

(b) Clamped and free (CCCF):

$$\begin{aligned} w=0 \quad {\text{and}}\quad \frac{\partial w}{\partial y}=0, \quad{\hbox{at}}\quad y=0,\end{aligned}$$

(7a-b)

$$\begin{aligned} \frac{1}{\xi^2}\frac{\partial^2 w}{\partial y^2}+\nu_x \frac{\partial^2 w}{\partial x^2}=0, \quad {\hbox{at}}\quad y=1,\end{aligned}$$

(7c)

$$\begin{aligned} \frac{\beta}{\xi^2}\frac{\partial^3 w}{\partial y^3}+(\alpha+2\eta)\frac{\partial^3 w}{\partial x^2\partial y}=0 , \quad{\hbox{at}}\quad y=1;\end{aligned}$$

(7d)

(c) Free and free (CFCF):

$$\begin{aligned} \frac{1}{\xi^2}\frac{\partial^2 w}{\partial y^2}+\nu_x \frac{\partial^2 w}{\partial x^2}=0, \quad{\hbox{at}}\quad y=0 \quad {\text{and}}\quad 1,\end{aligned}$$

(8a-b)

$$\begin{aligned} \frac{\beta}{\xi^2}\frac{\partial^3 w}{\partial y^3}+(\alpha+2\eta)\frac{\partial^3 w}{\partial x^2\partial y}=0 , \quad{\hbox{at}}\quad y=0 \quad {\text{and}}\quad 1.\end{aligned}$$

(8c-d)

Assuming a sinusoidal time response for free vibration,

$$\begin{aligned} w(x,y,t)=W(x,y) \mathtt {e}^{\mathtt {i}\lambda t}, \end{aligned}$$

(9)

the governing equation for the mode function becomes

$$\begin{aligned} \frac{\partial ^4 W}{\partial x^4}+\frac{2\alpha }{\xi ^2}\frac{\partial ^4 W}{\partial x^2 \partial y^2}+\frac{\beta }{\xi ^4}\frac{\partial ^4 W}{\partial y^4} -\lambda ^2 W=0, \end{aligned}$$

(10)

to be solved with the same boundary conditions.

3 Generalized integral transform solutions

The governing equation (10) combined with boundary conditions (5) with (6), (7) or (8), respectively, for CSCF, CCCF and CFCF is solved by employing the generalized integral transform technique (GITT). The integral transform kernels are based on the appropriate auxiliary eigenvalue problems, namely the fourth-order Sturm–Liouville equation with a complete and orthogonal base. The governing equation is integral-transformed in each coordinate direction through the multiplication of respective eigenfunctions together with the integration in its domain. It should be noted that the integration by parts combined with transformed free boundary terms of plate is employed in the generated terms of the transformed governing equation to incorporate the plate free boundary condition as it is not satisfied by the beam functions. Finally, the truncated transformed equations form a system of homogeneous linear algebraic equations, which is solved through a standard eigensystem algorithm to obtain the eigenvalues and eigenvectors.

3.1 Auxiliary eigenvalue problems

The auxiliary eigenvalue problem in the ‘x’ coordinate is the same for all three problems above, as follows:

$$\begin{aligned} \frac{{\text{d}}^4 X_i(x)}{{\text{d}} x^4}=\mu^4_i X_i (x) \quad{\mbox{and}} \quad 0<x<1,\end{aligned}$$

(11a)

$$X_i (0)= \frac{{\text{d}} X_i(0)}{{\text{d}} x}=0,$$

(11b-c)

$$X_i(1)= \frac{{\text{d}} X_i(1)}{{\text{d}} x}=0,$$

(11d-e)

and the eigenfunctions $X_{i}(x)$ and eigenvalues $\mu _i$ of problem (11) are given in the Appendix.

For the three sets of homogeneous boundary conditions, the auxiliary eigenvalue problem in the ‘y’ coordinate is defined by the same governing equation:

$$\begin{aligned}&\frac{\text {d}^4 Y_{kj}(y)}{\text {d} y^4}=\phi ^4_{kj} Y_{kj} (y), \quad 0<y<1, \\&\quad \text{ and } \quad k=1,2,3, \end{aligned}$$

(12)

and different boundary conditions as follows:

(a) CSCF boundary conditions ($k=1$):

$$Y_{1j} (0)= \frac{\text{d}^2 Y_{1j}(0)}{\text{d} y^2}=0,$$

(13a-b)

$$\frac{\text{d}^2 Y_{1j}(1)}{\text{d} y^2}= \frac{\text{d}^3 Y_{1j}(1)}{\text{d} y^3}=0;$$

(13c-d)

(b) CCCF boundary conditions ($k=2$):

$$Y_{2j} (0)= \frac{\text{d} Y_{2j}(0)}{\text{d} y}=0,$$

(14a-b)

$$\frac{\text{d}^2 Y_{2j}(1)}{\text{d} y^2}= \frac{\text{d}^3 Y_{2j}(1)}{\text{d} y^3}=0;$$

(14c-d)

(c) CFCF boundary conditions ($k=3$):

$$\frac{\text{d}^2 Y_{3j}(0)}{\text{d} y^2}= \frac{\text{d}^3 Y_{3j}(0)}{\text{d} y^3}=0,$$

(15a-b)

$$\frac{\text{d}^2 Y_{3j}(1)}{\text{d} y^2}= \frac{\text{d}^3 Y_{3j}(1)}{\text{d} y^3}=0,$$

(15c-d)

where $Y_{kj}(y)$ and $\phi _{kj}$ are the eigenfunctions and eigenvalues of problem (12) with boundary conditions (13), (14) or (15), and presented in the Appendix for SF, CF and FF boundary conditions, respectively.

3.2 Orthogonality property

The normalized eigenfunctions $X_i(x)$ and $Y_{kj}(y)$ satisfy the following orthogonality property:

$$\begin{aligned}&\int ^{1}_{0} X_i(x)X_m(x)\text {d}x=\delta _{im}, \\&\quad \text{ and } \quad i, m=1,2,3, \ldots , \quad \quad \end{aligned}$$

(16)

and

$$\begin{aligned}&\int ^{1}_{0} Y_{kj}(y)Y_{kn}(y)\text {d}y=\delta _{jn}, \\&\quad k=1,2,3\quad \text {and}\quad j,n =1, 2, 3, \ldots , \end{aligned}$$

(17)

with $\delta$ being the Kronecker delta function.

3.3 Generalized integral transform pairs

Based on the eigenvalue problems, the following generalized integral transform pairs are defined, first in the x direction and second in the y direction:

$$\begin{aligned} {\tilde{W}}_{m}(y)&=\int ^{1}_{0}W(x,y)X_m(x)\text {d}x, \quad \text {transform}, \end{aligned}$$

(18a)

$$\begin{aligned} W(x,y)&=\sum ^{\infty }_{m=1}X_m(x){\tilde{W}}_{m}(y), \quad \text {inverse}, \end{aligned}$$

(18b)

$$\begin{aligned} {\bar{W}}_{mn}&=\int ^{1}_{0}{\tilde{W}}_{m}(y)Y_{kn}(y)\text {d}y, \ \quad \text {transform}, \end{aligned}$$

(18c)

$$\begin{aligned} {\tilde{W}}_{m}(y)&=\sum ^{\infty }_{n=1}Y_{kn}(y){\bar{W}}_{mn}, \ \quad \text {inverse}, \\&\text{ and } \quad m, n=1,2,3,\ldots \end{aligned}$$

(18d)

where ${Y}_{kn}(y)$ represents ${Y}_{1n}(y)$, ${Y}_{2n}(y)$ and ${Y}_{3n}(y)$ for the boundary conditions of CSCF, CCCF and CFCF, respectively.

3.4 Transformed governing equations

The dimensionless governing equation (10) is integral-transformed first in the ‘x’ direction of the plate, being operated by $\int_{0}^{1} {X_{i} (x)\_{\text{d}}x}$, with application of the inverse formula in Eq. (18):

$$\begin{aligned}&\mu ^4_{i}{\tilde{W}}_{i}(y)+\frac{2\alpha }{\xi ^2}\sum ^{\infty }_{m=1}F_{im}\frac{\partial ^2 {\tilde{W}}_{m}(y)}{\partial y^2}+\frac{\beta }{\xi ^4}\frac{\partial ^4 {\tilde{W}}_{i}(y)}{\partial y^4} \\&\quad -\lambda ^2 {\tilde{W}}_{i}(y) =0, \quad \text{ and }\quad i=1,2,3,\ldots \end{aligned}$$

(19)

For each set of the CSCF, CCCF and CFCF boundary conditions, Eq. (19) is then operated by $\int_{0}^{1} {Y_{{ki}} (y)\_{\text{d}}y}$, with the inverse formulas in Eq. (18) applied:

$$\begin{aligned}&\mu ^4_{i}{\bar{W}}_{ij}+\frac{2\alpha }{\xi ^2}\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}F_{ijmn}{\bar{W}}_{mn} \\&\quad +\frac{\beta }{\xi ^4}\int ^{1}_{0}\frac{\partial ^4 {\tilde{W}}_{i}(y)}{\partial y^4}Y_{kj}(y)\text {d}y -\lambda ^2{\bar{W}}_{ij}=0, \\&\qquad k=1,2,3 \quad \text{ and }\quad i,j=1,2,3,\ldots \end{aligned}$$

(20)

Integration by parts on the third term in Eq. (20) is carried out:

$$\begin{aligned}&\int ^{1}_{0}\frac{\partial ^4 {\tilde{W}}_{i}(y)}{\partial y^4}Y_{kj}(y)\text {d}y = \left[ Y_{kj}(y)\frac{\partial ^3 {\tilde{W}}_{i}(y)}{\partial y^3} \right] ^1_0 \\&\quad -\left[ Y_{kj}^{'}(y)\frac{\partial ^2 {\tilde{W}}_{i}(y)}{\partial y^2}\right] ^1_0+ \left[ Y_{kj}^{''}(y)\frac{\partial {\tilde{W}}_{i}(y)}{\partial y} \right] ^1_0 \\&\quad -\left[ Y_{kj}^{'''}(y) {\tilde{W}}_{i}(y)\right] ^1_0+{\bar{W}}_{ij} \phi ^4_{kj}, \; \text{ and }\; k=1,2,3. \end{aligned}$$

(21)

Applying the generalized integral transform process on the plate free boundary conditions (6, 7 and 8), with the inverse formulas in Eq. (18) applied, we obtain

$$\begin{aligned}&\frac{\partial ^2 {\tilde{W}}_{i}(y)}{\partial y^2}=-\xi ^2\nu _x\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}{\bar{W}}_{mn}Y_{kn}(y)F_{im}, \end{aligned}$$

(22a)

$$\begin{aligned}&\frac{\partial ^3 {\tilde{W}}_{i}(y)}{\partial y^3}=-\frac{\xi ^2}{\beta }(\alpha +2\eta )\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}{\bar{W}}_{mn}Y_{kn}^{'}(y)F_{im}, \end{aligned}$$

(22b)

where the coefficient $F_{im} = \int ^{1}_{0} X_i X_m^{''}\text {d}x$.

(a) CSCF boundary conditions ($k=1$):

Equation (21) is simplified by applying the boundary conditions (6a-b) and (13):

$$\begin{aligned} \int ^{1}_{0}\frac{\partial ^4 {\tilde{W}}_{i}(y)}{\partial y^4}Y_{1j}(y)\text {d}y&= \left| Y_{1j}(y)\frac{\partial ^3 {\tilde{W}}_{i}(y)}{\partial y^3} \right| _{y=1} \\&\quad -\left| Y_{1j}^{'}(y)\frac{\partial ^2 {\tilde{W}}_{i}(y)}{\partial y^2} \right| _{y=1}+{\bar{W}}_{ij} \phi ^4_{1j}. \ \end{aligned}$$

(23)

A system of linear algebraic equations is obtained by introducing Eqs. (23 and 22) into the transformed governing equation (20):

$$\begin{aligned}&\mu ^4_{i}{\bar{W}}_{ij}+\frac{2\alpha }{\xi ^2}\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}F_{ijmn}{\bar{W}}_{mn} \\&\quad +\frac{\beta \nu _x}{\xi ^2} Y_{1j}^{'}(1)\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}Y_{1n}(1)F_{im}{\bar{W}}_{mn} \\&\quad -\frac{\alpha +2\eta }{\xi ^2}Y_{1j}(1)\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}Y_{1n}^{'}(1)F_{im}{\bar{W}}_{mn} \\&\quad +\frac{\beta }{\xi ^4} \phi ^4_{1j}{\bar{W}}_{ij} -\lambda ^2{\bar{W}}_{ij}=0. \end{aligned}$$

(24)

(b) CCCF boundary conditions ($k=2$):

Similarly, Eq. (21) is simplified by applying boundary conditions (7a-b) and (14):

$$\begin{aligned} \int ^{1}_{0}\frac{\partial ^4 {\tilde{W}}_{i}(y)}{\partial y^4}Y_{2j}(y)\text {d}y&= \left| Y_{2j}(y)\frac{\partial ^3 {\tilde{W}}_{i}(y)}{\partial y^3} \right| _{y=1} \\&\quad -\left| Y_{2j}^{'}(y)\frac{\partial ^2 {\tilde{W}}_{i}(y)}{\partial y^2} \right| _{y=1}+{\bar{W}}_{ij} \phi ^4_{2j}. \end{aligned}$$

(25)

A system of algebraic equations is obtained by introducing Eqs. (25 and 22) into the transformed governing equation (20):

$$\begin{aligned}&\mu ^4_{i}{\bar{W}}_{ij}+\frac{2\alpha }{\xi ^2}\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}F_{ijmn}{\bar{W}}_{mn} \\&\quad +\frac{\beta \nu _x}{\xi ^2} Y_{2j}^{'}(1)\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}Y_{2n}(1)F_{im}{\bar{W}}_{mn} \\&\quad -\frac{\alpha +2\eta }{\xi ^2}Y_{2j}(1)\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}Y_{2n}^{'}(1)F_{im}{\bar{W}}_{mn} \\&\quad +\frac{\beta }{\xi ^4} \phi ^4_{2j}{\bar{W}}_{ij} -\lambda ^2{\bar{W}}_{ij}=0. \end{aligned}$$

(26)

(c) CFCF boundary conditions ($k=3$):

Finally, Eq. (21) is simplified by applying boundary condition (15):

$$\begin{aligned}&\int ^{1}_{0}\frac{\partial ^4 {\tilde{W}}_{i}(y)}{\partial y^4}Y_{3j}(y)\text {d}y = \left[ Y_{3j}(y)\frac{\partial ^3 {\tilde{W}}_{i}(y)}{\partial y^3} \right] ^1_0 \\&\quad -\left[ Y_{3j}^{'}(y)\frac{\partial ^2 {\tilde{W}}_{i}(y)}{\partial y^2} \right] ^1_0+{\bar{W}}_{ij} \phi ^4_{3j}. \end{aligned}$$

(27)

A similar system of linear algebraic equations is obtained by introducing Eqs. (27 and 22) into the transformed governing equation (20):

$$\begin{aligned}&\mu ^4_{i}{\bar{W}}_{ij}+\frac{2\alpha }{\xi ^2}\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}F_{ijmn}{\bar{W}}_{mn} \\&\quad +\frac{\beta \nu _x}{\xi ^2} (Y_{3j}^{'}(1)\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}Y_{3n}(1)F_{im}{\bar{W}}_{mn} \\&\quad -Y_{3j}^{'}(0)\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}Y_n(0)F_{im}{\bar{W}}_{mn}) \\&\quad -\frac{\alpha +2\eta }{\xi ^2}(Y_{3j}(1)\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}Y_{3n}^{'}(1)F_{im}{\bar{W}}_{mn} \\&\quad -Y_{3j}(0)\sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1}Y_n^{'}(0)F_{im}{\bar{W}}_{mn}) \\&\quad +\frac{\beta }{\xi ^4} \phi ^4_{3j}{\bar{W}}_{ij} -\lambda ^2{\bar{W}}_{ij}=0. \end{aligned}$$

(28)

The coefficients are defined by the following integrals:

$$\begin{aligned} F_{ijmn}&= \int ^{1}_{0} X_i X_m^{''}\text {d}x\int ^{1}_{0} Y_j Y_n^{''}\text {d}y, \end{aligned}$$

(29a)

$$\begin{aligned} F_{im}&= \int ^{1}_{0} X_i X_m^{''}\text {d}x, \end{aligned}$$

(29b)

which can be calculated analytically from integral formulas [16, 40].

3.5 Solution of the transformed equations

The infinite systems of linear algebraic equations are truncated to a sufficiently large finite order NW in both directions, for computational purposes. The truncated equations (24), (26) and (28) can be written in matrix form as follows:

$$\begin{aligned} (\mathbf{K} -\lambda ^2 \mathbf{I} ) \mathbf{W} = 0, \end{aligned}$$

(30)

which forms a standard eigenvalue system. The eigenvalues and eigenvectors of the system (30) can be readily obtained by using the Mathematica package [39]. The ith mode function $W^{(i)}(x,y)$ corresponding to dimensionless frequency $\lambda ^{(i)}$ can be thus constructed by using the inverse defined by Eq. (18):

$$\begin{aligned}&W^{(i)}(x,y) = \sum ^{\infty }_{m=1}\sum ^{\infty }_{n=1} X_m(x)Y_{kn}(y){\bar{W}}^{(i)}_{mn}, \\&\quad \text{ and }\quad k=1,2,3, \qquad \quad \end{aligned}$$

(31)

where ${\bar{W}}^{(i)}_{mn}$ are the components of the ith eigenvector $\mathbf{W} ^{(i)}$.

Table 1 Convergence of the natural frequencies ($\lambda =\omega a^2 \sqrt{\rho /D}$) for the isotropic square plates with boundary conditions CSCF, CCCF and CFCF

Table 2 Natural frequencies ($\lambda =\omega a^2 \sqrt{\rho /D_x}$) for the orthotropic rectangular plates with boundary conditions CSCF, CCCF and CFCF (NW = 80)

4 Results and discussion

4.1 Convergence behavior of the solution

Firstly, the convergence behaviors of the first five natural frequencies for the isotropic square plate free vibration with boundary conditions CSCF, CCCF and CFCF are studied by using the GITT approach. The GITT solutions in Eqs. (24, 26 and 28) are examined up to truncation terms NW = 80, in comparison with Leissa solutions [1] and finite element solutions, as shown in Table 1. Three-dimensional linear-elastic finite element analysis is performed by using the Abaqus/Standard 6.14-3 package [41]. To apply the classical thin plate theory in the finite element model, the plate thickness is taken as 1/100th of the edge length of the square plate. The plate is discretized by using 100 S4R elements in both x and y directions. The physical parameters for the isotropic square plate are selected as $\rho =7800$ kg m$^{-3}$, E = 210 GPa, $\nu =0.3$. Table 1 shows that the first five natural frequencies of free vibration of the three cases considered converge to the third significant digit. The natural frequencies obtained by the converged GITT solutions (NW = 80) agree very well with the reference finite element solutions, to at least third significant digit. There are only small differences at the fourth significant digits. Meanwhile, the natural frequencies obtained by Leissa [1] differ from both our GITT solutions and the reference finite element solutions at the third significant digit. As it is known that the Rayleigh–Ritz method generates upper bound solutions from the exact solutions and the natural frequencies calculated by the present method have smaller values than Leissa’s results, it can be concluded that the integral transform solutions are more accurate than the Rayleigh–Ritz solutions when there is at least a free edge.

4.2 Natural frequencies of the orthotropic plates

The first six natural frequencies of the orthotropic rectangular thin plates with boundary conditions CSCF, CCCF and CFCF obtained by GITT are presented in Table 2. The convergence of the GITT solutions is examined up to truncation term NW = 80, for the aspect ratio a/b = 0.4, 2/3, 1.0, 1.5 and 2.5. To demonstrate the validity and accuracy of the proposed GITT approach, three-dimensional linear-elastic finite element analysis is performed in the Abaqus/Standard 6.14-3 package [41]. In x and y directions, 100 and $100 b/a\, S4R$ elements are used, respectively. The physical parameters for the orthotropic rectangular plate are selected as $\rho =7800$ kg m$^{-3}$, $E_x=200$ GPa, $E_y=800$ GPa, $\nu _x=0.075$, $\nu _y=0.3$ and $G_{xy}=174$ GPa. It can be seen in Table 2 that similar to the cases for the isotropic rectangular plate, the integral transform solutions agree very well with the reference finite element solutions, for the first six natural frequencies for orthotropic plates with different aspect ratios and three sets of boundary conditions with one or two free edges.

5 Conclusions

Free vibration of orthotropic rectangular thin plates with a pair of opposite edges clamped and one or two edges free is analyzed by using generalized integral transform technique. Numerically stable expressions for the eigenfunctions of Euler–Bernoulli beams are adopted as base functions along each direction with corresponding boundary conditions, thus overcoming the numerical difficulties with traditional expressions for the eigenfunctions in combinations of hyperbolic and trigonometric functions and allowing expansions to arbitrarily higher orders. More accurate natural frequencies have been obtained in comparison with the classical Leissa solutions obtained by Ritz–Rayleigh method. Examples show that the GITT solutions agree with reference finite element solutions to at least third significant digits for both examples, isotropic square plates and orthotropic rectangular plates with different aspect ratios. It is concluded that by including additional terms generated by integration by parts due to the difference between the plate and beam boundary conditions at a free edge, the integral transform solutions recover the loss of accuracy suffered by using the beam functions in the Rayleigh–Ritz methods when there is a free edge in a rectangular plate, and thus yield accurate natural frequencies of free vibration of orthotropic thin rectangular plates with one or two free edges.

Appendix

(a) CC (clamped edges):

The eigenfunctions $X_i(x)$ for a pair of clamped edges in the ‘x’ direction are given by solving problem (11) analytically [35,36,37]:

$$\begin{aligned} X_i(x)&= (-1)^{i}\cos (\mu _ix)-\sin (\mu _ix) \cot \left( \frac{\mu _i}{2}\right) ^{(-1)^i} \\&\quad -\frac{(-1)^i e^{-\mu _ix}}{1-(-1)^i e^{-\mu _i}}+\frac{e^{-\mu _i(1-x)}}{1-(-1)^i e^{-\mu _i}}. \end{aligned}$$

(32)

The transcendental equations for the eigenvalues $\mu _i$ are given by

$$\begin{aligned} (-1)^i \tan \left( \frac{\mu _i}{2}\right) =\frac{1-e^{-\mu _i}}{1+e^{-\mu _i}} \quad \text{ and } \quad i=1,2,3,\ldots \end{aligned}$$

(33)

(b) SF (simply supported and free edges):

The eigenfunctions $Y_{1j}(y)$ for a pair of simply supported and free edges in the ‘y’ direction are given by solving problem (12 and 13) analytically [35,36,37]:

$$\begin{aligned} Y_{11}(y)&= \root \of {3} y \quad \text{ and } \\ Y_{1j}(y)&= \root \of {2}\left( \sin (\phi _{1j} y)-\frac{e^{-\phi _{1j}}\sin (\phi _{1j})}{1-e^{-2\phi _{1j}}}e^{-\phi _{1j} y} \right. \\&\quad \left. +\frac{e^{-\phi _{1j}(1-y)}\sin (\phi _{1j})}{1-e^{-2\phi _{1j}}}\right) . \end{aligned}$$

(34)

The transcendental equations for the eigenvalues $\phi _{1j}$ are given by

$$\begin{aligned}&\phi _{11}=0, \\&\tan (\phi _{1j})=\frac{1-e^{-2\phi _{1j}}}{1+e^{-2\phi _{1j}}} \quad \text{ and } \quad j=2,3,4,\ldots \end{aligned}$$

(35)

(c) CF (clamped and free edges):

The eigenfunctions $Y_{2j}(y)$ for a pair of clamped and free edges in the ‘y’ direction are given by solving problem (12 and 14) analytically [35,36,37]:

$$\begin{aligned} Y_{2j}(y)&= \cos (\phi _{2j} y)-\frac{1+(-1)^{j} e^{-\phi _{2j}}}{1-(-1)^{j} e^{-\phi _{2j}}}\sin (\phi _{2j} y) \\&\quad - \frac{1}{1-(-1)^{j} e^{-\phi _{2j}}}e^{-\phi _{2j} y}+ \frac{(-1)^{j}}{1-(-1)^{j} e^{-\phi _{2j}}}e^{-\phi _{2j}(1-y)}. \end{aligned}$$

(36)

The transcendental equations for the eigenvalues $\phi _{2j}$ are given by

$$\begin{aligned} \cos (\phi _{2j})= \frac{-2 e^{-\phi _{2j}}}{1+e^{-2\phi _{2j}}} \quad \text{ and } \quad j=1,2,3,\ldots \end{aligned}$$

(37)

(d) FF (free and free edges):

The eigenfunctions $Y_{3j}(y)$ for a pair of two free edges in the ‘y’ direction are given by solving problems (12 and 15) given by [35,36,37]

$$\begin{aligned} Y_{31}(y)&= 1, \quad Y_{32}(y)=\root \of {3}(1-2y) \quad \text{ and } \\ Y_{3j}(y)&= \cos (\phi _{3j} y)-\frac{1+(-1)^{j} e^{-\phi _{3j}}}{1-(-1)^{j} e^{-\phi _{3j}}}\sin (\phi _{3j} y) \\&\quad + \frac{1}{1-(-1)^{j} e^{-\phi _{3j}}}e^{-\phi _{3j} y}- \frac{(-1)^{j}}{1-(-1)^{j} e^{-\phi _{3j}}}e^{-\phi _{3j}(1-y)}. \end{aligned}$$

(38)

The transcendental equations for the eigenvalues $\phi _{3j}$ are given by

$$\begin{aligned}&\phi _{31}=\phi _{32}=0, \\&(-1)^j \tan \left( \frac{\phi _{3j}}{2}\right) =\frac{1-e^{-\phi _{3j}}}{1+e^{-\phi _{3j}}} \quad \text{ and } \quad j=3,4,5,\ldots \end{aligned}$$

(39)