Ion Acoustic Shock Wave Excitations Around the Critical Values in an Unmagnetized Pair–Ion Plasma

Abstract

This work deals with the ion-acoustic shock waves (IASWs) around the critical values in an unmagnetized pair–ions plasma with ($\alpha , q$)-distributed electrons by formulating the correct stationary solution of Burgers-type equations with higher-order corrections. By considering higher-order correction of the reductive perturbation technique, the modified Burgers(mB)-, and mixed modified Burgers(mmB)-type equations are derived. With the changes of viscosity coefficients of positive and negative ions, the electrostatic IASWs and normalized electric fields are investigated around the critical values. The current studies might be very useful to understand the behavior of shocks around the critical values in the F- and D-regions of Earth’s ionosphere, and the later experimental verification in plasma laboratory.

1 Introduction

It is well confirmed that plasmas with negative ions (NIs) have attracted a lot of interest from the investigators because of extensive range of technological tools such as a neutral metal source [1], semiconductor and material processing [2], Q-machine plasmas [3], etc. Production of NIs by the inclusion of a small amount of $SF_6$ gas to low levels ($\approx 0.2 eV$) of potassium plasma in a Q-machine is already confirmed in Ref. [4]. Goeler and Ohe [5] generated a CsCl beam into a hot tungsten plate of a Q-plasma machine that produces plasma containing $Cs^+$, $Cl^-$ and electrons. In addition, NIs are found in the astrophysical environments, particularly in the D-, and F-region of the Earth’s ionosphere [6,7,8,9,10]. It is a convincing evidence that the Cassini spacecraft has confirmed the exitance of heavy NIs in the upper region of Titan's atmosphere [6]. Due to the existence of pair ions not only in laboratory but also in many space and astronomical environment, many researchers [10,11,12,13,14,15] investigated the propagation of IASWs in plasmas composing of various types of positive ions (PIs), (e.g., $K ^+$, $Cs^+$, $C_{60}^{+}$, etc.) and NIs (e.g., $SF_6 ^-$, $Cs^-$, $C_{60}^{-}$, etc.). However, the most reliable method is the formation of shocks for a reason that it spreads further. Actually, the IASWs are produced in plasmas because the relative velocity between the rarefaction wave and the plasma overtakes its IA speed, where the frequency of the rarefaction wave and the surrounding medium is comparatively the same. Adak et al. [14] reported IASWs in the $(C_{60}^{+}, C_{60}^{-})$ plasma by obtaining the KdV Burgers equation. Hussain et al. [15] theoretically described IASWs in negative ions plasma having nonextensive electrons. Recently, Alam and Talukder [11] investigated collisions between two IASWs by suggesting that the plasma system consists of pair ions and isothermal electrons. Furthermore, the energy of electrons may be nonthermal and less (subthermal) or greater (superthermal) than its isothermal energy in many environments. When the energy of electrons becomes subthermal or superthermal, one can use the nonextensive velocity distribution function to determine the density function of electron as $N_e=N_{e0}\left[ 1+(q-1)\left( e\Phi /k_B T_e\right) \right] ^{\frac{(q+1)}{2(q-1)}}$, where $\Phi$, $N_{e0}$, q, $T_e, e$ and $k_B$ are the electrostatic potential, unperturbed electron density, strength of nonextensivity, electron temperature, electron charge and Boltzmann constant, respectively [16]. The effects of electron nonextensivity on IASWs have already studied by many researchers [16,17,18,19,20]. For instance, Ferdousi et al. [20] have reported the effects of electron nonextensivity on the properties of IASWs in an unmagnetized three-component plasma. They have shown that SWEs are significantly modified and both compressive and rarefective shock waves are supported by the influence of the strength of nonextensivity. But, the nonextensive distribution function fails to address the physical issues for the nonthermal electron populations. As a result, one can consider model an electron distribution with a population of fast particle by taking the Cairns velocity distribution function [21,22,23] leading to $N_e=N_{e0}\left[ 1-(4\alpha /1+3\alpha )\left( e\Phi /k_B T_e\right) \right.$$\left.+(4\alpha /1+3\alpha )\left( e\Phi /k_B T_e\right) ^2\right] \exp \left( e\Phi /k_B T_e\right)$, where $\alpha$ is a parameter determining the fast particles present in the model considered. Later, Tribeche et al. [24] have proposed a unique distribution function, the so-called the $(\alpha , q)$-velocity distribution function by generalizing the work of Cairns et al. [21], which provides a better fit of the space observations due to the flexibility provided by the nonextensivity parameter. They have obtained electron density by integrating $(\alpha , q)$-velocity distribution function over all velocity space as

$$\begin{aligned} N_e=&\;N_{e0}\left[ 1+(q-1)\frac{e\Phi }{k_B T_e}\right] ^{\frac{(q+1)}{2(q-1)}}\biggl[ 1-\frac{16q\alpha }{3-14q+15q^2+12\alpha }\left( \frac{e\Phi }{k_B T_e}\right) \\&+\frac{16q(2q-1)\alpha }{3-14q+15q^2+12\alpha }\left( \frac{e\Phi }{k_B T_e}\right) ^2\biggr] . \end{aligned}$$

One can easily reduce the above electron density to the nonextensive and nonthermal electron density by setting $\alpha =0$ and $q\rightarrow 1$, respectively. Thus, a unique distribution function, like $(\alpha , q)$-velocity distribution function [24] can be assumed for examining all the cases of electrons energies. Very recently, Hafez et al. [10] proposed an NI plasma for understanding the nature of shocks and overtaking collisions of multi-shocks by deriving a Burgers-like equation. They reported that the compressive and rarefactive electrostatic shocks are supported in the aforementioned plasma system. But, they ignored the features of electrostatic shocks not only around the critical values (CVs) but also at the CVs. Also, the shock waves phenomena around CVs are reported by incorrectly defined solution of mB and mmB equations in most of the previous studies [25,26,27], which is not useful for further verification in laboratory plasmas. It is therefore essential to study shock wave propagation in the plasmas around CVs by formulating the appropriate solutions of mB and mmB equations.

Thus, this work explores the electrostatic nonlinear propagation of IASWs, not only around CVs but also at CVs in a pair ions plasma system, by deriving mB- and mmB-type equations with their useful solutions. The effect of some parameters on the shocks around CVs and almost at CVs are investigated.

2 Governing Equations

To achieve our goal, the following normalized model equations are considered, by assuming PI ($M_{+i}$ and temperature $T_{+i}$), NI (like $SF_{6}^{-}$ with mass $M_{-i}$ and temperature $T_{-i}$) and $(\alpha , q)$-distributed electrons, along with $1=N_{r1}+N_{r2}$, where $N_{r1}=N_{-i0}/N_{+i0}$, $N_{r2}=N_{e0}/N_{+i0}$, $N_{+i0}(N_{-i0})$ and $N_{e0}$ are respectively the PIs (NIs) and electrons unperturbed densities [10]:

$$\begin{aligned}&\frac{\partial N_{ji}}{\partial t}+\frac{\partial (N_{ji} U_{ji})}{\partial z} =0 ,j=+,-,\end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial U_{+i}}{\partial t}+U_{+i} \frac{\partial U_{+i}}{\partial z}+\frac{\partial {\Phi }}{\partial z}+\mu _{+i}\frac{\partial ^2 U_{+i}}{\partial z^2}=0,\end{aligned}$$

(2)

$$\begin{aligned}&\frac{\partial U_{-i}}{\partial t}+U_{-i} \frac{\partial U_{-i}}{\partial z}-M_{\pm }\frac{\partial {\Phi }}{\partial z}+\frac{\delta _{ei}}{N_{-i}}\frac{\partial N_{-i}}{\partial z}+\mu _{-i}\frac{\partial ^2 U_{-i}}{\partial z^2}=0,\end{aligned}$$

(3)

$$\begin{aligned}\frac{\partial ^2\Phi }{\partial z^2} =&\;N_{pi}-N_{ni}-N_{r2}\biggl\{ \left[ 1+(q-1)\Phi \right] ^{\frac{(q+1)}{2(q-1)}} \nonumber \\&\times \left[ 1-\frac{16q\alpha }{3-14q+15q^2+12\alpha }\Phi \right.\\&\left.+\frac{16q(2q-1)\alpha }{3-14q+15q^2+12\alpha }\Phi ^2\right] \biggr\} , \end{aligned}$$

(4)

where,

$$\begin{aligned} M_{\pm }= \frac{M_{+i}}{M_{-i}}, \delta _{ei}=\frac{T_e}{\left( 1-N_{r1}\right) T_{-i}}. \end{aligned}$$

(5)

Here, $N_{+i}$ ($N_{-i}$) and $N_{e}$ are respectively the normalized PIs (NIs) and electrons densities normalized by $N_{+i0}$, $U_{+i}$ ($U_{-i}$) is the normalized PIs (NIs) fluid velocity normalized by the PI speed $C_{+is} =\sqrt{k_B T_e/M_{\pm }}\sqrt{\left( N_{r1}+N_{r2}\right) /N_{r2}(1-N_{r1})}$, $\Phi$ is the normalized electrostatic potential, $\Phi \rightarrow e \Phi /k_B T_{e}$, t is the time variable normalized by $\omega ^{-1}_{+i} =\lambda _{De}/C_{+is}$, z is the space variable normalized by $\lambda _{De}=\sqrt{k_B T_{e}/4\pi N_{e0} e^2}$, and $\mu _{+i}$ ($\mu _{-i}$) is the normalized PIs (NIs) viscosity coefficient normalized by $\omega ^{-1}_{+i}/M_{\pm }N_{+i0}C_{+is}^2$ ($\omega ^{-1}_{+i}/M_{-i}N_{-i0}C_{+is}^2$). Additionally, one can use (i) $q\rightarrow 1$ and $\alpha =0$ for the Maxwell-Boltzmann distributed electrons, (ii) $q\rightarrow 1$ and $\alpha \ne 0$ for the Cairns distributed electrons and (iii) $\alpha =0$ for superthermal ($0<q<1$) and subthermal ($q>1$) electrons, respectively, where q is the strength of nonextensivity and $\alpha$ is measuring the population of nonthermal electrons.

3 Mathematical Analysis

3.1 Formation of mBE with Stationary Wave Solution

In order to study the shock wave phenomena around the critical values, one can consider the stretching coordinates by taking the higher-order correction of reductive perturbative method [25] as

$$\begin{aligned} X=\epsilon ^2(z-V_p t),T=\epsilon ^4 t, \end{aligned}$$

(6)

and the expansions for physical quantities as

$$\begin{aligned} \left[ \begin{array}{c} N_{+i} \\ N_{-i} \\ U_{+i} \\ U_{+i} \\ \Phi \\ \end{array}\right] =\left[ \begin{array}{c} 1 \\ N_{r1} \\ 0 \\ 0 \\ 0 \\ \end{array}\right] + \sum _{i}^{\infty }\epsilon ^i \left[ \begin{array}{c} N_{+i}^{(i)} \\ N_{-i}^{(i)} \\ U_{+i}^{(i)} \\ U_{-i}^{(i)} \\ \Phi ^{(i)} \\ \end{array}\right] , \end{aligned}$$

(7)

where $V_p$ and $\epsilon$ are the IA linear phase speed and a small quantity measuring the weakness of dissipation. By systematically inserting Eqs. (6) and (7) into Eqs. (1)−(4), the different order of $\epsilon$ equations are easily determined. The $O(\epsilon ^3)$-order equations gives the following expressions for $N_{pi}^{(1)}$, $N_{ni}^{(1)}$, $U_{ni}^{(1)}$ and $V_p$:

$$\begin{aligned} N_{+i}^{(1)}=\frac{1}{V_p^2}\Phi ^{(1)},U_{+i}^{(1)}=\frac{1}{V_p}\Phi ^{(1)}, N_{-i}^{(1)}=-\frac{N_{r1}M_{\pm }}{V_p^2-\delta _{ei}}\Phi ^{(1)}, U_{-i}^{(1)}=-\frac{V_p M_{\pm }}{V_p^2-\delta _{ei}}\Phi ^{(1)},\end{aligned}$$

(8)

$$\begin{aligned} V_p=\sqrt{\frac{\left( 1+N_{r1}M_{\pm }+\delta _{ei}N_{r2}\Omega _1\right) \pm \sqrt{\left( 1+N_{r1}M_{\pm }+\delta _{ei}N_{r2}\Omega _1\right) ^2-4N_{r2}\Omega _1\delta _{ei}}}{2N_{r2}\delta _{ei}}}, \end{aligned}$$

(9)

where

$$\begin{aligned} \Omega _1=\left[ \frac{q+1}{2}-\frac{16q\alpha }{3-14q+15q^2+12\alpha }\right] . \end{aligned}$$

(10)

It is obviously found from Eq. (9) that $V_p$ is strongly dependent on $N_{r1}$, $M_{\pm }$, $\delta _{ei}$, $N_{r2}$, $\alpha$ and q, but not on $\mu _{+i}$ and $\mu _{-i}$. It is validated for $\left( 1+N_{r1}M_{\pm }+\delta _{ei}N_{r2}\Omega _1\right) ^2- 4N_{r2}\Omega _1\delta _{ei}\ge 0$. Again, the $O(\epsilon ^4)$-order equations (ignored for convenience) yields the following relations:

$$\begin{aligned}&N_{+i}^{(2)}=\frac{1}{V_p^2}\left[ \frac{3}{2V_p^2}\left\{ \Phi ^{(1)}\right\} ^2+\Phi ^{(2)}\right] ,\nonumber \\&U_{+i}^{(2)}=\frac{1}{V_p^2}\left[ \frac{1}{2V_p^2}\left\{ \Phi ^{(1)}\right\} ^2+\Phi ^{(2)}\right] ,\nonumber \\&N_{-i}^{(2)}=\frac{N_{r1}M_{\pm }}{V_p^2-\delta _{ei}} \left[ \frac{M_{\pm }(3V_p^2-\delta _{ei})}{2(V_p^2-\delta _{ei})^2}\left\{ \Phi ^{(1)}\right\} ^2-\Phi ^{(2)}\right] ,\nonumber \\&U_{-i}^{(1)}=\frac{V_p M_{\pm }}{V_p^2-\delta _{ei}} \left[ \frac{M_{\pm }(V_p^2+\delta _{ei})}{2(V_p^2-\delta _{ei})^2}\left\{ \Phi ^{(1)}\right\} ^2-\Phi ^{(2)}\right] ,\nonumber \\&-C_f\left\{ \Phi ^{(1)}\right\} ^2=0, \end{aligned}$$

(11)

where

$$\begin{aligned} C_f=\left[ \frac{3}{V_p^4}-\frac{3N_{r1}V_p^2M_{\pm }^2}{\left( V_p^2-\delta _{ei}\right) ^3} +\frac{\delta _{ei}N_{r1}M_{\pm }^2}{\left( V_p^2-\delta _{ei}\right) ^3}-2N_{r2}\Omega _2\right] , \end{aligned}$$

(12)

and

$$\begin{aligned} \Omega _2=&\left[ \frac{(q+1)(3-q)}{8}-\frac{q+1}{2}\times \frac{16q\alpha }{3-14q+15q^2+12\alpha }\right. \\&\left.+\frac{16q(2q-1)\alpha }3-14q+15q^2+12\alpha \right] . \end{aligned}$$

(13)

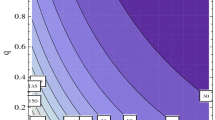
It is noted that one can determine the critical values (CVs) by setting $C_f=0$. But, it is very difficult to formulate the mathematical expression for CV. Figure 1 shows the variation of $C_f$ with regard to q and $\alpha$ by considering the other parameters constant. It is obviously found from Fig. 1 that the CVs only occur when the electron energy becomes less than its thermal energy, that is, for the subthermal electrons based on the considered parametric values as in Ref. [10, 11]. For instance, the CV $q_c$ for q is determined as $q_c=3.098638852$ by considering $\alpha = 0$, $M_{\pm } = 3.75$, $T_{-i}= 0.05eV$, $T_e = 0.19eV$, $N_{r1}=0.5$ and $N_{r2}= 0.01$. One can also find the other CV as $q_c=6.176859718$ by considering $\alpha = 0$, $M_{\pm } = 3.75$, $T_{-i}= 0.05eV$, $T_e = 0.1eV$, $N_{r1}=0.5$ and $N_{r2}= 0.1$. It is also provided that the CVs are only supported for subthermal electrons.

Fig. 1

Variation of $C_f$ with regard to q and $\alpha$. The other parameters are considered as $M_{r}=3.75$, $T_{ni}=0.05eV$, $T_{e}=0.2eV$, $N_{r1}=0.5$ and $N_{r2}=0.01$

Finally, the $O(\epsilon ^5)$-order provides the following equations:

$$\begin{aligned}& \frac{1}{V_p^2}\frac{\partial \Phi ^{(1)}}{\partial T}-V_p \frac{\partial N_{+i}^{(3)}}{\partial X}+\frac{\partial U_{+i}^{(3)}}{\partial X}+\frac{6}{V_p^5}\left\{ \Phi ^{(1)}\right\} ^2 \\& \frac{\partial \Phi ^{(1)}}{\partial X}+\frac{2}{V_p^3}\frac{\partial }{\partial X}\left[ \Phi ^{(1)}\Phi ^{(2)}\right] =0,\end{aligned}$$

(14)

$$\begin{aligned} \frac{1}{V_p}\frac{\partial \Phi ^{(1)}}{\partial T}-V_p \frac{\partial U_{+i}^{(3)}}{\partial X}+\frac{\partial \Phi ^{(3)}}{\partial X}+\frac{3}{2V_p^4}\left\{ \Phi ^{(1)}\right\} ^2 \\ \frac{\partial \Phi ^{(1)}}{\partial X}+\frac{1}{V_p^2}\frac{\partial }{\partial X}\left[ \Phi ^{(1)}\Phi ^{(2)}\right] +\frac{\mu _{+i}}{V_p}\frac{\partial ^2 \Phi ^{(1)}}{\partial X^2}=0,\end{aligned}$$

(15)

$$\begin{aligned}& -\frac{N_{r1} M_{\pm }}{V_p^2-\delta _{ei}}\frac{\partial \Phi ^{(1)}}{\partial T}-V_p \frac{\partial N_{-i}^{(3)}}{\partial X}+N_{r1}\frac{\partial U_{-i}^{(3)}}{\partial X}-\frac{6N_{r1}V_p^3M_{\pm }^3}{\left( V_p^2-\delta _{ei}\right) ^4} \\& \left\{ \Phi ^{(1)}\right\} ^2 \frac{\partial \Phi ^{(1)}}{\partial X}+\frac{2N_{r1}V_p M_{\pm }^2}{\left( V_p^2-\delta _{ei}\right) ^2}\frac{\partial }{\partial X}\left[ \Phi ^{(1)}\Phi ^{(2)}\right] =0,\end{aligned}$$

(16)

$$\begin{aligned}&-\frac{V_p M_{\pm }}{V_p^2-\delta _{ei}}\frac{\partial \Phi ^{(1)}}{\partial T}-V_p \frac{\partial U_{-i}^{(3)}}{\partial X}+\frac{\delta _{ei}}{N_{r1}} \frac{\partial N_{-i}^{(3)}}{\partial X}-M_{\pm }\frac{\partial \Phi ^{(3)}}{\partial X} \\&-\frac{\mu _{-i}V_pM_{\pm }}{V_p^2-\delta _{ei}}\frac{\partial ^2 \Phi ^{(1)}}{\partial X^2}+\frac{M_{\pm }^2}{\left( V_p^2-\delta _{ei}\right) }\frac{\partial }{\partial X}\left[ \Phi ^{(1)}\Phi ^{(2)}\right] \nonumber \\&+\left[ -\frac{3V_p^2M_{\pm }^3\left( V_p^2+\delta _{ei}\right) }{2\left( V_p^2-\delta _{ei}\right) ^4}+\frac{3\delta _{ei}M_{\pm }^3\left( 3V_p^2-\delta _{ei}\right) }{2\left( V_p^2-\delta _{ei}\right) ^4} \right.\\&\left.\qquad-\frac{\delta _{ei}M_{\pm }^3}{\left( V_p^2-\delta _{ei}\right) ^3}\right] \left\{ \Phi ^{(1)}\right\} ^2 \frac{\partial \Phi ^{(1)}}{\partial X}=0,\end{aligned}$$

(17)

$$\begin{aligned} 0=&-N_{r2}\Omega _1\frac{\partial \Phi ^{(3)}}{\partial X}-3N_{r2}\Omega _3\left[ \Phi ^{(1)}\right] ^2\frac{\partial \Phi ^{(1)}}{\partial X} \\ &-2N_{r2}\Omega _2\frac{\partial }{\partial X}\left[ \Phi ^{(1)}\Phi ^{(2)}\right] +\frac{\partial N_{+i}^{(3)}}{\partial X}-\frac{\partial N_{-i}^{(3)}}{\partial X}, \end{aligned}$$

(18)

where,

$$\begin{aligned} \Omega _3=&\left[ \frac{(q+1)(3-q)(5-q)}{48}-\frac{2q\alpha (q+1)(3-q)}{3-14q+15q^2+12} \right.\\&\left.+\frac{8q(2q-1)\alpha (q+1)}{3-14q+15q^2+12}\right] . \end{aligned}$$

(19)

By simplifying the above equations, the following equation is derived:

$$\begin{aligned} A\frac{\partial \Phi ^{(1)}}{\partial T}+B\left\{ \Phi ^{(1)}\right\} ^2\frac{\partial \Phi ^{(1)}}{\partial X }+C\frac{{\partial }^2\Phi ^{(1)}}{\partial X^2}=0, \end{aligned}$$

(20)

which is the mB-type equation. The coefficients of Eq. (20) are determined as

$$\begin{aligned}A=&\;2\left[ \frac{V_p^2-\delta _{ei}}{V_p}+\frac{N_{r1}V_p^3M_{\pm }}{\left( V_p^2-\delta _{ei}\right) }\right] ,\nonumber \\B=&\;\frac{15(V_p^2-\delta _{ei})}{2V_p^4}-3N_{r2}\Omega _3V_p^2(V_p^2-\delta _{ei}) \\&+\frac{3N_{r1}V_p^2M_{\pm }^3\left( 5V_p^4-2V_p^2\delta _{ei}+\delta _{ei}^2\right) }{2\left( V_p^2-\delta _{ei}\right) ^4} \\&+\frac{\delta _{ei}N_{r1}M_{\pm }^3V_p^2}{\left( V_p^2-\delta _{ei}\right) ^3},\nonumber \\C=&\;\frac{\mu _{+i}\left( V_p^2-\delta _{ei}\right) }{V_p}+\frac{N_{r1}\mu _{-i}V_p^3M_{\pm }}{\left( V_p^2-\delta _{ei}\right) }. \end{aligned}$$

(21)

In the previous literature [25,26,27], the solution of mB equation (see Appendix) is incorrectly defined, which is not useful for further verification in laboratory plasmas. To determine the correct stationary shock wave solution of Eq. (20), one can convert Eq. (20) by considering $\Phi ^{(1)}(X,T)=\Psi (\zeta )$ with $\zeta =X-V_rT$ ( $V_r$ is the constant speed of reference frame) to the following form:

$$\begin{aligned} C\frac{d\Psi }{d\zeta }=V_r A \Psi -\frac{B}{3}\Psi ^3. \end{aligned}$$

(22)

This implies that

$$\begin{aligned} \int {\frac{C}{ V_r A \Psi -\frac{B}{3}\Psi ^3}}d\Psi =\int d\zeta . \end{aligned}$$

(23)

By simplifying Eq. (23), the stationary shock wave solution of Eq. (20) is obtained as

$$\begin{aligned} \Phi ^{(1)}=\sqrt{\Phi _A\left\{ 1+\tan h\left( \frac{\zeta }{\Phi _W}\right) \right\} }, \end{aligned}$$

(24)

where $\Phi _A=\left( 3V_rA/2B\right)$ and $\Phi _W=\left( C/V_rB\right)$ are respectively the amplitude and thickness of IASWs around the critical values. The verification of the obtained solution is given in Appendix.

Fig. 2

Electrostatic mB shocks around the critical value $q_c=3.098638852$, that is $q=3.5$ for different values of (a) $\mu _{-i}$ and (b) $\mu _{+i}$, with $M_{r}=3.75$, $T_{ni}=0.05$, $T_{e}=0.19$, $N_{r1}=0.5$, $N_{r2}=0.01$ and $V_r=0.01$

Fig. 3

Effect of the reference speed $V_r$ on electrostatic mB shocks around the critical value $q_c=3.098638852$, that is $q=3.5$, with $M_{r}=3.75$, $T_{ni}=0.05$, $T_{e}=0.19$, $N_{r1}=0.5$, $N_{r2}=0.01$, $\mu _{-i}=0.05$, and $\mu _{+i}=0.3$

Fig. 4

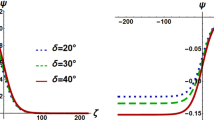
Variation of the normalized electric field around the critical value $q_c=3.098638852$, that is $q=3.5$, for different values of (a) $\mu _{-i}$ and (b) $\mu _{+i}$, with the same typical values of Fig. 1

Fig. 5

Electrostatic mmB shocks (a) $q=6<q_c=6.176859718$ and (b) $q=6.5>q_c=6.176859718$, with $M_{r}=3.75$, $T_{ni}=0.05$, $T_{e}=0.1$, $N_{r1}=0.5$, $N_{r2}=0.1$, $V_r=0.1$, $\mu _{-i}=0.01$ and $\mu _{+i}=0.5$

Fig. 6

Effect of (a) $\mu _{-i}$ and (b) $\mu _{+i}$ on the mmB shocks at $q=6.5$

3.2 Formation of mmB-Type Equation with Wave Solution

One can easily find that Eq. (20) is not useful to study the shock wave phenomena not only at CVs but also around CVs. To study the electrostatic shocks not only around CVs but also at CVs, one needs to derive another evolution equation. To do so, one can take $C_{f}=C_{f}^0$ for q (say) around its $q_c$ as

$$\begin{aligned} C_{f}^0=h\left( \frac{\partial C_{f}}{\partial q}\right) _{q=q_c}|q-q_c|=SG\epsilon , \end{aligned}$$

(25)

where $|q-q_v|\equiv \epsilon$ (because $|q-q_c|$ is small quantity), $S=1(-1)$ for $q>q_c(q<q_c)$ and $G=\left( \frac{\partial C_{f}}{\partial q}\right) _{q=q_c}$. As a result, one can re-evaluate from Eq. (4) by adding $\rho ^{(2)}\equiv -\varepsilon ^3 \frac{1}{2}SG\Phi ^2$ with the $O(\epsilon ^5)$ equation and yields

$$\begin{aligned} 0=&-N_{r2}\Omega _1\frac{\partial \Phi ^{(3)}}{\partial X}+SG\Phi ^{(1)}\frac{\partial \Phi ^{(1)}}{\partial X}-3N_{r2}\Omega _3\left[ \Phi ^{(1)}\right] ^2\frac{\partial \Phi ^{(1)}}{\partial X}\\&-3N_{r2}\Omega _2\frac{\partial }{\partial X}\left[ \Phi ^{(1)}\Phi ^{(2)}\right] +\frac{\partial N_{+i}^{(3)}}{\partial X}-\frac{\partial N_{-i}^{(3)}}{\partial X}, \end{aligned}$$

(26)

Now, simplifying Eqs. (14)–(17) and (26), one obtains

$$\begin{aligned} A\frac{\partial \Phi ^{(1)}}{\partial T} +SD\Phi ^{(1)}\frac{\partial \Phi ^{(1)}}{\partial X} +B\left\{ \Phi ^{(1)}\right\} ^2\frac{\partial \Phi ^{(1)}}{\partial X}+C\frac{{\partial }^2\Phi ^{(1)}}{\partial x^2}=0, \end{aligned}$$

(27)

where

$$\begin{aligned} D=V_p^2\left( V_p^2-\delta _{ei}\right) \left( \frac{\partial C_{f}}{\partial q}\right) _{q=q_c}. \end{aligned}$$

(28)

Equation (27) is so-called the mmB-type equation because the additional nonlinear term is occurred with the mBE. One can easily convert mmB-type equation not only to mB-type equation but also to B-type equation. It is noted that Eq. (27) does not support the IASWs around CVs but also at CVs, which is the main advantage of this equation.

The appropriate stationary shock wave solution of mmB-type equation can be defined as

$$\begin{aligned} \Phi ^{(1)}=\sqrt{\Phi _{mA}\left\{ 1+\tan h\left( \frac{\zeta }{\Phi _{mW}}\right) \right\} }-\frac{SD}{2B}, \end{aligned}$$

(29)

where

$$\begin{aligned}\Phi _{mA}=&\left( 3Ck/4B\right),\Phi _W=\left( 2/k\right),\\ k=&\left[ S^2\left( \frac{D}{A}\right) ^2\pm \sqrt{s^4\left( \frac{D}{A}\right) ^4+32CV_r \left( \frac{B}{A}\right) ^2}\right] \div \left[ 4C\left( \frac{B}{A}\right) \right] . \end{aligned}$$

(30)

4 Discussion

This section explores the effect of $\mu _{+i}$, $\mu _{-i}$ and $V_r$ with physical explanation on the electrostatic shocks around CVs and at the neighborhood of CVs.

Figure 2a, b display the effect of $\mu _{+i}$ and $\mu _{-i}$ on the electrostatic IASWs around $q_c$. It is observed that $\mu _{+i}$ and $\mu _{-i}$ strongly plays an important role to the formation of monotonically shock waves around $q_c$. In addition, the thickness of shocks are remarkably increased and slightly increased with the increases of $\mu _{+i}$ and $\mu _{-i}$, respectively. It is noted that the effect of the viscosity coefficient of NIs and PIs on shock wave excitation can be determined on the basis of collective friction between the layers of the plasma concentration system. In fact, viscosity is the force of collective friction between layers of fluid in the aforementioned plasmas. With the decrease of $\mu _{+i}$ and $\mu _{-i}$, the collective friction force is decreased. As a result, the thickness of shocks is decreased. The effect of $V_r$ on electrostatic IASWs around $q_c$ is displayed in Fig. 3. Figure 3 obviously shows that the amplitude and thickness of IASWs are significantly increased with the increase of $V_r$. Finally, the variation of normalized electric field ($E=-grad\Phi$) around $q_c$ for different values of $\mu _{+i}$ and $\mu _{-i}$ is presented in Fig. 4. It is observed that the electric field becomes monotonically hump-shaped with the increase of $\mu _{+i}$ and $\mu _{-i}$. Consequently, the electric field is propagating narrowly with the increase of $\mu _{+i}$, but smoothly with the increase of $\mu _{-i}$ (See Fig. 4).

Figure 5a, b shows the shape of electrostatic ion acoustic mmB shocks for $q=6<q_c=6.176859718$ and $q=6.5>q_c=6.176859718$ with $M_{r}=3.75$, $T_{ni}=0.05$, $T_{e}=0.1$, $N_{r1}=0.5$, $N_{r2}=0.1$, $V_r=0.1$, $\mu _{-i}=0.01$ and $\mu _{+i}=0.5$. Whereas Fig. 6a, b display the effect of $\mu _{+i}$ and $\mu _{-i}$ on the electrostatic IASWs at the neighboring of $q_c$, that is at $q=6.5$. It is found that the monotonic correct solution of the shocks are only generated for the viscosity coefficient of NIs in which both amplitude and thickness are increased with the increase of the viscosity coefficient of NIs at the neighboring CVs. However, the amplitude and thickness of IASWs are decreased with the increase of the viscosity coefficient of PIs at the neighboring CVs. It might be predicted from this work that one can study the real features of shock wave excitations around CVs by formulating the correct solution of the mB and mmB equations.

To conclude, the plasma system involving pair-ions and generalized distributed electrons has been considered for reporting the features of electrostatic IASWs around CVs. To do so, the mB- and mmB-type equations have been obtained by employing the reductive perturbation method, which reveals the shocks only around the critical values in the plasmas. The correct stationary shock wave solutions of these equations are first time reported. The effect of $\mu _{+i}$, $\mu _{-i}$ and $V_r$ on the electrostatic mB and mmB shocks around and at the neighboring of CVs are discussed. It is found that the mB-type equation is supporting monotonic shocks around CVs in which the amplitude is unchanged but the thickness is increased with the increase of $\mu _{+i}$ and $\mu _{-i}$. Subsequently, the monotonically hump-shaped electric field is propagating narrowly and smoothly with the increase of $\mu _{+i}$ and $\mu _{-i}$, respectively, due to the correct solution of the mB-type equation. However, the mmB-type equation supports monotonic shocks around CVs with the influence of $\mu _{-i}$ only, in which both the amplitudes and the thickness are increased with the increase of $\mu _{-i}$ but decreased with the increase of $\mu _{+i}$. It may be concluded that the results presented in this work are not only very helpful to understand the broadband shocks noise in the D- and F-regions of the Earth’s ionosphere around the critical values, but also in plasma laboratory experiments.

Appendix

Verification of solution as in Eq. (23) with the aid of Maple 18:

$$\begin{aligned}&>\zeta :=X-V_r T\\&>\Phi _A:=\left( 3V_rA/2B\right) \\&>\Phi _W:=\left( C/V_rB\right) \\&>\Phi ^{(1)}=\sqrt{\Phi _A\left\{ 1+\tan h\left( \frac{\zeta }{\Phi _W}\right) \right\} }\\&>diff(\Phi ^{(1)},T)\\&>diff(\Phi ^{(1)},X)\\&>diff(\Phi ^{(1)},X,X)\\& >A*diff(\Phi ^{(1)},T)+B*(\Phi ^{(1)})^2 *diff(\Phi ^{(1)},X)+C*diff(\Phi ^{(1)},X,X)\\& 0 \end{aligned}$$

It is noted that the stationary solution

$$\begin{aligned} >\phi ^{(1)}=\sqrt{\left( \frac{3u_0}{2B}\right) \left\{ 1-\tan h\left( \frac{\zeta -u_0\tau }{\sqrt{\frac{C}{u_0}}}\right) \right\} } \end{aligned}$$

provided in the previous literature [25,26,27] does not satisfy the following modified Burgers equation:

$$\begin{aligned} \frac{\partial \phi ^{(1)}}{\partial \tau }+B\left\{ \phi ^{(1)}\right\} ^2\frac{\partial \Phi ^{(1)}}{\partial \zeta }=C\frac{{\partial }^2\phi ^{(1)}}{\partial \zeta ^2}, \end{aligned}$$

which clearly indicates that the above solution of mB equation is not useful for later experimental verification.