Head-on Collision of Ion-Acoustic Shock and Solitary Waves in Collisionless Plasma with Pair Ions and Electrons

Abstract

Unmagnetized collisionless plasma system consisting of positive and negative ions and electrons is considered to study the head-on collision of ion-acoustic shock and solitary waves (IASWs) and its effects on the formation of shock (monotonic and oscillatory) waves and phase shift. The soliton solution is derived from the two-sided Korteweg-de Vries Burger (KdVB) equations. The KdVB equations are obtained using extend Poincaré-Lighthill-Kuo (ePLK) method. It is assumed that the negative ions are immobile and the electrons follow the Boltzmann energy distribution in the plasma. The effects of plasma parameters such as density ratios and kinematic viscosities on electrostatic shock profiles, phase shift, amplitudes, and formation of shock (monotonic and oscillatory) as well as on the soliton solution are investigated. It is found that the density ratio of negative to positive ions plays a vital role on the formation of shock waves and phase shift after collision.

1 Introduction

The nonlinear propagation of ion-acoustic waves is one of the most studied aspects in plasma physics. It is not always an easy task to obtain direct solution of the hydrodynamic-like model equations which govern their evolution. It is obvious that the asymptotic technique is both simpler and more informative to obtain the solution of such evolution equations. In 1966, Washimi and Taniuti [1] used the reductive perturbation technique to derive Korteweg-de Vries (KdV) equation to study the wave propagation in plasma systems consisting of cold ions and hot electrons. Later on, the asymptotic technique is extensively used for making the complicated systems of partial differential equations (PDEs) more tractable model equations that describe the wave propagation when the combined effects of nonlinear steepening and dispersion balance each other to give rise to the formation of localized structures [2, 3]. On the other hand, recently, many authors are attracted to investigate the interactions between waves due to their potentiality with the extended Poincaré-Lighthill-Kuo (ePLK) method [4,5,6].

Plasmas with negative ions have drawn great interest of researchers due to the wide technological applications such as in neutral beam source [7], semiconductor and material processing [8], and so on. The presence of negative ions in plasmas is ascribed by [9,10,11] and it is noted that the negative ions significantly modify the characteristics of plasma phenomena. The negative ions are observed in space and astrophysical objects and in laboratory [9, 10, 12,13,14,15,16,17,18,19,20] plasmas as well. The production of negative ions in low-temperature laboratory experiments is observed by [14, 15, 21, 22]. Sato [23] has investigated the production of negative ions by introducing a small amount of SF₆ gas into low-temperature (≈ 0.2 eV) potassium plasma in Q-machine. Von Goeler et al. [17] have directed a beam of CsCl onto the hot tungsten plate of a Q-machine that forms plasma consisting of Cs⁺, Cl⁻, and electrons. On the other hand, the negative ions are also observed in space and astrophysical objects, such as in the D-region [24] and F-region of the Earth’s ionosphere. It has been observed by the Cassini spacecraft that heavy negative ions are present in the upper region of Titans atmosphere Coates [25]. However, the ion-acoustic (IA) shock waves (IASWs) were first observed in a novel plasma device such as in the double-plasma device [24]. Wong et al. [10] have studied experimentally the production of IA waves (IAWs) in presence of negative ions with ${\mathrm{SF}}_6^{-}$ species. Thus, the theoretical investigation on the properties of IAWs is reported by Angelo et al. [9], Angelo [19], and Galvez and Gary [20]. Song et al. [26] have also reported an experimental investigation of IAWs in Q-machine plasmas consisting of K⁺, ${\mathrm{SF}}_6^{-}$, and electrons. They observed that the phase velocity of the IA “fast” mode [9, 10] increases with increasing density ratio of negative to positive ions. The fast wave may form negative-potential solitary waves [27, 28], and when the nonlinear steepening is considered, in addition to dissipation, it will either disperse or more significantly form a shock [29]. Collisionless means that the mean free path for binary Coulomb collisions is usually much larger than the typical size of the system. Bret [30] has shown that the collisionless plasmas behave like collisional ones and collisionless shock forms when two collisionless plasma shells collide, that depend on critical density. If the relative speed between the rarefaction wave and ambient plasma exceeds the IA speed at the location where the densities of the rarefaction wave and ambient medium are similar, then the plasma shocks can be formed. The electrostatic shocks and double layers are formed [31], when the plasma is unmagnetized or weakly magnetized. Dieckmann et al. [32] have investigated the formation of shock waves experimentally in collisionless plasmas. Shah et al. [33] have studied the propagation characteristics of positron-acoustic shock waves in an unmagnetized collisionless dense plasma consisting of non-relativistic inertial cold positrons, ultra-relativistic degenerate electrons and hot positron fluid, and non-degenerate positively and negatively charged immobile ions, as well as [34] investigated experimentally the formation of shocks. Gill et al. [35] have studied the IASWs considering collisionless unmagnetized relativistic quantum electron-positron-ion plasma employing the quantum hydrodynamic model. However, due to its importance, the production and properties of shock waves are investigated theoretically and experimentally for space, astrophysical, and laboratory plasmas [36,37,38,39]. The productions of shocks in Q-machine with negative ions are reported [34, 40]. Adak et al. [41, 42] have studied the magnetosonic shocks and investigated the effect of ion-ion interactions on the dynamics of nonlinear IAWs in fully collisional pair-ion (${\mathrm{C}}_{60}^{+}$, ${\mathrm{C}}_{60}^{-}$) plasmas along with KdV Burger equation using reductive perturbation method and found that the positive-(negative) potential IAWs exists when T₋ > T₊ (T₋ < T₊). Hossain et al. [43] have investigated the nonlinear IA monotonic as well oscillatory shock waves in negative-ion plasmas with nonextensive electrons. Saeed and Mushtaq [44] have investigated the linear and nonlinear properties of low-frequency IAWs in pair-ion plasmas with Boltzmann-distributed electrons along with Kadomtsev-Petviashvili (KP) equation and found that the structure of the IAWs is significantly affected by the ratio of electron density and temperature. The collision of counter-propagating solitary waves was studied theoretically [45, 46] and experimentally [47] and it was found that both (compressive and rarefactive) solitons lag in phase but the smaller soliton lags more than the larger ones. To the best of our knowledge, no one has studied the head-on collision of IA solitary and shock waves in plasma systems consisting of positive ions (K⁺) and negative ions (${\mathrm{SF}}_6^{-}\Big)$ with Boltzmann energy-distributed electrons. This report is organized as follows: assumptions and hydrodynamic fluid equations are represented in section 2. Derivation of the evolution equations and phase shifts with analytical solution are provided in section 3. Results and discussion are displayed in section 4. Conclusion is drawn in section 5.

2 Assumptions and Hydrodynamic Fluid Equations

Unmagnetized collisionless three-component plasma system consisting of positive and negative ions with Boltzmann energy-distributed electrons is considered. The normalized hydrodynamic fluid equations and Poisson’s equation for the concerned plasma system are, respectively, given by

$$ \frac{\partial {n}_{1i}}{\partial t}+\frac{\partial \left({n}_{1i}{v}_{1i}\right)}{\partial x}=0, $$

(1)

$$ \frac{\partial {n}_{2i}}{\partial t}+\frac{\partial \left({n}_{2i}{v}_{2i}\right)}{\partial x}=0, $$

(2)

$$ \frac{\partial {v}_{1i}}{\partial t}+{v}_{1i}\frac{\partial {v}_{1i}}{\partial x}+\frac{\partial \phi }{\partial x}+{\eta}_{1i}\frac{\partial^2{v}_{1i}}{\partial {x}^2}=0, $$

(3)

$$ \frac{\partial {v}_{2i}}{\partial t}+{v}_{2i}\frac{\partial {v}_{2i}}{\partial x}-{m}_{12i}\frac{\partial \phi }{\partial x}+\frac{T_{2 ie}}{n_{2i}}\frac{\partial {n}_{2i}}{\partial x}+{\eta}_{2i}\frac{\partial^2{v}_{2i}}{\partial {x}^2}=0, $$

(4)

$$ \frac{\partial^2\phi }{\partial {x}^2}={n}_{1i}-{n}_{2i}-{n}_e $$

(5)

where, n_1i, n_2i, n_e, v_1i, v_2i, and ϕ are the densities of positive and negative ions, electrons, velocities of positive and negative ions, and electrostatic potential, respectively. n_1i0, n_2i0, and n_e0 are the unperturbed densities of positive and negative ions and electrons, respectively. The charge neutrality condition is considered as n_1i0 = n_2i0 + n_e0. It can be converted to n_21i + n_e1i = 1, n_21i = n_2i0/n_1i0, n_e1i = n_e0/n_1i0, m_12i = m_1i/m_2i, and T_e2i = T_e/(1 − n_21i)T_2i. m_1i and m_2i are the masses of positive and negative ions, T_1i and T_2i are the temperatures of positive and negative ions, and T_e is the temperature of electrons, respectively. The densities n_2i and n_e are normalized by n_1i0, ϕ is normalized by k_BT_e/e, space coordinate is normalized by the electron Debye length ${\lambda}_{De}=\sqrt{k_B{T}_e/4\pi {e}^2{n}_{e0}}$, ion velocity is normalized by the positive-IA speed ${c}_s=\sqrt{k_B{T}_e/{m}_{1i}}$$\sqrt{\left({n}_{e1i}+{n}_{21i}\right)/{n}_{e1i}\left(1-{n}_{21i}\right)}$, and time coordinate is normalized by the positive-ion plasma frequency ${\omega}_{p1i}^{-1}={\lambda}_{De}/{c}_s$. The quantity $\sqrt{k_B{T}_e/{m}_{1i}}$, would be the positive-IA speed in the absence of negative ions, e is the electronic charge and k_B is the Boltzmann constant. η_1i and η_2i are the normalized kinematic viscosities of positive and negative ions, respectively, obtained introducing in Eqs. (3) and (4), where ${\eta}_{1i}={\eta}_{d1i}{\omega}_{p1i}/{m}_{1i}{n}_{1i}{c}_s^2$, ${\eta}_{2i}={\eta}_{d2i}{\omega}_{p2i}/{m}_{2i}{n}_{2i}{c}_s^2$. η_d1i, and η_d2i are the dynamic viscosities of the positive and negative ions, respectively. It is assumed that T_e ≥ T_1i ≫ T_2i [34]. Due to the effects of negative ions, the electron shielding is reduced and this effect was demonstrated for the propagation and damping of linear IAWs in collisionless negative plasma with ${\mathrm{SF}}_6^{-}$, which was observed in single-ended Q-machine plasmas [23, 26].The ion Landau damping is stronger for IAWs as obtained theoretically [48, 49] and experimentally in a Q-machine plasma of T_e ≈ T_1i, which has a big ballistic contribution to the wave propagation. In the single-ended Q-machine plasma of T_e ≥ T_1i with ion flow [23], the ion Landau damping is strong for IAWs but the ballistic effect can be neglected [50, 51]. In the presence of negative ions, the factor T_e ≈ T_e/(1 − n_21i) [34] is responsible for the increase of phase velocity, as a result, the Landau damping of IAWs decreases, which is equivalent to the increase of T_e/T_1i caused by electron heating through electron cyclotron resonance [52]. The mass of negative ion (${\mathrm{SF}}_6^{-}\Big)$ (mass number, 146) is much larger than the positive-ion mass (K⁺) (mass number, 39). Thus, one can assume that the negative ion is immobile and the IA mode is a positive-IA (PIA) mode. Thus, no loss of generality occurs by assuming that T_1i ≈ 0 instead of T_e/T_1i ≥ 1, because in presence of negative ions T_e is replaced by T_e/(1 − n_21i).

3 Derivation of Evolution Equations and Analytical Solution

It is assumed that there are two solitons S_L (propagates toward left) and S_R (propagates toward right) in the considered plasma system, approaching toward each other. Initially (t →  − ∞), they are asymptotically far apart and propagate toward each other. After some time, they interact and collide (t = 0) and then depart. As the collisions of solitons are elastic, the amplitudes of solitons will remain unchanged due to the interaction between them, but after the collision each soliton acquires an additional phase shift. There are two ways of interaction between the two solitons in one-dimensional system. One is head-on collision, in which the angle between the two propagating solitons is equal to π, and the other is overtaking collision, in which the angle between the two propagating solitons is equal to 0. The phenomena pertaining to overtaking collision is beyond the scope of this study. To study the effects of head-on collisions on IA solitary waves (IASWs), the electrostatic resonance and their corresponding phase shifts can be derived from the two-sided Korteweg-de Varies Burger (KdVB) equations considering the plasma system composing of unmagnetized collisionless positive ions and negative ions with Boltzmann energy-distributed electrons using ePLK method. With respect to the ePLK method the stretched variables can be expanded as

$$ {\displaystyle \begin{array}{c}\xi =\varepsilon \left(x-{v}_pt\right)+{\varepsilon}^2{\varphi}_{10}\left(\zeta, \tau \right)+{\varepsilon}^3{\varphi}_{11}\left(\xi, \zeta, \zeta \right)+\cdots \cdots \cdots \\ {}\zeta =\varepsilon \left(x+{v}_pt\right)+{\varepsilon}^2{\varphi}_{20}\left(\xi, \tau \right)+{\varepsilon}^3{\varphi}_{21}\left(\xi, \zeta, \zeta \right)+\cdots \cdots \cdots \\ {}\tau ={\varepsilon}^3t\kern0.50em \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{array}}\Big\}, $$

(6)

and the dependent variables can be expanded around the equilibrium values in powers of ε as

$$ \left.\begin{array}{c}{n}_{1i}=1+{\varepsilon}^2{n}_{1i}^{(1)}+{\varepsilon}^3{n}_{1i}^{(2)}+{\varepsilon}^4{n}_{1i}^{(3)}+\cdots \cdots \\ {}\kern1em {n}_{2i}={n}_{21i}+{\varepsilon}^2{n}_{2i}^{(1)}+{\varepsilon}^3{n}_{2i}^{(2)}+{\varepsilon}^4{n}_{2i}^{(3)}+\cdots \cdots \\ {}{v}_{1i}={\varepsilon}^2{v}_{1i}^{(1)}+{\varepsilon}^3{v}_{1i}^{(2)}+{\varepsilon}^4{v}_{1i}^{(3)}+\cdots \cdots \cdots \cdots \\ {}{v}_{2i}={\varepsilon}^2{v}_{2i}^{(1)}+{\varepsilon}^3{v}_{2i}^{(2)}+{\varepsilon}^4{v}_{2i}^{(3)}+\cdots \cdots \cdots \cdots \\ {}\phi ={\varepsilon}^2{\phi}^{(1)}+{\varepsilon}^3{\phi}^{(2)}+{\varepsilon}^4{\phi}^{(3)}+\cdots \cdots \cdots \cdots \\ {}{n}_e={n}_{e1i}{e}^{{\phi T}_{2 ie}}\kern12.5em \end{array}\right\}, $$

(7)

where v_p is the phase velocity of IASWs. From Eq. (6), the following operators are obtained

$$ \left.\begin{array}{c}{\partial}_t={\varepsilon}^3{\partial}_{\tau }-{v}_p\varepsilon \left({\partial}_{\xi }-{\partial}_{\zeta}\right)+{v}_p{\varepsilon}^3\left({\partial}_{\zeta }{\varphi}_{10}{\partial}_{\xi }-{\partial}_{\xi }{\varphi}_{20}{\partial}_{\zeta}\right)+\cdots \cdots \\ {}{\partial}_x=\varepsilon \left({\partial}_{\xi }+{\partial}_{\zeta}\right)+{\varepsilon}^3\left({\partial}_{\zeta }{\varphi}_{10}{\partial}_{\xi }+{\partial}_{\xi }{\varphi}_{20}{\partial}_{\zeta}\right)+\cdots \cdots \kern5.5em \end{array}\right\}. $$

(8)

As η_1i and η_2i in Eqs. (3) and (4) are small, therefore one may consider η_1i = εη₁ and η_2i = εη₂. Inserting Eqs. (6)–(8) into Eqs. (1)–(5), one can obtain a set of partial differential equations (PDEs) in terms of ε. Now, collecting the terms of equal powers of ε, the smallest order of ε yields

$$ -{v}_p{\partial}_{\xi }{n}_{1i}^{(1)}+{v}_p{\partial}_{\zeta }{n}_{1i}^{(1)}+{\partial}_{\xi }{v}_{1i}^{(1)}+{\partial}_{\zeta }{v}_{1i}^{(1)}=0, $$

(9)

$$ -{v}_p{\partial}_{\xi }{v}_{1i}^{(1)}+{v}_p{\partial}_{\zeta }{v}_{1i}^{(1)}+{\partial}_{\xi }{\phi}^{(1)}+{\partial}_{\zeta }{\phi}^{(1)}=0, $$

(10)

$$ -{v}_p{\partial}_{\xi }{n}_{2i}^{(1)}+{v}_p{\partial}_{\zeta }{n}_{2i}^{(1)}+{n}_{21i}{\partial}_{\xi }{v}_{2i}^{(1)}+{n}_{21i}{\partial}_{\zeta }{v}_{2i}^{(1)}=0, $$

(11)

$$ -{v}_p{\partial}_{\xi }{v}_{2i}^{(1)}+{v}_p{\partial}_{\zeta }{v}_{2i}^{(1)}-{m}_{21i}{\partial}_{\xi }{\phi}^{(1)}-{m}_{21i}{\partial}_{\zeta }{\phi}^{(1)}=0, $$

(12)

$$ {n}_{1i}^{(1)}-{n}_{2i}^{(1)}-{n}_{e1i}{T}_{e2i}{\phi}^{(1)}=0. $$

(13)

Solving Eqs. (9)–(13), one can determine the following relations consisting of different plasma parameters as

$$ \left.\begin{array}{c}\kern1em {\phi}^{(1)}={\phi}_{\xi}^{(1)}+{\phi}_{\zeta}^{(1)},\kern0.5em {n}_{1i}^{(1)}=1/{v}_p^2\left[{\phi}_{\xi}^{(1)}+{\phi}_{\zeta}^{(1)}\right]\kern0.5em ,{v}_{1i}^{(1)}=1/{v}_p\left[{\phi}_{\xi}^{(1)}-{\phi}_{\zeta}^{(1)}\right]\ \\ {}\ {n}_{2i}^{(1)}=-{n}_{21i}{m}_{21i}/{v}_p^2\left[{\phi}_{\xi}^{(1)}+{\phi}_{\zeta}^{(1)}\right],{v}_{2i}^{(1)}=-{m}_{21i}/{v}_p\left[{\phi}_{\xi}^{(1)}-{\phi}_{\zeta}^{(1)}\right]\end{array}\right\}, $$

(14)

and the phase velocity is obtained as ${v}_p={\left[\left(1+{n}_{21i}{m}_{21i}\right)/{n}_{e1i}{T}_{e2i}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$. In these expressions ${\phi}_{\xi}^{(1)}\left(\xi, \tau \right)\approx {\phi}_{\xi}^{(1)}$ and ${\phi}_{\zeta}^{(1)}\left(\zeta, \tau \right)\approx {\phi}_{\zeta}^{(1)}$ represent the right and left propagating waves, respectively. Taking the next higher order of ε, one can obtain the following relations:

$$ \left.\begin{array}{c}\kern1em {\phi}^{(2)}={\phi}_{\xi}^{(2)}+{\phi}_{\zeta}^{(2)},\kern0.5em {n}_{1i}^{(2)}=1/{v}_p^2\left[{\phi}_{\xi}^{(2)}+{\phi}_{\zeta}^{(2)}\right]\kern0.5em ,{v}_{1i}^{(2)}=1/{v}_p\left[{\phi}_{\xi}^{(2)}-{\phi}_{\zeta}^{(2)}\right]\\ {}\ {n}_{2i}^{(2)}=-{n}_{21i}{m}_{21i}/{v}_p^2\left[{\phi}_{\xi}^{(2)}+{\phi}_{\zeta}^{(2)}\right],{v}_{2i}^{(2)}=-{m}_{21i}/{v}_p\left[{\phi}_{\xi}^{(2)}-{\phi}_{\zeta}^{(2)}\right]\end{array}\right\}. $$

(15)

The next higher order of ε provides

$$ {\partial}_{\tau }{n}_{1i}^{(1)}-{v}_p{\partial}_{\xi }{n}_{1i}^{(3)}+{v}_p{\partial}_{\zeta }{n}_{1i}^{(3)}+{\partial}_{\xi }{v}_{1i}^{(3)}+{\partial}_{\zeta }{v}_{1i}^{(3)}+{\partial}_{\xi}\left({n}_{1i}^{(1)}{v}_{1i}^{(1)}\right)+{\partial}_{\zeta}\left({n}_{1i}^{(1)}{v}_{1i}^{(1)}\right)+{v}_p{\partial}_{\zeta }{\varphi}_{10}{\partial}_{\xi }{n}_{1i}^{(1)}-{v}_p{\partial}_{\xi }{\varphi}_{20}{\partial}_{\zeta }{n}_{1i}^{(1)}+{\partial}_{\zeta }{\varphi}_{10}{\partial}_{\xi }{v}_{1i}^{(1)}+{\partial}_{\xi }{\varphi}_{20}{\partial}_{\zeta }{v}_{1i}^{(1)}=0, $$

(16)

$$ {\partial}_{\tau }{n}_{2i}^{(1)}-{v}_p{\partial}_{\xi }{n}_{2i}^{(3)}+{v}_p{\partial}_{\zeta }{n}_{2i}^{(3)}+{n}_{21i}{\partial}_{\xi }{v}_{2i}^{(3)}+{n}_{21i}{\partial}_{\zeta }{v}_{2i}^{(3)}+{\partial}_{\xi}\left({n}_{2i}^{(1)}{v}_{2i}^{(1)}\right)+{\partial}_{\zeta}\left({n}_{2i}^{(1)}{v}_{2i}^{(1)}\right)\kern3.25em +{v}_p{\partial}_{\zeta }{\varphi}_{10}{\partial}_{\xi }{n}_{2i}^{(1)}-{v}_p{\partial}_{\xi }{\varphi}_{20}{\partial}_{\zeta }{n}_{2i}^{(1)}+{n}_{21i}{\partial}_{\zeta }{\varphi}_{10}{\partial}_{\xi }{v}_{2i}^{(1)}+{n}_{21i}{\partial}_{\xi }{\varphi}_{20}{\partial}_{\zeta }{v}_{2i}^{(1)}=0, $$

(17)

$$ {\partial}_{\tau }{v}_{1i}^{(1)}-{v}_p{\partial}_{\xi }{v}_{1i}^{(3)}+{v}_p{\partial}_{\zeta }{v}_{1i}^{(3)}+{v}_{1i}^{(1)}{\partial}_{\xi }{v}_{1i}^{(1)}+{v}_{1i}^{(1)}{\partial}_{\zeta }{v}_{1i}^{(1)}+{\partial}_{\xi }{\phi}^{(3)}+{\partial}_{\zeta }{\phi}^{(3)}+{v}_p{\partial}_{\zeta }{\varphi}_{10}{\partial}_{\xi }{v}_{1i}^{(1)}\kern0.75em -{v}_p{\partial}_{\xi }{\varphi}_{20}{\partial}_{\zeta }{v}_{1i}^{(1)}+{\partial}_{\zeta }{\varphi}_{10}{\partial}_{\xi }{\phi}^{(1)}+{\partial}_{\xi }{\varphi}_{20}{\partial}_{\zeta }{\phi}^{(1)}+{\eta}_1{\partial}_{\xi \xi}{v}_{1i}^{(1)}+2{\eta}_1{\partial}_{\xi \zeta}{v}_{1i}^{(1)}+{\eta}_1{\partial}_{\zeta \zeta}{v}_{1i}^{(1)}=0, $$

(18)

$$ {\partial}_{\tau }{v}_{2i}^{(1)}-{v}_p{\partial}_{\xi }{v}_{2i}^{(3)}+{v}_p{\partial}_{\zeta }{v}_{2i}^{(3)}+{v}_{2i}^{(1)}{\partial}_{\xi }{v}_{2i}^{(1)}+{v}_{2i}^{(1)}{\partial}_{\zeta }{v}_{2i}^{(1)}-{m}_{21i}{\partial}_{\xi }{\phi}^{(3)}-{m}_{21i}{\partial}_{\zeta }{\phi}^{(3)}+{v}_p{\partial}_{\zeta }{\varphi}_{10}{\partial}_{\xi }{v}_{2i}^{(1)}-{v}_p{\partial}_{\xi }{\varphi}_{20}{\partial}_{\zeta }{v}_{2i}^{(1)}-{m}_{21i}{\partial}_{\zeta }{\varphi}_{10}{\partial}_{\xi }{\phi}^{(1)}-{m}_{21i}{\partial}_{\xi }{\varphi}_{20}{\partial}_{\zeta }{\phi}^{(1)}+{\eta}_2{\partial}_{\xi \xi}{v}_{2i}^{(1)}+2{\eta}_2{\partial}_{\xi \zeta}{v}_{2i}^{(1)}+{\eta}_2{\partial}_{\zeta \zeta}{v}_{2i}^{(1)}=0, $$

(19)

$$ {\partial}_{\xi \xi}{\phi}^{(1)}+2{\partial}_{\xi \zeta}{\phi}^{(1)}+{\partial}_{\zeta \zeta}{\phi}^{(1)}={n}_{1i}^{(3)}-{n}_{2i}^{(3)}-{n}_{e1i}{T}_{e2i}{\phi}^{(3)}-\frac{1}{2}{n}_{e1i}{T}_{e2i}^2{\left\{{\phi}^{(1)}\right\}}^2. $$

(20)

Combining Eqs. (16)–(20) and with help of Eq. (14), after some straightforward mathematical calculation, one can obtain

$$ \frac{1}{C}\left[\frac{n_{21i}}{v_p^2}{v}_{1i}^{(3)}-4{v}_p^2{v}_{2i}^{(3)}\right]=\int \left[{\partial}_{\tau }{\phi}_{\xi}^{(1)}+{C}_N{\phi}_{\xi}^{(1)}{\partial}_{\xi }{\phi}_{\xi}^{(1)}-{C}_D{\partial}_{\xi \xi \xi}{\phi}_{\xi}^{(1)}+{C}_{DP}{\partial}_{\xi \xi}{\phi}_{\xi}^{(1)}\right] d\zeta +\int \left[{\partial}_{\tau }{\phi}_{\zeta}^{(1)}-{C}_N{\phi}_{\zeta}^{(1)}{\partial}_{\zeta }{\phi}_{\zeta}^{(1)}+{C}_D{\partial}_{\zeta \zeta \zeta}{\phi}_{\zeta}^{(1)}-{C}_{DP}{\partial}_{\zeta \zeta}{\phi}_{\zeta}^{(1)}\right] d\xi +\iint \left[{C}_2{\partial}_{\zeta }{\varphi}_{10}+{C}_3{\phi}_{\zeta}^{(1)}\right]{\partial}_{\xi \xi}{\phi}_{\xi}^{(1)} d\xi d\zeta -\iint \left[{C}_2{\partial}_{\xi }{\varphi}_{20}+{C}_3{\phi}_{\xi}^{(1)}\right]{\partial}_{\zeta \zeta}{\phi}_{\zeta}^{(1)} d\xi d\zeta, $$

(21)

where ${C}_N=\left(3+{n}_{e1i}{T}_{e2i}^2{v}_p^2-3{n}_{21i}{m}_{21i}^2/{v}_p^4\right)/{C}_1$, ${C}_D={C}_1^{-1}$, ${C}_{DP}=\left({v}_p{\eta}_1+{n}_{21i}{m}_{21i}{\eta}_2/{v}_p^3\right)/{C}_1$, ${C}_2=\left(4{v}_p^2+4{n}_{21i}{m}_{21i}/{v}_p^2\right)/{C}_1$, ${C}_3=\left({n}_{21i}{m}_{21i}^2/{v}_p^4-1+{v}_p^4{n}_{e1i}{T}_{e2i}^2\right)/{C}_1$, and ${C}_1={v}_p+1+2{n}_{21i}{m}_{21i}/{v}_p^3$ . C_N, C_D, and C_DP represent the coefficient of nonlinearity, dispersion, and dissipation, respectively. The first and second terms in the right side of Eq. (21) are proportional to ζ and ξ, respectively, because the integrand of the first term is independent of ζ and the integrand of second term is independent of ξ. The fourth and fifth terms in the right side of Eq. (21) are non-secular, and they would be secular in the next higher order of ε. From Eq. (21), it is obtained

$$ {\partial}_{\tau }{\phi}_{\xi}^{(1)}+{C}_N{\phi}_{\xi}^{(1)}{\partial}_{\xi }{\phi}_{\xi}^{(1)}-{C}_D{\partial}_{\xi \xi \xi}{\phi}_{\xi}^{(1)}+{C}_{DP}{\partial}_{\xi \xi}{\phi}_{\xi}^{(1)}=0, $$

(22)

$$ {\partial}_{\tau }{\phi}_{\zeta}^{(1)}-{C}_N{\phi}_{\zeta}^{(1)}{\partial}_{\zeta }{\phi}_{\zeta}^{(1)}+{C}_D{\partial}_{\zeta \zeta \zeta}{\phi}_{\zeta}^{(1)}-{C}_{DP}{\partial}_{\zeta \zeta}{\phi}_{\zeta}^{(1)}=0, $$

(23)

$$ {C}_2{\partial}_{\zeta }{\varphi}_{10}+{C}_3{\phi}_{\zeta}^{(1)}=0,\kern1em {C}_2{\partial}_{\xi }{\varphi}_{20}+{C}_3{\phi}_{\xi}^{(1)}=0. $$

(24)

Equations (22) and (23) represent the oppositely propagating two-sided KdVB equations in the frame of references ξ and ζ, respectively. It is the fact that the dissipation arises due to the cause of dissipative mechanism, such as wave-particle interaction, the effects of turbulence, dust fluctuations in dusty plasma, multi-ion streaming, Landau damping, and anomalous viscosity that leads to Burger’s term. In this study, the Burger’s term arises in Eqs. (22) and (23) due to the presence of viscosity of ion species and it is responsible for the formation of shock in the IAWs. The solution of Eqs. (22) and (23) is obtained as [53]

$$ {\phi}_{\xi}^{(1)}=\frac{3{C}_{DP}^2}{25{C}_N{C}_D}\left\{{\mathit{\operatorname{sech}}}^2\left[\frac{1}{2}\left(-\frac{C_{DP}}{5{C}_D}\xi +\frac{6{C_{DP}}^2}{125{C_D}^2}\tau \right)\right]+2\left[1-\mathit{\tanh}\left\{\frac{1}{2}\left(-\frac{C_{DP}}{5{C}_D}\xi +\frac{6{C_{DP}}^2}{125{C_D}^2}\tau \right)\right\}\right]\right\}, $$

(25)

$$ {\phi}_{\zeta}^{(1)}=\frac{3{C}_{DP}^2}{25{C}_N{C}_D}\left\{{\mathit{\operatorname{sech}}}^2\left[\frac{1}{2}\left(-\frac{C_{DP}}{5{C}_D}\zeta -\frac{6{C_{DP}}^2}{125{C_D}^2}\tau \right)\right]+2\left[-1-\mathit{\tanh}\left\{\frac{1}{2}\left(-\frac{C_{DP}}{5{C}_D}\zeta -\frac{6{C_{DP}}^2}{125{C_D}^2}\tau \right)\right\}\right]\right\}. $$

(26)

Equation (24) yields

$$ {\varphi}_{10}=-\frac{C_3}{C_2}{\int}_{-\infty}^{\zeta }{\phi}_{\zeta}^{(1)}d\overset{.}{\zeta },{\varphi}_{20}=-\frac{C_3}{C_2}{\int}_{+\infty}^{\xi }{\phi}_{\xi}^{(1)}d\overset{.}{\xi }. $$

(27)

After head-on collision, the phase shift of the solitons can be determined as

$$ \left.\begin{array}{c}\Delta {\varphi}_{10}=-{\varepsilon}^2\frac{6{C}_3{C_{DP}}^2}{25{C}_2{C}_N{C}_D}\\ {}\Delta {\varphi}_{20}={\varepsilon}^2\frac{6{C}_3{C_{DP}}^2}{25{C}_2{C}_N{C}_D}\end{array}\right\}. $$

(28)

3.1 Monotonic, Oscillatory, and Soliton Solutions

In the limit C_D → 0, Eq. (22) reduces to

$$ {\partial}_{\tau }{\phi}_{\xi}^{(1)}+{C}_N{\phi}_{\xi}^{(1)}{\partial}_{\xi }{\phi}_{\xi}^{(1)}+{C}_{DP}{\partial}_{\xi \xi}{\phi}_{\xi}^{(1)}=0. $$

(29)

Equation (29) represents the well-known Burger equation.

Let us consider,

$$ {\phi}_{\xi}^{(1)}\left(\xi, \tau \right)={\phi}^1\left(\chi \right),\kern1em \chi =\xi -{V}_0\tau, $$

(30)

where V₀ is the speed of the reference frame. Inserting Eq. (30) into Eq. (29), one can obtain

$$ {C}_{DP}{d}_{\chi \chi}{V}_0+{C}_N{\phi}^1{d}_{\chi }{\phi}^1-{V}_0{d}_{\chi }{\phi}^1=0. $$

(31)

The solution of Eq. (31) is

$$ {\phi}^1=\frac{V_0}{C_N}\left\{1-\mathit{\tanh}\left(\frac{\xi -{V}_0\tau }{\frac{2{C}_{DP}}{V_0}}\right)\right\}. $$

(32)

Similarly, the solution for Eq. (23) yields

$$ {\phi}^2=\frac{V_0}{C_N}\left\{1+\mathit{\tanh}\left(\frac{\zeta +{V}_0\tau }{\frac{2{C}_{DP}}{V_0}}\right)\right\},\kern1.75em $$

(33)

where $\frac{V_0}{C_N}$ and $\frac{2{C}_{DP}}{V_0}$ represent the amplitude and width of the monotonic shock wave, respectively.

Also using Eq. (30) in Eq. (22), it is found that

$$ -{V}_0{d}_{\chi }{\phi}^1+\frac{1}{2}{C}_N{d}_{\chi }{\left\{{\phi}^1\right\}}^2+{C}_D{d}_{\chi \chi \chi}{\phi}^1-{C}_{DP}{d}_{\chi \chi}{\phi}^1=0. $$

(34)

Integrating once, Eq. (34) yields

$$ -{V}_0{\phi}^1+\frac{1}{2}{C}_N{\left\{{\phi}^1\right\}}^2+{C}_D{d}_{\chi \chi}{\phi}^1-{C}_{DP}{d}_{\chi }{\phi}^1=0. $$

(35)

Introducing ϕ¹ = ϕ₁ + ϕ₀ (ϕ₁ ≪ ϕ₀) into Eq. (35) and using the equilibrium condition ϕ₀ = 2V₀/C_N, one can determine

$$ {C}_D{d}_{\chi \chi}{\phi}_1-{C}_{DP}{d}_{\chi }{\phi}_1+{V}_0{\phi}_1=0, $$

(36)

putting ϕ₁ = e^Lχ in Eq. (36), it is found that

$$ {C}_D{L}^2-{C}_{DP}L+{V}_0=0. $$

(37)

Therefore, $L=\frac{C_{DP}}{2{C}_D}\pm \frac{C_{DP}}{2{C}_D}\sqrt{\left({C_{DP}}^2-4{C}_D{V}_0\right)}$; the critical value of the dissipation coefficient is predicted as ${C}_{DPc}=2\sqrt{C_D{V}_0}$ . From this condition, it is observed that the IAWs have monotonic shock for C_DPc < C_DP and oscillatory shock for C_DPc > C_DP. The solution of Eq. (34) for oscillatory shock (C_DPc > C_DP) is determined as

$$ {\phi}^1=\frac{2{V}_0}{C_N}+{C}_{4a}{e}^{\frac{C_{DP}}{2{C}_D}\left(\xi -{V}_0\tau \right)}\mathit{\cos}\left\{{\left({V}_0/{C}_D\right)}^{1/2}\left(\xi -{V}_0\tau \right)\right\}. $$

(38)

Similarly, the solution for Eq. (23) can be obtained as

$$ {\phi}^2=\frac{2{V}_0}{C_N}+{C}_{4a}{e}^{\frac{C_{DP}}{2{C}_D}\left(\zeta +{V}_0\tau \right)}\mathit{\cos}\left\{{\left({V}_0/{C}_D\right)}^{1/2}\left(\zeta +{V}_0\tau \right)\right\}. $$

(39)

In special circumstances, if the dispersion dominates and the dissipation diminishes as (C_DP → 0), then the Burger terms from KdVB equations [(22), (23)] can be neglected, and under this situation Eqs. (22) and (23) are converted to the following form

$$ {\partial}_{\tau }{\phi}_{\xi}^{(1)}+{C}_N{\phi}_{\xi}^{(1)}{\partial}_{\xi }{\phi}_{\xi}^{(1)}-{C}_D{\partial}_{\xi \xi \xi}{\phi}_{\xi}^{(1)}=0, $$

(40)

$$ {\partial}_{\tau }{\phi}_{\zeta}^{(1)}-{C}_N{\phi}_{\zeta}^{(1)}{\partial}_{\zeta }{\phi}_{\zeta}^{(1)}+{C}_D{\partial}_{\zeta \zeta \zeta}{\phi}_{\zeta}^{(1)}=0. $$

(41)

Equations (40) and (41) are the well-known two-sided KdV equations and they admit the soliton solutions as

$$ {\phi}_{\xi}^{(1)}=\frac{3{v}_0}{C_N}\mathit{\sec}{h}^2\left(\frac{\xi -{v}_0\tau }{2\sqrt{\frac{C_D}{v_0}}}\right)\;\mathrm{and}\;{\phi}_{\zeta}^{(1)}=\frac{3{v}_0}{C_N}\mathit{\sec}{h}^2\left(\frac{\zeta +{v}_0\tau }{2\sqrt{\frac{C_D}{v_0}}}\right). $$

(42)

4 Results and Discussion

The plasma system consisting of negative ions with positive ions and electrons is considered to study the effects of plasma parameters such as density ratios, kinematic viscosity of positive and negative ions on the head-on collision of counter-propagating IASWs, formation of shock waves, phase shift after head-on collision, and amplitudes, as well on the soliton solution. Due to this, we take into account the typical values m_21i = 3.74, T_2i = 0.05, T_e = 0.2, 0 ≤ n_e1i ≤ 1, 0 ≤ n_21i ≤ 1, η₁ = 0.35, 0.25, 0.213, 0.188, and 0.179, and η₂ = 0.001 − 0.004, 0.050, and 0.1 − 0.4.

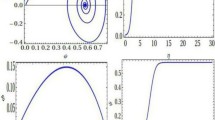
At C_N = 0, the critical density ratio of positive to negative ions is equal to n_21i = n_21i(c) = 0.64607(≈0.65) for T_2i = 0.05, T_e = 0.2, m_21i = 3.74, η₁ = 0.35, η₂ = 0.003, and n_e1i = 0.35, which is in good agreement with the experimental [34] value (n_21ic = 0.65). Figure 1 signifies the effect of density ratio on the phase velocity of the fast positive-ion-acoustic (PIA) mode. It is observed that the phase velocity is increasing (decreasing) with increasing of n_21i (n_e1i). It is also seen that for n_e1i > 0.45, the phase velocity remains unchanged. The phase velocity increases with the increase of n_21i to a point where the damping is weak, which is a significant modification of the PIA mode in the limit n_21i → 1, as T_e ≈ T_e/(1 − n_21i) [23, 26]. These are the conditions for the formation of a shock. This result is consistent with the experimental [34] results. Figure 2a, b, displays the effects of n_21i and η₁, respectively, on amplitudes. From Fig. 2a, it is observed that the amplitudes of IASWs are increasing in the range 0 to 0.2 and then decreasing with increasing n_21i but for n_e1i, the amplitudes of IASWs decrease. This means that the electrons contribute to the restoring force in the range 0 < n_e1i < 0.2 with respect to its small number density and then increasing the restoring force in the range n_e1i > 0.2. According to the charge neutrality condition, the density of electrons decreases while the density ratio of negative to positive ions increases, causes the reduction in restoring force that provides the inertialess electrons; as a result, the nonlinearity increases. For the balance between the effects of dispersion and nonlinearity, it needs to balance with the enhancement of nonlinearity of the plasma. This finally leads to the decrease in amplitudes of the IASWs. It is seen from Fig. 2b that the amplitudes of IASWs are decreasing due to the effect of positive-ion kinematic viscosity.

Fig. 1

Effects of n_21i on v_p of the PIA mode taking v₀ = 0.005, m_21i = 3.74, η₁ = 0.30, η₂ = 0.05, T_2i = 0.05, and T_e = 0.2

Fig. 2

The amplitudes of IASWs for various values of an_21i = 0.01, 0.04, and 0.10 taking v₀ = 0.005, m_21i = 3.74, η₁ = 0.30, η₂ = 0.05, T_2i = 0.05, T_e = 0.2, and T_2ie = T_e/(1—n_21i)T_2i, bη_21i = 0.188, 0.250, and 0.350, taking n_21i = 0.1, n_e2i = 0.5, and other parameters similar to a

Figures 3, 4, 5, and 6 describe the spatiotemporal evolution of electrostatic shock profiles (ϕ⁽¹⁾) (i.e., the head-on collision of two IASWs) in ξ − ζ plane considering the effects of n_21i, n_e1i, T_2i, T_e, η₁, η₂, and m_21i. It is demonstrated in Fig. 3 and Fig. 4 that the widths of the shocks are increasing with increasing n_21i, as well as the height of the shocks is also increasing in the range 0 ≤ n_21i < 0.65 but the opposite result is observed in the range 0.65 < n_21i < 1. Figure 5 depicts the effects of kinematic viscosity (η₂) of the negative-ion density on the formation of shock. It is observed that the widths of the shock waves decrease with the increase of η₂, maintaining the almost equal height. Figure 6 illustrates that the widths (heights) are increasing (decreasing) with the enhancement of n_e1i in IASWs. The strength of shocks increases for the enhancement of n_21i because the electrons gain energy due to the increase (decrease) of density of negative ions (electrons) in the concerned plasma system, as shown in Figs. 3 and 4. It is also observed that the compressive and rarefactive IA shocks are formed that are concerned with the PIA mode de pending on n_21i, n_e1i, and η₂ in the presence of negative ions. Hence, the compressive and rarefactive shocks correspond to the compression and depressi on of the positive-ion density that are guided by the compression and depression of the electron density, respectively. This finding is in good agreement with the experimental results [34].The effect of the negative-ion viscosity on the formation of shock can be elucidated on the basis of communal friction force between the layers of the considered plasma system. In fact, the viscosity is a communal friction force between fluid layers in the considered electron pair-ion plasma. Due to increasing negative-ion viscosity, the frictional force increases, causes the decrease of the shock width which is shown in Fig. 5. On the other hand, due to the depopulation of ion density, the density of electron increases, as a result the driving force increases that provided by the ions’ inertia in IASWs. Thus the amplitude of the shock decreases, which is depicted in Fig. 6. After head-on collision, if the velocity of the traveling soliton becomes slower (faster), then the phase shift would be positive (negative). Figure 7 displays the effects of n_21i, n_e1i, η₁, and η₂ on phase shifts of IASWs after head-on collision. Figure 7a illustrates that the phase shifts are increasing (decreasing) with increasing the density ratios n_21i and n_e1i. While Fig. 7b indicates that the phase shifts are increasing with increasing η₁ but η₂ shows insignificant effect on the phase shift. It is to be noted that for both cases the phase shift is compressive, this means that the post-collisional part of the trajectories leads the initial trajectories. It is to be noted that the phase shift is significantly modified due to the effects of n_21i, n_e1i, and η₁. Figure 8 shows the post-collisional spatiotemporal potential profiles of the counter-propagating IASWs. It is observed from this figure that the soliton S_R travels toward right direction and the soliton S_L travels toward left direction. Also the mesial line (i.e., separation line) clearly demarcates the two stages of collisions, one of it is the pre-collisional and the other is post-collisional potential profiles. This means that the propagating IASWs change their propagating plane due to collision. For the condition C_DPc < C_DP (n_21i > 0.311, T_2i = 0.05, V₀ = 0.0099, m_21i = 3.74, η₁ = 0.35, η₂ = 0.1, n_e1i = 0.6, and T_e = 0.2, the monotonic shock is formed. The head-on collision of the monotonic shock solutions as a function of n_21i is presented in Fig. 9. It is seen from these figures that the heights of the monotonic shocks (φ) are increasing with increasing n_21i maintaining almost equal widths. Since, the dispersive coefficient becomes negligible and dissipative coefficient becomes dominant in the considered plasma system, thus the monotonic shock is formed. Figure 10 illustrates the spatiotemporal evolution of the electrostatic potential profiles (ϕ⁽¹⁾) of soliton solutions. It is observed that both hump and dip-shaped rarefactive solitons exist for the effect of τ. As the dispersion coefficient becomes dominant to the propagation in the concerned plasma system, thus the hump and dip-shaped solitons are obtained. The hump or dip-shaped solitary structure arises due to the balance between the effects of nonlinearity and the dispersion. For n_21i < 0.311, T_2i = 0.05, V₀ = 0.0099, m_21i = 3.74, η₁ = 0.35, η₂ = 0.1, n_e1i = 0.6, and T_e = 0.2, the condition C_DP < C_DPc holds, thus the oscillatory shock is formed. Figure 11 depicts the temporal formation of shocks of the IASWs. The amplitudes and widths of the oscillatory shocks (φ⁽¹⁾) are decreasing with increasing τ as shown in Fig. 11. The negative-ion density can be realized as the depopulation of positive ions in the considered plasma system, hence the driving force (provides electrons) of the IASWs decreases, consequently the amplitudes of oscillatory shocks are decreased. Figure 12 shows the effect of negative-ion density on the electrostatic potential profiles ( ϕ⁽¹⁾ ) along with their range of validity of the IASWs. For n_21i = 0.60 and n_21i = 0.67, it can be seen that −0.015 ≤ ϕ⁽¹⁾ ≤ 0.015 and −0.017 ≤ ϕ⁽¹⁾ ≤ 0.017 as shown in Fig. 12a, b, respectively. Figure 12c depicts the potential profiles in the range −150 ≤ ϕ⁽¹⁾ ≤ 150 for n_21i(c) = 0.646, which is unexpected because the range of ϕ⁽¹⁾ is −1 ≤ ϕ⁽¹⁾ ≤ 1. The positive-ion density jumps into compressive shocks for n_21i < n_21i(c) and negative-ion density jumps into rarefactive shocks for n_21i > n_21i(c). Consequently, it is remarkable to note that the threshold for the formation of shock lies in the range −0.60 ≤ n_21i ≤ 0.67, which is in good agreement with the experimental value of n_21i = 0.65 [34]. Superposition of waves is one of the fundamental concepts in wave mechanics [54] and optics [55]. When two or more waves propagating in a medium arrive at the same point simultaneously, a new wave is produced and the net displacement of the medium is equal to the algebraic sum of displacements of individual waves arriving at that point. This is called the principle of superposition and holds good as long as the amplitude of the waves is not too large. If two sinusoidal waves having the same frequency and amplitude are traveling to each other in the same medium then, using the principle of superposition, the net displacement of the medium is the sum of the two waves. In head-on collision of two counter-propagating solitary waves in the same medium initially (t →  − ∞), the solitons are asymptotically far away from each other, that is one is at ζ →  − ∞ and ξ = 0 (the soliton traveling to right direction), the other is at ξ →  + ∞ and ζ = 0 (the soliton traveling to left direction). At t = 0, they collide at a point and then according to the principle of superposition, the resultant amplitude of the soliton becomes equal to the sum of the amplitudes of the two initial solitary waves. Figure 13 depicts the collision processes of two solitary waves for (a) n_21i = 0.54 (b) n_21i = 0.75, taking typical values of plasma parameters as n_e1i = 0.98, T_2i = 0.05, T_e = 0.20, η₁ = 0.35, η₂ = 0.003, m_21i = 3.74, and T_2ie = T_e/(1 − n_21i)T_2i. From the figure, it is observed that the amplitude is decreased due to the effect of n_21i but follows the principle of superposition. Besides, in the case of shock waves, the counter-propagating solitons change their propagation plane due to collision, therefore the linear superposition principle does not hold.

Fig. 3

Electrostatic potential profile (ϕ⁽¹⁾) of IASWs for an_21i = 0.54 bn_21i = 0.04 taking n_e1i = 0.35, T_2i = 0.05, T_e = 0.20, η₁ = 0.35, η₂ = 0.003, m_21i = 3.74, and T_2ie = T_e/(1 − n_21i)T_2i. The right column is the contour plot of the left column

Fig. 4

Electrostatic potential profile (ϕ⁽¹⁾) of IASWs for an_21i = 0.70 and bn_21i = 0.78 taking η₂ = 0.003, T_2i = 0.05, T_e = 0.20, η₁ = 0.35, m_21i = 3.74, n_e1i = 0.35, and T_2ie = T_e/(1 − n_21i)T_2i. The right column is the contour plot of the left column

Fig. 5

Electrostatic potential profile (ϕ⁽¹⁾) of IASWs for aη₂ = 0.001 and bη₂ = 0.003 taking n_e1i = 0.35, n_21i = 0.04, T_2i = 0.05, T_e = 0.20, η₁ = 0.35, m_21i = 3.74, and T_2ie = T_e/(1 − n_21i)T_2i. The right column is the contour plot of the left one

Fig. 6

Electrostatic potential profiles (ϕ⁽¹⁾) of IASWs for an_e1i = 0.35 and bn_e1i = 0.90 taking η₂ = 0.003, T_2i = 0.05, T_e = 0.20, η₁ = 0.35, m_21i = 3.74, and T_2ie = T_e/(1 − n_21i)T_2i. The right column is the contour plot of the left column

Fig. 7

Changes of Δφ₂ of IASWs for an_21i = 0.02, 0.08, 0.20, 0.50, 0.65, and 0.90 taking η₁ = 0.35, η₂ = 0.004, T_2i = 0.05, T_e = 0.20, m_21i = 3.74, and n_e1i = 0.80 and bη₁ = 0.179, 0.188, and 0.213 taking η₂ = 0.004, T_2i = 0.05, T_e = 0.20, n_21i = 0.04, m_21i = 3.74, n_e1i = 0.80, and T_21e = T_e/(1 − n_21i)T_2i

Fig. 8

Propagating process of IASWs for right (R) and left (L) traveling solitons after head-on collision, taking η₁ = 0.35, η₂ = 0.004, T_2i = 0.05, T_e = 0.20, n_21i = 0.04, m_21i = 3.74, n_e1i = 0.80, and T_21e = T_e/(1 – n_21i)T_2i

Fig. 9

Monotonic shock formation (φ) for an_21i = 0.40 and bn_21i = 0.98 taking T_2i = 0.05, V₀ = 0.0099, m_21i = 3.74, η₁ = 0.35, η₂ = 0.10, n_e1i = 0.60, T_e = 0.20, and T_2ie = T_e/(1 − n_21i)T_2i. The right column is the contour plot of the left column

Fig. 10

Effect on electrostatic potential (ϕ⁽¹⁾) of soliton solution for aτ = 0, n_21i = 0.98, T_2i = 0.05, V₀ = 0.005, m_21i = 3.74, η₁ = 0.35, η₂ = 0.3, n_e1i = 0.60, T_e = 0.20, T_21e = T_e/(1 − n_21i)T_2i, bτ = 1 and other parameters same as a, cτ = 3, n₂₁ = 0.09, and the other parameters same as a, and dτ=2 and other parameters same as a

Fig. 11

Formation of oscillatory shocks [φ⁽¹⁾] for τ = 10, 20, and 30 taking n_21i = 0.08, T_2i = 0.05, v₀ = 0.0099, m_21i = 3.74, η₁ = 0.35, η₂ = 0.10, n_e1i = 0.60, T_e = 0.20, C_4a = 0.0001, and T_2ie = T_e/(1 – n_21i)T_2i

Fig. 12

Electrostatic potential profiles (ϕ⁽¹⁾) of IASWs for an_21i = 0.60, bn_21i = 0.67, and cn_21i = 0.646, taking n_e1i = 0.35, T_2i = 0.05, T_e = 0.20, η₁ = 0.35, m_21i = 3.74, n_21i = 0.04, η₂ = 0.001, and T_2ie = T_e/(1 − n_21i)T_2i

Fig. 13

Interactions of solitons for an_21i = 0.54, bn_21i = 0.75 taking n_e1i = 0.98, T_2i = 0.05, T_e = 0.20, η₁ = 0.35, η₂ = 0.003, m_21i = 3.74, and T_2ie = T_e/(1 − n_21i)T_2i. The right column is the contour plot of the left column

5 Conclusion

The head-on collision between two IASWs, phase shift after collision, shock (monotonic and oscillatory) formation, and soliton solution is investigated in a plasma system composing positive and negative ions, and electrons. In order to solve the problems, two-sided KdVB equations are derived employing extended PLK method. It is also found that the head-on collision between two solitons obeys the linear superposition principle in the considered plasma system but does not hold for shock waves. The phase velocity increases with the increase of n_21i, which ensures that the fast PIA mode as well as the amplitudes of ion-acoustic shock waves (IASWs) are significantly modified by n_21i and η₁. Both compressive and rarefactive shocks produced for the effects of plasma parameters agree well with the experimental results and the phase shift significantly modified by the parameters, as well as they become compressive in each case. The counter-propagating shock waves change their propagation plane due to collision and the threshold lies in the range −0.60 ≤ n_21i ≤ 0.67 and the result is consistent with the experimental value n_21i = 0.65. Also, both the hump and dip-shaped rarefactive solitons exist in the soliton solution. The results obtained might be useful to understand the shock formation experiment in the laboratory as well as in the space plasma consisting of positive and negative ions, and electrons. It may also be useful to understand the features of broadband shock noise in the D- and F-regions of the Earth’s ionosphere.