1 Introduction

The investigations of flow over the disk and cone surfaces are regularly experienced in several industrial processes. Just restricted consideration has been centered on this sort of study. The fluid flows through a cone have propelled consideration because of ongoing enhancements in creative technologies. Fluid flows have fantastic applications in many engineering and modern fields. Spinning cone has wide-extending usage in different fields of progressive nanotechnology and designing like nuclear reactor cooling system, flash pyrolysis of biomass, fluid atomizers in oil burners, and chemical industries. The capability of noteworthy advancement equipment like fluid degasser, rotating cone, centrifugal film evaporators, centrifugal disc atomizers, and rotating packed-bed reactors that are noticeably impacted relies on the disseminations of pressure and the natural fluid motion. Himasekhar et al. [1] offered to solve the fluid flow past an upright cone in a gyrating system. The fluid flow past a rotating disk and cone with thermal analysis has been deliberated by Wang [2]. The joint investigations of mass and heat transfer analysis in the rotational system using cone apparatus were discussed by Roy and Anilkumar [3]. The fixed twisting cross-flow vortices were first detected by Gregory et al. [4] past a gyrating disk, and this work is further improved by Turkyilmazoglu et al. [5,6,7]. Takhar et al. [8] inspected the fluid flow using the thermophysical properties of gases. Hayat et al. [9] inspected the irreversibility portrayal of the convective fluid flow through a turning cone.

The scrutiny of fluid movement because of turning disk has been getting progressively famous in fluid dynamic exploration for the interest not only practical as well as scholastic. The flow above a rotating plate is important on account of its extensive presentations in various operations like mechanical, geothermal, and innovative zones. Hayat et al. [10] mathematically explored the MHD nanofluid flow because of a pivoting disk with a slip impact. Also, Imtiaz et al. [11] deliberated the warm radiation impacts for the nanofluid flow between stretchable disk. Mahanthesh et al. [12] researched and analyzed the impact of the CNTs near a pivoting stretchable plate. Rehman et al. [13] examined the flow over a pivoting circle with the effect of MHD. Asma et al. [14] have studied the magnetized nanofluid flow over a spinning disk activation energy.

Bioconvection is the impulsive arrangement of base fluid profiles, like declining paths. It consists of mainly two assortments of up spinning micro-organisms that typically functional in bioconvection investigate plump algae and firm oxytactic microorganism. The appliance of bioconvection includes numerous practices like fuels, bio reactors, oil reclamation, biomicrosystems, and the product of plants. Kuznetsov [15] examined the flow suspension of bioconvection nanofluids considering water based directed on oxytactic microbes. Using a level surface to design the nanoparticles involving gyrotactic microorganisms simulated by Basir et al. [16]. Khan et al. [17] evaluated the bioconvection because of the joint effect of nanoparticles with gyrotactic microbes that revealed the conductivity will upsurge with growing the buoyancy factor within the existence of convective form. Zuhra et al. [18] investigated the heat enhancement with the thermophoresis factor of second-grade fluid by the influence of nanoparticles and gyrotactic microbes.

Bhattacharyya et al. [19] researched the Casson fluid with the MHD impact scientifically. They found that expansion of the magnetic factor causes an increment in the scope of the mass exchange parameter for which steady flow is conceivable. Nadeem et al. [20] developed qualities of Casson fluid for boundary layer heat exchange fluid flow in participation with radiation towards an exponential extended casing. The exact model was proposed by Casson [21] while examining the flow curves of deferments of shades in lithographic paints. It accounts for that Casson’s constitutive condition depicted precisely the silicon suspensions [22].

Cone-plate gadgets, in which flow creates in hole between a pivoting cone and a fixed plate, are utilized in viscometry [23,24,25]. Medication utilizes such gadgets for sustaining endothelial cells that develop a single layer over the non-pivoting plate, though the cone turns gradually to renovate the nourishing fluid and concurrently did not harm the cells [26,27,28]. Shevchuk et al. [29] described the heat transmission and hydrodynamics in a centrifugal flow between parallel turning discs in the case when the tangential inlet flow velocity is bigger than the tangential disc velocity. Disk and cone viscometers and stream chamber gadgets are customarily used to measure and examine shear reactions on cells and fluids, which differs with flow phenomena, for example, angular velocity, cone angle, and the slit between the cone and disk were deliberated by Spruell et al. [30]. Thien [31] reported the flow of Oldroyd-B fluid using the disk and cone-apparatus. Turkyilmazoglu [32] reported the rate of heat transfer phenomena using the cone-disk apparatus is a gyrating system. Gul et al. [33] have extended the above idea using the CNT-nanofluids and observed the heat and mass transfer analysis.

The above studies witness that no exertion so far has been made to examine the 3D flow model for the fluid between the disk-cone gap in a gyrating system with thermophoresis and Brownian motion about the disk and cone as moving or stationary, under the influence of magnetic field. The originality of the current work is pointed out as follows:

  1. 1.

    The existing models [32, 33] are extended with the thermophoresis analysis and Brownian motion in a 3D-fluid flow model.

  2. 2.

    The Darcy-Forchheimer and magnetic field also added to the basic flow model.

  3. 3.

    The non Newtonian Casson fluid has been used, while the existing literature [32, 33] is limited to the Newtonian fluid.

  4. 4.

    The present work is also extended to the mass transfer analysis and gyrotactic microorganisms.

  5. 5.

    For the solution of the proposed problem HAM technique has been used.

2 Problem Formulation

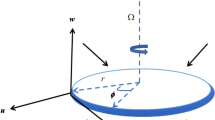
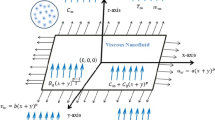
The Darcy-Forchheimer Casson nanofluid flow between the disk-cone gap is considered in a gyrating system. The upright magnetic field is imposed to the flow arrangement. The disk and cone apparatus are considered to be rotating or in rest. The geometry of the fluid is revealed in Fig. 1.

Fig. 1
figure 1

Physical interpretation of the problem

Full size image

All the assumptions of the published work [32] are used as liker radially flexible wall temperature \(T_{w} = T_{\infty } + cr^{m}\) at the disk and \(T_{\infty }\) is the ambient temperature. The mass transfer and bi-convection equations are also in countered with \(C_{w} = C_{\infty } + cr^{m}\) and \(n_{w} = n_{\infty } + cr^{m}\) at the wall.

The basic equations are defined as [17, 18, 32, 33]:

$$\frac{\partial u}{{\partial r}} + \frac{u}{r} + \frac{\partial w}{{\partial z}} = 0,$$
(1)
$$u\frac{\partial u}{{\partial r}} + w\frac{\partial u}{{\partial z}} - \frac{{v^{2} }}{r} + \frac{1}{{\rho_{f} }}\frac{\partial p}{{\partial r}} = \upsilon_{f} \left( {1 + \frac{1}{\beta }} \right)\left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{{\partial r}} - \frac{u}{{r^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right) - \frac{{\upsilon_{f} }}{{k^{*} }}u - F^{*} u^{2} - \frac{{\sigma_{f} }}{{\rho_{f} }}B_{0}^{2} u,$$
(2)
$$u\frac{\partial v}{{\partial r}} + w\frac{\partial v}{{\partial z}} + \frac{uv}{r} = \upsilon_{f} \left( {1 + \frac{1}{\beta }} \right)\left( {\frac{{\partial^{2} v}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial v}{{\partial r}} - \frac{v}{{r^{2} }} + \frac{{\partial^{2} v}}{{\partial z^{2} }}} \right) - \frac{{\upsilon_{f} }}{{k^{*} }}v - F^{*} v^{2} - \frac{{\sigma_{f} }}{{\rho_{f} }}B_{0}^{2} v,$$
(3)
$$u\frac{\partial w}{{\partial r}} + w\frac{\partial w}{{\partial z}} + \frac{1}{{\rho_{f} }}\frac{\partial p}{{\partial z}} = \upsilon_{f} \left( {1 + \frac{1}{\beta }} \right)\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{{\partial r}} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right),$$
(4)
$$\begin{gathered} u\frac{\partial T}{{\partial r}} + w\frac{\partial T}{{\partial z}} = \left( {\frac{{k_{f} }}{{\rho c_{p} }}} \right)_{f} \left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \tau \left[ {D_{b} \left( {\frac{\partial T}{{\partial r}}\frac{\partial C}{{\partial r}} + \frac{\partial T}{{\partial z}}\frac{\partial C}{{\partial z}}} \right) + \frac{{D_{t} }}{{T_{\infty } }}\left( {\left( {\frac{\partial T}{{\partial r}}} \right)^{2} + \left( {\frac{\partial T}{{\partial z}}} \right)^{2} } \right)} \right], \hfill \\ \end{gathered}$$
(5)
$$u\frac{\partial C}{{\partial r}} + w\frac{\partial C}{{\partial z}} = D_{b} \left( {\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial C}{{\partial r}} + \frac{{\partial^{2} C}}{{\partial z^{2} }}} \right) + \frac{{D_{t} }}{{T_{\infty } }}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right),$$
(6)
$$u\frac{\partial n}{{\partial r}} + w\frac{\partial n}{{\partial z}} = D_{m} \frac{{\partial^{2} n}}{{\partial z^{2} }} - \frac{{b^{*} W_{c} }}{{\left( {C_{w} - C_{\infty } } \right)}}\left( {\frac{\partial n}{{\partial z}}\frac{\partial c}{{\partial z}} + n\frac{{\partial^{2} C}}{{\partial z^{2} }}} \right),$$
(7)

Now, \(u,\;v,{\text{ and w}}\) are the velocity elements along x, y, and z directions, respectively, and \(\rho\) represents the density of base fluid, \(\beta_{0}\) is the strength of the magnetic field, and \(\nu_{f}\), \(\alpha_{f}\), \(\left( {\rho c_{p} } \right)_{f}\), and \(\mu_{f}\) are the kinematic viscosity, thermal diffusivity, heat capacity, and dynamic viscosity. \(\sigma\) is the electrical conductivity. \(F^{*} ,\;k^{*} ,\;\beta ,\;D_{b} ,\;D_{t} ,\,{\text{and}}\,\tau\) are the non-uniform inertia coefficient, porous medium permeability, Casson parameter, coefficient of the Brownian diffusion, coefficient of the thermophoretic diffusion, and ratio of the nanoparticles and effective heat capacity, while BCs are

$$\begin{gathered} u = 0,\,v = \omega r,w = 0,\,T = T_{w} \,, C = C_{w} \,,\,n = n_{w} \,\,at\,\,{\text{z = 0}}, \hfill \\ u = 0, \, v = \Omega r,w = 0,T = T_{\infty } \,,\,C = C_{\infty } ,n = n_{\infty } \,at\,\,z = r\tan \gamma . \hfill \\ \end{gathered}$$
(8)

The following transformation for the model work are introduced as [32, 33]

$$\begin{gathered} \,\,u = \frac{{\upsilon_{f} F(\eta )}}{r}{\text{ = U}}_{w} F(\eta ){,}\,\,v = \frac{{\upsilon_{f} G(\eta )}}{r} = {\text{U}}_{w} G(\eta ),\,\,w = \frac{{\upsilon_{f} H(\eta )}}{r} = {\text{U}}_{w} H(\eta ), \hfill \\ {\text{ p = }}\frac{{\rho \upsilon_{f}^{2} P}}{{r^{2} }} = {\text{U}}_{w}^{2} \rho P,\,\,\eta = \frac{z}{r},\,\,\Theta = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\,\,\phi = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }},J = \frac{{n - n_{\infty } }}{{n_{w} - n_{\infty } }}. \hfill \\ \end{gathered}$$
(9)

Transformed equations are

$$H^{\prime} - \eta F^{\prime} = 0,$$
(10)
$$(1 + \eta^{2} )F^{\prime\prime} + 3\eta F^{\prime} + \left( {1 + \frac{1}{\beta }} \right)\left( {\eta FF^{\prime} - HF^{\prime} + F^{2} - G^{2} } \right) + \left( {2p + \eta p^{\prime} - MF - F_{1} F - KrF} \right) = 0,$$
(11)
$$(1 + \eta^{2} )G^{\prime\prime} + 3\eta G^{\prime} - \left( {1 + \frac{1}{\beta }} \right)\left( {\eta FG^{\prime} - HG^{\prime}} \right) - MG - F_{1} G - KrG = 0,$$
(12)
$$(1 + \eta^{2} )H^{\prime\prime} + 3\eta H^{\prime} + \left( {1 + \frac{1}{\beta }} \right)\left( {\eta FH^{\prime} - HH^{\prime} + H + FH} \right) - p^{\prime} = 0,$$
(13)
$$(1 + \eta^{2} )\Theta^{\prime\prime} + \eta \,\Theta^{\prime} - \Pr \Theta^{\prime}\left( {H - \eta F} \right) - \Pr N_{b} \left( {\eta^{2} + 1} \right)\Theta^{\prime}\Phi^{\prime} - N_{t} \Pr \left( {1 + \eta^{2} } \right)\Theta^{{\prime}{2}} = 0,$$
(14)
$$\left( {1 + \eta^{2} } \right)\phi^{\prime\prime} + \eta \,\phi^{\prime} - Sc\left( {H - \eta F} \right)\phi^{\prime} + \frac{{N_{t} }}{{N_{b} }}\left( {\left( {1 + \eta^{2} } \right)\Theta^{\prime\prime} + \eta \,\Theta^{\prime}} \right) = 0$$
(15)
$$J^{\prime\prime} - \Pr L_{b} \left( {H - \eta F} \right)J^{\prime} - P_{e} \left( {J^{\prime}\phi^{\prime} + J\phi^{\prime\prime}\left( {1 + \Omega_{1} } \right)} \right) = 0$$
(16)

Correspondingly physical conditions are

$$\left. \begin{gathered} F(0) = 0,\,H(0) = 0,\,G(0) = {\text{Re}}_{w} ,\,\Theta (0) = \phi (0) = J(0) = 1 \hfill \\ F(\eta_{0} ) = \,H(\eta_{0} ) = \Theta (\eta_{0} ) = \phi (\eta_{0} ) = J(\eta_{0} ) = 0,\,G(\eta_{0} ) = {\text{Re}}_{\Omega } \hfill \\ \end{gathered} \right\}$$
(17)

Dimensionless parameters:

$$\begin{gathered} \,Ec = \frac{{U_{w}^{2} }}{{Cp\left( {T_{w} - T_{\infty } } \right)}},M = \frac{{\upsilon_{f} \sigma^{*} B_{0}^{2} }}{{\rho_{f} U_{w}^{2} }},\Pr = \frac{{\mu_{f} Cp}}{{k_{f} }}, \hfill \\ N_{b} = \frac{{\tau D_{b} (C_{w} - C_{\infty } )}}{\upsilon },N_{T} = \frac{{\tau D_{T} (T_{w} - T_{\infty } )}}{{\upsilon T_{\infty } }},Sc = \frac{{\upsilon_{f} }}{{D_{f} }}, \hfill \\ L_{b} = \frac{\alpha }{{D_{m} }},P_{e} = \frac{{bW_{c} }}{{D_{m} }},Re_{\omega } = \frac{{r^{2} \omega }}{\nu },Re_{\Omega } = \frac{{r^{2} \Omega }}{\nu }. \hfill \\ \end{gathered}$$
(18)

Above the symbols \(M,\;Ec,\;L_{b} ,\;Sc,\;\Pr ,\;N_{b} ,\;N_{T} ,\;{\text{Re}}_{w} ,\;Re_{\Omega } ,\;{\text{and}}\,P_{e} \,\,\,\), respectively, denote magnetic parameter, Eckert number, Lewis number, Schmith number and Prandtl number, Brownian motion parameter, thermophoretic parameter, rotation parameter at the disk surface, and the rotation parameter at the cone surface.

2.1 Quantities of Interest

The Nusselt and Sherwood numbers \(Nu_{d} ,Sh_{d}\) at the disk surface and the same numbers at the cone surface are denoted by \(Nu_{c} ,Sh_{c}\). Motile of the microorganism at the disk surface is \(J^{\prime}(0)\), and motile of the microorganism at the cone surface is as [18, 32, 33]

$$Nu_{d} = - \Theta^{\prime}(0),Nu_{c} = - \Theta^{\prime}(\eta_{0} ),Sh_{d} = - \Phi^{\prime}(0),\,\,Sh_{c} = - \Phi^{\prime}(\eta_{0} ),Nn_{d} = - J^{\prime}(0),\,\,Nn_{c} = - J^{\prime}(\eta_{0} )$$
(19)

3 HAM Solution

The problem solution in Eqs. (10–16) using the physical conditions (17) is obtained by way of the homotopy analysis method HAM [34,35,36,37,38,39,40]. Trail solution:

$$\begin{gathered} F_{0} \left( \eta \right) = 0,G_{0} \left( \eta \right) = \frac{{\left( {{\text{Re}}_{\Omega } - {\text{Re}}_{\omega } } \right)}}{{\eta_{0} }}\eta + {\text{Re}}_{\omega } ,H_{0} \left( \eta \right) = 0,\Theta_{0} \left( \eta \right) = \frac{{\eta_{0} - \eta }}{{\eta_{0} }}, \hfill \\ \phi_{0} \left( \eta \right) = \frac{{\eta_{0} - \eta }}{{\eta_{0} }},J_{0} \left( \eta \right) = \frac{{\eta_{0} - \eta }}{{\eta_{0} }}. \hfill \\ \end{gathered}$$
(20)
$$L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F^{\prime\prime}},L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G^{\prime\prime}},L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H^{\prime\prime}} ,{\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }} {(}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } {) = }\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta ^{\prime\prime}}{\text{,L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} {(}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } {) = }\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi^{\prime\prime}} \, ,{\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} }} {(}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} {) = }\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J^{\prime\prime}}$$
(21)
$$\begin{gathered} L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }} (e_{1} + e_{2} \eta ) = 0,{\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }} (e_{3} + e_{4} \eta ) = 0,{\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }} (e_{5} + e_{6} \eta ) = 0,{\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }} (e_{7} + e_{8} \eta ) = 0, \hfill \\ \,\,\,{\text{L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} (e_{9} + e_{10} \eta ) = 0 \, ,{\text{ L}}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} }} (e_{11} + e_{12} \eta ) = 0. \hfill \\ \end{gathered}$$
(22)

The non-linear operators are reasonably designated as \({\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }} ,{\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }} ,{\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }} ,{\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }} ,\,{\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} {\text{ and}}\,{\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} }}\).

$$\begin{gathered} \, {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }} \, \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ),G(\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} (\eta ;\zeta )} \right] = (1 + \eta^{2} )\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{\eta \eta } + 3\eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{\eta } \hfill \\ + \left( {1 + \frac{1}{\beta }} \right)\left( {\eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{\eta } - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{\eta } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F^{2}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G^{2}} } \right) + \left( {2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} + \eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{\eta } - M\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} - F_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F^{2}} - Kr\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} } \right) \hfill \\ \end{gathered}$$
(23)
$$\begin{gathered} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }} \, \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta )} \right] = (1 + \eta^{2} )\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{\eta \eta } - \left( {1 + \frac{1}{\beta }} \right)\left( {\eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{\eta } - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{\eta } } \right) - M\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} \hfill \\ - F_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G^{2}} - Kr\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} \hfill \\ \end{gathered}$$
(24)
$$\begin{gathered} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }} \, \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} (\eta ;\zeta )} \right] = \left( {1 + \eta^{2} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{\eta \eta } + 3\eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{\eta } \hfill \\ + \left( {1 + \frac{1}{\beta }} \right)\left( {\eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{\eta } - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{\eta } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} } \right) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{\eta } \hfill \\ \end{gathered}$$
(25)
$$\begin{gathered} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ;\zeta )} \right] = (1 + \eta^{2} )\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{\eta \eta } + \eta \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{\eta } - \Pr \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{\eta } \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} - \eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} } \right) \hfill \\ - \Pr N_{b} \left( {\eta^{2} + 1} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{\eta } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{\eta } - N_{t} \Pr \left( {1 + \eta^{2} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta_{\eta}^{2}} \hfill \\ \end{gathered}$$
(26)
$$\begin{gathered} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (\eta ;\zeta )} \right] = \left( {1 + \eta^{2} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{\eta \eta } + \eta \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{\eta } \hfill \\ - Sc\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} - \eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{\eta } + \frac{{N_{t} }}{{N_{b} }}\left( {\left( {1 + \eta^{2} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{\eta \eta } + \eta \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{\eta } } \right) \hfill \\ \hfill \\ \end{gathered}$$
(27)
$$\begin{gathered} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} }} \, \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta )} \right] = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}_{\eta \eta } - \Pr L_{b} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} - \eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}_{\eta } \hfill \\ - P_{e} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}_{\eta } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{\eta } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{\eta \eta } \left( {1 + \Omega_{1} } \right)} \right) \hfill \\ \end{gathered}$$
(28)

For Eqs. (11–14), the 0th-order system is written as

$$(1 - \zeta )L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{0} (\eta )} \right] = p\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }} \, \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ),G(\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} (\eta ;\zeta )} \right]$$
(29)
$$(1 - \zeta )L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} (\eta ;\zeta ) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{0} (\eta )} \right] = p\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }} \, \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta )} \right]$$
(30)
$$(1 - \zeta )L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta ) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{0} (\eta )} \right] = p\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }} \, \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} (\eta ;\zeta )} \right]$$
(31)
$$(1 - \zeta ) \, L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (\eta ;\zeta ) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{0} (\eta )} \right] = p\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ;\zeta )} \right]$$
(32)
$$(1 - \zeta ) \, L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ;\zeta ) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{0} (\eta )} \right] = p\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} {\rm N}_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (\eta ;\zeta )} \right]$$
(33)
$$(1 - \zeta ) \, L_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} (\xi ;\zeta ) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}_{0} (\xi )} \right] = p\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} }} N_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} }} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ;\zeta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta )} \right]$$
(34)

While BCs are

$$\begin{gathered} \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta )} \right|_{\eta = 0} = 0, \, \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta )} \right|_{\eta = 0} = 0,\left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} (\eta ;\zeta )} \right|_{\eta = 0} = {\text{Re}}_{w} , \hfill \\ \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (\eta ;\zeta )} \right|_{\eta = 0} = \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ;\zeta )} \right|_{\eta = 0} = \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} (\eta ;\zeta )} \right|_{\eta = 0} = 1 \hfill \\ \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta_{0} ;\zeta )} \right|_{{\eta_{0} = \tan \gamma }} = \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta_{0} ;\zeta )} \right|_{{\eta_{0} = \tan \gamma }} = \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (\eta_{0} ;\zeta )} \right|_{{\eta_{0} = \tan \gamma }} = \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta_{0} ;\zeta )} \right|_{{\eta_{0} = \tan \gamma }} = \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} (\eta_{0} ;\zeta )} \right|_{{\eta_{0} = \tan \gamma }} = 0, \hfill \\ \left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} (\eta_{0} ;\zeta )} \right|_{{\eta_{0} = \tan \gamma }} = {\text{Re}}_{\Omega } , \hfill \\ \end{gathered}$$
(35)

While the embedding constraint is \(\zeta \in [0,1][0,1]\), to regulate for the solution convergence \(\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }} ,\;\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }} ,\;\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }} ,\) \(\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } }} ,\;\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }}\), and \(\hbar_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} }}\) are used. When \(\zeta = 0{\text{ and }}\zeta = 1\), we have

$$\begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;1) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} (\eta ;1) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} (\eta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;1) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (\eta ;1) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (\eta ){ ,} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ;1) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} (\eta ;1) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} (\eta ), \hfill \\ \end{gathered}$$
(36)

Expand the \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ) \, ,\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} (\eta ;\zeta ),\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta ),\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (\eta ;\zeta ),\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ;\zeta )\), and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} (\eta ;\zeta )\) through Taylor’s series for \(\zeta = 0\)

$$\begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta ;\zeta ) \, = \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{0} (\eta ) + \sum\nolimits_{n = 1}^{\infty } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{n} (\eta )\zeta^{n} } \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} (\eta ;\zeta ) \, = \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{0} (\eta ) + \sum\nolimits_{n = 1}^{\infty } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{n} (\eta )\zeta^{n} } \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta ) \, = \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{0} (\eta ) + \sum\nolimits_{n = 1}^{\infty } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{n} (\eta )\zeta^{n} } \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (\eta ;\zeta ) \, = \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{0} (\eta ) + \sum\nolimits_{n = 1}^{\infty } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{n} (\eta )\zeta^{n} } \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ;\zeta ) \, = \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{0} (\eta ) + \sum\nolimits_{n = 1}^{\infty } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{n} (\eta )\zeta^{n} } \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} (\eta ;\zeta ) \, = \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}_{0} (\eta ) + \sum\nolimits_{n = 1}^{\infty } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}_{n} (\eta )\zeta^{n} } \hfill \\ \end{gathered}$$
(37)
$$\begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{n} (\eta ) \, = \left. {\frac{1}{n!}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (\eta ;\zeta )}}{\partial \eta }} \right|_{p = 0} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{n} (\eta ) \, = \left. {\frac{1}{n!}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} (\xi ;\zeta )}}{\partial \eta }} \right|_{p = 0} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{n} (\eta ) \, = \left. {\frac{1}{n!}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta ;\zeta )}}{\partial \eta }} \right|_{p = 0} , \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{n} (\xi ) \, = \left. {\frac{1}{n!}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (\eta ;\zeta )}}{\partial \eta }} \right|_{p = 0} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }_{n} (\xi ) \, = \left. {\frac{1}{n!}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta ;\zeta )}}{\partial \eta }} \right|_{p = 0} {,}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}_{n} (\xi ) \, = \left. {\frac{1}{n!}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} (\eta ;\zeta )}}{\partial \eta }} \right|_{p = 0} {. } \hfill \\ \end{gathered}$$
(38)

While BCs are

$$\begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (0) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (0) = 0,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} (0) = {\text{Re}}_{w} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (0) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (0) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} (0) = 1\,\,and \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} (\eta_{0} ) = \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\eta_{0} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta } (\eta_{0} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\eta_{0} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} (\eta_{0} ) = 0,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} (\eta_{0} ) = {\text{Re}}_{\Omega } . \hfill \\ \end{gathered}$$
(39)

Now

$$\begin{aligned} \Re_{n}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }} \left( \eta \right) &= 2\left( {1 + \frac{1}{\lambda }} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}{^{\prime\prime\prime}_{n - 1}} + 3\eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}{^{\prime}_{n - 1}} \\&+ \left( {1 + \frac{1}{\beta }} \right)\left( {\eta \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F^{\prime}_{j}} } - \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F^{\prime}_{j}} } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}{_{{^{n - 1} }}^{2}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}{_{{^{n - 1} }}^{2}} } \right) \hfill \\& + \left( {2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{n - 1} + \eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}{^{\prime}_{n - 1}} - M\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{n - 1} - F_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}{_{n - 1}^{2}} - Kr\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{n - 1} } \right) \hfill \\ \end{aligned}$$
(40)
$$\begin{aligned} \Re_{n}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }} \left( \eta \right) &= (1 + \eta^{2} )\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}{^{\prime\prime}_{n - 1}} \\&- \left( {1 + \frac{1}{\beta }} \right)\left( {\eta \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}{^{\prime}_{j}} } - \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}{^{\prime}_{j}} } } \right) \\&- M\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{n - 1} - F_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}{_{n - 1}^{2}} - Kr\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{n - 1} \hfill \\ \end{aligned}$$
(41)
$$\begin{aligned}\Re_{n}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }} \left( \eta \right) &= \left( {1 + \eta^{2} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}{^{\prime\prime}_{n - 1}} + 3\eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}{^{\prime}_{n - 1}} \\&+ \left( {1 + \frac{1}{\beta }} \right)\left( \begin{gathered} \eta \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}{^{\prime}_{w - 1 - j}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{j} } \hfill \\ - \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H^{\prime}_{j}} } + \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{n - 1} + \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{w - 1 - j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{j} } \hfill \\ \end{gathered} \right) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}{^{\prime}_{n - 1}}\end{aligned}$$
(42)
$$\begin{aligned} \Re_{n}^{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta}} (\eta ) = (1 + \eta^{2} )\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta}{^{{\prime}{\prime}}_{n - 1}} + + \eta \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta}{^{\prime}_{n - 1}} - \Pr \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta}{^{\prime}_{w - 1 - j}}} \left( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{j} - \eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{j} \right) \hfill \\ - \Pr N_{b} \left( {\eta^{2} + 1} \right)\sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta}{^{\prime}_{w - 1 - j}}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi }{^{\prime}_{j}} - N_{t} \Pr \left( {1 + \eta^{2} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta}{^{\prime{2}}_{n - 1}} ,\end{aligned}$$
(43)
$$\begin{aligned}\Re_{n}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } }} \left( \eta \right)& = \left( {1 + \eta^{2} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi}{^{\prime\prime}_{n - 1}} + \eta \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi}{^{\prime}_{n - 1}} \\&- Sc\sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi}{^{\prime}_{w - 1 - j}} } \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{j} - \eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{j} } \right) + \\&+ \frac{{N_{t} }}{{N_{b} }}\left( {\left( {1 + \eta^{2} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta}{^{\prime\prime}_{n - 1}} + \eta \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta}{^{\prime}_{n - 1}} } \right)\end{aligned}$$
(44)
$$\begin{aligned}\Re_{n}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J} }} \left( \eta \right)& = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}{^{\prime\prime}_{n - 1}} - \Pr L_{b} \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}{^{\prime}_{w - 1 - j}} } \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H}_{j} - \eta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{j} } \right) \\&- P_{e} \left( {\sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}{^{\prime}_{w - 1 - j}} } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi}{^{\prime}_{j}} + \sum\limits_{j = 0}^{w - 1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}_{w - 1 - j} } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi}{^{\prime\prime}_{j}} \left( {1 + \Omega_{1} } \right)} \right)\end{aligned}$$
(45)
$${\text{While}}\,\chi_{n} = \left\{ \begin{gathered} 0,{\text{ if }}\zeta \le {1} \hfill \\ 1,{\text{ if }}\zeta > {1}{\text{.}} \hfill \\ \end{gathered} \right.$$
(46)

4 Results and Discussions

The system (10) to (16) is numerically solved by homotopy analysis technique. Noticeable performances of the interesting constraints on velocity, fixation, concentration, the density of self-moving microorganisms, and temperature are graphically investigated.

4.1 Velocity Profile

Figure 1 displays the physical draught of the work. Conspicuous behaviors of various relevant factors like magnetic factor \(\left( M \right)\), Casson factor \(\left( \beta \right)\), porosity parameter \(\left( {Kr} \right)\), and inertial factor \(\left( {F_{1} } \right)\) on \(F\left( \eta \right)\,\) and \(G\left( \eta \right)\) are examined in Figs. 2−9. Figures 2 and 3 display the influence of magnetic parameter \(\left( M \right)\) on \(F\left( \eta \right)\,\) and \(G\left( \eta \right)\) correspondingly. Here for escalating estimations of magnetic factor, \(\left( M \right)\) improves the opposing force (Lorentz force) to decline the flow and consequently both components of the velocity are condensed. Figures 2 and 3 have also indicated that advanced estimations of the Casson parameter enhance more resistance to the system. In fact, these outcomes in tougher frictional force causing a decline in \(\left( {\,F\left( \eta \right)\;{\text{and}}\,G\left( \eta \right)} \right)\). Physically, the advanced fluid viscosity for expanding estimations of \(\beta\) ends-up in progress of the yield stress, which in turn stands answerable for the given variety in the two velocities of fluid \(\left( {\,F\left( \eta \right)\;{\text{and}}\,G\left( \eta \right)} \right)\). Figures 4 and 5 reveal the impacts of \(F_{1}\) and \(Kr\) on \(F\left( \eta \right)\,\) and \(G\left( \eta \right)\), respectively. The permeable medium played out a key part during fluid flow events. Fundamentally, the porosity factor upsets the limit layer flow of fluid which, thus, delivered resistance to the fluid flow and, from now on, a decrease in the speed of the fluid. Besides, \(F_{1}\) and \(Kr\) reduced the fluid flow at the outward of the inside the conical gap and the exteriors of disk and cone. This conduct happened in light of the fact that the permeable medium was added to the flow wonders which diminished the coefficient of inertia, and thus, the fluid velocity was diminished. In particular, the impact of Casson parameter \(\beta\) on \(H\left( \eta \right)\,\) is exposed in Fig. 6. The amassed estimations of the Casson factor, i.e., the declining yield stress, subdue the velocity field \(H\left( \eta \right)\,\). It is perceived that \(H\left( \eta \right)\,\) and the associated boundary layer thickness are declining function of \(\beta\).

Fig. 2
figure 2

Impacts of \(M\) and \(\beta\) on \(F(\eta )\) when \(Kr = 0.4,F_{1} = 0.4\)

Full size image
Fig. 3
figure 3

Impacts of \(M\) and \(\beta\) on \(G(\eta )\) when \(Kr = 0.4,F_{1} = 0.4\)

Full size image
Fig. 4
figure 4

Impacts of \(F_{1}\) and \(Kr\) on \(F(\eta )\) when \(M = 0.5,\beta = 0.3\)

Full size image
Fig. 5
figure 5

Impacts of \(F_{1}\) and \(Kr\) on \(G(\eta )\) when \(M = 0.1,\beta = 0.3\)

Full size image
Fig. 6
figure 6

Impact of \(\beta\) on \(H\left( \eta \right)\,\) when \(M = 0.1,Kr = 0.3\)

Full size image
Fig. 7
figure 7

Impact of \(\Pr\) on \(\Theta (\eta )\) when \(N_{t} = 0.8,\,\,N_{b} = 0.7\)

Full size image
Fig. 8
figure 8

Impact of \(N_{b}\) and \(N_{t}\) on \(\Theta (\eta )\) when \(\Pr = 10.1\,\)

Full size image
Fig. 9
figure 9

Impact of \(Sc\) on \(\phi (\eta )\) when \(N_{t} = 0.4,\,\,N_{b} = 0.5\)

Full size image

4.2 Temperature Profile

Prominent behaviors of numerous pertinent parameters like \(\left( {\Pr } \right)\), \(\left( {N_{b} } \right)\), and \(\left( {N_{t} } \right)\) on the temperature field \(\Theta \left( \eta \right)\). The performance of the thermal distributions for the variety of the \(\left( {\Pr } \right)\) can be commenced in Fig. 7. It is perceived that the thermal field reduces with expanding \(\left( {\Pr } \right)\). The constraint \(\left( {\Pr } \right)\) declines the thermal field for the larger values. For all estimations of \(\left( {\Pr } \right)\), wall temperature gradient is negative, which implies that the heat is constantly moving from the shallow to the ambient fluid. The important improvement is noted in temperature distribution \(\Theta \left( \eta \right)\) when Brownian factor \(\left( {N_{b} } \right)\) is upsurges as shown in Fig. 8. Since, an expansion in the strength of the Brownian movement measure causes a compelling development of the nanoparticles which progresses the thermal efficiency of the fluid. The thermophoresis marvel has a noteworthy commitment in numerous productions. The thermophoresis is a movement cycle of heated fluid particles towards the cool area, because of which the temperature increments. Figure 8 depicts the consequence of \(\left( {N_{t} } \right)\) on \(\Theta \left( \eta \right)\). It is due to the fact that heat radiation has a profound effect on the fluid temperature and it creates the shallow heat flux, which results in enhancement of the temperature. Influence of \((Nb)\) and \((Nt)\) on thermal profile is portrayed in Fig. 8. One can detect from the figure that rise in values of \((Nb)\) and \((Nt)\) improves the thermal gradient. Here, due to Brownian motion and thermophoresis, analysis affects the interaction of nanoparticles and generates additional heat which results in the enrichment of temperature. \((Nt)\) strengthens the thermophoresis forces which carry the nanoparticles from warmer region to the chiller region, and Brownian motion is the effect of individual motion of the small particles, which upshots in reduction of thermal boundary layer thickness, and hence, the temperature enrichment is detected for increasing values of \((Nb)\) and \((Nt)\).

4.3 Concentration Profile

Figure 9 is the outcome of Schmidt constraint \(Sc\) on the concentration field \(\left( {\phi \left( \eta \right)} \right)\). Growing the estimation of Sc drops the concentration \(\left( {\phi \left( \eta \right)} \right)\) of fluid. Expanding \(Sc\) prompts the lower estimation of the concentration field since diminishes in Brownian diffusivity has the opposite connection along \(Sc\). In Fig. 10, the outcomes are enforced for concentration field for dissimilar estimations of \(\left( {N_{t} } \right)\). It is seen that expansion in the estimation of \(N_{t}\), the concentration of nanoparticles upgraded. The thermophoresis wonder is frequently found in the different physical circumstances where the transfer of heat achieves more significance. Because of higher temperature close to the shallow, the fluid particles move to the contingency cool surface because of the gradient temperature and accordingly concentration distribution improved. An ascent in the nanoparticle concentration distribution is examined. Brownian motion \(N_{b}\) quantity contributions on concentration \(\left( {\phi \left( \eta \right)} \right)\) are captured in Fig. 10. As Brownian movement is the irregular movement of the particles in base fluid, by enhancing \(N_{b}\), concentration profile \(\left( {\phi \left( \eta \right)} \right)\) is decreased.

Fig. 10
figure 10

Impact of \(N_{b}\) and \(N_{t}\) on \(\phi (\eta )\) when \(Sc=0.4,\,\,\Pr=6.4\)  

Full size image

4.4 Motile Microorganism

The impact of \(P_{e}\) and \(L_{b}\) upon the motile microorganism profile \(J(\eta )\) is shown in Fig. 11. Since the increasing values of \(P_{e}\) and \(L_{b}\) cause a reduction in diffusion of micro-organism, this ultimately results in reduction of density of micro-organism. Hence, the density of micro-organism reveals a reducing response to augmented values of \(P_{e}\) and \(L_{b}\) as shown in Figs. 11 and 12. Figure 12 indicates the effect of \(\Omega_{1}\) on \(J(\eta )\). This is clear from the figure that the thicknesses of boundary layer of both the micro-organisms and density decay for amassed approximations of \(\Omega_{1}\).

Fig. 11
figure 11

Impact of \(L_{b}\) and \(P_{e}\) on \(J(\eta )\) when \(\Omega_1=0.4\)  

Full size image
Fig. 12
figure 12

Impact of \(\Omega_{1}\) on \(J(\eta )\) when \(P_{e} = 0.7,L_{b} = 0.5\)

Full size image

4.5 Tables Discussion

Table 1 shows the influence of Brownian factor \((N_{b} )\) and thermophoretic factor on the Nussult number for both cone and disk. For increasing values of \((Nb)\) and \((Nt)\), Nusselt number is rising. In fact, the heat transfer rate augmented with the larger magnitude of these parameters and consequently the Nusselt number increases.

Table 1 Nusselt number at various values of embedded parameters
Full size table

Table 2 displays the influence of Schmidt number \(Sc\), Brownian factor \(N_{b}\), and thermophoretic parameter on Sherwood number for both cone and disk. For cumulative values of Schmidt number \(Sc\) and \(N_{b}\), Sherwood number is decreasing for both cone and disk. For amassed estimations of thermophoretic factor, Nussult number is rising. Table 3 shows the impression of bioconvection Lewis number, bioconvection concentration difference parameter, and bioconvection Peclet number on the local density number \(\left( {Nn_{x} } \right)\) for both cone and disk. For rising estimations of bioconvection Lewis number, bioconvection concentration difference constraint, and bioconvection Peclet number, the local density number \(\left( {Nn_{x} } \right)\) is decreasing for both cone and disk.

Table 2 The rate of mass transfer at various values of physical parameters
Full size table
Table 3 Local density number \(\left( {Nn_{x} } \right)\) at various values of embedded parameters
Full size table

5 Conclusions

Here we analyzed the bioconvectional Darcy-Forchheime Casson nanofluid flow between a cone and disk with gyrotactic microorganisms. The magnetic field is imposed perpendicular to the flow field. The transformed equations are solved through HAM technique. The followings are the main observations of the present study.

  • For the rising estimations of Casson factor \(\beta\), porosity factor \(\left( {Kr} \right)\), and inertial parameter \(\left( {F_{1} } \right)\) and magnetic factor \(\left( M \right)\), the velocity profile decreases.

  • The temperature decreases with increasing \(\left( {\Pr } \right)\) while for increasing values of \(\left( {N_{b} } \right)\) and \(\left( {N_{t} } \right)\), \(\Theta \left( \eta \right)\) is decreasing.

  • By enhancing \(N_{b}\), concentration profile, \(\left( {\phi \left( \eta \right)} \right)\) is decreasing, while for increasing of thermophoresis parameter \(\left( {N_{t} } \right)\) ,concentration profile \(\left( {\phi \left( \eta \right)} \right)\) is increasing.

  • Density of motile micro-organism reveals a reducing response to amplified values of \(P_{e} ,\Omega_{1}\) and \(L_{b}\).

  • The small value of concentration profile leads by increasing \(Sc\) because declines in Brownian diffusivity have the inverse relation with \(Sc\).

  • The heat transfer rate enhances with the larger magnitude of the \(\left( {N_{b} } \right)\) and \(\left( {N_{t} } \right)\). Physically, the heat transfer rate augmented with the larger magnitude of these parameters, and consequently, the Nusselt number increases.

  • The cumulative values of Schmidt number \(Sc\) and \(N_{b}\) and Sherwood number are decreasing for both cone and disk apparatus.

  • Rising estimations of Lewis number, bioconvection, and Peclet number, the local density number \(\left( {Nn_{x} } \right)\), are decreasing for both cone and disk apparatus.