1 Introduction

The Brusselator mathematical model given by:

$$ \begin{array}{@{}rcl@{}} \dot{x} &=& \alpha - \left( 1 + \beta \right) x + x^{2} y, \\ \dot{y} &=& \beta x - x^{2} y, \end{array} $$
(1)

was proposed by Prigogine and Lefever [1], being a model for chemical reactions with oscillations, therefore maintaining a prolonged non-equilibrium state. For a complete description of the x, y dimensionless variables and the α, β positive control parameters, we suggest consulting Hannon and Ruth [2]. As explicitly shown in Epstein and Pojman [3], the Brusselator is a four-step chemical reaction which represents for example the Belousov-Zhabotinsky reaction [4], besides several others.

In this paper, we deal with a sinusoidally forced Brusselator given by:

$$ \begin{array}{@{}rcl@{}} \dot{x} &=& \alpha - \left( 1 + \beta \right) x + x^{2} y + F \cos \omega t, \\ \dot{y} &=& \beta x - x^{2} y, \end{array} $$
(2)

where F and ω are respectively amplitude and angular frequency of an external periodic forcing. System (2) was recently investigated by Luo and Guo [5], from the point of view of analytical solutions of some periodic evolutions. Reference [5] presents for example, the bifurcation tree of period 1 to period 8 evolutions through frequency-amplitude characteristics for system (2), among other equally important results.

Our main goal in this paper is to investigate numerically the (ω, F) parameter plane of system (2), with α = 0.4, β = 1.2 kept fixed, in the search for regions of multistability [6]. Therefore, our contribution to advance knowledge of the forced Brusselator considers (ω, F) parameter planes, which are cross sections of the (α, β, ω, F) four-dimensional parameter space of system (2). As we will see in detail in the next section, each (ω, F) parameter plane is constructed by considering a mesh of one million points. The characterization of the dynamical behavior of each of these points, chaos or regularity, in each parameter plane, will be done by the respective Lyapunov exponents spectrum, computed by the algorithm described in Wolf et al. [7]. From there, it will be possible to identify, by a simple visual inspection, the existence of parameter regions of occurrence of multistability in the forced Brusselator model (2).

The rest of the paper is organized as follows. Section 2 is dedicated to investigate aspects related to the multistability phenomenon. Parameter planes, basins of attraction, bifurcation diagrams, and phase-space portraits are presented and discussed in this section. The paper is summarized in Section 3.

2 Multistability in the Forced Brusselator

Multistability is an interesting phenomenon connected with nonlinear dynamics, meaning the coexistence of two or more attractors in the phase space, for a kept fixed set of parameters present in the related mathematical model. Coexisting attractors may be of the same type (stable equilibrium point, periodic, quasiperiodic, or chaotic) or not, having been detected in several different discrete- and continuous-time systems, modeled by different sets of mathematical equations [8,9,10,11,12,13,14,15]. Therefore, multistability is a typical phenomenon of nonlinear dynamical systems that arises as a consequence of its sensitive dependence on initial conditions. The final state of multistable systems depends on the initial conditions, being the set of initial conditions that takes the system to a particular final state called the basin of attraction of that state.

Our aim in this section is to report on the occurrence of multistability in system (2), and on coexisting periodic and chaotic attractors and its respective basins of attraction. Before presenting the results, we will write (2) for the forced Brusselator model in a more suitable form to perform all the necessary numerical manipulations. With this purpose, we consider a new variable, z = ωt, to obtain the transformed set:

$$ \begin{array}{@{}rcl@{}} \dot{x} &=& \alpha - \left( 1 + \beta \right) x + x^{2} y + F \cos z, \\ \dot{y} &=& \beta x - x^{2} y,\\ \dot{z} &=& \omega, \end{array} $$
(3)

in order to perform all the necessary numerical computations.

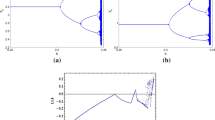
Figure 1 shows three versions of a same (ω, F) parameter plane of system (2), for which α = 0.4, β = 1.2, 0.75 ≤ ω ≤ 1.00, and 0.05 ≤ F ≤ 0.15. Each of the three versions was obtained in a different way, but in all of them the dynamical behavior of each point was characterized by the magnitude of the largest Lyapunov exponent (LLE). For the diagram in Fig. 1a, the initial condition for the necessary numerical integration of system (3) was the same for any pair (ω, F). Diagrams in Fig. 1b and c in turn were obtained by following the attractor along lines of F kept fixed.

Fig. 1
figure 1

Stability domains in the (ω, F) parameter plane of the forced Brusselator, for α = 0.4, β = 1.2. In each diagram, color is related with the magnitude of the largest Lyapunov exponent, as the respective color bar. In a, the initial condition is the same for any pair (ω, F). In b, the attractor is followed, and ω is increased for each kept fixed F. In c, the attractor is followed, and ω is decreased for each kept fixed F

Full size image

Obtaining the diagram in Fig. 1b, for example, starts at (ω, F) = (0.75, 0.05), with a given arbitrary initial condition. Then, system (3) was numerically integrated using the fourth-order Runge-Kutta algorithm, the corresponding time series was obtained, and the associated LLE was calculated. From a technical point of view, the computation of the LLE is done by using the Gram-Schmidt orthogonalization procedure, and includes determining the magnitude of expansion and contraction rates along the unstable and stable directions of the respective phase space. Speaking explicitly, the computation was done by using a FORTRAN code which is based on the ODE program that appears in Appendix A, page 310 of Ref. [7]. In the following, ω was incremented, and the system (2) was initialized with the final point (x, y, z) in the time series for the anterior ω value. System (3) was numerically integrated for the new point (ω, F), and the respective LLE was calculated. The procedure of increasing ω was repeated until its highest value ω = 1.00 is reached. Then, F was incremented, with the procedure being repeated until the pair (ω, F) = (1.00,0.15) is considered in computing. The diagram in Fig. 1c was obtained by a similar procedure, but now starting at (ω, F) = (1.00,0.15). Parameter ω was decreased until ω = 0.75. Considering F values up to 0.05, the procedure is repeated until the final point (ω, F) = (0.75,0.05) is reached. As we said before in the “Introduction” section, each diagram in Fig. 1 was discretized in a grid of 1 × 106 points equally spaced, i.e., in each diagram the LLE was computed for 1 × 106 (ω, F) pairs of parameters.

The color in diagrams of Fig. 1 is related to the magnitude of the LLE. Yellow/red color is associated to a positive LLE, while black color indicates a zero LLE, always according to the scale shown in the column at the right side, in each diagram. As is known [7], a positive LLE corresponds to a chaotic behavior, and a zero LLE means periodicity (or quasiperiodicity, when the second LLE also is null, which is not the case here). Therefore, regardless of the considered diagram in Fig. 1, we can see an oval-shaped chaotic region in yellow/red, surrounded by a periodic region in black. Embedded in the chaotic region, we may observe some few periodic stripes in black: the most apparent identified by a number that means the period of the respective stripe. Each of these numbers, for each parameter plane in Fig. 1, was obtained through bifurcation diagrams constructed for points along a horizontal straight line F = 0.1, for 0.75 ≤ ω ≤ 1.00.

As an example, Fig. 2 shows the bifurcation diagram related to the parameter plane in Fig. 1b, constructed for points along the red straight line drawn there. In Fig. 2 are plotted the local maxima of the variable y, represented by ym, as a function of the parameter ω. Such points (the local maxima) are coincident with those where the the variable y changes from increasing to decreasing as the parameter ω varies. They are determined by using the derivative of y with respect to t, specifically where the derivative changes sign from positive to negative.

Fig. 2
figure 2

Bifurcation diagram related to the parameter plane in Fig. 1b. Plotted are the local maxima of y as a function of ω. Points are considered along the line F = 0.1 in Fig. 1b

Full size image

As can be verified in Figs. 1b and 2, when we consider the increase of ω along the red straight line F = 0.1, the transition from periodic motion to chaotic motion occurs via a period-doubling bifurcation route at ω ≈ 0.82. Such figures also show that the transition from chaotic motion to periodic motion occurs via a reverse period-doubling bifurcation route at ω ≈ 0.95. Thus, for F = 0.1, ω increasing from 0.75, following the attractor, the oval-shaped chaotic region extends from ω ≈ 0.82 to ω ≈ 0.95. It is important to note that the ω values for both period-chaos and chaos-period transitions are almost the same, for the cases equal initial condition for every pair (ω, F) (diagram in Fig. 1a) and following the attractor decreasing ω (diagram in Fig. 1c). This behavior is repeated, even when considering different values for F (different horizontal lines) in diagrams of Fig. 1.

There are, however, some differences between the diagrams in Fig. 1. For example, we can note that the area inside the rectangle at the top right is clearly painted differently in each diagram. The dot marked with the red plus sign, namely (ω, F) = (0.938,0.130), is located in a periodic region of Fig. 1b, and in a chaotic region of Fig. 1c. Therefore, a given point in the (ω, F) parameter plane of system (2) may display different long-term behaviors, which are considered increasing (Fig. 1b) and decreasing (Fig. 1c) of ω for F kept fixed. In other words, for this case where the parameters in system (2) are kept fixed as (α, β, ω, F) = (0.2, 1.4, 0.938, 0.130), we can have two different attractors in the (x, y) phase space: one being chaotic, the other periodic. This is the signature of the multistability phenomenon.

The basin of attraction of an attractor is defined as being the set of initial conditions leading a given dynamical system to a long-time behavior that approaches that attractor. Therefore, behavior of the long-time state of a given system can be different, chaotic or regular, depending on which basin of attraction the initial condition belongs. Figure 3 shows the (x0, y0) basins of attraction of the forced Brusselator system (2) for the set of parameters marked with a red plus sign in diagrams of Fig. 1, i.e., for (α, β, ω, F) = (0.2, 1.4, 0.938, 0.130). In this plot, black and red colors are associated respectively with periodic and chaotic motion. Therefore, initial conditions chosen in the black region of Fig. 3 lead system (2) to periodic attractors, while initial conditions chosen in the red region of the same Fig. 3 lead to chaotic attractors. The basins of attraction plot in Fig. 3 were obtained by computing the LLE on a mesh of 500 × 500 (x0, y0) initial conditions. The criterion used to discriminate between periodic and chaotic dynamical behaviors was to assume that LLE in the range (− 0.005, 0.005) is related to periodic attractors, while those that are more positive are related to chaotic attractors.

Fig. 3
figure 3

Basins of attraction of system (2), for parameters related to the dot marked with a red plus sign in diagrams of Fig. 1. The diagram shows the coexistence of periodic and chaotic attractors. Black and red are related respectively with periodicity and chaos

Full size image

Figure 4 shows two attractors for system (2). The one shown in Fig. 4a is periodic, while the one shown in Fig. 4b is chaotic. The initial conditions are (x0, y0) = (0.2, 3.35) (point P in Fig. 3) and (x0, y0) = (1.3, 2.7) (point C in Fig. 3), respectively, for the periodic and the chaotic attractors. The Lyapunov exponents spectra are 0, − 0.01, − 0.44 and 0.04, 0, − 0.54 respectively for the periodic case and for the chaotic case. Ten thousand points were used to generate the periodic trajectory in Fig. 4, while to generate the chaotic trajectory used two hundred thousand points.

Fig. 4
figure 4

Two attractors related to system (2). a A periodic attractor, corresponding to the initial condition (x0, y0) = (0.2, 3.35), point P in Fig. 3. b A chaotic attractor, corresponding to the initial condition (x0, y0) = (1.3, 2.7), point C in Fig. 3

Full size image

3 Summary

In this paper, we have investigated a four-parameter nonlinear dynamical system, namely a periodically forced Brusselator, which is modeled by a set of two nonautonomous first-order ordinary differential equations. A given cross section of the four-dimensional parameter space has been used to demonstrate the occurrence of multistability in this system. The dynamical behavior of each point of this cross section was characterized by the value of the related largest Lyapunov exponent. In addition, basins of attraction have been used to show the coexistence of periodic and chaotic attractors in the related phase space.