A novel chaos control strategy for discrete-time Brusselator models

Abstract

This article deals with the dynamical analysis of discrete-time Brusselator models. Euler’s forward and nonstandard difference schemes are implemented for discretization of Brusselator system. We investigate the local dynamics related to equilibria of both discrete-time models. Furthermore, with the help of bifurcation theory and center manifold theorem, explicit parametric conditions for directions and existence of flip and Hopf bifurcations are investigated. A novel chaos control method is implemented in order to control chaos in discrete-time Brusselator models under the influence of flip and Hopf bifurcations. Numerical simulations are provided to illustrate theoretical discussion and effectiveness of newly introduced chaos control strategy.

1 Introduction

Recently, many authors have studied the models of nonlinear oscillatory behavior related to chemical reactions [1]. These chemical reactions play important role due to their similarities with neuronal and biological networks. Moreover, many nonlinear models related to these chemical reactions have complex and chaotic behavior [2]. The Belousov–Zhabotinsky reaction which is commonly known as BZ reaction [3,4,5], is a family of reactions representing the traditional example of non-equilibrium thermodynamics and such type of reactions yield nonlinear chemical oscillator. The oscillatory behavior of Brusselator reaction is similar to BZ reaction. The Brusselator reaction is an oscillating chemical reaction that was first studied by Prigogine and Lefever in 1968 [6] (see also [7]). Moreover, this model is the minimal mathematical system that can incorporate the oscillating behavior. In general, the Brusselator chemical reaction is described by the following steps:

$$\begin{aligned}&A\longrightarrow X,\ B+X\longrightarrow Y+D,\\&2X+Y\longrightarrow 3X,\ X\longrightarrow E. \end{aligned}$$

Assume that concentrations of A and B are constants and reversible reactions are neglected, then aforementioned reaction displays oscillatory behavior in two species X and Y. Under these assumptions, we have only two varying concentrations which are represented by X and Y. This is minimum number required for an isothermal oscillatory system [8]. Furthermore, the two reaction rate equations describing how the concentrations of X and Y vary with respect to time $\tau$ are given as follows:

$$\begin{aligned} \frac{d[X]}{d\tau }=k_1[A]_0-k_2[B]_0[X]+k_3[X]^2[Y]-k_4[X], \end{aligned}$$

and

$$\begin{aligned} \frac{d[Y]}{d\tau }=k_2[B]_0[X]-k_3[X]^2[Y]. \end{aligned}$$

Moreover, the concentrations [A] and [B] are assumed to be constants, and equal to their initial values represented by $[A]_0$ and $[B]_0$. In order to obtain the dimensionless forms for aforementioned reaction rate equations, we consider the following transformations:

$$\begin{aligned}{}[X]\longrightarrow x,\ [Y]\longrightarrow y,\ \tau \longrightarrow t= & {} \tau k_3,\\ \alpha =\frac{[A]_0 k_1}{k_3},\ \beta =\frac{[B]_0 k_2}{k_3},\ k_3= & {} k_4. \end{aligned}$$

Furthermore, we assume that the initial concentrations related to A and B are greater, then the maximum rate concentrations for X and Y are described by the following differential equations:

$$\begin{aligned} \frac{dx}{dt}&=\alpha -(1+\beta )x+x^2 y, \nonumber \\ \frac{dy}{dt}&=\beta x-x^2 y, \end{aligned}$$

(1.1)

where $\alpha$ and $\beta$ are positive constants, which are proportional to the concentrations of chemical reactants A and B, respectively. Moreover, the dimensionless variables x and y are proportional to the chemical reactants X and Y, respectively. The nonlinear equations may have a stable limit cycle for certain values the parameters $\alpha$ and $\beta$. This system exhibits oscillatory changes in the concentrations of X and Y depending upon the values of $\alpha$ and $\beta$. System (1.1) has unique positive equilibrium point $\left( \alpha ,\frac{\beta }{\alpha }\right)$. By standard mathematical calculation yields that the unique positive equilibrium point of (1.1) is locally asymptotically stable if and only if $\beta <1+\alpha ^2$. Moreover, system (1.1) undergoes Andronov–Hopf bifurcation in the neighborhood of $\beta =1+\alpha ^2$ at its positive equilibrium point, and oscillations are observed for $\beta >1+\alpha ^2$ [9].

It is worthwhile to note that discrete-time models governed by difference equations are more appropriate than the continuous one due to their efficient computational results and rich dynamical behavior [10, 11]. Moreover, this argument also works effectively in the case of nonlinear oscillatory behavior related to chemical reactions [12,13,14]. Therefore, we study stability, bifurcation analysis and chaos control related to two discrete counterparts of (1.1).

In [15], Kang and Pesin studied a discrete version of Brusselator model governed by the reaction–diffusion equations. Zafar et al. [16] implemented the classical fourth order Runge–Kutta method and non-standard finite difference scheme to system (1.1). Sanayei [17] investigated chaos control for a Brusselator chemical reaction model under the influence of a sinusoidal force acted on the reaction as a chaotic oscillator. In [18], Xu et al. discussed Turing instability and pattern formation in a semi-discrete Brusselator model. Moreover, in [19], Yu and Gumel investigated Hopf bifurcation and double-Hopf bifurcations of a chemical oscillator arising from the series coupling of two Brusselators. Similarly, we refer to [20,21,22,23,24,25,26,27,28,29,30,31] for some interesting investigations related to various variants of Brusselator models.

According to the definition of Strogatz [32], chaos requires three ingredients, that is, periodic long-term behavior, deterministic system, and sensitive dependence on initial conditions. The last item is equivalent to stating that nearby trajectories diverge exponentially (positive Lyapunov exponent). Continuous systems in a 2-dimensional phase space cannot experience such a divergence, hence chaotic behaviors can only be observed in deterministic continuous systems with a phase space of dimension 3, at least. That is why, there is no chance of chaotic behavior in continuous system (1.1). On the other hand, in a discrete map it is well known that chaos occurs also in one-dimension. Therefore, discrete-time chaotic systems, such as the logistic map, exhibit chaos whatever their dimension.

Aforementioned investigations reveal that it is an interesting mathematical study related to period-doubling bifurcation, Neimark–Sacker bifurcation and chaos control for discrete counterparts of system (1.1). In order to discuss the rich dynamical study of the system (1.1), we consider the discrete counterparts of (1.1). For this, we apply forward Euler’s method to the system (1.1) as follows:

$$\begin{aligned} x_{n+1}&=x_n+h\left( \alpha -(1+\beta )x_n+x_n^2 y_n\right) , \nonumber \\ y_{n+1}&=y_n+ h\left( \beta x_n-x_n^2 y_n\right) , \end{aligned}$$

(1.2)

where $0<h<1$ represents step size for Euler’s method. Furthermore, in order to obtain a dynamically consistent discrete-time model, a nonstandard difference scheme yields the following discrete-time model:

$$\begin{aligned} x_{n+1}&=\frac{h\alpha +x_n+h x_n^2y_n}{1+h(1+\beta )}, \nonumber \\ y_{n+1}&=\frac{y_n+\beta h x_n}{1+h x_{n}^{2}}. \end{aligned}$$

(1.3)

In [33], Din investigated local stability of equilibria, flip and Hopf bifurcations, and chaos control for discrete-time glycolysis models. Moreover, Din et al. [34] discussed qualitative behavior including stability analysis, bifurcation analysis and chaos control in discrete-time models related to chlorine dioxide–iodine–malonic acid reaction. In both [33] and [34], step size is taken as bifurcation parameter. In order to discuss chaos control, one cannot apply OGY method while keeping step size ( that is, h) as bifurcation parameter. In order to remove this deficiency, a new hybrid chaos control technique is implemented for systems (1.2) and (1.3).

The main contributions of this article are summarized as follows:

• A novel dynamically consistent discrete-time Brusselator model (1.3) is proposed which undergoes Hopf bifurcation at its unique positive steady-state.

• A novel hybrid control technique is introduced for controlling chaos under the influence of flip and Hopf bifurcations in systems (1.2) and (1.3).

• The effectiveness of proposed strategy is illustrated through suitable numerical simulations, and its comparison with existing hybrid control strategy.

The remaining discussion in this paper is organized as follows. In Sect. 2, we discuss the local dynamical behaviors of (1.2) and (1.3) at their positive steady-states. In Sect. 3, bifurcation theory related to normal forms and center manifold theorem are implemented to discuss existence and directions of flip (period-doubling) for the system (1.2) at its positive steady-state. Section 4 is related to Neimark–Sacker (Hopf) bifurcations for systems (1.2) and (1.3) at their positive steady-states. Moreover, a novel chaos control technique is introduced in Sect. 5. Finally, numerical simulations are provided in Sect. 6 in order to illustrate the theoretical discussion for the systems (1.2) and (1.3).

2 Local stability analysis

In this section, we discuss the local dynamical behaviors of systems (1.2) and (1.3). For this, first we investigate steady-states related to these systems. The steady-states of (1.2) solve the following 2-dimensional algebraic system:

$$\begin{aligned} x = x+h\left( \alpha -(1+\beta )x+x^2 y\right) ,\ y = y+ h\left( \beta x-x^2 y\right) , \end{aligned}$$

(2.1)

Solving (2.1) yields $E=\left( \alpha ,\frac{\beta }{\alpha }\right)$ as the unique steady-state for the system (1.2). Moreover, variational matrix of (1.2) at E is computed as follows:

$$\begin{aligned} J(E)=\left[ \begin{array}{cc} 1+h (\beta -1 ) &{} h \alpha ^2 \\ -h \beta &{} 1-h \alpha ^2 \end{array} \right] . \end{aligned}$$

Furthermore, the characteristic polynomial of J(E) is given as follows:

$$\begin{aligned} P(\lambda )=\lambda ^2-\left( 2-h \left( 1+\alpha ^2-\beta \right) \right) \lambda +1-h-h \alpha ^2+h^2 \alpha ^2+h \beta . \end{aligned}$$

(2.2)

Moreover, from (2.2) it follows that

$$\begin{aligned} P(1)= & {} h^2 \alpha ^2>0, \end{aligned}$$

(2.3)

$$\begin{aligned} P(-1)= & {} 4+h \left( \alpha ^2(h-2)+2 (\beta -1 )\right) , \end{aligned}$$

(2.4)

and

$$\begin{aligned} P(0)=1-h-h \alpha ^2+h^2 \alpha ^2+h \beta . \end{aligned}$$

(2.5)

Furthermore, keeping in view the relations between coefficients and roots for a quadratic equation [35,36,37,38,39,40], the following Lemma is presented:

Lemma 2.1

Consider the quadratic polynomial $\mathbb {P}(\mu )=\mu ^2-p\mu +q$, satisfying $\mathbb {P}(1)>0$ such that $\mu _1$, $\mu _2$ are roots of $\mathbb {P}(\mu )=0$. Then, the following statements hold true:

• (a) $|\mu _1|<1$ and $|\mu _2|<1$ iff $\mathbb {P}(-1)>0$ and $\mathbb {P}(0)<1$.

• (b) $|\mu _1|<1$ and $|\mu _2|>1$, or $|\mu _1|>1$ and $|\mu _2|<1$ iff $\mathbb {P}(-1)<0$.

• (c) $|\mu _1|>1$ and $|\mu _2|>1$ iff $\mathbb {P}(-1)>0$ and $\mathbb {P}(0)>1$.

• (d) $\mu _1=-1$ and $|\mu _2|\ne 1$ iff $\mathbb {P}(-1)=0$ and $\mathbb {P}(0)\ne \pm 1$.

• (e) $\mu _1$ and $\mu _2$ are complex and $|\mu _1|=|\mu _2|=1$ iff $p^2-4q<0$ and $\mathbb {P}(0)=1$.

Moreover, from (2.3) we have that $P(1)=h^2 \alpha ^2>0$. Thus, Lemma 2.1 can be implemented to prove the following results.

Lemma 2.2

For the steady-state $E=\left( \alpha ,\frac{\beta }{\alpha }\right)$ of (1.2), the following statements hold true:

• (i) $\left( \alpha ,\frac{\beta }{\alpha }\right)$ is a sink if and only if

  $$\begin{aligned} 4+h^2\alpha ^2+2h\beta >2h\alpha ^2+2h, \end{aligned}$$

  and

  $$\begin{aligned} h\alpha ^2+\beta <1+\alpha ^2. \end{aligned}$$

• (ii) $\left( \alpha ,\frac{\beta }{\alpha }\right)$ is a saddle point if and only if

  $$\begin{aligned} 4+h^2\alpha ^2+2h\beta <2h\alpha ^2+2h. \end{aligned}$$

• (iii) $\left( \alpha ,\frac{\beta }{\alpha }\right)$ is a repeller if and only if

  $$\begin{aligned} 4+h^2\alpha ^2+2h\beta >2h\alpha ^2+2h, \end{aligned}$$

  and

  $$\begin{aligned} h\alpha ^2+\beta >1+\alpha ^2. \end{aligned}$$

• (iv) Assume that $\lambda _1$ and $\lambda _2$ be roots of (2.2), then $\lambda _1=-1$ and $|\lambda _2|\ne 1$ if and only if

  $$\begin{aligned} h= & {} \frac{1+\alpha ^2-\beta \pm \sqrt{\alpha ^4+(\beta -1)^2-2 \alpha ^2(1+\beta )}}{\alpha ^2},\\&h\alpha ^2+\beta \ne 1+\alpha ^2, \end{aligned}$$

  and

  $$\begin{aligned} 2+h^2 \alpha ^2+h \beta \ne h+h \alpha ^2. \end{aligned}$$

• (v) Suppose that $\lambda _1$ and $\lambda _2$ be roots of (2.2), then $\lambda _1$ and $\lambda _2$ are complex with absolute values equal to 1 if and only if

  $$\begin{aligned} h=\frac{1+\alpha ^2-\beta }{\alpha ^2}, \end{aligned}$$

  and

  $$\begin{aligned} \alpha ^4+(\beta -1 )^2<2 \alpha ^2(1+\beta ). \end{aligned}$$

Next, we discuss the dynamical behavior of (1.3) at its positive steady-state $\left( \alpha ,\frac{\beta }{\alpha }\right)$. For this, the variational matrix of (1.3) at $\left( \alpha ,\frac{\beta }{\alpha }\right)$ is computed as follows:

$$\begin{aligned} M\left( \alpha ,\frac{\beta }{\alpha }\right) =\left[ \begin{array}{cc} \frac{1+2 h \beta }{1+h (1+\beta )} &{} \frac{h \alpha ^2}{1+h (1+\beta )} \\ -\frac{h \beta }{1+h \alpha ^2} &{} \frac{1}{1+h \alpha ^2} \end{array} \right] . \end{aligned}$$

Furthermore, the characteristic polynomial of $M\left( \alpha ,\frac{\beta }{\alpha }\right)$ is calculated as follows:

$$\begin{aligned} F(\lambda )=\lambda ^2-\left( 2+\frac{1}{1+h \alpha ^2}-\frac{1+2 h}{1+h+h \beta }\right) \lambda +\frac{1+h \left( 2+h \alpha ^2\right) \beta }{\left( 1+h \alpha ^2\right) (1+h+h \beta )}. \end{aligned}$$

(2.6)

From (2.6), we have

$$\begin{aligned} F(1)= & {} \frac{h^2 \alpha ^2}{\left( 1+h \alpha ^2\right) (1+h+h \beta )}>0,\\ F(-1)= & {} \frac{4+h \left( 2+6 \beta +\alpha ^2 (2+h+4 h \beta )\right) }{\left( 1+h \alpha ^2\right) (1+h+h \beta )}>0, \end{aligned}$$

and

$$\begin{aligned} F(0)=\frac{1+h \left( 2+h \alpha ^2\right) \beta }{\left( 1+h \alpha ^2\right) (1+h+h \beta )}>0. \end{aligned}$$

Moreover, dynamical behavior of (1.3) at its steady-state $\left( \alpha ,\frac{\beta }{\alpha }\right)$ is described in the following Lemma.

Lemma 2.3

For the system (1.3) the following results hold true:

• (i) The steady-state $\left( \alpha ,\frac{\beta }{\alpha }\right)$ for (1.3) is a sink if and only if

  $$\begin{aligned} \frac{1+h \left( 2+h \alpha ^2\right) \beta }{\left( 1+h \alpha ^2\right) (1+h+h \beta )}<1. \end{aligned}$$

• (ii) The steady-state $\left( \alpha ,\frac{\beta }{\alpha }\right)$ for (1.3) cannot be a saddle point for all $\alpha ,\ \beta >0$ and $0<h<1$.

• (iii) $\left( \alpha ,\frac{\beta }{\alpha }\right)$ is a source if and only if

  $$\begin{aligned} \frac{1+h \left( 2+h \alpha ^2\right) \beta }{\left( 1+h \alpha ^2\right) (1+h+h \beta )}>1. \end{aligned}$$

• (iv) Suppose that $\lambda _1$ and $\lambda _2$ be roots of (2.6), then $\lambda _1$ and $\lambda _2$ are complex with absolute values equal to 1 if and only if

  $$\begin{aligned} h=\frac{\beta -1-\alpha ^2}{\alpha ^2}, \end{aligned}$$

  and

  $$\begin{aligned} \alpha ^4 (4 \beta -1)+2 \alpha ^2 \left( 1+\beta -4 \beta ^2\right) +(\beta -1)(1+\beta (3+4\beta ))>0. \end{aligned}$$

3 Flip bifurcation

In this section, center manifold theorem and bifurcation theory are implemented in order to investigate the existence and direction of period-doubling(flip) bifurcation at positive steady-state $\left( \alpha ,\frac{\beta }{\alpha }\right)$ of the system (1.2). For this, we choose h as bifurcation parameter and taking into account the following conditions:

$$\begin{aligned}&h\equiv h_1=\frac{1+\alpha ^2-\beta \pm \sqrt{\alpha ^4+(\beta -1)^2-2 \alpha ^2(1+\beta )}}{\alpha ^2}, \end{aligned}$$

(3.1)

$$\begin{aligned}&h_1\alpha ^2+\beta \ne 1+\alpha ^2, \end{aligned}$$

(3.2)

and

$$\begin{aligned} 2+h_1^2 \alpha ^2+h_1 \beta \ne h_1(1+\alpha ^2). \end{aligned}$$

(3.3)

Let us consider

$$\begin{aligned} \Omega _{PD}=\left\{ (\alpha ,\beta ,h_1)\in \mathbb {R}_{+}^{3}:(3.1), (3.2)\,\ \hbox {and}\,\ (3.3)\,\ \hbox {are satisfied}\right\} . \end{aligned}$$

If $(\alpha ,\beta ,h_1)\in \Omega _{PD}$, then roots of (2.2) are $\lambda _1=-1$ and

$$\begin{aligned} \lambda _2:=\frac{\alpha ^2-1-\left( \alpha ^2-\beta \right) ^2\pm L \left( 1+\alpha ^2-\beta \right) +2 \beta }{\alpha ^2}, \end{aligned}$$

where

$$\begin{aligned} L=\sqrt{\alpha ^4+(-1+\beta )^2-2 \alpha ^2 (1+\beta )}. \end{aligned}$$

Assume that $(\alpha ,\beta ,h_1)\in \Omega _{PD}$, then (1.2) is described by the following mapping:

$$\begin{aligned} \left( \begin{array}{c} U \\ V \\ \end{array} \right) \rightarrow \left( \begin{array}{c} U+h_1\left( \alpha -(1+\beta )U+U^2 V\right) \\ V+ h_1\left( \beta U-U^2 V\right) \\ \end{array} \right) . \end{aligned}$$

(3.4)

Moreover, denote by $\bar{h}$ as bifurcation parameter satisfying $|\bar{h}|\ll 1$, then perturbation mapping for (3.4) is described as follows:

$$\begin{aligned} \left( \begin{array}{c} U \\ V \\ \end{array} \right) \rightarrow \left( \begin{array}{c} U+(h_1+\bar{h})\left( \alpha -(1+\beta )U+U^2 V\right) \\ V+ (h_1+\bar{h})\left( \beta U-U^2 V\right) \\ \end{array} \right) . \end{aligned}$$

(3.5)

By taking into account the transformations $x=U-\alpha$ and $y=V-\frac{\beta }{\alpha }$, then it follows from (3.5) that:

$$\begin{aligned} \left[ \begin{array}{c} x \\ y \\ \end{array} \right] \rightarrow \left[ \begin{array}{cc} 1+h_1 (\beta -1 ) &{} h_1 \alpha ^2 \\ -h_1 \beta &{} 1-h_1 \alpha ^2 \end{array} \right] \left[ \begin{array}{c} x \\ y \\ \end{array} \right] +\left[ \begin{array}{c} f_1(x,y, \bar{h}) \\ f_2(x,y,\bar{h})\\ \end{array} \right] , \end{aligned}$$

(3.6)

where

$$\begin{aligned} f_1(x,y,\bar{h})= & {} \frac{h_1\beta }{\alpha }x^2+2h_1\alpha x y+h_1 x^2y+(\beta -1)x\bar{h}+\alpha ^2y\bar{h}\\&+\frac{\beta }{\alpha } x^2 \bar{h}+2\alpha x y\bar{h}+O\left( (|x|+|y|+|\bar{h}|)^4\right) , \end{aligned}$$

and

$$\begin{aligned} f_2(x,y,\bar{h})= & {} -\frac{h_1\beta }{\alpha }x^2-2h_1\alpha x y-h_1x^2y-\beta x\bar{h}-\alpha ^2 y\bar{h}\\&-\frac{\beta }{\alpha } x^2 \bar{h}-2\alpha x y\bar{h}+O\left( (|x|+|y|+|\bar{h}|)^4\right) . \end{aligned}$$

For the conversion of the matrix $\left[ \begin{array}{cc} 1+h_1 (\beta -1 ) &{} h_1 \alpha ^2 \\ -h_1 \beta &{} 1-h_1 \alpha ^2 \end{array} \right]$ into normal form, we consider the following transformation

$$\begin{aligned} \left( \begin{array}{c} x \\ y \\ \end{array} \right) =T\left( \begin{array}{c} u \\ v \\ \end{array} \right) , \end{aligned}$$

(3.7)

where

$$\begin{aligned} T=\left( \begin{array}{cc} h_1\alpha ^2 &{} h_1\alpha ^2 \\ h_1(1-\beta ) &{} \lambda _2-1+h_1(1-\beta ) \\ \end{array} \right) \end{aligned}$$

be a non-singular matrix. From (3.6) and (3.7), we obtain

$$\begin{aligned} \left( \begin{array}{c} u \\ v \\ \end{array} \right) \rightarrow \left( \begin{array}{cc} -1 &{} 0 \\ 0&{} \lambda _2\\ \end{array} \right) \left( \begin{array}{c} u \\ v \\ \end{array} \right) +\left( \begin{array}{c} f_3(u,v,\bar{h}) \\ f_4(u,v,\bar{h})\\ \end{array} \right) , \end{aligned}$$

(3.8)

where

$$\begin{aligned} f_3(u,v,\bar{h})= & {} \left( {\frac{\beta \left( h_{1}({\alpha }^{2}-\beta +1)+\lambda _ {{2}}-1 \right) }{{\alpha }^{3} \left( \lambda _{{2}}-1 \right) }}\right) x^2 +\left( {\frac{2\left( h_{1}({\alpha }^{2}-\beta +1)+\lambda _{{2}}-1\right) }{ \alpha \left( \lambda _{{2}}-1 \right) }} \right) x y\\&+\left( {\frac{h_{1}({\alpha }^{2}-\beta +1)+\lambda _{{2}}-1}{{ \alpha }^{2} \left( \lambda _{{2}}-1 \right) }}\right) x^2y \\&+\left( \frac{\beta h_{1}\left( {\alpha }^{2}-\beta +2 \right) +\left( \lambda _{{2}}-1 \right) \left( \beta -1\right) -h_{1}}{h_{1}{ \alpha }^{2} \left( \lambda _{{2}}-1 \right) } \right) x\bar{h}\\&+ \left( {\frac{h_{1} \left( {\alpha }^{2}-\beta +1 \right) +\lambda _{{2}}-1}{h_ {1}\, \left( \lambda _{{2}}-1 \right) }}\right) y\bar{h} +\left( {\frac{\beta \left( h_{1}({\alpha }^{2}-\beta +1)+\lambda _ {{2}}-1 \right) }{{\alpha }^{3}h_1\left( \lambda _{{2}}-1 \right) }}\right) x^2\bar{h}\\&+\left( {\frac{2\left( h_{1}({\alpha }^{2}-\beta +1)+\lambda _{{2}}-1\right) }{ \alpha h_1\left( \lambda _{{2}}-1 \right) }}\right) x y\bar{h}+O\left( (|u|+|v|+|\bar{h}|)^4\right) ,\\ f_4(u,v,\bar{h})= & {} \left( {\frac{\beta h_{1}\left( {\alpha }^{2}-\beta +1 \right) }{{\alpha } ^{3} \left( 1-\lambda _{{2}}\right) }} \right) x^2+\left( {\frac{2 h_{1}\left( {\alpha }^{2}-\beta +1 \right) }{\alpha \, \left( 1- \lambda _{{2}}\right) }} \right) x y\\&+\left( {\frac{h_{1}\left( {\alpha }^{2}-\beta +1 \right) }{{\alpha }^{2} \left( 1-\lambda _{{2}}\right) }} \right) x^2 y +\left( {\frac{{\alpha }^{2}\beta -{\beta }^{2}+2\,\beta -1}{{\alpha }^{2} \left( 1-\lambda _{{2}}\right) }}\right) x\bar{h}\\&+\left( {\frac{{\alpha }^{2}-\beta +1}{1-\lambda _{{2}}}}\right) y\bar{h}+\left( {\frac{\beta \, \left( {\alpha }^{2}-\beta +1 \right) }{{\alpha }^{3} \left( 1-\lambda _{{2}}\right) }}\right) x^2\bar{h}\\&+\left( {\frac{2\left( {\alpha }^{2}-\beta +1 \right) }{\alpha \left( 1- \lambda _{{2}}\right) }}\right) x y\bar{h}+O\left( (|u|+|v|+|\bar{h}|)^4\right) ,\\ x= & {} h_1\alpha ^2(u+v),\ y=-(2+h_1(\beta -1))u+(\lambda _2-1-h_1(\beta -1))v. \end{aligned}$$

For the implementation of the center manifold theorem [41] to (3.8), let $W^c(0,0,0)$ denotes the center manifold of (3.8) evaluated at (0, 0) in a small neighborhood of $\bar{h}=0$. Then, $W^c(0,0,0)$ is computed as follows:

$$\begin{aligned} W^c(0,0,0)=\left\{ (u,v,\bar{h})\in \mathbb {R}^3:v=s_1u^2+s_2u\bar{h}+s_3\bar{h}^2+O\left( (|u|+|\bar{h}|)^3\right) \right\} , \end{aligned}$$

where

$$\begin{aligned} s_1= & {} -{\frac{h_{1}^{2}\alpha \left( {\alpha }^{2}-\beta +1 \right) \left( h_{1}\,\beta -2\,h_{1}+4 \right) }{ \left( \lambda _{{2}}-1 \right) ^{2}}},\\ s_2= & {} {\frac{{\alpha }^{2}h_{1}-2\,{\alpha }^{2}+2\,\beta -2}{ \left( \lambda _ {{2}}-1 \right) ^{2}}},\ s_3=0. \end{aligned}$$

Furthermore, the map restricted to the center manifold $W^c(0,0,0)$ is given as follows:

$$\begin{aligned} F: u\rightarrow -u+m_1u^2+m_2u\bar{h}+m_3u^2\bar{h}+m_4u\bar{h}^2+m_5u^3+O\left( (|u|+|\bar{h}|)^4\right) , \end{aligned}$$

where

$$\begin{aligned} m_1= & {} -{\frac{h_{1}\alpha \left( h_{1}\,{\alpha }^{2}-\beta \,h_{1}+h_{1}+\lambda _{{2}}- 1 \right) \left( \beta \,h_{1}-2\,h_{1}+4 \right) }{ \lambda _{{2}}-1}},\\ m_2= & {} {\frac{{\alpha }^{2}{h_{1}}^{2}-2\,{\alpha }^{2}h_{1}+2\,\beta \,h_{1}-2 \,h_{1}-2\,\lambda _{{2}}+2}{h_{1}\, \left( \lambda _{{2}}-1 \right) }},\\ m_3= & {} {\frac{\alpha \beta h_1\left( {\alpha }^{2}h_{1}-\beta \,h_{1}+h_{1}+\lambda _{{ 2}}-1 \right) \left( 2s_{{2}}h_{1}+1 \right) }{ \lambda _{{2}}-1}}\\&-{\frac{ 2h_{1}\alpha s_{2}\left( {\alpha }^{2}h_{1}-\beta \,h_{1}+h_{1}+\lambda _{{2}} -1 \right) \left( \beta \,h_{1}-h_{1}+2 \right) }{\lambda _{{2}}-1}}\\&-{\frac{ 2\alpha \left( h_1({\alpha }^{2}-\beta +1)+\lambda _{{2}} -1 \right) \left( h_1s_2(\beta h_1-h_1-\lambda _2+1)+h_1(\beta -1)+2\right) }{\lambda _{{2}}-1}}\\&+{\frac{s_{{1}} \left( h_1({\alpha }^{2}h_{1}+{\alpha }^{2}\lambda _{{2}}- {\alpha }^{2}-\beta \lambda _{{2}}+\beta +\lambda _{{2}}-1)+\lambda _2(\lambda _2-2)+1 \right) }{h_{1}\left( \lambda _{{2}}-1 \right) }},\\ m_4= & {} {\frac{s_{{2}} \left( h_{1} \left( {\alpha }^{2}h_{1}+{\alpha }^{2} \lambda _{{2}}-{\alpha }^{2}-\beta \,\lambda _{{2}}+\beta +\lambda _{{2}}-1 \right) +\lambda _{{2}} \left( \lambda _{{2}}-2 \right) +1 \right) }{h_ {1}\, \left( \lambda _{{2}}-1 \right) }}, \end{aligned}$$

and

$$\begin{aligned} m_5=-{\frac{h_{1}\alpha \left( h_{1}({\alpha }^{2}-\beta +1)+\lambda _{{2}}- 1 \right) \left( h_1( \alpha \beta h_{1}-\alpha h_{1}+2\beta s_{{1}}+2\alpha -4 s_{{1}})-2s_1(\lambda _{{2}}-3) \right) }{\lambda _{{2}}-1}}. \end{aligned}$$

Next, we define the following two nonzero real numbers:

$$\begin{aligned} l_1=\left( \frac{\partial ^2f_1}{\partial u \partial \bar{h}}+\frac{1}{2}\frac{\partial F}{\partial \bar{h}}\frac{\partial ^2F}{\partial u^2}\right) _{(0,0)} ={\frac{{\alpha }^{2}h_{1}^{2}-2\,{\alpha }^{2}h_{1}+2\,\beta \,h_{1}-2 \,h_{1}-2\,\lambda _{{2}}+2}{h_{1}\, \left( \lambda _{{2}}-1 \right) }}, \end{aligned}$$

and

$$\begin{aligned} l_2=\left( \frac{1}{6}\frac{\partial ^3F}{\partial u^3}+\left( \frac{1}{2}\frac{\partial ^2F}{\partial u^2}\right) ^2\right) _{(0,0)} =m_1^2+m_5. \end{aligned}$$

Due to aforementioned computation, we have the following result about period-doubling bifurcation of system (1.2).

Theorem 3.1

Suppose that $l_1\ne 0$ and $l_2\ne 0$, then system (1.2) undergoes period-doubling bifurcation at the unique positive equilibrium point when parameter h varies in small neighborhood of $h_1$. Furthermore, if $l_2>0$, then the period-two orbits that bifurcate from $\left( \alpha ,\frac{\beta }{\alpha }\right)$ are stable, and if $l_2<0$, then these orbits are unstable.

4 Hopf bifurcation

This section is related to investigate the conditions for the existence and direction of Hopf bifurcation at positive steady-state $\left( \alpha ,\frac{\beta }{\alpha }\right)$ of system (1.2). In order to obtain the parametric conditions for existence of Hopf bifurcation, the point $\left( \alpha ,\frac{\beta }{\alpha }\right)$ should be non-hyperbolic such that the variational matrix evaluated at $\left( \alpha ,\frac{\beta }{\alpha }\right)$ has both complex eigenvalues with absolute values equal to 1. For this, first we suppose that

$$\begin{aligned} h\equiv h_2:=\frac{1+\alpha ^2-\beta }{\alpha ^2}. \end{aligned}$$

Secondly, we assume that the following inequality holds true:

$$\begin{aligned} \alpha ^4+(\beta -1 )^2<2 \alpha ^2(1+\beta ). \end{aligned}$$

Under aforementioned conditions, both roots of (2.2) are complex having absolute values equal to 1. Assume that

$$\begin{aligned} \Omega _{NS}=\left\{ (\alpha ,\beta ,h_2)\in \mathbb {R}^{3}_{+}:h_2=\frac{1+\alpha ^2-\beta }{\alpha ^2},\ \alpha ^4+(\beta -1 )^2<2 \alpha ^2(1+\beta )\right\} . \end{aligned}$$

Let $(\alpha ,\beta ,h_2)\in \Omega _{NS}$, then (1.2) is described by the following mapping:

$$\begin{aligned} \left[ \begin{array}{c} U \\ V \\ \end{array} \right] \rightarrow \left[ \begin{array}{c} U+h_2\left( \alpha -(1+\beta )U+U^2 V\right) \\ V+ h_2\left( \beta U-U^2 V\right) \\ \end{array} \right] . \end{aligned}$$

(4.1)

Next, we take $\tilde{h}$ as the bifurcation parameter, then perturbation mapping for (4.1) is described as follows:

$$\begin{aligned} \left[ \begin{array}{c} U \\ V \\ \end{array} \right] \rightarrow \left[ \begin{array}{c} U+(h_2+\tilde{h})\left( \alpha -(1+\beta )U+U^2 V\right) \\ V+ (h_2+\tilde{h})\left( \beta U-U^2 V\right) \\ \end{array} \right] , \end{aligned}$$

(4.2)

where $|\tilde{h}|<<1$ represents the small perturbation parameter. Under the transformations $x=U-\alpha$ and $y=V-\frac{\beta }{\alpha }$ the map (4.2) is converted into the following form:

$$\begin{aligned} \left[ \begin{array}{c} x \\ y \\ \end{array} \right] \rightarrow \left[ \begin{array}{cc} 1+(h_2+\tilde{h})(\beta -1 ) &{} (h_2+\tilde{h}) \alpha ^2 \\ -(h_2+\tilde{h}) \beta &{} 1-(h_2+\tilde{h}) \alpha ^2 \end{array} \right] \left[ \begin{array}{c} x\\ y\\ \end{array} \right] + \left[ \begin{array}{c} g_{1}(x,y)\\ g_{2}(x,y)\\ \end{array} \right] , \end{aligned}$$

(4.3)

where

$$\begin{aligned} g_1(x,y)= & {} \frac{(h_2+\tilde{h})\beta }{\alpha }x^2+2(h_2+\tilde{h})\alpha x y+(h_2+\tilde{h}) x^2y+O\left( (|x|+|y|)^4\right) , \end{aligned}$$

and

$$\begin{aligned} g_2(x,y)= & {} -\frac{(h_2+\tilde{h})\beta }{\alpha }x^2-2(h_2+\tilde{h})\alpha x y-(h_2+\tilde{h})x^2y+O\left( (|x|+|y|)^4\right) . \end{aligned}$$

Furthermore, the characteristic equation for the variational matrix of (4.3) at its fixed point (0, 0) is given as follows:

$$\begin{aligned} \begin{array}{rcl} \mu ^2-\varphi (\tilde{h})\mu +\psi (\tilde{h})=0, \end{array} \end{aligned}$$

(4.4)

where

$$\begin{aligned} \varphi (\tilde{h})=2-(h_2+\tilde{h}) \left( 1+\alpha ^2-\beta \right) , \end{aligned}$$

and

$$\begin{aligned} \psi (\tilde{h})=1-(h_2+\tilde{h})-(h_2+\tilde{h}) \alpha ^2+(h_2+\tilde{h})^2 \alpha ^2+(h_2+\tilde{h}) \beta . \end{aligned}$$

Assume that $(\alpha ,\beta ,h_2)\in \Omega _{NS}$, then roots of (4.4) are computed as follows:

$$\begin{aligned} \mu _1:=\frac{\varphi (\tilde{h})-i\sqrt{4\psi (\tilde{h})-\left( \varphi (\tilde{h})\right) ^2}}{2}, \end{aligned}$$

and

$$\begin{aligned} \mu _2:=\frac{\varphi (\tilde{h})+i\sqrt{4\psi (\tilde{h})-\left( \varphi (\tilde{h})\right) ^2}}{2}. \end{aligned}$$

Furthermore, we obtain that

$$\begin{aligned} |\mu _{1}|=|\mu _{2}|=\sqrt{1-(h_2+\tilde{h})-(h_2+\tilde{h}) \alpha ^2+(h_2+\tilde{h})^2 \alpha ^2+(h_2+\tilde{h}) \beta }. \end{aligned}$$

Moreover, with simple computations it follows that

$$\begin{aligned} \bigg (\frac{d|\mu _{1}|}{d\tilde{h}}\bigg )_{\tilde{h}=0}=\bigg (\frac{d|\mu _{2}|}{d\tilde{h}}\bigg )_{\tilde{h}=0}= \frac{1}{2} \left( 1+\alpha ^2-\beta \right) \ne 0. \end{aligned}$$

Moreover, we suppose that $\varphi (0)\ne 0$ and $\varphi (0)\ne -1$, then it follows that

$$\begin{aligned} 1+\alpha ^2\ne \beta +\sqrt{2}\alpha ,\ \hbox {and}\,\ 1+\alpha ^2\ne \beta +\sqrt{3}\alpha . \end{aligned}$$

(4.5)

Suppose that $(\alpha ,\beta ,h_2)\in \Omega _{NS}$ and conditions (4.5) hold true, then it follows that $\varphi (0)\ne \pm 2,0,-1$. Thus, we have $\mu _{1}^{k}, \mu _{2}^{k}\ne 1$ for all $k=1,2,3,4$ at $\tilde{h}=0$. Due to these assumptions, it follows that the roots of (4.4) do not lie in the intersection of the unit circle with the coordinate axes when $\tilde{h}=0$. Suppose that $\kappa$ and $\omega$ denote real and imaginary parts of $\mu _2$ at $\tilde{h}=0$, respectively, then we have

$$\begin{aligned} \kappa :=\frac{1}{2} \left( 2-\frac{\left( 1+\alpha ^2-\beta \right) ^2}{\alpha ^2}\right) , \end{aligned}$$

and

$$\begin{aligned} \omega :=\frac{\left( 1+\alpha ^2-\beta \right) \sqrt{2 \alpha ^2 (1+\beta )-\alpha ^4-(1-\beta )^2}}{2\alpha ^2}. \end{aligned}$$

Now, we consider the following transformation:

$$\begin{aligned} \left( \begin{array}{c} x \\ y \\ \end{array} \right) \rightarrow \left( \begin{array}{cc} (h_2+\tilde{h}) \alpha ^2 &{} 0\\ \kappa -1+(h_2+\tilde{h})(1-\beta ) &{} -\omega \\ \end{array} \right) \left( \begin{array}{c} u\\ v\\ \end{array} \right) . \end{aligned}$$

(4.6)

Implementation of transformation (4.6), the normal form of (4.3) is computed as follows:

$$\begin{aligned} \left( \begin{array}{c} u \\ v \\ \end{array} \right) \rightarrow \left( \begin{array}{cc} \kappa &{} -\omega \\ \omega &{} \kappa \\ \end{array} \right) \left( \begin{array}{c} u\\ v\\ \end{array} \right) + \left( \begin{array}{c} \tilde{P}(u,v)\\ \tilde{Q}(u,v)\\ \end{array} \right) , \end{aligned}$$

(4.7)

where

$$\begin{aligned} \tilde{P}(u,v)&=\frac{\beta }{\alpha ^3}x^{2}+\frac{2}{\alpha }xy+\frac{1}{\alpha ^2}x^{2}y+O((|u|+|v|)^{4}),\\ \tilde{Q}(u,v)&=\bigg (\frac{\beta (\alpha ^4 \tilde{h}+\alpha ^4-\alpha ^2\beta \tilde{h}-2\alpha ^2\beta +\alpha ^2\tilde{h}+\alpha ^2\kappa +\alpha ^2+\beta ^2-2\beta +1)}{\omega \alpha ^5}\bigg )x^{2}\\&\quad +\bigg (\frac{2(\alpha ^4\tilde{h}+\alpha ^4-\alpha ^2\beta \tilde{h}-2\alpha ^2\beta +\alpha ^2\tilde{h} +\alpha ^2\kappa +\alpha ^2+\beta ^2-2\beta +1)}{\omega \alpha ^3}\bigg )xy\\&\quad +\bigg (\frac{\alpha ^4\tilde{h}+\alpha ^4-\alpha ^2\beta \tilde{h}-2\alpha ^2\beta +\alpha ^2\tilde{h} +\alpha ^2\kappa +\alpha ^2+\beta ^2-2\beta +1}{\omega \alpha ^4}\bigg )x^2 y\\&\quad +O((|u|+|v|)^{4}),\\ x&=(h_2+\tilde{h})\alpha ^2 u,\ \hbox {and}\,\ y=\left( \kappa -1+(h_2+\tilde{h})(1-\beta )\right) u-\omega v. \end{aligned}$$

We compute the following Lyapunov first exponent at $(u,v,\tilde{h})=(0,0,0)$ as follows:

$$\begin{aligned} \mathbb {L}_1=\bigg [-Re\bigg (\frac{(1-2\mu _{1})\mu _{2}^{2}}{1-\mu _{1}}\zeta _{20}\zeta _{11}\bigg )- \frac{1}{2}|\zeta _{11}|^{2}-|\zeta _{02}|^{2}+Re(\mu _{2}\zeta _{21})\bigg ], \end{aligned}$$

where

$$\begin{aligned} \zeta _{20}= & {} \frac{1}{8}\left[ \tilde{P}_{uu}-\tilde{P}_{vv}+2\tilde{Q }_{uv}+ i\left( \tilde{Q}_{uu}-\tilde{Q}_{vv}-2\tilde{P} _{uv}\right) \right] ,\\ \zeta _{11}= & {} \frac{1}{4}\left[ \tilde{P}_{uu}+\tilde{P}_{vv}+ i\left( \tilde{Q}_{uu}+\tilde{Q}_{vv}\right) \right] ,\\ \zeta _{02}= & {} \frac{1}{8}\left[ \tilde{P}_{uu}-\tilde{P}_{vv}-2\tilde{Q }_{uv}+ i\left( \tilde{Q}_{uu}-\tilde{Q}_{vv}+2\tilde{P} _{uv}\right) \right] , \end{aligned}$$

and

$$\begin{aligned} \zeta _{21}=\frac{1}{16}\left[ \tilde{P}_{uuu}+\tilde{P}_{uvv}+ \tilde{Q}_{uuv}+\tilde{Q}_{vvv}+ i\left( \tilde{Q}_{uuu}+ \tilde{Q}_{uvv}-\tilde{P}_{uuv}-\tilde{P}_{vvv}\right) \right] . \end{aligned}$$

Furthermore, the partial derivatives related to $\tilde{P}$ and $\tilde{Q}$ at $(u,v,\tilde{h})=(0,0,0)$ are computed as follows:

$$\begin{aligned} \tilde{P}_{uu}= & {} -\frac{(2(\alpha ^2-\beta +1))(\alpha ^2\beta -2\alpha ^2\kappa -\beta ^2+3\beta -2)}{\alpha ^3},\\ \tilde{Q}_{uv}= & {} -\frac{2(\alpha ^4-2\alpha ^2\beta +\alpha ^2\kappa +\alpha ^2+\beta ^2-2\beta +1)(\alpha ^2-\beta +1)}{\alpha ^3},\\ \tilde{Q}_{uu}= & {} -\frac{2(\alpha ^4-2\alpha ^2\beta +\alpha ^2\kappa +\alpha ^2+\beta ^2-2\beta +1) (\alpha ^2-\beta +1)(\alpha ^2\beta -2\alpha ^2\kappa -\beta ^2+3\beta -2)}{\alpha ^5\omega },\\ \tilde{P}_{uv}= & {} -\frac{2\omega (\alpha ^2-\beta +1)}{\alpha },\ \tilde{P}_{uuu}=-\frac{6(\alpha ^2-\beta +1)^2(\alpha ^2\beta -\alpha ^2\kappa -\beta ^2+2\beta -1)}{\alpha ^4},\\ \tilde{Q}_{uuv}= & {} -\frac{2(\alpha ^4-2\alpha ^2\beta +\alpha ^2\kappa +\alpha ^2+\beta ^2-2\beta +1)(\alpha ^2-\beta +1)^2}{\alpha ^4},\\ \tilde{Q}_{uuu}= & {} -\frac{6(\alpha ^4-2\alpha ^2\beta +\alpha ^2\kappa +\alpha ^2+ \beta ^2-2\beta +1)(\alpha ^2\beta -\alpha ^2\kappa -\beta ^2+2\beta -1)(\alpha ^2-\beta +1)^2}{\alpha ^6\omega },\\ \tilde{P}_{uuv}= & {} -\frac{2\omega (\alpha ^2-\beta +1)^2}{\alpha ^2},\\ \tilde{Q}_{vvv}= & {} \tilde{Q}_{uvv}=\tilde{P}_{vvv}=\tilde{P}_{uvv}=\tilde{P}_{vv}=\tilde{Q}_{vv}=0. \end{aligned}$$

Keeping in view aforementioned calculations and implementing bifurcation theory [42,43,44,45,46], we have the following result which gives criterion of Hopf bifurcation at $\left( \alpha ,\frac{\beta }{\alpha }\right)$ for the system (1.2).

Theorem 4.1

Suppose that (4.5) holds true and $\mathbb {L}_1\ne 0$, then system (1.2) undergoes Hopf bifurcation at $\left( \alpha ,\frac{\beta }{\alpha }\right)$ when h varies in a small neighborhood of $h_2=\frac{1+\alpha ^2-\beta }{\alpha ^2}$. Moreover, if $\mathbb {L}_1<0$, then an attracting invariant closed curve bifurcates from $\left( \alpha ,\frac{\beta }{\alpha }\right)$ for $h>h_2$, and if $\mathbb {L}_1>0$, then a repelling invariant closed curve bifurcates from $\left( \alpha ,\frac{\beta }{\alpha }\right)$ for $h<h_2$.

Next, we consider the following set for the system (1.3):

$$\begin{aligned} \Psi _{NB}=\left\{ (\alpha ,\beta ,h_3):h_3=\frac{\beta -1-\alpha ^2}{\alpha ^2},\ \Lambda (\alpha ,\beta )>0,\ \alpha>0,\ \beta >0\right\} , \end{aligned}$$

where

$$\begin{aligned} \Lambda (\alpha ,\beta ):=\alpha ^4(4 \beta -1)+2 \alpha ^2 \left( 1+\beta -4 \beta ^2\right) +(\beta -1)(1+\beta (3+4\beta )). \end{aligned}$$

Moreover, we consider the mapping

$$\begin{aligned} \left[ \begin{array}{c} X \\ Y \\ \end{array} \right] \rightarrow \left[ \begin{array}{c} \frac{(h_3+\hat{h})\alpha +X+(h_3+\hat{h}) X^2 Y}{1+(h_3+\hat{h})(1+\beta )}\\ \frac{Y+\beta (h_3+\hat{h}) X}{1+(h_3+\hat{h}) X^{2}} \\ \end{array} \right] , \end{aligned}$$

(4.8)

where $|\hat{h}|<<1$ is small bifurcation parameter for (1.3). Furthermore, the transformations $x=X-\alpha$ and $y=Y-\frac{\beta }{\alpha }$ convert (4.8) into the following form:

$$\begin{aligned} \left[ \begin{array}{c} x \\ y \\ \end{array} \right] \rightarrow \left[ \begin{array}{cc} \frac{1+2 (h_3+\hat{h}) \beta }{1+(h_3+\hat{h}) (1+\beta )}&{} \frac{(h_3+\hat{h}) \alpha ^2}{1+(h_3+\hat{h}) (1+\beta )} \\ -\frac{(h_3+\hat{h}) \beta }{1+(h_3+\hat{h}) \alpha ^2}&{} \frac{1}{1+(h_3+\hat{h}) \alpha ^2} \end{array} \right] \left[ \begin{array}{c} x\\ y\\ \end{array} \right] + \left[ \begin{array}{c} H_{1}(x,y)\\ H_{2}(x,y)\\ \end{array} \right] , \end{aligned}$$

(4.9)

where

$$\begin{aligned} H_1(x,y)&=\left( \frac{(h_3+\hat{h})\beta }{\alpha (1+(h_3+\hat{h})(1+\beta ))}\right) x^2 +\left( \frac{2\alpha (h_3+\hat{h})}{1+(h_3+\hat{h})(1+\beta )}\right) xy\\&\quad +\left( \frac{h_3+\hat{h}}{1+(h_3+\hat{h})(1+\beta )}\right) x^2 y+O\left( (|x|+|y|)^4\right) , \end{aligned}$$

and

$$\begin{aligned} H_2(x,y)&=\left( \frac{(\alpha ^2(h_3+\hat{h})-1)\beta (h_3+\hat{h})}{\alpha (\alpha ^2(h_3+\hat{h})+1)^2}\right) x^2 -\left( \frac{2\alpha (h_3+\hat{h})}{(\alpha ^2(h_3+\hat{h})+1)^2}\right) xy\\&\quad -\left( \frac{\beta (h_3+\hat{h})^2(\alpha ^2(h_3+\hat{h})-3)}{(\alpha ^2(h_3+\hat{h})+1)^3}\right) x^3+ \left( \frac{(h_3+\hat{h})(3\alpha ^2(h_3+\hat{h})-1)}{(\alpha ^2(h_3+\hat{h})+1)^3}\right) x^2 y\\&\quad +O\left( (|x|+|y|)^4\right) . \end{aligned}$$

The characteristic polynomial for variational matrix of (4.9) at (0, 0) is computed as follows:

$$\begin{aligned} \rho ^2-\left( 2+\frac{1}{1+H \alpha ^2}-\frac{1+2 H}{1+H+H \beta }\right) \rho +\frac{1+H \left( 2+H \alpha ^2\right) \beta }{\left( 1+H \alpha ^2\right) (1+H+H\beta )}=0, \end{aligned}$$

(4.10)

where

$$\begin{aligned} H:=h_3+\hat{h}. \end{aligned}$$

The roots of (4.10) are given as follows:

$$\begin{aligned} \rho _1=\frac{\zeta (\hat{h})-i\sqrt{4\vartheta (\hat{h})-\left( \zeta (\hat{h})\right) ^2}}{2}, \end{aligned}$$

and

$$\begin{aligned} \rho _2=\frac{\zeta (\hat{h})+i\sqrt{4\vartheta (\hat{h})-\left( \zeta (\hat{h})\right) ^2}}{2}, \end{aligned}$$

where

$$\begin{aligned} \zeta (\hat{h})=2+\frac{1}{1+H \alpha ^2}-\frac{1+2 H}{1+H+H \beta }, \end{aligned}$$

and

$$\begin{aligned} \vartheta (\hat{h})=\frac{1+H \left( 2+H \alpha ^2\right) \beta }{\left( 1+H \alpha ^2\right) (1+H+H\beta )}. \end{aligned}$$

Then, we obtain that

$$\begin{aligned} |\rho _{1}|=|\rho _{2}|=\sqrt{\frac{1+H \left( 2+H \alpha ^2\right) \beta }{\left( 1+H \alpha ^2\right) (1+H+H\beta )}}. \end{aligned}$$

Furthermore, suppose that $\alpha ^2\ne \beta$, then with simple computations it follows that

$$\begin{aligned} \bigg (\frac{d|\rho _{1}|}{d\hat{h}}\bigg )_{\hat{h}=0}=\bigg (\frac{d|\rho _{2}|}{d\hat{h}}\bigg )_{\hat{h}=0}= \frac{\alpha ^2 \left( 1+\alpha ^2-\beta \right) }{2 \left( \alpha ^2-\beta \right) \left( 1+\left( \alpha ^2-\beta \right) \beta \right) }\ne 0. \end{aligned}$$

Moreover, we suppose that $\zeta (0)\ne 0$ and $\zeta (0)\ne -1$, then it follows that

$$\begin{aligned} 2+\frac{1}{\beta -\alpha ^2 }+\frac{2+\alpha ^2-2 \beta }{\beta ^2-1-\alpha ^2\beta }\ne 0,\ \hbox {and}\,\ 3+\frac{1}{\beta -\alpha ^2 }+\frac{2+\alpha ^2-2 \beta }{\beta ^2-1-\alpha ^2\beta }\ne 0. \end{aligned}$$

(4.11)

Suppose that $(\alpha ,\beta ,h_2)\in \Psi _{NS}$ and conditions (4.11) hold true, then it follows that $\zeta (0)\ne \pm 2,0,-1$. Thus, we have $\rho _{1}^{k}, \rho _{2}^{k}\ne 1$ for all $k=1,2,3,4$ at $\hat{h}=0$. Due to these assumptions, it follows that the roots of (4.10) do not lie in the intersection of the unit circle with the coordinate axes when $\hat{h}=0$. Suppose that $\varepsilon$ and $\xi$ denote real and imaginary parts of $\rho _2$ at $\hat{h}=0$, respectively, then we have

$$\begin{aligned} \varepsilon :=\frac{1}{2} \left( 2+\frac{1}{\beta -\alpha ^2}+\frac{2+\alpha ^2-2 \beta }{\beta ^2-1-\alpha ^2 \beta }\right) , \end{aligned}$$

and

$$\begin{aligned} \xi :=\frac{\left( 1+\alpha ^2-\beta \right) \sqrt{\alpha ^4 (1-4 \beta ) +2\alpha ^2 \left( 4 \beta ^2-1-\beta \right) +(1-\beta )(1+\beta (3+4 \beta ))}}{2 \left( \alpha ^2-\beta \right) \left( 1+\left( \alpha ^2-\beta \right) \beta \right) }. \end{aligned}$$

Now, we consider the following transformation:

$$\begin{aligned} \left( \begin{array}{c} x \\ y \\ \end{array} \right) \rightarrow \left( \begin{array}{cc} \frac{(h_3+\hat{h}) \alpha ^2}{1+(h_3+\hat{h}) (1+\beta )} &{} 0\\ \varepsilon - \frac{1+2 (h_3+\hat{h}) \beta }{1+(h_3+\hat{h}) (1+\beta )}&{} -\xi \\ \end{array} \right) \left( \begin{array}{c} u\\ v\\ \end{array} \right) . \end{aligned}$$

(4.12)

Implementation of transformation (4.12), the normal form of (4.9) is computed as follows:

$$\begin{aligned} \left( \begin{array}{c} u \\ v \\ \end{array} \right) \rightarrow \left( \begin{array}{cc} \varepsilon &{} -\xi \\ \xi &{} \varepsilon \\ \end{array} \right) \left( \begin{array}{c} u\\ v\\ \end{array} \right) + \left( \begin{array}{c} \tilde{F}(u,v)\\ \tilde{G}(u,v)\\ \end{array} \right) , \end{aligned}$$

(4.13)

where

$$\begin{aligned} \tilde{F}(u,v)&=\frac{\beta }{\alpha ^3}x^{2}+\frac{2}{\alpha }xy+\frac{1}{\alpha ^2}x^{2}y+O((|u|+|v|)^{4}),\\ \tilde{G}(u,v)&=\left( \frac{\beta (\beta \epsilon H-2\beta H+\epsilon H+\epsilon -1)}{\alpha ^3\xi (1+H(1+\beta ))}- \frac{H\beta (\alpha ^2H-1)}{\xi \alpha (\alpha ^2H+1)^2}\right) x^{2}\\&\quad +\left( \frac{2(\beta \epsilon H-2\beta H+\epsilon H+\epsilon -1)}{\alpha \xi (1+H(1+\beta ))}+\frac{2H\alpha }{\xi (\alpha ^2 H+1)^2}\right) xy +\left( \frac{\xi (\alpha ^2 H+1)^2}{\xi (\alpha ^2 H+1)^3}\right) x^3\\&\quad +\left( \frac{\beta \epsilon H-2\beta H+\epsilon H+\epsilon -1}{\alpha ^2\xi (1+H(1+\beta ))}-\frac{H(3\alpha ^2 H-1)}{\xi (\alpha ^2 H+1)^3}\right) x^2 y +O((|u|+|v|)^{4}),\\ x&=\frac{(h_3+\hat{h}) \alpha ^2}{1+(h_3+\hat{h}) (1+\beta )} u,\ \hbox {and}\,\ y=\left( \varepsilon -\frac{1+2 (h_3+\hat{h}) \beta }{1+(h_3+\hat{h}) (1+\beta )}\right) u-\xi v. \end{aligned}$$

We compute the following Lyapunov first exponent for system (1.3) at $(u,v,\hat{h})=(0,0,0)$ as follows:

$$\begin{aligned} \mathbb {L}_2=\bigg [-Re\bigg (\frac{(1-2\rho _{1})\rho _{2}^{2}}{1-\rho _{1}}\chi _{20}\chi _{11}\bigg )- \frac{1}{2}|\chi _{11}|^{2}-|\chi _{02}|^{2}+Re(\rho _{2}\chi _{21})\bigg ], \end{aligned}$$

where

$$\begin{aligned} \chi _{20}= & {} \frac{1}{8}\left[ \tilde{F}_{uu}-\tilde{F}_{vv}+2\tilde{G }_{uv}+ i\left( \tilde{G}_{uu}-\tilde{G}_{vv}-2\tilde{F} _{uv}\right) \right] ,\\ \chi _{11}= & {} \frac{1}{4}\left[ \tilde{F}_{uu}+\tilde{F}_{vv}+ i\left( \tilde{G}_{uu}+\tilde{G}_{vv}\right) \right] ,\\ \chi _{02}= & {} \frac{1}{8}\left[ \tilde{F}_{uu}-\tilde{F}_{vv}-2\tilde{G }_{uv}+ i\left( \tilde{G}_{uu}-\tilde{G}_{vv}+2\tilde{F} _{uv}\right) \right] , \end{aligned}$$

and

$$\begin{aligned} \chi _{21}=\frac{1}{16}\left[ \tilde{F}_{uuu}+\tilde{F}_{uvv}+ \tilde{G}_{uuv}+\tilde{G}_{vvv}+ i\left( \tilde{G}_{uuu}+ \tilde{G}_{uvv}-\tilde{F}_{uuv}-\tilde{F}_{vvv}\right) \right] . \end{aligned}$$

Keeping in view aforementioned computation, we have the following result related to Hopf bifurcation for the system (1.3).

Theorem 4.2

Suppose that $\mathbb {L}_2\ne 0$ and 4.11 is satisfied, then (1.3) undergoes Hopf bifurcation at $\left( \alpha ,\frac{\beta }{\alpha }\right)$ as h varies in a small neighborhood of $h_3=\frac{\beta -1-\alpha ^2}{\alpha ^2}$. Moreover, if $\mathbb {L}_2<0$, then an attracting invariant closed curve bifurcates from $\left( \alpha ,\frac{\beta }{\alpha }\right)$ for $h>h_3$, and if $\mathbb {L}_2>0$, then a repelling invariant closed curve bifurcates from $\left( \alpha ,\frac{\beta }{\alpha }\right)$ for $h<h_3$.

5 Chaos control

In order to control chaos under the influence of flip and Hopf bifurcations one can design a controller that can modify the bifurcation properties for a given nonlinear dynamical system and in a result some desired dynamical properties can be obtained [47]. Chen and Yu [48] proposed linear time-delayed state-feedback control for chaotic systems. In [49], Abed et al. implemented non-linear state-feedback control for controlling chaos under the influence of flip bifurcation. Wen et al. [50] investigated washout-filter controller for controlling Hopf bifurcation for discrete-time systems. Luo et al. [51] proposed hybrid control methodology for controlling chaos under the influence of flip bifurcation in discrete-time systems. Ott et al. [52] introduced a feedback control method for controlling chaos in discrete-time systems and this method is known as OGY method. Pole-placement methodology was proposed by Romeiras et al. [53] (also see [54]), which may be treated as generalized OGY method.

In case of mathematical biology, bifurcations and unstable fluctuations have always been regarded as unfavorable phenomena, as they are harmful for the breeding of biological population [55]. For this reason, we modify the hybrid control strategy to control chaos under the influence of flip bifurcation and Neimark–Sacker bifurcation. The classical hybrid control strategy introduced by Luo et al. [51], in which the parameter perturbation and state feedback are combined and used to control the period-doubling bifurcations and chaos in a discrete nonlinear dynamical system [40, 56]. Moreover, in [40] the authors used hybrid control strategy for controlling Neimark–Sacker bifurcation in a discrete-time prey–predator system. For some more applications of feedback control strategies related to discrete-time models, we refer to [57,58,59,60,61,62].

In this section, a novel hybrid control strategy is introduced. Like hybrid control technique, the proposed strategy consists of feedback control and parameters perturbation. Moreover, this novel scheme is applicable for controlling chaos under the influence of both period-doubling and Neimark–Sacker bifurcations. The method works as follows. Consider an n-dimensional discrete dynamical system of the form:

$$\begin{aligned} X_{k+1}=F\left( X_k,\delta \right) , \end{aligned}$$

(5.1)

where $X_k=(x_k^{1},x_k^{2},\ldots ,x_k^{n})\in \mathbb {R}^n$ and $\delta \in \mathbb {R}$ denotes bifurcation parameter for the system (5.1). We apply both parameters perturbation and state feedback control to system (5.1) as follows:

$$\begin{aligned} X_{k+1}=D\bigg (\exp \big (-\alpha _i(x_k^{i}-x_i^*)\big )\bigg )F^{(m)}\left( X_k,\delta \right) , \end{aligned}$$

(5.2)

where $D\bigg (\exp \big (-\alpha _i(x_k^{i}-x_i^*)\big )\bigg )$ is $n\times n$ diagonal matrix with diagonal entries $\exp \big (-\alpha _i(x_k^{i}-x_i^*)\big )$, $i=1,2,\ldots ,n$, $(x_1^*,x_2^*,\ldots ,x_n^*)$ be equilibrium point of (5.1), $\alpha _1,\alpha _2,\ldots ,\alpha _n$ are control parameters and $F^{(m)}$ is mth iteration of $F(\cdot )$.

In order to implement the control strategy (5.2) to system (1.2), we take $n=2$ and $m=1$. Moreover, assume that $(x^*,y^*)=\left( \alpha ,\frac{\beta }{\alpha }\right)$ be steady-state of system (1.2) in chaotic region under the influence of flip or Hopf bifurcations. Then, related controlled system for (1.2) is written as follows:

$$\begin{aligned} x_{n+1}&=\exp \left( -a(x_n-x^*)\right) f(x_n,y_n,h),\nonumber \\ y_{n+1}&=\exp \left( -b(y_n-y^*)\right) g(x_n,y_n,h), \end{aligned}$$

(5.3)

where $f(x_n,y_n,h)=x_n+h\left( \alpha -(1+\beta )x_n+x_n^2 y_n\right)$, $g(x_n,y_n,h)=y_n+ h\left( \beta x_n-x_n^2 y_n\right)$ and $a,\ b\in \mathbb {R}$ are controlling parameters. Then, variational matrix for the controlled system (5.3) at $(x^*,y^*)=\left( \alpha ,\frac{\beta }{\alpha }\right)$ is computed as follows:

$$\begin{aligned} \left( \begin{array}{cc} 1-a \alpha +h (\beta -1) &{} h \alpha ^2 \\ -h \beta &{} 1-h \alpha ^2-\frac{b \beta }{\alpha } \end{array} \right) . \end{aligned}$$

(5.4)

Moreover, the characteristic polynomial of (5.4) is computed as follows:

$$\begin{aligned} \mathbb {T}(\lambda )&=\lambda ^2-\left( 2-a \alpha -h \left( 1+\alpha ^2-\beta \right) -\frac{b \beta }{\alpha }\right) \lambda +1-h-a \alpha -h \alpha ^2\nonumber \\&\quad +h^2 \alpha ^2+a h \alpha ^3+a b \beta +h \beta -\frac{b \beta }{\alpha }+\frac{b h \beta }{\alpha }-\frac{b h \beta ^2}{\alpha }. \end{aligned}$$

(5.5)

In this case, the curves of marginal stability are given by

$$\begin{aligned} C_1: h \alpha ^3 (h+a \alpha )+b (h+a \alpha ) \beta -b h \beta ^2= & {} 0,\\ C_2: \alpha (h+a \alpha -2)\left( h \alpha ^2-2\right) +(2 h \alpha +b (h-2+a \alpha )) \beta -b h \beta ^2= & {} 0, \end{aligned}$$

and

$$\begin{aligned}&C_3: \alpha \left( -a \alpha +h \left( -1+\alpha ^2 (-1+h+a \alpha )\right) \right) \\&\quad +\,(h \alpha +b (-1+h+a \alpha )) \beta -b h \beta ^2=0. \end{aligned}$$

Then, stable eigenvalues lie within the bounded regions in ab-plane bounded by the hyperbolic curves $C_1,C_2,C_3$ for particular parametric values. Thus instead of unique bounded region, one might obtain two possible stability regions. Moreover, the following Lemma gives conditions for local asymptotic stability of positive equilibrium $\left( \alpha ,\frac{\beta }{\alpha }\right)$ of the controlled system (5.3).

Lemma 5.1

The positive equilibrium $\left( \alpha ,\frac{\beta }{\alpha }\right)$ of the controlled system (5.3) is locally asymptotically stable, if the following condition holds true:

$$\begin{aligned}&\left| 2-a \alpha -h \left( 1+\alpha ^2-\beta \right) -\frac{b \beta }{\alpha }\right|<2-h-a \alpha -h \alpha ^2\\&\quad +\,h^2 \alpha ^2+a h \alpha ^3+a b \beta +h \beta -\frac{b \beta }{\alpha }+\frac{b h \beta }{\alpha }-\frac{b h \beta ^2}{\alpha }<2. \end{aligned}$$

Similarly, implementation of control strategy (5.2) to system (1.3) gives the following related controlled system:

$$\begin{aligned} x_{n+1}&=\exp \left( -a(x_n-x^*)\right) \left( \frac{h\alpha +x_n+h x_n^2y_n}{1+h(1+\beta )}\right) ,\nonumber \\ y_{n+1}&=\exp \left( -b(y_n-y^*)\right) \left( \frac{y_n+\beta h x_n}{1+h x_{n}^{2}}\right) , \end{aligned}$$

(5.6)

where $(x^*,y^*)=\left( \alpha ,\frac{\beta }{\alpha }\right)$. Then, variational matrix for the controlled system (5.6) at $(x^*,y^*)=\left( \alpha ,\frac{\beta }{\alpha }\right)$ is computed as follows:

$$\begin{aligned} \left( \begin{array}{cc} \frac{1+2 h \beta }{1+h+h \beta }-a \alpha &{} \frac{h \alpha ^2}{1+h (1+\beta )} \\ -\frac{h \beta }{1+h \alpha ^2}&{} \frac{1}{1+h \alpha ^2}-\frac{b \beta }{\alpha } \end{array} \right) . \end{aligned}$$

(5.7)

Moreover, the characteristic polynomial of (5.7) is computed as follows:

$$\begin{aligned} \mathbb {S}(\lambda )&=\lambda ^2+\left( a \alpha -\frac{1}{1+h \alpha ^2}+\frac{b \beta }{\alpha }-\frac{1}{1+h+h \beta }-\frac{2 h \beta }{1+h+h \beta }\right) \lambda \nonumber \\&\quad -\frac{a \alpha }{1+h \alpha ^2}+a b \beta +\frac{1}{\left( 1+h \alpha ^2\right) (1+h+h \beta )}-\frac{b \beta }{\alpha (1+h+h \beta )} \nonumber \\&\quad +\frac{2 h \beta }{\left( 1+h \alpha ^2\right) (1+h+h \beta )}-\frac{2 b h \beta ^2}{\alpha (1+h+h \beta )}+\frac{h^2 \alpha ^2 \beta }{\left( 1+h \alpha ^2\right) (1+h (1+\beta ))}.\nonumber \\ \end{aligned}$$

(5.8)

Moreover, the following Lemma gives conditions for local stability of steady-state $\left( \alpha ,\frac{\beta }{\alpha }\right)$ for the controlled system (5.6).

Lemma 5.2

The positive equilibrium $\left( \alpha ,\frac{\beta }{\alpha }\right)$ for the controlled system (5.6) is locally stable, if the following condition holds true:

$$\begin{aligned}&\left| a \alpha -\frac{1}{1+h \alpha ^2}+\frac{b \beta }{\alpha }-\frac{1}{1+h+h \beta }-\frac{2 h \beta }{1+h+h \beta }\right|<1-\frac{a \alpha }{1+h \alpha ^2}+a b \beta \\&\quad +\,\frac{1}{\left( 1+h \alpha ^2\right) (1+h+h \beta )}\\&\quad -\,\frac{b \beta }{\alpha (1+h+h \beta )}+\frac{2 h \beta }{\left( 1+h \alpha ^2\right) (1+h+h \beta )}-\frac{2 b h \beta ^2}{\alpha (1+h+h \beta )}\\&\quad +\,\frac{h^2 \alpha ^2 \beta }{\left( 1+h \alpha ^2\right) (1+h (1+\beta ))}<2. \end{aligned}$$

6 Numerical simulation and discussion

Example 6.1

First, we choose $\alpha =3.2$, $\beta =3.1$, $h\in [0.25,0.348]$ and taking initial values $(x_0,y_0)=(3.2,0.986)$, then system (1.2) undergoes flip bifurcation at (3.2, 0.96875) as h varies in a small neighborhood of $h_1=0.303724$. For $(\alpha ,\beta ,h)=(3.2,3.1,0.303724)$, the roots of (2.2) are $\lambda _1=-1$ and $\lambda _2=0.52769$. Moreover, $l_1=21.2990196$ and $l_2=-749.7017252<0$. Furthermore, bifurcation diagrams and largest Lyapunov exponents (LLE) are depicted in Fig. 1.

Fig. 1

Bifurcation diagrams and largest Lyapunov exponents for system (1.2) with $\alpha =3.2$, $\beta =3.1$, $h\in [0.25,0.348]$ and $(x_0,y_0)=(3.2,0.986)$. a Bifurcation diagram for $x_n$, b bifurcation diagram for $y_n$ and c largest Lyapunov exponents

Next, for $(\alpha ,\beta ,h)=(3.2,3.1,0.347)$ the controlled system (5.3) is rewritten as follows:

$$\begin{aligned} x_{n+1}&=\exp \left( -a(x_n-3.2)\right) \left( x_n+0.347\left( 3.2-4.1x_n+x_n^2 y_n\right) \right) ,\nonumber \\ y_{n+1}&=\exp \left( -b(y_n-0.96875)\right) \left( y_n+ 0.347\left( 3.1 x_n-x_n^2 y_n\right) \right) . \end{aligned}$$

(6.1)

The variational matrix for (6.1) is computed as follows

$$\begin{aligned} \left( \begin{array}{cc} 1.7287 -3.2 a &{} 3.55328 \\ -1.0757 &{} -2.55328-0.96875 b \end{array} \right) . \end{aligned}$$

In this case, (5.5) reduces to

$$\begin{aligned} \mathbb {T}(\lambda )=\lambda ^2+(0.825+3.2 a+0.97b)\lambda -0.592+8.171 a-1.675 b+3.1 a b. \end{aligned}$$

Stability conditions of Lemma 5.1 yield that steady-state (3.2, 0.96875) of (6.1) is locally stable if

$$\begin{aligned} -0.38<a\le -0.146,\ \frac{2.59\times 10^{23}-1.3\times 10^{24} a}{-2.73\times 10^{23}+5.047\times 10^{23} a}<b<\frac{-3.2\times 10^{24}-2.96\times 10^{25} a}{-1.84\times 10^{24}+8.076\times 10^{24} a}, \end{aligned}$$

or

$$\begin{aligned} -0.146<a<0.242,\ \frac{2.59\times 10^{23}-1.33\times 10^{24} a}{-2.73\times 10^{23}+5.047\times 10^{23} a}<b<\frac{1.08\times 10^{24}-1.29\times 10^{25} a}{-6.89\times 10^{24}+8.08\times 10^{24} a}, \end{aligned}$$

or

$$\begin{aligned} 0.84<a<1.23,\ \frac{-3.2\times 10^{24}-2.96\times 10^{25} a}{-1.84\times 10^{24}+8.08\times 10^{24} a}<b<\frac{2.59\times 10^{23}-1.33\times 10^{24} a}{-2.73\times 10^{23}+5.05\times 10^{23} a}, \end{aligned}$$

or

$$\begin{aligned} 1.23\le a<1.46,\ \frac{1.08\times 10^{24}-1.29\times 10^{25} a}{-6.89\times 10^{24}+8.08\times 10^{24} a}<b<\frac{2.59\times 10^{23}-1.3\times 10^{24} a}{-2.73\times 10^{23}+5.05\times 10^{23} a}. \end{aligned}$$

Moreover, the hyperbolic curves of marginal stability are given as

$$\begin{aligned} C_1: 1.23299 -0.705928 b+a (11.3705 +3.1 b)= & {} 0,\\ C_2: 0.416172+2.64343 b-a (4.9705 +3.1 b)= & {} 0, \end{aligned}$$

and

$$\begin{aligned} C_3: 1.59159+1.67468 b-a(8.1705 +3.1 b)=0. \end{aligned}$$

Two possible stability regions bounded by these hyperbolic curves are depicted in Fig. 2.

Fig. 2

Stability regions for the controlled system (6.1)

Fig. 3

Bifurcation diagrams and largest Lyapunov exponents for system (1.2) with $\alpha =0.5$, $\beta =1.1$, $h\in [0.4,1]$ and $(x_0,y_0)=(0.5,2.199)$. a bifurcation diagram for $x_n$, b bifurcation diagram for $y_n$ and c largest Lyapunov exponents

Fig. 4

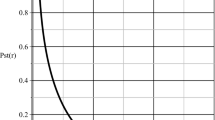
Phase portraits of (1.2) with $\alpha =0.5$, $\beta =1.1$, $h=\{0.57,0.6, 0.61,0.7\}$, $x_0=0.5,\ y_0=2.199$. a $h=0.57$, b $h=0.6$, c $h=0.61$ and d $h=0.7$

Fig. 5

Stability region for the controlled system (6.2)

Example 6.2

Next, we choose $\alpha =0.5$, $\beta =1.1$, $h\in [0.4,1]$ and $(x_0,y_0)=(0.5,2.199)$. Then system (1.2) undergoes Hopf bifurcation as h varies in a small neighborhood of $h_2=0.6$. At $(\alpha ,\beta ,h)=(0.5,1.1,0.6)$ roots of (2.2) are calculated as follows $\lambda _1=0.955-0.296606 i$ and $\lambda _2=0.955 +0.296606 i$ with absolute values 1. The bifurcation diagrams and LLE are shown in Fig. 3. Moreover, for $\alpha =0.5$, $\beta =1.1$, $h=0.57$, $h=0.6$, $h=0.61$ and $h=0.7$ phase portraits of (1.2) are shown in Fig. 4.

Next, for $(\alpha ,\beta ,h)=(0.5,1.1,0.95)$ the controlled system (5.3) is rewritten as follows:

$$\begin{aligned} x_{n+1}&=\exp \left( -a(x_n-0.5)\right) \left( x_n+0.95\left( 0.5-2.1x_n+x_n^2 y_n\right) \right) ,\nonumber \\ y_{n+1}&=\exp \left( -b(y_n-2.2)\right) \left( y_n+ 0.95\left( 1.1 x_n-x_n^2 y_n\right) \right) . \end{aligned}$$

(6.2)

The variational matrix for (6.2) is computed as follows

$$\begin{aligned} \left( \begin{array}{cc} 1.095 -0.5 a &{} 0.2375 \\ -1.045 &{} 0.7625 -2.2 b \end{array} \right) . \end{aligned}$$

In this case, (5.5) reduces to

$$\begin{aligned} \mathbb {T}(\lambda )=\lambda ^2-(1.8575-0.5 a-2.2 b)\lambda +1.08313-0.38125a-2.409b+1.1a b. \end{aligned}$$

Moreover, the hyperbolic curves of marginal stability are given as

$$\begin{aligned} C_1: 0.225625-0.209 b+a (0.11875+1.1 b)= & {} 0,\\ C_2: 3.94063 -4.609 b-a(0.88125-1.1 b)= & {} 0, \end{aligned}$$

and

$$\begin{aligned} C_3: 0.083125 -2.409 b-a(0.38125-1.1 b)=0. \end{aligned}$$

The unique stability region bounded by these hyperbolic curves is depicted in Fig. 5. In particular, if we select $b=-0.0001$, then steady-state (0.5, 2.2) of (6.2) is stable if and only if $0.218602< a< 4.4716$.

Example 6.3

Taking $\alpha =0.8$, $\beta =2.1$, $h\in [0.1,1]$ and $(x_0,y_0)=(0.8,2.6249)$, then system (1.3) undergoes Hopf bifurcation as h varies in a small neighborhood of $h_3=0.71875$. At $(\alpha ,\beta ,h)=(0.8,2.1,0.71875)$, (1.3) has steady-state (0.8, 2.625), and roots of (2.6) are computed as follows $\lambda _1=0.964925-0.262526 i$ and $\lambda _2=0.964925+0.262526 i$ with absolute values equal to 1. In this case, LLE and bifurcation diagrams are depicted in Fig. 6. Moreover, for $\alpha =0.8$, $\beta =2.1$, $h=0.71875$, $h=0.6$, $h=0.3$ and $h=0.1$ various phase portraits for (1.3) are depicted in Fig. 7.

Fig. 6

Bifurcation diagrams and largest Lyapunov exponents for system (1.3) with $\alpha =0.8$, $\beta =2.1$, $h\in [0.1,1]$ and $(x_0,y_0)=(0.8,2.6249)$. a Bifurcation diagram for $x_n$, b bifurcation diagram for $y_n$ and c largest Lyapunov exponents

Fig. 7

Phase portraits of (1.3) with $\alpha =0.8$, $\beta =2.1$, $h=\{0.71875,0.6, 0.3,0.1\}$, $x_0=0.8,\ y_0=2.6249$. a $h=0.71875$, b $h=0.6$, c $h=0.3$ and d $h=0.1$

Finally, we select $(\alpha ,\beta ,h)=(0.8,2.1,0.3)$ to see the effectiveness of newly introduced control strategy (5.6) for system (1.3). In this case, system (5.6) is written as follows:

$$\begin{aligned} x_{n+1}&=\exp \left( -a(x_n-0.8)\right) \left( \frac{0.24+x_n+0.3 x_n^2y_n}{1.93}\right) ,\nonumber \\ y_{n+1}&=\exp \left( -b(y_n-2.625)\right) \left( \frac{y_n+0.63 x_n}{1+0.3 x_{n}^{2}}\right) . \end{aligned}$$

(6.3)

The variational matrix for (6.3) is computed as follows

$$\begin{aligned} \left( \begin{array}{cc} 1.17098 -0.8 a &{} 0.0994819 \\ -0.528523 &{} 0.838926 -2.625 b \end{array} \right) . \end{aligned}$$

In this case, (5.8) reduces to

$$\begin{aligned} \mathbb {S}(\lambda )= & {} \lambda ^2-(2.00991-0.8 a-2.625 b)\lambda +1.03494-0.671141a\\&-\,3.07382b+2.1a b. \end{aligned}$$

Moreover, the hyperbolic curves of marginal stability are given as

$$\begin{aligned} C_1: 0.0250381-0.448822 b+a (0.128859+2.1 b)= & {} 0,\\ C_2: 4.04485-5.69882 b-a (1.47114-2.1 b)= & {} 0, \end{aligned}$$

and

$$\begin{aligned} C_3: 0.0349442-3.07382 b-a (0.671141-2.1 b)=0. \end{aligned}$$

The unique stability region bounded by these hyperbolic curves is depicted in Fig. 8.

Fig. 8

Stability region for the controlled system (6.3)

7 Concluding remarks

We have investigated the dynamical behavior related to discrete-time Brusselator models (1.2) and (1.3). A dynamically consistent nonstandard difference scheme is implemented in order to obtain model (1.3). Bifurcation theory related to normal forms is implemented for investigation of Hopf bifurcation for both models. Moreover, it is proved that system (1.2) undergoes flip bifurcation. A novel chaos control strategy (5.2) is presented for controlling flip and Hopf bifurcations. In order to show effectiveness of proposed chaos control scheme, a comparison with existing chaos control techniques is presented as follows. For this, first we compare it with OGY method [52]. In order to apply OGY method to (1.2), we take $(\alpha ,\beta ,h)=(0.5,1.1,0.95)$. In this case, the control system via OGY method is written as follows:

$$\begin{aligned} x_{n+1}&=x_n+\left( 0.95-k_1(x_n-0.5)-k_2(y_n-2.2)\right) \left( 0.5-2.1x_n+x_n^2 y_n\right) ,\nonumber \\ y_{n+1}&=y_n+ \left( 0.95-k_1(x_n-0.5)-k_2(y_n-2.2)\right) \left( 1.1 x_n-x_n^2 y_n\right) , \end{aligned}$$

(7.1)

where $k_1$ and $k_2$ represent control parameters. The variational matrix for (7.1) at (0.5, 2.2) is computed as follows:

$$\begin{aligned} J(0.5,2.2)=\left( \begin{array}{cc} 1.095 &{} 0.2375 \\ -1.045 &{} 0.7625 \end{array} \right) . \end{aligned}$$

Moreover, regulator poles [63] for J(0.5, 2.2) are given by $0.92875\pm 0.469626 i$ with absolute value $1.04073>1$. Thus OGY method fails to control chaos under the influence of Hopf bifurcation in system (1.2).

Next, for same parametric values, an application of hybrid control method [51] yields the following control system:

$$\begin{aligned} x_{n+1}&=A\left( x_n+\left( 0.5-2.1x_n+x_n^2 y_n\right) \right) +(1-A)x_n,\nonumber \\ y_{n+1}&=A\left( y_n+ \left( 1.1 x_n-x_n^2 y_n\right) \right) +(1-A)y_n, \end{aligned}$$

(7.2)

where $0<A<1$ denotes control parameter. The variational matrix for (7.2) at (0.5, 2.2) is computed as follows:

$$\begin{aligned} V(0.5,2.2)=\left( \begin{array}{cc} 1+0.095 A &{} 0.2375 A \\ -1.045 A &{} 1-0.2375 A \end{array} \right) . \end{aligned}$$

The characteristic polynomial for V(0.5, 2.2) is computed as follows:

$$\begin{aligned} P(\lambda )=\lambda ^2-\left( 2-0.1425 A\right) \lambda +1-0.1425 A+0.225625 A^2. \end{aligned}$$

The roots $P(\lambda )$ have absolute values less than unity if and only if $0< A < 0.631579$. Thus hybrid control strategy can control chaos in open interval $\bigg ]0,0.631579\bigg [$ only. Whereas in Example 6.2, newly proposed control strategy (5.2) implemented to (1.2) for the same parametric values and stability region is depicted in Fig. 5. Therefore, the proposed chaos control method is for better than both existing techniques and applicable to larger class of discrete-time models.