Abstract
Let R be a commutative ring with unity, M be a unitary R-module and G a finite abelian group (viewed as a \({\mathbb {Z}}\)-module). The main objective of this paper is to study properties of mod-annihilators of M. For \(x \in M\), we study the ideals \([x : M] =\{r\in R ~|~ rM\subseteq Rx\}\) of R corresponding to mod-annihilator of M. We investigate as when [x : M] is an essential ideal of R. We prove that the arbitrary intersection of essential ideals represented by mod-annihilators is an essential ideal. We observe that [x : M] is injective if and only if R is non-singular and the radical of R/[x : M] is zero. Moreover, if essential socle of M is non-zero, then we show that [x : M] is the intersection of maximal ideals and \([x : M]^2 = [x : M]\). Finally, we discuss the correspondence of essential ideals of R and vertices of the annihilating graphs realized by M over R.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A nonzero ideal in a commutative ring is called essential if it intersects with every other nonzero ideal nontrivially. The study of essential ideals in a ring R is a classical problem. For instance, Green and Van Wyk in [8] characterized essential ideals in certain classes of commutative and non-commutative rings. The authors in [5, 12] studied essential ideals in C(X), where C(X) denotes the set of continuous functions on X. They topologically characterized the scole and essential ideals. Moreover, essential ideals have been investigated in rings of measurable functions [14] and \(C^{*}\)-algebras [11]. For more on essential ideals, see [4, 9, 10, 21].
Throughout, R is a commutative ring (with \(1 \ne 0\)) and all modules are unitary unless otherwise stated. \([N : M] = \{r\in R~ |~ rM \subseteq N\}\) denotes an ideal of R. The symbols \(\subseteq \) and \(\subset \) have usual set theoretic meaning as containment and proper containment. We will denote the ring of integers by \({\mathbb {Z}}\), positive integers by \({\mathbb {N}}\) and the ring of integers modulo n by \({\mathbb {Z}}_n\). For basic definitions from ring and module theory we refer to [7, 25].
For a R-module M and \(x\in M\), set \([x : M] =\{r\in R ~|~ rM\subseteq Rx\}\), which clearly is an ideal of R and an annihilator of the factor module M/Rx, whereas the annihilator of M denoted by ann(M) is [0 : M].
Recently in [17], the elements of a module M have been classified into full-annihilators, semi-annihilators and star-annihilators. We recall a definition concerning full-annihilators, semi-annihilators and star-annihilators of a module M.
Definition 1.1
An element \(x\in M\) is a
-
(i)
full-annihilator, if either \(x = 0\) or \([x : M][y : M]M = 0\), for some nonzero \(y\in M\) with \([y : M] \ne R\),
-
(ii)
semi-annihilator, if either \(x = 0\) or \([x : M] \ne 0\) and \([x : M][y : M]M = 0\), for some nonzero \(y\in M\) with \( 0 \ne [y : M] \ne R\),
-
(iii)
star-annihilator, if either \(x = 0\) or \(ann(M) \subset [x : M]\) and \([x : M][y : M]M = 0\), for some nonzero \(y\in M\) with \(ann(M) \subset [y : M] \ne R\).
We denote by \(A_f(M)\), \(A_s(M)\) and \(A_t(M)\), respectively, the sets of full-annihilators, semi-annihilators and star-annihilators for any module M over R and call these annihilators as mod-annihilators. We set \(\widehat{A_{f}(M)} = A_f(M){/} \{0\}\), \(\widehat{A_{s}(M)} = A_s(M){/} \{0\}\) and \(\widehat{A_t(M)} = A_t(M){/} \{0\}\).
This paper is organized as follows. In Sect. 2, we study the correspondence of essential ideals in R and submodules of M represented by mod-annihilators. For some finite abelian group G (viewed as a \({\mathbb {Z}}\)-module), we determine the value of n such that \([x : G] = n{\mathbb {Z}}\), where \(x \in G\). We characterize all \({\mathbb {Z}}\)-module M such that [x : M] is an essential ideal of R. Furthermore, we discuss when [x : M] as a R-module is injective. Also, if essential socle of M is non-zero, then we prove that [x : M] is the intersection of maximal ideals and \([x : M]^2 = [x : M]\). In Sect. 3, we discuss the correspondence of essential ideals of R and the vertices of the annihilating graphs realized by modules over commutative rings. We conclude this paper with a discussion on some problems in this area of research.
2 Essential ideals represented by mod-annihilators
In this section, we discuss the correspondence of essential ideals in R represented by elements of \(\widehat{A_{f}(M)}\), and submodules of M generated by elements of \(\widehat{A_{f}(M)}\). We characterize essential ideals corresponding to \({\mathbb {Z}}\)-modules. We discuss the cases of finite abelian groups where essential ideals which are represented by elements of \(\widehat{A_{f}(M)}\) corresponding to submodules of M are isomorphic. If M is a non-simple R-module, then for \(x\in \widehat{A_{f}(M)}\), we show that an ideal [x : M] considered as an R-module is injective. We also study essential ideals represented by mod-annihilators over hereditary and regular rings.
By Definition 1.1, we see that there is a correspondence of ideals in R represented by elements of \(\widehat{A_{f}(M)}\), \(\widehat{A_{s}(M)}\), and \(\widehat{A_{t}(M)}\) and cyclic submodules of M generated by elements of sets \(\widehat{A_{f}(M)}\), \(\widehat{A_{s}(M)}\), and \(\widehat{A_{t}(M)}\). Furthermore, the containment \(A_t(M) \subseteq A_s(M) \subseteq A_f(M)\) is clear, so our main emphasis is on the set \(\widehat{A_{f}(M)}\). However, one can study these sets separately for any module M.
Let \(\lambda = (\lambda _1, \lambda _2, \ldots , \lambda _r)\) be a partition of n denoted by \(\lambda \vdash n\). For any \(\mu \vdash n\), we have an abelian group of order \(p^n\) and conversely every abelian group corresponds to some partition of n. In fact, if \(H_{\mu , p} = {\mathbb {Z}}/p^{{\mu }_1}{\mathbb {Z}} ~\oplus ~ {\mathbb {Z}}/p^{{\mu }_2}{\mathbb {Z}} ~\oplus ~ \cdots ~\oplus ~ {\mathbb {Z}}/p^{{\mu }_r}{\mathbb {Z}}\) is a subgroup of \(G_{\lambda , p} = {\mathbb {Z}}/p^{\lambda _1}{\mathbb {Z}} \oplus {\mathbb {Z}}/p^{\lambda _2}{\mathbb {Z}} \oplus \cdots \oplus {\mathbb {Z}}/p^{\lambda _r}{\mathbb {Z}}\), then \(\mu _1 \le \lambda _1, \mu _2 \le \lambda _2, \ldots , \mu _r \le \lambda _r\). If these inequalities hold, we write \(\mu \subset \lambda \), that is a “containment order”on partitions. For example, a p-group \({\mathbb {Z}}/p^{5}{\mathbb {Z}} ~\oplus ~ {\mathbb {Z}}/p{\mathbb {Z}} ~\oplus ~ {\mathbb {Z}}/p{\mathbb {Z}}\) is of type \(\lambda = (5, 1, 1)\). The possible types for its subgroup are \((5, 1, 1), (4, 1, 1), (3, 1, 1), (2, 1, 1), (1, 1, 1), 2(5, 1), 2(4, 1), 2(3,1), 2(2, 1), 2(1, 1), (5), (4), (3), (2), 2 (1)\). Note that the types (5, 1), (4, 1), (3, 1), (2, 1), (1, 1) are appearing twice in the sequence of partitions for a subgroup.
Let \(\lambda = (1, 1, \ldots , 1) = (1^n)\). A group of type \(\lambda \) is nothing but the \({\mathbb {Z}}/p{\mathbb {Z}}\)-vector space \({\mathbb {Z}}/p{\mathbb {Z}} \oplus {\mathbb {Z}}/p{\mathbb {Z}} \oplus \cdots \oplus {\mathbb {Z}}/p{\mathbb {Z}}\). Its subgroups are of type \((1^r )\), where \(0\le r \le n\). The essential ideals corresponding to subspaces of vector space \({\mathbb {Z}}/p{\mathbb {Z}}\oplus {\mathbb {Z}}/p{\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}/p{\mathbb {Z}}\) (represented by elements of the set \(A_f({\mathbb {Z}}/p{\mathbb {Z}}\oplus {\mathbb {Z}}/p{\mathbb {Z}} \oplus \cdots \oplus {\mathbb {Z}}/p{\mathbb {Z}})\) are same. In fact, \([x : {\mathbb {Z}}/p{\mathbb {Z}}\oplus {\mathbb {Z}}/p{\mathbb {Z}}~\oplus ~ \cdots ~\oplus ~ {\mathbb {Z}}/p{\mathbb {Z}}] = ann({\mathbb {Z}}/p{\mathbb {Z}}\oplus {\mathbb {Z}}/p{\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}/p{\mathbb {Z}}) = p{\mathbb {Z}}\).
More generally, for a finite abelain p-group of the type \({\mathbb {Z}}/p^{\alpha }{\mathbb {Z}}\oplus {\mathbb {Z}}/p^{\alpha }{\mathbb {Z}} \cdots \oplus {\mathbb {Z}}/p^{\alpha }{\mathbb {Z}}\), where \(\alpha \ge 2\), the essential ideals represented by elements of the set \(A_f({\mathbb {Z}}/p^{\alpha }{\mathbb {Z}}\oplus {\mathbb {Z}}/p^{\alpha }{\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}/p^{\alpha }{\mathbb {Z}}) = p^{\alpha }{\mathbb {Z}}\).
A finite abelian p-group is isomorphic to the group of the form \({\mathbb {Z}}/p^{\alpha _1}{\mathbb {Z}}\oplus {\mathbb {Z}}/p^{\alpha _2}{\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}/p^{\alpha _n}{\mathbb {Z}}\) whereas a finitely generated abelian p-group with Betti number n is of the from \({\mathbb {Z}}/p^{\alpha _1}{\mathbb {Z}}\oplus {\mathbb {Z}}/p^{\alpha _2}{\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}/p^{\alpha _n}{\mathbb {Z}} \oplus {\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}\). It is very difficult to determine the exact ideals represented by mod-annihilators of sets \(A_f({\mathbb {Z}}/p^{\alpha _1}{\mathbb {Z}}\oplus {\mathbb {Z}}/p^{\alpha _2}{\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}/p^{\alpha _n}{\mathbb {Z}})\) and \(A_f({\mathbb {Z}}/p^{\alpha _1}{\mathbb {Z}}\oplus {\mathbb {Z}}/p^{\alpha _2}{\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}/p^{\alpha _n}{\mathbb {Z}} \oplus {\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}})\). However, it is clear from the definition of mod-annihilators that for some \(x \in A_f({\mathbb {Z}}/p^{\alpha _1}{\mathbb {Z}}\oplus {\mathbb {Z}}/p^{\alpha _2}{\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}/p^{\alpha _n}{\mathbb {Z}} \oplus {\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}})\), delete \([x : {\mathbb {Z}}/p^{\alpha _1}{\mathbb {Z}}\oplus {\mathbb {Z}}/p^{\alpha _2}{\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}/p^{\alpha _n}{\mathbb {Z}} \oplus {\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}]\) is some ideal in \({\mathbb {Z}}\).
Using the description given above, we now characterize all essential ideals represented by elements of \(\widehat{A_f(M)}\) and corresponding to \({\mathbb {Z}}\)-modules.
Lemma 2.1
If M is any \({\mathbb {Z}}\)-module, then [x : M] is an essential ideal if and only if [x : M] is non-zero for all \(x\in \widehat{A_f(M)}\).
Proof
Let M be a \({\mathbb {Z}}\)-module. Clearly, M is an abelian group in a unique way. For all \(x\in \widehat{A_f(M)}\), we have \([x : M] = n{\mathbb {Z}}\), \(n\in {\mathbb {N}}\). The ideal \(n{\mathbb {Z}}\) intersects non-trivially with any ideal \(m{\mathbb {Z}}\), \(m\in {\mathbb {N}}\) in \({\mathbb {Z}}\). So, if M is a non-simple \({\mathbb {Z}}\)-module, then for every \(x\in M\), it follows that [x : M] is an essential ideal. Note that M is simple if and only if \(\widehat{A_f(G)} = \emptyset \).
If possible, suppose \([x : M] = \{0\}\), then [x : M] does not intersect non-trivially with non-trivial ideals of \({\mathbb {Z}}\), a contradiction.\(\square \)
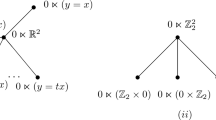
Since it is possible to have some finitely generated \({\mathbb {Z}}\)-modules such that the set of mod-annihilators is equal to zero only which of course by definition is not an essential ideal. Consider a \({\mathbb {Z}}\)-module \(M = {\mathbb {Z}}\oplus {\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}\), which is a direct sum of n copies of \({\mathbb {Z}}\). It is easy to verify that \(\widehat{A_f(M)} = {\widehat{M}}\) with \([x : M][y : M]M = 0 \) for all \(x, y\in M\). The cyclic submodules generated by elements of \(\widehat{A_f(M)}\) are simply lines with integral coordinates passing through the origin in the hyperplane \({\mathbb {R}}\oplus {\mathbb {R}}\oplus \cdots \oplus {\mathbb {R}}\) and these lines intersect at the origin only. Thus, for each \(x \in M\), it follows that [x : M] is not an essential ideal in \({\mathbb {Z}}\). In fact [x : M] is a zero-ideal in \({\mathbb {Z}}\).
For any R-module M and \(x\in \widehat{A_f(M)}\), it would be interesting to characterize essential ideals [x : M] represented by elements of \(\widehat{A_f(M)}\) such that the intersection of all essential ideals is again an essential ideal. It is easy to see that a finite intersection of essential ideals in any commutative ring is an essential ideal. But an infinite intersection of essential ideals need not to be an essential ideal, even a countable intersection of essential ideals in general is not an essential ideal, as can be seen in [5]. If the cardinality of M is finite over R, then the submodules determined by elements of \(\widehat{A_f(M)}\) are finite and therefore the ideals corresponding to submodules are finite in number. Thus, we conclude that for every \(x\in \widehat{A_f(M)}\), the intersection of essential ideals [x : M] in R is an essential ideal. For the other case, that is, if the cardinality of M is infinite over R, we have the following result. Note that, a nonzero submodule of a module M is said to be an essential submodule of M if it intersects non-trivially with other nonzero submodules of M.
Theorem 2.2
Let M be an R-module such that every proper submodule of M is cyclic over R. For \(x\in \widehat{A_f(M)}\), if the submodule generated by x intersects non-trivially with every other nonzero submodule of M, then [x : M] is an essential ideal in R.
Proof
Assume that \(\bigcap \nolimits _{0\ne x\in M} Rx \ne 0\). If \(\widehat{A_f(M)} = \phi \), then M is simple, a contradiction. Let \(x\in \widehat{A_f(M)}\) and let Rx be the submodule generated by x. Since Rx intersects non-trivially with every other submodule, so there exists \(y\in \widehat{A_f(M)}\) such that \(Rx \cap Ry \ne 0\). It suffices to prove the result for \(Rx \cap Ry\). Let \(z\in Rx \cap Ry\) and let [x : M], [y : M], [z : M] be ideals of R corresponding to submodules Rx, Ry and Rz. Then \([z : M]\subseteq [x : M]\cap [y: M] \ne 0\), which implies [x : M] intersects non-trivially with every nonzero ideal corresponding to the submodule generated by an element of \(\widehat{A_f(M)}\). For any other ideal I of R, it is clear that \(IM = \{\sum \nolimits _{finite}am : a\in I, ~m\in M\} = Ra\) for some \(a\in M\). Thus I corresponds to the cyclic submodule generated by \(a\in M\). It follows that \([x : M]\cap I \ne 0\), for every nonzero ideal of R and we conclude that [x : M] is an essential ideal for each \(x\in \widehat{A_f(M)}\).\(\square \)
The converse of Theorem 2.2 is not true in general. We can easily construct examples from \({\mathbb {Z}}\)-modules such that an ideal corresponding to the submodule generated by some element of \(\widehat{A_f(M)}\) is an essential ideal, but the intersection of all submodules determined by elements of \(\widehat{A_f(M)}\) is empty. However, if every ideal [x : M], where \(x\in \widehat{A_f(M)}\), corresponds to an essential submodule of M, then we have a non-zero intersection.
Corollary 2.3
Let M be an R-module.
-
(i)
For \(x\in \widehat{A_f(M)}\), if the cyclic submodule Rx intersects with every other cyclic nonzero submodule of M non-trivially, then [x : M] is an essential ideal in R.
-
(ii)
The intersection \(\bigcap \nolimits _{x\in \widehat{A_f(M)}}[x : M]\) is an essential ideal in R if and only if every submodule of M is essentially cyclic over R.
In the preceding results, we proved that “arbitrary intersection of essentials ideals is an essential ideal”. We formulated this theory of essential ideals using the concept of mod-annihilators and mainly the theory involves study of cyclic submodules of M. It is interesting to develop a similar theory that would employ the other finitely generated submodules of M. So, motivated by [5], we have the following question regarding essential ideals represented by elements of \(\widehat{A_f(M_N)}\), where \(\widehat{A_f(M_N)} = \{r\in R ~|~ rM\subseteq N\}\), N is a finitely generated submodule of M.
Problem 2.4
Let M be an R-module. For \(x\in \widehat{A_f(M_N)}\), characterize essential ideals [x : M] in R such that their intersection is an essential ideal.
For an R-module M, let Z(M) denote the following.
If \(Z(M) = M\), then M is said to be singular and if \(Z(M) = 0\), then M is said to be non-singular. By rad(M), we denote the intersection of all maximal submodules of M. So, rad(R) is the Jacobson radical J(R) of a ring R. The socle of an R-module M denoted by Soc(M) is the sum of simple submodules or equivalently the intersection of all essential submodules. To say that Soc(M) is an essential socle is equivalent to saying that every cyclic submodule of M contains a simple submodule of M. An essential socle of M is denoted by essoc(M).
Lemma 2.5
Let M be an R-module with \(essoc(M)\ne 0\), \(\bigcap \nolimits _{0\ne x\in M} Rx \ne 0\). Then for \(x\in \widehat{A_f(M)}\), R/[x : M] is a singular module.
Proof
Since \(\bigcap \nolimits _{0\ne x\in M} Rx \ne 0\) and \(essoc(M)\ne 0\), therefore, \(\widehat{A_f(M)} \ne \emptyset \). Thus, [x : M] is an essential ideal. Moreover, \(Z\big (R/[x : M]\big ) = R/[x : M]\). Therefore, R/[x : M] is a singular module.\(\square \)
A ring R is said to be a regular ring if for all \(a \in R\), \(a^2x = a\) for some \(x\in R\).
Lemma 2.6
[24] A commutative ring R with unity is regular if and only if every simple R-module is injective.
Now, we consider singular simple R-modules (ideals) which are injective, and obtain some properties of essential ideals corresponding to submodules generated by elements of \(\widehat{A_f(M)}\).
Theorem 2.7
Let M be an R-module with \(essoc(M)\ne 0\) and \(\bigcap \nolimits _{0 \ne x\in M} Rx \ne 0\). Then every singular simple R-module [x : M], \(x\in \widehat{A_f(M)}\) is injective if and only if \(Z(R) = 0\) and \(rad(R/[x : M]) = 0\).
Proof
We have \(essoc(M)\ne 0\) and \(\bigcap \nolimits _{0\ne x\in M} Rx \ne 0\), so that \(\widehat{A_f(M)} \ne \emptyset \). Therefore corresponding to every cyclic submodule generated by elements of \(\widehat{A_f(M)}\), we have an ideal in R. For \(x\in \widehat{A_f(M)}\), suppose all singular simple R-modules [x : M] are injective. If for some \(z\in \widehat{A_f(M)}\), \(I = [z : M]\subseteq Z(R)\) is a simple R-module, then \(Z(I) = I\). This implies that I is injective and thus a direct summand of R. However, the set Z(R) is free from nonzero idempotent elements. Therefore, \(I = 0\) and so \(Z(R) = 0\). For \(x\in \widehat{A_f(M)}\), clearly \(A = [x : M]\) is an essential ideal of R. Thus, by Lemma 2.5, R/A is a singular module and so is every submodule of R/A. Therefore every simple submodule of R/A is injective, which implies that every simple submodule is excluded by some maximal submodule. Thus we conclude that \(rad(R/A) = 0\).
For the converse, we again consider the correspondence of cyclic submodules of M and ideals of R. Let \({\tilde{I}}\) be a singular simple R-module corresponding to the submodule of M. In order to show that \({\tilde{I}}\) is injective, we must show that for every essential ideal A in R corresponding to the submodule determined by an element \(x\in \widehat{A_f(M)}\), every \(\varphi \in Hom_R(A, {\tilde{I}})\) has a lift \(\psi \in Hom_R(R, {\tilde{I}})\) such that the following diagram commutes.

Let \(K = ker(\varphi )\). We claim that K is an essential ideal of R. For, if \(K \cap J = \{0\}\), for some nonzero ideal J of R, then \(I^{*} = J \cap A \ne 0\) and \(I^{*} \cap K = \{0\}\). This implies that \(I^{*}\subseteq \varphi (I^{*}) \subseteq {\tilde{I}}\), a contradiction, since \({\tilde{I}}\) is a singular simple submodule and \(Z(R) = 0\). For \(\mu \ne 0\), it is clear that \(\varphi \) induces an isomorphism \(\mu : A/K \longrightarrow {\tilde{I}}\). So, A/K is a simple R-submodule of R/K. By our assumption, \(rad(R/K) = 0\), so there is a maximal submodule M/K such that \(R/K = A/K \oplus M/K\). Let \(g : R \longrightarrow R/K\) be a canonical map and let \(p : R/K \longrightarrow A/K\) be a projection map. Then, we have \(pg : R \longrightarrow A/K\). Therefore the composition \(\psi = \mu pg : R \longrightarrow {\tilde{I}}\) is the required lift such that the above diagram commutes.\(\square \)
Now, we discuss some interesting consequences of the preceding theorem.
Theorem 2.8
Let M be an R-module with \(essoc(M)\ne 0\), \(\bigcap \nolimits _{0\ne x\in M} Rx \ne 0\) and for \(x\in \widehat{A_f(M)}\), let every singular simple R-module [x : M] be injective. Then every ideal [x : M] is an intersection of maximal ideals, \(J(R)^{2} = 0\) and \([x : M]^{2} = [x : M]\).
Proof
For any \(x\in \widehat{A_f(M)}\), clearly [x : M] is an essential ideal in R. Therefore, \(J(R) \subseteq [x : M]\), since J(R) is contained in every essential ideal of R. On the other hand, intersection of all essential ideals in R is Socle of R, therefore \(J(R) \subseteq Soc(R)\). This implies that \(J(R)^{2} = 0\) and [x : M] is the intersection of maximal ideals in R. Suppose that \([x : M]^{2} \ne [x : M]\), for an essential ideal [x : M] of R. By Theorem 2.7, \(Z(R) = 0\) and therefore for every essential ideal I, we have \(I \subseteq I^2\). In particular, \([x : M] \subseteq [x : M]^2\) for each \(x\in \widehat{A_f(M)}\). It follows that \([x : M]^2\) is an essential ideal and is the intersection of maximal ideals in R. Finally, if \(y\in [x : M]^2\), \(y\notin [x : M]\), there is some maximal ideal P of R such that \([x : M] \subseteq P\), \(y\notin P\). Then \(R = Ry + P\), that is, \(1 = ry + m\). This implies that \(y = yry + ym\in P\), a contradiction. Hence we conclude that \([x : M]^{2} = [x : M]\).\(\square \)
Corollary 2.9
Let M be an R-module, where R is hereditary. For \(x\in \widehat{A_f(M)}\), if [x : M] is an essential ideal of R and \(J(R)^2 = 0\), then every singular simple R-module [x : M] is injective.
Proof
Let R be hereditary. From [7], the exact sequence
splits for any \(x\in R\). Since \(J(R)^{2} = 0\) and R/J(R) is an artinian ring, therefore \(J(R) \subseteq Soc(R)\). But any essential ideal of R contains Soc(R). So, \(J(R) \subseteq [x : M]\). This implies that R/[x : M] is a completely reducible R-module and therefore \(rad(R/[x : M]) = 0\). Thus, by Theorem 2.7, every singular simple R-module [x : M] is injective.\(\square \)
Next, we consider the modules over regular rings.
Theorem 2.10
Let M be an R-module such that every submodule of M is cyclic over R and \(\bigcap \nolimits _{0\ne x\in M} Rx \ne 0\). The following are equivalent.
-
(i)
R is regular.
-
(ii)
\(A^2 = A\) for each ideal A of R.
-
(iii)
\([x : M]^{2} = [x : M]\) for each \(x\in \widehat{A_f(M)}\).
Proof
The equivalence of (i) and (ii) is clear and certainly (ii) implies (iii). Thus, we just need to show that (iii) implies (ii). By Theorem 2.7, [x : M] is an essential ideal for each \(x\in \widehat{A_f(M)}\). Suppose that \([x : M]^{2} = [x : M]\). Choose J to be maximal ideal of R such that \(A\cap J = 0\), where A is some non essential ideal of R. Then \(A + J\) is an essential ideal of R. Therefore, again by Theorem 2.7, \(A + J\) corresponds to some submodule of M and we have \(A + J = [z : M]\) for some \(z\in M\). So, \((A + J)^2 = A^2 + J^2 = A + J\). If \(x \in A\), then \(x = \sum \nolimits _{finite}ab ~+ \sum \nolimits _{finite}mn\), where \(a, b\in A\) and \(m, n\in J\). Therefore,
This implies that \(x\in A^2\) and we conclude that \(A = A^2\).\(\square \)
Corollary 2.11
Let M be an R-module with \(essoc(M)\ne 0\) and \(\bigcap \nolimits _{x\in M} Rx \ne 0\). Then every singular simple R-module [x : M], where \(x\in \widehat{A_f(M)}\), is injective if and only if R is regular.
Proof
By Theorem 2.8, if every singular simple R-module [x : M] is injective, then for \(x\in \widehat{A_f(M)}\), we have \([x : M]^{2} = [x : M]\). Therefore, by Theorem 2.10, R is regular. If R is regular, then by Lemma 2.6 every simple R-module is injective.\(\square \)
3 Representation of essential ideals by vertices of annihilating graphs
In this section, we give a brief discussion on representation of essential ideals by vertices of graphs realized by modules over commutative rings.
A simple graph \(\Gamma \) consists of a vertex set \(V(\Gamma )\) and an edge set \(E(\Gamma )\), where an edge is an unordered pair of distinct vertices of \(\Gamma \). One of the areas in algebraic combinatorics introduced by Beck [6] is to study the interplay between graph theoretical and algebraic properties of an algebraic structure. Continuing the concept of associating a graph to an algebraic structure, another combinatorial approach of studying commutative rings was given by Anderson and Livingston in [2]. They associated a simple graph to a commutative ring R with unity called the zero-divisor graph denoted by \(\Gamma (R)\) with vertex set \(Z^{*}(R) = Z(R){/} \{0\}\), where two distinct vertices \(x,~ y\in Z^{*}(R)\) are adjacent in \(\Gamma (R)\) if and only if \(xy = 0\). The study of graph theoretical parameters and spectral properties in zero-divisor graphs of commutative rings are explored in [1,2,3, 15, 16, 18, 20, 22]. In [2, 18], authors have discussed chromatic number, clique number and metric dimensions of zero-divisor graphs associated with finite commutative rings whereas [16, 22] are related to eigenvalues and Laplacian eigenvalues of zero-divisor graphs associated to finite commutative rings of type \({\mathbb {Z}}_n\) for \(n = p^{N_1}q^{N_2}\), where \(p < q\) are primes and \(N_1, N_2\) are positive integers. The extension of zero-divisor graphs to non-commutative rings and semigroups can be found in [13, 23].
The combinatorial properties of zero-divisors discovered in [6] have also been investigated in module theory. In [17], the authors introduced annihilating graphs realized by modules over commutative rings known as full-annihilating, semi-annihilating and star-annihilating graphs, denoted by \(ann_f(\Gamma (M))\), \(ann_s(\Gamma (M))\) and \(ann_t(\Gamma (M))\). The vertices of annihilating graphs are elements of sets \(\widehat{A_{f}(M)}\), \(\widehat{A_{s}(M)}\) and \(\widehat{A_{t}(M)}\) respectively, where two vertices x and y are adjacent if and only if \([x : M][y : M]M = 0\). The three simple graphs: full-annihilating, semi-annihilating and star-annihilating with vertex sets: \(\widehat{A_f(M)}, \widehat{A_s(M)}, \widehat{A_t(M)}\) are natural generalizations of the zero-divisor graph introduced in [2]. This concept was further studied in [19].
We call a vertex x, an essential vertex in \(ann_f(\Gamma (M))\) if the ideal represented by x is essential in R. Recall that a graph \(\Gamma \) is said to be a complete if there is an edge between every pair of distinct vertices.
By Definition 1.1, we see the containment \(ann_t(\Gamma (M)) \subseteq ann_s(\Gamma (M)) \subseteq ann_f(\Gamma (M))\) as induced subgraphs of the graph \(ann_f(\Gamma (M))\), since \(A_t(M) \subseteq A_s(M) \subseteq A_f(M)\). If \(ann_f(\Gamma (M))\) is a finite graph, then by [17, Theorem 3.3 and Example 2.2], \(|\widehat{A_{f}(M)}| = |\widehat{A_{s}(M)}|\) and annihilating graphs \(ann_f(\Gamma (M))\), \(ann_s(\Gamma (M))\) coincide, whereas the graph \(ann_t(\Gamma (M))\) with vertex set \(\widehat{A_{t}(M)}\) may be different. For a \({\mathbb {Z}}\)-module \(M = {\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}\), we have by Definition 1.1\([x : M][y : M]M = 0\) for all \(x, y\in \widehat{A_f(M)}\). Therefore \(ann_f(\Gamma (M))\) is a complete graph whereas the graph \(ann_s(\Gamma (M))\) is an empty graph. Thus for finitely generated infinite modules, graphs \(ann_f(\Gamma (M))\) and \(ann_s(\Gamma (M))\) are different.
As discussed in Sect. 2, for a module \(M = {\mathbb {Z}}\oplus \cdots \oplus {\mathbb {Z}}\), the ideal [x : M] represented by a vertex \(x\in \widehat{A_f(M)}\) of the graph \(ann_f(\Gamma (M))\) is not an essential ideal. So, x is not an essential vertex of the graph \(ann_f(\Gamma (M))\). On the other hand, every vertex of a \({\mathbb {Z}}\)-module \({\mathbb {Z}}_p \oplus {\mathbb {Z}}_q\) is an essential vertex of the graph \(ann_f(\Gamma ({\mathbb {Z}}_p \oplus {\mathbb {Z}}_q))\), where p and q are any two primes.
Finally, Problem 2.4 can be restated in the graph theoretical version as follows.
Problem 3.1
Characterize all annihilating graphs realized by a module M such that every vertex \(x \in \widehat{A_f(M_N)}\) of an annihilating graph is an essential vertex.
4 Conclusion
In this paper, we formulated a new approach of recognition of essential ideals in a commutative ring R. This formulation of essential ideals corresponds to mod-annihilators of a R-module M. It is interesting to characterize essential ideals such that their arbitrary intersection is an essential ideal, since it is specified in [5] that an arbitrary intersection of essential ideals may not be an essential ideal. Furthermore, we obtained the results related to ideals [x : M] of R, where x is a mod-annihilator of M and discussed the representation of vertices of annihilating graphs by essential ideals of R. Apart from the research problems which we mentioned in Sects. 2 and 3, the following problems could be investigated for the future work.
1. Let G be a finite abelian p-group (viewed as a finite \({\mathbb {Z}}\)-module) of rank at least 3. Determine the value of n for the essential ideal \([x : G] = n{\mathbb {Z}}\), where \(x \in G\).
2. Let G be any finite abelian group (viewed as a finite \({\mathbb {Z}}\)-module). Determine the value of n for the essential ideal \([x : G] = n{\mathbb {Z}}\), where \(x \in G\).
References
Aijaz, M., Pirzada, S., Somasundaram, A.: Zero divisor graphs of unitary R-modules over commutative rings. AKCE Int. J. Graphs Combin. (in press)
Anderson, D.F., Livingston, P.S.: The zero-divisor graph of a commutative ring. J. Algebra 217, 434–447 (1999)
Anderson, D.F., Levy, R., Shapiro, J.: Zero-divisor graphs, von Neumann regular rings, and Boolean algebras. J. Pure Appl. Algebra 180, 221–241 (2003)
Azarpanah, F.: Essential ideals in C(X). Period. Math. Hung. 31, 105–112 (1995)
Azarpanah, F.: Intersection of essential ideals in C(X). Proc. Am. Math. Soc. 125, 2149–2154 (1997)
Beck, I.: Coloring of commutative rings. J. Algebra 116, 208–226 (1988)
Cartan, H., Eilenberg, S.: Homological Algebra. Princeton University Press, Princeton (1956)
Green, B.W., Van Wyk, L.: On the small and essential ideals in certain classes of rings. J. Aust. Math. Soc. Ser. A 46, 262–271 (1989)
Hongin, F., Stewart, P.: Graded rings and essential ideals. Acta Math. Sin. 9(4), 344–351 (1993)
Jain, S.K., Lopez-permouth, S.R., Rizvi, S.T.: Continuous rings with ACC on essentials is left Artinian. Proc. Am. Math. Soc. 108(3), 192–195 (1990)
Kaneda, M., Paulsen, V.I.: Characterization of essential ideals as operator modules over \(C^{*}-algebras\). J. Oper. Theory 49, 245–262 (2003)
Karamzadeh, O.A.S., Rostami, M.: On the intrinsic topology and some related ideals of C(X). Proc. Am. Math. Soc. 93(1), 179–184 (1985)
Meyer, F.D., Meyer, L.D.: Zero-divisor graphs of semigroups. J. Algebra 283, 190–198 (2005)
Momathan, E.: Essential ideals in rings of measurable functions. Commun. Algebra 38, 4739–4746 (2010)
Pirzada, S., Rather, A Bilal, Chishti, T.A.: On distance Laplacian spectrum of zero divisor graphs of \({\mathbb{Z}}_{n}\). Carpathian Math. Publ. 13(1), 48–57 (2021)
Pirzada, S., Wani, Bilal A., Somasundaram, A.: On the eigenvalues of zero divisor graph associated to finite commutative ring \(Z_{p^{M}q^{N}}\). AKCE Int. J. Graphs Combin. 18(1), 1–16 (2021)
Pirzada, S., Raja, Rameez: On graphs associated with modules over commutative rings. J. Korean Math. Soc. 53(5), 1167–1182 (2016)
Pirzada, S., Raja, Rameez: On the metric dimension of a zero-divisor graph. Commun. Algebra 45(4), 1399–1408 (2017)
Raja, Rameez, Pirzada, S.: On annihilating graphs associated with modules over commutative rings. Algebra Colloq. 29(2) (2022) (in press)
Pirzada, S., Aijaz, M., Imran Bhat, M.: On zero divisor graphs of the rings \(Z_{n}\). Afr. Mat. 31, 727–737 (2020)
Puczylowski, E.R.: On essential extensions of rings. Bull. Aust. Math. Soc. 35, 379–386 (1987)
Rather, B.A., Pirzada, S., Naikoo, T.A., Shang, Y.: On Laplacian eigenvalues of the zero-divisor graph associated to the ring of integers modulo n. Mathematics 9(482), 1–17 (2021)
Redmond, S.P.: The zero-divisor graph of a non-commutative ring. Int. J. Commut. Rings 1(4), 203–211 (2002)
Resenberg, A., Zelinsky, D.: Finiteness of the injective hull. Math. Z. 70, 372–380 (1959)
Wisbauer, R.: Foundations of Modules and Ring Theory. Gordon and Breach, Reading (1991)
Acknowledgements
The authors are grateful to the anonymous referees for their valuable suggestions which improved the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Raja, R., Pirzada, S. Essential ideals represented by mod-annihilators of modules. Afr. Mat. 33, 52 (2022). https://doi.org/10.1007/s13370-022-00988-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13370-022-00988-9