Introduction

Many problems related to energy and geophysical industries (such as thermal insulation, geophysical flows, petroleum resource, polymer processing, etc.) needed the analysis of mixed convective thermal and solutal transport phenomena of non-Newtonian fluids in a porous medium along different geometries. In particular, the majority of the real fluids (cosmetic products, grease, body fluids, and much more) exhibit a non-Newtonian behavior. Various fluid models have been suggested and studied to describe the dynamics of non-Newtonian fluids. Among them, Ostwald-de-Waele power-law fluid is one and it has substantial applications in many engineering industries such as oil reservoir engineering, chemical engineering, manufacturing processes, etc., because it characterizes the flow pattern of certain non-Newtonian fluids which contradict to Newton’s law of viscosity like polymer melt and glass, etc. A comprehensive evaluation of free/mixed convective thermal and mass transport phenomena of power-law fluid flow along different geometries embedded in a Darcy/non-Darcy porous medium, has been discussed and exposed by the many authors to mention few, Shenoy [1, 2], Gorla and Kumari [3], Ibrahim et al. [4], Kumari and Nath [5], Cheng [6], Kairi and RamReddy [7].

The analysis of heat transfer with convective thermal boundary condition is an important and useful consideration in the gas turbines, nuclear plants, heat exchangers related industries, due to the realistic nature of this condition. In this mechanism, heat is supplied to the convecting fluid through a bounding surface with a finite heat capacity, which provides a convective heat transfer coefficient (namely, Biot number). In view of these applications, Makinde [8] considered convective thermal boundary condition for the analysis of thermal and mass transfer on MHD fluid flow over a moving vertical plate, whereas Munir et al. [9] scrutinized the influence Biot number and Joule heating effect on the peristaltic flow of a viscous fluid along an asymmetric channel. Recently, Hayat et al. [10] utilized convective boundary condition in the analysis of fluid characteristics of power-law fluid along a stretching sheet with suspended nanoparticles.

The main streams of thermal systems are processed at high-level temperatures and in such situations, the density relation with temperature and concentration may become nonlinear. This nonlinear variation in temperature–concentration-dependent density relation gives a strong influence to the fluid flow characteristics (for more details see [11, 12]). Partha [13] studied the influence of dispersion and cross-diffusion effects with the nonlinear Boussinesq approximation (known as nonlinear convection) to the viscous fluid flow. A Darcy–Forchheimer model considered in the analysis of nonlinear convection and thermophoresis in a regular fluid by Kameswaran et al. [14] and concluded that the boundary layer thickness of temperature and concentration is reduced with enhancing values of nonlinear concentration and temperature parameters. More recently, RamReddy and Pradeepa [15] analyzed the influence of nonlinear convection and convective thermal boundary condition on saturated micropolar fluid emerged in porous media by taking into homogeneous-heterogeneous reactions.

In present days, the researchers are attracted to scrutinize the free/mixed convective flow of Newtonian and non-Newtonian fluids along non-identical geometries (such as inclined surfaces, discs, V-shaped prisms and bluff bodies, among them inclined plate is the first preference) in a porous medium. Since, the inclined plate is used in various industrial fields like chemical processing, electrical systems, iron removal, brine clarification, etc. The analysis of fluid flow characteristics over a inclined plate was pioneered by Cheng [16]. Further, Chamka et al. [17], Rahman et al. [18], Murthy et al. [19], Pal and Chatterjee [20], and in recent times, Sui et al. [21] considered problems on inclined plate with different Newtonian/non-Newtonian fluid and physical conditions.

Based on the previous studies, it is relevant to discuss the mixed convective thermal and solutal transport phenomena in a power-law fluid flow along an inclined plate with a Biot number effect. Also, the nonlinear Boussinesq approximation is considered in the formulation of fluid flow equations with a Darcy-Forchhiemer’s model. This kind of investigation is useful in the mechanism of combustion, solar collectors which are performed at high-level temperatures.

Fig. 1
figure 1

Schematic diagram of the problem

Full size image

Mathematical Modeling

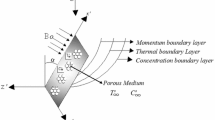
An incompressible, two-dimensional, steady, mixed convective flow of power-law fluid along an inclined semi-infinite plate embedded in a non-Darcy porous medium is considered. The semi-infinite plate is inclined about vertical direction with an angle \(\Omega \), as projected in Fig. (1). The plate is either heated or cooled from left by convection from a fluid of temperature \(T_f\) with \({T_f}> {T_{\infty }}\) corresponding to a heated surface and \({T_f}< {T_{\infty }}\) corresponding to a cooled surface, respectively. It is further assumed that the concentration of the ambient fluid is of uniform magnitude, \(C_{\infty }\), the unknown wall concentration of the plate is \(C_w\). In Fig. 1, M.B.L. represent momentum boundary layer, while T.B.L. and C.B.L. represents thermal and concentration boundary layers, respectively.

A power-law fluid is a type of generalized Newtonian fluid for which the shear stress \({{\tau }_{xy}}\) can be expressed as \({{\tau }_{xy}}={{\mu }^{*}}{{\left| \frac{\partial u}{\partial y} \right| }^{n-1}}\frac{\partial u}{\partial y}\). Here, \({{\mu }^{*}}\) is called the consistency coefficient and n is the power-law index. The dimension of \({{\mu }^{*}}\) depends on the value of n which is non-dimensional. When \(n=1\), the fluid become the Newtonian fluid with a dynamic coefficient of viscosity \({{\mu }^{*}}\). Therefore, deviation of n from a unity indicates the degree of deviation from Newtonian fluid behavior. That is for \(n<1\), the fluid is pseudo-plastic and for \(n>1\), the fluid is dilatants. The governing equations for the flow, heat and mass transfer of a power-law fluid saturated non-Darcy porous medium (Shenoy [2], Murthy and Singh [22], Chen [23] ) are given by

$$\begin{aligned}&{\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0} \end{aligned}$$
(1)
$$\begin{aligned}&{{{u}^{n}}+\frac{b\sqrt{{{K}_{p}}}}{\nu }{{u}^{2}}= -\frac{{{K}_{p}}}{\mu }\left( \frac{\partial p}{\partial x}+\rho {{g}^{*}}\cos \Omega \right) } \end{aligned}$$
(2)
$$\begin{aligned}&{{{v}^{n}}+\frac{b\sqrt{{{K}_{p}}}}{\nu }{{v}^{2}}= -\frac{{{K}_{p}}}{\mu }\left( \frac{\partial p}{\partial y} \right) } \end{aligned}$$
(3)
$$\begin{aligned}&{u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \left( \frac{{{\partial }^{2}}T}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{y}^{2}}} \right) } \end{aligned}$$
(4)
$$\begin{aligned}&{u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D\left( \frac{{{\partial }^{2}}C}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}C}{\partial {{y}^{2}}} \right) } \end{aligned}$$
(5)

along with the nonlinear Boussinesq approximation (Partha [13])

$$\begin{aligned} {\rho = {{\rho }_{\infty }}\left[ 1-{{\beta }_{0}}\left( T-{{T}_{\infty }} \right) -{{\beta }_{1}}{{\left( T-{{T}_{\infty }} \right) }^{2}}-{{\beta }_{2}}\left( C-{{C}_{\infty }} \right) -{{\beta }_{3}}{{\left( C-{{C}_{\infty }} \right) }^{2}} \right] } \end{aligned}$$
(6)

along with the associated boundary conditions

$$\begin{aligned} v= & {} 0, \quad - {k_f}\frac{\partial T}{\partial y} = {h_f}({T_f} - T),\quad C= C_w \quad \text{ at } \quad y=0\nonumber \\ u= & {} {u_\infty },\quad T={T_\infty }, \quad C={C_\infty } \quad \text{ as } \quad y\rightarrow \infty \end{aligned}$$
(7)

where (u, v) are the Darcian velocities, \(\rho \) is the density, p is the pressure, \(K_p\) is the permeability, C is the concentration, \(\textit{D}\) is the solutal diffusivity, \(\nu \) is the kinematic viscosity, \({h_f}\) is the convective heat transfer coefficient, \(\alpha \) is the thermal diffusivity, \(\textit{b}\) is the empirical constant, \(\Omega \) is the inclination of angle, \(g^*\) is the acceleration due to gravity, T is the temperature, \({k_f}\) is the thermal conductivity, \(u_\infty \) is the free stream velocity. Further, the first and second order thermal and solutal coefficients are taken as \(\beta _0\) and \(\beta _1\), \(\beta _2\) and \(\beta _3\), respectively.

Experimental and numerical studies on convective heat transfer in porous media show that thermal boundary layers exist adjacent to the heated or cooled bodies. When the thermal boundary layer is thin (i.e., \({x}\gg {y}\sim {\delta _{T}}\) , \({\delta _{T}}\) is the boundary layer thickness), boundary layer approximations analogous to classical boundary layer theory can be applied (Nield and Bejan [24]). Near the boundary, the normal component of seepage velocity is small compared with the other component of the seepage velocity and the derivatives of any quantity in the normal direction are large compared with derivatives of the quantity in the direction of the wall. Now, making use of the boundary layer assumptions, nonlinear Boussinesq approximations and eliminating pressure gradient from the momentum equations, the governing Eqs. (2)–(5) reduces to

$$\begin{aligned} \frac{\partial {{u}^n}}{\partial y}+\frac{b{\sqrt{K_{p}}}}{\nu }\frac{{\partial }{u^2}}{\partial y}= & {} \frac{{K_p} {g^{*}}}{\nu }\left\{ \left[ {\beta _0}+ 2{\beta _1}{\left( {T - {T_\infty }} \right) }\right] \frac{{\partial }T}{\partial y} \right. \nonumber \\&\left. + \left[ {\beta _2}+ 2{\beta _3}{\left( {C - {C_\infty }} \right) }\right] \frac{{\partial }C}{\partial y} \right\} \mathrm{cos}\Omega \end{aligned}$$
(8)
$$\begin{aligned} u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}= & {} \alpha \frac{{\partial ^2}T}{\partial {y^2}} \end{aligned}$$
(9)
$$\begin{aligned} u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y}= & {} D\frac{{\partial ^2}C}{\partial {y^2}} \end{aligned}$$
(10)

By defining stream function \({\psi (x,y)}\) as \(\displaystyle {u = \frac{{\partial \psi }}{{\partial y}}}\) and \(\displaystyle {v = - \frac{{\partial \psi }}{{\partial x}}}\), the continuity equation (1) is automatically satisfied. To convert the system of dimensional equations (8)–(10) into system of the equations in the non-dimensional form, we considered the following dimensionless non-similarity transformations (for more details, see. Huang et al. [25], Chamkha et al. [26], Prasad et al. [27])

$$\begin{aligned} \begin{aligned}&\displaystyle {\xi = \frac{x}{L}},\, \,\,\, \displaystyle {\eta = \frac{y}{L}\,{{ Pe}^{\frac{1}{2}}\,{\xi }^{\frac{-1}{2}}}},\,\,\, \displaystyle {\psi (\xi ,\eta ) ={\alpha \, {{\xi }^{\frac{1}{2}}\,{ Pe}^{\frac{1}{2}}}\,f(\xi ,\eta )}}\\&\displaystyle {T(\xi ,\eta )= {T_{\infty }}+\left( {T_f} - {T_\infty }\right) \,\theta (\xi ,\eta )},\,\,\,\,\, \displaystyle {C(\xi ,\eta )= {C_{\infty }}+\left( {C_w} - {C_\infty }\right) \,\phi (\xi ,\eta )} \end{aligned} \end{aligned}$$
(11)

Substituting the transformations (11) into (8)–(10), the resultant dimensionless momentum, energy and concentration equations can be presented as

$$\begin{aligned} n\,\left( {f'}\right) ^{n-1}\;f''+2{F_{0}Pe}f'\;f''= & {} {{\lambda }^{n}}\left[ { (1 + 2\,{\alpha _1}\theta ){\theta '} + {{\mathcal {B}}} (1 + 2\,{\alpha _2}\phi ){\phi '}} \right] \cos \Omega \end{aligned}$$
(12)
$$\begin{aligned} \theta ''+ \frac{1}{2}f\theta '= & {} \xi \left( {{f'}\frac{\partial \theta }{\partial \xi } - \frac{\partial f}{\partial \xi }\theta '} \right) \end{aligned}$$
(13)
$$\begin{aligned} \frac{1}{Le}{\phi ''} + \frac{1}{2}f{\phi '}= & {} \xi \left( {{f'}\frac{\partial \phi }{\partial \xi } - \frac{\partial f}{\partial \xi }{\phi '}} \right) \ \end{aligned}$$
(14)

Boundary conditions (7) in terms of f, \(\theta \), and \(\phi \) become

$$\begin{aligned} \begin{aligned} f(\xi ,0)&= - 2\,{\xi }{\left( {\frac{\partial f}{\partial \xi }} \right) _{\eta = 0}},\,\, \theta '(\xi , 0) = - Bi\,{\xi ^{\frac{1}{2}}}\left[ 1 - \theta (\xi ,0) \right] ,\phi (\xi ,0) = 1,\,\\ f'(\xi ,\infty )&= 1,\,\,\theta (\xi ,\infty ) = 0,\,\,\phi (\xi ,\infty ) = 0. \end{aligned} \end{aligned}$$
(15)

In usual definitions, \(Ra=(L/\alpha )\left( [{K_p}{g^*}{\beta _0}({T_f} - {T_\infty })]/{\nu }\right) ^{1/n}\) is the global Rayleigh number, \(Pe = ({u_\infty \,L})/{\alpha }\) is the global Peclet’s number, \(Pe_d=({u_\infty }d)/\alpha \) is the pore diameter-dependent Peclet number, \({\alpha _1} = {\beta _1}({T_f} - {T_\infty })/{\beta _0}\) is the nonlinear density-temperature parameter, \(\lambda = Ra/Pe\) is the mixed convection parameter is the \({{\mathcal {B}}} = {\beta _2}({C_w} - {C_\infty })/\left( {{\beta _0}({T_f} - {T_\infty })} \right) \) is the Buoyancy ratio, \({\alpha _2} = {\beta _3}({C_w} - {C_\infty })/{\beta _2}\) is the nonlinear density-concentration parameter, \(F_{0}Pe=f_{0}{(Pe_d)^{2-n}}\) \(\left[ f_{0}=\left( (b\sqrt{K_p})/\nu \right) (\alpha /d)^{2-n}\right] \) is the non-Darcian parameter(Forchheimer number), \(Le=(\alpha /D)\) is the diffusivity ratio(or Lewis number), \(Sc = \nu /D\) is the Schmidt number, \(\xi \) is the streamwise coordinate, \(Pr = \nu /\alpha \) is the Prandtl number, \(Bi = {h_f} L/({k_f} \,\,Pe^{1/2})\) is the Biot number, respectively.

Non-dimensional Nusselt number \(\displaystyle {Nu_x =\frac{-x}{(T_f-T_{\infty })}\left[ \frac{\partial T}{\partial y}\right] _{y=0}}\) and the Sherwood number \(\displaystyle {Sh_{x}=\frac{- x}{(C_w-C_{\infty })}\left[ \frac{\partial C}{\partial y}\right] _{y=0}}\) are given by

$$\begin{aligned} \displaystyle {Nu\, {Pe^{\frac{-1}{2}}}= - {\xi ^{\frac{1}{2}}}\theta '(\xi , \, 0)},\,\, \displaystyle {Sh \, {Pe^{\frac{-1}{2}}}= -{\xi ^{\frac{1}{2}}}\phi '(\xi , \, 0)}. \end{aligned}$$
(16)

Numerical Solutions

Numerical solution to Eqs. (12)–(14) together with (15) has been evaluated with Successive Linearisation Method (SLM) (see. Makukula et al. [28], Awad et al. [29], Khidir et al. [30]) along with Local non-similarity procedure (Sparrow and Yu [31], Minkowycz and Cheng [32]).

Local Non-similarity Procedure

The preliminary approximate solution can be found from local similarity equations for a particular case of \(\xi<<1\), the terms containing \(\xi \frac{\partial }{\partial \xi }\) are supposed to be negligible. Then the first level truncation or local similarity equations from (12) to (15) are

$$\begin{aligned}&\left[ n\,\left( {f'}\right) ^{n-1}+2{F_{0}Pe}f'\right] \;f''- {{\lambda }^{n}}\left[ { (1 + 2\,{\alpha _1}\theta ){\theta '} + {{\mathcal {B}}} (1 + 2\,{\alpha _2}\phi ){\phi '}} \right] \cos \Omega =0 \qquad \end{aligned}$$
(17)
$$\begin{aligned}&\theta ''+ \frac{1}{2}f\theta '=0 \end{aligned}$$
(18)
$$\begin{aligned}&\frac{1}{Le}{\phi ''} + \frac{1}{2}f{\phi '}=0 \end{aligned}$$
(19)

The corresponding boundary conditions are

$$\begin{aligned} \begin{aligned} f(\xi ,0)&= 0,\,\, \theta '(\xi , 0) = - Bi\,{\xi ^{\frac{1}{2}}}\left[ 1 - \theta (\xi ,0) \right] ,\phi (\xi ,0) = 1,\,\\ f'(\xi ,\infty )&= 1,\,\,\theta (\xi ,\infty ) = 0,\,\,\phi (\xi ,\infty ) = 0. \end{aligned} \end{aligned}$$
(20)

The local non-similarity ordinary nonlinear differential equations in the second level truncation is discovered by introducing new variables to recall the omitted expressions from the first level truncation i.e., take \(\displaystyle {U = \frac{\partial f}{\partial \xi }, V = \frac{\partial \theta }{\partial \xi }, W = \frac{\partial \phi }{\partial \xi }}\). Thus the second level truncation is

$$\begin{aligned}&\left[ n\,\left( {f'}\right) ^{n-1}+2{F_{0}Pe}f'\right] \;f''- {{\lambda }^{n}}\left[ { (1 + 2\,{\alpha _1}\theta ){\theta '} + {{\mathcal {B}}} (1 + 2\,{\alpha _2}\phi ){\phi '}} \right] \cos \Omega =0\qquad \end{aligned}$$
(21)
$$\begin{aligned}&\theta ''+ \frac{1}{2}f\theta ' = \xi \left( {V\,f' - U\,\theta '} \right) \end{aligned}$$
(22)
$$\begin{aligned}&\frac{1}{Le}{\phi ''} + \frac{1}{2}f{\phi '} = \xi \left( {W\,f' - U\,\phi '} \right) \end{aligned}$$
(23)

The corresponding boundary conditions are

$$\begin{aligned} \begin{aligned}&f(\xi ,0) = - 2\,\xi \, U(\xi ,\eta ),\,\,\theta '\left( {\xi ,0} \right) = - Bi\,{\xi ^{\frac{1}{2}}}\left[ {1 - \theta ( {\xi ,0})} \right] ,\,\,\phi (\xi ,0) = 1,\\&\quad f'(\xi ,\infty ) = 1,\,\,\theta (\xi ,\infty ) = 0,\,\phi (\xi ,\infty ) = 0. \end{aligned} \end{aligned}$$
(24)

The two level local non-similarity technique is accomplished with a third level of truncation, for this we differentiate equations (21)–(24) with respect to \(\xi \) and omit the partial derivatives of \(\displaystyle {U,V,W}\). Then the resultant equations are

$$\begin{aligned}&\begin{aligned}&n(n-1)\left( {f'}\right) ^{n-2}\;f''U'+n\left( {f'}\right) ^{n-1}\;U''+2{F_{0}Pe}(f''\;U' +U''\;f')\\&\quad -{{\lambda }^{n}}\left[ {V'+ 2\,{\alpha _1}(V {\theta '}+\theta {V'} )+ {{\mathcal {B}}} (W' + 2\,{\alpha _2}(W {\phi '}+\phi {W'}))} \right] \cos \Omega =0 \end{aligned} \end{aligned}$$
(25)
$$\begin{aligned}&V'' + \frac{3}{2}U\theta ' + \frac{1}{2}V'\;f - V\; f' = \xi \left( U'\;V - U\;V' \right) \end{aligned}$$
(26)
$$\begin{aligned}&\frac{1}{Le}W'' + \frac{3}{2}U\phi ' + \frac{1}{2}W'\; f- W\; f' = \xi \left( U'\;W - U\;W' \right) \end{aligned}$$
(27)

The corresponding boundary conditions are

$$\begin{aligned} \begin{aligned} U(\xi ,0)&= 0,\; V'\left( {\xi ,0} \right) = Bi{\xi ^{\frac{1}{2}}}V\left( {\xi ,0} \right) + \frac{1}{2}Bi\;{\xi ^{\frac{{ - 1}}{2}}}[\theta (\xi ,0) - 1], W(\xi ,0) = 0,\\ U'(\xi ,\infty )&= 0,\;V\left( {\xi ,\infty } \right) = 0,\;W(\xi ,\infty ) = 0 \end{aligned} \end{aligned}$$
(28)

Successive Linearization Method

The coupled nonlinear ordinary differential equations (21)–(23) and (25)–(27) along with the boundary conditions (24) and (28) are evaluated using Successive Linearization Method. First, it linearise the non-similarity equation and then it utilizes Chebyshev collocation method for the approximate solution.

Successive Linearization

Let us consider an independent vector \({\mathbb {Q}}(\eta ) = [{f\left( \eta \right) ,\,\theta \left( \eta \right) ,\phi (\eta ),U(\eta ),V(\eta )},\) \({\,W(\eta )}] \) and assume that it can be represented as

$$\begin{aligned} {\mathbb {Q}}(\eta ) = {{\mathbb {Q}}_k}(\eta ) + \sum \limits _{m = 0}^{k - 1} {{\mathbb {Q}}_m(\eta )} \ \end{aligned}$$
(29)

where \({{\mathbb {Q}}_k}(\eta ),\,k = 1,2,3\ldots .\), are unknown vectors, those are determined by recursively evaluating the linearised version of the non-similarity equations and presuming that \({{\mathbb {Q}}_m}(\eta ),\,(0\le m \le k-1)\) are expected from antecedent iterations. The initial guesses \({\mathbb {Q}}_0(\eta )\) is selected so that it satisfy the boundary conditions (24) and (28). By imposing Eq. (29) in Eqs. (21)–(28) and considering only linear terms, we obtain the linearised equations to be evaluated are

$$\begin{aligned}&{\tilde{p}_{1,k - 1}}{f_k}'' + {\tilde{p}_{2,k - 1}}{f_k}'+ {\tilde{p}_{3,k - 1}}{\theta _k}' + {\tilde{p}_{4,k - 1}}{\theta _k} + {\tilde{p}_{5,k - 1}}{\phi _k}'+ {\tilde{p}_{6,k - 1}}{\phi _k} = \tilde{z}_{1,k - 1}\qquad \end{aligned}$$
(30)
$$\begin{aligned}&{\tilde{q}_{1,k - 1}}{f_k} + {\tilde{q}_{2,k - 1}}{\theta _k}'' + {\tilde{q}_{3,k - 1}}{\theta _k}' +{\tilde{q}_{4,k - 1}}{U_k} + {\tilde{q}_{5,k - 1}}{V_k} = {\tilde{z}_{2,k - 1}}\ \end{aligned}$$
(31)
$$\begin{aligned}&{\tilde{a}_{1,k - 1}}{f_k} + {\tilde{a}_{2,k - 1}}{\phi _k}'' + {\tilde{a}_{3,k - 1}}{\phi _k}' +{\tilde{a}_{4,k - 1}}{U_k} + {\tilde{a}_{5,k - 1}}{W_k} = {\tilde{z}_{3,k - 1}}\ \end{aligned}$$
(32)
$$\begin{aligned}&\begin{aligned}&\tilde{b}_{1,k-1}{f_k}'' + {\tilde{b}_{2,k - 1}}{f_k}' +{\tilde{b}_{3,k - 1}}{\theta _k}'+ {\tilde{b}_{4,k - 1}}{\theta _k}+ {\tilde{b}_{5,k - 1}}{\phi _k}' + {\tilde{b}_{6,k - 1}}{\phi _k} + {\tilde{b}_{7,k - 1}}{U_k}''\quad \qquad \\&\quad + {\tilde{b}_{8,k - 1}}{U_k}' + {\tilde{b}_{9,k - 1}}{V_k}' + {\tilde{b}_{10,k - 1}}{V_k} + {\tilde{b}_{11,k - 1}}{W_k}' + {\tilde{b}_{12,k - 1}}{W_k} = {\tilde{z}_{4,k - 1}} \end{aligned} \end{aligned}$$
(33)
$$\begin{aligned}&\begin{aligned}&{\tilde{c}_{1,k - 1}}{f_k} + {\tilde{c}_{2,k - 1}}{\theta _k}' + {\tilde{c}_{3,k - 1}}{U_k}' + {\tilde{c}_{4,k - 1}}{U_k} + {\tilde{c}_{5,k - 1}}{V_k}'' + {\tilde{c}_{6,k - 1}}{H_k}'\\&\quad + {\tilde{c}_{7,k - 1}}{V_k} = {\tilde{z}_{5,k- 1}} \end{aligned} \end{aligned}$$
(34)
$$\begin{aligned}&\begin{aligned}&{\tilde{d}_{1,k - 1}}{f_k} + {\tilde{d}_{2,k - 1}}{\phi _k}' + {\tilde{d}_{3,k - 1}}{U_k}' + {\tilde{d}_{4,k - 1}}{U_k} + {\tilde{d}_{5,k - 1}}{W_k}'' + {\tilde{d}_{6,k - 1}}{W_k}' \\&\quad + {\tilde{d}_{7,k - 1}}{W_k} = {\tilde{z}_{6,k - 1}} \end{aligned} \end{aligned}$$
(35)

The linearised boundary conditions are

$$\begin{aligned} \begin{aligned} {f_k}(0)&= {f_k}^\prime (0) = {f_k}^\prime (\infty ) = 0,\, Bi\,{\xi ^{\frac{1}{2}}}{\theta _k}(0)+{\theta _k}^\prime (0) = 0,\,\,{\theta _k}(\infty ) = 0,\\ {\phi _k}(0)&= {\phi _k}(\infty ) = 0,\,{U_k}(0) = {U_k}^\prime (0) = {U_k}'(\infty ) = 0, \; \\&\quad - \frac{1}{2}Bi\,{\xi ^{\frac{{ - 1}}{2}}}{\theta _k}(0) + {V_k}'(0) - Bi\,{\xi ^{\frac{1}{2}}}{V_k}(0) = 0,\,{V_k}(\infty ) = 0,\,{W_k}(0) = {W_k}(\infty ) = 0\, \end{aligned} \end{aligned}$$
(36)

Here the coefficient parameters \({\tilde{p}_{s,k - 1}},\,{\tilde{q}_{s,k - 1}},\,{\tilde{a}_{s,k - 1}},\,{\tilde{b}_{s,k - 1}},\,{\tilde{c}_{s,k - 1,}}\,{\tilde{d}_{s,k - 1}}\), and \({\tilde{z}_{s,k - 1}}\) which depend on the \({\mathbb {Q}}_0(\eta )\) and on the \({{\mathbb {Q}}_k}(\eta )\) derivatives.

Chebyshev Collocation Scheme

We solve linearised equations (30)–(35) by an established procedure, namely Chebyshev collocation scheme (Canuto et al. [33]). In the context of numerical implication, the original region \([0, \infty )\) is truncated to [0, L] for large value of L, and further the truncated region [0, L] is transformed into \([-1, 1]\) using the following mapping

$$\begin{aligned} \frac{\eta }{L} = \frac{{\tau + 1}}{2},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 1 \le \tau \le 1 \end{aligned}$$
(37)

In this procedure, The Chebyshev polynomials \({T_m}(\tau ) = \cos [m\,\,\,{\cos ^{ - 1}}\tau ]\) are used to approximate the unknown functions \({\mathbb {Q}}_k(\eta )\) and these polynomials are collocated at \(K+1\) Gauss–Lobatto points in the interval \([-1,1]\) and those are defined as

$$\begin{aligned} {\tau _\textit{m}} = \cos \frac{{\pi \textit{m}}}{K},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\textit{m} = 0,1,\ldots ,K \end{aligned}$$
(38)

The unknown function \({\mathbb {Q}}_k(\eta )\) is imprecise at the collocation points by

$$\begin{aligned} {\mathbb {Q}}_k(\tau ) = \sum \limits _{j = 0}^K {{\mathbb {Q}}{_k}({\tau _j}){T_j}({\tau _m})} ,\,\,\,\,\,\,\,\,\,\,\,\,m = 0,1,\ldots ,K \end{aligned}$$
(39)

and

$$\begin{aligned} \frac{d^{\mathbb {S}}}{d{\eta ^{\mathbb {S}}}}{\mathbb {Q}}_k(\tau ) = \sum \limits _{r = 0}^K {\mathbf{D}}_{rm}^{\mathbb {S}} {\mathbb {Q}}_k(\tau _r),\,\,\,\,\,\,\,\,\,\,m = 0,1,2,\ldots ,K \end{aligned}$$
(40)

where \({\mathcal {D}}\) is the Chebyshev spectral derivative matrix such that \({\mathbf{D}} = (2/L){{\mathcal {D}}}\) and \({\mathbb {S}}\) is the order of differentiation. After employing Eqs. (37)–(40) into linearized form of equations (30)–(35), the resultant solution is

$$\begin{aligned} {\tilde{\mathbf{Y}}}_k = {\tilde{\mathbf{B}}}_{k - 1}^{ - 1}{{{\tilde{\mathbf{Z}}}}_{k - 1}} \end{aligned}$$
(41)

In Eq. (41), \({\tilde{\mathbf{B}}}_{k - 1}\) is a \((6N + 6)\times (6N + 6)\) matrix, \({{{\tilde{\mathbf{Y}}}}_k}\) and \({\tilde{\mathbf{Z}}}_{k - 1}\) are \((6N + 1)\times 1\) column vectors defined by

$$\begin{aligned} {{\tilde{\mathbf{B}}}_{k - 1}}&= \left[ {{{\tilde{\mathbf{B}}}_{ij}}} \right] ,\,\,i,j = 1,2,\ldots , 6,\,\,\,{{{\tilde{\mathbf{Y}}}}_k} = \left[ {{\tilde{\mathbb {F}}}{_k}\,\,{\tilde{\Theta } _k}\,\,{\tilde{\Phi } _k}\,\,{\tilde{\mathbb {U}}}{_k}\,\,{\tilde{\mathbb {V}}}{_k}\,\,{\tilde{\mathbb {W}}}{_k}}\right] {\,^T},\,\,\nonumber \\ {\tilde{\mathbf{Z}}_{k - 1}}&= \left[ {{\tilde{\mathbf{z}}_{1,k - 1}}\,\,{\tilde{\mathbf{z}}}_{2,k - 1}}\,\,{\tilde{\mathbf{z}}}_{3,k - 1}\,\,{\tilde{\mathbf{z}}}_{4,k - 1}\,\,{\tilde{\mathbf{z}}}_{5,k - 1}\,\,{\tilde{\mathbf{z}}}_{6,k - 1} \right] ^T \end{aligned}$$
(42)

Results and Discussion

The validation of the present results is cross verified with previously established results (Chaoyang et al. [34], Murthy [35]) in the absence of nonlinear convection parameters as shown in Tables 1 and 2. From those two tables, we have noticed that the error between these two (present and previously published) numerical results is negligible so that the numerical practice which we made by SLM is an appropriate scheme for the present analysis. The impacts of the considered parameters (such as nonlinear convection parameters (\(\alpha _1\),\(\alpha _2\)), the inclination of angle (\(\Omega \)) and Biot number (Bi), etc.) are determined through Figs. 2a, b, c, 3a, b, c, 4a, b, c, 5a, b, c, 6a, b, c for the boundary layer profiles. Also, the physical quantities of the flow, Nusselt and Sherwood numbers (i.e, \(Nu\, {Pe^{\frac{-1}{2}}}\) and \(Sh \, {Pe^{\frac{-1}{2}}}\)) are projected in Figs. 7a, b, 8a, b for the same values.

The practicability of non-similarity transformations (see Eq. (11)) in the present analysis is addressed by the Figs. 2a–c. Boosting the value of streamwise coordinate (\(\xi =0.1, 0.5, 1.0\)), the velocity component increases, whereas the thermal and solutal boundary layer thickness decreases. Further, the wall temperature always tends to 1 as \(\xi \rightarrow \infty \) and also, the changes in these profiles clearly proven that the present results are non-similar. It means that the solutions are not unique for different values of \(\xi \).

The images placed in Figs. 3a–c, exhibit the dependence of NDT parameter (\(\alpha _1=0, 2,6\)) and power-law index (\(n=0.5, 1.0, 1.5\)) on the boundary layer profiles. It reveals that the variation of the power-law index is considerable and enhances the momentum boundary layer thickness, whereas it diminishes thermal and solutal boundary layer thickness. With respect to the variation of \(\alpha _1\), the dimensionless velocity increases more at the surface of the inclined plate and it reaches unity for \(\eta _{max}\) value, the same result shown in the Fig. 3a. From Fig. 3b–c, one can notice that the increment of \(\alpha _1\) leads to reduce the temperature and solutal boundary layer thicknesses, and also the temperature and concentration gradients are more in the absence of \(\alpha _1\) as compared to its presence. Responses of boundary layer profiles for NDC parameter (\(\alpha _2=0, 3, 7\)) are portrayed to the three different values of the power-law index in Fig. 4a–c. The results of this set of figures repeat the same kind of behavior as like \(\alpha _1\) in all three profiles, but then the dominance, of \(\alpha _2\) is more of these three boundary layer profiles and in all three kinds fluids (pseudoplastic, Newtonian, dilatant fluid) compared to \(\alpha _1\) influence.

Table 1 Comparison of \(-\theta '(0,\,0)\) for various values of \(\lambda \) when \({F_0}Pe=0\), \({{\mathcal {B}}}=0\), \(\alpha _1=0\), \(\alpha _2=0\), \(Bi\rightarrow \infty \), and \(\Omega =0\)
Full size table
Table 2 Comparison of \(f'(0,\,0)\), \(-\theta '(0,\,0)\) and \(-\phi '(0,\,0)\) for different values of \(\mathcal {B}\), Le, \(\lambda \) when \(F_{0}Pe=1.0\), \(\alpha _1=0\), \(\alpha _2=0\), \(n=1\) , \(Bi\rightarrow \infty \), and \(\Omega =0\)
Full size table
Fig. 2
figure 2

Effect of \(\xi \) for different values n on the a velocity, b temperature, and c concentration with the fixed values of \({\alpha _1}=1\), \({\alpha _2}=1\), \(Bi=0.2\), \(\Omega =30^{\circ }\)

Full size image
Fig. 3
figure 3

Effect of \({\alpha }_1\) for different values n on the a velocity, b temperature, and c concentration with the fixed values of \(Bi=0.2\), \({\alpha }_2=1\), \(\Omega =30^{\circ }\), \(\xi =0.5\)

Full size image
Fig. 4
figure 4

Effect of \({\alpha }_2\) for different values n on the a velocity, b temperature, and c concentration with the fixed values of \(Bi=0.2\), \({\alpha }_1=1\), \(\Omega =30^{\circ }\), \(\xi =0.5\)

Full size image
Fig. 5
figure 5

Effect of Bi for different values n on the a velocity, b temperature, and c concentration with the fixed values of \({\alpha _1}=1\), \({\alpha _2}=1\), \(\Omega =30^{\circ }\), \(\xi =0.5\)

Full size image
Fig. 6
figure 6

Effect of \(\Omega \) for different values n on the a velocity, b temperature, and c concentration with the fixed values of \({\alpha _1}=1\), \({\alpha _2}=1\), \(Bi=0.2\), \(\xi =0.5\)

Full size image
Fig. 7
figure 7

Effect of \({\alpha }_1\) and \({\alpha }_2\) for different values n on the a heat transfer rate, and b mass transfer rate, against \(\xi \) with the fixed values of \(Bi=0.5\) and \(\Omega =30^{\circ }\)

Full size image
Fig. 8
figure 8

Effect of Bi and \(\Omega \) for different values n on the a heat transfer rate, and b mass transfer rate, against \(\xi \) with the fixed values of \({\alpha _1}=1\) and \({\alpha _2}=1\)

Full size image

Figure 5a–c illustrate the impact of the convective heat transfer coefficient (i.e Biot number \(Bi=0.05, 1.0, 20\)) on the non-dimensional velocity, temperature, and concentration for the pseudoplastic, Newtonian, and dilatant fluids. The rise in the Biot number changes the magnitude of the velocity in the increasing direction as depicted in Fig. 5a. The utility of convective thermal boundary condition is possible in two ways, one as an isothermal condition and another possibility is a non-isothermal condition. Because the isothermal condition is a limiting result of the Biot number when \(h_f\) tends to infinity (stated by Aziz [36]) and this is proven again by Fig. 5b. It means, there is a drastic change in temperature distribution at the surface of the plate when the Biot number approaches to a large value. The effect of the Biot number on the concentration profile is displayed in Fig. 5c and it depicts that the concentration profile decreases within the boundary layer when the Biot number increases from least to a large value. For a fixed value of the Biot number (for three values of Bi), the enhancement of power-law index leads to increase the velocity distribution, whereas it decreases the temperature and concentration distributions within the boundary layers, and according to above boundary specified condition these profiles are asymptotically reaching the ambient fluid conditions at \(\eta _{max}\). As convective coefficient enhances from \(Bi<1\) (thermally thin case) to \(Bi>1\) (thermally thick case), the temperature of the flow increases whereas the concentration decreases as shown in Fig. 5b–c, respectively. Obtained results for temperature and concentration profiles are subjectively equal with those of Makinde and Aziz [37] work.

The orientation of the plate is displaced from vertical to horizontal with reference to the angle(\(\Omega =0^{\circ }, 40^{\circ }, 80^{\circ }\)) and the resulting variations in boundary layer profiles are portrayed in Fig. 6a–c. The physical reason for the depletion of velocity profile with respect inclination angle is that the thermal and concentration buoyancy falls down [as considered in Eq. (8)] when the inclination of angle changed from \(\Omega =0^{\circ }\) to \(90^{\circ }\). The same illustration is noticed from Fig. 6a. Moreover, from Fig. 6a, one can observe that the maximum buoyancy force occurs to the temperature and concentration differences along the vertical plate only. It is observed from Fig.6b, c that the concentration and temperature enhance with rising values of inclination of angle. In the case of an inclination of angle, the thermal and concentration distributions results are identically equal to the work of Chamkha et al. [17], Chen [38].

The variation in physical quantities (specifically, \(Nu\, {Pe^{\frac{-1}{2}}}\) and \(Sh \, {Pe^{\frac{-1}{2}}}\)) of the present analysis are collected through the graphs Figs. 7a, b, 8a, b for different values of the considered parameters (for, \(\alpha _1=0, 6\); \(\alpha _2= 0, 5\); \(Bi=0.05, 1.0\); and \(\Omega = 0^{\circ }, 60^{\circ }\)). With respect to the pseudoplastic fluid, the magnitude of heat transfer rate (\(Nu\, {Pe^{\frac{-1}{2}}}\)) slightly increased when the \(\alpha _1\) is increased from zero to a nonzero value and the same kind of variation appeared for \(\alpha _2\), but then influence of \(\alpha _2\)is more compared to \(\alpha _1\) effect, as projected in Fig. 7a. In the case of other two fluids (Newtonian and dilatant fluids) the influence of these parameters is same. On the other side, for a fixed value of these two parameters, the heat transfer rate is more for dilatant compared to Newtonian and pseudoplastic fluids. The illustrations of Fig. 7b for Sherwood number (\(Sh \, {Pe^{\frac{-1}{2}}}\)), it is also showing same results as \(Nu\, {Pe^{\frac{-1}{2}}}\) affect. Fig. 8a, b demonstrate that the \(Nu\, {Pe^{\frac{-1}{2}}}\) and \(Sh \, {Pe^{\frac{-1}{2}}}\) show the opposite trend when the plate is displaced from vertical to a horizontal position with reference to the angle \(\Omega \). But then in the case of Bi variation of these two quantities is same and both the transfer rates are increased. However, for a fixed value of either Bi or \(\Omega \), both the \(Nu\, {Pe^{\frac{-1}{2}}}\) and \(Sh \, {Pe^{\frac{-1}{2}}}\) fall down when power-law index moves from \(n<1\) to \(n>1\).

Conclusions

In the present study, the nonlinear Boussinesq approximation is considered in the analysis of heat and mass transfer phenomena of an Ostwald-de-Waele model power-law fluid flow over a convectively heated inclined plate in a non-Darcy porous medium. The impact of pertinent parameters on the velocity, temperature, concentration, heat, and mass transfer rates have been analyzed. The major notice is that the impact of NDC parameter is prominent on the physical quantities(specifically, Nusselt and Sherwood number) of the present model, compared therewith NDT parameter and these two effects are more influenced in pseudoplastic fluids. The variation of the Biot number leads to enhance all pertinent characteristics except the concentration profile. However, the velocity, heat, and mass transfer rates diminish, whereas the thermal and solutal boundary layer thicknesses enhance with the increase of inclination of angle. This kind of analysis has important applications in aerosol technology, high-temperature polymeric mixtures, which are associated with temperature–concentration-dependent density.