1 Introduction

In the reform and development of the transportation industry, the emergence of driverless technology is of epoch-making significance. As technology in Artificial Intelligence has developed, driverless technology has received increasing attention from researchers. The Society of Automotive Engineers (SAE) has identified six degrees of driving automation for driverless vehicles, ranging from L0 to L5. Many academics and professionals in relevant disciplines are focusing their research on achieving L5 level of fully autonomous vehicles. The driverless system is an intelligent control system that integrates various advanced theoretical technologies such as environment perception, high precision positioning, path planning and trajectory tracking [1]. The main requirement for safe operation of driverless vehicles is environment perception technology, which depends on on-board sensors to generate the surrounding environment as well as the vehicle status [2,3,4]. In the constructed perception system, different sensors demonstrate their individual benefits and provide the necessary conditions for the subsequent trajectory tracking work [5, 6].

A key component of autonomous technology, trajectory tracking technology strives to preserve the stability of the vehicle's lateral and longitudinal control [7, 8]. Currently, the commonly used trajectory tracking control methods are PID control, sliding mode control, model predictive control (MPC), fuzzy control, etc. [9, 10]. Among the above four control methods, PID control provides the widest range of applications. Out of the four control strategies mentioned above. PID control is utilized to control the vehicle longitudinal motion in trajectory tracking by decoupling the vehicle motion, which to some extent increases tracking accuracy [11]. Since, there is a certain time delay in the vehicle steering, then using PID control in the steering motion can offset this disturbance [12]. Although PID control has some superiority in improving the trajectory tracking accuracy and anti-jamming, PID control is a linear control method with limitations, so its application to complex nonlinear systems will decrease the controller's regulation accuracy. Sliding mode control belongs to the nonlinear control method, which is how it differs from PID control. By evenly dividing the driving torque of the wheels during steering, the sliding mode control for vehicle steering can effectively lower the danger of vehicle rollover [13]. The vehicle steering stability was improved by using the Kalman filter to determine the tire sideslip angle, while taking the road adhesion coefficient into account [14]. The wheel slip rate does not soon converge to the ideal value when the vehicle is abruptly braked, so the sliding mode control does not guarantee the resilience of the system [15]. By its essence, fuzzy control does not only mean nonlinear control, but also belongs to the category of intelligent control. By establishing a fuzzy control rule base, the corresponding parameters are dynamically adjusted in the trajectory tracking controller to secure the flexibility and safety of vehicle driving [16]. Likewise, fuzzy control is applied to the vehicle steering, and the lateral stability of the vehicle can be greatly improved by designing a torque distribution control system [17, 18]. The vehicle's tracking accuracy will be decreased by the fuzzy control system's incompleteness, since there will be several unanticipated disturbances in its trajectory.

It is important to note that in the tracking trajectory control, not only the kinematic and dynamic constraints of the vehicle model should be considered, but also the control variables output by the controller should satisfy the above constraints [19]. While, model predictive control, a traditional control approach, has a strong capability to handle constraints, the aforementioned three methods nevertheless have significant limits in how they handle constraints. This method can predict the future output of the multi-constrained system based on the existing model, the current state of the system, and the future control variables [20]. Model predictive control theory relies on its distinct advantages to be ideally adapted for both technologies, whether it is path planning or trajectory tracking [21].

Among them, in terms of path planning, adding reinforcement learning algorithms to MPC controllers enables real-time path planning [22, 23]. Efficiency of the MPC controller was significantly improved with the addition of a planning algorithm to the MPC trajectory tracking controller [24, 25].

In vehicle trajectory tracking control, MPC trajectory tracking controller analyzes the vehicle stability and sets reasonable constraints by optimizing the function, which makes it widely used for trajectory tracking of driverless vehicles [26, 27]. By linearizing the processing vehicle model, the vehicle can reach the steady state in time during the tracking trajectory to avoid the phenomenon of vehicle overspeed and control saturation [28]. In transverse and longitudinal coupled control, the differential game theory is used to enable each MPC trajectory tracking controller to generate an adapted control based the corresponding cost, and to continuously correct the driving trajectory during each control cycle [29]. For longitudinal control in which multiple objectives are considered, oversimplification of the vehicle longitudinal motion model can cause velocity oscillations, and real time control of the on-board electronic control unit is further achieved by transforming these problems into MPC optimization solutions [30]. In the transverse control of the vehicle, a preview model to output the optimal front wheel angle and speed is created, which can achieve the steadiness in vehicles [31, 32]. When the vehicle driving environment is in extreme conditions, the Kalman filter algorithm is utilized to predict the road surface grip coefficient in time, and the vehicle speed corresponded with different road surface grip coefficients is gotten by plotting the vehicle mass lateral deflection angle and lateral deflection angle velocity phase plane stability diagram, so that the vehicle can be kept stable under extreme conditions [33]. Although the driving stabilization and convenience of the vehicle were strengthen with the processing of the model and the coupled control of the vehicle motion in the above study, the accuracy of the tracking trajectory was not further improved.

Currently, regarding the improvement of trajectory tracking accuracy, the MPC controller cost weights can be adaptively adjusted using fuzzy control, which improves the tracking accuracy and ensures vehicle steadiness [34]. In the MPC trajectory tracking controller, the corresponding weights are dynamically adjusted, while considering the curvature of the reference trajectory to better the accurate trajectory tracking [35]. The vehicle's tire stability will decrease when it is driven on a slick surface. By restraining the tire slip angle, the MPC trajectory tracking controller can optimize the slip angle in time and reduce the vehicle steering error [36, 37]. On the basis of the least squares method, the corresponding parameters in the MPC controller are estimated according to the recursive idea as a way to improve the tracking accuracy [38]. By estimating as well as dynamically adjusting some parameters, the error is reduced, but the computational effort is slightly increased, and most importantly, the optimized of objective function is not considered. In complex nonlinear vehicle control systems, intelligent optimization algorithms combined with intelligent fuzzy modeling will further improve the performance of trajectory tracking controllers [39, 40].

The key to the optimization of the objective function in the MPC trajectory tracking controller is the selection of the prediction time domain and control time domain, because the values of different time domains determine the accuracy of the vehicle tracking trajectory [41]. In previous studies, the values of these two parameters often depended on personal experience. This method is inefficient and has large errors. In the current study, control time domain is adjusted using matrix chunking and applied to the quadratic solution. This method only considers the choice of the control time domain and ignores the adjustment of the prediction time domain [42]. In fact, use of intelligent optimization algorithms is a good choice in terms of objective function optimization. Based on the dynamics model, the optimal time domain is obtained by optimizing the objective function through the particle swarm optimization (PSO) algorithm, but the PSO algorithm tends to fall into local optimal solutions and does not guarantee global convergence [43]. In contrast to the PSO algorithm, sparrow search algorithm (SSA) as an emerging heuristic optimization algorithm, has shown excellent results in function optimization [44]. In addition to the function optimization function, the algorithm can be applied to robot path planning to find the optimal path [45, 46]. Although the sparrow search algorithm is simple in structure and easy to implement, the algorithm itself has some randomness and slow convergence speed.

In this research, an enhanced sparrow search algorithm-based optimization approach of MPC trajectory tracking controller for unmanned vehicles is proposed to address the issues raised by the aforementioned study. The key contributions of this study, as compared to earlier ones, are as follows.

(1) To implement the unmanned vehicle trajectory tracking, the vehicle's dynamics model is established, as well an objective function with restrictions, and a full MPC trajectory tracking controller are built.

(2) Throughout and beyond this paper, traditional SSA has been improved in three ways. The improved algorithm accelerates the convergence speed and enhances the search capability.

(3) Using improved sparrow search algorithm to optimize the objective function in MPC trajectory tracking controller. Solving for the prediction time domain and control time domain corresponding to the optimal fitness value. The simulation demonstrates that the proposed method reduces the deviation from real trajectory and reference trajectory of the vehicle.

Essay is structured like below. In Sect. 2, the dynamics model of the vehicle is established to prepare for subsequent trajectory tracking. Section 3 constructs the MPC trajectory tracking controller. The sparrow search algorithm is initially introduced in Sect. 4, followed by a discussion of its drawbacks and suggestions for improvements, and lastly, the introduction of the optimization process. Section 5 simulates and verifies the method proposed in this paper and analyzes the results. The paper is shown in Sect. 6.

2 Vehicle Dynamics Model

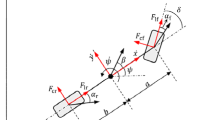
When the driverless vehicle tracks the reference trajectory, the vehicle motion must conform to the actual situation and satisfy the vehicle dynamics constraints. A vehicle dynamics model is developed in this study to represent the reality of vehicle motion, which is shown in Fig. 1.

Fig. 1
figure 1

Vehicle dynamics model

Full size image

Equations for the dynamics of the vehicle are.

$$\begin{aligned}m\ddot{y}&=-m\dot{x}\dot{\varphi }+2\left[{C}_{cf}\left(\delta -\frac{\dot{y}+{l}_{f}\dot{\varphi }}{\dot{x}}\right)+{C}_{cr}\left(\frac{{l}_{r}\dot{\varphi }-\dot{y}}{\dot{x}}\right)\right]\\ m\ddot{x}&=m\dot{y}\dot{\varphi }+2\left[{C}_{lf}{s}_{f}+{C}_{cf}\left(\delta -\frac{\dot{y}+{l}_{f}\dot{\varphi }}{\dot{x}}\right)\delta +{C}_{lr}{s}_{r}\right]\\ I\ddot{\varphi }&=2\left[{l}_{f}{C}_{cf}\left(\delta -\frac{\dot{y}+{l}_{f}\dot{\varphi }}{\dot{x}}\right)\delta -{l}_{r}{C}_{cr}\left(\frac{{l}_{r}\dot{\varphi }-\dot{y}}{\dot{x}}\right)\right]\\ \dot{Y}&=\dot{x}sin\varphi +\dot{y}cos\varphi \\ \dot{X}&=\dot{x}cos\varphi -\dot{y}sin\varphi \end{aligned}$$
(1)

Among them, \(m\) is the body mass, \(\varphi\) represents the yaw angle, \({C}_{lf}\) and \({C}_{lr}\) represent the longitudinal cornering stiffness of the front and rear tires, \({C}_{cf}\) and \({C}_{cr}\) is the lateral cornering stiffness of the front and rear tires, \({l}_{f}\) and \({l}_{r}\) denotes the distance from the center of mass of the vehicle to the front and rear axles, \(I\) represents the rotational inertia, \(\delta\) indicates the wheel turning angle. \({s}_{f}\) and \({s}_{r}\) represent the slip rate of the front and rear tires of the wheel.

Under Eq. (1), it suffices to known that the system state quantity \(\xi ={\left[\dot{y},\dot{x},\varphi ,\dot{\varphi },Y,X \right]}^{T}\), and the control quantity \(u=\updelta\)[47]. Its ordinary form is:

$$\begin{array}{c}\dot{\xi }=F\left(\xi ,u\right)\end{array}$$
(2)

The forward Eulerian discretization of Eq. (2) is applied to obtain.

$$\begin{array}{c}\xi \left(k+1\right)=\xi \left(k\right)+Tf\left(\xi \left(k\right),u\left(k\right)\right)\end{array}$$
(3)

where T is the system sampling time.

Linearize Eq. (3) and let it expand at the point \(\left({\xi }_{0},{u}_{0}\right)\)

$$\begin{array}{c}{\widetilde{\xi }}_{0}\left(k+1\right)=F\left({\widetilde{\xi }}_{0}\left(k\right),{u}_{0}\left(k\right)\right)\end{array}$$
(4)
$$\begin{aligned}\xi \left(k+1\right)&=F\left({\widetilde{\xi }}_{0}\left(k\right),{u}_{0}\left(k\right)\right)\\ & \quad +\frac{\partial F}{\partial \xi }{|}_{{\widetilde{\xi }}_{0}\left(k\right), \qquad {u}_{0}\left(k\right)}\left(\xi \left(k\right)-{\widetilde{\xi }}_{0}\left(k\right)\right)\\ & \quad +\frac{\partial F}{\partial u}{|}_{{\widetilde{\xi }}_{0}\left(k\right),{u}_{0}\left(k\right)}\left(u\left(k\right)-{u}_{0}\left(k\right)\right)\end{aligned}$$
(5)

Let \(\frac{\partial F}{\partial \xi }{|}_{{\widetilde{\xi }}_{0}\left(k\right),{u}_{0}\left(k\right)}={A}_{k,0}\), \(\frac{\partial F}{\partial u}{|}_{{\widetilde{\xi }}_{0}\left(k\right),{u}_{0}\left(k\right)}={B}_{k,0}\).

Then Eq. (5) can be rewritten as

$$\begin{aligned}\xi \left(k+1\right)&=F\left({\widetilde{\xi }}_{0}\left(k\right),{u}_{0}\left(k\right)\right)+{A}_{k,0}\left(\xi \left(k\right)-{\widetilde{\xi }}_{0}\left(k\right)\right)\\ & \quad +{B}_{k,0}\left(u\left(k\right)-{u}_{0}\left(k\right)\right)\end{aligned}$$
(6)

Equation (6) minus Eq. (4) yields

$$\begin{array}{c}\left\{\begin{array}{c}\xi \left(k+1\right)={A}_{k,0}\xi \left(k\right)+{B}_{k,0}u\left(k\right)+{d}_{k,0}\left(k\right)\\ {d}_{k,0}\left(k\right)={\widetilde{\xi }}_{0}\left(k+1\right)-{A}_{k,0}{\widetilde{\xi }}_{0}\left(k\right)-{B}_{k,0}{u}_{0}\left(k\right)\end{array}\right.\end{array}$$
(7)

The above is the expansion at the point \(\left({\xi }_{0},{u}_{0}\right)\), now choose any point \(\left({\xi }_{t},{u}_{t}\right)\) to obtain the expansion.

$$\begin{array}{c}\left\{\begin{array}{c}\xi \left(k+1\right)={A}_{k,t}\xi \left(k\right)+{B}_{k,t}u\left(k\right)+{d}_{k,t}\left(k\right)\\ {d}_{k,t}\left(k\right)={\widetilde{\xi }}_{t}\left(k+1\right)-{A}_{k,t}{\widetilde{\xi }}_{t}\left(k\right)-{B}_{k,t}{u}_{t}\left(k\right)\end{array}\right.\end{array}$$
(8)
$${\text{Among them}} {A}_{k,t} =\left[\begin{array}{cccccc}\frac{-2({C}_{cr}+{C}_{cf})}{m\dot{x}}& \frac{\partial {F}_{\dot{y}}}{\partial \dot{x}}& 0& -\dot{x}+\frac{2({l}_{r}{C}_{cr}-{l}_{f}{C}_{cf})}{m\dot{x}}& 0& 0\\ \dot{\varphi }-\frac{2{C}_{cf}\delta }{m\dot{x}}& \frac{\partial {F}_{\dot{x}}}{\partial \dot{x}}& 0& \dot{y}-\frac{2{l}_{f}{C}_{cf}\delta }{m\dot{x}}& 0& 0\\ 0& 0& 0& 1& 0& 0\\ \frac{2({l}_{r}{C}_{cr}-{l}_{f}{C}_{cf})}{I\dot{x}}& \frac{\partial {F}_{\dot{\varphi }}}{\partial \dot{x}}& 0& \frac{-2({{l}_{f}}^{2}{C}_{cf}+{{l}_{r}}^{2}{C}_{cr})}{I\dot{x}}& 0& 0\\ \mathit{cos}\left(\varphi \right)& sin(\varphi )& \dot{x}\mathit{cos}\left(\varphi \right)-\dot{y}sin(\varphi )& 0& 0& 0\\ -sin(\varphi )& \mathit{cos}\left(\varphi \right)& -\dot{y}\mathit{cos}\left(\varphi \right)-\dot{x}\mathit{sin}\left(\varphi \right)& 0& 0& 0\end{array}\right]$$
$${B}_{k,t}=\left[\begin{array}{cc}\frac{2{C}_{cf}}{m}& \begin{array}{cc}\frac{2{C}_{cf}(2\delta -\frac{\dot{y}+{l}_{f}\dot{\varphi }}{\dot{x}})}{m}& \begin{array}{cc}0& \begin{array}{cc}\frac{2{l}_{f}{C}_{cf}}{I}& \begin{array}{cc}0& 0\end{array}\end{array}\end{array}\end{array}\end{array}\right]$$
$$\frac{\partial{F}_{\dot{y}}}{\partial \dot{x}}=\frac{(2{C}_{cf}\left(\dot{y}+{l}_{f}\dot{\varphi}\right)+2{C}_{cr}\left(\dot{y}-{l}_{r}\dot{\varphi}\right))}{m{\dot{x}}^{2}}-\dot{\varphi}$$
$$\frac{\partial{F}_{\dot{x}}}{\partial \dot{x}}=\frac{2{C}_{cf}\delta (\dot{y}+{l}_{f}\dot{\varphi})}{m{\dot{x}}^{2}}$$
$$\frac{\partial{F}_{\dot{\varphi }}}{\partial \dot{x}}=\frac{2{l}_{f}{C}_{cf}\left(\dot{y}+{l}_{f}\dot{\varphi}\right)-2{l}_{r}{C}_{cr}\left(\dot{y}-{l}_{r}\dot{\varphi}\right)}{I{\dot{x}}^{2}}$$

Let \(\widehat{\xi}\left(k+1\right)=\left[\begin{array}{c}\xi (k+1)\\u(k)\end{array}\right]\), we can get

$$\begin{aligned} &\widehat{\xi}\left(k+1\right)=\left[\begin{array}{c}{A}_{k,t}\xi \left(k\right)+{B}_{k,t}u\left(k\right)+{d}_{k,t}\left(k\right)\\ u\left(k-1\right)+\Delta u\left(k\right)\end{array}\right]\\ & =\left[\begin{array}{cc}{A}_{k,t}& {B}_{k,t}\\ 0& 1\end{array}\right]\left[\begin{array}{c}\xi \left(k\right)\\ u\left(k-1\right)\end{array}\right]+\left[\begin{array}{c}{B}_{k,t}\\ 1\end{array}\right]\Delta u\left(k\right)+\left[\begin{array}{c}{d}_{k,t}\\ 0\end{array}\right]\end{aligned}$$
(9)

A new linear time-varying prediction model with control increments can be constructed from the above Eq. (9). As shown.

$$\begin{array}{c}\left\{\begin{array}{c}\widehat{\xi }\left(k+1\right)=\widehat{A}\widehat{\xi }\left(k\right)+\widehat{B}\Delta u\left(k\right)+{d}_{k}\\ \eta \left(k\right)=C\widehat{\xi }\left(k\right)\end{array}\right.\end{array}$$
(10)

Among them, \(\widehat{A}=\left[\begin{array}{cc}{A}_{k,t}& {B}_{k,t}\\ 0& 1\end{array}\right]\), \(\widehat{B}=\left[\begin{array}{c}{B}_{k,t}\\ 1\end{array}\right]\).

3 Design of MPC Trajectory Tracking Controller

3.1 Design Objective Function

Through continuous iterative inference Eq. (10), a system output expression with prediction time domain (\({N}_{p}\)) and control time domain (\({N}_{c}\)) can be obtained:

$$\begin{array}{c}Y=\Psi \xi +\Theta \Delta U+\Gamma \phi \end{array}$$
(11)

In Eq. (11):

$$\begin{aligned} \Psi & = \left[ {\begin{array}{*{20}c} {C\hat{A}} \\ {\begin{array}{*{20}c} {C\hat{A}^{2} } \\ {\begin{array}{*{20}c} \cdots \\ {\begin{array}{*{20}c} {C\hat{A}^{{N_{c} }} } \\ {\begin{array}{*{20}c} \cdots \\ {C\hat{A}^{{N_{P} }} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right], \\ \Delta U & = \left[ {\begin{array}{*{20}c} {\Delta u\left( k \right)} \\ {\Delta u\left( {k + 1} \right)} \\ {\begin{array}{*{20}c} \vdots \\ {\Delta u\left( {k + N_{c} - 1} \right)} \\ \end{array} } \\ \end{array} } \right],\phi = \left[ {\begin{array}{*{20}c} {d_{k} } & {d_{{k + 1}} } & {\begin{array}{*{20}c} \cdots & {d_{{k + N_{p} + 1}} } \\ \end{array} } \\ \end{array} } \right]^{T} \\ \Theta & = \left[ {\begin{array}{*{20}c} {C\hat{B}} & 0 & 0 & 0 \\ {C\hat{A}\hat{B}} & {C\hat{B}} & 0 & 0 \\ \cdots & \cdots & \ddots & \cdots \\ {C\hat{A}^{{N_{c} - 1}} \hat{B}} & {C\hat{A}^{{N_{c} - 2}} \hat{B}} & \cdots & {C\hat{B}} \\ {C\hat{A}^{{N_{c} }} \hat{B}} & {C\hat{A}^{{N_{c} - 1}} \hat{B}} & \cdots & {C\hat{A}\hat{B}} \\ \vdots & \vdots & \ddots & \vdots \\ {C\hat{A}^{{N_{P} - 1}} \hat{B}} & {C\hat{A}^{{N_{P} - 2}} \hat{B}} & \cdots & {C\hat{A}^{{N_{P} - N_{c} }} \hat{B}} \\ \end{array} } \right] \\ \Gamma & = \left[ {\begin{array}{*{20}c} C & \cdots & 0 \\ \vdots & \ddots & \vdots \\ {C\hat{A}^{{N_{p} - 1}} } & \cdots & C \\ \end{array} } \right] \\ \end{aligned}$$

It is worth noting that the MPC trajectory tracking controller are design to ensure that actual trajectory of the vehicle movement should be as close as possible to the reference trajectory. For this reason, it is necessary to add the optimization of the biases of the state quantities and the control quantities in the established objective function.

$$\begin{aligned}J&=\sum_{i=1}^{{N}_{p}}{\Vert \eta \left(t+i|t\right)-{\eta }_{ref}\left(t+i|t\right)\Vert }_{Q}^{2}\\ & \quad +\sum_{i=1}^{{N}_{c}-1}{\Vert \Delta U\left(t+i|t\right)\Vert }_{R}^{2}+\rho {\varepsilon }^{2}.\end{aligned}$$
(12)

where, on the right side of the equation, the first part represents the accuracy of the vehicle tracking a known trajectory, the second item represents the stationarity of the vehicle tracking a known trajectory, and the third item is the soft constraint, the purpose of which is to prevent the system from appearing a zero solution phenomenon. \(\eta\) is an actual state quantity generated by the actual motion of the vehicle, \({\eta }_{ref}\) represents the reference state quantity, \(\Delta U\) is control increment, \(Q\) and \(R\) are the weight matrix, \(\rho\) represents the weight coefficient, \(\varepsilon\) is the relaxation factor.

3.2 Design Constraints

Within the motion of the vehicle, the main consideration is the control quantity and the control increment constraints. The expressions of the two constraints are:

$$\begin{array}{c}\left\{\begin{array}{c}{u}_{min}\left({k}_{a}\right)\le u\left({k}_{a}\right)\le {u}_{max}\left({k}_{a}\right)\\ {\Delta u}_{min}\left({k}_{a}\right)\le \Delta u\left({k}_{a}\right)\le \Delta {u}_{max}\left({k}_{a}\right)\end{array}\right.\end{array}$$
(13)

In the above inequalities, \({k}_{a}=\text{0,1},2,\cdots ,{N}_{c}-1\).

The change of front wheel steering angle in driverless vehicle trajectory tracking is critical to the stability of the vehicle driving. To ensure that vehicles are safe while in motion, the front wheel turning angle need to are constrained:

$$\begin{array}{c}-2.5^\circ \le \delta \le +2.5^\circ \end{array}$$
(14)

Since, the model are solved to obtain the control increments, for which corresponding constraints must also contain control increments, converting the objective function to quadratic form is required.

By Eq. (11), let\(Y={\left[\begin{array}{cc}\eta (t+1)& \begin{array}{cc}\eta (t+2)& \begin{array}{cc}\cdots & \eta (t+{N}_{p})\end{array}\end{array}\end{array}\right]}^{T}\), \(Y_{ref} = \left[ {\begin{array}{*{20}c} {\eta_{ref} (t + 1)} & {\begin{array}{*{20}c} {\eta_{ref} (t + 2)} & {\begin{array}{*{20}c} \cdots & {\eta_{ref} (t + N_p )} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]^T\), and Eq. (12) can be reduced to:

$$\begin{array}{*{20}c} {J = \left[ {Y - Y_{ref} } \right]^T \overline{Q}\left[ {Y - Y_{ref} } \right] + \Delta U^T \overline{R}\Delta U + \varepsilon^T \rho \varepsilon } \\ \end{array}$$
(15)

Among them, \(\overline{Q} = \left[ {\begin{array}{*{20}c} Q & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & Q \\ \end{array} } \right]_{N_p \times N_p }\), \(\overline{R} = \left[ {\begin{array}{*{20}c} R & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & R \\ \end{array} } \right]_{N_c \times N_c }\).

Bringing Eq. (11) into Eq. (15), we get

$$\begin{aligned} J &= \left[ {\Psi \xi + \Theta \Delta U + {\Gamma }\phi - Y_{ref} } \right]^T \\ & \quad \overline{Q}\left[ {\Psi \xi + \Theta \Delta U + {\Gamma }\phi - Y_{ref} } \right] + \Delta U^T \overline{R}\Delta U + \varepsilon^T \rho \varepsilon \end{aligned}$$
(16)

Let \(E = Y_{ref} - { }\Psi \xi - {\Gamma }\phi\).

And so

$$\begin{aligned} J &= \left[ {\Theta \Delta U - E} \right]^T \overline{Q}\left[ {\Theta \Delta U - E} \right] + \Delta U^T \overline{R}\Delta U + \varepsilon^T \rho \varepsilon \\ & = \left[ {\Delta U^T \Theta^T - E^T } \right]\overline{Q}\left[ {\Theta \Delta U - E} \right] + \Delta U^T \overline{R}\Delta U + \varepsilon^T \\ &= \Delta U^T \left[ {\Theta^T \overline{Q}\Theta + \overline{R}} \right]\Delta U - 2E^T \overline{Q}\Theta \Delta U + E^T \overline{Q}E + \varepsilon^T \rho \varepsilon \\ \end{aligned}$$
(17)

Constructing Eq. (17) into quadratic form as

$$\begin{array}{*{20}c} {J = \frac{1}{2}\left[ {\begin{array}{*{20}c} {\Delta U} & \varepsilon \\ \end{array} } \right]H\left[ {\begin{array}{*{20}c} {\Delta U} \\ \varepsilon \\ \end{array} } \right] + f^T \left[ {\begin{array}{*{20}c} {\Delta U} \\ \varepsilon \\ \end{array} } \right] } \\ \end{array}$$
(18)

Among them, \(H = \left[ {\begin{array}{*{20}c} {2\Theta^T \overline{Q}\Theta + 2\overline{R}} & 0 \\ 0 & {2\rho } \\ \end{array} } \right]\), \(f = \left[ {\begin{array}{*{20}c} { - 2e^T \overline{Q}\Theta } & 0 \\ \end{array} } \right]^T\), \(e\) represents the tracking error in the prediction time domain.

4 Optimized MPC Trajectory Tracking Controller

4.1 Vehicle Tracking Trajectory Simulation Comparison in Different Time Domains

In the constructed objective function, prediction time domain and control time domain affect accuracy of the vehicle tracking reference trajectory. For these two parameters, the traditional method is to adjust and select relatively appropriate values through personal experience, but this method is too inefficient and may cause larger errors.

Taking the circular trajectory as an example, as seen in Fig. 2, different prediction time domains and control time domains have a great impact on the tracking of the reference trajectory of the driverless vehicle. When \(N_p = 12\), \(N_c = 5\), the vehicle driving trajectory will have large fluctuations, the tracking effect will become worse, and the vehicle stability will be reduced. Similarly, when \(N_p = 10\), \(N_c = 3\), the vehicle trajectory is still very volatile and has a large tracking error. Therefore, selecting the suitable prediction time domain and control time domain are important for the trajectory tracking of driverless vehicles.

Fig. 2
figure 2

Comparison of vehicle tracking trajectories in different time domains

Full size image

4.2 Sparrow Search Algorithm

Sparrow search algorithm is an emerging optimization algorithm that simulates the scavenging and anti-predation behavior in sparrows through continuously updating individual positions. The sparrow search algorithm features fewer control parameters, a simpler structure, and better local search performance than the conventional optimization algorithm [44]. It performs better than some classic algorithms in a few distinct search areas and is somewhat superior to them. Figure 3 depicts the algorithm's optimization procedure.

Fig. 3
figure 3

Sparrow search algorithm optimization process

Full size image

In the figure below, the producer indicates that in the process of searching, it will preferentially find food and provide all scroungers with a foraging area and direction. Its position update formula is:

$$\begin{array}{*{20}c} {X_{i,j}^{t + 1} = \left\{ {\begin{array}{*{20}c} {X_{i,j}^t {\text{*exp}}\left( {\frac{ - i}{{\alpha \cdot I_{{\text{max}}} }}} \right){\text{ if }}AV < ST} \\ {X_{i,j}^t + r_1 {*}L{\text{ if }}AV \ge ST} \\ \end{array} } \right.} \\ \end{array}$$
(19)

In Eq. (19), \(t\) refers to the iteration count of current, \(X_{i,j}^t\) represents positions at the j-th dimension of the i-th sparrow on t-th generation, \(\alpha \in (0,1)\), \(I_{max}\) is total number of optimization process iterations, and \(AV\) denotes warning value, \(ST\) indicates security value, \(r_1\) represents one random number, \(L\) denotes a \(1 \times d\) matrix, and \(d\) represents the dimension.

Scroungers will constantly be spying on producers, and as they find that producers have found great food, they will compete for the food. Its position update formula is:

$$\begin{aligned} &X_{i,j} \left( {t + 1} \right) \\ &\quad = \left\{ \begin{array}{ll} r_1 {\text{*exp}}\left( \frac{{x_w \left( t \right) - X_{i,j} \left( t \right)}}{i^2 } \right)& i > \frac{n}{2} \\ X_p \left( {t + 1} \right) + \left| X_{i,j} \left( t \right) - X_p \left( {t + 1} \right) \right|{*}A^+ {*}L & i \le \frac{n}{2} \\ \end{array} \right. \end{aligned}$$
(20)

where \(X_p \left( {t + 1} \right)\) represents position with an optimum fitness value in current finder, \(x_w \left( t \right)\) denotes the position with the worst global fitness, \(A\) represents a column vector with the same dimension as the individual sparrow, and \(n\) represents the population quantity.

Vigilantes will quickly move towards the safe area when aware of the danger to get a position in better. Its position optimization equation is:

$$X_{i,j} \left( {t + 1} \right) = \left\{ \begin{array}{*{20}c} X_b \left( t \right) + \beta {*}\left| {X_{i,j} \left( t \right) - X_b \left( t \right)} \right|& f_i > f_g \\ X_{i,j} \left( t \right) + K{*}\left( {\frac{{X_{i,j} \left( t \right) - X_w \left( t \right)}}{{\left( {f_i - f_w } \right) + \varepsilon }} }\right)& f_i = f_g \\ \end{array} \right.$$
(21)

Among them, \(X_b \left( t \right)\) represents current global optimal position, \(\beta\) indicates step size, \(K \in [ - 1,1]\), \(f_i\) denotes the fitness value assigned to the current sparrow individually. \(f_g\) and \(f_w\) are the current global best and worst fitness values respectively, \(\varepsilon\) indicates a small constant to prevent zeros in denominators.

4.3 Improved Good Point-Set

Traditional SSA populations are initialized with a high degree of randomness. This randomness often represents an uncertainty and the population is not uniformly distributed in space. Optimizing sparrow positions using good point set to enhance global search capability for algorithms.

$$\begin{array}{*{20}c} {r_j = mod\left( {2\cos \left( {\frac{2\pi j}{p}} \right),1} \right) } \\ \end{array}$$
(22)
$$\begin{array}{*{20}c} {P_m \left( i \right) = \left\{ {\left( {r_1 i_1 ,r_2 i_2 { }, \cdots ,r_m i_m } \right)} \right\} } \\ \end{array}$$
(23)
$$\begin{array}{*{20}c} {X_i^j = a_j + P_n \left( i \right)\left( {b_j - a_j } \right) } \\ \end{array}$$
(24)

Among them, \(1 < j < n\), \(i = 1,2,3, \cdots ,m\), \(n\) denotes the spatial dimension, \(m\) is the number of populations, \(r_j\) shows the good point, \(P_n\) means good point collection, \(a_j\) indicates the upper limit of the current dimension, \(b_j\) is the lower limit of the current dimension。

Since, the value of good points in the set of good points is determined by \(p\) and the value is not fixed. If the value of the good point is too large, the population will disperse to the spatial edge, and if the value of the good point is too small, the population will be clustered to the spatial center. For this reason, the range of values of good points is improved in this paper as follows.

$$\begin{array}{*{20}c} {p = n + \left( {\frac{m - t}{t}} \right) } \\ \end{array}$$
(25)

where, \(t\) represents the current number of iterations.

As the number of iterations increases, the populations are gradually distributed over the space.

4.4 Improved Producer Position Updates

During the conventional sparrow search algorithm location update when \(AV \ge ST\), the producer enters the search mode, and the parameter a in its position update formula has randomness, and the size of its value directly influences the speed of convergence as well algorithm accuracy.

To increase the convergence speed of algorithms, a larger value of \(\alpha\) can expand search range of the sparrow in preliminary iterations with algorithm, and the value of \(\alpha\) needs to be reduced in the late iteration in order to increase the convergence speed of traditional algorithm. Then, the improved \(\alpha\):

$$\begin{array}{*{20}c} {\alpha = \left( {1 - \frac{t}{{I_{max} }} + \varepsilon } \right) } \\ \end{array}$$
(26)

In the above equation, \(t\) refers to the iteration count of current, \(I_{max}\) is total number of optimization process iterations, \(\varepsilon\) indicates constant, the purpose is to prevent zero solution.

In addition, with the increase of the number of iterations, the local search ability of producers in sparrow population will be reduced, which will lead to the decline of population optimization ability. Therefore, the local search ability should be strengthened in the later iteration of the producer position update entering the search mode. Then, combined with formula (19), the improved finder position update formula is:

$$X_{i,j}^{t + 1} = \left\{ \begin{array}{*{20}c} X_{i,j}^t {*}exp\left( \frac{ - i}{{\left( {1 - \frac{t}{{I_{max} }} + \varepsilon } \right) \cdot I_{max} }} \right)^{\exp \left( \frac{1}{t} \right)} & if\quad AV < ST \\ X_{i,j}^t + r_1 {*}L& if\quad AV \ge ST \\ \end{array} \right.$$
(27)

4.5 Improved Vigilante Position Updates

When the sparrow realizes the danger, it must immediately approach the safe area. Due to randomness of the moving step length \(K\), the sparrow moves slowly and the short step length will lead to the decrease of the sparrow fitness value at the current position. The sparrow moves fast and the increase of the step length will lead to the decrease of the accuracy of the algorithm. In order to meet the need for location updates in different periods and to take into account the global search as well as the local search capability of the algorithm, Then, the improved \(K\):

$$\begin{array}{*{20}c} {K = b + \frac{a - b}{{1 + \exp \left( { - 0.05\left( {\frac{2t}{{T - 1}}} \right)} \right)}} } \\ \end{array}$$
(28)

In Eq. (28), \(a\) and \(b\) are the upper and lower population limits, respectively, and \(T\) is the number of iterations. When the algorithm optimization enters the late iteration, the value of \(K\) gradually decreases and the algorithm global search as well as local search capability will be gradually enhanced. The complete formula is as follows.

$$X_{i,j} \left( {t + 1} \right) = \left\{ {\begin{array}{ll} X_b \left( t \right) + \beta {*}\left| {X_{i,j} \left( t \right) - X_b \left( t \right)} \right|{ }&f_i > f_g \hfill \\ X_{i,j} \left( t \right) + b + \frac{a - b}{{1 + \exp \left( {\frac{ - 0.1t}{{T - 1}}} \right)}}{*}\left( {\frac{{X_{i,j} \left( t \right) - X_w \left( t \right)}}{{\left( {f_i - f_w } \right) + \varepsilon }}} \right){ }&f_i = f_g \hfill \\ \end{array} } \right.$$
(29)

4.6 Algorithm Combination

An optimization method of MPC trajectory tracking controller for driverless vehicles based on improved sparrow search algorithm is proposed in this paper. By using the optimization ability of the improved sparrow search algorithm, the objective function in the MPC trajectory tracking controller is optimized and the prediction time domain and control time domain corresponding to the optimal fitness value are obtained. The specific combination process is shown in Fig. 4.

Fig. 4
figure 4

Algorithm combination process

Full size image

Step 1: Generate an initial population and assign initial values.

Step 2: Initialization of sparrow positions and calculation with corresponding fitness assigns sparrow positions in each dimension to \(Np\) and \(Nc\) accordingly.

Step 3: Run the system model.

Step 4: The sum of position and yaw angle deviation between the reference trajectory and the actual trajectory output by the system is taken as the fitness value.

Step 5: It is judged whether the end condition is satisfied, and if yes, it ends; otherwise, steps (6) to (7) are executed.

Step 6: Iteratively update the position of the producer, scrounger, and vigilante.

Step 7: The new fitness value is calculated and sparrow position is updated, continue with steps (2) to (5).

5 Simulation Experiments and Analysis

5.1 Co-simulation of Carsim and Simulink

This paper chooses using Carsim and simulink in collaborative simulations. The simulation platform are shown in Fig. 5. Firstly, build the MPC trajectory tracking controller in Simulink and determine the inputs and outputs of the system to satisfy the vehicle motion; Then, build a vehicle model in Carsim and select inputs and outputs that match the MPC trajectory tracking controller. The front wheel steering angle and speed are output by the MPC trajectory tracking controller, which controls the vehicle tracking reference trajectory in Carsim. For better verification of the method proposed for this paper, the double lane change trajectory and the lane change trajectory are specially selected as the reference trajectory to verify the feasibility on the method. The system framework is shown in Fig. 6. The main parameters are shown in Table 1.

Fig. 5
figure 5

Co-simulation platform

Full size image
Fig. 6
figure 6

System framework

Full size image
Table 1 Main parameters
Full size table

5.2 Algorithm Performance Test Comparison

The optimization capability of ISSA must be tested before conducting joint simulations. In Table 2\(F_1 \sim F_3\) are single-peaked benchmark functions with only one optimal value, whose main investigation is the global search ability of the optimization algorithm. \(F_4 \sim F_6\) are multi-peaked benchmark functions, which contain multiple optimal values and are designed to evaluate the local search capability of the optimization algorithm.

Table 2 Description of benchmark functions
Full size table

Figure 7 compares the optimization capability of ISSA with PSO, SSA and the whale optimization algorithm (WOA) [48]. Among them, Fig. 7a–c show the comparison of the results of three optimization algorithms to optimize \(F_1 \sim F_3\), respectively, and it can be seen that ISSA can effectively find the minimum value and has a better global search capability. Figure 7d–f shows the comparison of the results of three optimization algorithms to optimize \(F_4 \sim F_6\), respectively. It can be seen that ISSA can quickly reach the convergence state and find the optimal value with better local search ability. In summary, it can be seen that ISSA has better global search and local search ability after testing and comparison.

Fig. 7
figure 7

Comparison of ISSA, SSA, WOA and PSO function optimization

Full size image

5.3 Track Double Lane Change Trajectories

Figure 8a shows the optimal values obtained by ISSA optimally solving the MPC trajectory tracking control model. The optimal value in Fig. 8a when the curve reaches convergence is 0.0773. Figure 8b represent the prediction time domain and control time domain obtained by ISSA to optimize the objective function. It should be particularly noted that the values of the \(N_p\) and \(N_c\) must be positive integers. Throughout the optimization iteration, when the curve reaches the final convergence state and stabilizes, the values should be taken according to the “rounding” rule. From the figure, the ISSA optimization objective function obtains the \(N_p = 16\), \(N_c = 3\).

Fig. 8
figure 8

ISSA-optimized MPC trajectory tracking controller under double lane change work conditions

Full size image

Figure 9a–d represent, comparison of MPC and ISSA + MPC tracking reference trajectory at vehicle speed of 36 km/h. \(N_p = 12\) and \(N_c = 3\) selected for MPC controller. In addition, this paper also designs and compares an MPC trajectory tracking controller based on neural network (NN-MPC) optimization. The optimization results of this method are \(N_p = 35\), \(N_c = 5\). The lateral trajectory generated by the MPC controller in Fig. 9a generated oscillations in the 7 ~ 15 s interval. The ISSA + MPC controller generates a smoother lateral trajectory. The lateral errors generated by MPC controller and NN-MPC controller in Fig. 9b and c as well as the wheel turning angle still fluctuate considerably, and the lateral acceleration shown in Fig. 9d is extremely unstable. However, the lateral error and lateral acceleration generated by ISSA + MPC gradually converge to zero, and the steering control is more stable.

Fig. 9
figure 9

Comparison of ISSA + MPC trajectory tracking effect under 36 km/h and 54 km/h velocity

Full size image

When the speed is increased to 54 km/h, the lateral trajectory generated by MPC controller in Fig. 9e still has fluctuations, and the lateral trajectory generated by ISSA + MPC controller is smoother and has a better tracking effect in the straight line interval. The lateral error and lateral acceleration generated by the ISSA + MPC controller in Fig. 9f and h do not fluctuate, and the lateral error is stable in the \(\pm 0.5\) m interval and tends to zero after 6s. The vehicle turning angle generated by the ISSA + MPC controller in Fig. 9g remains smooth. However, the lateral error, front wheel turning angle, and lateral acceleration generated by the MPC controller fluctuate continuously as the speed increases. The lateral error results generated by the three controllers are shown in Table 3.

Table 3 Maximum value of lateral error comparison
Full size table

5.4 Track Lane Change Trajectories

The optimal value in Fig. 10a when the curve reaches convergence is 0.0229817. Throughout the optimization iteration, when the curve reaches the final convergence state and stabilizes, the values should be taken according to the “rounding” rule. From the figure, the ISSA optimization objective function obtains the \(N_p = 13\), \(N_c = 13\). The optimization results of the NN-MPC controller are the same as those in Sect. 5.2.

Fig. 10
figure 10

ISSA-optimized MPC trajectory tracking controller under lane change work conditions

Full size image

Also, in this simulation the MPC controller is still chosen for \(N_p = 12\) and \(N_c = 5\). The lateral trajectory generated by the MPC controller in Fig. 11a at a vehicle speed of 36 km/h produced oscillations in the 15 ~ 20 s interval. The lateral trajectory generated by the ISSA + MPC controller remains smooth. The lateral errors generated by the MPC controller in Fig. 11b and c as well as the wheel turning angle still fluctuate considerably, and the lateral acceleration shown in Fig. 11d is extremely unstable. The lateral error generated by the NN-MPC controller is larger. Nevertheless, the lateral error and lateral acceleration generated by ISSA + MPC gradually converge to zero, and the steering control is more stabilized.

Fig. 11
figure 11

Comparison of ISSA + MPC trajectory tracking effect under 36 km/h and 54 km/h velocity

Full size image

While, the velocity increases to 54 km/h, the lateral trajectory generated by the MPC controller in Fig. 11e still fluctuates, and the lateral trajectory generated by the ISSA + MPC controller is flatter during the whole tracking process. The lateral acceleration of the lateral error generated by the ISSA + MPC controller in Fig. 11f and h does not fluctuate, and the lateral error stabilizes in the \(\pm 0.1\) m interval and tends to zero after 10 s. The vehicle turning angle generated by the ISSA + MPC controller in Fig. 11g is still smooth. Therefore, the lateral error, front wheel angle, and lateral acceleration generated by the MPC controller still fluctuate as the speed increases. The lateral error results generated by the three controllers are shown in Table 4.

Table 4 Maximum value of lateral error comparison
Full size table

6 Conclusion

In this paper, the effects of prediction time domain and control time domain in MPC trajectory tracking controller on vehicle trajectory tracking accuracy are investigated. By improving the traditional sparrow search algorithm and designing the performance evaluation function, an MPC trajectory tracking controller optimization method based on the improved sparrow search algorithm is proposed to improve the trajectory tracking accuracy. Through simulation analyzes, to draw the below concluded:

(1)In order to improve the convergence speed and search capability of the algorithm, the traditional sparrow search algorithm is improved. The simulation comparison of the tested optimized benchmark functions shows that ISSA outperforms SSA and WOA in function optimization.

(2)The simulation results show that when the vehicle speed is 36 km/h, the lateral error of the ISSA optimized MPC trajectory tracking controller is reduced by 68.98% and 81.08% compared with the MPC controller, and by 67.95% and 76.94% compared with the NN-MPC controller, respectively. When the vehicle speed is 54 km/h, the lateral error of the MPC controller is reduced by 65.44% and 86.76%, respectively, and that of the NN-MPC controller is reduced by 78.43% and 72.35%. The results show that the ISSA improved MPC trajectory tracking controller is superior to the traditional MPC controller and NN-MPC controller in terms of tracking accuracy.