Variable step MPC trajectory tracking control method for intelligent vehicle

Abstract

To improve the accuracy, real-time and stability of intelligent vehicle path tracking control algorithms, a variable Step Model Predictive Control method (VMPC) for path tracking based on Model Predictive Method (MPC) is proposed. A vehicle dynamics model considering path tracking was constructed, and a VMPC controller was designed based on the model. To address cumulative model error, the proposed control method employs a zero-order holder-based short-step discretization prediction model in the front part of the prediction interval and a first-order holder-based long-step discretization prediction model in the back part. Carsim/Simulink co-simulations were conducted to compare the performance of the proposed VMPC controller with that of a traditional MPC controller on double-lane roads and highways. The simulation results indicate that the proposed VMPC controller exhibits superior control precision, smoothness, real-time performance, and dynamic stability. The proposed method decreases 56.6% for the lateral error, 52.4% for the heading error, 28.5% for the sideslip angle, and 45.7% for the average solution time at most when compared to a standard MPC. Experiments were performed on a drive-by-wire integrated chassis platform, which confirmed that the proposed VMPC controller achieves desired tracking control accuracy for variable curvature paths in engineering applications.

1 Introduction

Recent advancements in artificial intelligence and the automobile industry have facilitated the development of intelligent driving technology [5, 7, 28]. The intelligent driving system, comprising environmental perception, high-precision positioning, behavior decision-making, and planning control, is integral to autonomous driving. Precise and stable tracking control of the planned path remains a key research focus and challenge in the field of intelligent vehicle planning and control.

To enhance the reliability and safety of intelligent vehicle path tracking, researchers have proposed various methods, including pure pursuit tracking control [31, 32], PID control [24], slide mode control (SMC) [10, 13], backstepping control [1], linear quadratic regulator (LQR) tracking control [34], and output feedback control [27, 33], etc. Notably, considering the relationship between the vehicle and the path, the forward viewpoint is heuristically selected to improve the tracking accuracy [2]. In [20,21,22,23], output feedback controllers for four in-wheel motors were designed to boost lateral stability and balance of the vehicle when the lane keeping system is working, but the real-time performance of the control is not considered. Although these methods have achieved significant results in the field of intelligent driving, they cannot effectively address the multi-constraint problem of vehicle dynamics.

Model Predictive Control (MPC) is a control strategy that uses a mathematical model of the system to predict its future behavior and optimize the control actions over a finite time horizon. It has been used in various fields such as process control, robotics, power systems, and transportation systems. The main advantages of MPC are its ability to handle constraints and optimize the system performance over a finite time horizon. It can account for system nonlinearities and uncertainties, and can handle multiple objectives and constraints simultaneously. Additionally, MPC is a closed-loop controller that can adaptively adjust the control actions based on the system’s actual performance. In transportation systems, MPC is used for path planning and control of autonomous vehicles [11, 35]. MPC can incorporate constraints into the control process, providing a solution to the multi-constraint problem and improving vehicle path tracking accuracy [3]. In the field of autonomous vehicles, these advantages have led to the widespread adoption of MPC. A multi-constraint MPC has been proposed to calculate the desired front wheel angle for path tracking, enabling high-speed path tracking for intelligent vehicles in [8]. In [12], an implicit linear model predictive control method was proposed. The controller can deal with the modeling error by using variable sampling time and variable prediction time domain. In [15], an obstacle avoidance path planning algorithm based on real-time output constraint model predictive control is proposed to alleviate the problem of drastic change of steering and improve the tracking accuracy. In [6], the authors proposed a linear time-varying model predictive controller considering steering characteristics. It has good adaptability under complex conditions and improves tracking stability and driving safety. In [18], an adaptive MPC has been developed to estimate tire cornering stiffness and road adhesion coefficient online, enhancing tracking accuracy and stability. In [9], a MPC lateral controller with adaptive preview characteristics was proposed. Cooperative path-planning and tracking controller for driverless vehicles via a distributed MPC was discussed in [14]. In [29], a nonlinear MPC and mixed-integer quadratic program were developed for the cooperative trajectory-planning problem for autonomous driving. A longitudinal vehicle speed auxiliary constraint based on the maximum ideal lateral acceleration was added to improve the path tracking performance. The authors presented a novel integrated path tracking control strategy for self-driving vehicles in [4]. The proposed strategy combines a multi-input multi-output linear model predictive control and a fuzzy logic switching system for improved vehicle stability. In [16], a real-time nonlinear model predictive control (NMPC) controller for all-wheel independent motor-drive electric vehicles. This controller enhances both vehicle longitudinal and lateral stability.

MPC control can ensure high tracking accuracy in intelligent vehicle path tracking [17]. However, the underlying principle of MPC involves the use of the current state and future control sequence of the constructed model to predict the future output sequence of the system. This approach involves an optimal solution process that results in an optimal solution during each prediction period [30]. Despite its advantages, it is challenging to ensure that the optimal solution is achieved within the control period due to the extensive calculation. Therefore, ensuring real-time performance is a crucial aspect of MPC control. How to improve the tracking accuracy of MPC and enhance its real-time performance remain an important area of research. Therefore, this paper proposed a novel VMPC method to improve the accuracy, real-time and stability for intelligent vehicle path tracking. The main contributions of this paper are as follows.

• An enhanced three-degree-of-freedom vehicle model that incorporates the lateral error and heading error associated with vehicle path tracking is built. The proposed vehicle dynamics reflects the motion state of the vehicle and effectively capture the impact of vehicle path tracking.

• A variable step size MPC controller is designed via the vehicle dynamics model considering path tracking. This approach leverages the vehicle dynamics model and incorporates variable step sizes for both short and long intervals to achieve prediction accuracy and real-time control.

• The effectiveness of the VMPC controller is verified through practical vehicle testing using a drive-by-wire integrated chassis experimental platform.

The rest of the paper is structured as follows: Section 2 outlines the construction of the vehicle dynamics model considering path tracking. Section 3 elucidates the design of the VMPC. Section 4 presents the simulation results and analysis. Section 5 introduces the experiments. And the conclusions are given in Sect. 6.

2 Vehicle dynamics model considering path tracking

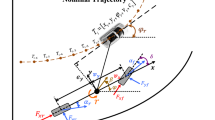
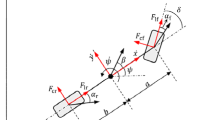
In most literature, a two-DOF models are built considering lateral forces and moments balance for vehicle dynamics analysis. For example, in [19], a two-DOF model at high vehicle speed was presented which includes the heading angle and sideslip angle. These models mainly focus on the lateral dynamics. A lateral vehicle dynamics model of two-DOF which was represented by the lateral position and yaw angle at higher vehicle speed was proposed in [25] which considered the lanes. A baseline model with lateral vehicle dynamics was proposed in [26] for path tracking. Inspired by these vehicle dynamics models, in this study, we employ a three-DOF model that accounts for vehicle velocity, lateral and yaw motion to reduce computational complexity and enhance lateral control accuracy during path tracking. This dynamics model combines the lateral dynamics model with path tracking model. Figures 1 and 2 depict this three-DOF model.

Fig. 1

Two wheels dynamics model

As shown in Fig. 1, according to Newton’s law, vehicle lateral force balance equation and torque balance equation are expressed as

$$\begin{aligned} \begin{aligned}&m(\ddot{y}+\dot{x} \dot{\varphi })=F_{yf}\cos \delta _{f} + F_{yr}\\&I_{z}\ddot{\varphi }= l_{f}F_{yf}\cos \delta _{f} - l_{r}F_{yr}, \end{aligned} \end{aligned}$$

(1)

where m is the vehicle mass, $I_z$ is the moment of inertia, $\delta _f$ is the front wheel angle, $\ddot{y}$ and $\dot{x}$ are the lateral acceleration and longitudinal velocity of the vehicle respectively, $\dot{\varphi }$ and $\ddot{\varphi }$ are the yaw rate and yaw angular acceleration respectively, $F_{xf}$ and $F_{xr}$ are the longitudinal forces of front and rear wheels respectively, $F_{yf}$ and $F_{yr}$ are the lateral forces of front and rear wheels respectively, $l_{f}$ is the distance from front axle to centroid, and $l_{r}$ is the distance from rear axle to centroid.

Under normal conditions, the tire remains within the elastic cornering region. Consequently, the tire cornering forces can be approximated as a linear function of the tire cornering angle.

$$\begin{aligned} \begin{aligned}&F_{yf} = 2C_{\alpha f}\alpha _{f} \\&F_{yr} = 2C_{\alpha r}\alpha _{r}, \end{aligned} \end{aligned}$$

(2)

where $C_{\alpha f}$ and $C_{\alpha r}$ are the cornering stiffnesses of the front wheel and rear wheel respectively, $\alpha _f$ and $\alpha _r$ are the side slip angles of the front wheel and rear wheel respectively.

For evaluating the path tracking effect, we introduce two metrics, the lateral error and heading error of vehicle path tracking. A kinematics model considering path tracking is established and depicted in Fig. 2.

Fig. 2

Path tracking model

Fig. 3

Lateral error and heading error of path tracking

As shown in Fig. 3, the lateral error and heading error of vehicle path tracking are

$$\begin{aligned} \begin{aligned}&e_{y} = -(X - X_{ref})\sin \varphi _{ref} + (Y-Y_{ref})\cos \varphi _{ref}\\&e_{\varphi } = \varphi - \varphi _{ref}, \end{aligned} \end{aligned}$$

(3)

where $e_{y}$ and $e_{\varphi }$ are the lateral error and heading error respectively, (X, Y) is the coordinates of centroid, $(X_{ref}, Y_{ref})$ is the coordinates of the reference point in the reference path, $\varphi$ is the heading angle of the vehicle, $\varphi _{ref}$ is the heading angle of the reference point.

To establish the three-DOF model considering path tracking, we combine the lateral error and heading error of vehicle path tracking with the two wheels dynamics model and calculate the transformation relationship between them. From the reference point, it is easy to know the reference lateral acceleration and the reference yaw rate.

$$\begin{aligned} \begin{aligned}&v_{x}=\dot{x}\\&a_{yref} = v_{x}^2 / R\\&\dot{\varphi }_{ref} = v_{x} / R, \end{aligned} \end{aligned}$$

(4)

where x is the longitudinal displacement, $v_{x}$ is the longitudinal velocity, $a_{yref}$ and $\dot{\varphi }_{ref}$ are the reference lateral acceleration and the reference yaw rate respectively, R is the road radius of curvature.

According to Eqs.(1)–(4), the derivative of the lateral error change rate is

$$\begin{aligned} \begin{aligned} \ddot{e}_{y}&= a_{y} - a_{yref} = (\ddot{y} + v_{x}\dot{\varphi }) - v_{x}^2 / {R} \\&= \ddot{y} + v_{x}(\dot{\varphi }- \dot{\varphi }_{ref}) = \ddot{y} + v_{x}\dot{e}_{\varphi }. \end{aligned} \end{aligned}$$

(5)

The lateral error change rate can be directly obtained by integrating from Eq.(5) as

$$\begin{aligned} \begin{aligned} \dot{e}_{y} = \dot{y} + v_{x}e_{\varphi } \end{aligned}. \end{aligned}$$

(6)

The heading error change rate is

$$\begin{aligned} \begin{aligned} \dot{e}_{\varphi } = \dot{\varphi }- \dot{\varphi }_{ref} = \dot{\varphi }- v_{x} / {R} \end{aligned}. \end{aligned}$$

(7)

The derivative of the heading error change rate can be obtained directly by differentiating Eq.(7) as

$$\begin{aligned} \begin{aligned} \ddot{e}_{\varphi } = \ddot{\varphi }- \ddot{\varphi }_{ref} \end{aligned}. \end{aligned}$$

(8)

According to Eqs.(5), (6), (7), and (8), one obtains

$$\begin{aligned} \begin{aligned} \ddot{y}&= \ddot{e}_{y} - v_{x}\dot{e}_{\varphi }\\ \dot{y}&= \dot{e}_{y} - v_{x}e_{\varphi }\\ \ddot{\varphi }&= \ddot{e}_{\varphi } + \ddot{\varphi }_{ref}\\ \dot{\varphi }&= \dot{e}_{\varphi } + \dot{\varphi }_{ref}. \end{aligned} \end{aligned}$$

(9)

Via Eqs.(3) and (9), the differential equations of motion for the path tracking dynamic model can be expressed as

$$\begin{aligned} \begin{aligned} \ddot{e}_{y}&= -\frac{2C_{\alpha f}+2C_{\alpha r}}{mv_{x}}\dot{e}_{y} + \frac{2C_{\alpha f}+2C_{\alpha r}}{m}e_{\varphi } \\&+ \frac{-2l_{f}C_{\alpha f}+2l_{r}C_{\alpha r}}{mv_{x}}\dot{e}_{\varphi } +\frac{2C_{\alpha f}}{m}\delta _{f} \\&+\left( \frac{-2l_{f}C_{\alpha f}+2l_{r}C_{\alpha r}}{mv_{x}} - v_{x}\right) \dot{\varphi }_{ref}\\ \ddot{e}_{\varphi }&= \frac{-2l_{f}C_{\alpha f}+2l_{f}C_{\alpha r}}{I_{z}v_{x}}\dot{e}_{y} + \frac{2l_{f}C_{\alpha f}-2l_{r}C_{\alpha r}}{I_{z}}e_{\varphi } \\&-\frac{2l_{f}^2C_{\alpha f}+2l_{r}^2C_{\alpha r}}{I_{z}v_{x}}\dot{e}_{\varphi } +\frac{2l_{f}C_{\alpha f}}{I_{z}}\delta _{f} \\&-\frac{2l_{f}^2C_{\alpha f}+2l_{r}^2C_{\alpha r}}{I_{z}v_{x}}\dot{\varphi }_{ref}. \end{aligned} \end{aligned}$$

(10)

According to the above model, we define the state variables of the model as $x(t) = [e_y,\dot{e}_{y}, e_\varphi ,\dot{e}_\varphi ]$ and the control variable as $u(t)=\delta _f(t)$. The time-varying vehicle dynamics model considering path tracking is transformed into a state space equation

$$\begin{aligned} \dot{x}(t)=Ax(t)+Bu(t)+W, \end{aligned}$$

(11)

where

$$\begin{aligned}{} & {} \begin{aligned} {A \!=\! \begin{bmatrix} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} \frac{-2C_{\alpha f}-2C_{\alpha r}}{mv_{x}(t)} &{} \frac{2C_{\alpha f}+2C_{\alpha r}}{m} &{} \frac{-2l_{f}C_{\alpha f}+2l_{r}C_{\alpha r}}{mv_{x}(t)}\\ 0 &{} 0 &{} 0 &{} 1\\ 0 &{} \frac{-2l_{f}C_{\alpha f}+2l_{r}C_{\alpha r}}{I_{z}v_{x}(t)} &{} \frac{2l_{f}C_{\alpha f}-2l_{r}C_{\alpha r}}{I_{z}} &{}{\frac{-2l_{f}^2C_{\alpha f}-2l_{r}^2C_{\alpha r}}{I_{z}v_{x}(t)}} \end{bmatrix}}, \end{aligned} \\{} & {} \begin{aligned} B = \begin{bmatrix} 0\\ \frac{2C_{\alpha f}}{m}\\ 0\\ \frac{2l_{f}C_{\alpha f}}{I_{z}} \end{bmatrix}, \end{aligned}\\{} & {} \begin{aligned} W = \begin{bmatrix} 0\\ \frac{-2l_{f}C_{\alpha f}+2l_{r}C_{\alpha r}}{mv_{x}(t)} - v_{x}(t)\\ 0\\ -\frac{2l_{f}^2C_{\alpha f}+2l_{r}^2C_{\alpha r}}{I_{z}v_{x}(t)} \end{bmatrix}\dot{\varphi }_{ref}(t). \end{aligned} \end{aligned}$$

This model can accurately reflect the motion state of the vehicle and consider the heading error and lateral error of path tracking, which can directly reflect the effect of vehicle path tracking.

3 VMPC controller design

3.1 Variable step discrete linear continuous system model

MPC is characterized by its utilization of a model to forecast future system states. In order to derive the state of the future system, the vehicle dynamics model considering path tracking should be discretized. Equation (11) is rewritten as

$$\begin{aligned} \begin{aligned}&\frac{dx(t)}{dt}=Ax(t)+f(t)\\&f(t)=Bu(t)+W\\&x(t_0)=\mathbb {K}, \end{aligned} \end{aligned}$$

(12)

where $\mathbb {K}$ is the initial value of the state at $t_0$.

Denote $t\in [kT,(k+1)T],t_0 = kT$, T is the sampling period of the system. The solution of the non-homogeneous state equation is

$$\begin{aligned} x((k+1)T)&= e^{AT}x(kT)\nonumber \\&+\int _{kT}^{(k+1)T}e^{A[(k+1)T-\tau ]}u(\tau )d\tau \cdot B\nonumber \\&+\int _{kT}^{(k+1)T}e^{A[(k+1)T-\tau ]}d\tau \cdot W. \end{aligned}$$

(13)

When employing MPC for tracking control, increasing the prediction time domain can enhance tracking accuracy. However, this also increases the complexity of MPC solution and negatively impacts real-time performance. To balance model prediction accuracy and real-time performance, we optimize the prediction horizon by dividing it into two parts, short-step and long-step discretization.

During the discretization process, the control variable u(t) varies within the sampling period based on the selected holder’s control quantities. Commonly used holders include zero-order holders (ZOH) and first-order holders (FOH).

The zero-order holder is

$$\begin{aligned} \begin{aligned} \text {ZOH}{:}{\left\{ \begin{array}{ll} u(t)=u(kT)=\text {Const}\\ t\in [kT,(k+1)T] \end{array}\right. }, \end{aligned} \end{aligned}$$

(14)

And the first-order holder is

$$\begin{aligned} \begin{aligned} \text { FOH}{:} {\left\{ \begin{array}{ll} u(t)=t(kT)+\dot{u}(kT)(t-kT)\\ \dot{u}(kT)=\frac{u[(k+1)T]-u(kT)}{T}]\\ t\in [kT,(k+1)T \end{array}\right. }. \end{aligned} \end{aligned}$$

(15)

During the sampling period, the ZOH maintains a constant control variable, while the FOH allows for linear changes in the control variable from its initial value. To ensure accuracy in the discrete model, short-step discretization based on ZOH is employed in the initial section of the divided prediction interval. In contrast, long-step discretization based on FOH is utilized in the latter section to provide a reasonable balance between accuracy and computational efficiency over an extended prediction time domain.

The solution of the non-homogeneous state equation obtained by short-step discretization based on ZOH is

$$\begin{aligned}{} & {} x(k+1)=A_s x(k)+B_{s1}u(k) +B_{s2}u(k+1)+W_s,\nonumber \\ \end{aligned}$$

(16)

where

$$\begin{aligned} \begin{aligned}&A_s=I+AT_s+\frac{1}{2!}A^2T_s^2+\cdots +\frac{1}{n!}A^nT_s^n,\\&B_{s1}=BT_s+\frac{1}{2!}ABT_s^2+\cdots +\frac{1}{n!}A^{n-1}BT_s^n,\\&B_{s2}=0,W_s\!=\!WT_s\!+\!\frac{1}{2!}AWT_s^2\!+\!\cdots \!+\!\frac{1}{n!}A^{n-1}WT_s^n,\\ \end{aligned} \end{aligned}$$

$T_s$ is the short-step discretization interval.

The solution of the non-homogeneous state equation obtained by long-step discretization based on FOH is

$$\begin{aligned}{} & {} x(k+1)=A_l x(k)+B_{l1}u(k)+ B_{l2}u(k+1)+W_l,\nonumber \\ \end{aligned}$$

(17)

where

$$\begin{aligned} \begin{aligned}&A_l=I+AT_l+\cdots +\frac{1}{n!}A^nT_l^n,\\&B_{l1}=\frac{1}{2}BT_l+\cdots +\frac{1}{n!(n+2)}A^nBT_l^{n+1},\\&B_{l2}=\frac{1}{2}BT_l+\cdots +\frac{1}{(n+1)!(n+2)}A^nBT_l^{n+1},\\&W_l=WT_l+\cdots \!+\!\frac{1}{n!}A^{n-1}WT_l^n, \end{aligned} \end{aligned}$$

$T_l$ is the long-step discretization interval.

To construct a VMPC prediction model, it is imperative to standardize the discretization results. This can be achieved through the utilization of a unified form of linear time-varying state space equation based on variable step discretization.

$$\begin{aligned}{} & {} x(k+1|t)=A(t)x(k|t)+B_{1}(t)u(k|t)\nonumber \\{} & {} \quad +B_{2}(t)u(k+1|t)+W. \end{aligned}$$

(18)

3.2 Construction of prediction model

According to Eq. (18), we select the current state and the control quantity at the previous moment as the discrete state quantity of the VMPC prediction model, and select the control increment at the current moment and the next moment as the discrete control quantity of the VMPC prediction model. The expression is

$$\begin{aligned} \xi (k|t) = \begin{bmatrix} x(k|t)\\ u(k-1|t) \end{bmatrix}, \varDelta U(k|t) = \begin{bmatrix} \varDelta u(k|t)\\ \varDelta u(k+1|t) \end{bmatrix}.\nonumber \\ \end{aligned}$$

(19)

The discrete control quantity is represented as a control increment to facilitate subsequent constraints on the control quantity and enhance the smoothness of the VMPC controller. The discrete state space equation is

$$\begin{aligned}{} & {} \xi (k+1|t) =\widetilde{A}(t)\xi (k|t) + \widetilde{B}(t)\varDelta U(k|t)+ \widetilde{W}(t),\nonumber \\ \end{aligned}$$

(20)

where

$$\begin{aligned}{} & {} \widetilde{A}(t) =\begin{aligned} \begin{bmatrix} A(t) &{} B_{1}(t)+B_{2}(t)\\ 0_{N_u \times N_x} &{} I_{N_u} \end{bmatrix} \end{aligned}, \\{} & {} \widetilde{B}(t)\!=\! \begin{bmatrix} B_{1}(t)+B_{2}(t) &{} B_{2}(t)\\ I_{N_u} &{} 0_{N_u \times N_u} \end{bmatrix}, \widetilde{W}(t)\!=\!\begin{bmatrix} W\\ 0_{N_u \times N_u} \end{bmatrix}. \end{aligned}$$

where $N_x$ and $N_u$ are the number of state variables and control variables respectively.

The output equation is

$$\begin{aligned} \eta (k|t)=C\xi (k|t), \end{aligned}$$

(21)

where C is the coefficient matrix,

$$\begin{aligned} C=\begin{aligned} \begin{bmatrix} 1&{} 0&{} 0&{} 0&{} 0\\ 0&{} 0&{} 1&{} 0&{} 0 \end{bmatrix} \end{aligned}. \end{aligned}$$

3.3 Prediction equation and output equation

The VMPC controller’s prediction horizon is divided into $N_p$ prediction steps. To enhance prediction accuracy, a short-step discretization based on ZOH is utilized for the 1st $\sim$ $N_s$ prediction steps, while a long-step discretization based on FOH is employed for the subsequent $N_{s+1} \sim N_p$ steps.

Utilizing Eq. (20), we can derive the state quantity of the proposed system throughout the prediction interval. Similarly, we can obtain the system’s output within the same interval by applying Eq. (21). The predicted output at a future time point is represented as

$$\begin{aligned} \begin{aligned} Y(t)=\psi _t\xi (t)+\theta _t U(t)+\gamma _t\phi (t), \end{aligned} \end{aligned}$$

(22)

where

$$\begin{aligned} \begin{aligned}&Y(t)= \begin{bmatrix} \eta (k+1|t) \\ \vdots \\ \eta (k+N_s-1|t)\\ \eta (k+N_s|t)\\ \vdots \\ \eta (k+N_p|t) \end{bmatrix}, U(t)= \begin{bmatrix} \varDelta U(k|t) \\ \vdots \\ \varDelta U(k+N_s-1|t) \\ \varDelta U(k+N_s|t) \\ \vdots \\ \varDelta U(k+N_c-1|t) \end{bmatrix},\\&\phi (t)= \begin{bmatrix} \widetilde{W}_s(t) \\ \vdots \\ \widetilde{W}_s(t) \\ \widetilde{W}_l(t) \\ \vdots \\ \widetilde{W}_l(t) \end{bmatrix}, \psi _t= \begin{bmatrix} C\widetilde{A}_s(t) \\ \vdots \\ C\widetilde{A}_s^{N_s}(t)\\ C\widetilde{A}_l(t)\widetilde{A}_s^{N_s}(t) \\ \vdots \\ C\widetilde{A}_l^{N_p-N_s}(t)\widetilde{A}_s^{N_s}(t) \end{bmatrix}, \\&\theta _t= \begin{bmatrix} C\widetilde{B}_s(t) &{} 0 &{} \cdots &{} 0 \\ C\widetilde{A}_s(t) \widetilde{B}_s(t) &{}C\widetilde{B}_s(t) &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \begin{aligned}C\widetilde{A}_l^{N_p-N_s}(t)\\ \widetilde{A}_s^{N_s-1}(t)\widetilde{B}_s(t)\end{aligned} &{} \begin{aligned}C\widetilde{A}_l^{N_p-N_s}(t)\\ \widetilde{A}_s^{N_s-2}(t)\widetilde{B}_s(t)\end{aligned} &{} \cdots &{} \begin{aligned} &{}C\widetilde{A}_l^{N_p-N_c}(t)\\ {} &{}\widetilde{B}_l(t) \end{aligned} \end{bmatrix}, \\&\gamma _t= \begin{bmatrix} C &{} 0 &{} \cdots &{} 0 \\ C\widetilde{A}_s(t) &{} C &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \begin{aligned} &{}C\widetilde{A}_l^{N_p-N_s}(t)\\ {} &{}\widetilde{A}_s^{N_s-1}(t) \end{aligned} &{} \begin{aligned} &{}C\widetilde{A}_l^{N_p-N_s}(t)\\ {} &{}\widetilde{A}_s^{N_s-2}(t) \end{aligned} &{} \cdots &{} C \end{bmatrix}. \end{aligned} \end{aligned}$$

3.4 Objective function and constraint conditions

The primary goal of the path tracking control system is to enable rapid and smooth tracking of the target path by the vehicle. To achieve this, both the system state quantity error and the incremental weighting optimization of the system control quantity must be considered. Considering the complexity of the multi-objective optimization problems, there may be no feasible solution in the calculation process. The possible reasons for the potential infeasibility in multi-objective optimization problems may include the following aspects. Firstly, due to the limitation of constraint conditions, there may be no solution that satisfies all objectives and constraints simultaneously. Secondly, in some cases, the optimization algorithm may only find local optimal solutions rather than global optimal solutions. Thirdly, during the solution process, numerical stability issues may arise, causing the algorithm to fail to converge to an effective solution. Given the complexity of multi-objective optimization problems and the potential infeasibility during computation, a relaxation factor is incorporated into the objective function. The main roles of the relaxation factor include the following aspects. Firstly, when the initial state of the system is not within the feasible region, or when certain constraints cannot be satisfied due to changes in the environment or system parameters, the relaxation factor allows the controller to slightly violate the constraints at certain moments, thus maintaining the continuity and stability of the control. This flexibility enables the algorithm to tolerate certain system uncertainties and external disturbances to enhance system robustness. Secondly, for multi-objective optimization problems, there may be conflicts between performance indicators and constraints. By adjusting the relaxation factor, a trade-off can be achieved between performance optimization and constraint satisfaction. When the relaxation factor is large, the control system focuses more on performance optimization while relaxing the requirements for constraints. When the relaxation factor is small, the control system focuses more on satisfying the constraints, potentially sacrificing some performance. Thus, we define the system’s multi-objective optimization function as follows.

$$\begin{aligned} \begin{aligned} J(t)=&\sum _{i=1}^{N_p} \Vert \eta (k+i|t) -\eta _{ref} (k+i|t) \Vert _Q^2 \\ {}&+\sum _{i=0}^{N_c-1} \Vert \varDelta U (k+i|t) \Vert _R^2 + \rho \varepsilon ^2, \end{aligned} \end{aligned}$$

(23)

where Q is the state weighting matrix, R is the control weighting matrix, $N_c$ is the number of sampling points of the control horizon, $N_p$ is the number of sampling points of the prediction horizon, $\rho$ is the weight coefficient, $\varepsilon$ is the relaxation factor.

To meet the performance indicators of vehicle steering control smoothness and vehicle path tracking accuracy, it is necessary to constrain the output, control increment and control quantity of the path tracking control system. The constraints are designed as

$$\begin{aligned} \begin{aligned}&\varDelta U_{\min } \le \varDelta U(k+i|t) \le \varDelta U_{\max } \\&u_{\min } \le u(k+i|t) \le u_{\max }\\&\eta _{\min } \le \eta (k+i|t) \le \eta _{\max } \\&\varepsilon _{\min } \le \varepsilon \le \varepsilon _{\max }. \end{aligned} \end{aligned}$$

(24)

The first inequality represents the control increment constraint with the constraint boundary determined by the smoothness of vehicle steering control. The second inequality denotes the control constraint with the constraint boundary reflecting the physical limitations of vehicle steering. The third inequality signifies the system output constraint with the constraint boundary determined by the desired path tracking accuracy. The fourth inequality states that the relaxation factor should be constrained within a certain range to avoid causing instability or slow convergence rate in the algorithm.

To solve this multi-objective optimization, it must be reformulated as a standard quadratic programming. The VMPC multi-objective optimization can be summarized as

$$\begin{aligned} \begin{aligned}&\min \left( \frac{1}{2} \varDelta U(t)_{\varepsilon }^T \widetilde{H}_t\varDelta U(t)_{\varepsilon }+ \tilde{f}_t ^T \varDelta U(t)_{\varepsilon }\right) \\&{\left\{ \begin{array}{ll} A_{qp} \varDelta U(t)_{\varepsilon } \le b_{qp} \\ lb \le \varDelta U(t)_{\varepsilon } \le ub \end{array}\right. }, \end{aligned} \end{aligned}$$

(25)

where

$$\begin{aligned} \begin{aligned}&\widetilde{H}_t= \begin{aligned} \begin{bmatrix} \theta _t^T Q_Q\theta _t+R_R &{} 0 \\ 0 &{} \rho \end{bmatrix} \end{aligned}, \begin{aligned} \tilde{f}_t = \begin{bmatrix} \theta _t^T Q_Q(E_t+G_t) \\ 0 \end{bmatrix} \end{aligned}, \\ {}&A_{qp} = \begin{aligned} \begin{bmatrix} I_{N_c} &{} 0 \\ -I_{N_c}&{} 0 \\ \theta _t &{} 0 \\ - \theta _t &{} 0 \end{bmatrix} \end{aligned}, b_{qp} = \begin{aligned} \begin{bmatrix} U_{max} - U(k-1|t) \\ -U_{min} + U(k-1|t) \\ Y_{max} - \psi _t\xi (t) - \gamma _t\phi (t) \\ - Y_{min} + \psi _t\xi (t) + \gamma _t\phi (t) \end{bmatrix} \end{aligned}, \\ {}&\varDelta U(t)_{\varepsilon } = \begin{aligned} \begin{bmatrix} \varDelta U(t)\\ \varepsilon \end{bmatrix} \end{aligned}, lb = \begin{aligned} \begin{bmatrix} \varDelta U_{Min} \\ \varepsilon _{min} \end{bmatrix} \end{aligned}, ub = \begin{aligned} \begin{bmatrix} \varDelta U_{Max} \\ \varepsilon _{max} \end{bmatrix} \end{aligned}, \end{aligned} \end{aligned}$$

where $\widetilde{H}_t$ is the quadratic objective matrix, $\widetilde{f}_t$ is the linear target vector, $A_{qp}$ is the linear inequality constraint matrix, $b_{qp}$ is the linear inequality constraint vector, lb and ub are the upper bound of optimization objective and lower bound of optimization objective respectively.

In each cycle, the above constrained multi-objective function is solved. The output of the VMPC controller is

$$\begin{aligned} u(k|t)=u(k-1|t) + [1 \quad 0] \varDelta U(k|t). \end{aligned}$$

(26)

During the control period, the input at the next sampling time can be recalculated from Eq. (26) by the rolling optimization characteristics. Through iterative optimization, the vehicle is able to track the target path.

4 Simulation and analysis

In this section, we conduct a co-simulation with Carsim and MATLAB/Simulink to evaluate the accuracy, stability, and robustness of the VMPC controller in path tracking control under two conditions, a double-lane road and a high-speed road with both straight and curved sections. Simulation results are compared with those of the MPC controller to assess the performance of the VMPC controller. The paramters of an used E-Class sedan are shown in Table 1 and the parameters of the VPMC are shown in Table 2.

Table 1 The parameters of an used E-Class sedan

Table 2 The parameters of the VMPC

4.1 Double lane road condition

In the double-lane road simulation experiment, we tested the performance of the VMPC controller at vehicle velocities of 15 km/h, 50 km/h, and 70 km/h. The curvature of the used double-lane road is shown in Fig. 4.

Fig. 4

The curvature of the used double lane road in simulation

Fig. 5

The vehicle trajectory on the double lane road at 15 km/h

Fig. 6

The lateral error at 15 km/h

Fig. 7

The heading error at 15 km/h

Figure 5 illustrates the vehicle trajectory on the double-lane road at 15 km/h. One finds that the max trajectory tracking error of the Y axle is about 0.02 m with the MPC controller, while 0.01m with the VMPC controller. Figures 6 and 7 compare the lateral and heading errors with the two controllers. As shown in these figures, the lateral error with the MPC controller ranges from $-$0.052 to 0.048 m, while that with the VMPC controller is maintained between $-$0.032 and 0.027 m. The heading error with the MPC controller is maintained between $-$1.413 and 2.261 deg, while that with the VMPC controller is maintained between $-$1.234 and 1.897 deg. These results demonstrate that the VMPC controller exhibits higher trajectory, lateral and heading tracking accuracy when tracking a double-lane road at low vehicle velocity.

Fig. 8

The sideslip angle at 15 km/h

Fig. 9

The front wheel angle at 15 km/h

Figures 8 and 9 compare the sideslip angle and front wheel angle with the two controllers. The sideslip angle with the MPC controller exhibits oscillations with multiple large peaks and a larger angle amplitude. In contrast, the sideslip angle with the VMPC controller changes gently and is maintained between $-$0.27 and 0.90 deg. These results indicate that the VMPC controller provides higher lateral stability and more stable steering at low vehicle velocity.

Fig. 10

The solution time at 15 km/h

Figure 10 presents a comparison of the solution times between the two controllers. The average solution time of the VMPC controller is about 4.92 ms, which is significantly less than 9.46 ms of the MPC controller. This indicates that the VMPC controller exhibits superior real-time performance compared to the MPC controller at low vehicle velocity.

Fig. 11

The vehicle trajectory on the double lane road at 50 km/h

Fig. 12

The lateral error at 50 km/h

Fig. 13

The heading error at 50 km/h

Figure 11 illustrates the vehicle trajectory on the double-lane road at 50 km/h. One finds that the max trajectory tracking error of the Y axle is about 0.05 m with the MPC controller, while 0.03m with the VMPC controller. Figures 12 and 13 compare the lateral and heading errors of the two controllers. As shown in these figures, the lateral error with the MPC controller ranges from $-$0.087 to 0.048 m, while that with the VMPC controller is maintained between $-$0.034 and 0.038 m. The heading error with the MPC controller is maintained between $-$1.744 and 1.321 deg, while that with the VMPC controller is maintained between $-$0.747 and 0.934 deg. These results demonstrate that the VMPC controller exhibits higher trajectory, lateral and heading tracking accuracy when tracking a double-lane road at medium vehicle velocity.

Remark 1

In Fig. 13, there are oscillations in areas with large curvature because of model approximation error. As aforementioned, the VMPC controller’s prediction horizon is divided into $N_p$ prediction steps. the short-step discretization based on ZOH is utilized for the 1st $\sim$ $N_s$ prediction steps, while the long-step discretization based on FOH is employed for the subsequent $N_{s+1} \sim N_p$ steps. When the VMPC uses the long-step discretization interval to discretize the model to approximate system behavior, it reduces computational complexity. However, this approximation method may introduce errors with large curvature. In areas with large curvature, this approximate model may not accurately describe the actual dynamics of the system, leading to oscillations when tracking the reference trajectory by the control system. When the vehicle velocity is low, $N_s$ should be larger. But for comparison under different vehicle velocities, we set $N_s$ as 12, which leads to obvious oscillations at 50 km/h. If $N_s$ is increased, the oscillations will be significantly attenuated or even disappear. If the oscillations are too large, it will cause passengers to feel the vehicle swaying left and right. Figure 13 shows that the amplitudes of these oscillations are small. Therefore, it will not cause passengers to feel the sway of the vehicle in this case.

Figures 14 and 15 compare the sideslip angle and front wheel angle of the two controllers. The sideslip angle of the MPC controller exhibits oscillations with multiple large peaks and a larger angle amplitude. In contrast, the sideslip angle of the VMPC controller changes gently and is maintained between $-$0.5 and 0.5 deg with a smaller angle amplitude. These results indicate that the VMPC controller provides higher lateral stability and more stable steering at medium vehicle velocity.

Fig. 14

The sideslip angle at 50 km/h

Fig. 15

The front wheel angle at 50 km/h

Figure 16 presents a comparison of the solution times between the two controllers. The average solution time for the VMPC controller is about 5.07 ms, which is significantly less than 8.38 ms of the MPC controller. This indicates that the VMPC controller exhibits superior real-time performance compared to the MPC controller at medium vehicle velocity.

Fig. 16

The solution time at 50 km/h

Figure 17 depicts the vehicle trajectory on a double-lane road at 70 km/h. One finds that the max trajectory tracking error of the Y axle is about 0.17 m with the MPC controller, while 0.1 m with the VMPC controller. Figures 18 and 19 provide a comparison of lateral and heading errors between the two controllers. As shown in the figures, in large curvature curves, the lateral error with the MPC controller ranges from $-$0.195 to 0.223 m, while its heading error exhibits significant fluctuations when transitioning from curves to straight roads, with a maximum heading error of 10.54 deg. In contrast, the lateral error with the VMPC controller remains between $-$0.105 and 0.192 m, and both lateral and heading errors quickly converge to 0 when transitioning from curves to straight roads. These results demonstrate that the VMPC controller provides better lateral and heading tracking stability at higher speeds under this condition.

Fig. 17

The vehicle trajectory on the double lane road at 70 km/h

Fig. 18

The lateral error at 70 km/h

Fig. 19

The heading error at 70 km/h

Figures 20 and 21 present a comparison of the sideslip angle and front wheel angle between the two controllers. As shown in the diagrams, for the VMPC controller, the peak and trough values of the sideslip angle are 3.92 deg and $-$7.33 deg, respectively. In contrast, for the MPC controller, the peak and trough values of the sideslip angle are 4.72 deg and $-$11.03 deg, respectively. The VMPC controller exhibits smaller oscillation amplitude and shorter convergence time to 0. The front wheel angle output by the MPC controller ranges from $-$13.43 to 12.70 deg with slower convergence of front wheel angle oscillations when transitioning from curves to straight roads. In contrast, the front wheel angle output by the VMPC controller ranges from $-$10.44 to 10.90 deg with smaller oscillations and faster convergence. These results indicate that VMPC control provides higher lateral stability and more stable steering under this condition.

Fig. 20

The sideslip angle at 70 km/h

Fig. 21

The front wheel angle at 70 km/h

Figure 22 presents a comparison of solution times between the two controllers. The average solution time of the VMPC controller is about 5.71 ms, while that of the MPC controller is 9.52 ms. This demonstrates that the VMPC controller exhibits superior real-time performance compared to the MPC controller under this condition.

Fig. 22

The solution time at 70 km/h

Remark 2

One can find that there are oscillations for the heading error at 50 km/h in Fig. 13, but no oscillations at 70 km/h in Fig. 19. The main reasons are the settings of the prediction horizon and relaxation factor. Of course, there are other factors to influence this phenomenon. In our simulations, we choose the prediction horizon and relaxation factor focusing on the range of 60–120 km/h according to the practice. On the other hand, there are no oscillations at low vehicle velocity as shown in Fig. 7. Our simulation results show that the oscillations become serious just at 50 km/h. In order to fully reflect the performance of the algorithm, we give the simulation result at 50 km/h, not 60 km/h, and explain the reason via Remark 1.

4.2 High-speed road condition

We simulate the vehicle under two high-speed lane road conditions, 100 km/h and 120 km/h. Figure 23 depicts the vehicle trajectory on the high-speed road at 100 km/h. Figures 24 and 25 provide a comparison of lateral and heading errors between the two controllers. The lateral error generated by the MPC controller is larger than that generated by the VMPC controller. Notably, in the third turn, the maximum lateral error with the MPC controller reaches 0.349 m, while that with the VMPC controller is only 0.2 m. The heading error with the MPC controller oscillates near 0 when entering curves, while that with the VMPC controller remains at approximately ± 0.4 deg. These results demonstrate that the VMPC controller can maintain high tracking accuracy when tracking multiple curves at high vehicle velocity.

Fig. 23

The vehicle trajectory on the double lane road at 100 km/h

Fig. 24

The lateral error at 100 km/h

Fig. 25

The heading error at 100 km/h

Figures 26 and 27 present a comparison of the sideslip angle and front wheel angle between the two controllers at 100 km/h. As shown in the figures, the trends in changes of sideslip angle and front wheel angle are consistent. The control effects of the MPC and VMPC controllers for sideslip angle and front wheel angle are similar. However, the sideslip angle and front wheel angle with the VMPC controller exhibit smoother changes in curves, with significantly smaller fluctuations compared to those with the MPC controller. the partially enlarged detail of Fig. 26 indicates that the fluctuation of the sideslip angle with the MPC controller is about 0.5 deg, while the fluctuation of the sideslip angle with the VMPC controller is about 0.3 deg. As shown in Fig. 27, the partially enlarged detail indicates that the fluctuation of the front wheel angle with the MPC controller is about 0.8 deg, while the fluctuation of the front wheel angle with the VMPC controller is about 0.4 deg. The front wheel angle with the VMPC controller is slightly larger than that with the MPC controller when transitioning from straight roads to curves, for example, as shown in Fig. 27, at the 19.9 s, the front wheel steering angle is about 3.5 deg with MPC controller, while the front wheel steering angle is about 4.1 deg with VMPC controller.This ensures tracking accuracy on curves while keeping the riding stability of the vehicle at high vehicle velocity.

Fig. 26

The sideslip angle at 100 km/h

Fig. 27

The front wheel angle at 100 km/h

Figure 28 presents a comparison of solution times between the two controllers. The average solution time of the VMPC controller is about 5.85 ms, while that of the MPC controller is about 8.64 ms. This demonstrates that the VMPC controller exhibits superior real-time performance compared to the MPC controller at high vehicle velocity.

Fig. 28

The solution time at 100 km/h

Figure 29 depicts the vehicle trajectory on the high-speed road at 120 km/h. As shown in Fig. 29, the VMPC controller tracks the reference path more closely on curves, particularly on the second and third curves. Figures 30 and 31 provide a comparison of lateral and heading errors between the two controllers. The lateral error generated by the MPC controller is larger than that generated by the VMPC controller. Notably, on the third turn, the maximum lateral error for the MPC controller reaches 0.349 m, while that for the VMPC controller is only 0.2 m. The heading error with the MPC controller oscillates near 0 when entering curves, while that with the VMPC controller remains at approximately± 0.4 deg. These results demonstrate that the VMPC controller can maintain high tracking accuracy when tracking multiple curves at high vehicle velocity.

Fig. 29

The vehicle trajectory on the double lane road at 120 km/h

Fig. 30

The lateral error at 120 km/h

Fig. 31

The heading error at 120 km/h

Figures 32 and 33 present a comparison of the sideslip angle and front wheel angle between the two controllers at 120 km/h. As shown in the diagrams, the trends in changes of sideslip angle and front wheel angle are consistent. The control effects of the MPC and VMPC controllers for sideslip angle and front wheel angle are similar. However, the sideslip angle and front wheel angle with the VMPC controller exhibit smoother changes in curves, with significantly smaller fluctuations compared to those with the MPC controller. the partially enlarged detail of Fig. 32 indicates that the fluctuation of the sideslip angle with the MPC controller is about 1.0 deg, while the fluctuation of the sideslip angle with the VMPC controller is about 0.5 deg. As shown in Fig. 33, the partially enlarged detail indicates that the fluctuation of the front wheel angle with the MPC controller is about 4.1 deg, while the fluctuation of the front wheel angle with the VMPC controller is about 1.8 deg. The front wheel angle with the VMPC controller is slightly larger than that with the MPC controller when transitioning from straight roads to curves, for example, as shown in Fig. 33, at the 24.5 s, the front wheel steering angle is about 5.9 deg with MPC controller, while the front wheel steering angle is about 8.3 deg with VMPC controller. This ensures tracking accuracy on curves while keeping the riding stability of the vehicle at high vehicle velocity.

Fig. 32

The sideslip angle at 120 km/h

Fig. 33

The front wheel angle at 120 km/h

Figure 34 shows a comparison of solution times between the two controllers. The average solution time of the VMPC controller is 5.85 ms, while that of the MPC controller is 8.64 ms. This demonstrates that the VMPC controller exhibits superior real-time performance compared to the MPC controller at high vehicle velocity.

In summary, the VMPC path tracking controller outperforms the traditional MPC controller in terms of tracking accuracy, real-time, control stability, and vehicle velocity robustness.

Fig. 34

The solution time at 120 km/h

5 Practical vehicle test

To further validate the control performance of the VMPC controller, a path tracking experiment was conducted on a drive-by-wire integrated chassis platform, as shown in Fig. 35. The platform comprises a laser radar, IMU, computing platform, steering motor, drive motor, USB-CAN, CAN bus, MCU, and remote controller. The length, width and height of the platform are 2340 mm, 1320 mm and 710 mm respectively. The controller was developed based on the ROS (Robot Operating System) and C++ under Ubuntu operating system.

Fig. 35

The drive-by-wire integrated chassis experimental platform

Figure 36 presents a comparison between the actual driving trajectory and reference trajectory of the platform. To ensure safety, the vehicle velocity was maintained at 15 km/h and the reference path included both straight and curve segments. From Fig. 36 one can obtain that the actual driving trajectory coincides with the reference trajectory. The tracking accuracy is high in straight sections and sections with small curvature, and is slightly worse in sections with large curvature which is consistent with the simulation results.

Fig. 36

The driving path and the reference path

Figures 37and 38 depict the lateral and heading errors during the tracking process respectively. As shown in the figures, the lateral error remains between $-$0.2 and 0.2 m and the heading error remains between $-$2.7 and 2.9 deg in straight sections and sections with smaller curvature. In large curvature sections, the lateral error is controlled between$-$0.4 and 0.6 m, and the heading error is controlled between$-$7.8 and 5.2 deg. The reason for the poor tracking accuracy in the large curvature sections may be the decrease of lidar positioning accuracy for the large turning radius and open space. Compared with the simulation results, the experimental results show lower accuracy. The reasons are complex such as differences between the experimental and simulation environments, errors in sensors and actuators, and disparities in vehicle dynamics model. On the whole, the experimental results demonstrate that the control performance of the VMPC path tracking controller on an actual vehicle agrees with simulation result, exhibiting good tracking accuracy.

Fig. 37

the lateral error in the tracking process

Fig. 38

the heading error in the tracking process

6 Conclusions

• (1) To enhance the accuracy, real-time performance, and stability of path tracking, we propose a model predictive control method based on variable discrete step size.

• (2) We adopt a vehicle model that accounts for path tracking. During model discretization, we optimize the prediction interval by balancing the model’s prediction accuracy and real-time performance. The prediction interval is divided into short-step and long-step discretization sections. The former employs ZOH while the latter utilizes FOH.

• (3) We conduct Carsim/Simulink co-simulations on double-lane and high-speed roads. The results demonstrate that our VMPC controller exhibits superior tracking accuracy, stability, and real-time performance. To further validate VMPC’s control efficacy, we perform a path tracking experiment on a drive-by-wire integrated chassis platform. The practical vehicle experimental results confirm that VMPC’s control effect on the practical vehicle is consistent with simulation results and exhibits good tracking accuracy.