1 Introduction

The centrifugal pump is one of the crucial energy conversion devices utilized in almost all commercial and agricultural applications, including the nuclear industry, petroleum, agriculture, chemical and cryogenic propellant pumping, among others. The most critical research areas for centrifugal pumps are safety and dependable operation.

The fluid–structure interaction (FSI) would impact the accuracy and dependability of the unsteady flow simulation and rotor deformation analysis. The energy transfer between fluid and solid may be neglected due to a lack of understanding of fluid–structure interaction. Examining the performance of centrifugal pumps by applying the FSI method is crucial. A fluid–structure interaction method with a strong two way has been employed to understand better the influence interface between fluids and structures in the low specific speed centrifugal pump. The FSI has the advantage of describing the interaction of a deformable structure submerged in a fluid, where the fluid and structure movements interact. Consequently, the interaction between the rotating impeller and the static volute in centrifugal pumps and the energy loss during pump operation due to the variation in the number of blades must be thoroughly studied.

Numerous engineering issues have been resolved using FSI techniques. The application of several partitioned FSI simulation methodologies to the pump impeller was also investigated. The outcomes of one-way and two-way coupling strategies were assessed and compared.

The study by Benra et al. [1] used one-way and two-way coupling approaches to examine the deflection of an impeller in a single-blade centrifugal pump. The findings revealed notable disparities between the solution obtained by one-way coupling and the actual outcomes. The two-way coupling approach generally produced results that closely approximated reality, whereas the one-way coupling approach demonstrated reasonable results only for specific values in certain instances. The investigation by Pozarlik et al. [2] examined the distinctions between one-way and two-way interaction in the typical gas turbine combustion chamber. The study’s findings showed that using a one-way approach may serve as a valuable approximation for predicting the amplitude and vibration pattern of the structure. On the contrary, two-way interaction is recommended for analyzing the pressure distribution inside the combustion chamber. Pei et al. [3] employed FSI methods with strong two-way coupling to estimate the oscillation of the single-blade centrifugal pump generated by fluctuation pressure. Moreover, they compared the experimental and numerical findings under off-design conditions, and the results showed a good match. Yuan et al. [4] integrated simulations for transient flow and an oscillating structure using a two-way coupling technique to investigate the impact of fluid–structure interaction (FSI) on the fluid flow field and the structural stability of the rotating impeller.

Using the FSI robust two-way approach, Pei et al. [5] studied the stress and the strain in the rotating component of an axial-flow pump. They found that both values decreased drastically with increasing flow rates. Schneider et al. [6] applied the fluid–structure interaction approach to computing the warp and the equivalent stress in the impeller of a multistage pump under varied operating conditions. The results demonstrated that the exciting hydraulic forces created by the fluctuating pressure are the primary causes of vibration and noise in the pump. Pei et al. [7] studied the structural behavior of the single-blade centrifugal pump under several operating conditions.

In addition, the partitioned FSI technique was used to quantify the effectiveness of interaction on turbulent flow. Zhang et al. [8] noted that the impeller and the volute interface is the primary source of rising pressure fluctuation and flow-induced oscillation in centrifugal pumps. Birajdar et al. [9] established a one-way fluid–structure interaction technique for predicting the vibration under specific flow rates, and it was substantially associated with empirical results. Wu et al. [10] carried out a numerical analysis of a centrifugal pump’s unsteady flow field and structural parameters employing a two-way coupling fluid–structure interaction approach under cavitation conditions. The way of cavitation impacts the blade loads and unstable radial force has been described. The results indicated that the average radial force increased with cavitation augmentation as the transition progressed. Zhou et al. [11] employed a two-way coupling method to explain the structural and rotor behaviors of the pump. The flow field and structural reaction were analyzed using a method to calculate turbulent flow and structural response simultaneously. Zhang et al. [12] investigated pressure pulsation in vertical axial flow pumps employing fluid–structure coupling and structural analysis. It provides a crucial theoretical foundation for optimizing the design and secure operation of vertical axial pumps. Liu et al. [13] used the two-way fluid–structure interaction approach to examine the diffuser centrifugal pump’s exterior features and interior flow field. With the fluid–structure interaction effect, the pressure fluctuation at the impeller output is more significant than in normal conditions.

Using CFX and ANSYS Workbench, Yuan et al. [14] analyzed three rotating impellers’ structural behavior and turbulent flow with different parameter designs. They concluded that the closed impeller was the least stable and had the best hydraulic performance. In contrast, the split impeller was the least stable and had the best hydraulic performance.

Since centrifugal pumps are energy conversion devices, their high energy consumption is mainly attributable to their revolving components. Consequently, a more energy-efficient operation of centrifugal pumps is necessary; accordingly, identifying the areas linked with losses plays a significant role in performance optimization research. A universal feature of the symmetry of the random process of entropy generation has been found. This property was created using the fluctuation concept and the second law of thermodynamics. In nonequilibrium systems, entropy production quantifies dissipation, which is inversely correlated to the output effectiveness of hydraulic machinery.

Numerous researchers have investigated the connection between energy loss and entropy generation. Li et al. [15] applied the entropy production concept to demonstrate that the splitter blades increase the pump’s hydraulic performance. Jia et al. and Zhao et al. [16,17,18] analyzed how different flow conditions affected the relationship between centrifugal pump internals and the energy dissipation rate during turbulent flow.

In examining the entropy generation of the multistage centrifugal pump, Yun et al. [19] discovered that the multistage centrifugal pump had better hydraulic efficiency with the guide ring than without the guide ring.

The impeller characteristics, such as the number of impeller blades, also substantially impact pump performance, and researchers have considered these factors in their works. Al-Obaidi [20, 21] performed a numerical analysis to evaluate how changing the impeller diameter and blade number might affect the pump’s operation in cavitation and noncavitation modes. The effects of using 3, 4 and 5 blades were studied. Research shows that increased flow rate and the number of blades lead to developing cavitation. The cavity length expands when the pressure at the impeller inlet is lowered. Impeller suction greatly affected cavitation at a five-blade number compared with other blades, especially with a high-flow discharge. Jafarzadeh et al. [22] examined the turbulent flow of a centrifugal pump to predict pressure and velocity fields. Several models have been used in numerical analysis, including the regular K-, the RNG and the RSM. The effect of the number of blades on the pump’s effectiveness was also investigated. The number of blades has been increased from five to seven. These models are more accurate than the classic k–ε model for predicting cavitation. Seven blades produced the highest head coefficient. Al-Obaidi et al. [23,24,25] investigated a numerical technique to conduct a qualitative and quantitative analysis of flow characteristics in axial-flow pumps. They studied the impact of varying impeller blade angles and diffusers on axial-flow pumps’ flow behavior. The numerical calculations provide theoretical insights that may inform axial-flow pumps’ further design and investigation. As far as the authors are aware, the study on the effects of blade numbers (up to 11-blade) remains a considerable gap in the design improvement of the centrifugal pump research area [26].

Although numerous researchers have examined the impact of augmented blade numbers on the hydraulic efficiency of centrifugal pumps, a lack of academic research particularly examines how the blade numbers affect centrifugal pumps’ structural response. The investigation into the FSI and entropy generation rate (EGR) methodologies when examining the blade numbers’ effect on pump performance needs further research. Hence, the present study investigates varied numbers of blades to analyze the impact of their modification on the performance and structural behavior of a centrifugal pump. This investigation has practical implications for the design and operation of such pumps, potentially leading to improvements in efficiency, stability, and internal energy loss visualization. First, simulation results are experimentally validated. Then, the pressure distribution, energy loss, and structural behavior are analyzed. This study employs entropy generation techniques and two-way fluid–structure interaction to investigate the impeller’s strength at various blade numbers. The findings of this study are valuable in terms of serving as a point of reference for impeller design and enhancing our understanding of the impact of varying blade numbers on the operational efficiency of centrifugal pumps.

2 Simulation of Three-Dimensional Model

2.1 Modeling of Three-Dimensional Centrifugal Pump

2.1.1 Fluid Domain

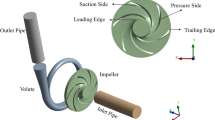
The fluid domain is a centrifugal pump with a low specific speed with an outlet impeller width of 17 mm, an output impeller diameter of 260 mm and an inlet impeller diameter of 80 mm. The impeller has six enclosed blades with a flow rate of 55 m3/h, a head of 20 m and a rotational speed of 1450 rpm. The fluid utilized was water. Zhang et al. [27, 28] previously operated the chosen pump in numerical investigation and experimental testing.

CFturbo V2020.1.1 was used to regenerate the investigated pump shape. Figure 1 shows the impeller and volute of the revised pump. The computational fluid domain of a centrifugal pump, as shown in Fig. 1, is divided into four sections: the inlet pipe, the volute, the impeller and the output pipe. Notably, the inlet and outlet pipe lengths are five times the pump’s suction diameter [29,30,31] to decrease the influence of boundary condition disturbances, provide a stable flow at the inlet, and deliver a fully developed flow at the outlet. Table 1 summarizes the centrifugal pump’s primary parameters. The monitoring points in the volute are depicted in Fig. 2.

Fig. 1
figure 1

The three-dimension model of the centrifugal pump

Full size image
Table 1 The parameter of the centrifugal pump
Full size table
Fig. 2
figure 2

The location of the monitoring point used in the simulation on the volute

Full size image

2.1.2 Solid Domain

The structure domain has been generated using SOLIDWORKS 2020 software. The rotor system consists primarily of the solid impeller (hub, shroud and blades) and the rotating shaft, as shown in Fig. 3, Table 2. The material properties of solid domain for the impeller and shaft used in structural analysis. The impeller and shaft’s introductory material is stainless steel, according to DIN 1.4408 stainless steel [10].

Fig. 3
figure 3

The solid domain of the centrifugal pump includes the impeller, rotating shaft and cylindrical supports

Full size image
Table 2 The material properties of solid domain
Full size table

2.2 Mesh Generation and Mesh Independence Verification

ANSYS fluent meshing is used to mesh the computational fluid domains into poly-hexacore grids. Figure 4 shows how the mesh refinement approach was used to control the boundary layer and produce the desired mesh size and boundary layer quality. In this research, the dimensionless distance, denoted by the y+ value, between the initial grid node and the wall has been considered. The maximum y+ value of the computational domain in the design flow conditions is 89 (Fig. 5). The value of y+ in this work is good enough to satisfy numerical simulation criteria [16, 19, 29, 32,33,34,35]. The grid independency check was done at the design point to avoid the grid number’s impact on the flow simulation results. Six grids were used to test the grid’s independence (Table 3).

Fig. 4
figure 4

Mesh of the fluid domain generated in the ANSYS fluent meshing

Full size image
Fig. 5
figure 5

Y+ at the centrifugal pump wall

Full size image
Table 3 The grid independence test scheme
Full size table

The optimum number of cells was determined by comparing the deviation between the results of the numerical head across six grid cell numbers. The head error for the grids is less than 1%. Therefore, the impact of the grid number on computation can be disregarded. Figure 6 illustrates that the deviation value stays constant as the number of grids rises. The mesh with 2,616,077 cells was chosen for further computations since they used fewer computer resources and were completed in less time. The head of six computational grids is shown in Fig. 6 under design conditions. However, utilizing ANSYS meshing, the structural regions are meshed in unstructured grids, with 1,010,264 grid elements, as shown in Fig. 7.

Fig. 6
figure 6

The mesh independence checking

Full size image
Fig. 7
figure 7

The mesh of the solid domain

Full size image

2.3 Numerical Setting and Boundary Conditions

ANSYS Fluent 21R2 is used to solve the unsteady Reynolds-averaged Navier–Stokes equation for the fluid calculations. The common turbulence selected was the k–ω model using SST near-wall formulation since it accurately predicts the flow near the wall [4, 36,37,38,39]. The inlet and outlet boundary conditions have been set to total pressure and mass flow rate, respectively. The computational impeller domain was configured to rotate at 1450 r/m. However, the remaining computational parts were considered to be static. Table 4 presents the fundamental simulation parameters used for flow field simulation. The coupled solver was used to model the flow, while the Green–Gauss node-based technique was used to calculate the gradients. The PRESTO! process was explored to correct the pressure difference between iterations, which may be implemented with a strongly whirling flow. The second-order upwind approach was chosen due to its more precise computation. The impeller-volute contact was set up using sliding mesh [40], which adjusts the relative location of the rotor and stator at each time step.

Table 4 CFD simulation parameters used in the ANSYS fluent
Full size table

The exact time step size is set for fluid field simulation and dynamic structure analysis [4, 41]. It cannot capture some minor changes in the pressure by using a large time step size. However, the computing time will also significantly rise if the time steps are too small [42]. Consequently, considering computer configuration, the time step size independence was examined by utilizing the pump head under three different time steps, including ∆t = 0.00011494 s, 0.00023 s, 0.000345 s which is equivalent to (T/120, T/180, T/360) where T = 0.0414 s. The result indicated that with the time step size variance, the pump head’s discrepancy is smaller than 1.6%, as shown in Table 5. Hence, considering the simulation time and accuracy, a 0.000345 s was adopted, which is 1/120 of the impeller rotational period T and an angle of 3° of the impeller rotations per time step [3, 10, 20, 43, 44].

Table 5 The time step size independence test
Full size table

The overall simulation duration was set to 7T of the impeller rotation cycles when the results were stable and reliable [44, 45]. The convergence residual is set to 1 × 10−5 to determine if the simulation is convergent. Moreover, the maximum number of iterations has been set to 10 for each time step to keep the residuals around 10–5 [40].

2.3.1 Turbulence Model

In the engineering domain, all flow-related issues must adhere to the principles of mass, momentum and energy conservation. The subject of investigation in this research study pertains to a three-dimensional, incompressible turbulent flow. The turbulence model chosen for the computational modeling is the shear stress transport (SST) k–\(\omega\) model since this equation is appropriate for calculating the parameter in the pump simulation. The fundamental governing equations of the SST k–\(\omega\) model can be expressed as follows [46, 47]:

$$ \frac{{\partial \left( {\rho k} \right)}}{\partial t} + \frac{\partial }{{\partial x_{j} }}\left( {\rho u_{j} k} \right) = \frac{\partial }{{\partial x_{j} }}\left( {\Gamma_{k} \frac{\partial k}{{\partial x_{j} }}} \right) + P_{k} - \Upsilon_{k} $$
(1)
$$ \frac{{\partial \left( {\rho \omega } \right)}}{\partial t} + \frac{\partial }{{\partial x_{i} }}\left( {\rho u_{i} \omega } \right) = \frac{\partial }{{\partial x_{j} }}\left( {\Gamma_{\omega } \frac{\partial \omega }{{\partial x_{j} }}} \right) + D_{\omega } + P_{\omega } - \Upsilon_{\omega } $$
(2)

In the given equations, the variable k represents the turbulent kinetic energy, while ω denotes the dissipation rate. Additionally, \(P_{k}\) and \(P_{\omega }\) refer to the generation parts, whereas \(D_{\omega }\) represents the diffusion part. \(\Upsilon_{k}\) and \(\Upsilon_{\omega }\) represent the turbulent viscosity, while t denotes the time. The variables \(u_{i}\) and \(u_{j}\) represent the average turbulent velocity, and \(x_{i}\) and \(x_{j}\) represent the coordinate components. \(\Gamma_{k}\) and \(\Gamma_{\omega }\) represent the coefficient of effective diffusion.

3 Fluid–Structure Interaction Calculation

When the flow-induced deflection of the structure has a non-negligible effect on the flow performance, requiring the coupling of the flow calculation (CFD) and the structural analysis (CSD) to capture the entire phenomenon, the fluid–structure interaction can efficiently handle this multi-physics problem. The fluid–structure interaction is characterized by the shared boundaries between the fluid and mechanical models. The created load of the solid surface should be derived from prior computational fluid dynamics. Sequentially, the loads derived from the structural analysis may influence the findings of the fluid investigation. Fluid–structure interaction has two main types: one-way and two-way approaches. The two-way coupling method is more reliable since it accounts for the whole phenomenon but is costly and requires much computational time. Figure 8 depicts the one-time step of the strong two-way coupling approach.

Fig. 8
figure 8

The strategy of the two-way FSI in the current simulation

Full size image

The governing matrix equations for finite elements are represented as follows [11, 48]:

$$ \left[ {M_{{\text{S}}} } \right]\left\{ {\ddot{U}} \right\} + \left[ {K_{{\text{S}}} } \right]\left\{ U \right\} = \left\{ {F_{{\text{S}}} } \right\} + \left[ R \right]\left\{ P \right\}{ } $$
(3)
$$ \left[ {M_{{\text{f}}} } \right]\left\{ {\ddot{P}} \right\} + \left[ {K_{f} } \right]\left\{ P \right\} = \left\{ {F_{{\text{S}}} } \right\} - \rho_{O} \left[ R \right]\left\{ {\ddot{U}} \right\} $$
(4)

where \(M_{{\text{S}}}\), \(U\), \(\ddot{U}\), \(K_{{\text{S}}}\), \(F_{{\text{S}}}\), \(P\), \(M_{{\text{f}}}\), \(K_{f}\), \(F_{{\text{S}}}\), \(\rho_{O}\), and \(R\) represent the solid mass, displacement, acceleration, stiffness matrix, solid node force, pressure, fluid mass, damping matrix, fluid node force, fluid density, and positive surface area linked with every grid node, respectively.

4 Energy Loss Analysis and Entropy Equations

The centrifugal pump generates mechanical energy by rotating its impeller, a portion of which is subsequently transferred into fluid power while also experiencing losses. The concept of loss, in this case, may be quantified by the measure of entropy generation [16, 32, 49, 50]. The concept of entropy generation measures the irreversibility inherent in a system and provides insight into the dissipation of energy that occurs throughout fluid flow processes. The metrics pertaining to entropy generation are used to assess energy dissipation and facilitate the identification of energy losses inside the centrifugal pump. The method of generating entropy may be divided into two distinct components: entropy generation via heat transfer and entropy generation via dissipation. The temperature in the impeller is virtually constant, so heat transfer-induced entropy generation is disregarded [29, 51,52,53].

The entropy generation of the centrifugal pump may be divided into two components: the entropy generation resulting from viscous dissipation, denoted as \(S_{{\overline{D}}}^{ \cdot \prime \prime \prime }\), and the entropy generation resulting from turbulent dissipation, denoted as \(S_{{\mathop D\limits{\prime} }}^{ \cdot \prime \prime \prime }\). The equation used for the computation of the local entropy generation per unit volume of the pump is as follows [29, 50]:

$$ {\text{EGR}} = S_{D}^{ \cdot \prime \prime \prime } = S_{{\overline{D}}}^{ \cdot \prime \prime \prime } + S_{{\acute{\mathop D\limits }}}^{ \cdot \prime \prime \prime } $$
(5)
$$ \begin{aligned} S_{{\overline{D}}}^{ \cdot \prime \prime \prime } = & \frac{\mu }{{\overline{T}}}\left\{ {2\left[ {\left( {\frac{{\partial \overline{u}}}{\partial x}} \right)^{2} + \left( {\frac{{\partial \overline{v}}}{\partial y}} \right)^{2} + \left( {\frac{{\partial \overline{\omega }}}{\partial z}} \right)^{2} } \right]} \right. \\ & \; + \left( {\frac{{\partial \overline{u}}}{\partial y} + \frac{{\partial \overline{v}}}{\partial x}} \right)^{2} + \left( {\frac{{\partial \overline{u}}}{\partial z} + \frac{{\partial \overline{\omega }}}{\partial x}} \right)^{2} + \left. {\left( {\frac{{\partial \overline{v}}}{\partial z} + \frac{{\partial \overline{\omega }}}{\partial y}} \right)^{2} } \right\} \\ \end{aligned} $$
(6)
$$ \begin{aligned} S_{\acute{\mathop D } }^{{ \cdot \prime \prime \prime }} = & \frac{\mu }{{\bar{T}}}\left\{ {2\left[ {\overline{{\left( {\frac{{\partial \acute{\mathop u}}}{{\partial x}}} \right)^{2} }} + \overline{{\left( {\frac{{\partial \acute{\mathop v}}}{{\partial y}}} \right)^{2} }} + \overline{{\left( {\frac{{\partial \acute{\mathop \omega}}}{{\partial z}}} \right)^{2} }} } \right]} \right. \\ & \; + \overline{{\left( {\frac{{\partial \acute{\mathop u}}}{{\partial y}} + \frac{{\partial \acute{\mathop v}}}{{\partial x}}} \right)^{2} }} + \overline{{\left( {\frac{{\partial \acute{\mathop u}}}{{\partial z}} + \frac{{\partial \acute{\mathop \omega}}}{{\partial x}}} \right)^{2} }} + \left. {\overline{{\left( {\frac{{\partial \acute{\mathop v}}}{{\partial z}} + \frac{{\partial \acute{\mathop \omega}}}{{\partial y}}} \right)^{2} }} } \right\} \\ \end{aligned} $$
(7)

Equation (6) encompasses the mean velocity gradients, commonly denoted as direct dissipation. The phenomenon under consideration may be understood as the mean flow field’s dissipation of entropy generation. Equation (7) incorporates the gradients of the fluctuating velocities, hence characterizing the dissipation of entropy generation within the fluctuating component of the flow field. The numerical solution cannot accurately capture the fluctuating velocity described in Eq. (5). Hence, within the SST k–ω turbulence model, the evaluation of the local entropy generation resulting from the velocity field variations can be mathematically represented, as shown in Eq. (8).

$$ S_{{\acute{\mathop D} }}^{ \cdot \prime \prime \prime } = \beta \frac{\rho \omega k}{T} $$
(8)

The variables k, ω and β denote the turbulent kinetic energy, vortex frequency and a constant value of 0.09. The total entropy generation (TEG) is defined as the integral of the local entropy generation across the volume, as shown by the following representation:

$$ S_{{\overline{D}}}^{ \cdot } = \mathop \int \limits_{V}^{1} S_{{\overline{D}}}^{ \cdot \prime \prime \prime } {\text{d}}V $$
(9)
$$ S_{{\acute{\mathop D} }}^{ \cdot } = \mathop \int \limits_{V}^{1} S_{{\mathop D{\prime} }}^{ \cdot \prime \prime \prime } {\text{d}}V $$
(10)
$$ {\text{TEG}} = S_{D}^{ \cdot } = S_{{\overline{D}}}^{ \cdot } + S_{{\acute{\mathop D\limits} }}^{ \cdot } $$
(11)

where V explains the path of the fluid flow.

5 Results and Discussion

5.1 Validation and Performance Curve

The head coefficient ψ is indicated to compare the experimental findings from [28] with the numerical results obtained from unsteady numerical simulation to test the work validation. The equation for the head coefficient is as follows [54]:

$$ \psi = 2Hg/u_{2}^{2} $$
(12)

where u2 is the circumferential velocity of the impeller outlet, and g is the acceleration gravity.

Figure 9 shows that although the experimental values are somewhat higher than the numerical findings of the head coefficient, both follow the same general pattern. This comparison indicated that the current simulation results reasonably agree with the previous experimental data. The simulation method can predict the flow behavior and provide acceptable results. However, the minor underestimation from the simulation results attributed to the friction losses, inaccurate geometry, a hypothetical CFD model and fluctuations in fluid properties might all contribute to this divergence [55,56,57]. Understanding and addressing these factors are crucial for refining and improving the model’s predictive accuracy. Therefore, these aspects can be considered for further improvements.

Fig. 9
figure 9

The validation of the head coefficient between experimental [28] and current simulation

Full size image

The centrifugal pump’s hydraulic parameters, including pump head, shaft power and pump efficiency, have been considered for various blade numbers. Figure 10 shows the centrifugal pump’s head and shaft power for the six models. The head and shaft power rise as the blade number increases. Moreover, the following equation has been used to calculate the hydraulic efficiency of the centrifugal pump for each of the six models [22]:

$$ \eta = \left( {\rho QgH/P_{{{\text{sh}}}} } \right) \times 100 $$
(13)

where Psh represents the consumed shaft power.

Fig. 10
figure 10

The head and the shaft power vary with the blade number

Full size image

Figure 11 shows pump efficiency with a variety of blade numbers. It can be observed that the impeller with seven blades has the best efficiency.

Fig. 11
figure 11

The pump efficiency at different blade numbers

Full size image

5.2 Flow Behavior Analysis

5.2.1 Pressure Fluctuation

Strong pressure pulsations may result from the impeller and the volute interface interaction. Unsteady numerical simulations were run with four to nine blades at a flow rate of 55 m3/h and a shaft speed of 1450 rpm to examine the unsteady pressure field and explore how the number of blades affects the unsteady pressure field. The unsteady pressure distributions inside the four monitoring points (V1, V2, V3 and V4) chosen at the volute, as seen in Fig. 12, are given and studied to examine the dependence on the number of blades.

Fig. 12
figure 12

Pressure fluctuation with time for different blade numbers at the monitoring points a V1, b V2, c V3 and d V4

Full size image

Figure 12 depicts a time-domain diagram of pressure fluctuations at the four monitoring points during the last rotational cycle. It is worth noting that the pressure fluctuation amplitude of the impeller with eight blades is greater than that of the other blades at points V1, V2 and V4 near the volute tongue. The amplitude of pressure pulsations at monitoring point V4 for the impeller with seven blades is somewhat more significant than that of the other impellers.

Even though the pressure fluctuation of the impeller with seven blades reaches a higher peak, the impeller’s mean pressure with eight blades is the highest (Fig. 13). The pressure fluctuation shows a different attitude at monitoring point V3 at the pump outlet. The impeller with nine blades has a greater pressure fluctuation amplitude than the other blades (Fig. 13). The number of waves and blades is correlated with the pressure’s periodic fluctuations. Additionally, each monitoring site in the volute has a distinct peak phase because a blade does not cross each monitoring point simultaneously.

Fig. 13
figure 13

The amplitude of the mean pressure at monitoring points

Full size image

5.2.2 Analysis of Frequency Domain

In addition, blade numbers are used in the calculation of the passing frequency of the blades, which is an essential component of pump design for determining whether the natural frequency of the blades is harmonics or sub-harmonics [58]. Additionally, it is utilized to assess if the pump operates at the highest level of efficiency [59]. The frequency of the blades passing may be represented as:

$$ f_{{\text{b}}} = {\raise0.7ex\hbox{${Zn}$} \!\mathord{\left/ {\vphantom {{Zn} {60}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${60}$}} $$
(14)

Z is the blade numbers, n is the rotational speed, and fb is the blade passing frequency [60].

Figure 14 shows the unsteady pressure’s frequency domain following a fast Fourier transform (FFT) with various blade numbers. Since the impeller rotates at 1450 rpm, the rotating frequency (fb) of the six models (Table 6) specifies the magnitude of pressure pulsations at their fundamental frequencies. The difference in the domain frequencies of the blades’ pressure fluctuations can be attributed to their separation. It can be shown that the highest pressure fluctuation amplitude for all monitoring points in the volute is at a blade passing frequency (BPF). Moreover, the impeller with four blades reaches a high peak at monitoring points V1, V2 and V3. However, the impeller with seven blades reaches the highest peak at monitoring point V4, far from the volute tongue. The analysis of the collected unsteady pressure data shows that the amplitude of the pressure pulsations at the pump outlet decreases as the number of blades rises.

Fig. 14
figure 14

The frequency of the pressure fluctuation at the monitoring points a V1, b V2, c V3 and d V4

Full size image
Table 6 The amplitude of the frequency at the monitoring points
Full size table

5.2.3 Pressure Distribution

To further investigate the effect of fluid–solid interaction on the internal flow behavior of the centrifugal pump, the middle section of the centrifugal pump on the XY plane at Z = 0.05 m was selected as the examination plane to analyze the flow characteristics inside the centrifugal pump.

Figure 15 depicts the cloud diagram of the static pressure behavior under different blade numbers. The figure illustrates that across all models, the pressure distribution trend of the impeller and volute exhibits a fundamental consistency, with higher pressure seen on the blade’s pressure side than the suction side. The variation in static pressure between the impeller inlet and impeller outlet is more noticeable. The location of the minimum static pressure region consistently occurs at the impeller inlet, regardless of variations in the blade number. The pressure inside the impeller increases as the impeller rotates, resulting in an expansion of pressure with increasing radius. This expansion of pressure creates a noticeable static pressure gradient inside the impeller. The static pressure will progressively increase until it reaches its maximum value when entering the volute.

Fig. 15
figure 15

Static pressure distribution with blade number a Z = 4, b Z = 5, c Z = 6, d Z = 7, e Z = 8 and f Z = 9

Full size image

The flow characteristics are significantly influenced by the asymmetry produced by the volute case’s presence and the volute tongue’s positioning. While the impact of the volute tongue is noticeable, a very consistent pressure distribution is observable around the impeller. Notably, the nonuniform properties of the pressure fields found between the circumference of the impeller and the volute are a consequence of the interaction between the rotor and stator.

Analyzing the pressure distribution of six distinct impeller configurations shows that the overall pressure magnitude of the impeller’s cross section at every blade number is highest at the impeller with nine blades compared with the other models, and that clearly explains in Fig. 15. It is noticeable that the monitoring point’s (V3) pressure is highest when the impeller with nine blades is in operation.

5.3 Entropy Generation Analysis

5.3.1 Total Entropy Generation

The centrifugal pump device’s total entropy generation (TEG) at various blade numbers was calculated. The total entropy generation in each component of the centrifugal pump of the six models under different blade numbers is shown in Fig. 16. Moreover, the proportion of the total entropy for each component of the centrifugal pump is shown in Fig. 17. Comparing the total entropy produced by the centrifugal pump’s inlet and outlet pipes and its impeller and volute, it was discovered that the inlet pipe produced the least entropy loss in all cases, with the tendency to decrease slightly as the number of blades increased. That means the pump’s inlet has little or no influence on the total entropy generation. However, the volute generated the maximum losses for all six models. It increases with increasing blade number, as shown in Fig. 16. That indicates the volute is not a good pair or suitable for matching the impeller [61, 62]. Moreover, the total entropy of all components of the centrifugal pump (inlet and outlet pipes, impeller and volute) increases with the increase in the blade number since increasing the blade number would lead to an increase in the blade walls that increases the wall friction with the pumped fluid. It is vital to note that the entropy generation due to wall friction also significantly adds to losses [62].

Fig. 16
figure 16

Distribution of TEG for pump components

Full size image
Fig. 17
figure 17

The proportion of TEG for pump components

Full size image

5.3.2 Entropy Generation Rate

The entropy generation rate (EGR) is examined numerically under various blade numbers to provide a comprehensive understanding of the properties that constitute the energy lost by the centrifugal pump. Figure 18 presents the EGR distribution under the six models. The EGR has startling irregularity in both the impeller and the volute. Figure 18 demonstrates that the EGR in the region at the impeller inlet with four blades is bigger than in the other models. It fills almost the whole entrance of the impeller flow channel and then decreases until it vanishes as the number of blades increases.

Fig. 18
figure 18

Distribution of EGR with blade number a Z = 4, b Z = 5, c Z = 6, d Z = 7, e Z = 8 and f Z = 9

Full size image

The EGR in the impeller is located at the leading edge, owing to a modest incidence angle in the passage. Because it is not rounded at the trailing edge, the fluid will strike the blade vertically, producing energy loss. The blades’ inlet and outlet are the primary locations where the energy lost is concentrated.

The flow separation occurs at the blade’s front edge suction surface and gradually diffuses into the impeller’s outlet in the passage because the inlet flow angle is less than the installation angle of the blade. This situation results in a significant separation loss. The backflow at the impeller outlet causes a significant amount of energy loss at the blade outlet. The entropy generation rate can be found at the impeller–volute interface since it is affected by rotor–stator interaction. Energy loss begins on the spiral portion of the volute’s wall once the fluid has passed through the tongue of the volute.

The losses are the most concentrated in the areas closest to the impeller’s inlet and outlet. Additionally, the amount of energy lost in the area close to the hub and the shroud is more than in the center part. As a result, the impeller–volute interface’s rotor–stator interaction significantly impacts the impeller inlet. Furthermore, it is crucial to comprehend how the velocity profiles affect the EGR on various spans, as shown in Fig. 19.

Fig. 19
figure 19

EGR and velocity vector distribution in different spans with blade numbers a Z = 4, b Z = 5, c Z = 6, d Z = 7, e Z = 8 and f Z = 9

Full size image

There is a strong correlation between velocity streamlines and entropy distribution. From span 0.5 to span 0.9, the zones with high entropy levels had a similar velocity pattern. The blade-to-blade view offers a unique vantage point for examining the flow dynamics between adjacent blades while maintaining a constant relative distance between the hub and shroud surfaces. There is a notable correspondence seen between the velocity streamlines and the EGR. The areas with high entropy values had a comparable range of vortices from 0.5 to 0.9. As seen in Fig. 19, a wide variety of vortices formed close to the working surface of the impeller blades, blocking up over half of the impeller flow route and leading to significant energy loss. The blade wake flow also causes the loss at the impeller exit. Despite vortices on the pressure surface, the low flow velocity causes the pressure surface to lose less energy than the suction surface. The impeller’s suction side (SS) determines the highest energy loss rate (EGR), which improves with an increase in blade number and causes high energy loss in the impeller flow channels.

In addition, the presence of flow separation zones in the velocity plots indicates a significant level of vortex strength, which implies that the velocity profiles impact the EGR. The largest EGR is at the trailing edge of the impeller’s suction side (SS), resulting in significant energy loss inside the impeller’s flow passages. Due to the increase in relative velocity and impact loss near the shroud, the EGR on the SS of the impeller blade increases as its proximity to the shroud increases.

5.4 Analysis of Structure Behavior

5.4.1 Analysis of Total Deformation

Figure 20 illustrates the distribution diagram of structural deformation for various blade numbers. The impeller is deformed around the edge region. The deformation gradually increases along the direction of the increasing radius of the impeller. In each model, the impeller’s outlet experiences the most significant deformation. The maximum deformation position of the impeller has a different trend for each model, and the deformation changes significantly. Variation of blade number has a significant effect on the maximum total deformation of the impeller.

Fig. 20
figure 20

Total deformation distribution with blade number a Z = 4, b Z = 5, c Z = 6, d Z = 7, e Z = 8 and f Z = 9

Full size image

Figure 20 clearly shows that the maximum deformation occurs in a different quadrant of the XY plane. The maximum deflection would vary with the variation of blade number. It shows at the first and fourth quadrants of the impeller with four blades. The maximum total deformation of impellers with five and eight-blade numbers has almost a similar attuite. The maximum deflection is shown at the third and fourth quadrants of the XY plane. Moreover, the impellers with six and seven blades also have the same attuite.

The maximum total deformation almost happened at a similar location as the impellers with five and eight blades but with a little deviation to the third quadrant. Finally, the maximum total deformation of the impeller with nine blades is shown at the first and second quadrants with the minimum value compared with the other models.

Figure 21 depicts the maximum deformation variation curve for rotor systems with various numbers of blades. With an increase in blade number, the maximum total deformation initially decreases and then increases (Fig. 21), showing that the rotor system deformation changed dramatically with the variation of blade number. Maximum deformation varies substantially with different blade numbers. Among the six impeller cases, the impeller with six blades has the largest maximum deformation, and the maximum deformation is 0.097 mm. However, the nine-blade impeller has a minimum value of 0.046 mm.

Fig. 21
figure 21

The maximum value of a total deformation for different blade numbers

Full size image

Figure 22 shows the time-domain diagram of fluctuations of the average total deformation for the last rotational cycle of the testing models under different blade number. It is observed to see that the fluctuation is periodic. The number of waves and blades corresponds, with one exception of the impeller with nine blades which shows that the number of waves is six, which is less than the number of blades, so that would encourage investigation of the centrifugal pump with blade number more than nine. Moreover, it is evident that the phases of the peaks are different, and the impeller with seven blades shows the highest peak. This situation is because each blade passes the monitoring point at a different time.

Fig. 22
figure 22

The average of total deformation fluctuation with blade number

Full size image

5.4.2 Analysis of Equivalent Stress

Figure 23 illustrates the impeller’s equivalent stress distribution for various numbers of blades. Relative stress values are highest at the blade-cover junction and lowest at the rotating shaft. Under different numbers of blades, the equivalent stress distribution of the impeller is nearly the same, which is a more consistent and center-symmetric distribution. The arrangement of the hub joint and the impeller blades clearly show stress concentration areas. Moreover, the maximum value of the equivalent stress of all testing models shows at the cylindrical support: a of the rotating shaft, which closes to the rotating impeller of the centrifugal pump, as shown in Fig. 24.

Fig. 23
figure 23

Equivalent stress distribution at the impeller with blade number a Z = 4, b Z = 5, c Z = 6, d Z = 7, e Z = 8 and f Z = 9

Full size image
Fig. 24
figure 24

Equivalent stress distribution at support: a with blade number a Z = 4, b Z = 5, c Z = 6, d Z = 7, e Z = 8 and f Z = 9

Full size image

Figure 25 shows the curve of the maximum equivalent stress of the solid rotating structure of the centrifugal pump. The solid structure’s maximum equivalent stress changes significantly as the number of blades rises. The maximum equivalent stress of the impeller with seven blades was much higher than that of other cases, with a value of 16.74 MPa. Moreover, the impeller with nine blades shows a minimum value of 5.74 MPa.

Fig. 25
figure 25

Maximum equivalent stress with blade number

Full size image

Figure 26 shows the time-domain diagram of fluctuations of the average equivalent stress for the last rotational cycle of the testing models under different blade numbers. The fluctuations of the average of the equivalent stress would be the same as the pressure and the fluctuations of the equivalent stress. It is noted that the oscillation is periodic and that the wave number corresponds to the number of the blades. Moreover, the impeller of nine blades also shows that the number of waves is six, which is less than the number of blades and fluctuates with minimum value.

Fig. 26
figure 26

Average of equivalent stress fluctuation with blade number

Full size image

6 Conclusion

In conclusion, this numerical investigation explored the effects of varying blade numbers on the hydraulic and structural performance of a centrifugal pump, considering energy loss. The main findings can be summarized as follows:

  1. (a)

    Hydraulic performance:

    • The head and shaft power steadily increase with the rise in blade numbers.

    • Notably, the impeller with nine blades attains maximum values, showing a 5.4% increase in head and a 7.9% increase in shaft power relative to the original model.

    • Efficiency peaks with seven blades, demonstrating a 0.27% improvement over the original model.

  2. (b)

    Pressure pulsations:

    • Pressure pulsations vary with blade numbers, with the eight-bladed impeller showing the highest values near the volute tongue.

    • Monitoring points at different locations reveal distinct pressure fluctuation behaviors, emphasizing the influence of blade number variation.

  3. (c)

    Entropy generation:

    • Entropy generation analysis highlights the importance of blade number on entropy distribution.

    • The inflow pipe exhibits the lowest total entropy, while the highest is observed at the volute.

    • The entropy generation rate on the suction side rises near the shroud due to velocity effects.

  4. (d)

    Structural analysis:

    • Equivalent stress and total deformation are minimized in the nine-blade impeller under given operating conditions.

    • Distortion increases gradually with the expansion of the impeller radius.

    • Maximum equivalent stress consistently occurs near the root of the blade’s connection with the hub.

  5. (e)

    Limitations and future directions:

    • The study acknowledges limitations in computational capacity, particularly regarding two-way fluid–structure coupling.

    • Including this coupling method is deemed crucial for advancing centrifugal pump performance analysis.

    • Future research should explore the influence of other parameters and incorporate fluid–structure interaction aspects for a more comprehensive understanding.

This study provides valuable insights into the interaction between blade numbers, hydraulic performance and structural behavior in centrifugal pumps. The findings contribute to the current understanding of pump dynamics and lay the groundwork for future research, emphasizing the importance of considering fluid–structure interaction for a more realistic analysis.