1 Introduction

One of the fundamental components of nanotechnology is nanofluid, which is a possible heat transfer fluid. Carbon nanotubes are used in boiler exhaust flue gas recovery, nuclear systems cooling, engine transmission oil, electronic cooling, high power lasers, biomedical applications, polymer extraction, and fiber equipment, and in a cooling bath, crystals develop and cool on infinite metallic plates, lubrications, drilling, and solar water heating. These are some of the many applications of carbon nanotubes.

Carbon nanotubes (CNTs) based nanofluid as a heat transfer system. Carbon nanotubes are a commonly used fullerene allotrope with a lengthy and cylindrical chemical structure made up of sheets of graphite. There are two categories of CNTs, SWCNTs, and MWCNTs. The thermophysical properties of carbon nanotubes are subservient along with graphene sheets getting aligned consecutively within the tube, which results in this kind of material executing the properties of metal or semiconductor explored by Waqar et al. [1]. Iijima [2] explores the chemical process and heat radiation effect on nanofluid flow, which relies on time along with changing fluid characteristics. Baughman et al. [3] investigated the heat transmission with magnetohydrodynamics and the flow of carbon nanotube suspensions of nanoparticles over a stretching sheet (linear).

The study of the (magnetohydrodynamics) electrically conductive fluid flow driven by a stretched sheet is essential in modern metallurgy applications, plastic sheet drawings, metal-working processes, and so on. In each of these techniques, a cooling speed has a significant impact on the final product’s condition. Sarpakaya was the first to investigate the flow of magnetohydrodynamics in this specific case. The Jeffrey fluid model is preferred in several cases since convicted derivatives are replaced with time derivatives. The multi-phase flow of the Jeffrey fluid was investigated by Nazeer et al. [4] within a magnetized horizontal surface. A numerical investigation of the effects of activation energy and microorganisms on a Jeffrey nanofluid squeezing flow contained by two parallel disks using a chemical process was done by Chu et al. [5]. Abbas et al. [6] examined Darcy Forchheimer’s electromagnetic stretched flow of carbon nanotubes across an inclined cylinder while taking entropy optimization and quartic chemical reaction into account. Hayat et al. [7] present heat transfer and boundary layer flow in a nanoparticle-enhanced Jeffrey fluid. Turkyilmazoglu [8], in his paper, considered parallel external flow to explore Jeffrey fluid flow with heat transfer. In the latter, which included several physical parameters, exact solutions of the linear or exponential systems were provided. With the aid of the Brinkman model, Mahabaleshwar et al. [9] investigated the behavior of velocity profiles due to slip parameters in Newtonian liquid flow over shrinking /stretching sheets in the penetrable media. Mahabaleshwar et al. [10] explored Newtonian fluid flow and the magnetohydrodynamics effect caused by a superlinear stretched sheet. Siddheshwar et al. [11] conducted an analytical study on the magnetohydrodynamics flow across a stretched sheet of a viscoelastic fluid embedded in a porous media.

Mahabaleshwar et al. [12] contributed to the inclined magnetohydrodynamics effect, thermal radiation effects, and Stefan blowing effects on Newtonian fluids. Siddheshwar et al. [13] presented a new perspective approach for a nonlinear boundary layer that arises in stretched surface problems with non-Newtonian/Newtonian liquids. Ramesh et al. [14, 15] used a semi-infinite flat sheet to investigate a precise remedy for 2D viscous boundary layer flow along with the magnetic effect. Mahantesh et al. [16] proposed the second-order slip flow across a stretched surface with heat transfer. Mahabaleshwar [17, 18] investigated a new exact solution for the flow of a fluid through porous media for a variety of boundary conditions. An investigation of electrically conducting viscoelastic fluid flow over a porous media barrier that is linearly expanded [19,20,21]. Anuar et al. [22] studied the heat transfer of carbon nanotubes over an exponentially stretching/shrinking sheet with a suction and slip effect. Anwar et al. [23] investigated the unsteady magnetohydrodynamics flow of Jeffery fluid flow with wall velocity and Newtonian fluid. Fluid flow and heat transfer of carbon nanotubes along with a flat plate with a Navier slip boundary were investigated by Khan et al. [24]. Shalini et al. [25] studied the unsteady magnetohydrodynamics chemically reacting mixed convection nanofluids flow past an inclined pours stretching sheet with slip effect and variable thermal radiation and heat source. The effects of inclined Lorentz force and thermal radiation on natural convection inside a porous container with a micropolar nano liquid and an elliptical tilted heater are investigated by Yana et al. [26]. Unsteady MHD flow for Casson fluid with porous media with stretching/shrinking plate with mass transpiration and Brinkman ratio is investigated by Anusha et al. [27, 28]. Mahabaleshwar [29] investigated the inclined Lorentz force and Schmidt number on chemically reactive Newtonian fluid flow on a stretchable surface when Stefan blowing and thermal radiation are significant. Thermal management for conjugate heat transfer of curved solid conductive panel coupled with different cooling systems using non-Newtonian power law nanofluid applicable to photovoltaic panel systems. The recent works related to MHD and porous media can be found in these studies [30,31,32,33,34].

Further, the effects of carbon nanotube-based nanofluids on mass transpiration, radiation, and the inclined field of magnetism in the presence of Jeffery fluid flow are discussed. The discussion is established over a stretching/shrinking sheet. Furthermore, the velocity profiles, skin friction, and heat transfer on the plate are examined to discuss the effect that the different physical governing parameters, such as the Prandtl number, or the magnetic field, have on them, and to introduce the consequences of the physical parameters imposed on the velocity profiles.

The main purpose and motivation of this paper is to address the magnetohydrodynamics effect on fluid flow over a stretching surface in the presence of CNTs. Using these CNTs, the present problem is examined with the help of analytical results. The main reason to accompany CNTs is due to its extraordinary electrical and heat conductivity properties. The complimentary error function was utilized to get a solution for temperature profile. The organization of the present work is to provide the new results on carbon nanotubes and examine these results in the analytical approach.

The first section includes an introduction, and in Sect. 2, the physical model and solution are discussed; Sect. 3 comprises results and a discussion of the graphical representation, and the conclusions of the current study are presented in Sect. 4.

2 Physical Model and Solution

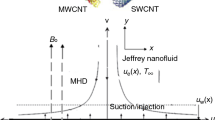
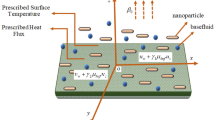
In a water/oil-based nanofluid containing both single- and multi-wall carbon nanotubes, consider two-dimensional flows over a flat plate with heat transfer. The stretching/shrinking sheet is parallel to the y = 0 plane. The flow is induced by a stretching/shrinking sheet caused by the simultaneous application of two equal and opposite forces along the x-axis. A uniform surface heat flux is applied to the plate surface. It is assumed that the flow is laminar, continuous, and incompressible. Thermal equilibrium is considered between the base fluid and the carbon nanotubes [35,36,37].

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0,$$
(1)
$$u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}\,\,\, = \,u_{e} \frac{{\partial u_{e} }}{\partial x}\, + \frac{{\nu_{nf} }}{{\left( {\chi_{1} + 1} \right)}}\left[ {\frac{{\partial^{2} u}}{{\partial y^{2} }} + \chi_{2} \left( {u\frac{{\partial^{3} u}}{{\partial x\partial y^{2} }} + v\frac{{\partial^{3} u}}{{\partial y^{3} }} - \frac{{\partial^{2} u}}{{\partial y^{2} }}\frac{\partial u}{{\partial x}} + \frac{{\partial^{2} u}}{\partial x\partial y}\frac{\partial u}{{\partial y}}} \right)} \right] - \frac{{\sigma_{nf} B_{0}^{2} }}{{\rho_{nf} }}{\text{Sin}}^{2} \left( \tau \right)\left( {u - u_{e} } \right),$$
(2)
$$\left( {\rho C_{{\text{p}}} } \right)_{nf} \left( {v\frac{\partial T}{{\partial y}} + u\frac{\partial T}{{\partial x}}} \right) = \,k_{nf} \frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{{\partial q_{{\text{r}}} }}{\partial y}.$$
(3)

Here, \(\left( {u,v} \right)\) stand for \(\left( {x,y} \right)\) directional velocity components correspondingly, \(U_{{\text{w}}} (x)\) is surface velocity, \(\chi_{1}\) is the relaxation ratio, \(\chi_{2}\) denotes retardation time, effective kinematic viscosity \(\nu_{nf}\), \(T\) is temperature, and \(\left( {\rho C_{{\text{p}}} } \right)_{nf}\) and \(k_{nf}\) denotes heat capacity and thermal conductivity, respectively. The following are effective nanofluid properties with base fluid containing a solid volume fraction of the CNTs: [38]

$$\left. \begin{gathered} \nu_{nf} = \frac{{\mu_{nf} }}{{\rho_{nf} }},\,\,\rho_{nf} = \phi \rho_{{{\text{CNT}}}} + \rho_{f} \left( {1 - \phi } \right), \hfill \\ \alpha_{nf} = \frac{{\kappa_{nf} }}{{\left( {\rho C_{p} } \right)_{nf} }},\,\,\,\left( {\rho C_{p} } \right)_{nf} = \left( {\rho C_{p} } \right)_{f} \left( {1 - \phi } \right) + \left( {\rho C_{p} } \right)_{{{\text{CNT}}}} \phi , \hfill \\ \frac{{\sigma_{nf} }}{{\sigma_{f} }} = 1 - \frac{{3\phi \left( {1 - \frac{{\sigma_{{{\text{CNT}}}} }}{{\sigma_{f} }}} \right)}}{{\frac{{\sigma_{{{\text{CNT}}}} }}{{\sigma_{f} }} - 2 + \left( {1 - \frac{{\sigma_{{{\text{CNT}}}} }}{{\sigma_{f} }}} \right)\phi }}, \hfill \\ \frac{{k_{nf} }}{{k_{f} }} = \frac{{2\phi \frac{{k_{{{\text{CNT}}}} }}{{k_{{{\text{CNT}}}} - \kappa_{f} }}\log \frac{{k_{f} + k_{{{\text{CNT}}}} }}{{2\kappa_{f} }} + 1 - \phi }}{{1 + 2\phi \frac{{k_{f} }}{{k_{{{\text{CNT}}}} - k_{f} }}\log \frac{{k_{{{\text{CNT}}}} + k_{f} }}{{2k_{f} }} - \phi .}} \hfill \\ \end{gathered} \right\}$$
(4)

Using [37] diffusion approximation, the radiative heat flux is determined by Mahabaleshwar et al. [29]:

$$q_{r} = - \frac{{16\,\sigma^{*} }}{{3k^{*} }}T_{\infty }^{3} \,\frac{\partial T}{{\partial y}},$$
(5)

where, \(k^{*}\) and \(\sigma^{*}\) is the mean absorption coefficient and Stefan–Boltzmann constant, respectively. The Taylor’s series expansion of the term \(T^{4}\) being a linear function of temperature is expressed as follows by Mahabaleshwar et al. [29]:

$$T^{4} = T_{\infty }^{4} + 4\left( {T - T_{\infty } } \right)T_{\infty }^{4} + .....$$
(6)

Omitting high-order terms in Eq. (6) leaving the initial term in \(\left( {T - T_{\infty } } \right)\), \(T^{4}\) can be estimated by:

$$T^{4} \cong 4TT_{\infty }^{3} - 3T_{\infty }^{4} ,$$
(7)

Employing Eqs. (6–7), Eq. (3) can be rewritten as,

$$v\frac{\partial T}{{\partial y}} + u\frac{\partial T}{{\partial x}} = \frac{{k_{nf} }}{{(\rho C_{{\text{p}}} )_{nf} }}\left( {1 + \frac{{16T_{\infty }^{3} \,\sigma^{*} }}{{3k^{*} k_{nf} }}} \right)\frac{{\partial^{2} T}}{{\partial y^{2} }}.$$
(8)

2.1 Boundary Conditions

With the boundary conditions

$$\begin{gathered} \left. {\,\,u\, = \,U_{w} (x)\,\, = \,\,dcx + \Gamma_{1} \frac{\partial u}{{\partial y}} + \Gamma_{2} \frac{{\partial^{2} u}}{{\partial y^{2} }},\,\,\,} \right\}\,\,{\text{at}}\,\,y = 0 \hfill \\ \,\,v = v_{w} ,\,\,\,\,\,T = T_{w} \left( x \right), \hfill \\ \left. {\,\,\,u \to u_{e} \left( x \right)\, = \,\,xa,\,\,\,\,\,\,\,\,\,\,\frac{\partial u}{{\partial y}}\,\,\, \to 0,\,\,\,\,\,\,T \to T_{\infty } .} \right\}{\text{at y}} \to \infty \hfill \\ \end{gathered}$$
(9)

where \(\Gamma_{1}\)and \(\Gamma_{2}\) are first-order and second-order slip parameters, following suitable similarity variables are introduced as follows:

$$\begin{aligned} \eta = \sqrt {\frac{{c\,(\gamma_{1} + 1)}}{{\nu_{f} }}} \,y,\,\,\,u = \,xcf_{\eta } (\eta ),\\ v = - \sqrt {\frac{{\nu_{f} \,c\,}}{{(1 + \gamma_{1} )}}} f(\eta ),\,\,\,\theta = \frac{{T - T_{{_{\infty } }} }}{{T_{{_{w} }} - T_{{_{\infty } }} }},\,\, \end{aligned}$$
(10)
$$T_{w} \left( x \right) = T_{\infty } + bx,$$

The transformed Eqs. (2–3) and (8) are expressed as follows:

$$\begin{aligned} & f_{\eta \eta \eta } \varepsilon_{3} + ff_{\eta \eta }- \left( {f_{\eta } } \right)^{2} - \varepsilon_{3} \beta \left( {ff_{\eta \eta \eta \eta } - \left( {f_{\eta \eta } } \right)^{2} } \right) + \Lambda^{2} \\ &\quad - \left( {f_{\eta } - \Lambda } \right)\frac{{\varepsilon_{1} }}{{\varepsilon_{2} }}Q{\text{Sin}}^{2} \left( \tau \right) = 0, \hfill \\ &\quad \left( {\varepsilon_{5} + \,\frac{4}{3}Rd} \right)\theta_{\eta \eta } + \Pr \varepsilon_{4} f\theta_{\eta } \, = \,0,\,\, \hfill \\ &\quad \left( {\varepsilon_{5} + \,\frac{4}{3}Rd} \right)\theta_{\eta \eta } + \Pr \varepsilon_{4} \left( {f\theta_{\eta } - f_{\eta } \theta } \right) = 0. \hfill \\ \end{aligned}$$
(11)

The renovated boundary limitations

$$\begin{aligned} f\left( 0 \right)\, &= \,V_{c} \,\,,\,\,\,f_{\eta } \left( 0 \right) = L_{1} f_{\eta \eta } \left( 0 \right) + L_{2} f_{\eta \eta \eta } \left( 0 \right) + \,d, \hfill \\ \theta (0)\, &= \,1,\,\,\,f_{\eta } \left( \infty \right) = \Lambda ,\,\,f_{\eta \eta } \left( \infty \right)\, = 0\,\,\theta \left( \infty \right) = 0. \hfill \\ \end{aligned}$$
(12)

Here, \(\Lambda \, = \,\frac{a}{c}\) is a stagnation parameter, Prandtl number \(\Pr \, = \,\frac{{\nu_{f} }}{\alpha }\), \(L_{1} \,{\text{and}}\,L_{2}\) the slip parameter, \(\beta\) Deborah number, and wall transpiration \(v_{w} = - \sqrt {\frac{{c\nu_{f} }}{{1 + \gamma_{1} }}}\), Q Chandrasekhar number. Hence, the boundaries are the governing boundaries in the Jeffery fluid flow.

The major physical dimensionless parameters like skin friction coefficient \(Cf_{x}\) and Nusselt number \(Nu_{x}\) are well-stated as,

$$Cf_{x} = \frac{{\tau_{w} }}{{\rho_{nf} u_{e}^{2} (x)}},$$
(13)
$$Nu_{x} = \frac{{xq_{w} }}{{\left( {T_{w} - T_{\infty } } \right)\alpha }}.$$
(14)
$$\begin{gathered} {\text{where}}, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tau_{w} = \mu_{nf} \left. {\left( {\frac{\partial u}{{\partial y}}} \right)} \right|_{y = 0} ,\,\,q_{w} = - \alpha_{nf} \left. {\left( {\frac{\partial T}{{\partial y}}} \right)} \right|_{y = 0} . \hfill \\ \end{gathered}$$

We get Eq. (15) after applying the similarity transformation Eq. (10)

$$Cf_{x} \,{\text{Re}}_{x}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \,\, = \,\varepsilon_{3} \,f_{\eta \eta } (0),\,\,\,Nu_{x} \,{\text{Re}}_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \, = \, - \frac{{\varepsilon_{4} }}{{\varepsilon_{5} }}\theta_{\eta } (0).$$
(15)

2.2 Solution of Momentum Problem

Our examination is fundamentally founded on classical Crane’s solution \(f(\eta ) = 1 - exp\left( { - \lambda \eta } \right),\)

[39]. Here, \(V_{c} = Q = \beta = \Lambda = L_{1} = L_{2} = 0\) in the most basic flow condition as a consequence, and we can execute an explanation of the procedure for the general case

$$f(\eta )\, = \,V_{c} + \Lambda \eta + \frac{d - \Lambda }{{\lambda (1 + L_{1} \lambda + L_{2} \lambda^{2} )}}\left( {1 - exp\left( { - \lambda \eta } \right)} \right)$$
(16)

We get the mathematical equation relating the actual boundaries by substituting Eq. (11) first of (16)

$$(d - \Lambda )\,\left\{ \begin{gathered} (1 + L_{1} \lambda + L_{2} \lambda^{2} )\,\,\left[ { - \frac{{\varepsilon_{1} }}{{\varepsilon_{2} }}Q{\text{Sin}}^{2} \left( \tau \right) + \lambda \left( {\varepsilon_{3} \lambda - V_{c} + \varepsilon_{3} \beta V_{c} \lambda^{2} } \right)} \right] + \,\,\,\,d\left( { - 1 + \varepsilon_{3} \beta \lambda^{2} } \right) \hfill \\ - \Lambda - 2\Lambda L_{1} \lambda + 2\Lambda L_{2} \lambda^{2} - \varepsilon_{3} \beta \Lambda \lambda^{2} + \,\,\,\,\eta \Lambda \lambda \left( {1 + L_{1} \lambda + L_{2} \lambda^{2} } \right)\left( { - 1 + \varepsilon_{3} \beta \lambda^{2} } \right) \hfill \\ \end{gathered} \right\}.$$
(17)

As a consequence, the form and number of solutions will be determined by the polynomial roots (17).

For the specific case, Λ = 0, (12) converts

$$\left( {\varepsilon_{3} \beta \lambda^{2} - 1} \right)d(1 + L_{1} \lambda + L_{2} \lambda^{2} ) + \,\left( { - \frac{{\varepsilon_{1} }}{{\varepsilon_{2} }}Q{\text{Sin}}^{2} \tau + \lambda \left( {\varepsilon_{3} \lambda - V_{c} + \varepsilon_{3} \beta V_{c} \lambda^{2} } \right)} \right)\,\,\,\, = 0$$
(18)

Provided the reduced form Eqs. (11) and the energy Eq. (15), a further solution can be found supposing linear wall temperature.

2.3 Solution of Energy Problem

$$\theta = exp\left( { - \lambda \eta } \right),$$
(19)

that produces

$$d\Pr \varepsilon_{4} \, + \left[ {\Pr \varepsilon_{4} V_{c} - \lambda \left( {\varepsilon_{5} + \frac{4}{3}Rd} \right)\lambda (1 + L_{1} \lambda + L_{2} \lambda^{2} )} \right] = 0,$$
(20)

It is simple to get between (18) and (20).

$$\lambda = \,\sqrt {\frac{{\left( {\varepsilon_{5} + \frac{4}{3}Rd} \right) - \Pr \varepsilon_{4} \varepsilon_{3} \pm \sqrt {\left( {\left( {\varepsilon_{5} + \frac{4}{3}Rd} \right) - \Pr \varepsilon_{4} \varepsilon_{3} } \right)^{2} + 4\Pr \beta \frac{{\varepsilon_{1} \varepsilon_{4} \varepsilon_{3} }}{{\varepsilon_{2} }}Q{\text{Sin}}^{2} \tau \left( {\varepsilon_{5} + \frac{4}{3}Rd} \right)} }}{{2\beta \varepsilon_{3} \left( {\varepsilon_{5} + \frac{4}{3}Rd} \right)}}} ,$$
(21)
$$V_{c} \, = \,\frac{{\lambda \left( {\varepsilon_{5} + \frac{4}{3}Rd} \right)}}{{Pr\varepsilon_{4} }} - \frac{d}{{\lambda (1 + L_{1} \lambda + L_{2} \lambda^{2} )}}.$$

As a consequence, one can get

$$\left. \begin{aligned} f(\eta )\, = & V_{c} + \frac{d - \Lambda }{{\lambda (1 + L_{1} \lambda + L_{2} \lambda^{2} )}}\left( {1 - Exp[ - \lambda \eta ]} \right), \\ \theta = & Exp[ - \lambda \eta ]. \\ \end{aligned} \right\}$$
(22)

Temperature is unaffected by these parameters because \(\lambda\) is independent of \(L_{1} ,L_{2}\) and \(D\). The corresponding suction parameter Vc, on the other hand, will change as these parameters change.

After that, the physically interesting parameters are determined.

$$- f_{\eta \eta } (\eta )\, = \,\frac{{\left( {d - \Lambda } \right)\lambda }}{{(1 + L_{1} \lambda + L_{2} \lambda^{2} )}},\,\,\, - \theta_{\eta } (0) = \lambda .$$
(23)

As a consequence, on expanding the slip parameter, the coefficient of skin friction, and variations in wall shear and Nusselt number, just as velocity and temperature distributions, the Jeffrey fluid will evolve to f in the case of \(\Lambda = 1\) as well as d = 1. \(f(\eta )\, = \,V_{c} + \eta\) any Q,\(L_{1} ,L_{2}\), \(V_{c}\) and \(\lambda\) are real. A temperature solution is also given when these two variables are added together.

$$\theta (\eta ) = \frac{{Erfc\left[ {\sqrt {\frac{{Pr\varepsilon_{4} }}{{2\left( {\varepsilon_{5} + \frac{4}{3}Rd} \right)}}} \left( {V_{c} + \eta } \right)} \right]}}{{Erfc\left[ {\sqrt {\frac{{Pr\varepsilon_{4} }}{{2\left( {\varepsilon_{5} + \frac{4}{3}Rd} \right)}}} \,\,V_{c} } \right]}},$$
(24)

The complementary error function is denoted by Erfc. As a result, we obtain the same expression.

$$- \theta_{\eta } (0) = \,\frac{{ - \sqrt {\frac{2}{\pi }} \sqrt {\frac{{Pr\varepsilon_{4} }}{{\left( {\varepsilon_{5} + \frac{4}{3}Rd} \right)}}} Exp\left[ { - \frac{Pr}{{\left( {\varepsilon_{5} + \frac{4}{3}Rd} \right)}}} \right]}}{{Erfc\left[ {\sqrt {\frac{{Pr\varepsilon_{4} }}{{2\left( {\varepsilon_{5} + \frac{4}{3}Rd} \right)}}} \,\,V_{c} } \right]}}.$$
(25)

3 Result and Discussion

The Jeffery fluid flow known as non-Newtonian flows with heat transfer is analytic and steady. A comprehensive mathematical model of the carbon nano-multi-wall carbon nanotube-based nano-liquids due to stretching/shrinking sheets with radiations has been presented in this research paper. The systems of PDEs Eqs. (1), (2), and (3) are transformed into a set of nonlinear ODEs via similarity variables. The exact analytical solution is investigated the different combinations of physical parameters viz. Exact analytical explanations for velocity and energy profiles can be achieved by using the appropriate similarity variable. As a result of the multiple graphs that will be presented and discussed below on the subject, we now understand the technology involved in such fascinating dynamics. Furthermore, similar visuals provide a comparison of the transverse, axial, and temperature profiles of single-wall carbon nanotubes and multi-wall carbon nanotubes, for which the solid volume fraction will be fixed, with dashed and solid lines indicating the solutions for single-wall carbon nanotubes and multi-wall carbon nanotubes, respectively (Fig. 1). A comparison of the present study and existing works by other authors is illustrated in Table 1.

Fig. 1
figure 1

Geometry of the flow

Full size image

Figures 2, 3 depict the axial and transverse velocity versus similarity variables for different entities of Chandrasekhar’s number’s Q. In Fig. 2a, b with fixed Pr = 6.2 for base fluid water for single-wall carbon nanotubes and multi-wall carbon nanotubes, it is identified that the velocity field increases for the raise of the different values of Chandrasekhar’s number’s Q. As one can see, \(f\left( \eta \right)\) increases as Chandrasekhar’s number’s Q also rises, and, for the suction case, the boundary layer thickness is shifted away from the x-axis. It is similarly noticed that \(f_{\eta } (\eta )\) improves water and kerosene oil nano-liquid for multi-wall carbon nanotubes as compared with single-wall carbon nanotubes. Figure 3a,b illustrates the effect of Chandrasekhar’s number’s Q on \(f_{\eta } (\eta )\), for large estimates of the Chandrasekhar’s number’s Q, velocity \(f_{\eta } (\eta )\) and its related boundary layer decrease. Chandrasekhar’s numbers affect the extent of the boundary layer thickness, which decreases in a stretching/shrinking surface when the parameter Q increases.

Fig. 2
figure 2

a Curves of transverse profile for different values of Q. b Curves of transverse for various values of Q

Full size image
Fig. 3
figure 3

a Impact of Chandrasekhar number on velocity profile for stretching sheet. b Impact of Chandrasekhar number on velocity profile for shrinking sheet

Full size image

The action of the radiation parameter Rd on \(f_{\eta } (\eta )\) is depicted in Fig. 4a, b. The velocity profile for SWCNTs and MWCNTs using base liquid water indicates a reduction in the behavior of the radiation parameter. The consequence of the radiation field is to develop the stretching sheet and reduction it for the sheet with shrinking. The radiation parameter affects the extent of the boundary layer thickness, which decreases in a stretching/shrinking surface when the parameter Q increases.

Fig. 4
figure 4

a Impact of radiation on velocity profile for stretching sheet. b Impact of radiation on velocity profile for shrinking sheet

Full size image

Figure 5 portrays the effect of the temperature profile and raise of Chandrasekhar’s number’s Q for both single-wall carbon nanotubes and multi-wall carbon nanotubes. For higher values of Chandrasekhar’s number’s Q, the temperature distribution and associated boundary layer thickness decrease. It is observed that the temperature and boundary layer density rise in SWCNTs and MWCNTs when the volume fraction increases and the boundary layer thickness also decreases. Figure 6 represents the impact of mass transpiration \(V_{c}\) on the temperature profile \(\theta\). In both the SWCNTs and MWCNTs cases, temperature decreases concerning \(V_{c}\). This is because of the way that fluid has a lower thermal conductivity for comprehensive mass transpiration, which lessens conduction and the thickness of the thermal boundary layer, lowering the temperature. It is observed that the temperature and boundary layer density rise in SWCNTs and MWCNTs. When the volume fraction increases, the boundary layer thickness also decreases. Figure 7 portrays the impacts of Prandtl number Pr on the Nusselt number with the variation of mass transportation \(V_{c}\). It could be seen that the graph of the mass transpiration reduces the thermal layer thickness improving the frequency of heat transfer. When the \(V_{c}\) increases, the extent boundary layer also increases on the stretching/shrinking surface. Additionally, for a given value of Pr, Nu is always higher with multi-wall carbon nanotubes and with single-wall carbon nanotubes. Figure 8 features the skin friction with the variation of Prandtl number Pr for different values of Chandrasekhar’s number’s Q. The skin friction increments with dense volume fraction and diminishes with Navier slip because of an increase in carbon nanotube density with solid volume fraction. In effect, one can always find a combination of the governing parameter for which null values either of the skin friction coefficient or the Nusselt number can be obtained, which would convert the sheet either in a frictionless or in an adiabatic wall, respectively (Table 1).

Fig. 5
figure 5

Impact of Q on the temperature profile

Full size image
Fig. 6
figure 6

Impact of Q on the temperature profile

Full size image
Fig. 7
figure 7

Nusselt number versus mass transpiration \(V_{{\text{c}}}\) for stretched sheet

Full size image
Fig. 8
figure 8

Skin friction coefficient versus Prandtl number \(\Pr\) for stretching sheet

Full size image
Table 1 Comparison of the present study and related works by other authors
Full size table

4 Concluding Remarks

A theoretical investigation of the magnetohydrodynamics flow and heat exchange of CNT-based nano-liquid through a variable thicker surface is discussed in this paper. For the suspension of nanoparticles, water is utilized as the base fluid. Saturation in base fluid is accounted for by two types of CNTs, namely SWCNTs and MWCNTs. This has allowed us to obtain the analytical solution to the problem, explore how the solutions are influenced by the governing physical parameters, and identify the following impacts:

  • The effects of several parameters on the heat transfer of magnetohydrodynamics Jeffery nanofluid flow of water-based SWCNTs and MWCNTs due to stretching/shrinking surface.

  • The transverse velocity will decrease with an increase in the magnetic constraint in the case of the stretching/shrinking sheet.

  • The special focus on differences between single- and multi-walled carbon nanotubes in a systematic and qualitative manner.

  • As Chandrasekhar’s number’s Q is expanded, multi-wall carbon nanotubes cause an increase in the velocity field relative to multi-wall carbon nanotubes.

  • For both SMWCNTs and MWCNTs, the temperature profile increases as the radiation estimator is increased.

  • In the case of the stretching parameter, the dual solution for the skin friction and Nusselt number factors of the carbon nanofluids across the surface is observed to be greater.

  • This paper is extended to the stability analysis and adding new fluids like ternary fluid and hybrid nanofluid.

  • This paper is solved analytically, and you can go through this paper to solve numerical method for different cases.

  • In future, more analytical results are examined along with carbon nanotubes; also, these experiments are examined under different fields like, medicine, engineering, industries, and so on.