Introduction

The mixture of nanoparticle in a base fluid is named as nanofluid which works efficiently in cooling the system which is in high temperature range and has many thermal applications. Introduction of the MHD force will affect more on the flow due to development of Lorentz force. Magnetohydrodynamic (MHD) flow plays an important part in the production of petroleum products and processes of metallurgy. It is to note that the final product that is formed is dependent on the rate of cooling followed by these processes. In order to separate the metallic materials from the nonmetallic materials, this field of magnetism is used to refine the molten metals. The carbon nanotubes (CNTs) based nanofluid as a heat transfer system. CNTs are a well-known allotrope of family of fullerene exhibiting long and hollow chemical structure compromising of graphene sheets. In a broader sense, two kinds of CNTs exist viz., single and multi-walled. The thermophysical properties of CNTs are subservient along with graphene sheets getting aligned in a sequential manner within the tube which results in this kind of materials to execute properties of metal or semiconductor. Ebaid and Sharif [1] investigated MHD transfer of heat and flow of CNTs-suspended nanofluids over stretching sheet (linear). The flow of MHD in such a particular case was first explored by Sarpakaya [2] and Mahabaleshwar [3,4,5]. Tiwari et al. [6] investigated the Marangoni convection MHD flow of CNTs through a porous medium with radiation.

Stretching sheet problems are very applicable in many industrial processes such as electronic cooling process, heat exchange between devices, and cooling of engines. Because of this reason, many researchers show an interest on stretching sheet problems. Crane [7] and Sakiadis [8] are pioneers in the investigation of stretching sheet problems. Hayat et al. [9] examined stagnation point of viscous nanofluid over a nonlinear stretching surface with variable thickness.

Hamad [10] and Fang and Zhang [11] examine the MHD flow due to shrinking sheet and shrinking sheet, respectively. Vinay Kumar et al. [12] have investigated the impact of MHD and mass transpiration on the slip flow. Sneha et al. [13] have examined the stagnation point flow over a Jeffrey fluid flow through a stretching/shrinking sheet. Turkyilmazoglu et al.[14] examined the MHD flow, heat and mass transfer of viscoelastic fluid with slip over the stretching surface and got the multiple solutions. Recently, Reddy et al.[15] examine the numerical analysis of the MHD flow of CNT nanofluid over a nonlinear inclined stretching/shrinking sheet with heat generation and viscous dissipation. Norzawary et al.[16] examined on the stagnation point flow in CNTs with suction/injection impacts over a stretching/shrinking sheet.

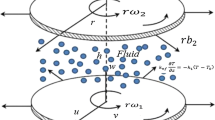
Mahabaleshwar et al.[17] made the article on the MHD flow with carbon nanotubes by considering the effect of mass transpiration and radiation on it. Mahabaleshwar et al.[18] investigates the MHD flow and mass transfer due to porous media. Turkyilmazoglu [19] studied on exact solution for flow of Jeffrey fluid. The Novelty of the present research is to examine the MHD flow and heat transfer of Jeffrey fluid due to a stretching/shrinking surface with CNTs considering the effects of thermal radiation and Navier’s slip. And the motivation is to add the effects CNTs and slips to previous works of momentum and energy with constant and linear wall temperature.  Secondly, to provide an analytic solution of the resulting nonlinear system is novel. Moreover, the influence for various physical features as magnetic parameter, mass transpiration, radiation and Prandtl number parameter are presented on the field of flow and analysed thereafter. Investigate the important physical parameters Nusselt number and skin friction (Fig. 1).

Fig. 1
figure 1

Schematic diagram of the flow problem

Full size image

Physical model and explanations

The steady MHD flow and heat transfer of Jeffrey fluid with CNTs due to a stretching/shrinking surface moving with deforming wall velocity \(u_{w} (x)\) is examined and the phenomena of heat transfer with thermal radiation are investigated. The magnetic field of strength \(B_{0}\) is applied perpendicular to the fluid flow. The fluid flow is along x-axis and y-axis is perpendicular to it. The sheet is stretched/shrinked with the velocity which is proportional to the distance from the origin \(c\). The momentum and temperature governing equations can be modelled as Saif et al. [20], Rao et al. [21], and Maranna et al. [22].

$$\frac{\partial u}{{\partial x}} + \frac{\partial u}{{\partial y}} = 0,$$
(1)
$$\rho_{{n{\text{f}}}} \left( {u\frac{\partial u}{{\partial x}} + {\text{v}}\frac{\partial u}{{\partial y}}} \right) = \rho_{{{\text{nf}}}} u_{{\text{e}}} \frac{{\partial u_{{\text{e}}} }}{\partial x} + \frac{{\mu_{{\text{f}}} }}{{1 + \Gamma_{1} }}\left[ {\frac{{\partial^{2} u}}{{\partial y^{2} }} + \Gamma_{2} \left( {u\frac{{\partial^{3} u}}{{\partial x\partial y^{2} }} - \frac{\partial u}{{\partial x}}\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{\partial u}{{\partial y}}\frac{{\partial^{2} u}}{\partial x\partial y} + {\text{v}}\frac{{\partial^{3} u}}{{\partial y^{3} }}} \right)} \right] - \frac{{\sigma_{{{\text{nf}}}} B_{0}^{2} }}{{\rho_{{{\text{nf}}}} }}\left( {u - u_{{\text{e}}} } \right)$$
(2)
$$u\frac{\partial T}{{\partial x}} + {\text{v}}\frac{\partial T}{{\partial y}} = \,\frac{{\kappa_{{{\text{nf}}}} }}{{\left( {\rho c_{p} } \right)_{{{\text{nf}}}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{1}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{nf}}}} }}\frac{{\partial q_{{\text{r}}} }}{\partial y},$$
(3)

with B.Cs as follows:

$${\begin{array}{*{20}c} {u = dcx + A\frac{{\partial u}}{{\partial y}},\quad v = v_{{\text{w}}} ,\quad T = T_{{\text{w}}} \left( x \right)\quad \quad y = 0} \\ {u \to u_{\text{e}} \left( x \right) = ax,\quad \frac{{\partial u}}{{\partial y}} \to 0,\quad T \to T_{\infty } \quad \quad y \to \infty } \\ \end{array} }$$
(4)

here, \(u_{\text{e}} \left( x \right) = ax\) is the potential flow and wall temperature field \(T_{{\text{w}}} \left( x \right)\) is either kept at constant \(T_{{\text{w}}}\) or linearly proportional with x as follows: \(T_{{\text{w}}} \left( x \right) = T_{{\text{w}}} + bx\), \({\text{v}}_{{\text{w}}} = - \left( {\frac{{c\nu_{{\text{f}}} }}{{\left( {1 + \omega_{1} } \right)}}} \right)^{\frac{1}{2}} S\) is wall transpiration, where \({\text{v}}_{{\text{w}}} < 0\) for suction and \({\text{v}}_{{\text{w}}} > 0\) for injection. \(\Gamma_{1}\) and \(\Gamma_{2}\) are material parameters of Jeffrey fluid.

The suitable similarity transformations [19] are as follows:

$$\eta = \left( {\frac{{c\left( {1 + \Gamma_{1} } \right)}}{{\nu_{f} }}} \right)^{\frac{1}{2}} y,\,\,u = cx\frac{\partial f}{{\partial \eta }},\,\,{\text{v}} = - \left( {\frac{{c\nu_{\text{f}} }}{{\left( {1 + \Gamma_{1} } \right)}}} \right)^{\frac{1}{2}} f\left( \eta \right),\,\,\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}$$
(5a)

The radiative heat flux \(q_{\text{r}}\) is obtained by using the approximation of Rosseland for radiation as in [23,24,25,26],

$$q_{{\text{r}}} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{\partial y}$$
(5b)

T is implicit that the temperature varies within the flow, where the term \(T^{4}\) is the linear function of the temperature. Therefore, on using Taylor series expansion to the term \(T^{4}\) about \(T_{\infty }\) and on ignoring the higher order terms to get,

$$T^{4} \cong 4T_{\infty }^{3} T - 3T_{\infty }^{4}$$

Then, Eq. (3) reduces to

$$u\frac{\partial T}{{\partial x}} + {\text{v}}\frac{\partial T}{{\partial y}} = \,\frac{{\kappa_{{{\text{nf}}}} }}{{\left( {\rho c_{\text{p}} } \right)_{{{\text{nf}}}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{1}{{\left( {\rho c_{\text{p}} } \right)_{{{\text{nf}}}} }}\frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }}\frac{{\partial^{2} T}}{{\partial y^{2} }},$$
(5c)

On the implementation of similarity transformations (5a) and Eq. (5b) to governing Eqs. (2) and (3), we obtain,

$$\frac{{C_{2} }}{{C_{1} }}\frac{{\partial^{3} f}}{{\partial \eta^{3} }} + f\left( \eta \right)\frac{{\partial^{2} f}}{{\partial \eta^{2} }} - \left( {\frac{\partial f}{{\partial \eta }}} \right)^{2} + \beta \frac{{C_{2} }}{{C_{1} }}\left[ {\left( {\frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right)^{2} - f\left( \eta \right)\frac{{\partial^{4} f}}{{\partial \eta^{4} }}} \right] - M\left( {\frac{\partial f}{{\partial \eta }} - \lambda } \right)\frac{{C_{3} }}{{C_{1} }} + \lambda^{2} = 0,$$
(6)
$$\left( {C_{5} + N_{{\text{R}}} } \right)\frac{{\partial^{2} \theta }}{{\partial \eta^{2} }} + \Pr C_{{4}} f\frac{\partial \theta }{{\partial \eta }} = 0,\;\left( {{\text{for}}\quad T_{{\text{w}}} \left( x \right) = T_{{\text{w}}} } \right)$$
(7)
$$\left( {C_{5} + \,N_{{\text{R}}} } \right)\frac{{\partial^{2} \theta }}{{\partial \eta^{2} }} + \Pr C_{{4}} \left( {f\frac{\partial \theta }{{\partial \eta }} - \frac{\partial f}{{\partial \eta }}\theta } \right) = 0,\,\,\,\,\left( {for\,\,\,T_{{\text{w}}} \left( x \right) = T_{{\text{w}}} + bx} \right)$$
(8)

also B.Cs are as follows:

$$\left. {\begin{array}{*{20}l} {f\left( \eta \right) = V_{{\text{c}}} ,} \hfill & {\frac{\partial f}{{\partial \eta }} = d + L_{1} \frac{{\partial^{2} f}}{{\partial \eta^{2} }},} \hfill & {\theta \left( \eta \right) = 1\;{\text{at}}\;\eta = 0} \hfill \\ {\frac{\partial f}{{\partial \eta }} = \lambda ,} \hfill & {\frac{{\partial^{2} f}}{{\partial \eta^{2} }} = 0,} \hfill & {\theta \left( \eta \right) = 0\;{\text{as}}\;\eta \to \infty } \hfill \\ \end{array} } \right\}$$
(9)

here, \(\beta = \Gamma_{2} c\) is Deborah number, \(\lambda = \frac{a}{c}\) is stagnation/strength parameter, \(M = \frac{{\sigma_{{\text{f}}} B_{0}^{2} }}{{\rho_{{\text{f}}} c}}\) is magnetic parameter, \(C_{1} = \frac{{\rho_{{{\text{nf}}}} }}{{\rho_{{\text{f}}} }}\) and \(C_{2} = \frac{{\mu_{{{\text{nf}}}} }}{{\mu_{{\text{f}}} }}\),\(C_{3} = \frac{{\sigma_{{{\text{nf}}}} }}{{\sigma_{{\text{f}}} }}\), \(C_{4} = \frac{{\left( {\rho c_{{\text{P}}} } \right)_{{{\text{nf}}}} }}{{\left( {\rho c_{P} } \right)_{{\text{f}}} }}\), \(C_{5} = \frac{{\kappa_{{{\text{nf}}}} }}{{\kappa_{{\text{f}}} }}\). \(P_{{\text{r}}} \, = \,\frac{{\nu_{{\text{f}}} }}{{\alpha_{\text{f}} }}\) is Prandtl number. \(V_{{\text{c}}}\) is mass transpiration parameter, for suction case \(V_{{\text{c}}} > 0\) and for injection case \(V_{{\text{c}}} < 0\), \(d\) is stretching/shrinking parameter, where \(d > 0\) for stretching and \(d < 0\) for shrinking, respectively. \(L_{1} = A\left( {\frac{{c\left( {1 + \Gamma_{1} } \right)}}{{\nu_{{\text{f}}} }}} \right)^{\frac{1}{2}}\) is first order slip. And nanofluid quantities are given by,

Here, \(\varphi\) is solid volume fraction of nanofluid. The physical quantities of interest, the skin friction coefficient and local Nusselt number, respectively, given by,

$$C_{{\text{f}}} = \frac{{\nu_{f} }}{{a^{2} x^{2} }}\left( {\frac{\partial u}{{\partial y}}} \right)_{{{\text{y}} = 0}} = \frac{c}{{a^{2} x}}\left( {c\nu_{{\text{f}}} \left( {1 + \Gamma_{1} } \right)} \right)^{\frac{1}{2}} \left( {\frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right)_{{{\upeta } = 0}} ,Nu_{{\text{x}}} = - x\left( {\frac{{c\left( {1 + \Gamma_{1} } \right)}}{{\nu_{{\text{f}}} }}} \right)^{\frac{1}{2}} \left( {\frac{\partial \theta }{{\partial \eta }}} \right)_{{{\upeta } = 0}}$$
(10)

Additionally the skin friction and Nusselt number can be determined from \(- \left( {\frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right)_{{{\upeta } = 0}}\) and \(- \left( {\frac{\partial \theta }{{\partial \eta }}} \right)_{{{\upeta } = 0}}\)

Analysis of momentum equation

The present work is related to classical Crane’s [10] solution for the simple flow, that is for \(\lambda = S = L_{1} = 0\) and \(d = 1\). For the general case, the solution form of momentum equation is as below and to get the physical solution there is an additional constraint as \(\delta > 0\),

$$f\left( \eta \right) = V_{{\text{c}}} + \lambda \eta + \frac{d - \lambda }{{\delta \left( {1 + L_{1} \delta } \right)}}\left[ {1 - {\text{exp}}\left( { - \delta \eta } \right)} \right]$$
(11)

Applying of Eq. (11) into Eq. (6) gives, \(C_{1} ,C_{2} ,C_{3} ,C_{4} ,C_{5}\)

$$(d - \lambda )\,\left\{ {\left( {1 + L_{1} \delta } \right)\,\,\left[ { - \frac{{C_{3} }}{{C_{1} }}M + \delta \left( {\frac{{C_{2} }}{{C_{1} }}\delta - V_{{\text{c}}} + \frac{{C_{2} }}{{C_{1} }}\beta S\delta^{2} } \right)} \right] + \,\,d\left( { - 1 + \frac{{C_{2} }}{{C_{1} }}\beta \delta^{2} } \right)} \right.\left. { - \lambda - 2\lambda L_{1} \delta - \frac{{C_{2} }}{{C_{1} }}\beta \lambda \delta^{2} + \,\,\eta \lambda \delta \left( {1 + L_{1} \delta } \right)\left( { - 1 + \frac{{C_{2} }}{{C_{1} }}\beta \delta^{2} } \right)} \right\} = 0$$
(12)

For the special case \(\lambda = 0\), Eq. (12) got the form as follows:

$$d\left( { - 1 + \frac{{C_{2} }}{{C_{1} }}\beta \delta^{2} } \right)\left( {1 + L_{1} \delta } \right) + \,\left[ { - \frac{{C_{3} }}{{C_{1} }}M + \delta \left( {\frac{{C_{2} }}{{C_{1} }}\delta - V_{{\text{c}}} + \frac{{C_{2} }}{{C_{1} }}\beta S\delta^{2} } \right)} \right]\,\,\,\, = 0$$
(13)

Analysis of heat transfer

These momentum and temperature solutions got match with the examined work of Turkyilmazoglu [3, 6]. In the case of linear wall concentration, Eqs. (8) and (11) can lead us to obtain an additional solution by taking the assumption,

$$\theta \left( \eta \right) = {\text{exp}}\left( { - \delta \eta } \right)$$
(14)

Applying Eq. (11) and (14) in Eq. (8) will imply,

$$C_{4} \Pr d + \left( {1 + L_{1} \delta } \right)\delta \left[ {C_{4} V_{c} \Pr - \left( {C_{5} + N_{R} } \right)\delta } \right] = 0,$$
(15)

Equation (13) and (15) gives the relations,

$$\delta = \,\sqrt {\frac{{\left( {C_{5} + N_{{\text{R}}} } \right) - \Pr \frac{{C_{4} C_{2} }}{{C_{1} }} \pm \sqrt {\left( {\left( {C_{5} + N_{{\text{R}}} } \right) - \Pr \frac{{C_{4} C_{2} }}{{C_{1} }}} \right)^{2} + 4{\text{Pr}}\beta \frac{{C_{2} C_{3} C_{4} }}{{C_{1}^{2} }}\left( {C_{5} + N_{{\text{R}}} } \right)M} }}{{2\beta \frac{{C_{2} }}{{C_{1} }}\left( {C_{5} + N_{{\text{R}}} } \right)}}} ,$$
(16)

and

$$S = - \frac{d}{{\delta \left( {1 + L_{1} \delta } \right)}} + \frac{{\delta \left( {C_{5} + N_{R} } \right)}}{{C_{4} \Pr }}$$
(17)

Here, \(\delta\) and S is influenced by all used physical parameters.

And clearly for the above studied special case \(\lambda = 0\), the velocity and concentration fields becomes,

$$f\left( \eta \right) = V_{{\text{c}}} + \frac{d}{{\delta \left( {1 + L_{1} \delta } \right)}}\left[ {1 - {\text{exp}}\left( { - \delta \eta } \right)} \right],$$
(18)

and

$$\phi \left( \eta \right) = {\text{exp}}\left( { - \delta \eta } \right)$$
(19)

Here, \(\delta > 0\) and S are given by Eqs. (16) and (17). For this case, skin friction and Sherwood numbers becomes,

$$- \left( {\frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right)_{\eta = 0} = \frac{\delta d}{{1 + L_{1} \delta }}\quad {\text{and}}\quad - \left( {\frac{\partial \phi }{{\partial \eta }}} \right)_{\eta = 0} = \delta$$
(20)

The Jeffrey fluid will change to following f in case of \(\lambda = d = 1\).

$$f(\eta )\, = V_{\text{c}} + \eta ,$$
(21)

Temperature profile is given by,

$$\theta (\eta ) = \frac{{{\text{Erfc}}\left[ {\sqrt {\frac{{\Pr C_{4} }}{{2\left( {C_{5} + N_{{\text{R}}} } \right)}}} \left( {V_{{\text{c}}} + \eta } \right)} \right]}}{{{\text{Erfc}}\left[ {\sqrt {\frac{{\Pr C_{4} }}{{2\left( {C_{5} + N_{{\text{R}}} } \right)}}} \,V_{{\text{c}}} } \right]}},$$
(22)

The function Erfc denotes the complementary error function. From Eq. (22) the Nusselt number will be obtained as follows:

$$- \theta_{\eta } (0) = \,\frac{{ - \sqrt {\frac{{2\Pr C_{4} }}{{\pi \left( {C_{5} + N_{{\text{R}}} } \right)}}} {\text{Exp}}\left[ { - \frac{Pr}{{\left( {C_{5} + N_{{\text{R}}} } \right)}}} \right]}}{{{\text{Erfc}}\left[ {\sqrt {\frac{{\Pr C_{4} }}{{2\left( {C_{5} + N_{{\text{R}}} } \right)}}} \,\,V_{{\text{c}}} } \right]}}.$$
(23)

Result and discussion

The current work examine the MHD slip flow and heat transfer of Jeffrey fluid due to a stretching/shrinking surface with CNTs considering the effects of thermal radiation and Navier’s slip. Further consider the effects of nanofluid by adding CNTs. This leads to offer higher thermal conductivity than base fluid and considered nanofluid is formed by suspending two types of CNTs, i.e. SWCNTs and MWCNTs in the base fluid water. The structure of the problem is equation of momentum and temperature which are then converted into a set of ODE’s to imitate the MHD flow of carbon nanotubes. Magnetic parameter \(\left( M \right)\), radiation parameter \(\left( {N_{R} } \right)\), and Navier slip \(\left( {L_{1} } \right)\) effect significantly on the structure of solution of the problem. And investigate the important physical parameters Nusselt number and skin friction. In all plots, black curves denote SWCNTs and red curves denote MWCNTs. Moreover, the thermophysical properties are mentioned in Table 1. The present research is good agreement with already existing literature [19].

Table 1 Thermophysical properties of CNTs [22]
Full size table

Figures 2 and 3, respectively, demonstrate the transverse and axial velocity for different entities of magnetic parameter M. In Fig. 2, Pr is fixed at 6.2 for base fluid water for SWCNTs and MWCNTS. It can be seen that velocity profiles increases with raise in M for stretching boundary. Similarly, we can also notice that velocity profiles decreases with raise in M for shrinking boundary. Transverse velocity improves for water and kerosene oil nanofluid for SWCNT than MWCNT. If MWCNT nanofluids have higher effective velocities than the SWCNT-deferred nanofluids, and this might assist in industrial applications and medical benefits. But axial velocity has no much difference for SWCNTs and MWCNTs. The impact of Radiation parameter \(N_{\text{R}}\) on axial velocity \(f_{\eta } (\eta )\) is examined in Fig. 4. The axial velocity profile for SWCNTs and MWCNTs using base liquid water indicates a reduction for the behaviour of \(N_{\text{R}}\). The consequence of increase of \(N_{\text{R}}\) on axial velocity will be, increased \(f_{\eta } (\eta )\) for stretching boundary and decreased \(f_{\upeta } (\eta )\) for shrinking boundary.

Fig. 2
figure 2

The transverse velocity profile \(f\left( \eta \right)\) for various values of magnetic parameter \(M\) due to a stretching sheet and b shrinking sheet

Full size image
Fig. 3
figure 3

The axial velocity profile \(f_{{\upeta }} \left( \eta \right)\)for various values of magnetic parameter \(M\) due to a stretching sheet and b shrinking sheet

Full size image
Fig. 4
figure 4

The transverse velocity profile Pr\(f_{{\upeta }} \left( \eta \right)\) for various values of radiation parameter \(N_{\text{R}}\) due to a stretching sheet and b shrinking sheet

Full size image

Figure 5a depicts the skin friction \(C_{\text{f}}\) verses Prandtl number Pr for different values of M. The skin friction is more for SWCNTs than for MWCNTs and is negative. With the increase in M, the skin friction will decrease. In the similar way, the variation of skin friction \(C_{\text{f}}\) verses M for different values of Pr is as shown in Fig. 5b. With the increase in Pr, the skin friction will decrease. \(C_{\text{f}}\) will increase with dense of volume fraction and decreases with Navier slip because of an increase in CNT density with solid volume fraction.

Fig. 5
figure 5

The Skin friction coefficient \(C_{{\text{f}}}\) a versus \({\text{Pr}}\) for different values of \({\text{M}}\) and b \(C_{{\text{f}}}\) a versus \(M\) for different values of \(Pr\) due to stretching sheet

Full size image

Figure 6 portrays the effect of M and \(V_{\text{C}}\) on temperature profile \(\theta \left( \eta \right)\). From Fig. 6a, the observations can be made are, raise in M for both SWCNT and MWCNTs will result in decrease of thermal boundary layer thickness. For lower value of M, there is a temperature difference for SWCNTs and MWCNTs, further can be seen that on increasing M, the difference is negligible.

Fig. 6
figure 6

The temperature profile \(\theta \left( \eta \right)\) for various values of radiation parameter \(N_{{\text{R}}}\) due to a stretching sheet and b shrinking sheet

Full size image

Figure 6b represents the impact of \(V_{\text{C}}\) on temperature profile \(\theta \left( \eta \right)\). In both the SWCNT and MWCNT cases, temperature decreases with increase in \(V_{\text{C}}\). This is because of the way that fluid has a lower thermal conductivity for a comprehensive mass transpiration, which lessens conduction and the thickness of the thermal boundary layer, lowering the temperature.

Figure 7 depicts the effect of Pr on Nusselt number which plot versus mass transpiration \(V_{\text{C}}\). It can be observed the improvement in the rate of heat transfer as \(V_{\text{C}}\) increases. And also Nusselt number will be more for more value of Pr and the Nusselt number for SWCNTs is less than that for MWCNTs.

Fig. 7
figure 7

The Nusselt number \(- \theta_{{\upeta }} \left( 0 \right)\) verses mass transpiration \(V_{{\text{C}}}\) for various values of \(\Pr\) due to stretching sheet

Full size image

Conclusions

The examination of MHD slip flow and heat transfer of Jeffrey fluid due to a stretching/shrinking surface with CNTs considering the effects of thermal radiation and Navier’s slip will result in some observations. Further consider the effects of nanofluid by adding CNTs to offer higher thermal conductivity than base fluid. The governing partial differential equations for momentum and energy are transformed into ordinary differential equations using a similarity transformation. These equations are solved analytically. MWCNT suspended nanofluids have evolved faster velocities than SWCNT suspended nanofluids, indicating that they may be beneficial in a few applications. Primary research has shown that MWCNT nanoparticles can reach the tumour faster than SWCNT nanoparticles in the treatment of disorder. Magnetic parameter \(\left( M \right)\), radiation parameter \(\left( {N_{\text{R}} } \right)\), and Navier slip \(\left( {L_{1} } \right)\) effect significantly on the structure of solution of the problem is discussed. And investigate the important physical parameters Nusselt number and skin friction.

  • Velocity profiles increases with increase in magnetic field for stretching boundary and decreases with increase in magnetic field for shrinking boundary.

  • The axial velocity profile for SWCNTs and MWCNTs using base liquid water indicates a reduction for the behaviour of radiation parameter.

  • Increase of radiation parameter on axial velocity will results in, axial velocity increased for stretching boundary and decreased for shrinking boundary.

  • The skin friction is more for SWCNTs than for MWCNTs and is negative.

  • Increase of magnetic field or Prandtl number will decrease the skin friction.

  • In both the SWCNT and MWCNT cases, temperature decreases with increase in mass transpiration.

  • The rate of heat transfer will improve as mass transpiration increases. And also Nusselt number will be more for more value of Prandtl number.

  • Nusselt number for SWCNTs is less than that for MWCNTs

A number of previous studies serve as the limiting example for this investigation.

(a)\(\mathop {\lim }\limits_{\begin{subarray}{l} M \to 0, \\ \phi \, \to 0, \\ q_{\text{r}} \to 0, \end{subarray} }\){Results of present works}\(\to\){ Results of Turkyilmazoglu [19]}.

Further extensions of the current work can be implemented incorporating new physical mechanisms, such as an external Newtonian/non-Newtonian fluid rheology with various parameter.