Effect of Thermal Radiation on the Flow of a Boussinesq Couple Stress Nanofluid Over a Porous Nonlinear Stretching Sheet

Abstract

In this article, we propose a mathematical model for the flow and heat transfer characteristics of a non-Newtonian fluid past a porous and nonlinearly stretching sheet. The fluid is assumed to be immersed in a graphene-water nanofluid in the presence of mass transpiration and thermal radiation. A set of suitable similarity transformations are used to reduce the nonlinear partial differential equations system to a nonlinear loosely-coupled ordinary differential equation system. The heat transfer characteristics are studied with two types of boundary conditions, namely the Prescribed Surface Temperature and the Prescribed Surface Heat Flux. The exact solution to the momentum nonlinear ordinary differential equation is obtained by Wentzel-Kramers-Brillouin method. The temperature equation is solved analytically by converting it to a Gaussian-confluent hypergeometric differential equation. The effects of the porous medium parameter, power of the surface temperature, prescribed heat flux on the velocity, and the temperature field are some of the important findings of this investigation. The current research has its applications in the manufacturing industry, liquid film condensation process, metal spinning etc.

Introduction and Motivation

The study of steady laminar non-Newtonian fluids has become popular due the enormous applications in the field of metallurgy, polymer extrusion of plastic sheets, conveyor belts, etc. (see [1]). The problem was initially considered by Sakiadis [2, 3] and Siddheshwar et al. [4], and references therein describe such a flow phenomenon. Later, Crane [5] investigated the problem that consists viscous flow with surfaces (such as a slit) moving with a velocity that is being proportional to the distance from the slit. Numerous applications of nonlinear stretching sheet have important roles in designing of astronaut suits and biochemical protective suits and other allied industries. In view of such applications, in the current study we consider the boundary layer flow of nonlinear sheets. Mahabaleshwar et al. [6, 7] investigated stretching sheet problems with a variety of boundary conditions. Andersson [8] studied the stretching sheet problem of viscous flow in the presence of partial slip, for which an exact analytical solution was obtained. Kumaran and Ramanaiah [9] and Kelson [10] analytically examined solutions for the problem of quadratic stretching sheets. Siddheshwar et al. [11] and Singh et al. [12] analytically investigated the porous stretching sheet problem with mass transpiration.

The aforementioned investigations are for the flow and heat transfer issues in nonporous medium. There are many practical applications involving the fluid flow through porous media. Recently, problems involving stretching sheets in the presence of porous media are getting lot of attention. Mahabaleshwar et al. [13] investigated the second-grade, non-Newtonian fluid flow and heat transfer characteristics due to a stretching sheet through a porous medium in the presence of an external magnetic field. Later, Mahabaleshwar et al. [14, 15] studied the fluid flow passing through a semi-infinite porous media with a slipping boundary, the solid being proportionally sheared, and the fluid being injected at the boundary. Apart from these investigations, many authors have studied several new types of problems, and by using the obtained results, they concluded that nanofluids offer an enhanced thermal conductivity than the base fluids. Rahman et al. [16] investigated nanofluid flow past a permeable exponentially shrinking/stretching surface with second order slip using Buongiorno’s method. Mahabaleshwar et al. [17] and Benos [18] investigated the effect of magnetic effects on the flow of a nanofluid driven by stretching/shrinking sheet with suction. Reza-E-Rabbi et al. [19] investigated the fluid flow behaviour in the attendance of nanoparticles. Reza-E-Rabbi et al. [20] worked on stretching sheet problem with MHD Casson fluid flow. Arifuzzaman et al. [21] worked on porous medium with radiative heat grade fluid in the presence of MHD. Also Rana et. al. [22] studied the effects of bioconvection of microorganisms on Williamson’s fluid flow in the presence of nanoparticles.

Graphene-family of nanomaterials are widely used in many engineering applications including in biomedical field, and many studies are available in the literature about the biocompatibility and toxicity of graphene nanoparticles. So far a number of investigations on graphene nanofluids about their thermal conductivity, viscosity, electrical conductivity, biotoxicity are at one’s disposal in the literature. Motivated by the investigations available in the literature [23,24,25,26,27,28,29]], the present paper conducted an extension of the theoretical work of Siddheshwar and Mahabaleshwar [30]. In [30], the authors have utilized the WKB method to obtain analytical solutions. The present work describes a steady nonlinear stretching of a couple stress fluid flow in the presence of a porous medium. We have considered the thermal radiation in the energy equation, and nanoparticles’ thermophysical properties considered to achieve better heat transfer rate.

Physical Model

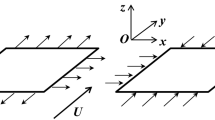
The current investigation is quiescent, laminar, and boundary layer flow of an electrically conducting incompressible non-Newtonian fluid on a nonlinear stretching sheet in the porous media. Figure 1 depicts physical configuration of the problems considered in this study. In beginning the fluid is at stationary but the motion take place due the stretching sheet effect.

Fig. 1

Schematic diagram of the porous stretching boundary

By considering the above assumptions, the quiescent flow along the nonlinear sheet is (see Mahabaleshwar et al.[7])

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0, $$

(1)

$$ \rho_{nf} \left( {u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}} \right) = \mu_{nf} \frac{{\partial^{2} u}}{{\partial y^{2} }} - \eta_{0} \frac{{\partial^{4} u}}{{\partial y^{4} }} - \frac{{\mu_{nf} }}{K^{\prime}}u. $$

(2)

The imposed boundary conditions are, (see [31] and [32])

$$\begin{array}{ll}u = \beta x + \alpha {x^2},\,v = {v_c} + \delta {\kern 1pt} x&\quad {\rm{at}} y = 0\\u = 0&\quad {\rm{as}}\;y \to \infty .\end{array}$$

(3)

The physical parameters are defined in the nomenclature. Consider the new dimension variables,

$$ U = \frac{u}{{\sqrt {\beta \nu_{f} } }},\;V = \frac{v}{{\sqrt {\beta \nu_{f} } }},\;X = x\sqrt {\frac{\beta }{{\nu_{f} }}} ,\;Y = y\sqrt {\frac{\beta }{{\nu_{f} }}} ,\;\alpha^{*} = \frac{\alpha }{\beta }\sqrt {\frac{{\nu_{f} }}{\beta }} ,\;\delta^{*} = \frac{\delta }{2\beta }, $$

(4a)

The applied similarity transformations are given by

$$ \psi = \sqrt {\beta \nu_{f} } xf\left( \eta \right) - \frac{\delta }{2}x^{2} f_{y} \left( \eta \right),\;\psi^{*} = \frac{\psi }{{\nu_{f} }}, $$

(4b)

By using above Eq. (4a,b) in the Eqs. (1) to (3), then they are transformed into the following form:

$$ \frac{\partial U}{{\partial X}} + \frac{\partial V}{{\partial Y}} = 0, $$

(5)

$$ U\frac{\partial U}{{\partial X}} + V\frac{\partial U}{{\partial Y}} = \frac{{\gamma_{1} }}{{\gamma_{2} }}\frac{{\partial^{2} U}}{{\partial Y^{2} }} - \frac{C}{{\gamma_{2} }}\frac{{\partial^{4} U}}{{\partial Y^{4} }} - \frac{{\gamma_{1} }}{{\gamma_{2} }}\Lambda U. $$

(6)

The of boundary conditions is given by

$$\begin{array}{ll}U = X + {\alpha ^*}{X^2},\,\,\,\,V = {V_C} + 2{\delta ^*}{\kern 1pt} X&\quad {\rm{at}}\;Y = 0\\U = 0&\quad {\rm{as}}\;Y \to \infty .\end{array}$$

(7)

Solutions of Eq. (7) by using Eq. (4a,b) is given below

$$U = X{f_Y} + {\delta ^*}{X^2}{f_{YY}},$$

(8)

$$ V = - f + 2\delta^{*} Xf_{Y} , $$

(9)

After substituting Eqs. (8) and (9) in (6), the respective results can be obtained in the form of the following nonlinear ordinary differential with constant coefficients:

$$ Cf_{YYYYY} - \gamma_{1} f_{YYY} + \gamma_{2} f_{Y}^{2} - \gamma_{2} ff_{YY} + \gamma_{1} \Lambda f_{Y} = 0, $$

(10)

$$ Cf_{YYYYY} - \gamma_{1} f_{YYYY} + \gamma_{2} f_{Y} f_{YY} - \gamma_{2} ff_{YYY} + \gamma_{1} \Lambda f_{YY} = 0, $$

(11)

and

$$ f_{YY}^{2} - f_{Y} f_{YYY} = 0. $$

(12)

The imposed boundary conditions given in (7) are transformed into

$$ f\left( 0 \right) = - V_{C} ,\;f_{Y} \left( 0 \right) = 1,\;f_{YY} \left( 0 \right) = - \frac{{\alpha^{*} }}{{2\delta^{*} }},\;f_{Y} \left( \infty \right) = 0,\;f_{YY} \left( \infty \right) = 0. $$

(13)

The simplified form of Eq. (12) can be rewritten as

$$ \frac{{f_{YY} }}{{f_{Y} }} = \frac{{f_{YYY} }}{{f_{YY} }}. $$

(14)

With the help of the above equation, the exact analytical solution of Eq. (10) can be derived as

$$ f\left( Y \right) = A + B\exp ( - RY). $$

(15)

Here,

$$ A = - V_{C} + \frac{1}{R}{, }\;B = - \frac{1}{R}. $$

(16)

Note that Eq. (15) is also an analytical solution of Eq. (10) provided,

$$ CR^{4} - \gamma_{1} R^{2} - V_{C} R\gamma_{1} + \left( {\gamma_{1} \Lambda + \gamma_{2} } \right) = 0, $$

(17)

and

$$ V_{C} = \frac{{\left( {\gamma_{2} + \gamma_{1} \Lambda } \right) - \gamma_{1} R^{2} + CR^{4} }}{{R\gamma_{2} }}, $$

(18)

By using Eqs. (8) and (9), the flow pattern in the area around the stretching sheet is obtained and given as follows:

$$ \psi^{*} = Xf(Y) - \delta^{*} X^{2} f_{Y} (Y). $$

(19)

When $\psi^{*} = a$, the Eq. (19) converted into the following form

$$ Y = \frac{1}{R}Ln\left\{ {\frac{{X\left( {\frac{1}{R} + \delta^{*} X} \right)}}{{\frac{X}{R} - XV_{C} - a}}} \right\}. $$

(20)

Analysis of Heat Transfer

The heat equation is given by

$$ \left( {\rho C_{P} } \right)_{nf} \left( {u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}}} \right) = \kappa_{nf} \frac{{\partial^{2} T}}{{\partial y^{2} }} + Q_{0} \left( {T - T_{\infty } } \right) - \frac{{\partial q_{r} }}{\partial y}, $$

(21a)

The heating process considered in the present analysis is dependent on the thermal boundary conditions. Two different heating processes, namely, PST and PHF cases, are considered in this analysis; see that some of the other investigations conducted on PST and PHF cases are Siddheshwar and Mahabaleshwar [30] and Rollins and Vajravelu [32].

Subject to the boundary conditions

$$ {\rm{PST}}:\;T = T_{w} \left( x \right) = T_{\infty } + AX^{s} \;at\;y = 0,\;T \to T_{\infty } \;as\,\,y \to \infty , $$

(21b)

$$ {\rm{PHF}}:T - T_{\infty } = DX^{s} \sqrt {\frac{{\gamma_{f} }}{\beta }} G\left( \eta \right)\;at\;y = 0,\;T \to T_{\infty } ,\;as\;y \to \infty . $$

(21c)

PST (Prescribed Surface Temperature)

Using equation (4), the above energy equation defined in Eq. 21(a) transformed into the following form

$$ \Pr \gamma_{3} \left( {U\frac{\partial \theta }{{\partial X}} + V\frac{\partial \theta }{{\partial Y}}} \right) = \left( {\gamma_{4} + Rd} \right)\frac{{\partial^{2} \theta }}{{\partial Y^{2} }} + Ni\theta . $$

(22)

Here, $Rd = \frac{{16\sigma T_{\infty }^{3} }}{{3\kappa_{f} k^{*} }}$, which is called the radiation parameter, can be solved using Rosseland’s approximation (see Mahabaleshwar et al. [7, 33, 34], Anusha et al. [35]).

The constant parameters defined in Eqs. (10), (11) and (22) are given by

$$ \gamma_{1} = \frac{{\mu_{nf} }}{{\mu_{f} }} = \frac{1}{{\left( {1 - \phi } \right)^{2.5} }}, $$

$$ \gamma_{2} = \frac{{\rho_{nf} }}{{\rho_{f} }} = 1 - \phi + \phi \frac{{\rho_{s} }}{{\rho_{f} }}, $$

$$ \gamma_{3} = \frac{{\left( {\rho C_{P} } \right)_{nf} }}{{\left( {\rho C_{P} } \right)_{f} }} = 1 - \phi + \phi \frac{{\left( {\rho C_{P} } \right)_{s} }}{{\left( {\rho C_{P} } \right)_{f} }}, $$

and

$$ \gamma_{4} = \frac{{k_{nf} }}{{k_{f} }} = \frac{{k_{s} + 2k_{f} + 2\phi \left( {k_{s} - k_{f} } \right)}}{{k_{s} + 2k_{f} - \phi \left( {k_{s} - k_{f} } \right)}}, $$

using transformation,

$$ \theta = A_{1} X^{s} \Theta \left( Y \right). $$

(23)

Substituting the above transformation into equation (22), it is transformed into

$$ \left( {\gamma_{4} + Rd} \right)\Theta_{YY} + \left( {\Pr \gamma_{3} f - 2\delta^{*} X\Pr \gamma_{3} f^{\prime}} \right)\Theta_{Y} + \left( {Xs\delta^{*} \Pr \gamma_{3} f^{\prime\prime} - s\Pr \gamma_{3} f^{\prime} + Ni} \right)\Theta = 0. $$

(24)

Equating the coefficients of $X^{0} ,X^{1}$ results in the following nonlinear ODEs with constant coefficients:

$$ \left( {\gamma_{4} + Rd} \right)\Theta_{YY} + \Pr \gamma_{3} f\Theta_{Y} - \left( {s\Pr \gamma_{3} f^{\prime} - Ni} \right)\Theta = 0, $$

(25)

$$ \Pr \gamma_{3} \delta^{*} sf_{YY} \Theta - 2\Pr \gamma_{3} \delta^{*} f_{Y} \Theta_{Y} = 0. $$

(26)

On simplifying Eq. (26) and dividing by $f_{Y} \Theta$, the above equation takes the form as

$$ \frac{{f_{YY} }}{{f_{Y} }} = \frac{2}{s}\frac{{\Theta_{Y} }}{\Theta }, $$

(27)

With the help of the above equation, the solution of $\Theta$ is given by

$$ \Theta \left( Y \right) = \exp \left( { - RY} \right). $$

(28)

Now, consider the new transformation,

$$ X = - \frac{\Pr }{{R^{2} }}\exp \left( { - RY} \right). $$

(29)

Substituting Eq. (29) in Eq. (25), then the Eq. (25) converted into the following form

$$ X\left( {\gamma_{4} + Rd} \right)\Theta_{XX} + \left( {\left( {\gamma_{4} + Rd} \right) - \frac{{\Pr A\gamma_{3} }}{R} - \gamma_{3} X} \right)\Theta_{X} + \left( {s\gamma_{3} + \frac{Ni}{{R^{2} }}X^{ - 1} } \right)\Theta = 0. $$

(30)

Boundary conditions defined in Eqs. 21(a) reduces to

$$ \Theta \left( 0 \right) = 1,\,\,\,\,\,\,\,\,\,\,\Theta \left( \infty \right) = 0. $$

(31)

Using Eq. (31) in Eq. (30), then to yield as

$$ \Theta \left( X \right) = \left( { - \frac{{R^{2} }}{\Pr }X} \right)^{{m_{1} }} \frac{{F\left[ {\frac{a + b}{2} - s,1 + b,\gamma_{3} X} \right]}}{{F\left[ {\frac{a + b}{2} - s,1 + b, - \frac{\Pr }{{R^{2} }}} \right]}}, $$

(32)

where

$$ m_{1} = \frac{a + b}{2},\,\,\,\,\,a = \frac{{\Pr \gamma_{3} A}}{{R\left( {\gamma_{4} + Rd} \right)}},\,\,\,\,\,b = \frac{1}{{R\left( {\gamma_{4} + Rd} \right)}}\sqrt {\Pr^{2} \gamma_{3}^{2} A^{2} - 4Ni\left( {\gamma_{4} + Rd} \right)} . $$

(33)

In terms of Y the Eq. (32) can be rewritten as

$$ \Theta \left( Y \right) = \exp \left( { - Rm_{1} Y} \right)\frac{{F\left[ {\frac{a + b}{2} - s,1 + b, - \gamma_{3} \frac{\Pr }{{R^{2} }}\exp \left( { - RY} \right)} \right]}}{{F\left[ {\frac{a + b}{2} - s,1 + b, - \frac{\Pr }{{R^{2} }}} \right]}}. $$

(34a)

The Nondimensional wall temperature gradient $\Theta_{Y} \left( 0 \right)$ obtained from Eq. (34) is given by

$$ \Theta_{Y} \left( 0 \right) = - \left( {R\left( {\frac{a + b}{2}} \right) - \frac{{\Pr \gamma_{3} }}{R}\left( {\frac{a + b - 2s}{{2\left( {1 + b} \right)}}} \right)\frac{{F\left( {\frac{a + b}{2} - s + 1,2 + b, - \frac{{\Pr \gamma_{3} }}{{R^{2} }}} \right)}}{{F\left( {\frac{a + b}{2} - s,1 + b, - \frac{{\Pr \gamma_{3} }}{{R^{2} }}} \right)}}} \right). $$

(34b)

The local Nusselt number $Nu$ is defined as

$$ Nu = \frac{{Xq_{w} }}{{k_{f} \left( {T_{w} - T_{\infty } } \right)}}, $$

(35)

$$ q_{w} = - k_{nf} \left( {\frac{\partial T}{{\partial y}}} \right)_{y = 0} + \left( {q_{r} } \right)_{w} , $$

(36)

Equating Eqs. (35) and (36) to obtain the local Nusselt number in the following form:

$$ \frac{Nu}{{\sqrt {{\rm{Re}} x} }} = - \left( {\gamma_{4} + Rd} \right)\Theta_{Y} \left( 0 \right). $$

(37)

PHF (Prescribed Surface Heat Flux)

Using the same transformation defined in Eq. (23), the energy equation defined in Eq. 21(a) reduced to

$$ X\left( {\gamma_{4} + Rd} \right)G_{XX} + \left( {\left( {\gamma_{4} + Rd} \right) - \frac{{\Pr A\gamma_{3} }}{R} - \gamma_{3} X} \right)G_{X} + \left( {s\gamma_{3} + \frac{Ni}{{R^{2} }}X^{ - 1} } \right)G = 0. $$

(38)

The corresponding boundary condition defined in Eq. 21(c) reduces to

$$ G_{Y} \left( 0 \right) = - 1,\,\,\,{\rm{and}}\,\,\,G\left( \infty \right) = 0. $$

(39)

By using Eq. (39), the solution of Eq. (38) can be obtained in terms of Kummer’s function

$$ G\left( Y \right) = \frac{{\exp \left( { - Rm_{1} Y} \right)F\left( {m_{1} - s,1 + b,\frac{{ - \Pr \gamma_{3} }}{{R^{2} }}\exp \left( { - RY} \right)} \right)}}{{Rm_{1} F\left( {m_{1} - s,1 + b,\frac{{ - \Pr \gamma_{3} }}{{R^{2} }}} \right) - \frac{{\left( {m_{1} - s} \right)}}{{\left( {1 + b} \right)}}\frac{{\Pr \gamma_{3} }}{R}F\left( {m_{1} - s + 1,2 + b,\frac{{ - \Pr \gamma_{3} }}{{R^{2} }}} \right)}}. $$

(40)

Wentzel-Kramer-Brillouin (WKB) Method

The matched asymptotic expansion (MAE) is obtained by using the WKB approximation in the case of large Pr for both PST and PHF cases, whereas the MAE is not possible to find in the case of small Pr because the solution is converted to O (1) on a length scale of order 1/Pr. In this case, the solution of large Prandtl numbers can be used in industrial applications. Therefore, solutions of heat transfer characteristics are essential, and the solution of the asymptotic limit for large $\Pr$ is also essential. Here, an exact solution can be obtained for the PST and PHF cases. See the related work illustrated by Sharma and Nageswara [36].

PST

The boundary layer expansion along with the boundary condition is given by

$$ \left( {\gamma_{4} + Rd} \right)\Theta_{YY} + \Pr \gamma_{3} f\Theta_{Y} - \left( {\Pr \gamma_{3} sf_{Y} - Ni} \right)\Theta = 0, $$

(41)

$$ \Theta \left( 0 \right) = 1,\,\,\,\,\Theta \left( \infty \right) \to 0. $$

(42)

By considering $\Pr = 1/\varepsilon$, (where $\varepsilon$ is very small) in Eq. (41), then Eq. (41) can be reduced as

$$ \varepsilon \left( {\gamma_{4} + Rd} \right)\Theta_{YY} + \gamma_{3} f\Theta_{Y} - \left( {\gamma_{3} sf_{Y} - \varepsilon Ni} \right)\Theta = 0. $$

(43)

The highest-order derivative of $\varepsilon$ represents the boundary layer behavior at $Y = 0$

$$ f\left( Y \right) = A + B\exp ( - RY), $$

(44)

where $A = - \left( {V_{C} } \right) + \frac{1}{R}\,{ > }\,{0,}\,\,{\rm{ B}} = - \frac{1}{R}\, < \,0.$ If $A > \left| B \right|$, $Y$ has no value in in $\left[ {0,\infty } \right)$. However, when $A < \left| B \right|$, $f\left( Y \right)$ vanishes at $Y^{*} = R^{ - 1} Ln\left\{ {\left| \frac{B}{A} \right|} \right\}$. The nature of the solution of Eq. (41) converted because of this turning point at $Y^{*} = Y$. The case $A = \left| B \right|$ provides $Y^{*} = 0$.

By the WKB method, uniform expansion can be found in case $A > \left| B \right|$.

$$ {\rm{Let}}\;\Theta \left( Y \right) = \exp \left\{ { - \frac{1}{2\varepsilon }\int\limits_{0}^{Y} {f\left( Z \right)dZ} } \right\}\Phi \left( Y \right). $$

(45)

The useful formulation of Eq. (43) can be written as

$$ \begin{gathered} \varepsilon^{2} \left( {\gamma_{4} + Rd} \right)\Phi_{YY} + \left( {\gamma_{3} - \left( {\gamma_{4} + Rd} \right)} \right)\varepsilon f\Phi_{Y} + \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {\frac{{\left( {\gamma_{4} + Rd} \right)}}{4}f^{2} - \frac{1}{2}\gamma_{3} f^{2} - \varepsilon \left( {s\gamma_{3} + \frac{{\left( {\gamma_{4} + Rd} \right)}}{2}} \right)f_{Y} + \varepsilon^{2} Ni} \right)\Phi = 0. \hfill \\ \end{gathered} $$

(46)

By using the WKB hypothesis, a uniform estimation in the limit of small $\varepsilon$[2] is found. Assumption of the solution is given by

$$ \Phi \left( Y \right) = \exp \left( {\frac{1}{\varepsilon }\sum\limits_{n = 0}^{\infty } {\varepsilon^{n} Q_{n} \left( Y \right)} } \right). $$

(47)

On applying Eq. (47) into Eq. (46), then the equation converted to the following form:

$$ \begin{gathered} \left( {\gamma_{4} + Rd} \right)\left( {Q_{0} } \right)_{Y}^{2} + 2\varepsilon \left( {\gamma_{4} + Rd} \right)\left( {Q_{0} } \right)_{Y} \left( {Q_{1} } \right)_{Y} + \varepsilon \left( {\gamma_{4} + Rd} \right)\left( {Q_{0} } \right)_{YY} + \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\gamma_{3} f\left( {Q_{0} } \right)_{Y} + \gamma_{3} \varepsilon f\left( {Q_{1} } \right)_{Y} - \left( {\gamma_{4} + Rd} \right)f\left( {Q_{0} } \right)_{Y} - \left( {\gamma_{4} + Rd} \right)\varepsilon f\left( {Q_{1} } \right)_{Y} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \left( {\frac{1}{4}\left( {\gamma_{4} + Rd} \right)f^{2} - \frac{1}{2}\gamma_{3} f^{2} - \varepsilon \left( {s\gamma_{3} + \frac{1}{2}\left( {\gamma_{4} + Rd} \right)} \right)} \right)f_{Y} + O\left( {\varepsilon^{2} } \right). \hfill \\ \end{gathered} $$

(48)

The $O\left( 1 \right)\,{\rm{and}}\,O\left( \varepsilon \right)$ equations are, respectively

$$ \left( {\gamma_{4} + Rd} \right)\left( {Q_{0} } \right)_{Y}^{2} + \gamma_{3} f\left( {Q_{0} } \right)_{Y} - \left( {\gamma_{4} + Rd} \right)f,\left( {Q_{0} } \right)_{Y} = \frac{1}{2}\gamma_{3} f^{2} - \frac{1}{4}\left( {\gamma_{4} + Rd} \right)f^{2} , $$

(49)

$$ 2\left( {\gamma_{4} + Rd} \right)\left( {Q_{0} } \right)_{Y} \left( {Q_{1} } \right)_{Y} + \left( {\gamma_{4} + Rd} \right)\left( {Q_{0} } \right)_{YY} + \gamma_{3} f\left( {Q_{1} } \right)_{Y} - \left( {\gamma_{4} + Rd} \right)f\left( {Q_{1} } \right)_{Y} = \left( {s\gamma_{3} + \frac{1}{2}\left( {\gamma_{4} + Rd} \right)} \right)f_{Y} . $$

(50)

Up to $O\left( {\varepsilon^{2} } \right)$ equation the effect of Ni does not effect. The solution of Eq. (49), which offers the correct behavior at $\infty$ for $\Theta \left( Y \right)$, gives the result as

$$ \left( {Q_{0} } \right)_{Y} = - K_{1} \int\limits_{0}^{Y} {f\left( Z \right)} \,dZ, $$

(51)

where

$$ K_{1} = \frac{{k + \sqrt {k\left( {k - l} \right)} }}{2l} $$

and

$$ k = \gamma_{3} - \left( {\gamma_{4} + Rd} \right),\;l = \left( {\gamma_{4} + Rd} \right). $$

Using Eq. (51) in Eq. (50), Eq. (50) can be simplified as

$$ \left( {Q_{1} } \right)_{Y} = - \Gamma Lnf\left( Z \right), $$

(52)

where

$$ \Gamma = \frac{{s\gamma_{3} + \frac{1}{2}\left( {\gamma_{4} + Rd} \right) + K_{1} \left( {\gamma_{4} + Rd} \right)}}{{\gamma_{3} - \left( {\gamma_{4} + Rd} \right)\left( {2K_{1} + 1} \right)}}. $$

(53)

Thus, the representation of $\Phi \left( Y \right)$ is given by

$$ \Phi \left( Y \right) = C_{1} \left( {f\left( Z \right)} \right)^{ - \Gamma } \exp \left( { - \frac{{K_{1} }}{\varepsilon }\int\limits_{0}^{Y} {f\left( Z \right)dZ} } \right). $$

(54)

After substituting the boundary conditions at $Y = 0$, we obtain

$$ \Theta \left( Y \right) = \left( {\frac{A + B}{{A + B\exp \left( { - RY} \right)}}} \right)^{\Gamma } \exp \left( { - \frac{{(K_{1} + 1)}}{2\varepsilon }\left\{ {AY + \frac{B}{R}\left( {1 - \exp \left( { - RY} \right)} \right)} \right\}} \right) + O\left( \varepsilon \right). $$

(55)

PHF

The solution of the asymptotic expansion for the condition $A > \left| B \right|$ is given by

$$ G\left( Y \right) = \frac{{\varepsilon \left( {A + B} \right)^{\Gamma + 1} }}{{\left( {K_{1} + 1} \right)\left( {A + B} \right)^{2} - \varepsilon \Gamma RB}}\left( {f\left( Y \right)} \right)^{ - \Gamma } \exp \left( { - \frac{{\left( {K_{1} + 1} \right)}}{2\varepsilon }\left( {AY + \frac{B}{R}\left( {1 - \exp \left( { - RY} \right)} \right)} \right)} \right). $$

(56)

Results and Discussion

The linear porous stretching sheet problem is discussed in the current study along with the non-Newtonian fluid in the presence of graphene-water nanofluid. The nonlinear PDEs are converted into system of nonlinear ODEs by utilizing a set of similarity variables. The analytical solution for the momentum equations is obtained from different analytical methods, and the heat equation is solved by using two different conditions, namely, PST and PHF, and also for the case of large Prandtl number. The results of this present problem can be explained with the following graphical arrangements. Before explaining the result of the present work, it is worth mentioning that the parameter $\beta^{*}$ does not appear explicitly in the expressions of $\psi ,\,U\,\,{\rm{and}}\,\,V$ for no suction because the value of $\frac{{\beta^{*} }}{{\delta^{*} }}$ is unity. $\beta^{*}$ appears implicitly through R in the presence of suction.

Figures 2 and 3 indicate the plots of $\Theta \left( Y \right)$ versus Y for various values of $\Lambda \,\,{\rm{and}}\,\,s$ for the prescribed surface temperature. Figure 2 clearly indicates that the boundary value thickness increases with increasing values of the porous medium parameter $\Lambda$, and it moves away from the x axis. This effect is reversed in Fig. 3. This means that upon varying the values of constant power of the surface temperature s, the boundary value thickness decreases and moves toward the x axis. Figure 4 portrays that the temperature profile $G\left( Y \right)$ versus Y for various values of s for the prescribed heat flux. increasing the value of s and decreasing the nonlinear stretching.

Fig. 2

Temperature profile $\Theta \left( Y \right)$ versus Y for different values of porous medium parameter $\Lambda$ with $s = 1,\,\,V_{C} = 1,\,\,C = 1,\,\,\phi = 0.1\,\,Rd = 1,\,\,Ni = - 1\,\,{\rm{and}}\,\,\,\delta^{*} = 1.$

Fig. 3

Temperature profile $\Theta \left( Y \right)$ versus Y for various values of surface temperature $s$ with $\Lambda = 0.1,\,\,V_{C} = 1,\,\,C = 1,\,\,\phi = 0.1\,\,Rd = 1,\,\,Ni = - 1\,\,{\rm{and}}\,\,\,\delta^{*} = 1.$

Fig. 4

Temperature profile $\Theta \left( Y \right)$ versus Y for various values of $s$ with $\Lambda = 0.1,\,\,V_{C} = 1,\,\,C = 1,\,\,\phi = 0.1\,\,Rd = 1,\,\,Ni = - 1\,\,{\rm{and}}\,\,\,\delta^{*} = 1.$

Figure 5 highlights the boundary heating effect on heat transfer in the case of suction and in the absence of a heat source/sink. With this figure, it is clearly observed that the PST condition acts as effective cooling of the stretching sheet. Additionally, PHF-type heating increases the boundary layer temperature. Figures 6 and 7 reveal how the velocity field and streamlines are affected by the values of mass transpiration $V_{C}$. Figures 6a and 7a represent the different streamline patterns obtained by using the formula defined in Eq. (19), and Figs. 6b and 7b indicate the vector graphs. Both figures reveal that the flow pattern is roughly divided into two regions, one region is clearly controlled by the stretching rate of the sheet. This result is similar to the ones presented for the stretching problem many results in the literature.

Fig. 5

Temperature profile $\Theta \left( Y \right)/G\left( Y \right)$ on Y for PST and PHF

Fig. 6

Comparison of a the streamlines and b vector fields at the values $\Lambda = 0.1,\,\,s = 1,\,\,Rd = 2,\,\,\delta^{*} = 1,\,\,V_{C} = 1,\,\,Ni = 0.1,\,\,c = 1.$

Fig. 7

Comparison of a the streamlines and b vector fields at the values $\Lambda = 0.1,\,\,s = 1,\,\,Rd = 2,\,\,\delta^{*} = 1,\,\,V_{C} = 2,\,\,Ni = 0.1\,\,\,{\rm{and}}\,\,C = 1.$

Figure 8a and b represents the 3-dimensional graphs for the different values of mass transpiration $V_{C}$. Figure 9 highlighting the differences between the WKB solution and Kummer’s solution. The closeness of the solution can be observed with the help of the figure.

Fig. 8

3-D graphs for a $V_{C} = 1$ and b $V_{C} = 3$

Fig. 9

Comparison of Kummer’s function and WKB asymptotic solution

Concluding Remarks

The present investigation is an important effort to study the effects of thermal radiation on the steady flow of a non-Newtonian fluid in the presence of graphene-water nanofluids. We have also examined the mass transpiration. The analytical solutions are obtained for the momentum and energy equations. Some important conclusions of the present study are in the following order:

• It is worth noting that when the values of $\delta^{*} = C = \Lambda = 0$, the nanofluids are converted into a base fluid, the present problem is converted into the classical Crane problem [5]. Therefore, we can recover the solutions of Crane problem from the solution presented in this paper;

• On increasing the values of ‘s’, the streamlines form a pattern and entire behavior is divided into two regions, one is controlled by the stretching rate.

• Increasing the value of $V_{C}$ causes the linear stretching of streamlines.

• The PST condition acts as effective cooling of the stretching sheet.

• PHF-type heating increases the boundary layer temperature.

Table 1 Thermophysical properties of nanofluids (see Aly [37])