A Novel Fuzzy Cumulative Sum Control Chart with an α-Level Cut Based on Trapezoidal Fuzzy Numbers for a Real Case Application

Abstract

Statistical process control (SPC) is widely used to monitor production processes in many industries under certain conditions. When dealing with a quality characteristic for uncertainty, fuzzy numbers are used in the context of the statistical process control (SPC) to monitor a fuzzy production process. The aim of this paper is fourfold. One, a fuzzy $\overline{X} - R$ control chart with an α-level cut is used based on trapezoidal fuzzy numbers (TFNs) for detecting the large shifts in the fuzzy process mean. Second, a fuzzy cumulative sum (FCUSUM) control with an α-level cut based on TFNs is firstly developed for detecting the small shifts in the fuzzy process mean. Third, the fuzzy process capability indices (FPCIs) are presented to measure the fuzzy process performance. Finally, an ultra-fine calcite production process is controlled with both the fuzzy $\overline{X} - R$ control chart and the proposed FCUSUM control chart. The results of the fuzzy $\overline{X} - R$ control charts show that the fuzzy production process is in control, and large shifts in the fuzzy process mean were detected. On the other hand, the results of the FCUSUM charts show that the fuzzy production process is out of control, and small shifts in the fuzzy process mean were detected. FPCIs are also conducted, and the results of fuzzy C_pk indices show that the ultra-fine calcite production process is not capable of meeting specification limits.

1 Introduction

Statistical process control (SPC) is an important technique to provide a certain type of quality characteristics for many industries. For this purpose, control charts are used to monitor many processes in order to prevent defective products. Moreover, a number of processes should be operated with little variability around the desired target of the product’s quality characteristics. Therefore, the SPC is used to achieve variance reduction and provide continuous improvement for the processes when dealing with certain and uncertain conditions. Fuzzy control charts have been developed to control the process when considering uncertainty. In addition, this paper focuses on fuzzy control charts. This section consists of three sub-sections. Firstly, the literature review survey is provided for fuzzy $\overline{X} - R$, FEWMA, and FCUSUM control charts. Secondly, the fuzzy process capability analysis (FPCA) is reviewed. Finally, the importance of this study is presented with the novel control chart.

1.1 Literature Review of Fuzzy $\overline{X} - R$, FEWMA, and FCUSUM Control Charts

In the literature, the traditional control charts have been reviewed by Montgomery [1] when dealing with certain environments. These charts are able to detect assignable causes under certain conditions. On the other hand, fuzzy control charts have been used to monitor processes for uncertainty. Fuzzy variable charts for subgroups and fuzzy attribute charts have been applied to control processes. Particularly, Kanagawa et al. [2] proposed control charts for the process mean using linguistic data. After that, Gülbay et al. [3] proposed α‐cut fuzzy control charts for attributes. Along the same lines, Faraz and Moghadam [4] developed a fuzzy control chart for the process mean of a continuous variable with a warning line that is a suitable alternative to Shewhart $\overline{X}$ control charts. Individual control charts and moving range control charts are used when data come from individuals form of a process. For this situation, Erginel [5] presented fuzzy control limits for individual and moving range control charts with α‐cuts under a vague condition. Besides, Hryniewicz [6] briefly reviewed the fundamental problems of fuzzy sets in statistical quality control.

The mostly used traditional control charts are $\overline{X} - R$ and $\overline{X} - S$ under certain conditions. On the contrary, Şentürk and Erginel [7] developed fuzzy $\overline{X} - R$ and $\overline{X} - S$ control charts with α‐cuts for uncertainty. In addition, Shu and Wu [8] offered the fuzzy $\overline{X} - R$ control chart and constructed the fuzzy control limits from the resolution identity. Next, Şentürk et al. [9] proposed fuzzy $\tilde{u}$ control charts for attributes control charts. Erginel [10] also introduced fuzzy $\tilde{p}$ and $\tilde{n}p$ control charts for the attribute data when dealing with an uncertain condition. Then, Kaplan Göztok et al. [11] used a fuzzy $\overline{X} - R$ control chart for a production system. Besides, Özdemir [12] proposed a fuzzy $\overline{X} - S$ control chart with unbalanced fuzzy data.

Exponentially weighted moving average (EWMA) control charts and cumulative sum (CUSUM) control charts have been paid little attention to in the fuzzy environment [13]. An EWMA control chart is an effective tool to detect the small shifts in the process mean and the process standard deviation. In the fuzzy environment, Shu et al. [14] proposed a fuzzy-maximum generally weighted moving average control chart while considering both the randomness and fuzziness of imprecise sample data. Along the same lines, Şentürk et al. [15] developed a fuzzy exponentially weighted moving average (FEWMA) to detect the small shifts for univariate data under the fuzzy environment. Then, Hesamian et al. [16] proposed EWMA control charts based on normal fuzzy random variables. Next, Kaplan Göztok et al. [17] developed a FEWMA control chart with the α-level cuts for a large number of samples while using a unity technique.

A CUSUM control chart is another useful tool to detect the small shifts in the process mean and the process standard deviation. The two different approaches, which are the V-mask and the tabular CUSUM, are available in the literature [1]. Many users prefer the Tabular CUSUM over the V-mask procedure. The reason is that the tabular CUSUM can be quickly performed to detect the small shifts in the process mean. For fuzzy quality data, Wang [18] firstly proposed a CUSUM control chart. Traditional multivariate control charts are not useful when dealing with two or more related quality characteristics for uncertainty. Therefore, Ghobadi et al. [19] proposed a fuzzy multivariate CUSUM control chart to control multinomial linguistic quality characteristics. In a recent paper, Erginel and Şentürk [13] proposed fuzzy EWMA and fuzzy CUSUM control charts using fuzzy triangular numbers.

1.2 Literature Review of Fuzzy Process Capability Analysis (FPCA)

The traditional process capability analysis (PCA) by using C_p, C_pk, C_pm, and other indices was provided a comprehensive review in order to measure the process performance by Montgomery [1] while considering certain conditions. On the other hand, the fuzzy formulations of the process capability indices (PCIs) were used to evaluate the fuzzy process performance for uncertainty [20]. In addition to these studies, Yum [21, 22] presented a bibliography of process capability indices based on recently published studies, including fuzzy process capability indices (FPCIs) and their applications.

1.3 Research Motivating Concepts

The SPC is a powerful problem-solving tool in order to provide process stability and detects defective products and process shifts. The investigation of the process is significant for taking corrective actions for the small and large shifts when dealing with a fuzzy environment. Therefore, the aim of this paper is fourfold. One, we use fuzzy $\overline{X} - R$ control charts with an α-level cut based on trapezoidal fuzzy numbers (TFNs). Thus, we can detect large shifts in the monitored parameters: the fuzzy process mean and the fuzzy process variability. Two, as shown in the literature review section, we firstly propose a fuzzy cumulative sum control chart (FCUSUM) with an α-level cut based on TFNs. Therefore, we are able to detect the small shifts in the fuzzy process mean. Three, the fuzzy process mean, and standard deviation values are obtained. The fuzzy process capability indices (FPCIs) are also developed to measure the fuzzy process performance. Finally, an ultra-fine calcite production process is monitored using a novel and innovative methodology presented in this paper, including both the fuzzy $\overline{X} - R$ control chart and the proposed FCUSUM control chart. FPCIs are also conducted in order to evaluate the fuzzy production process.

This paper is organized as follows: One, the proposed methodology development is presented in Sect. 2. Then, a real case application for an ultra-fine calcite production process is monitored using the proposed methodology in Sect. 3. Finally, concluding remarks and further studies are drawn in Sect. 4.

2 Proposed Methodology Development

In this section, the four-phased methodology is presented as follows: (1) trapezoidal fuzzy numbers (TFNs) with an α-level cut, (2) the fuzzy $\overline{X} - R$ control chart, (3) the proposed fuzzy cumulative sum (FCUSUM) control chart, and (4) the fuzzy process capability indices.

2.1 Trapezoidal Fuzzy Numbers (TFNs) with an α-Level Cut

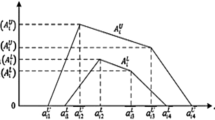
Types of fuzzy numbers may affect the results and efficiency of the problem [23, 24]. Thus, trapezoidal fuzzy numbers (TFNs) may give a better solution than triangular fuzzy numbers for a fuzzy production process. Therefore, TFNs are used in this paper. A TFN is denoted as a, b, c, and d. A trapezoidal membership function is denoted as follows:

$$ f\left( {x;a,b,c,d} \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {x \le a} \hfill \\ {\frac{x - a}{{b - a}},} \hfill & {a \le x \le b} \hfill \\ {1,} \hfill & {b \le x \le c} \hfill \\ {\frac{d - x}{{d - c}},} \hfill & {c \le x \le d} \hfill \\ {0,} \hfill & {d \le x} \hfill \\ \end{array} } \right\} $$

(1)

where $f\left( {x;a,b,c,d} \right)$ is the trapezoidal membership function. Figure 1 shows a TFN with an α-level cut for a sample.

Fig. 1

A TFN with an α-level cut for a sample

A TFN with an α-level cut is denoted as $a^{\alpha } ,b^{\alpha } ,c^{\alpha } ,\;{\text{and}}\;d^{\alpha }$. They are found as follows:

$$ a^{\alpha } = (b - a)\alpha + a $$

(2)

$$ b^{\alpha } = b $$

(3)

$$ c^{\alpha } = c $$

(4)

$$ d^{\alpha } = (d - c)\alpha + c $$

(5)

An α-level cut approach is useful to determine the tightness of the inspection for fuzzy control charts. Notice that selecting a higher α-level provides a tighter examination.

2.2 Fuzzy $\overline{X} - R$ Control Chart with an α-Level Cut Based on TFNs

The traditional control charts are sensitive to large process shifts, which are $1.5\sigma$ or more. The traditional $\overline{X}$ control chart is constructed using the following formulas:

$$ {\text{UCL}}_{{\overline{X}}} = \overline{\overline{X}} + A_{2} \overline{R} $$

(6)

$$ {\text{CL}}_{{\overline{X}}} = \overline{\overline{X}} $$

(7)

$$ {\text{LCL}}_{{\overline{X}}} = \overline{\overline{X}} - A_{2} \overline{R} $$

(8)

where ${\text{UCL}}_{{\overline{X}}}$, ${\text{CL}}_{{\overline{X}}}$, and ${\text{LCL}}_{{\overline{X}}}$ represent the upper control limit, the center line, and the lower control limit for the traditional $\overline{X}$ control chart. $\overline{\overline{X}}$ is the overall mean, $A_{2}$ is a value for the traditional $\overline{X}$ control chart and $\overline{R}$ is the average of the ranges. Please see Montgomery [1] for an $A_{2}$ value.

The equations of the traditional R control chart are denoted as follows:

$$ {\text{UCL}}_{R} = D_{4} \overline{R} $$

(9)

$$ {\text{CL}}_{R} = \overline{R} $$

(10)

$$ {\text{LCL}}_{R} = D_{3} \overline{R} $$

(11)

where ${\text{UCL}}_{R}$, $CL_{R}$, and $LCL_{R}$ are the upper control limit, the center line, and the lower control limit for the traditional R control chart. $D_{4}$ and $D_{3}$ are values for the traditional R control chart. Please see Montgomery [1] for $D_{4}$ and $D_{3}$ values.

The classical $\overline{X} - R$ control charts are adequate under certain conditions. On the other hand, the fuzzy $\overline{X} - R$ control charts using α-cuts are suitable for monitoring the fuzzy process for uncertainty. Therefore, Şentürk and Erginel [7] proposed fuzzy $\overline{X} - R$ control charts using α-cuts for a fuzzy environment. They used triangular fuzzy numbers. They stated that trapezoidal fuzzy numbers could be used for further research. In this paper, we use a fuzzy $\overline{X} - R$ control chart with an α-level cut based on trapezoidal fuzzy numbers. First of all, fuzzy $\overline{X}$ control limits are denoted as follows:

$$ \widetilde{{\text{U}}}{\text{CL}}_{{\overline{X}}}^{\alpha } = \left( {\overline{\overline{X}}_{a}^{\alpha } + A_{2} \overline{R}_{a}^{\alpha } ,\overline{\overline{X}}_{b}^{\alpha } + A_{2} \overline{R}_{b}^{\alpha } ,\overline{\overline{X}}_{c}^{\alpha } + A_{2} \overline{R}_{c}^{\alpha } ,\overline{\overline{X}}_{d}^{\alpha } + A_{2} \overline{R}_{d}^{\alpha } } \right) $$

(12)

$$ \widetilde{{\text{C}}}{\text{L}}_{{\overline{X}}}^{\alpha } = \left( {\overline{\overline{X}}_{a}^{\alpha } ,\overline{\overline{X}}_{b}^{\alpha } ,\overline{\overline{X}}_{c}^{\alpha } ,\overline{\overline{X}}_{d}^{\alpha } } \right) $$

(13)

$$ \widetilde{{\text{L}}}{\text{CL}}_{{\overline{X}}}^{\alpha } = \left( {\overline{\overline{X}}_{a}^{\alpha } - A_{2} \overline{R}_{a}^{\alpha } ,\overline{\overline{X}}_{b}^{\alpha } - A_{2} \overline{R}_{b}^{\alpha } ,\overline{\overline{X}}_{c}^{\alpha } - A_{2} \overline{R}_{c}^{\alpha } ,\overline{\overline{X}}_{d}^{\alpha } - A_{2} \overline{R}_{d}^{\alpha } } \right) $$

(14)

where $\widetilde{{\text{U}}}{\text{CL}}_{{\overline{X}}}^{\alpha }$, $\widetilde{{\text{C}}}{\text{L}}_{{\overline{X}}}^{\alpha }$, and $\widetilde{{\text{L}}}{\text{CL}}_{{\overline{X}}}^{\alpha }$ are the upper control limit, the center line, and the lower control limit for the fuzzy $\overline{X}$ control chart. $\overline{\overline{X}}_{a}^{\alpha } ,\overline{\overline{X}}_{b}^{\alpha } ,\overline{\overline{X}}_{c}^{\alpha } ,{\text{ and }}\overline{\overline{X}}_{d}^{\alpha }$ are the overall mean for a, b, c, and d fuzzy numbers with α-cuts. $\overline{R}_{a}^{\alpha } ,\overline{R}_{b}^{\alpha } ,\overline{R}_{c}^{\alpha } ,{\text{ and }}\overline{R}_{d}^{\alpha }$ are the averages of the ranges for a, b, c, and d fuzzy numbers with α-cuts.

Then, fuzzy R control limits are given as follows:

$$ \widetilde{{\text{U}}}{\text{CL}}_{{\overline{R}}}^{\alpha } = \left( {D_{4} \overline{R}_{a}^{\alpha } ,D_{4} \overline{R}_{b}^{\alpha } ,D_{4} \overline{R}_{c}^{\alpha } ,D_{4} \overline{R}_{d}^{\alpha } } \right) $$

(15)

$$ \widetilde{{\text{C}}}{\text{L}}_{{\overline{R}}}^{\alpha } = \left( {\overline{R}_{a}^{\alpha } ,\overline{R}_{b}^{\alpha } ,\overline{R}_{c}^{\alpha } ,\overline{R}_{d}^{\alpha } } \right) $$

(16)

$$ \widetilde{{\text{L}}}{\text{CL}}_{{\overline{R}}}^{\alpha } = \left( {D_{3} \overline{R}_{a}^{\alpha } ,D_{3} \overline{R}_{b}^{\alpha } ,D_{3} \overline{R}_{c}^{\alpha } ,D_{3} \overline{R}_{d}^{\alpha } } \right) $$

(17)

where $\widetilde{{\text{U}}}{\text{CL}}_{{\overline{R}}}^{\alpha }$, $\widetilde{{\text{C}}}{\text{L}}_{{\overline{R}}}^{\alpha }$, and $\widetilde{{\text{L}}}{\text{CL}}_{{\overline{R}}}^{\alpha }$ represent the upper control limit, the center line, and the lower control limit for the fuzzy R control chart.

2.3 Proposed Fuzzy Cumulative Sum (FCUSUM) Control Chart with an α-Level Cut Based on TFNs

In this paper, the tabular CUSUM is preferred over the V-mask CUSUM procedure. Actually, the tabular CUSUM is appropriate for many real-life applications [13]. The traditional CUSUM control chart catches the small shifts in the process mean. The tabular CUSUM is calculated as follows:

$$ C_{i}^{ + } = \max \left[ {0,\overline{x}_{i} - \left( {\tau - K} \right) + C_{i - 1}^{ + } } \right] $$

(18)

$$ C_{i}^{ - } = \min \left[ {0,\left( {\tau - K} \right) - \overline{x}_{i} + C_{i - 1}^{ - } } \right] $$

(19)

where K is the reference value and $K = {{\left( {\mu_{1} - \tau } \right)} \mathord{\left/ {\vphantom {{\left( {\mu_{1} - \tau } \right)} 2}} \right. \kern-0pt} 2}$. $C_{i}^{ + }$ is the upper deviation from the target $(\tau )$ for the ith period and $C_{i}^{ - }$ is the lower deviation from the target $(\tau )$ for the ith period. $C_{0}^{ + }$ and $C_{0}^{ + }$ are 0 for the starting values. $\overline{x}_{i}$ and $\mu_{1}$ denote the mean for the ith period and the mean value corresponding to the out of control state.

H represents the decision interval. The process is denoted as out of control if either $C_{i}^{ + }$ and $C_{i}^{ - }$ surpass H. Indeed, the appropriate choice of K and H is important for the performance of the CUSUM control chart. In the literature, a value for H is five times the process standard deviation $(\sigma )$ [1]. The tabular CUSUM control chart is constructed with the following equations:

$$ {\text{UCL}}_{{{\text{CUSUM}}}} = {{H\sigma } \mathord{\left/ {\vphantom {{H\sigma } 2}} \right. \kern-0pt} 2} $$

(20)

$$ {\text{CL}}_{{{\text{CUSUM}}}} = 0 $$

(21)

$$ {\text{LCL}}_{{{\text{CUSUM}}}} = {{ - H\sigma } \mathord{\left/ {\vphantom {{ - H\sigma } 2}} \right. \kern-0pt} 2} $$

(22)

where ${\text{UCL}}_{{{\text{CUSUM}}}}$, ${\text{CL}}_{{{\text{CUSUM}}}}$, and ${\text{LCL}}_{{{\text{CUSUM}}}}$ are the upper control limit, the center line, and the lower control limit for the tabular CUSUM control chart.

For the proposed fuzzy CUSUM control chart with an α-level cut based on TFNs, $C_{i}^{ + }$ and $C_{i}^{ - }$ are denoted as TFNs $\left( {C_{i}^{ + } \left( {a^{\alpha } } \right),C_{i}^{ + } \left( {b^{\alpha } } \right),C_{i}^{ + } \left( {c^{\alpha } } \right),C_{i}^{ + } \left( {d^{\alpha } } \right)} \right)$ and $\left( {C_{i}^{ - } \left( {a^{\alpha } } \right),C_{i}^{ - } \left( {b^{\alpha } } \right),C_{i}^{ - } \left( {c^{\alpha } } \right),C_{i}^{ - } \left( {d^{\alpha } } \right)} \right)$, respectively.

$$ C_{i}^{ + } \left( {a^{\alpha } } \right) = \max \left[ {0,\overline{x}_{{a^{\alpha } }} - \left( {\tau_{{a^{\alpha } }} - K} \right) + C_{i - 1}^{ + } \left( {a^{\alpha } } \right)} \right] $$

(23)

$$ C_{i}^{ + } \left( {b^{\alpha } } \right) = \max \left[ {0,\overline{x}_{{b^{\alpha } }} - \left( {\tau_{{b^{\alpha } }} - K} \right) + C_{i - 1}^{ + } \left( {b^{\alpha } } \right)} \right] $$

(24)

$$ C_{i}^{ + } \left( {c^{\alpha } } \right) = \max \left[ {0,\overline{x}_{{c^{\alpha } }} - \left( {\tau_{{c^{\alpha } }} - K} \right) + C_{i - 1}^{ + } \left( {c^{\alpha } } \right)} \right] $$

(25)

$$ C_{i}^{ + } \left( {d^{\alpha } } \right) = \max \left[ {0,\overline{x}_{{d^{\alpha } }} - \left( {\tau_{{d^{\alpha } }} - K} \right) + C_{i - 1}^{ + } \left( {d^{\alpha } } \right)} \right] $$

(26)

$$ C_{i}^{ - } \left( {a^{\alpha } } \right) = \min \left[ {0,\left( {\tau_{{a^{\alpha } }} - K} \right) - \overline{x}_{{a^{\alpha } }} + C_{i - 1}^{ - } \left( {a^{\alpha } } \right)} \right] $$

(27)

$$ C_{i}^{ - } \left( {b^{\alpha } } \right) = \min \left[ {0,\left( {\tau_{{b^{\alpha } }} - K} \right) - \overline{x}_{{b^{\alpha } }} + C_{i - 1}^{ - } \left( {b^{\alpha } } \right)} \right] $$

(28)

$$ C_{i}^{ - } \left( {c^{\alpha } } \right) = \min \left[ {0,\left( {\tau_{{c^{\alpha } }} - K} \right) - \overline{x}_{{c^{\alpha } }} + C_{i - 1}^{ - } \left( {c^{\alpha } } \right)} \right] $$

(29)

$$ C_{i}^{ - } \left( {d^{\alpha } } \right) = \min \left[ {0,\left( {\tau_{{d^{\alpha } }} - K} \right) - \overline{x}_{{d^{\alpha } }} + C_{i - 1}^{ - } \left( {d^{\alpha } } \right)} \right] $$

(30)

where $\tau_{{a^{\alpha } }}$, $\tau_{{b^{\alpha } }}$, $\tau_{{c^{\alpha } }}$, and $\tau_{{d^{\alpha } }}$ are target values for TFNs (a), (b), (c), and (d), respectively. Notice that the reference value (K) depends on the magnitude of the shift.

The fuzzy upper control limit ($\widetilde{{\text{U}}}{\text{CL}}_{{{\text{CUSUM}}}}$), the fuzzy center line ($\widetilde{{\text{C}}}{\text{L}}_{{{\text{CUSUM}}}}$), and the fuzzy lower control limit ($\widetilde{{\text{L}}}{\text{CL}}_{{{\text{CUSUM}}}}$) are denoted as follows:

$$ \widetilde{{\text{U}}}{\text{CL}}_{{{\text{CUSUM}}}} = \left( {{{H\sigma_{{a^{\alpha } }} } \mathord{\left/ {\vphantom {{H\sigma_{{a^{\alpha } }} } 2}} \right. \kern-0pt} 2},{{H\sigma_{{b^{\alpha } }} } \mathord{\left/ {\vphantom {{H\sigma_{{b^{\alpha } }} } 2}} \right. \kern-0pt} 2},{{H\sigma_{{c^{\alpha } }} } \mathord{\left/ {\vphantom {{H\sigma_{{c^{\alpha } }} } 2}} \right. \kern-0pt} 2},{{H\sigma_{{d^{\alpha } }} } \mathord{\left/ {\vphantom {{H\sigma_{{d^{\alpha } }} } 2}} \right. \kern-0pt} 2}} \right) $$

(31)

$$ \widetilde{{\text{C}}}{\text{L}}_{{{\text{CUSUM}}}} = \left( {0,0,0,0} \right) $$

(32)

$$\begin{aligned}&\widetilde{{\text{L}}}{\text{CL}}_{{{\text{CUSUM}}}}\\&\quad = \left( {{{ -H\sigma_{{a^{\alpha } }} } \mathord{\left/ {\vphantom {{ -H\sigma_{{a^{\alpha } }} } 2}} \right. \kern-0pt} 2},{{ -H\sigma_{{b^{\alpha } }} } \mathord{\left/ {\vphantom {{ -H\sigma_{{b^{\alpha } }} } 2}} \right. \kern-0pt} 2},{{ -H\sigma_{{c^{\alpha } }} } \mathord{\left/ {\vphantom {{ -H\sigma_{{c^{\alpha } }} } 2}} \right. \kern-0pt} 2},{{ -H\sigma_{{d^{\alpha } }} } \mathord{\left/ {\vphantom {{ -H\sigma_{{d^{\alpha } }} } 2}} \right. \kern-0pt} 2}} \right)\end{aligned}$$

(33)

where $\sigma_{{a^{\alpha } }} , \,\sigma_{{b^{\alpha } }} , \, \sigma_{{c^{\alpha } }},\;{\text{and}}\;\sigma_{{d^{\alpha }}}$ are the process standard deviations for TFNs (a),(b), (c), and (d) with α-cuts, respectively.

In practice, the process standard deviation $(\sigma )$ will not be known by practitioners. Therefore, the estimated standard deviations can be found as follows:

$$ \left( {\hat{\sigma }_{{a^{\alpha } }} ,\hat{\sigma }_{{b^{\alpha } }} ,\hat{\sigma }_{{c^{\alpha } }} ,\hat{\sigma }_{{d^{\alpha } }} } \right) = \left( {\frac{{\overline{R}_{a}^{\alpha } }}{{d_{2} }},\frac{{\overline{R}_{b}^{\alpha } }}{{d_{2} }},\frac{{\overline{R}_{c}^{\alpha } }}{{d_{2} }},\frac{{\overline{R}_{d}^{\alpha } }}{{d_{2} }}} \right) $$

(34)

where $\hat{\sigma }_{{a^{\alpha } }} , \, \hat{\sigma }_{{b^{\alpha } }} , \, \hat{\sigma }_{{c^{\alpha } }} ,\;{\text{and}}\;\hat{\sigma }_{{d^{\alpha } }}$ are the estimated standard deviations for TFNs (a), (b), (c), and (d) with α-cuts, respectively. Please see Montgomery [1] for $d_{2}$ values. Notice that other estimations methods can be used for the standard deviation. However, the method in Eq. (34) provides a good estimation performance for the process.

2.4 Fuzzy Process Capability Indices (FPCIs)

A process capability study is an important step to analyze and measure process performance. For this particular purpose, process capability ratios are widely used in many industries [1]. The C_p index is the most commonly used process capability ratio in the literature. The estimated $\hat{C}_{{\text{p}}}$ index is calculated as follows:

$$ \hat{C}_{{\text{p}}} = \frac{{{\text{USL}} - {\text{LSL}}}}{{6\hat{\sigma }}} $$

(35)

where USL and LSL represent the upper and lower specification limits, respectively. The C_pk index is another ratio to measure the process performance while considering the process mean as well. The estimated $\hat{C}_{{{\text{pk}}}}$ index is found as follows:

$$ \hat{C}_{{{\text{pk}}}} = \min \left( {C_{{{\text{pu}}}} ,C_{{{\text{pl}}}} } \right) = \min \left( {\frac{{{\text{USL}} - \overline{\overline{X}}}}{{3\hat{\sigma }}},\frac{{\overline{\overline{X}} - {\text{LSL}}}}{{3\hat{\sigma }}}} \right) $$

(36)

If the process capability ratio is 1.33 or higher for the existing process, the process is stable [1]. It is also noted that the C_pk index is not appropriate to measure centering. Further, a large value of the C_pk index does not provide information about the mean location in the interval. Therefore, the estimated $\hat{C}_{{{\text{pm}}}}$ index is used for centering and is denoted as follows:

$$ \hat{C}_{{{\text{pm}}}} = \frac{{{\text{USL}} - {\text{LSL}}}}{{6\hat{T}}} $$

(37)

where $\hat{\tau }$ denotes the square root of the expected standard deviation from the desired target $(\tau )$ and $\hat{T} = \sqrt {\hat{\sigma }^{2} + \left( {\overline{\overline{X}} - \tau } \right)}$.

We propose fuzzy capability indices (FCIs) based on TFNs using cuts to measure the process performance. The estimated fuzzy $\hat{\tilde{C}}_{{\text{p}}}$ is proposed as follows:

$$ \hat{\tilde{C}}_{{\text{p}}} = \left(\frac{{{\text{USL}}_{a} - {\text{LSL}}_{a} }}{{6\hat{\sigma }_{{a^{\alpha } }} }},\frac{{{\text{USL}}_{b} - {\text{LSL}}_{b}}}{{6\hat{\sigma }_{{b^{\alpha } }} }},\frac{{{\text{USL}}_{c} -{\text{LSL}}_{c} }}{{6\hat{\sigma }_{{c^{\alpha } }} }},\frac{{{\text{USL}}_{d} - {\text{LSL}}_{d} }}{{6\hat{\sigma }_{{d^{\alpha } }} }} \right) $$

(38)

The estimated fuzzy $\hat{\tilde{C}}_{{{\text{pk}}}}$ is proposed as follows:

$$ \hat{\tilde{C}}_{{{\text{pk}}}} = \left( \begin{gathered} \min \left( {\frac{{{\text{USL}}_{a} - \overline{\overline{X}}_{a}^{\alpha } }}{{3\hat{\sigma }_{{a^{\alpha } }} }},\frac{{\overline{\overline{X}}_{a}^{\alpha } - {\text{LSL}}_{a} }}{{3\hat{\sigma }_{{a^{\alpha } }} }}} \right),\min \left( {\frac{{{\text{USL}}_{b} - \overline{\overline{X}}_{b}^{\alpha } }}{{3\hat{\sigma }_{{b^{\alpha } }} }},\frac{{\overline{\overline{X}}_{b}^{\alpha } - {\text{LSL}}_{b} }}{{3\hat{\sigma }_{{b^{\alpha } }} }}} \right), \hfill \\ \min \left( {\frac{{{\text{USL}}_{c} - \overline{\overline{X}}_{c}^{\alpha } }}{{3\hat{\sigma }_{{c^{\alpha } }} }},\frac{{\overline{\overline{X}}_{c}^{\alpha } - {\text{LSL}}_{c} }}{{3\hat{\sigma }_{{c^{\alpha } }} }}} \right),\min \left( {\frac{{{\text{USL}}_{d} - \overline{\overline{X}}_{d}^{\alpha } }}{{3\hat{\sigma }_{{d^{\alpha } }} }},\frac{{\overline{\overline{X}}_{d}^{\alpha } - {\text{LSL}}_{d} }}{{3\hat{\sigma }_{{d^{\alpha } }} }}} \right) \hfill \\ \end{gathered} \right) $$

(39)

The estimated fuzzy $\hat{\tilde{C}}_{{{\text{pm}}}}$ is developed as:

$$ \begin{aligned} \hat{\tilde{C}}_{{{\text{pm}}}} = & \left( {\frac{{{\text{USL}}_{a} - {\text{LSL}}_{a} }}{{6\hat{T}_{{a^{\alpha } }} }},\frac{{{\text{USL}}_{b} - {\text{LSL}}_{b} }}{{6\hat{T}_{{b^{\alpha } }} }},\frac{{{\text{USL}}_{c} - {\text{LSL}}_{c} }}{{6\hat{T}_{{c^{\alpha } }} }},\frac{{{\text{USL}}_{d} - {\text{LSL}}_{d} }}{{6\hat{T}_{{d^{\alpha } }} }}} \right) \\ \, = & \left( \begin{gathered} \frac{{{\text{USL}}_{a} - {\text{LSL}}_{a} }}{{6\sqrt {\hat{\sigma }^{2}_{{a^{\alpha } }} + \left( {\overline{\overline{X}}_{a}^{\alpha } - \tau_{{a^{\alpha } }} } \right)} }},\frac{{{\text{USL}}_{b} - {\text{LSL}}_{b} }}{{6\sqrt {\hat{\sigma }^{2}_{{b^{\alpha } }} + \left( {\overline{\overline{X}}_{b}^{\alpha } - \tau_{{b^{\alpha } }} } \right)} }}, \hfill \\ \frac{{{\text{USL}}_{b} - {\text{LSL}}_{b} }}{{6\sqrt {\hat{\sigma }^{2}_{{c^{\alpha } }} + \left( {\overline{\overline{X}}_{c}^{\alpha } - \tau_{{c^{\alpha } }} } \right)} }},\frac{{{\text{USL}}_{b} - {\text{LSL}}_{b} }}{{6\sqrt {\hat{\sigma }^{2}_{{d^{\alpha } }} + \left( {\overline{\overline{X}}_{d}^{\alpha } - \tau_{{d^{\alpha } }} } \right)} }} \hfill \\ \end{gathered} \right) \\ \end{aligned} $$

(40)

3 A Real Case Application: An Ultra-Fine Calcite Production Process

3.1 Material and Data Collection

Micronized calcite is an inexpensive mineral filling material, and it is widely applied to many production processes, such as plastic, dye, and paper. In Turkey, calcites are good quality, and the reserves are hundreds of millions of tons. This situation may lead to a very important advantage for Turkey to produce very good quality products using micronized calcite.

Traditional ball-mill grinding technology is applied to obtain micronized calcite in industries. In this study, an ultra-fine calcite powder product was obtained by an industrial-scale ball mill from a grinding plant in Turkey. Data for d₅₀ (µm) and d₉₇ (µm) particle sizes were collected in four subgroups for each particle size for 20 days. These particle sizes (µm) values were measured by using Mastersizer 2000 (Malvern). Tables 1 and 2 show the collected data for d₅₀ (µm) and d₉₇ (µm) values, respectively. Note that the Minitab software was used in order to draw plots in this study.

Table 1 Collected data for d₅₀ (µm) values

Table 2 Collected data for d₉₇ (µm) values

The normality tests were performed for the collected data in Tables 1 and 2 because violating the normality assumption may result in incorrect conclusions for statistical process control charts. The Anderson–Darling normality tests were conducted to check the normality assumption for d₅₀ (µm) and d₉₇ (µm) values. The p values are 0.449 and 0.729 for d₅₀ (µm) and d₉₇ (µm), respectively. The p values are higher than the alpha values, which are 0.05. Therefore, both d₅₀ (µm) and d₉₇ (µm) values satisfy the normality assumptions. Figures 2 and 3 also verify normality assumptions.

Fig. 2

Normality plot for d₅₀ (µm) values

Fig. 3

Normality plot for d₉₇ (µm) values

For this application, fuzzy data are used because of the error rate in the measurement. Tables 3 and 4 show trapezoidal fuzzy numbers for d₅₀ (µm) and d₉₇ (µm) values, respectively. Tables 5 and 6 show trapezoidal fuzzy numbers with α-cuts for d₅₀ (µm) and d₉₇ (µm) values, respectively.

Table 3 Trapezoidal fuzzy numbers for d₅₀ (µm) values

Table 4 Trapezoidal fuzzy numbers for d₉₇ (µm) values

Table 5 Trapezoidal fuzzy numbers with α-cuts for d₅₀ (µm) values

Table 6 Trapezoidal fuzzy numbers with α-cuts for d₉₇ (µm) values

3.2 Results and Discussions for the Fuzzy $\overline{X} - R$ Control Chart

In this section, Eqs. (12) and (14) are used to construct $\overline{X}$ control limits, and Eqs. (15) and (17) are used to construct R control limits for the fuzzy $\overline{X} - R$ control chart.

3.2.1 Analysis of TFNs with α-Cuts for d₅₀ (µm) Values

Figure 4 shows the fuzzy $\overline{X} - R$ control charts using TFNs for d₅₀ (µm) values.

Fig. 4

a $\overline{X} - R$ control chart of $a_{1}^{\alpha }$, $a_{2}^{\alpha }$, $a_{3}^{\alpha }$, and $a_{4}^{\alpha }$ for d₅₀ (µm) values; b $\overline{X} - R$ control chart of $b_{1}^{\alpha }$, $b_{2}^{\alpha }$, $b_{3}^{\alpha }$, and $b_{4}^{\alpha }$ for d₅₀ (µm) values; c $\overline{X} - R$ control chart of $c_{1}^{\alpha }$, $c_{2}^{\alpha }$, $c_{3}^{\alpha }$, and $c_{4}^{\alpha }$ for d₅₀ (µm) values; d $\overline{X} - R$ control chart of $d_{1}^{\alpha }$, $d_{2}^{\alpha }$, $d_{3}^{\alpha }$, and $d_{4}^{\alpha }$ for d₅₀ (µm) values

Notice that the fifth point is below the LCL for each $\overline{X}$ control graph in Fig. 4. This situation was investigated, and there was not found any reason for the fifth point. The fifth point is also very close to the LCL. Therefore, it is concluded that the process is in control.

3.2.2 Analysis of TFNs with α-Cuts for d₉₇ (µm) Values

Figure 5 shows the fuzzy $\overline{X} - R$ control charts using TFNs for d₉₇ (µm) values.

Fig. 5

a $\overline{X} - R$ control chart of $a_{1}^{\alpha }$, $a_{2}^{\alpha }$, $a_{3}^{\alpha }$, and $a_{4}^{\alpha }$ for d₉₇ (µm) values; b $\overline{X} - R$ control chart of $b_{1}^{\alpha }$, $b_{2}^{\alpha }$, $b_{3}^{\alpha }$, and $b_{4}^{\alpha }$ for d₉₇ (µm) values; c $\overline{X} - R$ control chart of $c_{1}^{\alpha }$, $c_{2}^{\alpha }$, $c_{3}^{\alpha }$, and $c_{4}^{\alpha }$ for d₉₇ (µm) values; d $\overline{X} - R$ control chart of $d_{1}^{\alpha }$, $d_{2}^{\alpha }$, $d_{3}^{\alpha }$, and $d_{4}^{\alpha }$ for d₉₇ (µm) values

The seventh and nineteenth points are more than 3.00 standard deviations from the center line for each control graph in Fig. 5. The control charts in Fig. 5 are out of control because of the seventh and nineteenth points. The process investigation for d₉₇ (µm) values was investigated, and the worker error was reported. Therefore, the seventh and nineteenth points are removed from the fuzzy data. Then, the control charts were constructed. It is seen that the tenth point is out of control. Actually, the tenth point is very close to the LCL in Fig. 5. Then, the tenth point was also removed from the fuzzy data. Finally, all fuzzy data are in control, and the process improvement is achieved for d₉₇ (µm) values.

3.3 Results and Discussions for the Proposed FCUSUM Control Chart

$C_{i}^{ + }$ and $C_{i}^{ - }$ are calculated using Eqs. (23–30). Equations (31) and (33) are used for FCUSUM control limits. Note that K and H are denoted as 0.5 and 5, respectively.

3.3.1 Analysis of TFNs with α-Cuts for d₅₀ (µm) Values

The process standard deviation is unknown. Therefore, the estimated standard deviations for TFNs (a), (b), (c), and (d) with α-cuts are found using Eq. (34). The estimated standard deviations, $\hat{\sigma }_{{a^{\alpha } }} , \, \hat{\sigma }_{{b^{\alpha } }} , \, \hat{\sigma }_{{c^{\alpha } }} ,\;{\text{and}}\;\hat{\sigma }_{{d^{\alpha } }}$, are 0.188, 0.188, 0.188, and 0.188, respectively. In addition, $\tau_{{a^{\alpha } }}$, $\tau_{{b^{\alpha } }}$, $\tau_{{c^{\alpha } }}$, and $\tau_{{d^{\alpha } }}$ are specified as 3.34, 3.35, 3.55, and 3.56, respectively. Figure 6 shows the proposed FCUSUM control charts using TFNs d₅₀ (µm) values.

Fig. 6

a FCUSUM control chart of $a_{1}^{\alpha }$, $a_{2}^{\alpha }$, $a_{3}^{\alpha }$, and $a_{4}^{\alpha }$ for d₅₀ (µm) values; b FCUSUM control chart of $b_{1}^{\alpha }$, $b_{2}^{\alpha }$, $b_{3}^{\alpha }$, and $b_{4}^{\alpha }$ for d₅₀ (µm) values; c FCUSUM control chart of $c_{1}^{\alpha }$, $c_{2}^{\alpha }$, $c_{3}^{\alpha }$, and $c_{4}^{\alpha }$ for d₅₀ (µm) values; d FCUSUM control chart of $d_{1}^{\alpha }$, $d_{2}^{\alpha }$, $d_{3}^{\alpha }$, and $d_{4}^{\alpha }$ for d₅₀ (µm) values

In Fig. 6a–d, $C_{i}^{ + }$ and $C_{i}^{ - }$ values are denoted as blue and red points. Blue points denote in-control points, and red points denote out of control points. For each control chart in Fig. 6, the fuzzy UCL, the fuzzy CL, and the fuzzy LCL are 0.469, 0, and − 0.469, respectively. In Fig. 6, the production process for d₅₀ (µm) values is out of control because red points are above the fuzzy UCL. It is concluded that this process is not capable of meeting specifications to study under 1.0 standard deviations from the center line. For this production process, 3.00 standard deviation-based control limits are more appropriate to monitor d₅₀ (µm) values.

3.3.2 Analysis of TFNs with α-Cuts for d₉₇ (µm) Values

The process standard deviation is unknown for d₉₇ (µm) values. Thus, Eq. (34) is used to estimate the standard deviations for TFNs (a), (b), (c), and (d) with α-cuts. The estimated standard deviations, $\hat{\sigma }_{{a^{\alpha } }} , \, \hat{\sigma }_{{b^{\alpha } }} , \, \hat{\sigma }_{{c^{\alpha } }} ,\;{\text{and}}\;\hat{\sigma }_{{d^{\alpha } }}$, are 0.446, 0.446, 0.446, and 0.446, respectively. In addition, $\tau_{{a^{\alpha } }}$, $\tau_{{b^{\alpha } }}$, $\tau_{{c^{\alpha } }}$, and $\tau_{{d^{\alpha } }}$ are specified as 12.89, 12.90, 13.10, and 13.11, respectively. The proposed FCUSUM control charts using TFNs d₅₀ (µm) values are shown in Fig. 7.

Fig. 7

a FCUSUM control chart of $a_{1}^{\alpha }$, $a_{2}^{\alpha }$, $a_{3}^{\alpha }$, and $a_{4}^{\alpha }$ for d₉₇ (µm) values; b FCUSUM control chart of $b_{1}^{\alpha }$, $b_{2}^{\alpha }$, $b_{3}^{\alpha }$, and $b_{4}^{\alpha }$ for d₉₇ (µm) values; c FCUSUM control chart of $c_{1}^{\alpha }$, $c_{2}^{\alpha }$, $c_{3}^{\alpha }$, and $c_{4}^{\alpha }$ for d₉₇ (µm) values; d FCUSUM control chart of $d_{1}^{\alpha }$, $d_{2}^{\alpha }$, $d_{3}^{\alpha }$, and $d_{4}^{\alpha }$ for d₉₇ (µm) values

In Fig. 7a–d, $C_{i}^{ + }$ and $C_{i}^{ - }$ values are denoted as blue and red points. Blue points are in control, and red points are out of control. For each control chart in Fig. 7, the fuzzy UCL, the fuzzy CL, and the fuzzy LCL are 1.115, 0, and − 1.115, respectively. In Fig. 7, the production process for d₉₇ (µm) values is out of control because triangular-shaped red points are below the fuzzy LCL, and square-shaped red points are above the fuzzy UCL. This process is incapable of under 1.0 standard deviations from the center line. Therefore, it is concluded that this production process is not useful for detecting the small shifts in the fuzzy process mean for d₉₇ (µm) values.

3.4 Results and Discussions for the Proposed Fuzzy Process Capability Indices (FPCIs)

Table 7 denotes the upper specification limits (USLs) and the lower specification limits (LSLs) for d₅₀ and d₉₇ (µm) values of the plant.

Table 7 USL and LSL values of d₅₀ and d₉₇ (µm) values of the plant

Equations (37) and (38) are used to calculate the C_p and the C_pk indices, respectively. Table 8 shows the values of the C_p index for d₅₀ and d₉₇ (µm) values of the plant. Table 9 shows the values of the C_pk index for d₅₀ and d₉₇ (µm) values of the plant.

Table 8 Values of the fuzzy C_p index

Table 9 Values of the fuzzy C_pk index

This process capability analysis (PCA) is meaningful if the process is in control. Therefore, the PCA was conducted for the fuzzy $\overline{X} - R$ control charts. The production process is capable of meeting specification limits because all fuzzy C_p indices in Table 8 are greater than 1.33. Notice that the PCA is not meaningful because the process is out of control for the proposed FUSUM control chart.

In Table 9, fuzzy C_pk indices are smaller than 1.33 for d₅₀ (µm). Therefore, the process is not capable of meeting specifications. These results show that the fuzzy C_p index is not enough to draw a conclusion for the production process. In such situations, further action is necessary to be capable of meeting specifications for production systems. Particularly, the sample size could be increased. On the other hand, fuzzy C_pk indices are greater than 1.33 for d₉₇ (µm). Thus, the fuzzy production process is appropriate to meet the specifications for d₉₇ (µm) in terms of the fuzzy C_pk indices.

In some processes, fuzzy C_p and C_pk values may not be enough. For this reason, the fuzzy C_pm values are needed to conclude the fuzzy production process. Table 10 presents the values of the fuzzy C_pm index. All values in Table 10 are greater than 1.33 for d₅₀ (µm) and d₉₇ (µm). Hence, the fuzzy production meets the specifications regarding a measure of centering.

Table 10 Values of the fuzzy C_pm index

4 Concluding Remarks

In this paper, fuzzy control charts are proposed to monitor d₅₀ and d₉₇ (µm) particle size of ultra-fine calcite products in the ball mill. The four potential contributions are reported as follows: (1) A fuzzy $\overline{X} - R$ control chart is used with α-cuts based on trapezoidal fuzzy numbers. Large shifts in the fuzzy process mean can be detected while studying fuzzy $\overline{X} - R$ control charts. (2) An FCUSUM control chart is firstly proposed with α-cuts based on trapezoidal fuzzy numbers. Small shifts in the fuzzy process mean may be detected while considering FCUSUM control charts. (3) Fuzzy process capability indices (FPCIs) are proposed to measure the production process performance. (4) A real application is provided to illustrate the effectiveness of the proposed methodology.

Trapezoidal fuzzy numbers are used in this paper while providing a better solution and efficiency for monitoring the fuzzy production process. In addition, an α-level cut approach is suitable to determine the tightness control limits for the production process. The fuzzy SPC results of the ultra-fine calcite products show that the fifth point is below the LCL in Fig. 4, and the seventh and the nineteenth point are not between the control limits in Fig. 5. The reasons were found why these points were out of control. Then, further analysis was conducted while removing the seventh and nineteenth points. Next, the results of the ultra-fine calcite products show that the process is in control while using fuzzy $\overline{X} - R$ control charts. It is also investigated that the fuzzy $\overline{X} - R$ control charts are capable of detecting the large shift in the process. However, the process is out of control for FCUSUM control charts. Many red points are observed in Figs. 6 and 7, which are out of control. The ultra-fine calcite products are not capable of meeting the specifications under 1.0 standard deviations. This observation shows that the proposed FCUSUM control chart detects a small shift for the products. Also, the fuzzy $\overline{X} - R$ control charts are insufficient to provide stability and variance reduction for the products. The drawback may be eliminated using the proposed FCUSUM control chart.

Fuzzy capability analyses are proposed and conducted for the real case application in this paper. The values of the fuzzy C_p index are 1.773 and 1.868 for d₅₀ (µm) and d₉₇ (µm), respectively. According to the fuzzy C_p index, the process is capable of meeting specification limits while studying fuzzy $\overline{X} - R$ control charts. On the other hand, the values of the fuzzy C_pk index are 0.892 and 1.433 for d₅₀ (µm) and d₉₇ (µm), respectively. Thus, the fuzzy C_pk index shows that the process does not meet specification limits for d₅₀ (µm) while considering fuzzy $\overline{X} - R$ control charts. When measuring the location of the mean, the fuzzy C_pm index was analyzed. The fuzzy C_pm values are 1.720 and 1.837 for d₅₀ (µm) and d₉₇ (µm), respectively. Hence, the fuzzy C_pm index is suitable as a measure of centering for the real case application.

The limitation of this study is summarized as follows: In this study, the data were collected in four subgroups for 20 days. The sample size seems small; however, it is enough to draw a conclusion for the fuzzy process. Also, the number of subgroups may be increased for collected data. On the other hand, the four subgroups are appropriate for the fuzzy production process. Based on the analysis of the C_pk index, the large sample size may meet the specification limits of d₅₀ (µm) for the fuzzy $\overline{X} - R$ control chart. However, this situation cannot guarantee process stability and variance reduction. This limitation is overcome using the proposed FCUSUM control chart for the real case study while detecting many out of control points. The sample size is appropriate to monitor the process for the small shifts.

For further study, the fuzzy C_p, C_pk, and C_pm indices may not be enough in some fuzzy production processes. For this reason, the other fuzzy capability indices could be proposed and used for further study. Next, the variability of the production process should be reduced in order to meet the process specification limits. For this purpose, off-line quality improvement approaches, such as the design of experiments, could be useful to minimize the process variance while optimizing process parameters. Then, on-line quality control methods could be used to monitor production processes. As another further study, the sample size could be increased to minimize the process variance.