Development of a Fuzzy Exponentially Weighted Moving Average Control Chart with an α-level Cut for Monitoring a Production Process

Abstract

Statistical quality control is a useful approach that applies to statistical techniques for monitoring a production system. These charts are effective to monitor the process under certain conditions. On the other hand, the fuzzy set theory is an appropriate tool to deal with an uncertain situation. This paper is fourfold. First of all, triangular fuzzy numbers with an α-level cut technique are used for each sample. The α-level cut technique is sensitive to satisfy the process requirement. Second, a fuzzy exponentially weighted moving average (FEWMA) control chart is proposed with the α-level cut technique. The proposed FEWMA detects small shifts under uncertain situations while using a unity technique for samples. Third, the fuzzy target-focused process capability index (FC_pm) index is proposed to measure the fuzzy process performance. Then, a case study is presented to monitor a pumice block plant using the FEWMA control chart with the α-level cut and measure the process performance with the FC_pm index. Comparative studies are also presented. By using the proposed FEWMA control chart with the α-level cut, the accuracy and the flexibility of control specification limits are reported for the case study.

1 Introduction

Shewhart statistical quality controls are known as the traditional control charts to monitor a process under certain situations. Both the process mean and the process variability are considered together when dealing with numerical variables. In the literature, the X-bar and R charts are most widely used by practitioners and researchers [1]. However, these traditional charts do not work when data comes from uncertainty. For this particular situation, the fuzzy set theory is a powerful approach to monitor a production system.

1.1 Literature Review of Control Charts in the Fuzzy Set Theory

In the literature, Bradshaw [2] demonstrated how to interpret economic control limits in the context of the fuzzy set theory. Besides, Wang and Raz [3] applied the fuzzy set theory to develop quality control charts and construct control charts using linguistic variables for controlling the process average. Similarly, Kanagawa et al. [4] developed linguistic control charts for both the process average and the process variability. Besides, Franceschini and Romano [5] presented an online control of a process with control charts for linguistic variables. Along the same lines, Taleb and Limam [6] proposed control charts using linguistic data while considering fuzzy and probability theory. Besides, Gulbay et al. [7] developed α‐cut control charts for attributes. In contrast to the previously offered fuzzy control charts, Gulbay and Kahraman [8] proposed a direct fuzzy approach for fuzzy control charts. This approach prevents the loss of information from the samples. Then, Hou et al. [9] developed a technique to construct a control chart with a fuzzy score number while determining the design of nonconformity judging criteria and investigating the selection of fuzzy numbers. Furthermore, Fernandez [10] investigated the main aims of proposed fuzzy control charts in the relevant studies. Along the same lines, Hesamian et al. [11] presented a quality control process by using fuzzy random variables. For autocorrelated observations, Hryniewicz et al. [12] used fuzzy information in the design of control charts. Next, Zohoori et al. [13] presented an application of fuzzy adaptive control to monitor production time and cost performance. Finally, Choi et al. [14] offered a decision-making technique with fuzzy inference to ease process capability analysis by using the knowledge and perform a process capability control.

1.2 Literature Review of Variables Fuzzy Control Charts

In many applications, the moving average of two successive observations is used. Particularly, Erginel [15] proposed a fuzzy individual and moving range control charts with α-cuts. Along the same lines, Faraz and Moghadam [16] proposed a fuzzy chart for monitoring the process mean. For the problems of fuzzy control charts, Hryniewicz [17] provided a brief review of statistical quality control for fuzzy data, including challenges for the future. Next, Amirzadeh et al. [18] proposed a fuzzy p control chart with a mean degree of nonconformity. Then, Demirli and Vijayakumar [19] proposed a rule-based fuzzy inference system for the X-bar control chart. Besides, the fuzzy X-bar and R and X-bar and S control charts were studies by Senturk and Erginel [20], Erginel et al. [21], and Shu and Wu [22]. Besides, Taylan and Darrab [23] proposed fuzzy control charts in the tip shear carpet industry. Many quality characteristics could not be denoted as numerical variables. These quality characteristics are known as attributes. For fuzzy attributes control charts, such as p, np, and u, were developed by Senturk et al. [24] and Erginel [25]. Then, Shu et al. [26] proposed fuzzy $\overline{X}$ and s control charts while demonstrating a data-adaptability and human-acceptance for fuzzy data. Next, Ercan-Teksen and Anagun [27] developed c control charts with interval type-2 fuzzy numbers. Further, Fadaei and Poova [28] used the fuzzy operating characteristic to analyze the fuzzy u control chart performance. Then, Aslam and Khan [29] proposed a new variable control chart with a neutrosophic interval method for the automobile industry. For the uncertainty environment, Aslan et al. [30] offered a new moving average control chart for the normal distribution. In addition to these studies, Nasiri and Darestani [31] and Razali et al. [32] provided reviews of fuzzy control charts.

1.3 Literature Review of Time-Weighted Fuzzy Control Charts

The exponentially weighted moving average (EWMA) chart is used to detect small shifts in the process mean. It is also noted that this time-weighted chart is not greatly affected by low- or high-level values of variables. In the fuzzy set theory, Alipour and Noorossana [33] developed a fuzzy multivariate exponentially weighted moving average (F-MEWMA) control chart. Besides, Erginel and Senturk [34] proposed fuzzy EMWA and cumulative-sum (CUSUM) control charts. Then, Khan et al. [35] developed a fuzzy median EWMA control charts to detect small shifts for the process mean while monitoring the fuzzy oil packaging process. Furthermore, Hesamian et al. [36] developed the fuzzy EWMA by using normal fuzzy random variables where the fuzzy process mean and/or the fuzzy process variance is unknown. Next, Al-Refaie et al. [37] presented the alpha-cut EWMA by using fuzzy response observations in a manufacturing process for the mean shift with fuzzy logic.

1.4 Literature Review of Fuzzy Process Capability Indices

The process capability indices are useful to measure whether a process is capable of manufacturing items within the defined specification limits defined by the customer. In the literature, Kane [38] introduced the first capability index, C_p. The C_p index is defined by the ratio of the difference between the upper and the lower specification limits over the process standard deviation. The value of the C_p index denotes the process performance, such as satisfactory and unsatisfactory. On the other hand, the C_p index does not work where the process mean is located to the specification limits. To overcome this particular problem, the C_pk index is used [1]. The C_pk index is calculated based on the tolerance ($3\sigma$) to the control limits. However, the C_p and C_pk indices are not applicable while dealing with uncertainty. Therefore, Kaya and Kahraman [39] calculated the fuzzy C_p and C_pk indices with the triangular fuzzy numbers (TFNs). Besides, the results of the fuzzy C_p and C_pk indices are more accurate, sensitive, and flexible for uncertain situations.

In this paper, Sect. 2 presents research motivating concepts for this study. Next, the proposed FEWMA control chart with the α-level cut and the proposed fuzzy target-focused process capability index (FC_pm) index are presented in Sect. 3. Then, Sect. 4 illustrates a case study for monitoring a pumice block plant, including the results and discussions. Finally, concluding remarks are drawn in Sect. 5.

2 Research Motivating Concepts

As shown in the introduction section, little attention has been paid in the literature to detect small shifts under uncertain situations. Even though fuzzy X-bar and R and fuzzy X-bar and S control charts are widely used, these fuzzy charts may not be capable of small shifts in the process mean. Besides, fuzzy X-bar and R and fuzzy X-bar and S control charts can only react when the last data point is outside a lower or an upper control limit. Furthermore, the vast majority of previous studies do not present a unified approach to investigate two main aspects of fuzzy control processes, which are fuzzy process control charts and fuzzy process capability analyses. Therefore, the aim of this paper is fourfold. One, triangular fuzzy numbers are used with an α-level cut technique for each sample. The α-level cut technique can be sensitive to calculate control limits for satisfying the production process requirement. Two, a fuzzy exponentially weighted moving average (FEWMA) control chart is firstly proposed by using the α-level cuts while considering a unity technique for a large number of samples. The proposed FEWMA control chart is useful when the goal is to detect small shifts under uncertain situations. Besides, the proposed FEWMA control chart reaches a stable level at the steady-state values. Therefore, the accuracy and flexibility of control specification limits are observed. Three, the FC_pm index is firstly proposed to measure the process performance for a pumice block plant. Besides, this paper is the first research attempt to analyze important aspects of the fuzzy quality control process, such as a time-weighted fuzzy control chart with the α-level cut technique and fuzzy process capability analyses. Finally, a case study is presented to show the effectiveness of the proposed methodology for monitoring a pumice block plant.

3 Proposed Methodology Development

In this section, the three-phased proposed methodology is as follows: (1) triangular fuzzy numbers with an α-level cut, (2) the proposed FEWMA control chart with the α-level cut, and (3) the proposed FC_pm index.

3.1 Triangular Fuzzy Numbers with an α-level Cut

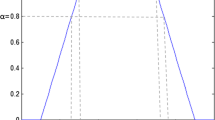
In this paper, triangular fuzzy numbers (TFNs) are used for obtaining the FEWMA control chart. Triangular fuzzy numbers are denoted as a, b, and c. The triangular membership function computes fuzzy membership values with a triangular membership function as follows:

$$ f(x;\,a,b,c) = \left\{ \begin{aligned} 0,\;x \le a \\ \frac{x - a}{b - a},\;a \le x \le b \\ \frac{c - x}{c - b},\;b \le x \le c \\ 0,\;c \le x \\ \end{aligned} \right\} $$

(1)

where $f(x;\,a,b,c)$ is the triangular membership function. In Fig. 1, a^α and c^α denote the endpoints of an α-level cut.

Fig. 1

TFN with an α-level cut for a sample

In Fig. 1, $a^{\alpha } ,b^{\alpha } ,\;{\text{and}}\;c^{\alpha }$ are found as follows:

$$ a^{\alpha } = (b - a)\alpha + a $$

(2)

$$ b^{\alpha } = b $$

(3)

$$ c^{\alpha } = (c - b)\alpha + b $$

(4)

3.2 FEWMA Control Charts with the α-level Cut

The EWMA control chart is a preferred technique to detect small shifts for the process mean. In this subsection, the FEWMA control chart with the α-level cut proposed by Senturk et al. [40] is reviewed and a new approach is developed for the FEWMA with the α-level cut.

3.2.1 The FEWMA Control Chart with the α-level Cut Proposed by Senturk et al. [40]

For the traditional EWMA control chart, the upper control limit (UCL), the center limit (CL), and the lower control limit (LCL) are found as follows [40]:

$$ {\text{UCL}} = \bar{\bar{X}} + A_{2} \bar{R}\sqrt {\frac{\lambda }{(2 - \lambda )}} $$

(5)

$$ {\text{CL}} = \bar{\bar{X}} $$

(6)

$$ {\text{LCL}} = \bar{\bar{X}} - A_{2} \bar{R}\sqrt {\frac{\lambda }{(2 - \lambda )}} $$

(7)

where $\bar{\bar{X}}$ is the overall mean, $\bar{R}$ is the average of the range for each sample, $A_{2}$ is a constant, and $0 \le \lambda \le 1$ is a constant. Notice that $\sigma$ is unknown.

In the fuzzy set theory, each sample or subgroup is denoted as a TFN. TFNs with the α-level cut are $X_{a}^{\alpha }$, $X_{b}^{\alpha }$, and $X_{c}^{\alpha }$ for each observation under uncertainty. For the FEWMA control chart with the α-level cut, the upper control limit (${\tilde{\text{U}}\text{CL}}$), the center limit (${\tilde{\text{C}}\text{L}}$), and the lower control limit (${\tilde{\text{L}}\text{CL}}$) are denoted as follows [40].

$$ \begin{aligned} {\tilde{\text{U}}\text{CL}} &= \left( {\bar{\bar{X}}_{a}^{\alpha } + A_{2} \bar{R}_{a}^{\alpha } \sqrt {\frac{\lambda }{(2 - \lambda )}} ,\bar{\bar{X}}_{b}^{\alpha } }\right.\\&\quad\left.{+ A_{2} \bar{R}_{b}^{\alpha } \sqrt {\frac{\lambda }{(2 - \lambda )}} ,\bar{\bar{X}}_{c}^{\alpha } + A_{2} \bar{R}_{c}^{\alpha } \sqrt {\frac{\lambda }{(2 - \lambda )}} } \right) \end{aligned} $$

(8)

$$ {\tilde{\text{C}}\text{L}} = \left( {\bar{\bar{X}}_{a}^{\alpha } ,\bar{\bar{X}}_{b}^{\alpha } ,\bar{\bar{X}}_{c}^{\alpha } } \right) $$

(9)

$$ \begin{aligned} {\tilde{\text{L}}\text{CL}} &= \left( {\bar{\bar{X}}_{a}^{\alpha } - A_{2} \bar{R}_{a}^{\alpha } \sqrt {\frac{\lambda }{(2 - \lambda )}} ,\bar{\bar{X}}_{b}^{\alpha } }\right.\\&\quad\left.{- A_{2} \bar{R}_{b}^{\alpha } \sqrt {\frac{\lambda }{(2 - \lambda )}} ,\bar{\bar{X}}_{c}^{\alpha } - A_{2} \bar{R}_{c}^{\alpha } \sqrt {\frac{\lambda }{(2 - \lambda )}} } \right) \end{aligned} $$

(10)

where $\bar{\bar{X}}_{a}^{\alpha }$, $\bar{\bar{X}}_{b}^{\alpha }$, and $\bar{\bar{X}}_{c}^{\alpha }$ are the overall means for $X_{a}^{\alpha }$, $X_{b}^{\alpha }$, and $X_{c}^{\alpha }$, respectively. $\bar{R}_{a}^{\alpha }$, $\bar{R}_{b}^{\alpha }$, and $\bar{R}_{c}^{\alpha }$ are the averages of the ranges for each sample. Notice that Erginel and Senturk [34] used the same equations in (8)–(10) for the FEWMA with the α-level cut.

3.2.2 The Proposed FEWMA Control Chart with the α-level Cut

When $\sigma$ is unknown, the specifications of the traditional EWMA control chart could be computed as follows:

$$ {\text{UCL}} = \bar{\bar{X}} + A_{2} \bar{R}\sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} $$

(11)

$$ {\text{CL}} = \bar{\bar{X}} $$

(12)

$$ {\text{LCL}} = \bar{\bar{X}} - A_{2} \bar{R}\sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} $$

(13)

In Eqs. (11) and (13), the term $\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]$ approaches unity as the number of samples i gets larger. Therefore, Eqs. (11) and (13) are recommended to compute the exact control limits for small values of the sample number i. The results of the case study in Sect. 4.3 show that the performance of the traditional EWMA control chart will be greatly improved using Eqs. (11) and (13) to detect an off-target process instantly after the traditional EWMA is run.

The proposed FEWMA control chart is a statistic to monitor the fuzzy production process when the aim is to detect small shifts in a fuzzy environment. Besides, a stable level at the steady-state values is reached by using the proposed FEWMA control chart. Control limits are also accurately and effectively observed with the proposed FEWMA control chart with the α-level cuts for the fuzzy process. For the proposed FEWMA control chart with the α-level cut strategy, the upper control limit (${\tilde{\text{U}}\text{CL}}^{\alpha }$), the center limit (${\tilde{\text{C}}\text{L}}^{\alpha }$), and the lower control limit (${\tilde{\text{L}}\text{CL}}^{\alpha }$) are developed as follows:

$$ {\tilde{\text{U}}\text{CL}}^{\alpha } = \left( \begin{array}{*{20}l} \bar{\bar{X}}_{a}^{\alpha } + A_{2} \bar{R}_{a}^{\alpha } \sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} ,\bar{\bar{X}}_{b}^{\alpha } + A_{2} \bar{R}_{b}^{\alpha } \sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} , \hfill \\ \bar{\bar{X}}_{c}^{\alpha } + A_{2} \bar{R}_{c}^{\alpha } \sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} \hfill \\ \end{array} \right) $$

(14)

$$ {\tilde{\text{C}}\text{L}}^{\alpha } = \left( {\bar{\bar{X}}_{a}^{\alpha } ,\bar{\bar{X}}_{b}^{\alpha } ,\bar{\bar{X}}_{c}^{\alpha } } \right) $$

(15)

$$ {\tilde{\text{L}}\text{CL}}^{\alpha } = \left( \begin{array}{*{20}l}\bar{\bar{X}}_{a}^{\alpha } - A_{2} \bar{R}_{a}^{\alpha } \sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} ,\bar{\bar{X}}_{b}^{\alpha } - A_{2} \bar{R}_{b}^{\alpha } \sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} , \hfill \\ \bar{\bar{X}}_{c}^{\alpha } - A_{2} \bar{R}_{c}^{\alpha } \sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} \hfill \\ \end{array} \right) $$

(16)

The fuzzy values of the FEWMA are calculated as follows:

$$ \tilde{z}_{i} = \left( {\lambda \bar{X}_{a}^{\alpha } + \left( {1 - \lambda } \right)z_{i - 1}^{a} ,\lambda \bar{X}_{b}^{\alpha } + \left( {1 - \lambda } \right)z_{i - 1}^{b} ,\lambda \bar{X}_{c}^{\alpha } + \left( {1 - \lambda } \right)z_{i - 1}^{c} } \right) $$

(17)

where $\tilde{z}_{i}$ is the fuzzy value for the FEWMA, $z_{0}^{a} = \bar{\bar{X}}_{a}^{\alpha }$, $z_{0}^{b} = \bar{\bar{X}}_{b}^{\alpha }$, and $z_{0}^{c} = \bar{\bar{X}}_{c}^{\alpha }$.

3.3 The Proposed FC_pm Index

After the results of the statistical control chart are analyzed, the process capability analysis is conducted to measure the process performance. Particularly, the target-focused process capability index, C_pm, measures the ability of a production process to cluster around the target value. This index is related to the process variation relative to the target value. The C_pm index is defined as follows [1]:

$$ C_{\text{pm}} = \frac{{{\text{USL}} - {\text{LSL}}}}{{6\sqrt {\sigma^{2} + \left( {\mu - \tau } \right)^{2} } }} $$

(18)

where USL and LSL represent the upper and lower specification limits, respectively. $\sigma^{2}$ is the process variation, $\mu$ is the process mean, and $\tau$ is the process target.

There may exist some situations where the target is the priority. In this paper, the C_pm index is reconsidered as follows:

$$ C_{\text{pm}} = \frac{{{\text{USL}} - {\text{LSL}}}}{{6\sqrt {w_{1} \sigma^{2} + w_{2} \left( {\mu - \tau } \right)^{2} } }} $$

(19)

where $0 \le w_{1} \le 1$ and $0 \le w_{2} \le 1$. $w_{1}$ and $w_{2}$ are constants defined by the user. Three special cases are reported as follows:

• 1. $w_{1} = w_{2} = 1$, this is the approach, which is denoted in Eq. (18).

• 2. $w_{1} = 1$ and $w_{2} = 0$, this is the C_p index (please see [1]).

• 3. $w_{1} = 0$ and $w_{2} = 1$, this is a new approach, which focuses on the process bias. The process bias is the difference between the process mean and the process target.

In the fuzzy set theory, the FC_pm index with the α-level cut is proposed as follows:

$$ {{{\text{F}}\tilde{{\text{C}}}}}_{\text{pm}}^{\alpha } = \left( \begin{array}{*{20}l} \frac{{{\text{USL}}_{a}^{\alpha } - {\text{LSL}}_{a}^{\alpha } }}{{6\sqrt {w_{1} \left( {\sigma_{a}^{\alpha } } \right)^{2} + w_{2} \left( {\mu_{a}^{\alpha } - \tau_{a}^{\alpha } } \right)^{2} } }},\frac{{{\text{USL}}_{b}^{\alpha } - {\text{LSL}}_{b}^{\alpha } }}{{6\sqrt {w_{1} \left( {\sigma_{b}^{\alpha } } \right)^{2} + w_{2} \left( {\mu_{b}^{\alpha } - \tau_{b}^{\alpha } } \right)^{2} } }}, \hfill \\ \frac{{{\text{USL}}_{c}^{\alpha } - {\text{LSL}}_{c}^{\alpha } }}{{6\sqrt {w_{1} \left( {\sigma_{c}^{\alpha } } \right)^{2} + w_{2} \left( {\mu_{c}^{\alpha } - \tau_{c}^{\alpha } } \right)^{2} } }} \hfill \\ \end{array} \right) $$

(20)

In practical applications, the process variance $\sigma^{2}$ is unknown. We will use $\bar{\bar{X}}_{a}^{\alpha } ,\bar{\bar{X}}_{b}^{\alpha } ,\bar{\bar{X}}_{c}^{\alpha }$ and $\left( {s_{a}^{\alpha } } \right)^{2} ,\left( {s_{b}^{\alpha } } \right)^{2} ,\left( {s_{c}^{\alpha } } \right)^{2}$ as estimates of $\mu_{a}^{\alpha } ,\mu_{b}^{\alpha } ,\mu_{c}^{\alpha }$ and $\left( {\sigma_{a}^{\alpha } } \right)^{2} ,\left( {\sigma_{b}^{\alpha } } \right)^{2} ,\left( {\sigma_{c}^{\alpha } } \right)^{2}$, respectively. Therefore, the estimate of the FC_pm is written as follows:

$$ {{{\text{F}}\tilde{\hat{{\text{C}}}}}}_{\text{pm}}^{\alpha } = \left( \begin{array}{*{20}l} \frac{{{\text{USL}}_{a}^{\alpha } - {\text{LSL}}_{a}^{\alpha } }}{{6\sqrt {w_{1} \left( {s_{a}^{\alpha } } \right)^{2} + w_{2} \left( {\bar{\bar{X}}_{a}^{\alpha } - \tau_{a}^{\alpha } } \right)^{2} } }},\frac{{{\text{USL}}_{b}^{\alpha } - {\text{LSL}}_{b}^{\alpha } }}{{6\sqrt {w_{1} \left( {s_{b}^{\alpha } } \right)^{2} + w_{2} \left( {\bar{\bar{X}}_{b}^{\alpha } - \tau_{b}^{\alpha } } \right)^{2} } }}, \hfill \\ \frac{{{\text{USL}}_{c}^{\alpha } - {\text{LSL}}_{c}^{\alpha } }}{{6\sqrt {w_{1} \left( {s_{c}^{\alpha } } \right)^{2} + w_{2} \left( {\bar{\bar{X}}_{c}^{\alpha } - \tau_{c}^{\alpha } } \right)^{2} } }} \hfill \\ \end{array} \right) $$

(21)

4 Case Study: Monitoring a Pumice Block Plant

4.1 Production System

Most of the Mediterranean countries have used basaltic tuffs with lime. Nowadays, the cement industry is one of the developed industries in Turkey with a growing interest in using tuffs. Recently, the trass cement of a Portland-pozzolan cement mixture was produced almost thirty percent of the total production [41]. It is known that Turkey is wealthy in the natural pozzolans, such as the basaltic pumice of the cement industry, in which Tertiary and Quaternary-age volcanic rocks cover almost 155,000 km² of the country. The potential of the natural pozzolan has not been adequately addressed even though there are a wide variety of geological-based studies done on the volcanic rocks [42]. Besides, the physical and chemical properties of pumice in Turkey are summarized in Tables 1 and 2.

Table 1 Physical properties of pumice in Turkey [43]

Table 2 Chemical properties of pumice in Turkey [43]

The lightweight concrete block production is produced with mechanized industry-based automation and accuracy, and this specific production has the standards for the products. The standards are denotations on sizes, fire resistance, properties of insulating, strength, and weather resistance. In Turkey, the natural lightweight aggregate is highly popular for the manufacturing of lightweight concrete blocks during recent years to utilize pumice aggregates. Besides, pumice aggregate may be applied to aggregates in concrete to meet the standards [44]. Pumice concrete is manufactured with the mixing of cement, pumice aggregate, and water. Pumice blocks are manufactured from pumice concrete.

The first phase of the pumice block production process is to produce several grades of pumice blocks in the quarry. The second phase is the breaking process. Then, the sieving process is to separate particles of different sizes. Next, pumice grading is to determine grades for pumice block products. The fifth phase is to mix cement, pumice aggregate, and water. Then, the pumice block production process is applied, including vibration and press. Next, pumice blocks are cured in the room temperature condition. Finally, pumice blocks are packed and delivered to customers. Figure 2 summarizes the process of pumice block production.

Fig. 2

Process of the pumice block production (Modified from [45])

4.2 Material

Pumice block products are produced under TS-EN 771/3 and CE standards in the ISO 9001-2008 system. They used in the inner and outer walls of all types of construction systems. Pumice blocks are known as highly insulated, energy-saving, and lightweight. In this research study, five samples were collected for each day and totaled twenty-four days. The samples were collected at regular intervals during the day. The proposed FEWMA control chart with the α-level cut was carried out for a plant in Turkey producing pumice blocks in dimensions of 150 × 390 × 190 mm (see Fig. 3). In the production process, the proposed FEWMA control chart with the α-level cut was established to determine whether the results from unit volume weights (kg/dm³) in a pumice block plant were under control or not.

Fig. 3

A pumice block product in a dimension of 150x390x190 mm

4.3 Results and Discussions

4.3.1 TFNs with the α-level Cuts

Data were collected for twenty-four samples with five groups. The results of the collected data are shown in Table 3 for pumice block products.

Table 3 Collected data for calculating unit volume weights (kg/dm³) of pumice block products

The normality test was performed for the collected data in Table 3. The Anderson–Darling normality test using Minitab software version 17 was performed to check the normality assumption. The pumice block production process satisfied the normality assumption because the p value is higher than the alpha value where the p value and the alpha value are 0.301 and 0.05, respectively. Figure 4 also shows the normality plot. Notice that Fig. 4 also verifies the normality assumption.

Fig. 4

Normality plot for the pumice block production process

The values of Table 3 were collected under uncertainty, and these values were converted the triangle fuzzy numbers according to ± 0.005 kg/dm³ values. For example, the value 0.555 kg/dm³ in Table 3 (Sample 1 for $X_{1}$) was converted to a TFN as (0.550, 0.555, 0.560) (kg/dm³). TFNs were used because of the differences between the workers and the error rate in the measurement. In Table 4, TFNs with the α-level cuts are shown when $\alpha = 0.9$. The α-level is defined as 0.9 by the researchers because this value can reflect the accurate control limits for the pumice block plant. For another industry process, such as a piston inner diameter production process, the α-level is 0.65 [20].

Table 4 The TFNs of the unit volume weights (kg/dm³) corresponding the measurements in Table 3 when $\alpha = 0.9$

4.3.2 The Results of the FEWMA Control Charts

The proposed FEWMA control chart without the α-level cuts is shown in Fig. 5. The following equations are used to determine control limits. Notice that the term $\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]$ is used in Eqs. (22) and (24).

Fig. 5

The proposed FEWMA control chart without the α-level cuts

$$ {\tilde{\text{U}}\text{CL}}_{{{\text{no}}\_{\text{cut}}}} = \left( \begin{array}{*{20}l} \bar{\bar{X}}_{a} + A_{2} \bar{R}_{a} \sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} ,\bar{\bar{X}}_{b} + A_{2} \bar{R}_{b} \sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} , \hfill \\ \bar{\bar{X}}_{c} + A_{2} \bar{R}_{c} \sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} \hfill \\ \end{array} \right) $$

(22)

$$ {\tilde{\text{C}}\text{L}}_{{{\text{no}}\_{\text{cut}}}} = \left( {\bar{\bar{X}}_{a} ,\bar{\bar{X}}_{b} ,\bar{\bar{X}}_{c} } \right) $$

(23)

$$ {\tilde{\text{L}}\text{CL}}_{{{\text{no}}\_{\text{cut}}}} = \left( \begin{array}{*{20}l} \bar{\bar{X}}_{a} - A_{2} \bar{R}_{a} \sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} ,\bar{\bar{X}}_{b} - A_{2} \bar{R}_{b} \sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} , \hfill \\ \bar{\bar{X}}_{c} - A_{2} \bar{R}_{c} \sqrt {\frac{\lambda }{(2 - \lambda )}\left[ {1 - \left( {1 - \lambda } \right)^{2i} } \right]} \hfill \\ \end{array} \right) $$

(24)

where ${\tilde{\text{U}}\text{CL}}_{{{\text{no}}\_{\text{cut}}}}$ is the upper control limits without the α-level cuts, ${\tilde{\text{C}}\text{L}}_{{{\text{no}}\_{\text{cut}}}}$ is the center limits without the α-level cuts, and ${\tilde{\text{L}}\text{CL}}_{{{\text{no}}\_{\text{cut}}}}$ is the lower control limits without the α-level cuts.

Figure 5 shows the mean value of the fuzzified results for the proposed FEWMA control chart without the α-level cuts. Notice from Fig. 5 that the control limits increase in width as the sample number increases from $i = 1,2, \ldots ,24$ until they reach the stable level at the steady-state values. In Fig. 5, the FEWMA control charts without the α-level cuts show that the pumice block plant is in control because there are no calculated points out of control limits.

For the FEWMA control chart, the α-level cuts proposed by Senturk et al. [40], the upper control limit (${\tilde{\text{U}}\text{CL}}$), the center limit (${\tilde{\text{C}}\text{L}}$), and the lower control limit (${\tilde{\text{L}}\text{CL}}$) are found as follows:

$$ {\tilde{\text{U}}\text{CL}} = \left( {0.569432,0.569932,0.570432} \right) $$

(25)

$$ {\tilde{\text{C}}\text{L}} = \left( {0.566308,0.566808,0.567308} \right) $$

(26)

$$ {\tilde{\text{L}}\text{CL}} = \left( {0.563185,0.563685,0.564185} \right) $$

(27)

According to the FEWMA control chart with the α-level cuts proposed by Senturk et al. [40], the process is in control. However, this approach uses the same control limits for each sample. Therefore, this control chart is not able to detect an off-target process after the FEWMA is started up.

For the proposed FEWMA control chart with the α-level cuts, Table 5 shows the determined control limits using Eqs. (11–13). Note that $\lambda = 0.1$, $\bar{R}_{a}^{\alpha } = \bar{R}_{b}^{\alpha } = \bar{R}_{c}^{\alpha } = 0.023875$, and $A_{2} = 0.577$. The control limits in Fig. 6 increase in width as the sample number increases from $i = 1,2, \ldots ,24$ until they stabilize at the steady-state value.

Table 5 Control limits for the pumice block production process

Fig. 6

The proposed FEWMA control chart with the α-level cuts

Figure 6 shows the mean value of the fuzzified results for the proposed FEWMA control chart with the α-level cuts. In Fig. 6, the process is in control because the fuzzy values of the FEWMA are between upper control limits and lower control limits. As shown in Fig. 6, the performance of the control chart can detect an off-target process after the first sample is analyzed. If the first observation was computed as 0.565, the process would be in control for the FEWMA control chart with the α-level cuts proposed by Senturk et al. [40]. However, the process would be out of control for the proposed FEWMA control chart with the α-level cuts when the first value of the FEWMA could be found 0.565. Therefore, the accuracy and efficiency were increased using the proposed FEWMA control chart with the α-level cuts. Using the cut strategy increases the values of the control limits for $\bar{\bar{X}}_{a}^{\alpha }$. On the other hand, using the cut strategy decreases the values of the control limits for $\bar{\bar{X}}_{c}^{\alpha }$. In Figs. 5 and 6, the cut level influences upper, center, and lower control limits for the pumice production process. Therefore, the choice of the cut level can be sensitive to obtain control limits for meeting the production process requirement.

The proposed FEWMA control chart with the α-level cuts is highly effective to control the pumice production process for finding causes of variation and corrective actions. In Fig. 6, the pumice production is in control; therefore, no corrective action is necessary. The proposed technique shows that the production process is stable due to no out of control points. In Fig. 6, the proposed FEWMA control chart with the α-level cuts points out no unusual condition arising in the pumice production process.

4.3.3 The Results of the Fuzzy Process Capability Analysis

The proposed FEWMA control chart with the α-level cuts is in control; however, the process capability analysis should be conducted to measure the process performance. For this particular purpose, the specification limits are used to check whether or not the observations are within specification limits. The upper specification limit (USL) and the lower specification limit (LSL) are specified in Table 6 by the researchers. These specification limits are appropriate for the pumice production process.

Table 6 Values of USL, LSL, $s$, $\tau$, and $\bar{\bar{X}}$

Within standard deviation is an estimate of the process variation within the subgroups. The within-subgroup variation should not be affected by changes to process input, such as the workers and the error rate in the measurement because we collect data properly. The fuzzy values of s can be found as follows:

$$ s = \left( {\frac{{\bar{R}_{a}^{\alpha } }}{{d_{2} }},\frac{{\bar{R}_{b}^{\alpha } }}{{d_{2} }},\frac{{\bar{R}_{c}^{\alpha } }}{{d_{2} }}} \right) $$

(28)

where $d_{2}$ is 2.326 (see [1]). The values of the estimated standard deviation, the mean and the target are given in Table 6. Note that the target values are determined by the user. The values of $\bar{\bar{X}}$ are found (please see Fig. 6).

The FC_pm index is determined based on Eq. (21) while considering the three different cases. Table 7 shows these values for the three different cases.

Table 7 Results of the FC_pm analysis with the three different cases

In Table 7, the first case denotes the FC_pm index, and the second case is the traditional fuzzy C_p index calculated by Kaya and Kahraman [39]. Besides, the C_p index is widely used in the industry [1]. However, the fuzzy C_p index does not consider the process bias. On the other hand, the third case in Table 7 is the proposed fuzzy capability index, which is based on the process bias. All cases indicate that the pumice block production process is adequate because all values in Table 7 are greater than 1.33 for the existing process [1]. It is also concluded that the proposed fuzzy capability index has a good performance based on the results in Table 7 to measure the fuzzy process while considering both the process variance and the process bias.

5 Concluding Remarks

The traditional control charts are applicable under certain conditions. However, the fuzzy control charts are useful for dealing with uncertain conditions. In this paper, a FEWMA control chart with an α-level cut is proposed to detect small shifts in the process mean for uncertainty while applying to a unity technique for samples. Then, the FC_pm index is proposed to measure the fuzzy production process performance. Next, a pumice block production process was analyzed. Then, the proposed FEWMA control chart with the α-level cut was applied to the pumice production process. In addition, the α-level is defined as 0.9 to obtain the accurate control limits for the pumice block plant. Then, the proposed FEWMA control chart with the α-level cut was compared to the previously offered FEWMA chart in the literature. The results of the case study showed superior performance for the proposed FEWMA control chart. Besides, the proposed FEWMA control chart with the α-level cuts shows no unusual condition arising in the pumice production process; therefore, the process is in control. Next, the process capability analysis was conducted to verify the process stability. The values of the proposed fuzzy capability index are 13.29, 31.83, and 80.49, respectively. Besides, the proposed fuzzy capability index is effective to measure the process performance, and the pumice production process is stable based on the values of the proposed fuzzy capability index.

For future research studies, trapezoidal fuzzy numbers could be used and the obtained results could be compared with the previous studies. Besides, a fuzzy multivariate control chart with an α-level cut could be developed for linguistic observations. Another future study could be to build a FEWMA control chart for reliability tests in a fuzzy environment.