1 Introduction

Nowadays, the design, modeling, and control research around continuum robots has received a lot of attention due to their appealing characteristics such as low inertia, high dexterity, flexibility, and, most importantly, their safety near humans when compared to robots with rigid links [1,2,3]. Additionally, their continuous structure and inherent compliance enable them to work in extremely congested environments and provide them with the ability to dexterously avoid obstacles. These features make them more suitable for a variety of applications including: medical and surgical applications [4, 5], inspection and manipulation [6,7,8] and so on.

A continuum robot has a complex structure that can be either soft or hard consisting of single section or a number of sections serially connected. The entire structure of continuum robot can be assimilated as piecewise curves, which can be either real or virtual, depending on the type of the robot. Currently, a variety of designs and prototypes of continuum robots have been developed with planar and spatial functionality such as Cable-Driven Continuum Robot (CDCR) [9], Tendon-Driven Continuum Robot (TDCR) [10], pneumatic continuum manipulator as Bionic Handling Assistant (BHA) [11] and concentric-tube continuum robot [12]. Nevertheless, due to their inherent complex behavior, they require extensive modeling and development in order to extract their full physical potential for practical applications.

From a modeling point of view, the Forward Kinematic (FK) problem of continuum robots is relatively easy to solve. As a result, many research projects have been carried out to solve it using different methods and theories based on some simplifications and hypotheses, such as Elliptic Integral Approach [13], Constant Curvature Kinematic Approach [14], Modal Approach [15] and Pseudo-Rigid Body Representation [16]. On the other hand, the Inverse Kinematic (IK) problem of continuum robots remains a major challenge due to highly coupled nonlinear equations of the forward kinematic. In fact, it is hard to solve this problem in a purely analytical way except in specific circumstances where the robot meets particular conditions, such as in [17,18,19,20]. In [17], the IK of multi-section continuum robot was analytically solved by considering it as a rigid-linkage system (i.e., each rigid-link connects the section's EPs) and assuming that the EP coordinates of all links are known and without considering their orientations. In [18], the IK of continuum structures was solved by using parametric curves approximated by mode shape functions assigned to restricted shapes and motions. The authors in [19] proposed a solution to the IK for inextensible bending segments under specific segment arrangement, and similarly, for a specified EP pose in [20]. In [21], the IK problem of continuum robots has been solved using Pythagorean Hodograph curves, in which the robot's shape is firstly reconstructed, and then the IKs are derived. However, these approaches do not tackle the redundancy problem; hence they cannot be used to find a general solution to the redundancy problem.

Alternatively, some researchers have resorted to use machine learning tools to solve the IKs of continuum robots. In [22], a neural network approach via a distal supervised learning architecture has been used to solve the IK problem of Compact Bionic Handling Assistant (CBHA) manipulator. In [23], a hybrid approach was used to solve the IK problem of the CBHA manipulator in which the robot was considered as a series of vertebrae, where a flexible link joined two successive vertebrae. In the same context, a goal babbling approach was used to solve IK problem of Bionic Handling Assistant (BHA) manipulator [24]. However, only one IK solution was provided among the redundancy varieties in these approaches, and which, in turn, cannot be used in general cases.

Additionally, other researchers have used numerical and optimization methods to solve the IKs problem and the redundancy resolution of continuum robots. In [25, 26], the IK problem for a planar and spatial CDCR has been formulated as an optimization issue dealing with a constant curvature assumption and using PSO method. In [27], a Sequential Quadratic Program (SQP)-based approach is used to approximate the IK of CBHA manipulator. These approaches, however, can only provide one optimal or non-optimal IK solution. Similarly, numerical methods based on the Jacobian matrix have been implemented to solve the IK problem of continuum robots [11, 28, 29], in which the FK equations are differentiated to find a linear transformation between actuator velocities and robot pose velocities and yet, these methods have only solved redundancy in one way, where changing the resolution criterion when computing the IK solution is difficult.

Based on the previously proposed approaches for solving the IK problem of continuum robots, we noticed that the majority of researchers have not thoroughly addressed the redundancy resolution, which is undeniably important. In this paper, a reliable algorithm is established and developed to address the shortcomings of previously proposed algorithms for solving the IK problem and redundancy resolution of continuum robots. It is a two-sub-algorithm: the first sub-algorithm collects and forms a tree of the reachable EP poses of the first \((n-1)\) sections for each robot's EP pose. The second sub-algorithm selects the optimal posture of the robot among the redundant varieties provided by the first one.

The following points summarize the advantages of the proposed algorithms: (1) unlike previous works [11, 28, 29], in which the ease of the model’s derivation is strongly related to the number of robot’s sections (i.e., increasing number of robot’s sections has a negative impact on the process of the IK problem’s resolution). On the other hand, these methods suffer generally from several shortcomings such as high calculation cost, the presence of local minima and instabilities close to the singularities; while the proposed algorithm has no links with the robot’s degree of redundancy and its characteristics, and does not require computing the Jacobian and even the gradient of the cost function; thus the common problem of singularities can be easily avoided. Besides, the re-generation of the initial population on the PSO method has been introduced to address the occurrence probability of local minima. Thus, the complexity of the continuum robot’s mechanism is no longer an obstacle to processing multi-sections which was previously considered as an unavoidable problem. (2) unlike [22,23,24] that require a massive database just to provide access to a significant number of possible solutions, the proposed algorithm is simple, complete and does not require any data to be applied, except for the treatment of the problem’s inputs. Essentially, it is a database builder, which allows researchers to easily build their own databases. (3) with the proposed algorithm, all IK solutions are obtained analytically and thus easily accessible, in contrast to works [25,26,27], where all these solutions are inaccessible and rely entirely on runtime.

The structure of this paper is as follows: the next section describes the structure of the considered continuum robot, namely CDCR, and presents briefly the kinematics models of its single section. Section 3 focuses on the development of the proposed algorithm and details the pseudo-codes of the first sub-algorithm. After that, the second sub-algorithm and its pseudo-codes related to the resolution of redundancy are presented in Sect. 4. Section 5 presents a series of numerical experiments on a class of continuum robots, namely cable-Driven Continuum Robot (CDCR). Finally, Sect. 6 outlines the main conclusions and future perspectives.

2 Kinematics of a Single Continuum Robot Section

This section provides a summary on the IK solution of a continuum robot with a single section. Commonly, this class of continuum robot consists of \(n\) sections; each section is actuated by three cables, namely CDCR, as depicted in Fig. 1.

Fig. 1
figure 1

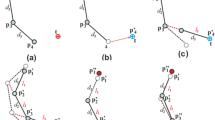
Multi-section continuum robot schematics. Panel a shows a class of a continuum robot with three sections, namely CDCR. Panel b shows a single section of CDCR with three driving cables. It consists of a number of units. Panel c shows a single unit modeled as a parallel 3UPS-1PU type robot. The Prismatic actuators for the kinematic chain UPS are considered active, whereas the central one of PU is considered as a passive

Full size image

From a structural point of view, the movable part of a single CDCR section is composed of a flexible backbone on which several equidistant spacer disks are rigidly mounted, each two disks form a unit. The whole section is actuated by three driving cables placed at 120 degree from each other. This arrangement of cables leads to performing two DoFs of bending and orientation motions.

In order to describe the robot’s configuration, references coordinate systems \({O}_{k}{X}_{k}{Y}_{k}{Z}_{k},\) where \(k=1, 2, \dots ,n\) is the section number, are attached at the end of each section. Additionally, one fixed base reference coordinate system \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\) (see Fig. 1a, b). Furthermore, we introduce local references coordinate systems \({o}_{j,k}{x}_{j,k}{y}_{j,k}{z}_{j,k}\), where \(j=1, 2, \dots ,m\) is the unit number, attached to the ends of each intermediate unit (see Fig. 1c).

As mentioned above, the objective is to calculate the actuator cable lengths as a function of \(\left\{{X}_{k},{Y}_{k},{Z}_{k}\right\}\), the Cartesian coordinates of the section’s endpoint \(k\), defined in its base reference coordinate system,\({O}_{k-1}{X}_{k-1}{Y}_{k-1}{Z}_{k-1}\), supposed fixed in this case. Various methods can be applied to accomplish this purpose, but most of them require quite complicated and mathematically lengthy steps [14, 30]. In this section, the IK of a single CDCR section is derived by assuming that each of its units is assimilated to a parallel 3UPS-1PU type robot [23, 26]. This model is a crucial part of the algorithm involved in this paper, which will be developed and explained through numerical experiments in the following sections.

For simplicity reasons, the bending shape of each section \(k\) is assumed to be a perfect arc of circle and variable in time. Thus, the length vector of the active prismatic actuator for each UPS \({(l}_{i,j,k}={A}_{i,j,k}{B}_{i,j,k})\), where \(i=1, 2, 3\) is the actuator cable number, which corresponds to the cable length variable vector in our case (see Fig. 1), it can be calculated using the Cartesian coordinates of the endpoint of each section \(k\) by the following relationship

$${l}_{i,j,k}={o}_{j-1,k}{o}_{j,k}+{\mathbf{R}}_{\mathbf{P}}\cdot {o}_{j,k}{A}_{i,j,k}-{o}_{j-1,k}{B}_{i,j,k},$$
(1)

where \({\mathbf{R}}_{\mathbf{P}}\) is the matrix defines the orientation of the moving platform relative to fixed platform unit \(\left(j,k\right)\), it can be expressed by.

$${\mathbf{R}}_{\mathbf{P}}=\mathbf{r}\mathbf{o}\mathbf{t}\left({x}_{j-1,k},{\Theta }_{j,k}\right)\cdot \mathbf{r}\mathbf{o}\mathbf{t}\left({y}_{j-1,k},{\Psi }_{j,k}\right),$$
(2)

where \(\mathbf{r}\mathbf{o}\mathbf{t}\) represents the rotation transformation, and \({\Theta }_{j,k}\) and \({\Psi }_{j,k}\) indicate pitch and roll angles, which correspond to the rotation around \({y}_{j,k}\)-axis and \({x}_{j,k}\)-axis, respectively, can be obtained by.

$${\Theta }_{j,k}={\mathrm{tan}}^{-1}\left(\frac{{-\mathrm{r}}_{31}}{{\mathrm{r}}_{11}}\right),$$
(3)
$${\Psi }_{j,k}={\mathrm{tan}}^{-1}\left(\frac{{-\mathrm{r}}_{23}}{{\mathrm{r}}_{22}}\right),$$
(4)

where \({\mathrm{r}}_{\mathfrak{m}\mathfrak{n}}\) is the element \((\mathfrak{m}, \mathfrak{n})\) of the matrix \(\mathbf{R}\) given by [14]

$$\begin{array}{c}\mathbf{R}=\mathbf{r}\mathbf{o}\mathbf{t}\left({z}_{j-1,k},{\varphi }_{k}\right)\cdot \mathbf{r}\mathbf{o}\mathbf{t}\left({y}_{j-1,k},{\theta }_{j,k}\right) \\ \cdot \mathbf{r}\mathbf{o}\mathbf{t}\left({z}_{j-1,k},{-\varphi }_{k}\right),\end{array}$$
(5)

where \({\theta }_{j,k}\) and \({\varphi }_{k}\) indicate bending and orientation angles. They can be obtained as a function of Cartesian coordinates as follows:

$${\theta }_{j,k}={\frac{2}{m}\mathrm{tan}}^{-1}\left(\frac{\sqrt{{X}_{k}^{2}+{Y}_{k}^{2}}}{{Z}_{k}}\right),$$
(6)
$${\varphi }_{k}={\mathrm{tan}}^{-1}\left(\frac{{Y}_{k}}{{X}_{k}}\right),$$
(7)

Finally, the total actuator cables’ length of the section \(k\) (i.e., the actuator space vector), which corresponds to the sum of vectors norm of Eq. (1), can be written as follows:

$${l}_{i,k}=\sum_{j=1}^{m}\sqrt{\left({{l}_{i,j,k}}^{T}\cdot {l}_{i,j,k}\right)},$$
(8)

For further use, the endpoint coordinates of each section relative to its base reference as a function of a bending and orientation angle are needed, which presents the forward kinematic model of a single continuum robot section. According to [14], this model can be expressed as

$$\left\{\begin{array}{c}{X}_{k}=\frac{{\ell}_{k}}{{\theta }_{k}}\left(1-\mathrm{cos}\left({\theta }_{k}\right)\right)\mathrm{cos}\left({ \varphi }_{k}\right),\\ {Y}_{k}=\frac{{\ell}_{k}}{{\theta }_{k}}\left(1-\mathrm{cos}\left({\theta }_{k}\right)\right)\mathrm{sin}\left({ \varphi }_{k}\right),\\ {Z}_{k}=\frac{{\ell}_{k}}{{\theta }_{k}}\mathrm{sin}\left({\theta }_{k}\right) , \end{array}\right.$$
(9)

in which \({\theta }_{k}=\sum_{j=1}^{n}\left({\theta }_{j,k}\right)\), and \({\ell}_{k}\) is the length of the continuum robot section.

3 IKs of Continuum Robots with All-Inclusive IK Solutions

As mentioned before, for a given operational configuration of the robot’s EP, there is an infinite number of IK solutions that the robot can reach and this will generally raise two problems: obtaining all-inclusive IK solutions for a given robot’s EP pose and the redundancy resolution (i.e., selecting an appropriate IK solution that satisfies a specific criterion for the robot, such as minimum variation of the actuator space vector, traveled distance, obstacle avoidance and so forth). Certainly, from a computational time point of view, the ideal is to use the analytical methods since they provide all IK solutions for a given robot’s EP pose. However, these methods generally remain unable to solve the IK problem of this class of redundant robots, which is undoubtedly a non-trivial problem to be solved.

As for the numerical methods, although they work independently of the robot’s redundancy, they still suffer from several shortcomings, such as high computational costs, running times, existence of local minima and instabilities close to singularities [11, 28, 29]. Moreover, redundancy resolution criteria for these methods are generally applied to derive a specific IK solution. However, to figure out this commonly encountered problem, a reliable algorithm has been developed, in this section, to provide all-inclusive IK solutions, for a given robot’s EP pose.

Since the proposed algorithm is strongly based on an optimization method, many optimization algorithms can be used, such as Genetic Algorithm (GA) [26], Particle Swarm Optimization (PSO) [31], Simulated Annealing (SA) [32], and so on. Although these algorithms have been successfully for solving a variety of real-world problems, each of them has some limitations. However, since PSO method is superior in terms of model complexity, accuracy, iteration and program simplicity in finding the optimal solution compared to other algorithms [33], it will be used to pick up the first randomly IK solution for the proposed algorithm.

In the following, we will introduce the preliminaries used in developing the proposed algorithm, namely PSO method and the cost function, boundary conditions and the physical limitations as well as the proposed algorithm itself.

3.1 PSO Method and the Cost Function

Standard PSO method is a population-based search algorithm, developed by Kennedy and Eberhart in 1995 [31]. This method is inspired by the social behavior of swarming animals such as flocks of birds, schools of fish, and even human social behavior. Generally, PSO method is quite simple and has a fast convergence with few parameters tuned compared to other optimization algorithms. However, it has not been shown to be effective in some challenging problems, especially the type of problems where the algorithm has to be applied in small increments in order to keep the algorithm's stability. Therefore, to increase the PSO performance, Shi and Eberhart [34] added another factor called the inertia weight concept, which will be used in this work.

In the PSO algorithm, the potential solution to the optimization problem is called a particle and the population of solutions is called a swarm. Each particle, is characterized by a position vector and a velocity vector . The quality of its position is determined by the value of the appropriate cost function. The particle memorizes the best reached position so far and it is denoted by . The best position found by all the particles in the swarm is denoted by \({gbest}_{\mathcal{D}}\). In the search space \(\mathcal{D}\), the velocities and positions of particles keep changing according to the following equations:

(10)
(11)

where and is the current position and velocity of the particle, respectively; \(\xi\) is the iteration number; \(\mathcal{D}\) is the dimension of the particle vector (here, \(\mathcal{D}=3\), i.e., along \(X-, Y-\) and \(Z\)-axis); \(\omega\) is the inertia weight rate; \({c}_{1}\) and \({c}_{2}\) are two positive constants, \({\lambda }_{1}\) and \({\lambda }_{2}\) are two random numbers; and \({gbest}_{\mathcal{D}}\) represent personal best and swarm best position, respectively.

figure i

Regardless of the time ‘s implementation issue, a common barrier to most optimization algorithms is the early convergence of solutions to local minima, which makes the algorithms inefficient in practical applications. However, to avoid the algorithm being trapped in local optima, the re-generating of population technique has been added to PSO method [35, 36], see algorithm 1.

As stated in the paper's title, the first goal is to provide all-inclusive IK solutions of continuum robot. Since the proposed algorithm is based on the PSO method, the appropriate cost function which enables the goal to be achieved can be expressed as.

$${C}_{f}=\Vert {\mathbb{X}}_{desired}-{\mathbb{X}}_{generated}\Vert ,$$
(12)

where \({\mathbb{X}}_{desired}\) and \({\mathbb{X}}_{generated}\) are the desired and generated position vector of the endpoint of the robot. The generated position vector is given by the fourth column of the homogeneous matrix defining the FKM of the continuum robot (for detailed derivation of the FKM refers to ref [37].).

3.2 Parameters Selection of PSO Method

Naturally, the performance and efficiency of the PSO method strongly depends on the choice of its parameters, namely constant parameters \({c}_{1}\) and \({c}_{2}\), inertia weight \(\omega\), swarm size, number of iterations. Therefore, these parameters should be carefully determined before starting the optimization process. As the parameters \({c}_{1}\) and \({c}_{2}\) give the tendency of the swarm to converge to local or global best solution, the two parameters are fixed after performing a pre-test of the algorithm by increasing their values with a step of 0.1 in a range [0.1, 3.0] and the fitness value was calculated. As a result, it was found that the value 1.2 is the best for both parameters. For the determination of inertial weight parameter, the method developed in [38] was used for reducing the inertia weight linearly from 0.9 to 0.4 throughout the implementation in order to explore the research space in the early stages and then exploit the optimum solution at the later ones. On the other hand, since the size of the swarm and the number of iterations are related to the complexity of the problem, that is, larger ratios obviously mean better performance with the selected swarm and the number of iterations and therefore, following multiple tests of the algorithm, and it was found that the values 15 and 45 are the lowest values of the convergence of the algorithm in a reasonable computation time.

3.3 Boundary Conditions and PHYSICAL Limitations

The Boundary conditions satisfying the achievement of the central backbone curve to the reference frame’s origin must be introduced to correlate the reference frame of the central backbone and the base’s reference. Furthermore, another required condition is the association of the desired point, which is located in the prescribed trajectory and the previously mentioned frames. Explicitly, a relationship between the frame of the central backbone, the base, and the prescribed trajectory’s specific position (point) that allows the robot to fulfill the task must be considered. Mathematically, these conditions can be expressed as follows:

$${\mathbb{X}}_{0}={\mathbb{X}}_{base}, { {\mathbb{X}}}_{n}={\mathbb{X}}_{desired},$$
(13)

where \({\mathbb{X}}_{base}\) and \({\mathbb{X}}_{desired}\) are the position of origin of the reference frame associated with the fixed base and the end reference frame of the robot, respectively.

Limitations such as those related to actuator variables, which are typically presented in rigid manipulators, can be considered to confirm the robot’s proper operation, especially in the case of a continuum robot with a large number of sections that may overlap. These limitations can be expressed as.

$${l}_{k}^{min}\le {l}_{i,k}\le {l}_{k}^{max},$$
(14)

3.4 Proposed Algorithm Step-By-Step

From a computational time point of view, the analytical approaches have been proved to be the ideal way to solve the inverse kinematics of continuum robots. Methodically, it is extremely difficult to solve their inverse kinematics, especially for those who have more than two sections. Solving the inverse kinematics of continuum robots generally leads to an infinite number of inverse kinematics solutions. Therefore, the alternative way is the development and the improvement of numerical and optimization approaches. Thus, this sub-section is dedicated to establishing and developing a reliably efficient algorithm capable of providing with all-inclusive IKs solutions of any multi-section continuum robots and; then, its redundancy can be easily resolved. The problem of the infinite number of IK solutions is transformed into a finite number by considering a set of the reachable positions of the EP poses of the first \((n-1)\) sections, which are defined and created one-by-one from the first section to the \((n-1)\)-thsection. It should be noted, here, that any numerically selected solution results in small errors.

Figure 2 summarizes the proposed algorithm approach which can be divided into two sub-algorithms with \(\left(\left(n-1\right)+1\right)\) steps. Sub-algorithm 1, with \(\left(n-1\right)\) steps, focuses on defining and creating the reachable positions of the EP poses of the first \(\left(n-1\right)\). In this sub-algorithm, the robot redundancy is decreased one-by-one by deleting the previous section. While sub-algorithm 2, with one step, is dedicated to the resolution of the redundancy, which will be presented in the next section. This sub-algorithm works with the outputs of sub-algorithm 1 and the robot EP pose.

Fig. 2
figure 2

Block diagram of algorithm providing with all-inclusive inverse kinematics’ solutions and the resolution of its redundancy

Full size image

However, it is known that the difficulty of deriving the inverse kinematic for any continuum robot increases as the number of its sections increases. So, in this paper, the proposed algorithm is applied to a three section continuum robot; hence, sub-algorithm 1 will have two steps. Therefore, according to block diagram depicted in Fig. 2, the first step gives the reachable EP poses of the first section, and the second one for determining the reachable EP poses of the second section. The procedure of each step can be achieved, respectively, by the following pseudo-code.

figure j

To summarize, sub-algorithm 1 collects and forms a tree of the reachable EP poses of the first \((n-1)\) sections for each robot’s EP pose, while sub-algorithm 2 selects the optimal posture of the robot based on a specific criterion from among the redundant varieties provided by sub-algorithm 1.

4 Resolution of Redundancy

In fact, any selected IK solution results in Cartesian and orientation errors; thus, the most accurate solution criterion is used in redundancy resolution process. This solution can be reliably used in various applications that do not require very high accuracy. In this context, to obtain the optimal posture of the robot in which its endpoint reaches the desired trajectory, the intermediate endpoints of the first \((n-1)\) sections can be selected among the redundant varieties, provided by sub-algorithm 1, according to a specific criterion, such as.

  • Minimum variation of the actuator space vector: this criterion can be expressed as

    $$l=\underset{i,k}{\mathrm{min}}\Vert {l}_{sum}-{l}_{sum}^{opt}\Vert ,$$
    (15)

    where \({l}_{sum}\) and \({l}_{sum}^{opt}\) are the sum of current and last continuum robot actuator space, respectively, i.e., the sum of cables length of all sections of the robot.

  • Minimum variation of traveled distances of the endpoints of the first \((n-1)\) sections: this criterion can be expressed in the general form as

    $$dist=\underset{k}{\mathrm{min}}\sum_{\mathrm{k}=1}^{\mathrm{n}}\Vert {P}_{k}-{P}_{k}^{opt}\Vert ,$$
    (16)

where \({P}_{k}\) and \({P}_{k}^{opt}\) are the current and last position of endpoint of the section \(k\), respectively.

To thoroughly describe the application of the two criteria that serve to generate the optimal posture of the robot for a given EP pose, the following pseudo-codes are presented:

figure k
figure l

4.1 Obstacle Avoidance

When the robot is operating in a restricted environment, the inverse kinematic involves generating an optimal posture allowing the robot to avoid the obstacles and reach the target. The obstacle avoidance strategy can be performed through two steps. First, a set of appropriate EP poses of the first \((n-1)\) sections, that the robot does not collide with the obstacles, is selected from the redundancy varieties provided by sub-algorithm 1.

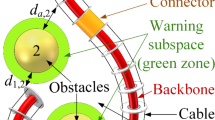
A simple manner to achieve the obstacle avoidance is to place some virtual spheres such that their gravity center is placed on the backbone curve of the robot (see Fig. 3), and then; if the distance between any obstacle and these spheres are greater than a given value compared to the sum of the radii of the obstacle and that of the spheres, the IK solution is retained, otherwise the solution is rejected. The obstacle avoidance strategy can be written in the general form as.

Fig. 3
figure 3

Obstacle avoidance strategy

Full size image
$${d}_{j,k}>{r}_{obs}+{r}_{j,k},$$
(17)

Then, the optimal posture that allows the robot to avoid the obstacles and achieves the specified target can be selected among the resulting set of EP poses of the first \((n-1)\) sections in which Eq. 16 will be satisfied using a certain criterion.

5 Numerical Experiments

The aim of this research work is to find all-inclusive IK solutions that allow the robot to track a given EP pose in its workspace (sub-algorithm 1), and then to solve the redundancy problem according to a given criterion (sub-algorithm 2).

The proposed algorithm that is dedicated to a CDCR with three sections begins with finding out the dimension of the problem at step 1 in sub-algorithm 1 which is \(\left(nb\_{P}_{1} \times 3\right)\), where \(nb\_{P}_{1}\) is the number of EP poses of Sect. 1. While at step 2, the dimension of the problem is \(\left(nb\_{P}_{2} \times 3\right)\) for each point of \(\left[MAT\_{P}_{1}\right]\), where \(\left[MAT\_{P}_{1}\right]\) is the matrix of all Sect. 1’s reachable EP poses that verify the inequality \(a{X}_{1}+b{Y}_{1}+c{Z}_{1}+d\ge 0\), where \({X}_{1},{ Y}_{1}\) and \({Z}_{1}\) are the Cartesian coordinates of the specific IK solution denoted \({P}_{1s}\). On the other hand, the reachable EP poses of Sect. 2, denoted \(\left[MAT\_{P}_{2}\right]\), are all points that verify the equality \(a{X}_{2}+b{Y}_{2}+c{Z}_{2}+d=0\), for each point of \(\left[MAT\_{P}_{1}\right]\), where \({X}_{2}, {Y}_{2}\) and \({Z}_{2}\) are the Cartesian coordinates of the specific point denoted \({P}_{2}\) (see, step 2 in sub-algorithm 1).

Regarding PSO method, the population is the set of possible reachable EP poses and the coordinates of the particle are the variables of the optimization problem, which represent in our case the specific accessible EP poses, denoted \({P}_{1s}\left({X}_{1},{Y}_{1},{Z}_{1}\right)\) and \({P}_{2}\left({X}_{2},{Y}_{2},{Z}_{2}\right)\) in sub-algorithm 1. Concerning the redundancy problem (i.e., sub-algorithm 2), the optimal posture of the robot, denoted \(\left[MAT\_{P}_{1}^{opt}\right]\) and \(\left[MAT\_{P}_{2}^{opt}\right]\) are selected according to a given criterion among redundancy varieties.

The proposed algorithm is tested through three numerical experiments utilizing a CDCR with three sections (see Fig. 1). The first example is considered to illustrate the block diagram depicted in Fig. 3 that showing the reachable EP poses of the two sections for a given robot’s EP pose. The second numerical experiment has been carried out in order to track a line-shaped trajectory in a free environment. The last is performed to reach a desired goal while avoiding a static obstacle in the robot's workspace, in which the collision and free-collision’s areas are illustrated. To select the optimal IK solution, in all examples, two criteria have been applied, namely minimum variation of the actuator space vector and traveled distance, and after that, their results have been compared. The numerical experiments have been performed in MATLAB software on a computer with the following specifications: Intel(R) Xeon(R) CPU E5-1620 0 @ 3.60 GHz, 16 Go of RAM, 64-bit operating system. The geometric parameters of CDCR are given in Table 1.

Table 1 Parameters of CDCR for the numerical experiments
Full size table

5.1 Illustration of the Block Diagram of the Proposed Algorithm: A Numerical Example

The purpose of this numerical example is to thoroughly illustrate the block diagram as it is shown in Fig. 3. To emphasize, the three-section continuum robot starts from its initial configuration\(\left[0 ; 0 ; 750\right]\), see Fig. 4a, to reach the desired goal located at\(\left[240 ; 150 ; 570\right]\). In fact, there is an infinite possible configuration. However, for simplicity reasons, three EP poses are exclusively taken for the first section, denoted\(\left[MAT\_{P}_{1}\right]\); and for each point of\(\left[MAT\_{P}_{1}\right]\), four EP poses are chosen for the second section, denoted\(\left[MAT\_{P}_{2,q}\right]\), in which the reachable EP poses \(\left[MAT\_{P}_{2,q}\right],\) with \(q=1, 2, 3,\) forms the matrix of all reachable EP poses of the second section, denoted\(\left[MAT\_{P}_{2}\right]\), see Fig. 4b. However, to select an optimal configuration, namely to pick up the most appropriate IK solution, among the considered varieties of solutions, criteria of minimum variation of the actuator space and traveled distance are granted. The obtained optimal achievable EP poses of Sects. 1 and 2 are given in Table 2 and which are displayed, respectively, in bold-black line and dashed-line in Fig. 4b.

Fig. 4
figure 4

Numerical example in the form of a tree illustrating the block diagram of the proposed algorithm

Full size image
Table 2 Optimal reachable EP poses of Sect. 1 and 2 satisfying both criteria to achieve the desired goal
Full size table

5.2 IKs for Tracking a Trajectory in Free Environment

This simulation experiment attempts at first to demonstrate the existence of infinite configurations of the robot, i.e., all possible IK solutions, from any starting pose to any destination pose on the trajectory. From a realistic view, it is not possible to reach all IK solutions; however, through the proposed algorithm, the problem can be reduced to a finite number of IK solutions by considering the sets of reachable EP poses of the two first sections. Before starting, it is obvious that when the robot is in a straight line, there is a unique configuration of the robot, which represents generally its initial configuration, where \({P}_{1}\) and \({P}_{2}\) represent the EP poses of the two first sections in this case, see Fig. 5a. Figure 5.b shows such a destination pose of the robot in which the sets of reachable EP poses of the two first sections are shown (red points). Besides, three random configurations of the robot, presented by its backbone, are depicted.

Fig. 5
figure 5

Representation of reachable EP poses of two first sections for such robot’s EP pose. Panel a shows the initial configuration of the CDCR presented by its central backbones. The green and cyan set points present the theoretical workspaces of the two first sections of the robot, respectively. Panel b shows the reachable EP poses of two first sections presented by the sets red points, i.e., set of \({P}_{1}\) and \({P}_{2}\), for such robot’s EP pose. Panel c shows three random configurations of the robot reached such pose on the line-shaped trajectory

Full size image

To illustrate more about Fig. 5b, let \(\left[MAT\_{P}_{1}\right]=4621\) EP poses for the first section and \(\left[MAT\_{P}_{2,q}\right]=300\) EP poses for the second section for each point of \(\left[MAT\_{P}_{1}\right]\). The dimension of the problem becomes \(4621\times 300\) possible configurations of the robot for such pose on the trajectory, which can be explained graphically in Fig. 5c.

To highlight the redundancy resolution aspect along the desired trajectory, two cases have been considered for a line-shaped trajectory \({[40t, 25t, 750- 30t]}^{T}(\mathrm{mm})\). Figure 6a and b illustrates the robot’s EP poses and its backbone deflection for tracking a line-shaped trajectory with two criteria, namely minimum variation of the actuator space vector and traveled distance, respectively.

Fig. 6
figure 6

Inverse position kinematics: a and b the robot’s EP pose tracks a line-shaped trajectory with minimum variation of the actuator space vector and the traveled distance of two first sections’ EP poses, respectively

Full size image

Figure 7 presents the variation of cable lengths (actuator space vectors) required to track the desired line-shaped trajectory with two considered criteria. From this Figure, it can be seen that the two criteria give the similar solution in finding IK solutions. Of course, the two solutions are very similar because practically and according to the given trajectory, it is the unique and optimal solution that can be obtained; and this indicates the computational efficiency of the proposed algorithm in finding IK solutions and redundancy resolution. However, the slight difference apparent in the lengths variation, especially in the second and third sections, is due to the small number of EP poses considered for the second section.

Fig. 7
figure 7

The required actuator space vectors to track the line-shaped trajectory for two criteria

Full size image

5.3 IKs for Reaching a Goal in Presence of Obstacle

In this numerical experiment, the proposed algorithm is evaluated against avoiding obstacles which can be encountered in the robot’s workspace. According to this numerical experiment, areas of collision and free-collision (obstacle avoidance) of the robot can be identified. Let us consider a static obstacle that is located at\({\mathbb{X}}_{obs}=\left[60 ; 70 ; 350\right] (\mathrm{mm})\), within the robot’s workspace (see Fig. 8), from the fixed reference frame and then, the robot starts from its initial state \(\left[0 ; 0 ; 750\right] (\mathrm{mm})\) to reach the desired goal\({\mathbb{X}}_{desired}=\left[240 ; 150 ; 570\right] (\mathrm{mm})\). Interestingly, to ensure that obstacles along the trajectory are avoided, the path must be subdivided into a large number of points. To achieve this purpose, the obstacle avoidance is provided at the point of destination. For visual representation, the red and green points, depicted in Fig. 8, present the collision and free-collision’s areas, respectively, of the robot with obstacle.

Fig. 8
figure 8

a and b Collision and free-collision’s areas for the robot (Red and green points present collision and free-collision’s areas, respectively)

Full size image

To avoid that obstacle, an additional constraint has been introduced to the optimization problem aiming at retaining the Euclidean distance between the obstacle's position and some points on the robot's backbone beyond a safety distance equal to 40 mm. However, to select the optimal configuration through which the robot does not collide with the obstacle and properly tracks the desired trajectory, the previously criteria, namely minimum variation of the actuator space vector and traveled distance are accorded. The reachable EP poses of the two first sections of the robot that satisfy the two aforementioned criteria are presented in Table 3. Besides, the actuator space vectors required to reach the desired goal for both criteria, namely minimum variation of the actuator space vector and traveled distance are given in Table 4.

Table 3 Reachable EP poses of Sects. 1 and 2 satisfying both criteria to reach the desired goal
Full size table
Table 4 Actuator space vectors required to reach the desired goal for both criteria
Full size table

6 Summary

Three numerical experiments are conducted on the IK problem and redundancy resolution for a class of continuum robots, namely Cable-Driven Continuum Robot (CDCR), to test and validate the proposed algorithm. The aim of the first example is to provide with an explicit illustration of the block diagram as it is shown in Fig. 3. The second one is dedicated to figuring out the redundant IK solutions and the redundancy resolution for tracking a trajectory without obstacle avoidance, while third one is considered for reaching a desired goal in the presence of obstacle. According to the achieved results, the proposed algorithm achieves good performance in terms of computational accuracy and efficiency in obtaining global IK solutions and redundancy resolution criteria, unlike the previously proposed approaches.

Regardless of the runtime, the main advantages of the proposed algorithm can be summarized as follows: (1) easy parameterization and simple build, (2) does not require any data to apply it except the treatment of the problem’s inputs, (3) no links with the degree of redundancy of the robot and its characteristics, (4) a database builder, and (5) it can be applied to any continuum robot regardless of its number of sections.

Comparatively, the so-called continuum robots are composed of hard or soft structure, which makes their characteristics and properties different, such as sizes, material, continuous/discontinuous shape, etc. On the other hand, these robots can be controlled by different inputs including pneumatic actuation, hybrid actuation (pneumatic + electric), cable/tendon actuation, and so on. Based on the aforementioned differences between the existing continuum robots’ proprieties, a comprehensive comparison cannot be fully considered by merely considering the results obtained in this work. Table 5 lists some contributions dealing with IK problem and redundancy resolution of continuum robots. Comparatively speaking, an overview of the previously developed continuum robot’s IK solutions is given in Table 5, which proved that the proposed algorithm is the best and can be used as an exhaustive method to solve the IK problem and its redundancy for continuum robots (despite the differences in characteristics and properties of the studied robots), and thus, it can be considered as an alternative and a sovereign remedy to compensate for the shortcoming experienced by the previously proposed algorithms.

Table 5 Some contributions dealing with IK problem and redundancy resolution of continuum robots
Full size table

7 Conclusion

In this paper, a novel reliable algorithm is proposed. It accurately provides with all-inclusive inverse kinematics’ solutions of continuum robots as well as the resolution of redundancy. Certainly, there are an infinite number of configurations through which the continuum robot’s EP pose can attain a specific pose within its workspace, in other words, an endless number of IK solutions are inevitably encountered for a given pose in the robot’s workspace. Through the proposed algorithm, the infinite number of the IK solutions can be reduced to a finite number by considering sets of reachable EP poses of the first \((n-1)\) sections. It consists of a two-sub-algorithm: the first sub-algorithm collects and forms a tree of the reachable EP poses of the first \((n-1)\) sections for each robot's EP pose. In this way, the robot’s sets EP poses are selected and built up one-by-one starting from the first section to \(\left(n-1\right)\)th section. The second sub-algorithm selects the optimal posture of the robot, among the redundant varieties solutions provided by the first sub-algorithm’s outputs, according to a specific criterion. However, since the proposed algorithm is strongly related to an optimization method, the Particle Swarm Optimization (PSO) method is adopted, to pick up the first specific IK solution, due to its particularly considerable advantages compared to other algorithms, particular: its implementation simplicity and its fast convergence that provides a low computation time.

To test and validate the efficiency of the proposed algorithm, three numerical experiments are carried out on a cable-Driven Continuum Robot (CDCR). The first example is explicitly provided to illustrate the functionality of the two sub-algorithms. While the second and third numerical experiments are performed for tracking a trajectory in a free environment as well as to reach a desired goal in the presence of obstacle within the robot’s workspace. In all simulations, IK, multiple IK solutions and redundancy resolution are thoroughly discussed. The obtained results showed that the proposed algorithm is computationally accurate and efficient in obtaining all-inclusive IK solutions and redundancy resolution of continuum robots.

In comparison with existing works about IK, that directly address the problem in this paper, and despite the differences in the above-mentioned properties and characteristics, the proposed algorithm can be considered as a comprehensive method for perfectly addressing the IK problem and its redundancy for continuum robots. Furthermore, the proposed algorithm can be applied to any kind of continuum robot regardless of the number of sections, which makes it a sovereign remedy for the IK problem and redundancy of continuum robots. One of the many advantages regarding the developed algorithm in this paper is that it can be adopted by researchers to directly build their database without using the forward kinematic which significantly helps to narrow down the unwanted singularities triggered by the forward kinematic during the build-up of the needed database, for instance, neural networks and growing gas techniques strongly depend on the database, thus a well-collected data helps to achieve accurate results.

In the future, we will address the issue of mobile continuum manipulators.