1 Introduction

Multisegment continuum manipulators, which consist of a series of flexible modules, possess theoretically infinite degrees of freedom and are capable of large structural deformations with high curvatures [1, 2]. Due to their inherent compliance and dexterity, multisegment continuum manipulators have the ability to bend and twist in multiple directions and can deform their bodies in a continuous manner to adapt to unstructured environments [3, 4]. These attractive characteristics make them exhibit broad application prospects for complex tasks in confined spaces where traditional rigid-link manipulators cannot access [5, 6], such as minimally invasive surgeries [7], on-orbit maintenance [8], and rescue operations [9]. Inspired by biological appendages, various cable-driven continuum manipulators [10,11,12] have been developed to perform compliant operations.

Although the great progress has been made in the design and manufacture of cable-driven continuum manipulators, there remains a lack of exploration on motion planning and control methods of these manipulators [13, 14], which hinders continuum manipulators from achieving their full potential in confined spaces. To further develop motion planning and control methods of continuum manipulators, it is necessary to first derive their dynamic models [1, 15]. Cable-driven continuum manipulators are primarily subject to bending and torsional deformations. By dividing them into a series of large deformation beam elements, a discrete dynamic modeling approach was proposed for continuum manipulators based on the Lagrangian formulation [11, 16]. The resulting dynamic models had the ability to accurately calculate elastic deformations and dynamic responses. However, the inherent compliance and dexterity of continuum manipulators lead to dynamic models characterized by strong nonlinearity and high dimensionality in both state and control spaces, significantly complicating the process of motion planning for these manipulators [14, 17].

Several effective motion planning methods have been developed for continuum manipulators in open spaces without obstacles [18, 19]. However, to generate collision-free paths for continuum manipulators in confined spaces, obstacle-avoidance constraints need to be introduced, which makes the motion planning problem more complex [20, 21]. Ouyang et al. [22] proposed a shape correspondence algorithm to regulate the manipulator configuration while successfully avoiding the collisions with obstacles. Subsequently, constrained motion planning methods [23, 24] were developed to generate a collision-free path for tip trajectory tracking. Despite achieving obstacle-avoidance motion planning for continuum manipulators, these studies solely focused on static obstacle avoidance. To enable continuum manipulators to perform tasks in dynamic environments, it is crucial to implement motion planning for dynamic obstacle avoidance. However, dynamic obstacles may collide multiple times with the continuum manipulator. The motion path of the manipulator needs to be adjusted in response to the movement of dynamic obstacles, which is more challenging than static obstacle avoidance. Hence, further research is still required on obstacle-avoidance motion planning for continuum manipulators in dynamic environments [14, 24].

Kinodynamic motion planning [25] aims to find an optimal path for a system subject to both kinematic and dynamic constraints, such as obstacle-avoidance conditions, dynamic equations, and input limitations. Based on this planning method, Allen and Pavone [26] developed an obstacle-avoidance framework utilizing an offline-online computation paradigm, and successfully applied it to a quadrotor unmanned aerial vehicle navigating in an indoor space with dynamic obstacles. Sharma et al. [27] proposed a solution to the motion planning and control problem for a team of carlike mobile robots traversing in dynamic environments with swarm avoidance. As can be seen from these application cases, the kinodynamic planning method exhibits a great performance in searching for optimal paths under complex constraints, and is a potential solution to motion planning for continuum manipulators in dynamic environments.

Based on the kinodynamic motion planning method, Li et al. [28] developed an improved algorithm for a tensegrity manipulator to generate a collision-free optimal path. However, for large overall motion planning, additional virtual targets had to be introduced to prevent this algorithm from diverging, which complicated the process of motion planning. It is still a challenge to achieve large overall motion planning for continuum manipulators without introducing additional virtual targets. Additionally, the obstacle-avoidance motion planning problem is essentially a nonlinear optimization problem (NOP), which can be addressed by intelligent optimization algorithms [29]. The particle swarm optimization (PSO) algorithm is frequently employed to solve this NOP because of its excellent cooperative search capability [30]. Using the PSO algorithm, Ekrem and Aksoy [31] effectively planned a collision-free trajectory for a six-degree-of-freedom robotic manipulator. However, the dynamic model of the continuum manipulator exhibits stronger nonlinearity and higher dimensionality in both state and control spaces. To achieve motion planning for continuum manipulators, a substantial number of particles need to be randomly initialized within the search space, which leads to a significant increase in computational complexity. Therefore, based on the above analyses, two critical issues must be addressed to effectively achieve obstacle-avoidance motion planning for continuum manipulators. The first issue is to develop an obstacle-avoidance planning algorithm that has excellent stability for large overall motion. The second issue is to enhance the search ability of the optimization algorithm, enabling it to solve high-dimensional NOPs with lower computational costs.

The objective of this paper is to develop a kinodynamic motion planning method for cable-driven multisegment continuum manipulators in confined spaces. Based on the instantaneous optimal control theory and the dynamic model, the kinodynamic motion planning problem for the continuum manipulator is first transformed into a NOP that minimizes the cost function in the presence of the obstacle-avoidance constraints and input limitation constraints. The workspace of the continuum manipulator is then divided into a safe subspace and a warning subspace. In the safe subspace, where the continuum manipulator stays far away from the obstacles, obstacle-avoidance constraints are automatically satisfied and do not need to consider. By introducing nonlinear complementarity function [32], the transformed NOP for the motion planning problem in the safe subspace is further reformulated as a mixed complementarity problem (MiCP), expressed as a set of nonlinear algebraic equations. This approach can significantly reduce computational costs in comparison with directly solving a NOP. On the other hand, the kinodynamic motion planning problem in the warning subspace must consider obstacle-avoidance constraints, and it exhibits strong nonlinearity and high dimensionality in both state and control spaces, resulting in a significant increase in computational complexity. To overcome this problem, an improved PSO algorithm with great search performance is developed by introducing normal distribution and adaptive parameters. This algorithm has the ability solve the strongly nonlinear kinodynamic motion planning problem in the warning subspace, while maintaining lower computational costs compared to the traditional PSO algorithm [31]. Finally, a combined kinodynamic motion planning method is proposed for continuum manipulators in both the safe and warning subspaces. The main contributions of this paper are summarized as follows:

  1. (1)

    A unified path optimization framework is proposed for the kinodynamic motion planning problem of multisegment continuum manipulators in confined space. This proposed framework has great stability for large overall motion planning, effectively addressing the highly nonlinear motion planning problem of continuum manipulators with both obstacle-avoidance constraints and input limitation constraints.

  2. (2)

    The motion planning problem in the safe subspace is transformed into a MiCP to solve, enabling it to rapidly generate paths while strictly satisfying system constraints. Additionally, an improved PSO algorithm with great search performance is developed by introducing normal distribution. This algorithm has the ability to solve the strongly nonlinear kinodynamic motion planning problem in the warning subspace, while maintaining lower computational costs.

The rest of this paper is organized as follows. Section 2 formulates the dynamic model of cable-driven multisegment continuum manipulators and derives obstacle-avoidance kinematic constraints. In Sect. 3, a combined kinodynamic motion planning method is developed for continuum manipulators in confined spaces in detail. Section 4 presents the numerical simulations for obstacle-avoidance motion planning of cable-driven multisegment continuum manipulators to illustrate the effectiveness and advantages of the proposed method. Finally, conclusions drawn from this investigation are provided in Sect. 5.

2 Dynamic model and kinematic constraints of multisegment continuum manipulators

As shown in Fig. 1, a cable-driven multisegment continuum manipulator consists of flexible backbones, disks with routing holes, driving cables, and connectors between two adjacent segments [11]. Each segment of the continuum manipulator can be independently actuated by cables. To accurately achieve kinodynamic motion planning for a continuum manipulator in confined space with obstacles, the dynamic model of a continuum manipulator needs to be derived first. The multisegment continuum manipulator is a multibody dynamic system. The disks and connectors on the manipulator segments are equivalent to rigid bodies. The dynamics of flexible backbones are derived based on the Euler–Bernoulli beam theory. To avoid the singularity problem in the large overall motion, the quaternion representation is adopted to describe the orientation of continuum manipulators.

Fig. 1
figure 1

A multisegment continuum manipulator and obstacles

Full size image

Based on the above modeling techniques and the Lagrangian formulation, the dynamic model of a cable-driven multisegment continuum manipulator has been derived in detail in our previous work [11] and could be formulated as a set of differential–algebraic equations:

$$ \left\{ \begin{gathered} {\mathbf{M}}\left( {\mathbf{q}} \right){{\ddot{\mathbf{q}}}} + {\mathbf{V}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}}} \right){\dot{\mathbf{q}}} + \frac{{\partial E\left( {\mathbf{q}} \right)}}{{\partial {\mathbf{q}}}} + \left[ {\frac{{\partial {{\varvec{\uppsi}}}\left( {\mathbf{q}} \right)}}{{\partial {\mathbf{q}}}}} \right]^{T} {{\varvec{\uplambda}}} = {\mathbf{Gu}} \hfill \\ {{\varvec{\uppsi}}}\left( {\mathbf{q}} \right) = {\mathbf{0}} \hfill \\ \end{gathered} \right. $$
(1)

where \({\mathbf{q}} \in {\mathbb{R}}^{n}\), \({\dot{\mathbf{q}}} \in {\mathbb{R}}^{n}\) and \({{\ddot{\mathbf{q}}}} \in {\mathbb{R}}^{n}\) denote the generalized coordinate, velocity and acceleration of the continuum manipulator, respectively. \({\mathbf{M}} \in {\mathbb{R}}^{n \times n}\) is the system mass matrix; \({\mathbf{V}} \in {\mathbb{R}}^{n \times n}\) includes the centrifugal-Coriolis and damping matrices of the system; \(E \in {\mathbb{R}}\) is the elastic potential energy of the system; \({{\varvec{\uppsi}}} \in {\mathbb{R}}^{m}\) is the vector of the system constraints; \({{\varvec{\uplambda}}} \in {\mathbb{R}}^{m}\) is the vector of Lagrange multipliers; \({\mathbf{G}} \in {\mathbb{R}}^{n \times s}\) is the input matrix for the cable actuation force \({\mathbf{u}} \in {\mathbb{R}}^{s}\). Here, n, m, and s are the number of generalized coordinates, system constraints, and actuation forces, respectively.

The proposed dynamic model provides a sound basis for kinodynamic motion planning of continuum manipulators. In addition, to avoid the collision with obstacles, the motion of the continuum manipulator needs to satisfy the obstacle-avoidance constraint. As shown in Fig. 1, the large three-dimensional deformation results in multiple potential collision points between the manipulator and the obstacles, which increases the difficulty of collision detection. In the kinodynamic motion planning process, the obstacle-avoidance condition between the ith potential collision point on the manipulator and the jth obstacle needs to be satisfied as follows:

$$ d_{i,j} \ge d_{s} ,\;\;\left( {i = 1,2, \ldots ,a;\;j = 1,2, \ldots ,b} \right) $$
(2)

where a represents the number of the potential collision points on the manipulator for an obstacle, and b represents the number of obstacles. Here, \(d_{s} \in {\mathbb{R}}\) is the critical safety distance. \(d_{i,j} \in {\mathbb{R}}\) denotes the distance between the ith potential collision point on the manipulator and the jth obstacle, and can be calculated by

$$ d_{i,j} = \sqrt {\left( {{\mathbf{r}}_{i} - {\overline{\mathbf{r}}}_{j} } \right)^{T} \left( {{\mathbf{r}}_{i} - {\overline{\mathbf{r}}}_{j} } \right)} $$
(3)

where \({\mathbf{r}}_{i} \in {\mathbb{R}}^{3}\) and \({\overline{\mathbf{r}}}_{j} \in {\mathbb{R}}^{3}\) are the position coordinates of the ith potential collision point and the jth obstacle, respectively. For a dynamic obstacle, the position coordinate \({\overline{\mathbf{r}}}_{j} \left( t \right)\) is time-varying. To successfully achieve obstacle avoidance, the kinematic constraint between the continuum manipulator and the obstacles needs to be satisfied as follows:

$$ {\mathbf{c}}\left( {\mathbf{q}} \right) = {\mathbf{d}}_{s} - {\mathbf{d}} \le {\mathbf{0}} $$
(4)

where \({\mathbf{c}} \in {\mathbb{R}}^{ab}\) denotes the obstacle-avoidance constraint of the continuum manipulator and can be expressed in terms of the generalized coordinates q. \({\mathbf{d}}_{s} \in {\mathbb{R}}^{ab}\) is vector of the critical safety distances. \({\mathbf{d}} \in {\mathbb{R}}^{ab}\) is vector of the actual distances between all potential collision points and obstacles, and can be expressed as

$$ {\mathbf{d}} = \left[ {d_{1,1} \;\;d_{1,2} \;\; \ldots \;\;d_{1,b} \;\; \ldots \;\;d_{a,1} \;\;d_{a,2} \;\; \ldots \;\;d_{a,b} } \right]^{T} $$
(5)

3 Combined kinodynamic motion planning method for multisegment continuum manipulators

In this section, based on the derived dynamic model and kinematic constraints, a combined kinodynamic motion planning method for a cable-driven multisegment continuum manipulator is proposed to achieve obstacle avoidance in confined spaces. The detailed derivation is as follows.

3.1 Discretization of the dynamic model

The dynamic model of the continuum manipulator, which is given by Eq. (1), can be rewritten as

$$ {\mathbf{g}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}},{{\ddot{\mathbf{q}}}},{{\varvec{\uplambda}}}} \right) = {\mathbf{f}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}},{{\ddot{\mathbf{q}}}},{{\varvec{\uplambda}}}} \right) - {\mathbf{B}}\left( {\mathbf{q}} \right){\mathbf{u}} = {\mathbf{0}} $$
(6)

where

$$ \displaystyle {\mathbf{f}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}},{{\ddot{\mathbf{q}}}},{{\varvec{\uplambda}}}} \right) = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}\left( {\mathbf{q}} \right){{\ddot{\mathbf{q}}}} + {\mathbf{V}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}}} \right){\dot{\mathbf{q}}} + \frac{{\partial E\left( {\mathbf{q}} \right)}}{{\partial {\mathbf{q}}}} + \left[ {\frac{{\partial {{\varvec{\uppsi}}}\left( {\mathbf{q}} \right)}}{{\partial {\mathbf{q}}}}} \right]^{T} {{\varvec{\uplambda}}}} \\ {{{\varvec{\uppsi}}}\left( {\mathbf{q}} \right)} \\ \end{array} } \right] $$
(7)

and

$$ {\mathbf{B}} = \left[ {\begin{array}{*{20}c} {{\mathbf{G}}^{T} } & {\mathbf{0}} \\ \end{array} } \right]^{T} \in {\mathbb{R}}^{{\left( {n + m} \right) \times s}} $$
(8)

is the augmented input matrix of the system.

To implement numerical integrations, the time domain T is equally discretized into S time intervals with the time-step length \(\eta = {T \mathord{\left/ {\vphantom {T S}} \right. \kern-0pt} S}\). At time \(t_{k} \;\left( {k = 1,\;2,\; \ldots \;,\;S} \right)\), the dynamic Eq. (6) can be expressed as

$$ {\mathbf{g}}\left( {{\mathbf{q}}_{k} ,{\dot{\mathbf{q}}}_{k} ,{{\ddot{\mathbf{q}}}}_{k} ,{{\varvec{\uplambda}}}_{k} } \right) = {\mathbf{f}}\left( {{\mathbf{q}}_{k} ,{\dot{\mathbf{q}}}_{k} ,{{\ddot{\mathbf{q}}}}_{k} ,{{\varvec{\uplambda}}}_{k} } \right) - {\mathbf{B}}\left( {{\mathbf{q}}_{k} } \right){\mathbf{u}}_{k} = {\mathbf{0}} $$
(9)

where the subscript k denotes the variable at time \(t_{k}\). To solve Eq. (9), the discretization scheme of the generalized-α method [33] is introduced as follows:

$$ \left\{ {\begin{array}{*{20}l} {{\mathbf{q}}_{k} = {\mathbf{q}}_{{k - 1}} + \eta \mathop {\dot{\mathbf{q}}} _{{k - 1}} + \eta ^{2} \left( {0.5 - \phi } \right){\mathbf{a}}_{{k - 1}} + \eta ^{2} \phi {\mathbf{a}}_{k} } \hfill \\ {\mathop {\dot{\mathbf{q}}} _{k} = \mathop {\dot{\mathbf{q}}} _{{k - 1}} + \eta \left( {1 - \gamma } \right){\mathbf{a}}_{{k - 1}} + \eta \gamma {\mathbf{a}}_{k} } \hfill \\ \end{array} } \right. $$
(10)

where \(\phi\), \(\gamma\) and \({\mathbf{a}}_{k}\) are the parameters of the generalized-α method. \({\dot{\mathbf{q}}}_{0}\) is the generalized velocity of the system at initial time. Substituting the discretization scheme (10) into Eq. (9), then Eq. (9) is transformed into a set of nonlinear algebraic equations, which can be solved by the Newton–Raphson iteration algorithm as follows:

$$ {\mathbf{x}}_{k}^{{\left( {j + 1} \right)}} = {{\varvec{\upzeta}}}_{k,1}^{\left( j \right)} + {{\varvec{\upzeta}}}_{k,2}^{\left( j \right)} {\mathbf{u}}_{k}^{\left( j \right)} $$
(11)

where

$$ {\mathbf{x}}_{k} = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}_{k}^{T} } & {{{\varvec{\uplambda}}}_{k}^{T} } \\ \end{array} } \right]^{T} \in {\mathbb{R}}^{n + m} $$
(12)

is a vector composed of the generalized coordinates and the Lagrange multipliers. The superscript j denotes the jth Newton–Raphson iteration. \({{\varvec{\upzeta}}}_{k,1}^{\left( j \right)}\) and \({{\varvec{\upzeta}}}_{k,2}^{\left( j \right)}\) can be expressed as

$$ \left\{ {\begin{array}{*{20}l} {\varvec{\zeta} _{{k,1}}^{{\left( j \right)}} = {\mathbf{x}}_{k}^{{\left( j \right)}} - \left[ {{\mathbf{g}}_{k}^{{\left( j \right)^{\prime } }} } \right]^{{ - 1}} {\mathbf{f}}_{k}^{{\left( j \right)}} } \hfill \\ {\varvec{\zeta} _{{k,2}}^{{\left( j \right)}} = \left[ {{\mathbf{g}}_{k}^{{\left( j \right)^{\prime } }} } \right]^{{ - 1}} {\mathbf{B}}_{k}^{{\left( j \right)}} } \hfill \\ \end{array} } \right. $$
(13)

where

$$ \left\{ \begin{gathered} {\mathbf{g}}_{k}^{\left( j \right)} = {\mathbf{g}}\left( {{\mathbf{x}}_{k}^{\left( j \right)} ,{\dot{\mathbf{x}}}_{k}^{\left( j \right)} ,{{\ddot{\mathbf{x}}}}_{k}^{\left( j \right)} } \right) \hfill \\ {\mathbf{f}}_{k}^{\left( j \right)} = {\mathbf{f}}\left( {{\mathbf{x}}_{k}^{\left( j \right)} ,{\dot{\mathbf{x}}}_{k}^{\left( j \right)} ,{{\ddot{\mathbf{x}}}}_{k}^{\left( j \right)} } \right) \hfill \\ {\mathbf{B}}_{k}^{\left( j \right)} = {\mathbf{B}}\left( {{\mathbf{x}}_{k}^{\left( j \right)} } \right) \hfill \\ {\mathbf{g}}_{k}^{\left( j \right)\prime \,} = \frac{{\partial {\mathbf{g}}_{k}^{\left( j \right)} }}{{\partial {\mathbf{x}}_{k}^{\left( j \right)} }} + \frac{{\partial {\mathbf{g}}_{k}^{\left( j \right)} }}{{\partial {\dot{\mathbf{x}}}_{k}^{\left( j \right)} }}\frac{{\partial {\dot{\mathbf{x}}}_{k}^{\left( j \right)} }}{{\partial {\mathbf{x}}_{k}^{\left( j \right)} }} + \frac{{\partial {\mathbf{g}}_{k}^{\left( j \right)} }}{{\partial {{\ddot{\mathbf{x}}}}_{k}^{\left( j \right)} }}\frac{{\partial {{\ddot{\mathbf{x}}}}_{k}^{\left( j \right)} }}{{\partial {\mathbf{x}}_{k}^{\left( j \right)} }} \hfill \\ \end{gathered} \right. $$
(14)

Thus far, the variable \({\mathbf{x}}_{k}\) is expressed in terms of the actuation force \({\mathbf{u}}_{k}\) according to Eq. (11), which establishes a mapping between generalized coordinates and actuation forces. This mapping provides an important foundation for kinodynamic motion planning of continuum manipulators.

3.2 Basic formulation for kinodynamic motion planning

To accurately accomplish complex tasks in confined spaces, the motion planning of continuum manipulators aims to find a path that minimizes the cost of the manipulators moving to the desired configuration. Furthermore, the motion planning also needs to simultaneously satisfy the dynamical Eqs. (1) and the obstacle-avoidance kinematic constraint (4). In addition, due to the tension-only cables and the actuators with limited output power, the actuation force is subject to a box constraint. Therefore, this is a typical kinodynamic motion planning problem. Based on the instantaneous optimal control theory, the cost function of such a planning problem is minimized at each time step. Consequently, at time \(t_{k}\), the kinodynamic motion planning problem for continuum manipulators in confined spaces can be formulated as

$$ \left\{ {\begin{array}{*{20}l} {\mathop {{\text{minimize}}}\limits_{{{\mathbf{u}}_{k} }} :\;\;J_{k} = \left( {{\mathbf{y}}_{k} - \widetilde{{\mathbf{y}}}_{k} } \right)^{T} {\mathbf{Q}}_{k} \left( {{\mathbf{y}}_{k} - \widetilde{{\mathbf{y}}}_{k} } \right) + {\mathbf{u}}_{k}^{T} {\mathbf{R}}_{k} {\mathbf{u}}_{k} + \Delta {\mathbf{u}}_{k}^{T} {\mathbf{W}}_{k} \Delta {\mathbf{u}}_{k} } \hfill & {\quad \left( {{\text{15a}}} \right)} \hfill \\ {{\text{subject}}{\mkern 1mu} {\text{to}}:\;\;{\mathbf{c}}_{k} \le {\mathbf{0}}} \hfill & {\quad \left( {{\text{15b}}} \right)} \hfill \\ {:\;\;{\mathbf{u}}_{{\min }} \le {\mathbf{u}}_{k} \le {\mathbf{u}}_{{\max }} } \hfill & {\quad \left( {{\text{15c}}} \right)} \hfill \\ \end{array} } \right. $$

where \({\mathbf{Q}}_{k} \in {\mathbb{R}}^{w \times w}\) is a positive semidefinite symmetric weighting matrix at time \(t_{k}\). \({\mathbf{R}}_{k} \in {\mathbb{R}}^{s \times s}\) and \({\mathbf{W}}_{k} \in {\mathbb{R}}^{s \times s}\) are positive definite symmetric weighting matrices at time \(t_{k}\). \(\Delta {\mathbf{u}}_{k} = {\mathbf{u}}_{k} - {\mathbf{u}}_{k - 1}\) is the increment in the actuation force in the kth time interval. \({\mathbf{c}}_{k}\) denotes the obstacle-avoidance constraint of continuum manipulators at time \(t_{k}\) and can be calculated by Eq. (4). \({\mathbf{u}}_{\min }\) and \({\mathbf{u}}_{\max }\) are the lower and upper bounds of the actuation force, respectively. \({\tilde{\mathbf{y}}}_{k} \in {\mathbb{R}}^{w}\) denotes the vector of the desired output variable at time \(t_{k}\). w is the number of the system output variables. \({\mathbf{y}}_{k} \in {\mathbb{R}}^{w}\) is the vector of the actual output variable at time \(t_{k}\).

There are mainly two operational modes for the continuum manipulator. The first mode is to control the tip of the manipulator to the desired pose, and the second mode is to control the manipulator shape to the desired configuration. For the first operational mode, the actual output variable \({\mathbf{y}}_{k}\) consists of the generalized coordinates and velocities of the manipulator tip. For the second operational mode, the actual output variable \({\mathbf{y}}_{k}\) consists of the manipulator curvature and its first derivative with respect to time, which are also nonlinear functions of the generalized coordinates and velocities. Consequently, the actual output variable \({\mathbf{y}}_{k}\) can be actually expressed in terms of the generalized coordinates and velocities of continuum manipulators for both operational modes as follows [11]:

$$ {\mathbf{y}}_{k} = {{\varvec{\Gamma}}}\left( {{\mathbf{x}}_{k}^{{\left( {j + 1} \right)}} ,\;{\dot{\mathbf{x}}}_{k}^{{\left( {j + 1} \right)}} } \right) $$
(16)

From Eqs. (10) and (11), it can be found that \({\mathbf{x}}_{k}^{{\left( {j + 1} \right)}}\) and \({\dot{\mathbf{x}}}_{k}^{{\left( {j + 1} \right)}}\) are both related to the actuation force \({\mathbf{u}}_{k}\). Consequently, \({\mathbf{y}}_{k}\) is essentially a function of the actuation force \({\mathbf{u}}_{k}\). Furthermore, \(J_{k} \in {\mathbb{R}}\) expressed in Eq. (15a) is the cost function of motion planning only with respect to the actuation force \({\mathbf{u}}_{k}\). The cost function given in this paper consists of three terms. The first item evaluates the errors between the actual and desired system output variables, and the second item is related to the energy consumed in the control process. Additionally, the continuum manipulator is usually required to move to the target configuration within a short time, which may cause the oscillation of the actuation forces, which is harmful to the continuum manipulator. The third term is used to weaken the oscillation of the actuation forces, making the manipulators move to the target configuration while maintaining stability. The constructed cost function comprehensively considers the motion planning error and the system actuation, which is beneficial for improving the performance of the kinodynamic motion planning.

Equation set (15) describes the kinodynamic motion planning problem for cable-driven multisegment continuum manipulators in confined spaces. Based on the distance between the manipulator and the obstacles, the workspace of the continuum manipulator is subdivided into a safe subspace and a warning subspace, as shown in Fig. 1. In the safe subspace, where the continuum manipulator stays far away from the obstacles, the obstacle-avoidance kinematic constraints are automatically satisfied. This is a significant difference from the motion planning problem in the warning subspace. In the following subsections, the kinodynamic motion planning problems for cable-driven multisegment continuum manipulators in the safe and warning subspaces are transformed into a MiCP and a NOP to solve, respectively.

3.3 Motion planning in the safe subspace

In this subsection, the motion planning problem for the continuum manipulator in the safe subspace is analyzed. The safe subspace is defined as a region in which the minimum distance between the manipulator and the obstacles is greater than the warning distance as follows:

$$ \mathop {\min }\limits_{i,j} d_{i,j} > d_{w} $$
(17)

where \(d_{i,j}\) can be calculated by Eq. (3). \(d_{w} \in {\mathbb{R}}\) is the warning distance and is set to be greater than the critical safety distance \(d_{s}\). When Eq. (17) holds, the kinematic constraints (15b) for obstacle avoidance will be automatically satisfied.

In addition, the actuation force of the continuum manipulator is subject to a box constraint (15c). However, the inequality constraints are difficult to be addressed in the motion planning. By introducing additional parameters, the inequality constraints for the actuation forces at time \(t_{k}\) can be equivalently transformed into a set of equality constraints as follows:

$$ \left\{ \begin{gathered} {\mathbf{u}}_{k} - {\mathbf{u}}_{\max } + {\overline{\boldsymbol{\alpha }}}_{k} = {\mathbf{0}} \hfill \\ {\mathbf{u}}_{\min } - {\mathbf{u}}_{k} + {\underline{\boldsymbol{\alpha }}}_{k} = {\mathbf{0}} \hfill \\ \end{gathered} \right. $$
(18)

where \({\overline{\boldsymbol{\alpha }}}_{k} \ge {\mathbf{0}} \in {\mathbb{R}}^{s}\) and \({\underline{\boldsymbol{\alpha }}}_{k} \ge {\mathbf{0}} \in {\mathbb{R}}^{s}\) are parameters at time \(t_{k}\), which can ensure that the actuation force satisfies the box constraint (15c). Substituting Eq. (18) into the cost function (15a) can yield an expanded cost function considering the actuation force limits. In the safe subspace, since Eq. (15b) is satisfied, the motion planning problem (15) for continuum manipulators can be transformed into a NOP without the obstacle-avoidance kinematic constraints as follows:

$$ \left\{ {\begin{array}{*{20}l} {\mathop {{\text{minimize}}}\limits_{{{\mathbf{u}}_{k} }} :\;\;\hat{J}_{k} = \left( {{\mathbf{y}}_{k} - \widetilde{{\mathbf{y}}}_{k} } \right)^{T} {\mathbf{Q}}_{k} \left( {{\mathbf{y}}_{k} - \widetilde{{\mathbf{y}}}_{k} } \right) + {\mathbf{u}}_{k}^{T} {\mathbf{R}}_{k} {\mathbf{u}}_{k} + \Delta {\mathbf{u}}_{k}^{T} {\mathbf{W}}_{k} \Delta {\mathbf{u}}_{k} } & {} \\ {+ \overline{{\varvec{\beta }}} _{k}^{T} \left( {{\mathbf{u}}_{k} - {\mathbf{u}}_{{\max }} + \overline{{\varvec{\alpha }}} _{k} } \right) + {{\underline{\varvec{\beta} } }}_{k}^{T} \left( {{\mathbf{u}}_{{\min }} - {\mathbf{u}}_{k} + {{\underline{\varvec{\alpha} } }}_{k} } \right)} & .{\quad \left( {{\text{19a}}} \right)} \\ {{\text{subject to: }}\;\;{\mathbf{u}}_{k} - {\mathbf{u}}_{{\max }} + \overline{{\varvec{\alpha }}} _{k} = {\mathbf{0}},\quad {\mathbf{u}}_{{\min }} - {\mathbf{u}}_{k} + {{\underline{\varvec{\alpha} } }}_{k} = {\mathbf{0}}} & {\quad\; \left( {{\text{19b}}} \right)} \\ \end{array} } \right. $$

where \(\hat{J}_{k} \in {\mathbb{R}}\) is the expanded cost function considering the actuation force limits at time \(t_{k}\). \({\overline{\varvec{\beta }}}_{k} \in {\mathbb{R}}^{s}\) and \({\varvec{\underline {\beta } }}_{k} \in {\mathbb{R}}^{s}\) are the parameters at time \(t_{k}\), and satisfy a complementarity relationship with the parameters \({\overline{\varvec{\alpha }}}_{k}\) and \({\varvec{\underline {\alpha } }}_{k}\) [34] as follows:

$$ \left\{ \begin{gathered} \overline{\varvec{\alpha }}_{{{k}}} \ge {\mathbf{0}},\;\overline{\varvec{\beta }}_{{{k}}} \ge {\mathbf{0}},\;\overline{\varvec{\alpha }}_{{{k}}}^{{{T}}} \overline{\varvec{\beta }}_{{{k}}} = {\mathbf{0}} \hfill \\ \varvec{\underline {\alpha } }_{{{k}}} \ge {\mathbf{0}},\;\varvec{\underline {\beta } }_{{{k}}} \ge {\mathbf{0}},\;\varvec{\underline {\alpha } }_{{{k}}}^{{{T}}} \varvec{\underline {\beta } }_{{{k}}} = {\mathbf{0}} \hfill \\ \end{gathered} \right. $$
(20)

To obtain the minimum value of the expanded cost function \(\hat{J}_{k}\) expressed in Eq. (19a), its variation with respect to \({\mathbf{u}}_{k}\) can be calculated by

$$ {{\partial \hat{J}_{k} } \mathord{\left/ {\vphantom {{\partial \hat{J}_{k} } {\partial {\mathbf{u}}_{k} }}} \right. \kern-0pt} {\partial {\mathbf{u}}_{k} }} = {\mathbf{0}} $$
(21)

Substituting Eqs. (19a) into (21) yields

$$ \left( {{{\partial {\mathbf{y}}_{k} } \mathord{\left/ {\vphantom {{\partial {\mathbf{y}}_{k} } {\partial {\mathbf{u}}_{k} }}} \right. \kern-0pt} {\partial {\mathbf{u}}_{k} }}} \right)^{T} {\mathbf{Q}}_{k} \left( {{\mathbf{y}}_{k} - {\tilde{\mathbf{y}}}_{k} } \right) + {\mathbf{R}}_{k} {\mathbf{u}}_{k} + {\mathbf{W}}_{k} \Delta {\mathbf{u}}_{k} + {{\left( {{\overline{\varvec{\beta }}}_{k} - {\varvec{\underline {\beta } }}_{k} } \right)} \mathord{\left/ {\vphantom {{\left( {{\overline{\varvec{\beta }}}_{k} - {\varvec{\underline {\beta } }}_{k} } \right)} 2}} \right. \kern-0pt} 2} = {\mathbf{0}} $$
(22)

where based on Eqs. (11) and (16), \({{\partial {\mathbf{y}}_{k} } \mathord{\left/ {\vphantom {{\partial {\mathbf{y}}_{k} } {\partial {\mathbf{u}}_{k} }}} \right. \kern-0pt} {\partial {\mathbf{u}}_{k} }}\) can be expressed by

$$ \frac{{\partial {\mathbf{y}}_{k} }}{{\partial {\mathbf{u}}_{k} }} = \frac{{\partial {\mathbf{y}}_{k} }}{{\partial {\mathbf{x}}_{k}^{{\left( {j + 1} \right)}} }}\frac{{\partial {\mathbf{x}}_{k}^{{\left( {j + 1} \right)}} }}{{\partial {\mathbf{u}}_{k} }} + \frac{{\partial {\mathbf{y}}_{k} }}{{\partial {\dot{\mathbf{x}}}_{k}^{{\left( {j + 1} \right)}} }}\frac{{\partial {\dot{\mathbf{x}}}_{k}^{{\left( {j + 1} \right)}} }}{{\partial {\mathbf{x}}_{k}^{{\left( {j + 1} \right)}} }}\frac{{\partial {\mathbf{x}}_{k}^{{\left( {j + 1} \right)}} }}{{\partial {\mathbf{u}}_{k} }} $$
(23)

Thus far, the NOP (19) for the motion planning of the continuum manipulator in the safe subspace is transformed into a MiCP [35] consisting of the actuation constraint Eq. (18), the complementarity relationship (20), and the governing Eq. (22).

The Fischer–Burmeister complementarity function [32]

$$ \rho = \sqrt {\tau^{2} + \chi^{2} } - \left( {\tau + \chi } \right) $$
(24)

is introduced to describe the complementarity relationship (20) between parameters, then Eq. (20) is equivalently transformed into

$$ \left\{ \begin{gathered} \sqrt {{\overline{\varvec{\alpha }}}_{k}^{2} + {\overline{\varvec{\beta }}}_{k}^{2} } - \left( {{\overline{\varvec{\alpha }}}_{k} + {\overline{\varvec{\beta }}}_{k} } \right) = {\mathbf{0}} \hfill \\ \sqrt {{\varvec{\underline {\alpha } }}_{k}^{2} + {\varvec{\underline {\beta } }}_{k}^{2} } - \left( {{\varvec{\underline {\alpha } }}_{k} + {\varvec{\underline {\beta } }}_{k} } \right) = {\mathbf{0}} \hfill \\ \end{gathered} \right. $$
(25)

By combining the actuation constraint Eq. (18), the governing Eq. (22), and the complementarity Eq. (25), the NOP (19) for the motion planning of the continuum manipulator in the safe subspace is finally transformed into a set of nonlinear algebraic equations expressed in terms of the actuation force and parameters as follows:

$$ \left\{ {\begin{array}{*{20}l} {\left( {\partial {\mathbf{y}}_{k} {\text{ }}/\partial {\mathbf{u}}_{k} } \right)^{T} {\mathbf{Q}}_{k} \left( {{\mathbf{y}}_{k} - \widetilde{{\mathbf{y}}}_{k} } \right) + {\mathbf{R}}_{k} {\mathbf{u}}_{k} + {\mathbf{W}}_{k} \Delta {\mathbf{u}}_{k} + \left( {\overline{{\varvec{\beta }}} _{k} - {\varvec{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\beta } }}_{k} } \right){\text{ }}/2{\text{ }} = {\mathbf{0}}} \hfill \\ {{\mathbf{u}}_{k} - {\mathbf{u}}_{{\max }} + \overline{{\varvec{\alpha }}} _{k} = {\mathbf{0}}} \hfill \\ {{\mathbf{u}}_{{\min }} - {\mathbf{u}}_{k} + {\varvec{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha } }}_{k} = {\mathbf{0}}} \hfill \\ {\sqrt {\overline{{\varvec{\alpha }}} _{k}^{2} + \overline{{\varvec{\beta }}} _{k}^{2} } - \left( {\overline{{\varvec{\alpha }}} _{k} + \overline{{\varvec{\beta }}} _{k} } \right) = {\mathbf{0}}{\text{ }}} \hfill \\ {\sqrt {{\varvec{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha } }}_{k}^{2} + {\varvec{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\beta } }}_{k}^{2} } - \left( {{\varvec{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha } }}_{k} + {\varvec{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\beta } }}_{k} } \right) = {\mathbf{0}}{\text{ }}} \hfill \\ \end{array} } \right.{\text{ }} $$
(26)

The motion planning problem in the safe subspace is transformed into a MiCP with actuation constraints to solve. The adoption of a nonlinear complementarity function enables the MiCP to be finally reformulated as a set of nonlinear algebraic Eqs. (26), which provides a new solution to the calculation of the actuation forces. Equation (26) can be solved by the Newton–Raphson iteration algorithm. Then, the actuation force \({\mathbf{u}}_{k}\) is obtained. Based on Eqs. (11), (16), and the discretization scheme of the generalized-α method [33], the optimal path for the motion planning of the continuum manipulator is also constructed. This approach, which transforms a planning problem into a MiCP, can rapidly achieve motion planning while strictly satisfying the system constraints.

3.4 Motion planning in the warning subspace

In this subsection, the motion planning problem for the continuum manipulator in the warning subspace is analyzed. The warning subspace, as shown in Fig. 1, is defined as a region in which the minimum distances between the manipulator and the obstacles do not satisfy Eq. (17). Since the continuum manipulator in this subspace is close to the obstacles, the obstacle-avoidance constraints must be considered during motion planning. Consequently, to achieve kinodynamic motion planning in the warning subspace, the NOP (15) with the obstacle-avoidance constraints needs to be solved. However, it is usually difficult to find the optimal solution to the constrained NOP. To avoid such a problem, the penalty function method [36] is used here to transform the constrained NOP (15) into a NOP without kinematic constraints. A penalty function

$$ \Phi \left( {d_{i,j} } \right) = \left\{ \begin{gathered} \left[ {1 - \left( {{{d_{i,j} } \mathord{\left/ {\vphantom {{d_{i,j} } {d_{s} }}} \right. \kern-0pt} {d_{s} }}} \right)^{6} } \right]^{3} ,\quad d_{i,j} < d_{s} \\ 0\quad \quad \quad \quad \quad \quad ,\quad d_{i,j} \ge d_{s} \\ \end{gathered} \right. $$
(27)

is introduced in this subsection. \(\Phi \in {\mathbb{R}}\) is expressed in terms of the distance \(d_{i,j}\) between the manipulator and the obstacles, which can be calculated by Eq. (3).

Substituting Eq. (27) into the cost function \(J_{k}\) expressed in Eq. (15a) can yield an expanded cost function with the penalty terms for the obstacle-avoidance constraints. Then, the NOP (15) for the kinodynamic motion planning is transformed into a NOP without obstacle-avoidance constraints as follows:

$$ \left\{ {\begin{array}{*{20}l} {\mathop {{\text{minimize}}}\limits_{{{\mathbf{u}}_{k} }} :\;\;\mathop {J_{k} }\limits^{\smile } = \left( {{\mathbf{y}}_{k} - \widetilde{{\mathbf{y}}}_{k} } \right)^{T} {\mathbf{Q}}_{k} \left( {{\mathbf{y}}_{k} - \widetilde{{\mathbf{y}}}_{k} } \right) + {\mathbf{u}}_{k}^{T} {\mathbf{R}}_{k} {\mathbf{u}}_{k} + \Delta {\mathbf{u}}_{k}^{T} {\mathbf{W}}_{k} \Delta {\mathbf{u}}_{k} + \sum\limits_{i} {\sum\limits_{j} {\upsilon {\mkern 1mu} \Phi _{k} \left( {d_{{i,j}} } \right)} } } \hfill & {\left( {{\text{28a}}} \right)} \hfill \\ {{\text{subject}}{\mkern 1mu} {\text{to}}:\;\;{\mathbf{u}}_{{\min }} \le {\mathbf{u}}_{k} \le {\mathbf{u}}_{{\max }} } \hfill & {\left( {{\text{28b}}} \right)} \hfill \\ \end{array} } \right. $$

where \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{J}_{k} \in {\mathbb{R}}\) is an expanded cost function with the penalty terms for the obstacle-avoidance constraint (15b). \(\upsilon \in {\mathbb{R}}\) is a penalty factor, which plays an important role in adjusting the strength of a penalty assigned to solutions that violate the constraints. By adjusting the penalty factor, the penalty function method can balance the trade-off between achieving an optimal solution for the expanded cost function and satisfying the obstacle-avoidance constraints [28].

Intelligent optimization algorithms can be used to deal with the NOP [29]. Due to its cooperative search capability utilizing both the local and global information, the PSO algorithm [37] is suitable for the motion planning problem of continuum manipulators and is adopted in this paper to solve Eq. (28). In the implementation of the standard PSO algorithm, each candidate solution to the NOP (28) is regarded as a particle. The positions and velocities of particles are randomly initialized within the search space. Then, these particles move through the search space based on the attractions to the best solutions separately found by each individual particle and the entire particle swarm. That is, the velocity and position of each particle are updated by the following rules [37]:

$$ \left\{ {\begin{array}{*{20}l} {v_{{j,e}}^{{\left( {i + 1} \right)}} = \omega ^{{\left( i \right)}} v_{{j,e}}^{{\left( i \right)}} + \varsigma _{1} \theta _{{1,e}} \left( {l_{{j,e}}^{{\left( i \right)}} - p_{{j,e}}^{{\left( i \right)}} } \right) + \varsigma _{2} \theta _{{2,e}} \left( {p_{{g,e}}^{{\left( i \right)}} - p_{{j,e}}^{{\left( i \right)}} } \right)} \hfill & {\quad \left( {{\text{29a}}} \right)} \hfill \\ {p_{{j,e}}^{{\left( {i + 1} \right)}} = p_{{j,e}}^{{\left( i \right)}} + v_{{j,e}}^{{\left( {i + 1} \right)}} } \hfill & {\quad \left( {{\text{29b}}} \right)} \hfill \\ \end{array} } \right. $$

where \(\omega\) is an inertia weight. \(\varsigma_{1}\) and \(\varsigma_{2}\) are acceleration coefficients. \(\theta_{1,e}\) and \(\theta_{2,e}\) are random numbers uniformly distributed between 0 and 1. \(l_{j,e} \in {\mathbb{R}}\) is the best position found by the jth particle at the eth dimension. \(p_{g,e} \in {\mathbb{R}}\) is the best position found by the entire particle swarm at the eth dimension. \({\mathbf{v}}_{j} = \left[ {v_{j,1} \;\,v_{j,2} \;\, \ldots \;\,v_{j,e} \;\, \ldots \;\,v_{j,s} } \right]^{T} \in {\mathbb{R}}^{s}\) and \({\mathbf{p}}_{j} = \left[ {p_{j,1} \;\,p_{j,2} \;\, \ldots \;\,p_{j,e} \;\, \ldots \;\,p_{j,s} } \right]^{T} \in {\mathbb{R}}^{s}\) denote the velocity and position of the jth particle, respectively. The particle position \({\mathbf{P}} = \left[ {{\mathbf{p}}_{1} \;\,{\mathbf{p}}_{2} \;\, \ldots \;\,{\mathbf{p}}_{j} \;\, \ldots \;\,{\mathbf{p}}_{\delta } } \right] \in {\mathbb{R}}^{s \times \delta }\) is a set of candidate solutions to the NOP (28) and \(\delta\) is the number of particles. The subscript j denotes the jth particle. The subscript \(e\;\left( {e = 1,\;2,\; \ldots \;,\;s} \right)\) denotes the eth dimension of each individual particle. The superscript i denotes the ith update.

Each particle position can be regarded as a candidate solution. Substituting the generated particle positions into Eq. (28a), the cost function value for each particle can be calculated. By iteratively updating the particle positions and searching for the minimum cost function value, the optimal solution can be obtained until the convergence criteria is satisfied. However, in the standard PSO algorithm [37], the set P of particle positions is initialized in a uniform random manner throughout the search space and the search performance of the PSO algorithm is obviously dependent on parameters. These characteristics reduce the convergence rate of the standard PSO algorithm to find the optimal solution to the kinodynamic motion planning problem. To solve the NOP (28) more stably, the PSO algorithm is improved in this paper from the following two aspects.

3.4.1 Introducing normal distribution in the initialization process

Since the control forces of the continuum manipulator vary continuously over time, the control force \({\mathbf{u}}_{k}\) is usually in the neighborhood of the actuation force \({\mathbf{u}}_{k - 1}\), as shown in Fig. 2. Therefore, in the initialization process of the particle swarm at time \(t_{k}\), particles should be densely distributed in a random manner within the neighborhood of the actuation force \({\mathbf{u}}_{k - 1}\), rather than distributed in a uniform random manner throughout the search space.

Fig. 2
figure 2

\({\mathbf{u}}_{k}\) located in the neighborhood of \({\mathbf{u}}_{k - 1}\)

Full size image

To have a stronger search capability within the neighborhood of the control force \({\mathbf{u}}_{k - 1}\) while also considering the global search capability of the PSO algorithm, a combination of the normal and uniform distributions is used in the position initialization process of the particle swarm at time \(t_{k}\) as follows:

$$ \left\{ \begin{gathered} {\mathbf{P}}_{\delta 1} \sim N\left( {{\mathbf{u}}_{k - 1} ,\;{{\varvec{\upsigma}}}^{2} } \right) \hfill \\ {\mathbf{P}}_{\delta 2} \sim U\left( {{\mathbf{u}}_{\min } ,\;{\mathbf{u}}_{\max } } \right) \hfill \\ \end{gathered} \right. $$
(30)

where \({\mathbf{P}}_{\delta 1} \in {\mathbb{R}}^{{s \times \delta_{1} }}\) consisting of \(\delta_{1}\) particles obeys normal distribution N with the mean value of the actuation force \({\mathbf{u}}_{k - 1}\) and the standard deviation of \({{\varvec{\upsigma}}}\). \({\mathbf{P}}_{\delta 2} \in {\mathbb{R}}^{{s \times \delta_{2} }}\) consisting of \(\delta_{2}\) particles obeys the uniform distribution U between \({\mathbf{u}}_{\min }\) and \({\mathbf{u}}_{\max }\). Here, \(\delta_{1} + \delta_{2} = \delta\). In addition, the actuation force \({\mathbf{u}}_{k - 1}\) and the actuation force \({\mathbf{u}}_{k}^{\left( j \right)}\) in the jth Newton–Raphson iteration are also candidate solutions to the NOP (28). Therefore, in the implementation of the improved PSO algorithm, the set of the particle positions is finally initialized as

$$ {\hat{\mathbf{P}}} = \left[ {{\mathbf{P}}_{\delta 1} \;\,{\mathbf{P}}_{\delta 2} \;\,{\mathbf{u}}_{k - 1} \;\,{\mathbf{u}}_{k}^{\left( j \right)} } \right] \in {\mathbb{R}}^{{s \times \left( {\delta + 2} \right)}} $$
(31)

The introduction of \({\mathbf{u}}_{k - 1}\) and \({\mathbf{u}}_{k}^{\left( j \right)}\) is the key to ensure the stability of the motion planning algorithm. Initializing the particle position according to Eq. (31) can improve the search efficiency of the algorithm. Furthermore, since the actuation force is subject to a box constraint (28b), each individual particle \({\mathbf{p}}_{j}\) in the position set \({\hat{\mathbf{P}}}\) must satisfy the following equation:

$$ {\mathbf{p}}_{j} = \left\{ \begin{gathered} {\mathbf{u}}_{\min } ,\;\,{\text{if}}\;{\mathbf{p}}_{j} \le {\mathbf{u}}_{\min } \hfill \\ {\mathbf{u}}_{\max } ,\;\,{\text{else}}\;{\text{if}}\;{\mathbf{p}}_{j} \ge {\mathbf{u}}_{\max } \hfill \\ {\mathbf{p}}_{j} ,\;\,\;\;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;\;j = 1,\;2,\; \ldots \;,\;\delta + 2 $$
(32)

The kinodynamic motion planning problem for multisegment continuum manipulators has highly nonlinear characteristics, which increases the difficulty of searching for the optimal solution. Since the optimal solution at time \(t_{k}\) is in the neighborhood of the actuation force \({\mathbf{u}}_{k - 1}\), introducing \({\mathbf{u}}_{k - 1}\) into the initialization position set \({\hat{\mathbf{P}}}\) can accelerate the convergence rate of the algorithm.

3.4.2 Using a chaotic map with an adaptive parameter in the search process

To avoid the PSO algorithm falling into a local optimal solution, a chaotic map is introduced into the search process [38]. After the initialization of the particle swarm, the cost function value for each particle can be calculated by Eq. (28a). Then, the particle swarm \({\hat{\mathbf{P}}}\) consisting of \(\delta + 2\) particles is divided into two populations. The first population contains the particles with \(\delta + 2 - \varphi\) smallest cost function values, and the second population contains the remaining \(\varphi\) particles. The velocity and position of the particle in the first population are still updated by Eq. (29). On the other hand, to further improve the search performance of the PSO algorithm, the position of the particle in the second population is updated based on a chaotic map.

To implement a chaotic map, the position \({\mathbf{p}}_{j}^{\left( h \right)}\) of the jth particle in the second population is first normalized by

$$ {\overline{\mathbf{p}}}_{j}^{\left( h \right)} = \frac{{{\mathbf{p}}_{j}^{\left( h \right)} - {\mathbf{u}}_{\min } }}{{{\mathbf{u}}_{\max } - {\mathbf{u}}_{\min } }} $$
(33)

Then, the normalized position \({\overline{\mathbf{p}}}_{j}\) is substituted into a logistic map [38] as follows:

$$ {\overline{\mathbf{p}}}_{j}^{{\left( {h + 1} \right)}} = 4{\overline{\mathbf{p}}}_{j}^{\left( h \right)} \left( {1 - {\overline{\mathbf{p}}}_{j}^{\left( h \right)} } \right) $$
(34)

where h denotes the hth iteration of the logistic map. The obtained variable \({\overline{\mathbf{p}}}_{j}^{{\left( {h + 1} \right)}}\) is further mapped to the search space by following equation:

$$ {\mathbf{p}}_{j}^{{\left( {h + 1} \right)}} = {\mathbf{u}}_{\min } + {\overline{\mathbf{p}}}_{j}^{{\left( {h + 1} \right)}} \left( {{\mathbf{u}}_{\max } - {\mathbf{u}}_{\min } } \right) $$
(35)

These two populations separately updated by Eqs. (29) and (35) are finally merged into a new combined population. This combined population is used to search for the optimal solution to the NOP (28), which can improve the global search performance of the PSO algorithm. However, an excessive number \(\varphi\) of particles updated by a chaotic map will reduce the convergence rate of the algorithm. Choosing an appropriate number \(\varphi\) for the kinodynamic motion planning is a thorny problem. To adjust algorithm parameters adaptively, the number \(\varphi\) of particles is set to linearly vary based on the proportion of feasible solutions in this paper. A feasible solution is defined as an actuation force that satisfies the obstacle-avoidance constraint (15b) of continuum manipulators. If the number of feasible solutions is small, it means that the obtained solution falls into a local subspace far from the feasible domain. In such a situation, to further improve the performance of the global search, more particles need to be updated by a chaotic map. Therefore, the number \(\varphi\) of particles is set to

$$ \varphi = \varphi_{1} + \left( {1 - \vartheta } \right)\left( {\varphi_{2} - \varphi_{1} } \right) $$
(36)

where \(\varphi_{1}\) and \(\varphi_{2}\) are the minimum and maximum numbers of particles updated by a chaotic map, respectively. \(\vartheta\) is the proportion of feasible solutions to the total number of particles.

By introducing normal distribution and a chaotic map with an adaptive parameter, the improved PSO algorithm proposed in this subsection has great local and global search capabilities, which accelerates the convergence rate of the algorithm and provides a sound basis for solving NOPs. In this paper, this improved PSO algorithm, as presented in Algorithm 1, is used to solve the kinodynamic motion planning problem (28) for the cable-driven multisegment continuum manipulator in the warning subspace. After the actuation force \({\mathbf{u}}_{k}\) is calculated by Eq. (28), the optimal path for the continuum manipulator can be further obtained by Eqs. (11), (16) and the discretization scheme of the generalized-α method [33].

Algorithm 1
figure a

The improved PSO algorithm

Full size image

3.5 Flowchart for the combined kinodynamic motion planning

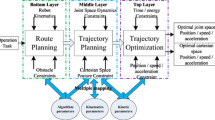
In this section, a combined kinodynamic motion planning method is proposed to achieve the obstacle avoidance of cable-driven multisegment continuum manipulators in confined spaces, as presented in Fig. 3. The workspace of the continuum manipulator is first divided into a safe subspace and a warning subspace based on the distances between the manipulator and the obstacles, namely Eqs. (5) and (17). In the safe subspace, the motion planning problem for continuum manipulators is transformed into a MiCP without the obstacle-avoidance kinematic constraints. By introducing a nonlinear complementarity function, the MiCP is further reformulated as a set of nonlinear algebraic Eqs. (26), which is solved by the Newton–Raphson iteration algorithm. This processing approach can rapidly generate paths while strictly satisfying the system constraints. In the warning subspace, the motion planning problem for continuum manipulators is transformed into a NOP (28) with the penalty terms for the obstacle-avoidance kinematic constraints. An improved PSO algorithm with a great search performance is proposed to solve the NOP (28), which significantly accelerates the convergence rate of the iterative process. After the MiCP (26) and the NOP (28) are solved, the actuation force and the optimal path for the obstacle avoidance of cable-driven multisegment continuum manipulators can be finally obtained.

Fig. 3
figure 3

Flowchart for the proposed combined kinodynamic motion planning method

Full size image

The proposed combined kinodynamic motion planning method provides a unified path optimization framework for obstacle-avoidance motion planning of continuum manipulators, which enables them to safely perform dexterous operations in confined spaces.

4 Numerical simulation

In this section, numerical simulations are conducted to analyze the performance of the combined kinodynamic motion planning method proposed in this paper. The aim is to plan a collision-free motion path for a cable-driven multisegment continuum manipulator from its initial to terminal configurations in the confined space with static and dynamic obstacles. To demonstrate the convergence and stability of the proposed method for the large overall motion, the desired configuration of the continuum manipulator is set to a configuration with large structural deformations. Simulation results for obstacle-avoidance motion planning of multisegment continuum manipulators, including dynamic responses and actuation forces, are presented to illustrate the effectiveness and advantages of the proposed method.

The continuum manipulator under consideration consists of four flexible segments. The geometric and material parameters of each manipulator segment are presented in Table 1. Moreover, each segment is driven by six equally spaced cables, as shown in Fig. 1. Consequently, the dimension of the cable actuation force u is 24. The weighting matrix for the motion planning problem defined by Eq. (15a) is set as \({\mathbf{R}} = {\mathbf{I}}_{24}\), where \({\mathbf{I}}_{k}\) denotes a k-dimension identity matrix. The warning distance \(d_{w}\) is set to 0.01 m. The dynamic model of the continuum manipulator is solved by the generalized-α method. The time-step length is 0.1 s, and the total simulation time is 100 s.

Table 1 Manipulator segment parameters
Full size table

The lower bound \({\mathbf{u}}_{\min }\) and the upper bound \({\mathbf{u}}_{\max }\) of the actuation forces are set as

$$ \left\{ \begin{gathered} {\mathbf{u}}_{\min } = {\mathbf{0}}_{24 \times 1} \hfill \\ {\mathbf{u}}_{\max } = 220{{\varvec{\Xi}}}_{24} \hfill \\ \end{gathered} \right. $$
(37)

where \({{\varvec{\Xi}}}_{k}\) denotes the vector \(\left[ {1\;\;1\;\; \ldots \;\;1} \right]^{T} \in {\mathbb{R}}^{k}\).

4.1 Motion planning for the manipulator tip

To perform detection tasks, the tip of continuum manipulators needs to be regulated to the desired pose. Therefore, the motion planning problem for the manipulator tip is studied in this subsection. The manipulator tip is required to track the given pose while avoiding the collisions between the manipulator and the obstacles. The desired tip trajectory is set to the lemniscate of Bernoulli as follows:

$$ \left\{ \begin{gathered} x = \rho \cos \theta \hfill \\ y = \rho \sin \theta \hfill \\ z = - 2.4 \hfill \\ \end{gathered} \right. $$
(38)

where \(\rho = 0.6\cos 2\theta\) and

$$ \theta = \left\{ \begin{gathered} \frac{\pi }{100}t,\quad \quad \quad \quad \quad \quad \;\,0 \le t \le 25 \hfill \\ - \frac{\pi }{100}\left( {t - 25} \right) + \frac{5\pi }{4},\;\;\;25 < t \le 50 \hfill \\ - \frac{\pi }{100}\left( {t - 50} \right) + \pi ,\quad \;\;50 < t \le 75 \hfill \\ \frac{\pi }{100}\left( {t - 75} \right) + \frac{7\pi }{4},\quad \;\,75 < t \le 100 \hfill \\ \end{gathered} \right. $$
(39)

The direction of the manipulator tip during motion is required to be always consistent with the negative z direction. Consequently, the quaternion of the manipulator tip is set as

$$ {\varvec{\varsigma }} = \left[ {\cos \left( {{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}} \right)\;\;0\;\;\sin \left( {{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}} \right)\;\;0} \right]^{T} $$
(40)

The output variable of the system at time \(t_{k}\) is given by

$$ {\mathbf{y}}_{k} = \left[ {{\mathbf{q}}_{e,k}^{T} \;\;{\dot{\mathbf{q}}}_{e,k}^{T} \;\;{\dot{\mathbf{q}}}_{m,k}^{T} } \right]^{T} $$
(41)

where \({\mathbf{q}}_{e} \in {\mathbb{R}}^{7}\) denotes the vector of the coordinates and the quaternion of the manipulator tip. \({\mathbf{q}}_{m}\) denotes the vector of the coordinates and the quaternion of the nodes except the manipulator tip. The introduction of \({\dot{\mathbf{q}}}_{m}\) is to increase the damping term, which can avoid the manipulator oscillation.

To minimize tracking errors of the manipulator tip at every moment and make its movement more stable, the weighting matrices Q and W for the motion planning problem defined by Eq. (15a) are set as

$$ \left\{ {\begin{array}{*{20}l} {{\mathbf{Q}} = {\text{diag}}\left( {5 \times 10^{{12}} {\mathbf{I}}_{7} ,\;5 \times 10^{{10}} {\mathbf{I}}_{7} ,\;10^{8} {\mathbf{I}}} \right)} \hfill \\ {{\mathbf{W}} = 10^{4} {\text{diag}}\left( {{\mathbf{I}}_{6} ,\;2{\mathbf{I}}_{6} ,\;3{\mathbf{I}}_{6} ,\;4{\mathbf{I}}_{6} } \right)} \hfill \\ \end{array} } \right.{\text{ }} $$
(42)

Two spherical obstacles with a radius of 0.1 m are considered, and their centroid coordinates are set as

$$ \left\{ {\begin{array}{*{20}l} {{\mathbf{O}}_{1} = \left[ {0.45\;\;\quad 0.15\;\; \quad{-1.20}} \right]^{T} {\text{ }}} \hfill \\ {{\mathbf{O}}_{2} = \left[ {0.40 + 0.32\cos \left( {\omega {\mkern 1mu} t} \right)\;\;\; - 0.15 + 0.32\sin \left( {\omega {\mkern 1mu} t} \right)\;\;\; {-1.68}} \right]^{T} } \hfill \\ \end{array} } \right. $$
(43)

where \(\omega = {{\pi t} \mathord{\left/ {\vphantom {{\pi t} {6000}}} \right. \kern-0pt} {6000}} + {{7\pi } \mathord{\left/ {\vphantom {{7\pi } {600}}} \right. \kern-0pt} {600}}\).

The dynamic responses of the continuum manipulator for different penalty factors are calculated to analyze the effect of this factor on obstacle-avoidance motion planning. The Euclidean distances between the manipulator and the obstacles are presented in Fig. 4. It can be found from Fig. 4 that the depth of the manipulator penetrating the obstacle gradually decreases with the increase in the penalty factor. The obstacle-avoidance constraints are well satisfied for a penalty factor \(\upsilon = 1 \times 10^{12}\). If the penalty factor is too large, solutions that violate the constraints will be assigned a very high cost, making it difficult for numerical solutions to converge [28]. Therefore, the penalty factor \(\upsilon\) is set to 1 × 1012 in this simulation example.

Fig. 4
figure 4

Euclidean distances between the manipulator and the obstacles for different penalty factors \(\upsilon\)

Full size image

The motion planning for a four-segment continuum manipulator is conducted by the proposed kinodynamic motion planning method. Four snapshots are presented to illustrate the motion of the continuum manipulator, as shown in Fig. 5. The trajectory of the manipulator tip forms the lemniscate of Bernoulli, and the tip direction is always consistent with the negative z direction during motion. Consequently, the tip of the continuum manipulator can be accurately regulated to the desired pose. The continuum manipulator is capable of large structural deformations, which provides a sound basis for tracking the complex trajectory. Moreover, the manipulator undergoes large overall motion and avoids the collisions with the obstacles. Therefore, the proposed method can effectively achieve large overall motion planning for the continuum manipulator.

Fig. 5
figure 5

Snapshots of a continuum manipulator for trajectory tracking

Full size image

The trajectory of the dynamic obstacle is a circle centered on (0.4 m, − 0.15 m) and with a radius of 0.32 m, as given by Eq. (43). There is a risk of multiple collisions between the continuum manipulator and these two obstacles, which significantly increases the difficulty of obstacle-avoidance motion planning. The Euclidean distances between the manipulator and the obstacle centroids are calculated to demonstrate the obstacle-avoidance effectiveness of the proposed motion planning method. As presented in Fig. 6a, a head-on collision between the manipulator and the second obstacle is imminent at point A. The proposed obstacle-avoidance motion planning method actively adjusts the manipulator to move away from the obstacle. Consequently, the distance between the manipulator and the second obstacle gradually increases between point A and point B. It is difficult for the manipulator to avoid a head-on collision with the obstacle, but the proposed method still successfully achieves obstacle avoidance. As the second obstacle moves, this distance decreases gradually between point B and point C. Additionally, in the motion process, the distances between the manipulator and the obstacles are always greater than or equal to the obstacle radius of 0.1 m, as shown in Fig. 6a. Therefore, the motion path generated by the proposed method can strictly satisfy the obstacle-avoidance constraints.

Fig. 6
figure 6

Euclidean distances between the manipulator and the obstacle centroids

Full size image

A motion path without obstacle avoidance is also generated for comparison. The Euclidean distances between the manipulator and the obstacle centroids are calculated during the manipulator moving along this path, as illustrated Fig. 6b. The distances are less than the obstacle radius of 0.1 m within the time intervals [30.9 s, 47.3 s] and [79.7 s, 84.5 s], which indicates that the manipulator penetrates the obstacles, as illustrated in the detail view in Fig. 6b. Based on the comparison between Fig. 6a and b, it can be found that the proposed motion planning method exhibits a great obstacle-avoidance performance.

The configurations of the continuum manipulator at 82.6 s are presented in Fig. 7 to further illustrate the obstacle-avoidance effectiveness of the proposed motion planning method. The tip of the continuum manipulator can accurately track the given trajectory regardless of whether the obstacle-avoidance constraints are considered or not. However, the manipulator penetrates the obstacle when obstacle avoidance is not considered. On the other hand, the manipulator, which moves along the path generated by the proposed method, avoids a collision with obstacle when the obstacle-avoidance constraint is considered. Therefore, it can be found from Figs. 6 and 7 that the proposed kinodynamic motion planning method can achieve trajectory tracking while successfully avoiding the collisions with obstacles.

Fig. 7
figure 7

Comparison between the configurations with and without obstacle avoidance

Full size image

The desired and actual trajectories of the manipulator tip are shown in Fig. 8a. The tip of the continuum manipulator strictly moves along the given trajectory. The tracking error varies between -6.6 × 10–3 m and 5.1 × 10–3 m, as presented in Fig. 8b. This tracking error is mainly caused by the phase difference and can be adjusted by the weighting matrix Q. The quaternion of the manipulator tip and its error are shown in Fig. 9. The maximum error is only 2.5 × 10–3, which indicates that the tip of the continuum manipulator can maintain the desired attitude well even for the large overall motion. Therefore, the proposed method can make the continuum manipulator accurately track the desired pose.

Fig. 8
figure 8

Trajectories and tracking error of the manipulator tip

Full size image
Fig. 9
figure 9

Quaternion and its error of the manipulator tip

Full size image

Each segment of the continuum manipulator is driven by six cables, as illustrated in Fig. 1. The actuation forces of the last two segments are shown in Fig. 10. \(u_{i,j}\) denotes the actuation force of the jth cable of the ith manipulator segment. A head-on collision between the manipulator and the second obstacle is imminent at 77.0 s, as shown in Fig. 6a. The proposed obstacle-avoidance motion planning method actively adjusts the actuation forces to keep the manipulator away from the obstacle. Therefore, there are sudden changes in the actuation forces between 77.0 s and 80.0 s, as shown in Fig. 10. In the motion process of the manipulator, the actuation force \(u_{3,5}\) reaches the upper bound of 220 N, as presented in Fig. 10b. In addition, all actuation forces are always between 0 and 220 N, which indicates that the proposed motion planning method can strictly satisfy the input limitations (37). The continuum manipulator successfully achieves trajectory tracking and avoids the collisions with the obstacles under the action of these actuation forces constructed by the proposed method.

Fig. 10
figure 10

Actuation forces of the last two segments

Full size image

4.2 Motion planning for the manipulator shape

To achieve complex tasks successfully in confined spaces, continuum manipulators need to deform to the desired configuration. Therefore, the motion planning problem for the manipulator shape is studied in this subsection. The aim is to plan a collision-free path so that the multisegment continuum manipulator can safely deform to the desired shape in confined spaces with static and dynamic obstacles.

Each segment of the continuum manipulator is required to bend around \(y_{m}\) and \(z_{m}\) directions, as shown in Fig. 1. The initial curvatures of the manipulator are set to zero. For the continuum manipulator with four segments, the eight desired average curvatures [11] at terminal time are set as

$$ {{\varvec{\upkappa}}}_{e} = \left[ {0.806\;\;0.806\;\; {-2.417}\;\;0\;\; {-1.611}\;\; {-2.417} \;\; {-1.611} \;\; {-2.417}} \right]^{T} $$
(44)

The output variable of the system at time \(t_{k}\) is given by

$$ {\mathbf{y}}_{k} = \left[ {{{\varvec{\upkappa}}}_{k}^{T} \;\;{\dot{\varvec{\upkappa }}}_{k}^{T} } \right]^{T} \in {\mathbb{R}}^{16} $$
(45)

where \({{\varvec{\upkappa}}}_{k}\) is the vector of the average curvatures of manipulator segments at time \(t_{k}\).

To smoothly deform the continuum manipulator to the desired configuration, the weighting matrices Q and W for the motion planning problem defined by Eq. (15a) are set as

$$ \left\{ {\begin{array}{*{20}l} {{\mathbf{Q}} = - 9.99 \times 10^{5} \left( {t - 100} \right)^{2} {\mathbf{I}}_{{16}} + 1 \times 10^{{10}} {\mathbf{I}}_{{16}} } \hfill \\ {{\mathbf{W}} = 2 \times 10^{6} {\mathbf{I}}_{{24}} } \hfill \\ \end{array} } \right. $$
(46)

Two spherical obstacles with a radius of 0.1 m are considered and their centroid coordinates are set as

$$ \left\{ {\begin{array}{*{20}l} {{\mathbf{O}}_{1} = \left[ {0.20\;\; - 0.10\;\; - 2.40} \right]^{T} } \hfill \\ {{\mathbf{O}}_{2} = \left[ {0.25\;\;0.50\;\; - 0.01t - 1.20} \right]^{T} } \hfill \\ \end{array} } \right.{\text{ }} $$
(47)

The penalty factor \(\upsilon\) is set to 1 × 1016 in this simulation example.

The collision-free path for a four-segment continuum manipulator is generated by the proposed kinodynamic motion planning method. To clearly observe the motion of the continuum manipulator in confined spaces, four snapshots are presented in Fig. 11. The continuum manipulator gradually deforms to the desired terminal configuration given by Eq. (44), which stays far away from its initial position. The curvatures of the continuum manipulator are actively regulated to avoid the collisions with the obstacles, which obviously results in a sudden change in the trajectory of the manipulator tip near the green obstacle, as shown in Fig. 11c. Therefore, the proposed method exhibits great convergence and stability performances even for large overall obstacle-avoidance motion planning.

Fig. 11
figure 11

Snapshots of a continuum manipulator during large overall motion

Full size image

The continuum manipulator moves along the path generated by the proposed kinodynamic motion planning method. The Euclidean distances between the manipulator and the obstacle centroids decrease first and then increase as the manipulator moves, as shown in Fig. 12a. The distances are always greater than or equal to the obstacle radius of 0.1 m, which indicates that the continuum manipulator successfully achieves obstacle avoidance. To illustrate the effectiveness of the proposed method, a motion path is planned for the manipulator moving to the desired configuration without obstacle avoidance. The Euclidean distance between the manipulator and the obstacle centroids given by Eq. (47) is also calculated when the manipulator moves along this generated path, as shown in Fig. 12b. The minimum Euclidean distances are only 0.042 m and 0.066 m at 16.2 s and 41.6 s, respectively, which are less than the obstacle radius of 0.1 m. This indicates that the manipulator penetrates the obstacles within the time intervals [13.0 s, 18.4 s] and [36.7 s, 47.0 s], as presented in the detail view in Fig. 12b.

Fig. 12
figure 12

Euclidean distances between the manipulator and the obstacle centroids

Full size image

The trajectories of the manipulator tip, which are generated by the motion planning with and without obstacle avoidance, are consistent in the zone where the manipulator is far away from the obstacle, as illustrated in Fig. 13. At point A, these two trajectories start to separate. The trajectory generated under the obstacle-avoidance constraint successfully avoids the collisions. From Figs. 12 and 13, it can be found that the proposed kinodynamic motion planning method can effectively make the continuum manipulator avoid the collisions with static and dynamic obstacles during the large overall motion.

Fig. 13
figure 13

Comparison between the tip trajectories with and without obstacle avoidance

Full size image

The actual average curvature is calculated for each manipulator segment during movement. \(\kappa_{i,1}\) and \(\kappa_{i,2}\) denote the actual average curvature of the ith manipulator segment about the \(y_{m}\) and \(z_{m}\) axes, respectively. The difference between the actual curvature and the desired terminal curvature gradually decreases to zero, as illustrated in Fig. 14. The maximum difference is only 0.017 m−1 at terminal time. In addition, the curvature of the third segment decreases slowly around 16 s, as shown in Fig. 14b. The curvature is actively regulated to avoid the collisions between the manipulator and the obstacle, as illustrated in Figs. 11, 12 and 13. Therefore, the proposed motion planning method can make the continuum manipulator accurately deform to the desired shape while achieving obstacle avoidance.

Fig. 14
figure 14

Difference between the actual and desired curvatures

Full size image

Each segment of the continuum manipulator is driven by six cables. The first three actuation forces of each segment are illustrated in Fig. 15. The proposed method actively regulates the actuation forces of the first three segments to avoid the collisions between the last two segments and the obstacles around 16 s and 47 s. In addition, all actuation forces are greater than or equal to zero, which is consistent with the fact that the cables can only be subject to tension. Moreover, the actuation forces constructed from the proposed method strictly satisfy the upper bound of 220 N. It can be found that the actuation forces \(u_{3,2}\) and \(u_{4,2}\) increase significantly after the actuation forces \(u_{3,3}\) and \(u_{4,3}\) reach the upper bound. This increment can compensate for the lack of actuation caused by input limitation, so that the continuum manipulator can still accurately deform to the desired shape. Therefore, the proposed method can utilize the full potential of unsaturated actuators to achieve high-precision control.

Fig. 15
figure 15

First three actuation forces of each segment

Full size image

To illustrate the advantages of the improved PSO algorithm presented in this paper, a comparison is conducted between this algorithm and the traditional PSO algorithm without normal distribution, as shown in Fig. 16. The variation of the average number of Newton–Raphson iterations is calculated under the different numbers of particles. As illustrated in Fig. 16, the improved PSO algorithm remains convergent to the optimal solution even with a small number of particles (for example, 20), whereas the traditional PSO algorithm exhibits divergence. The normal distribution is introduced into the improved PSO algorithm during the position initialization process of the particle swarm, resulting in particles being densely distributed in the domain where the optimal solution is most probable to be found. Therefore, the improved PSO algorithm can still find the optimal solution even for this high-dimensional NOP, using only 20 particles. Furthermore, when 40 or 60 particles are involved, the average number of Newton–Raphson iterations of the improved PSO algorithm is less than that of the traditional PSO algorithm, indicating a faster convergence to the optimal solution by the improved PSO algorithm. Therefore, the improved PSO algorithm exhibits a greater search performance and has the ability to solve the NOP with high dimensionality, while maintaining lower computational costs compared to the traditional PSO algorithm.

Fig. 16
figure 16

Average number of the Newton–Raphson iterations

Full size image

5 Conclusions

This paper proposes a combined kinodynamic motion planning method for cable-driven multisegment continuum manipulators in confined spaces with obstacles. The proposed method provides a unified path optimization framework for obstacle-avoidance motion planning of multisegment continuum manipulators. Numerical results indicate that the proposed method exhibits great stability performances even for large overall motion planning. Along the optimal path generated by the proposed kinodynamic motion planning method, continuum manipulators can accurately deform to the desired configuration while achieving obstacle avoidance within the input limitations. Therefore, the proposed method can effectively address the highly nonlinear obstacle-avoidance motion planning problem for multisegment continuum manipulators in confined spaces.

Multisegment continuum manipulators are typically equipped with grippers and sensors at their end to perform various operations and detection tasks in confined spaces, such as structural assembly and aircraft fuel tank inspections. The proposed method effectively implements obstacle-avoidance motion planning for both the configuration and the tip pose of the continuum manipulator, ensuring that the manipulator safely passes through confined spaces and accomplishes these complex tasks. Additionally, the excellent performance of the proposed method for large overall motion planning further enhances the autonomy and adaptability of the continuum manipulator to unstructured environments. Future work will involve extending motion planning to continuum manipulators in uncertain environments, including unpredictable obstacle motion. To achieve this goal, a combination of perception and decision-making is necessary, which puts forward greater demands on the algorithm.